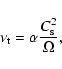A&A 413, 373-380 (2004)
DOI: 10.1051/0004-6361:20031515

Modeling the thermodynamical conditions in the Uranian subnebula - Implications for regular satellite composition

O. Mousis

CNRS-UMR 6091, Observatoire de Besançon, BP 1615, 25010 Besançon Cedex, France

Received 9 January 2003 / Accepted 12 September 2003

Abstract
We study the thermodynamical conditions existing in the Uranian subnebula from which the regular satellites were presumably formed, assuming it was produced by an earth-sized body impact on proto-Uranus (Stevenson 1984; Slattery et al. 1992). Two evolutionary turbulent models of the Uranian subnebula are constructed. Both are derived from the solar nebula analytical model of Dubrulle (1993) and Drouart et al. (1999). Each model provides a distinct chemical composition which depends on the assumed origin of the subdisk's material (proto-Uranus or impactor ejected material). Moreover, the evolution of the chemistry of C and N compounds is examined in order to assess the nature of major volatiles trapped into the ices of regular satellites. The temporal evolution of the D/H ratio in water is also explored in the Uranian subdisk, as a function of the gas phase composition. Such an analysis may provide constraints on the origin of the material which led to the formation of the regular satellite system.

Key words: planets and satellites: Uranus - solar system: formation - accretion, accretion disks

1 Introduction

The five large icy satellites of Uranus form the most distant regular satellite system of the outer Solar system. The bulk densities of Miranda, Ariel, Umbriel, Titania, and Oberon, lying between 1.2 and 1.7 g cm-3, suggest that the global ice/rock ratio of these satellites is close to 1 (Table 1). Different models of formation of the Uranian satellites have been proposed in order to explain their physical properties. Most of these models advocate the presence of a disk of material that surrounded Uranus during its early history and from which the regular satellites were formed (see the review of Pollack et al. 1991). An important characteristic of the Uranian system is the significant tilt of the giant planet rotation axis which can be linked to the formation of its regular satellites. Indeed, the fact that the regular satellites orbit in the equatorial plane of Uranus in the same direction as its tilted spin rapidly suggested that a circumplanetary disk may have been the consequence of material ejection by an earth-sized body impact on the giant planet (Stevenson 1984). The first quantitative simulations of the giant impact hydrodynamical effects on the envelope of Uranus were made by Korycansky et al. (1990), where Uranus was assumed to be still in its accretion phase at the time of the collision. These authors expressed difficulty in explaining at the same time the large obliquity of Uranus consecutive to a slanting impact and the formation of a circumplanetary disk with the fact that the planet was losing most of its envelope's mass. On the other hand, the giant impact simulations carried out by Slattery et al. (1992) led to quite different results by assuming an internal structure of Uranus close to today's one at the moment of the impact. Slattery et al. (1992) found that it was easy to produce the large tilt of the rotation axis as well as the formation of an icy debris disk surrounding the giant planet after its collision with an impactor whose mass lies between 1 and 3  $M_{\oplus}$. More recently, Canup & Ward (2000) argued that the mass of the disk made of orbiting particles engendered by the catastrophic collision could reach maximum values of 1 to 3 per cent of the total system mass and would be the result of the cooling and the condensation of an initially more radially extended disk than the last outer satellite orbital radius.

Table 1: Major regular satellites radii, densities, and per mass ice/rock ratios derived from Brown et al. (1991).

In this paper, the 1D solar nebula analytical model elaborated by Dubrulle (1993) is used to investigate the thermodynamical conditions existing in the protosatellite accretion disk surrounding Uranus, assuming it was produced by a giant collision. Given the uncertainties on the origin of the material forming the Uranian subnebula (proto-Uranus or impactor originating material), we consider two turbulent models which provide different chemical compositions. These models allow us to explore the evolution of carbon and nitrogen gas-phase chemistries in the Uranian subnebula and to deduce the nature of C and N volatiles trapped in icy planetesimals from which the regular satellites were presumably formed. The evolution of the D/H ratio in the vapor phase of water is also examined in the Uranian subnebula. Indeed, since it strongly depends on the chemical composition of the subdisk, such an analysis is likely to provide constraints on the origin of the material that formed the Uranian satellites.

The outline of the paper is as follows. In Sect. 2, a description of the structure and the evolution of the Uranian subnebula is given. Two different models, which provide different chemical compositions and thermodynamical parameters, are proposed. Section 3 is devoted to the investigation of the evolution of CO/CH4 and N2/NH3 ratios in both models of the Uranian subnebula. In Sect. 4, we discuss the trapping of C and N volatiles into the ices of the protosatellite disk. Section 5 is dedicated to the estimate of the D/H ratio in the water ice incorporated into regular satellites and its implications for the origin of the subnebula material. A summary is given in Sect. 6.

2 Origin and formation of the subnebula

2.1 Structure and evolution of the subnebula

Basing our work on prevous studies (Stevenson 1984; Slattery et al. 1992), we advocate the formation of a protosatellite disk consecutive to a giant impact on Uranus. For the disk, we use a time-dependent turbulent model adapted from Dubrulle (1993) and detailed in Drouart et al. (1999), in which a simplified description of the evolution of the solar nebula, following the formation of the Sun, is developed. This model was already employed to determine the thermodynamical conditions existing in the protosatellite accretion disks around Saturn and Jupiter (Mousis et al. 2002a,b; Mousis & Gautier 2003). The Uranian subnebula is considered as a geometrically thin gaseous disk for which temperature, pressure, surface density, and height radial profiles are determined once the initial mass  $M_{\rm D0}$ and radius $R_{\rm D}$ of the disk, as well as the coefficient of turbulent viscosity $\alpha$, are provided. The gas of the protosatellite disk is assumed to fall onto Uranus, generating, thanks to turbulent viscosity, a transport of the angular momentum outwards. Following Shakura & Sunyaev (1973), the turbulent viscosity  $\nu_{\rm t}$ is expressed in terms of Keplerian rotation frequency $\Omega$ and the sound velocity C$_{\rm s}$:

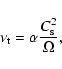\begin{displaymath}\nu_{\rm t}=\alpha\frac{C_{\rm s}^2}{\Omega}, \end{displaymath} (1)

where the value of the $\alpha$ parameter characterizes the assumed form of turbulence in the subdisk. The opacity law supplied in our model is taken from Ruden & Pollack (1991) and the time dependent accretion rate $\dot{M}$, on which the physical parameters of the subnebula depend, is inspired from Makalkin & Dorofeeva (1991). $\dot{M}$ follows a simple power law which is a function of the initial accretion rate $\dot{M}_0$ and the accretion timescale t0. Three parameters constrain $\dot{M}_0$ and t0: the initial mass of the disk  $M_{\rm D0}$, the coefficient of turbulent viscosity $\alpha$, and the radius of the subnebula $R_{\rm D}$. The time t=0 of the subnebula model is arbitrarily defined as the moment of occurrence of the giant impact.

2.2 Composition of the impact generated subnebula

The analytical turbulent model we use in order to determine the thermochemical parameters of the Uranian subnebula only takes into account gas and grains in its composition. Indeed, growing planetesimals reaching the centimeter to meter size are quickly decoupled from gas and their behaviours become independent of the evolution of the gaseous medium (Weidenschilling 1997). Consequently, we assume that refractory elements, like rocks or iron, are not included in the composition of the subdisk, since their rapid growth involved their separation from gas early in the subnebula's life.

In this study, two models of the Uranian subnebula are developed, each providing a different composition. The first model, hereafter labeled water-rich subnebula, is based on the conclusions of Slattery et al. (1992), who used hydrodynamic simulations to describe the evolution of the proto-Uranus and impactor system. Slattery et al. (1992) employed similar internal structure models, with respect to their sizes, for both proto-Uranus and impactor, which were derived from the interior models of Uranus developed by Hubbard & Marley (1989). We followed the prescription of Slattery et al. (1992), which consisted of selecting, among the dozens of results of their runs, those for which the rotation period of proto-Uranus consecutive to the impact is nearly similar to that of today. Most of the runs in compliance with this constraint revealed that the majority of the remaining orbiting material after the collision came from the impactor and was mainly composed of vaporized ices in orbit. Such a chemical composition of the initial gas phase of the Uranian subnebula should be close to that of the Oort comets. Indeed, since both Oort comets and the impactor are expected to be formed in the region of Uranus and Neptune, they probably shared a similar composition. Therefore, we infered from Iro et al. (2003) the abundances of major C and N molecules found in comets which could take part with H2O in the composition of the water-rich subnebula at t=0. In these conditions, CO, CH4, and NH3 gases are supposed to be the main C and N compounds in the subdisk, with abundances relative to H2O not exceeding 15% for CO, and 1.5% for both NH3 and CH4. Consequently, assuming that H2O was the major gas constituent, the gas mean molecular weight of the water-rich subnebula is about 18 g mole-1.

The second model, hereafter named water-poor subnebula, is based on the hypothesis of a blowout disk engendered by the giant collision, where a part of the giant planet's envelope was ejected into orbit to produce a satellite disk. In the blowout disk scenario proposed by Stevenson (1984), the H2-He-CH4-H2O atmosphere of proto-Uranus was shocked, involving the complete chemical conversion of the expelled methane into carbon monoxyde. As a consequence of this conversion, some oxygen was associated with carbon and reduced the quantity of water in the subnebula. Furthermore, assuming that NH3 exists in solar proportions in the atmosphere of Uranus (Gulkis et al. 1978), its conversion into N2 also occurred in the expelled part of the envelope, as a result of the heating due to the shock (Pollack et al. 1991). Table 2 reflects the abundances of major species at t = 0 in the water-poor subnebula which were inferred from the atmosphere of Uranus. The He/H2 ratio is deduced from Voyager measurements (Conrath et al. 1987). According to Baines et al. (1993), carbon is enriched 32 times compared to its solar value in the atmosphere of Uranus. Since O/H has never been measured in the atmosphere of Uranus, oxygen is conservatively assumed to be enriched, compared to its solar value, by the same factor as carbon. Such a composition leads to a mean molecular weight of 3.1 g mole-1 for the water-poor subnebula.

Table 2: Per volume abundances of He, O and C elements in the water-poor Uranian subnebula. He, CO, and H2O are the dominant species with hydrogen gas in the water-poor subnebula.

2.3 Thermodynamical parameters of the models

Canup & Ward (2000) estimated that the mass of particles resulting from the cooling of the impact-generated subdisk is between 1 and 3 per cent of the total system mass composed of both proto-Uranus and impactor. Consequently, we adopted the same intermediary value for the initial masses of the water-poor and water-rich subnebulae. This gives $M_{\rm D0}~=~0.02~M_{\rm Ur}$ (where  $M_{\rm Ur}$ is for Uranus mass), which is larger than the total mass of the Uranian satellite system ( $1.1 \times 10^{-4}~M_{\rm Ur}$). The radius of the water-rich subnebula is arbitrarily set to $R_{\rm D}~=~75~R_{\rm Ur}$ (where $R_{\rm Ur}$ is the Uranus radius), a value larger than the current orbit of Oberon, namely the outer regular Uranian satellite, which is located at 23 $R_{\rm Ur}$. Once the mass and the radius of the water-rich subnebula have been fixed, the initial accretion rate $\dot{M}_0$ and $\alpha$ are determined from the H/R < 0.3 condition defined by Mousis et al. (2002a), where H is the half-height of the disk and R the uranocentric distance. Indeed, this condition is necessary to maintain the validity of the evolutionary turbulent model, which must be consistent with the assumption of a geometrically thin disk. The hypothesis of a geometrically thin model for the Uranian subnebula is potentially restrictive but, at the present time, non-Keplerian geometrically thick models have not yet been elaborated. From the choice of  $M_{\rm D0}$ and $R_{\rm D}$ and from the condition H/R < 0.3, we derived a maximum value of $\dot{M}_0$ equal to $4\times 10^{-5}$ $M_{\rm Ur}$/yr. This fixed in turn the minimum value of $\alpha$ which is 10-5. On the other hand, adopting a substantially lower initial accretion rate would lead to a quasi-stationary model in which the high temperature in the whole subnebula would not favor the condensation of ices (see Fig. 1 at early times). Another way to ease the cooling of the water-rich subnebula would be to adopt a value for $R_{\rm D}$ larger than $75~R_{\rm Ur}$. Keeping the same values for the initial accretion rate and the mass of the water-poor subnebula, its radius and $\alpha$ are defined again from the H/R < 0.3 condition defined by Mousis et al. (2002a). This yields a much more extended radius in the water-poor subnebula case than in the water-rich subnebula. The characteristics of the two models are summarized in Table 3.

Table 3: Thermodynamical parameters of the water-rich and water-poor subnebulae.


  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{MS3475f1.ps} \end{figure} Figure 1: Temperature profiles throughout the water-rich subnebula characterized by the parameters $M_{\rm D} = 0.02~ M_{\rm Ur}$, $R_{\rm D} = 75~ R_{\rm Ur}$, and $\alpha = 10^{-5}$ for various values of t in years. The vertical bars designated by the letters M, A, U, T, and O correspond to the current orbits of Miranda, Ariel, Umbriel, Titania, and Oberon, respectively.
Open with DEXTER

Figures 1-3 exhibit radial profiles of temperature T, pressure P, and surface density $\Sigma$ respectively, at various epochs throughout the water-rich subnebula. Radial profiles of T, P and $\Sigma$ are similar for the water-poor subnebula, even if its radius is more extended than that of the water-rich subnebula. In both models, water remains in vapor phase at t = 0 and T, P, and $\Sigma$ decrease with time and with the uranocentric distance. The cooling of the water-rich subnebula allows the propagation front of crystalline water to reach the orbits of Oberon (22.3  $R_{\rm Ur}$), Titania (16.6  $R_{\rm Ur}$), Umbriel (10.1  $R_{\rm Ur}$), Ariel (7.3  $R_{\rm Ur}$), and Miranda (5  $R_{\rm Ur}$) at $t = 3\times 10^5$, $5 \times 10^5$, 106, $1.9 \times 10^6$, and $2.9\times 10^6$ years. In the case of the water-poor subnebula, crystalline water condenses at the same orbits at $t = 1.8\times 10^5$, $2.8\times 10^5$, $5.7\times 10^5$, $9.6\times 10^5$, and $1.6\times10^6$ years.

Both water-rich and water-poor Uranian subnebulae display structures similar to those detailed by Mousis et al. (2002a) and Mousis & Gautier (2003) for the Saturnian and Jovian subdisks. Figure 4 shows, as a function of time, the mass of gas and planetesimals contained in a ring of one $R_{\rm Ur}$ width in the water-poor subnebula, centered at a distance R of Uranus. This figure illustrates that, at each time, gas and planetesimals are mainly located in the outer part of the subdisk. This remark is also valid for the water-rich subnebula. In fact, such structures demand that the zone of formation of regular satellites was fed by planetesimals that migrated inwards from the outer part of the subnebula (Coradini et al. 1989). Indeed, following the mechanism invoked by Makalkin et al. (1999) in the case of the formation of Galilean satellites, the high efficiency of the capture of particles by the growing satellite embryos may have led to the accumulation of solid material on the orbits of regular satellites in the subdisk.

  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{MS3475f2.ps} \end{figure} Figure 2: Pressure profiles throughout the water-rich subnebula characterized by the same parameters as in Fig. 1, for various values of t in years.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{MS3475f3.ps} \end{figure} Figure 3: Surface density profiles throughout the water-rich subnebula characterized by the same parameters as in Fig. 1, for various values of t in years.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{MS3475f4.ps} \end{figure} Figure 4: Mass distribution in the water-poor subnebula as a function of time. Most of the mass is in the outer part of the subnebula.
Open with DEXTER

3 Evolution and trapping of C and N compounds in the Uranian subnebula

In this section, we examine the possibility of chemical conversions between CO and CH4 and N2 and NH3 in thermodynamical conditions derived from our two evolutionary turbulent models of the Uranian subnebula. The gas phase chemistries of carbon and nitrogen in a medium dominated by H2 are respectively described by the two reversible equations:

\begin{displaymath}{\rm CO+3H_2=CH_4+H_2O} \end{displaymath} (2)


\begin{displaymath}{\rm N_2+3H_2=2NH_3}. \end{displaymath} (3)

In the case of the water-rich subnebula, C and N chemical conversions are not possible since the subnebula medium is dominated by water in the vapor phase. This implies that at any epoch and as long as they stay in the gas phase, CO, CH4, and NH3 should remain the main C and N species in the water-rich subnebula, with the same initial abundances.

In the case of the water-poor subnebula, its hydrogen-dominated medium required us to check the possibility of CO  $\rightarrow$ CH4 and N2  $\rightarrow$ NH3 conversions. The gas phase chemistries of carbon and nitrogen in media dominated by H2 are represented in Figs. 5 and 6, respectively. At equilibrium, CO/CH4 and N2/NH3 ratios depend only upon local conditions of temperature and pressure (Prinn & Barshay 1977; Lewis & Prinn 1980; Smith 1998). CO/CH4 and N2/NH3 ratios of 1000, 1, and 0.001 are plotted in Figs. 5 and 6, and compared to the water-poor subnebula at t = 103, 104, and 105 years. On these figures, it can be seen that at early epochs and if the kinetics of chemical reactions are ignored, CO and CH4, and N2 and NH3 exist together in the water poor subnebula. With time, the part of the subnebula where CH4 and NH3 dominate increases, as it is indicated in Figs. 5 and 6.

  \begin{figure} \par\includegraphics[width=8.6cm,clip]{MS3475f5.ps} \end{figure} Figure 5: Calculated ratios of CO/CH4 in the water-poor subnebula at equilibrium. The solid line labelled CO-CH4 corresponds to the case in which the abundances of the two gases are equal. When moving towards the left side of the solid line, CO/CH4 increases, while when moving towards the right side of the solid line, CO/CH4 decreases. The dotted contours labelled -3, 0, 3 correspond to log10 CO/CH4 contours. Adiabats of our turbulent model of the Uranian subnebula are calculated at three epochs. The origin of time corresponds to the moment when the giant impact occured. The uranocentric distance, in $R_{\rm Ur}$, when CO/CH4 = 1, is indicated by arrows for t = 103 yr, t = 104 yr, and t = 105 yr.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{MS3475f6.ps} \end{figure} Figure 6: Same as in Fig. 5, but for calculated ratios of N2/NH3 atequilibrium.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{MS3475f7.ps} \end{figure} Figure 7: Chemical times profiles calculated for CO/CH4 and N2/NH3 conversions in the water-poor subnebula. The conversion of CO to CH4 and of N2 to NH3 is inhibited in the subdisk, except quite close to Uranus.
Open with DEXTER

However, taking into account the kinetics of C and N chemical conversions dramatically changes the situation. Indeed, based on the appropriate kinetic data described by Smith (1998), we calculated the chemical times that characterize the rates of  $\rm CO \rightarrow CH_4$ and $\rm N_2 \rightarrow NH_3$ conversions by using the temperature and pressure radial profiles at different epochs of the water-poor subnebula. These calculations, illustrated by Fig. 7, show that, assuming C and N are initially entirely in the forms of CO and N2 at t = 0 in the water-poor subnebula, their conversions into CH4 and NH3 can occur in a realistic timescale only quite close to Uranus and at early epochs. Considering the structure of the disk where most of the mass is located in its cold outer part (see Fig. 4), one can argue that the amount of CH4 and NH3 produced is too small to affect the initial abundances of CO and N2, even if transport by turbulent diffusion is taken into account.

Thus, both models of the Uranian subnebula have preserved during their evolution the CO/CH4 and N2/NH3 ratios they initially acquired, as long as no condensation or trapping of these species occurred. The next step is now to examine how C and N volatiles were trapped in the ices of the Uranian subnebula and subsequently in the regular satellites.

4 Trapping volatiles in regular satellites

In this section, we discuss the composition of ices other than pure water ice which may have been included in the regular satellites. The nature of C and N volatiles trapped in the regular icy satellites depends on the presumed origin and composition of the Uranian subnebula. Indeed, as it is stated in Sect. 3, carbon and nitrogen are assumed to have been mainly combined into CO and N2 in the gas phase of the water-poor subnebula, and into CO, CH4, and NH3 in the gas phase of the water-rich subnebula.

During the cooling of the water-poor subnebula, most of CO and N2 was trapped by H2O ice in the forms of CO-5.75H2O and N2-5.66H2O clathrate hydrates, respectively (Lunine & Stevenson 1985; Davidson et al. 1987). Figure 8 describes the temporal evolution of the crystallization radii of these ices throughout the water-poor subnebula. At t = 0, H2O, CO and N2 remain in the vapor phase in the whole subnebula. The cooling of this medium allows the condensation of water to start at t = 103 yr at the level of its outer edge. At this position, the trapping of CO and N2 by crystalline water in the forms of clathrate hydrates begins at $t = 3\times 10^3$ yr and $t = 4.5\times 10^3$ yr. With time, the condensation fronts of CO-5.75H2O and N2-5.66H2O clathrate hydrates propagate inwards. The clathration of CO occurs at the current orbits of Oberon (22.3  $R_{\rm Ur}$) and Miranda (5  $R_{\rm Ur}$) at t = 0.4 Myr and t = 2.6 Myr, respectively. In turn, N2 is trapped by crystalline water as a clathrate hydrate at t = 0.6 Myr and t = 4.2 Myr at the same orbits. This implies that, in the case of the water-poor subnebula, the incorporation in planetesimals of CO and N2 in the forms of clathrate hydrates should lead to the presence of important amounts of CO and N2 in the interiors of regular icy satellites. The resulting C/N ratio in these bodies should reflect the oversolar value present in the atmosphere of Uranus. Moreover, CH4/CO and NH3/N2 ratios should be negligible in the satellite ices.

  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{MS3475f8.ps} \end{figure} Figure 8: Formation radii of water ice, CO-5.75H2O and N2-5.66H2O clathrate hydrates in the water-poor subnebula, as a function of time. The stability curve of N2-5.66H2O clathrate hydrate is calculated assuming that N/H is solar and all nitrogen is in the form of N2. The abundances of H2O and CO are given in Table 2.
Open with DEXTER

A similar mechanism is invoked for the trapping conditions of C and N volatiles in the water-rich subnebula. Indeed, the cooling of this medium allows the formation of NH3-H2O hydrate, and CH4-5.75H2O and CO-5.75H2O clathrate hydrates at t = 0.42, 0.61 and 0.72 Myr respectively, at the current orbit of Oberon, if one assumes that NH3, CH4 and CO abundances are those prescribed in Sect. 2.2 for the water-rich subnebula. At the present orbit of Miranda, NH3-H2O, CH4-5.75H2O, and CO-5.75H2O never condense before t = 3.9, 5.6, and 6.6 Myr, respectively. This analysis implies that, in the case of the water-rich subnebula, CH4, CO, and NH3 should be the main C and N compounds trapped as hydrates or clathrate hydrates in the interiors of regular icy satellites. Furthermore, C/N should be oversolar in the satellite ices, since the trapping of C and N species in the water-rich subnebula must have preserved the initial mixing ratios.

5 Evolution of the D/H ratio in water in the Uranian subnebula

In the framework of the impact generated subdisk scenario, the prediction of the D/H ratio in the water ice incorporated in regular satellites may provide constraints on the origin of the material which led to their formation. Indeed, two different cases of deuterium enrichment, compared to the solar value, can be found in the H2O ices formed in the Uranian subnebula, each depending on the initial abundance of hydrogen. The enrichment factor f, defined as the ratio of D/H in deuterated water to D/H in hydrogen, is given by:

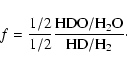\begin{displaymath}f={\rm\frac{1/2}{1/2}\frac{HDO/H_2O}{HD/H_2}\cdot} \end{displaymath} (4)

In the case of the water-rich subnebula, the main reservoir of deuterated molecules is H2O. As a consequence of the weak abundance of hydrogen in the subdisk, the isotopic exchange in vapor phase with deuterated hydrogen molecules is restricted to a very limited number of H2O molecules. In such conditions, the global D/H enrichment in water ice is almost equal to the initial value present in the ices of the impactor before it collided with the proto-Uranus. Assuming a comet-like composition for the ices of the impactor, the global D/H enrichment factor f present in the water ice of regular satellites should correspond to the average value infered from measurements realized in Oort comets. Taking into account the measurements made in Halley, Hyakutake and Hale-Bopp comets (Balsiger et al. 1995; Eberhardt et al. 1995; Bockelée-Morvan et al. 1998; Meier et al. 1998), and adopting (D/H) $_{\rm proto}$ = ( $2.35 \pm 0.3) \times 10^{-5}$ (Mousis et al. 2002b), f should be close to the value of 13.

In the case of the water-poor subnebula, the situation is quite different. Indeed, in opposition to the composition of the water-rich subnebula, hydrogen is the most important deuterium reservoir in the subdisk. In addition, the D/H ratio in hydrogen must reflect the value measured in the atmosphere of Uranus ( $5.5(_{-1.5}^{+3.5}) \times 10^{-5}$, Feuchtgruber et al. 1999). In these conditions, the evolution of f is ruled by the equation of diffusion previously detailed by Drouart et al. (1999) and Mousis et al. (2000), which is:

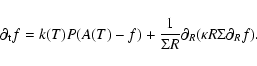\begin{displaymath}\partial_{\rm t}f=k(T)P(A(T)-f)+\frac{1}{\Sigma R} \partial_R (\kappa R \Sigma \partial_R f). \end{displaymath} (5)

The first member on the right side of Eq. (5) describes the isotopic exchange between HDO and H2. Function A(T) is the isotopic fractionation at equilibrium, k(T) is the rate of the isotopic exchange between HDO and H2, and P is the total pressure. A(T) is derived from the tabulations of Richet et al. (1977) and the rate k(T) is taken from the experimental determination of Lécluse & Robert (1994). The second member on the right side of Eq. (5) describes the turbulent diffusion throughout the water-poor subnebula. It depends on the local surface density  $\Sigma(R,t)$, and on the diffusivity $\kappa$. Following Drouart et al. (1999), $\kappa$ is assumed to be the ratio of the turbulent viscosity to the Prandtl number $P_{\rm R}$, which value is always close to unity.

Equation (5) is valid as long as H2O does not condense. Indeed, the isotopic exchange is inhibited between the vapor phase and the solid phase. This statement implies that the value of the enrichment in microscopic ices is the one obtained at the time and at the location of the condensation of vapor. As soon as grains reach the millimeter size, they begin to decouple from gas, continue to grow, and form planetesimals. Whatever the subsequent evolution of these bodies, their D/H ratio is that of microscopic grains. In other words, the D/H ratio in H2O ices contained in the Uranian satellites is that of these species when they condensed.

  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{MS3475f9.ps} \end{figure} Figure 9: Calculated deuterium enrichment factor f in H2O as a function of Uranocentric distance  $R_{\rm Ur}$, at various epochs in years, in the case of the water-poor subnebula. The initial enrichment factor f(R) = f0 at t = 0 is equal to 1. The integration of the equation of diffusion is calculated until the condensation radius of water is reached. When condensation occurs, the value of the enrichment is fixed.
Open with DEXTER

The enrichment factor f(R,t) is thus obtained by integrating Eq. (5), which requires spatial and temporal boundary conditions. Spatial boundary conditions are determined by setting $\partial f/\partial R$ = 0 at both $R~=~1~R_{\rm Ur}$ and $R~=~R_{\rm D}$. When condensation occurs within $R_{\rm D}$, we set $\partial f/\partial R = 0$ at the radius of condensation. Our scenario implies that, at the time of the collision with the impactor, the temperature following the impact was high enough to decompose in elements all the volatiles presents in the expelled material. This hypothesis seems realistic since Stevenson (1984) described a shocked gas following impact reaching temperatures as high as 104 K. Therefore, if the molecules have been exclusively produced from the recombination of elements in the initially hot water-poor Uranian subnebula, there is no initial fractionation between D/H ratios in water and molecular hydrogen (f=1). Setting f(R) = 1 at t = 0 when integrating Eq. (5) reveals that, as shown in Fig. 9, f(R,t) would never exceed 1.3 at the level of the regular satellite system in the life of the water-poor Uranian subnebula. This implies that water ice should not present a deuterium enrichment greater than 4.4 times the protosolar value in the water-poor subnebula.

Finally, we have shown that the value of the D/H ratio in the water ice incorporated in regular satellites strongly depends on the primordial composition of the protosatellite disk. Subsequent in situ measurements of the D/H ratio in the ices of these bodies should provide constraints on the scenario which led to their formation. Indeed, if the measured deuterium enrichment in water ice, compared to the solar value, is close to that of Oort comets, it can be presumed that, as is shown by Slattery et al. (1992), most of the subnebula material came from the impactor. On the other hand, the measurement of a substantially lower deuterium enrichment in water ice would signify that most of the material came from a hydrogen-rich subnebula. Such an observation would comply with the blowout disk hypothesis defended by Stevenson (1984).

6 Summary

Basing our work on the impact generated subdisk scenario, we have developed two evolutionary turbulent models of the Uranian subnebula. Both models are derived from the 1D alpha model described by Dubrulle (1993) and Drouart et al. (1999). These models are geometrically thin and present a similar initial accretion rate, but provide distinct chemical compositions. The first model, named water-rich subnebula, displays a gas phase composition dominated by water and is based on the assumption that the impactor was the main provider of the subdisk's material, as it is concluded by Slattery et al. (1992). On the other hand, the second model, labelled water-poor subnebula, exhibits a gas phase composition derived from the atmosphere of Uranus, which is presumed to have been the main supplier of the subdisk's material, as it is argued by Stevenson (1984).

During their temporal evolution, both models of the Uranian subnebula have preserved the CO/CH4 and N2/NH3 ratios they initially acquired. In the case of the water-rich subnebula, assuming an initial gas phase composition close to that of Oort comets, CO, CH4 and NH3 should remain the major C and N compounds in the subdisk. In the case of the water-poor subnebula, as a consequence of the heating suffered by the expelled part of the giant planet's envelope composing the subdisk, CO and N2 should remain the main C and N compounds. In both models of the Uranian subnebula, C and N volatiles were trapped as clathrate hydrates or hydrates in planetesimals before they became incorporated into the regular satellites.

Furthermore, the evolution of the D/H ratio in water has been investigated in both models of the Uranian subnebula. It is shown that the resulting value of the D/H ratio in water ice taking part in the regular satellite composition is strongly dependent on the nature of the main reservoir of deuterated molecules existing in the subdisk's gas phase. In other words, this involves that future measurements of such a ratio in the regular satellite ices may constrain the origin of the subnebula which led to their formation.

Acknowledgements
Many thanks are due to Daniel Gautier for helpful discussions about this work. I wish to acknowledge Guy Moreels, Céline Reylé and Jean-Marc Petit for their valuable comments on the manuscript.

References


Copyright ESO 2003