A&A 412, 727-734 (2003)
DOI: 10.1051/0004-6361:20031276
L. E. Kristensen1 -
M. Gustafsson1 -
D. Field1,![]() -
G. Callejo2,3 -
J. L. Lemaire2,3
-
G. Callejo2,3 -
J. L. Lemaire2,3
![]() -
L. Vannier2 -
G. Pineau des Forêts4
-
L. Vannier2 -
G. Pineau des Forêts4
1 - Department of Physics and Astronomy, University of Aarhus,
8000 Aarhus C, Denmark
2 -
Observatoire de Paris-Meudon, LERMA and UMR 8112 of the CNRS, 92195
Meudon Principal Cedex, France
3 -
Université de Cergy-Pontoise, LERMA and
UMR 8112 of the CNRS, 95806 Cergy Cedex, France
4 -
Institut d'Astrophysique Spatiale,
Université Paris XI, 91405 Orsay Cedex, France
Received 30 January 2003 / Accepted 11 August 2003
Abstract
Observations are reported of IR emission in H2, around
2 ![]() m in the K-band, obtained with the ESO 3.6 m telescope
using the ADONIS adaptive optics system. Data cover a region of the
Orion Molecular Cloud north of the Trapezium stars and SW of the
Becklin-Neugebauer object. Excellent seeing yielded diffraction
limited images in the v=2-1 S(1) line at 2.247
m in the K-band, obtained with the ESO 3.6 m telescope
using the ADONIS adaptive optics system. Data cover a region of the
Orion Molecular Cloud north of the Trapezium stars and SW of the
Becklin-Neugebauer object. Excellent seeing yielded diffraction
limited images in the v=2-1 S(1) line at 2.247 ![]() m. Excitation
temperature images were created by combining these data with similar
data for H2 emission in the v=1-0 S(1) line reported earlier
(Vannier et al. 2001). Shock models are used to estimate
densities in emitting clumps of material. In local zones with high
excitation temperatures, post-shock densities are found to be as
high as several times 108 cm-3, an order of magnitude denser
than our previous estimates. We propose that the
nature of these zones is dictated by the combined activity of
shocks, which create dense structures, and the powerful radiation
field of
m. Excitation
temperature images were created by combining these data with similar
data for H2 emission in the v=1-0 S(1) line reported earlier
(Vannier et al. 2001). Shock models are used to estimate
densities in emitting clumps of material. In local zones with high
excitation temperatures, post-shock densities are found to be as
high as several times 108 cm-3, an order of magnitude denser
than our previous estimates. We propose that the
nature of these zones is dictated by the combined activity of
shocks, which create dense structures, and the powerful radiation
field of ![]() 1C Ori which photoevaporates the boundaries of
these structures.
1C Ori which photoevaporates the boundaries of
these structures.
Key words: ISM: individual objects: OMC1 - ISM: kinematics and dynamics - ISM: molecules - shock waves - ISM: lines and bands
An understanding of how massive stars influence the formation of
compact bodies in the surrounding gas is based on the hypothesis that
outflows from massive stars may shock-compress the local gas,
triggering the formation of stars, brown dwarfs or free-floating
objects of planetary mass (Lucas & Roche 2000; Zapatero
Osorio et al. 2000; Boss 2001). This mechanism, if
operational, has far-reaching consequences for star formation in many
regions of the Galaxy and in external galaxies, making an important
contribution to the initial mass function (IMF) for objects in the low
mass range. The Galactic IMF has been extensively studied, especially
in Orion, e.g. Luhman et al. (2000), in which studies extend
down to 0.02 ![]() .
.
In recent work (Vannier et al. 2001, hereafter V2001), we
attempted quantitatively to test the shock compression hypothesis in
OMC1, examining the distribution of scale sizes of regions brightly
emitting in H2 (e.g. Allen & Burton 1993; Schild et al. 1997; Chen et al. 1998; Stolovy et al. 1998; Schultz et al. 1999) and using
theoretical shock models (Wilgenbus et al. 2000) to
reproduce the observed brightness of emission in the H2 v=1-0 S(1)
line at 2.121 ![]() m. The results in V2001 showed that clumps of gas
emitting in the v=1-0 S(1) line do not form a fractal size
distribution but rather display a preferred scale size lying between
1
m. The results in V2001 showed that clumps of gas
emitting in the v=1-0 S(1) line do not form a fractal size
distribution but rather display a preferred scale size lying between
1
![]() 4 to 1
4 to 1
![]() 8, that is 3
8, that is 3![]() 10-3 to
4
10-3 to
4![]() 10-3 pc given a distance to Orion of 460 pc (Bally et al. 2000). It was found that the passage of magnetic (C-type)
shocks, with velocities of
10-3 pc given a distance to Orion of 460 pc (Bally et al. 2000). It was found that the passage of magnetic (C-type)
shocks, with velocities of ![]() 30 kms-1, impinging on gas of
preshock number density 106 cm-3, could yield the very bright
H2 emission observed. The passage of the shock was found to
compress gas to number densities (
30 kms-1, impinging on gas of
preshock number density 106 cm-3, could yield the very bright
H2 emission observed. The passage of the shock was found to
compress gas to number densities (
![]() )
of several times
107 cm-3. V2001 found that one clump in the field (region 1,
below) may be gravitationally unstable and may be a potential site for
future low mass star formation. This result is consistent with the
stellar density in the Trapezium cluster, which would yield one star
on average in the volume of gas observed (Luhman et al. 2000).
)
of several times
107 cm-3. V2001 found that one clump in the field (region 1,
below) may be gravitationally unstable and may be a potential site for
future low mass star formation. This result is consistent with the
stellar density in the Trapezium cluster, which would yield one star
on average in the volume of gas observed (Luhman et al. 2000).
In the present work we consider, as in V2001, a small part of OMC1 in
a region centered ![]() 45
45
![]() north of the Trapezium cluster,
reporting data in the v=2-1 S(1) line at 2.247
north of the Trapezium cluster,
reporting data in the v=2-1 S(1) line at 2.247 ![]() m, at high spatial
resolution, obtained using adaptive optics.
m, at high spatial
resolution, obtained using adaptive optics.
A finding chart for the region observed, recorded in the v=1-0 S(1)
line, is given in Fig. 1. The brightest H2 emission is
centered around 10
![]() E of the reference star TCC0016 and is the
region originally designated as "Peak 2'' in Beckwith et al. (1978). BN lies 20
E of the reference star TCC0016 and is the
region originally designated as "Peak 2'' in Beckwith et al. (1978). BN lies 20
![]() 3 to the north-west of TCC0016,
that is, 0.045 pc.
3 to the north-west of TCC0016,
that is, 0.045 pc.
 |
Figure 1:
A finding chart, recorded at 2.121 |
| Open with DEXTER | |
The ADONIS Adaptive Optics (AO) system at the ESO 3.6 m telescope was
used for the observations, which took place on 27th to 29th December
1996. ADONIS was equipped with the infra-red Sharp-NICMOS camera (256
![]() 256 pixels). At the time of our observations the seeing was
exceptionally good, lying between 0.3 and 0.4 arcsec, and the lens set
was used which gave a resolution of 50 mas/pixel, with a field of view
of 12.8
256 pixels). At the time of our observations the seeing was
exceptionally good, lying between 0.3 and 0.4 arcsec, and the lens set
was used which gave a resolution of 50 mas/pixel, with a field of view
of 12.8
![]()
![]() 12.8
12.8
![]() .
Data recorded here in the H2v=2-1 S(1) line are used in conjunction with data in v=1-0 S(1), where
the latter have already been reported in V2001. In all sets of data, isolation
of spectral
lines and observation of the continuum at 2.179
.
Data recorded here in the H2v=2-1 S(1) line are used in conjunction with data in v=1-0 S(1), where
the latter have already been reported in V2001. In all sets of data, isolation
of spectral
lines and observation of the continuum at 2.179 ![]() m were achieved
using a Fabry-Perot interferometer with a resolution of
m were achieved
using a Fabry-Perot interferometer with a resolution of
![]() /1000, that is,
/1000, that is, ![]() 150 kms-1.
150 kms-1.
The northerly extent of the field which we were able to observe was
restricted by the availability of only a single star, ![]() 1 B
Ori, as a sufficiently bright reference for wavefront sensing. The
field reported here consists of a single frame
(12
1 B
Ori, as a sufficiently bright reference for wavefront sensing. The
field reported here consists of a single frame
(12
![]() 8
8![]() 12
12
![]() 8), centered 16
8), centered 16
![]() 8 E and
3
8 E and
3
![]() 4 S, relative to TCC0016 (see Fig. 1) and chosen for its
strong v=2-1 emission. The Strehl ratio, the ratio of the peak
intensity of the measured point-spread function (PSF) to the
theoretical maximum for a telescope with perfect optics and no
atmosphere, diminishes as the distance from the reference star
increases.
4 S, relative to TCC0016 (see Fig. 1) and chosen for its
strong v=2-1 emission. The Strehl ratio, the ratio of the peak
intensity of the measured point-spread function (PSF) to the
theoretical maximum for a telescope with perfect optics and no
atmosphere, diminishes as the distance from the reference star
increases. ![]() 1 Ori B lies at the south-eastern corner of our
image, with the north-west corner of our field
1 Ori B lies at the south-eastern corner of our
image, with the north-west corner of our field
![]() 45
45
![]() away. This corresponds to a size of the order of that
of the isoplanatic patch at 2
away. This corresponds to a size of the order of that
of the isoplanatic patch at 2 ![]() m, the area beyond which AO
correction may be significantly degraded. The size of the isoplanatic
patch depends on the outer scale of turbulence, a poorly characterized
parameter, and much larger isoplanatic patches have been reported.
It
turned out that the excellent seeing at the time of our observations
allowed us to achieve mean-diffraction limited correction throughout the
field, including faint objects. The resolution in our images
corresponds to a Strehl ratio between 0.37 and 0.5. In order to obtain
a representative point spread function, we chose to record
m, the area beyond which AO
correction may be significantly degraded. The size of the isoplanatic
patch depends on the outer scale of turbulence, a poorly characterized
parameter, and much larger isoplanatic patches have been reported.
It
turned out that the excellent seeing at the time of our observations
allowed us to achieve mean-diffraction limited correction throughout the
field, including faint objects. The resolution in our images
corresponds to a Strehl ratio between 0.37 and 0.5. In order to obtain
a representative point spread function, we chose to record
![]() 1 Ori D to the SE (see Fig. 1), rather than
1 Ori D to the SE (see Fig. 1), rather than
![]() 1 Ori B, since
1 Ori B, since ![]() 1 Ori D lies at a distance from
our field more representative for the full field than
1 Ori D lies at a distance from
our field more representative for the full field than ![]() 1 Ori
B. Numerous observations were performed of
1 Ori
B. Numerous observations were performed of ![]() 1 Ori D
throughout data taking, since it is important for data reduction to
use a PSF appropriate to the time of and therefore the seeing for any
particular image acquisition.
1 Ori D
throughout data taking, since it is important for data reduction to
use a PSF appropriate to the time of and therefore the seeing for any
particular image acquisition.
Data reduction to obtain a H2 image was performed so as to take account of any temporal variability of the sky background, spatial variations in the sensitivity of the detector (flat-fielding), differences in the sky brightness at different wavelengths and differing efficiencies of the detection system for the different Fabry-Perot settings. Dark counts were subtracted and bad pixels and noise due to cosmic rays removed.
Since we seek to ratio the images in v=1-0 and v=2-1 S(1), it is
essential that brightness estimates are as free as possible from
differential effects between the two lines. In this regard atmospheric
absorption in these lines must be considered. Data obtained
(Dec. 2000) on the Canada-France-Hawaii Telescope, using a combination
of the PUEO adaptive optics system and Fabry-Perot interferometry
("GriF''; Clénet et al. 2002), as well as extensive data in
Chrysostomou et al. (1997), reveal that OMC1 as a
whole contains H2 emission which shows velocity shifts, relative to
Earth, of between +60 to -10 km s-1. Using the atmospheric
absorption line atlas of Livingston & Wallace (1991), we
find that there is negligible absorption for the v=1-0 line in all
cases, save over a very narrow range of velocities around +30 kms-1
for which an absorption of ![]() 7% is found. For the
v=2-1 line, the situation is similar with a weak absorption feature
again of
7% is found. For the
v=2-1 line, the situation is similar with a weak absorption feature
again of ![]() 7% at around +33 kms-1. GriF data show that the
regions studied span the range of velocity which includes these
values. Thus differential absorption may introduce systematic errors
into estimates of excitation temperature, but of only a few per
cent. The effect cannot be accurately determined and we choose to
ignore it in the present work.
7% at around +33 kms-1. GriF data show that the
regions studied span the range of velocity which includes these
values. Thus differential absorption may introduce systematic errors
into estimates of excitation temperature, but of only a few per
cent. The effect cannot be accurately determined and we choose to
ignore it in the present work.
A further consideration is that the v=2-1 line will be less reddened
than the v=1-0 line. The factor between the two is
![]() (
(![]() 1/
1/![]() 2)-1.7 (Mathis 1990),
that is, the v=2-1 line may be overestimated by
2)-1.7 (Mathis 1990),
that is, the v=2-1 line may be overestimated by ![]() 10% compared
to the v=1-0 line. We present results here for data uncorrected for
this imprecisely known differential absorption. If included,
excitation temperatures estimated below would be reduced by
10% compared
to the v=1-0 line. We present results here for data uncorrected for
this imprecisely known differential absorption. If included,
excitation temperatures estimated below would be reduced by
![]() 5%. Absolute values of brightness may however be
underestimated due to dust obscuration (Rosenthal et al.
2000), but this does not in itself affect estimation
of excitation temperatures.
5%. Absolute values of brightness may however be
underestimated due to dust obscuration (Rosenthal et al.
2000), but this does not in itself affect estimation
of excitation temperatures.
Data for the v=2-1 S(1) line and at 2.179 ![]() m in the continuum,
free from H2 emission, were deconvolved with the appropriate
point-spread functions, using the technique of Subtractive Optimally
Localized Averages, SOLA (Pijpers 1999). This method has
been shown to preserve the smallest scales in the data more
effectively than the standard methods of Maximum Entropy and
Richardson-Lucy (Vannier 2001; Hook 1999 and
references therein), yielding otherwise very similar
results. Implementation of SOLA involves as input some "target''
resolution which it is the aim of deconvolution to achieve. If this
target represents too high a resolution, the penalty will be an
unacceptable level of noise. In the present data we were able, with
acceptable noise, to achieve a spatial resolution, uniform within the
image,
of 0
m in the continuum,
free from H2 emission, were deconvolved with the appropriate
point-spread functions, using the technique of Subtractive Optimally
Localized Averages, SOLA (Pijpers 1999). This method has
been shown to preserve the smallest scales in the data more
effectively than the standard methods of Maximum Entropy and
Richardson-Lucy (Vannier 2001; Hook 1999 and
references therein), yielding otherwise very similar
results. Implementation of SOLA involves as input some "target''
resolution which it is the aim of deconvolution to achieve. If this
target represents too high a resolution, the penalty will be an
unacceptable level of noise. In the present data we were able, with
acceptable noise, to achieve a spatial resolution, uniform within the
image,
of 0
![]() 15. Absolute fluxes were obtained by calibration using both the
standard star HD71264, at 08
15. Absolute fluxes were obtained by calibration using both the
standard star HD71264, at 08![]() 26
26![]() 18
18
![]() 15,
-05
15,
-05![]() 51
51![]() 49
49
![]() 8 (J2000), with a K magnitude of 8.538 (DENIS
Standard Stars: see
http://cdsweb.u-strasbg.fr/denis.html) and TCC0016,
whose K' band calibration is given in McCaughrean &
Stauffer (1994). Images of the v=2-1 S(1) emission were
obtained by subtraction of the deconvolved continuum image at 2.179
8 (J2000), with a K magnitude of 8.538 (DENIS
Standard Stars: see
http://cdsweb.u-strasbg.fr/denis.html) and TCC0016,
whose K' band calibration is given in McCaughrean &
Stauffer (1994). Images of the v=2-1 S(1) emission were
obtained by subtraction of the deconvolved continuum image at 2.179 ![]() m
from that at 2.247
m
from that at 2.247 ![]() m, noting that the continuum itself
shows very little emission save that from stars in the field. The
region is strongly illuminated by the Trapezium stars (see below) and
absence of continuum emission indicates that very small dust
particles, which show bright K-band emission in photon dominated
regions (PDRs: e.g. NGC 7023: Lemaire et al. 1996), are
absent in this part of OMC1 (Ferland 2001). Images extracted
in the same manner as described above, but for the v=1-0 S(1) line,
may be found in V2001.
m, noting that the continuum itself
shows very little emission save that from stars in the field. The
region is strongly illuminated by the Trapezium stars (see below) and
absence of continuum emission indicates that very small dust
particles, which show bright K-band emission in photon dominated
regions (PDRs: e.g. NGC 7023: Lemaire et al. 1996), are
absent in this part of OMC1 (Ferland 2001). Images extracted
in the same manner as described above, but for the v=1-0 S(1) line,
may be found in V2001.
Excitation temperature images were created by forming a ratio of the
v=2-1 and v=1-0 S(1) images. This places a stringent requirement on
registration of the separate images. Two stars in the field were used
for image registration, namely PSH132 and TCC0044 located 19
![]() E,
3
E,
3
![]() N and 14
N and 14
![]() E, 7
E, 7
![]() S respectively of TCC0016 (see
Fig. 1). Cuts through these stars show that superposition
of the two sets of data may be performed with an accuracy of
S respectively of TCC0016 (see
Fig. 1). Cuts through these stars show that superposition
of the two sets of data may be performed with an accuracy of ![]() 1
pixel on the full field. Thus ratio images could be made without
significant loss of spatial resolution. (Data recently acquired using the Canada-France-Hawaii Telescope have enabled us to perform registration of v=2-1 and 1-0 S(1) images using 10 stars in the field. Results confirm the registration of the images presented here.)
1
pixel on the full field. Thus ratio images could be made without
significant loss of spatial resolution. (Data recently acquired using the Canada-France-Hawaii Telescope have enabled us to perform registration of v=2-1 and 1-0 S(1) images using 10 stars in the field. Results confirm the registration of the images presented here.)
Referring to v=1, J=3 as level 1 and v=2, J=3 as level 2, both of the
same degeneracy, the excitation temperature may be expressed as
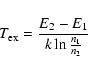 |
(1) |
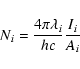 |
(2) |
![\begin{figure}
\par\includegraphics[width=11.8cm,clip]{cbcotemp2.eps}\end{figure}](/articles/aa/full/2003/49/aa3458/Timg27.gif) |
Figure 2:
An "excitation image'' of the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{zoom1.eps}\end{figure}](/articles/aa/full/2003/49/aa3458/Timg28.gif) |
Figure 3: a) A detail of region 1, identified in the excitation image in Fig. 2, b) corresponding emission in v=1-0 S(1) and c) in v=2-1 S(1). The line in Fig. 3a indicates the position of the cut taken in this image to form the data shown in Fig. 5a. The colour bars for brightness in b) and c) are in units of 10-5 Wm-2 sr-1 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{zoom2.eps}\end{figure}](/articles/aa/full/2003/49/aa3458/Timg29.gif) |
Figure 4: As in Fig. 3, but for region 2, see Fig. 2. The line in a) indicates the position of the cut taken in this image to form the data shown in Fig. 5b. The colour bars for brightness in b) and c) are in units of 10-5 Wm-2 sr-1 |
| Open with DEXTER | |
The resulting H2 excitation image can be seen in Fig. 2.
To avoid unacceptable levels of noise in forming this
image, all emission in the v=1-0 and v=2-1 S(1) lines weaker than
![]() Wm-2 sr-1 (
Wm-2 sr-1 (![]() 10% of the maximum in
the 2-1 line and
10% of the maximum in
the 2-1 line and ![]() 2% of the maximum in the 1-0 line) was
excluded. Details of two illustrative objects within Fig. 2 are shown in Figs. 3 and 4, which also show the
corresponding v=1-0 and 2-1 data. The data show surprisingly clear
excitation structure, ranging from
excitation temperatures of 1500 K to >5000 K. There is a
tendency for the emitting clumps of H2 to show a hot edge. In
addition, edges have a clear propensity to face south to south-west.
2% of the maximum in the 1-0 line) was
excluded. Details of two illustrative objects within Fig. 2 are shown in Figs. 3 and 4, which also show the
corresponding v=1-0 and 2-1 data. The data show surprisingly clear
excitation structure, ranging from
excitation temperatures of 1500 K to >5000 K. There is a
tendency for the emitting clumps of H2 to show a hot edge. In
addition, edges have a clear propensity to face south to south-west.
Cuts through objects 1 and 2 are shown in Figs. 5a, b,
which illustrate that the excitation temperature in these zones can
rise to more than 5000 K. Errors in the excitation temperatures quoted
here and subsequently are ![]() 10% for 3
10% for 3![]() .
Values of
.
Values of
![]() in hot zones lie in general around 3500 K to 4000 K. In cooler zones,
values of
in hot zones lie in general around 3500 K to 4000 K. In cooler zones,
values of
![]() congregate around 2500 K. A significant feature is
that the edge of hot zones tends to be very abrupt, as shown in Fig. 5b.
congregate around 2500 K. A significant feature is
that the edge of hot zones tends to be very abrupt, as shown in Fig. 5b.
 |
Figure 5:
a) A cut through the excitation image in Fig. 3a,
region 1, in a direction N-S, 1
|
| Open with DEXTER | |
A comparison may be made between excitation temperatures reported here
and the excitation temperature(s) deduced from Boltzmann plots, that is, of (Ni/gi)
vs. Ei, where Ni is the column density of level i, and
gi and Ei the multiplicity and energy of level i respectively, using the
ISO-SWS data of Rosenthal et al. (2000). The
latter data integrate the emission in an area in the plane of the sky
of ![]() 15
15
![]() by 30
by 30
![]() in the region of Peak 1. This region,
lying to the north of IRc2 (see Fig. 1) and about 3 times
larger than the present region, suffers excitation processes similar in nature
to those in Peak 2. The excitation temperature in the range of energies including
v=2, J=3,
spatially averaged over the ISO-SWS beam, is of the order of 3000 K in
Rosenthal et al. (2000) or 3300 K according to Le Bourlot et al.
(2002). It is evident therefore that the hot zones
observed in the present work, very small on the scale of the ISO-SWS
beam, are rather hotter than in general for OMC1 and represent a
different set of physical conditions than the average for OMC1 as a
whole.
in the region of Peak 1. This region,
lying to the north of IRc2 (see Fig. 1) and about 3 times
larger than the present region, suffers excitation processes similar in nature
to those in Peak 2. The excitation temperature in the range of energies including
v=2, J=3,
spatially averaged over the ISO-SWS beam, is of the order of 3000 K in
Rosenthal et al. (2000) or 3300 K according to Le Bourlot et al.
(2002). It is evident therefore that the hot zones
observed in the present work, very small on the scale of the ISO-SWS
beam, are rather hotter than in general for OMC1 and represent a
different set of physical conditions than the average for OMC1 as a
whole.
Absolute values of brightness of H2 emission in hot and cold zones
in Figs. 2-4 provide an additional diagnostic
of the prevalent physical conditions. The average value of brightness
of the v=1-0 S(1) line in hot zones with
![]() K is
K is
![]() Wm-2 sr-1 (1
Wm-2 sr-1 (1![]() )
whereas the
cooler zones possess a higher brightness of between 1 and
)
whereas the
cooler zones possess a higher brightness of between 1 and
![]() Wm-2 sr-1.
Wm-2 sr-1.
H2 emission in OMC1 arises from both heating through shocks (V2001
and see below), and from photon excitation in PDRs (Störzer &
Hollenbach 1999 (SH99); Sternberg &
Dalgarno 1989; Black & van Dishoeck 1987; Black
& Dalgarno 1976). PDRs are characterized by high excitation
temperatures, e.g. >5000 K for the S(1) v=2-1 and 1-0 lines, at any
rate for low number densities, that is, ![]() 104 cm-3(Sternberg & Dalgarno 1989). In the discussion that
follows, we consider first the influence of shocks and then turn to
the influence of the PDR generated by
104 cm-3(Sternberg & Dalgarno 1989). In the discussion that
follows, we consider first the influence of shocks and then turn to
the influence of the PDR generated by ![]() 1C Ori.
1C Ori.
Our aim is to identify shock conditions which reproduce the observed range of excitation temperatures using shock models. Our discussion proceeds with the proviso that shock models do not yet yield a definitive description of the origin of H2 emission. Indeed, models in general experience considerable difficulties in describing data for H2 emission spectrum in such objects as the Orion bullets (e.g. Tedds et al. 1999).
Since the region
may be permeated by magnetic fields (Norris 1984; Crutcher et al.
1999) and the gas is at least weakly ionized, shock
models include not only J-type (Hollenbach & McKee 1989; Lim et al. 2002) and but also continuous-type (C-type)
shock waves. The latter have been investigated by Draine et al. (1983), Pineau des Forêts et al. (1988),
Smith & Brand (1990),
Kaufman & Neufeld (1996a,b),
Timmerman (1998), Wilgenbus et al. (2000), whose
results were used in V2001, and most recently by Le Bourlot et al. (2002). The latter extends the work of Wilgenbus et al. (2000), showing that C-type shocks may propagate at
considerably greater velocities than was previously believed,
increasing the range from around 30 km s-1 to >50 km s-1depending on the gas density (see below). The model of Le Bourlot et al. (2002) used here abides by the relationship that the
transverse magnetic induction is given by
![]() ,
in contrast to the models reported for example in Smith (1991) and Smith et al. (1991) which invoke very high magnetic fields.
Using the new model of Le Bourlot et al. (2002), the range of C-type
shock speed and pre-shock gas density explored in the present work is therefore
considerably enlarged over that investigated using the results of
Wilgenbus et al. (2000) in V2001. The range of densities and
shock speeds covers preshock values of n=103 cm-3 to
107 cm-3 and shock speeds of 10 km s-1
,
in contrast to the models reported for example in Smith (1991) and Smith et al. (1991) which invoke very high magnetic fields.
Using the new model of Le Bourlot et al. (2002), the range of C-type
shock speed and pre-shock gas density explored in the present work is therefore
considerably enlarged over that investigated using the results of
Wilgenbus et al. (2000) in V2001. The range of densities and
shock speeds covers preshock values of n=103 cm-3 to
107 cm-3 and shock speeds of 10 km s-1
![]() ,
where
,
where
![]() is the maximum velocity at which a C-type shock is able to
propagate in the medium for any chosen pre-shock density, ranging from
is the maximum velocity at which a C-type shock is able to
propagate in the medium for any chosen pre-shock density, ranging from ![]() 50 km s-1 for n=103 cm-3 to
50 km s-1 for n=103 cm-3 to ![]() 24 km s-1 for
n=107 cm-3. The steady-state code treats, in planar geometry, the
hydrodynamics of the shock and the detailed chemistry in a
self-consistent manner, including for example the chemistry-dependent
cooling of the post-shock gas. Level population densities of H2ro-vibrational states are computed, in parallel with the chemical and
dynamical variables. In the models to which we refer below, the
ortho/para H2 ratio is assumed to be 3 in the pre-shocked gas. We note that these latest shock models, which include the most recent collisional cross-section data (Le Bourlot et al. 2002), overcome the difficulties experienced in earlier shock models (e.g. Burton et al. 1990) in treating high density regions of >105 cm-3.
24 km s-1 for
n=107 cm-3. The steady-state code treats, in planar geometry, the
hydrodynamics of the shock and the detailed chemistry in a
self-consistent manner, including for example the chemistry-dependent
cooling of the post-shock gas. Level population densities of H2ro-vibrational states are computed, in parallel with the chemical and
dynamical variables. In the models to which we refer below, the
ortho/para H2 ratio is assumed to be 3 in the pre-shocked gas. We note that these latest shock models, which include the most recent collisional cross-section data (Le Bourlot et al. 2002), overcome the difficulties experienced in earlier shock models (e.g. Burton et al. 1990) in treating high density regions of >105 cm-3.
We initially consider the possibility that in any clump, such as those
in Figs. 3 and 4, we are observing generic
structure in the emission of a shock, seen edgeways on, and that the observed excitation temperature structure reflects the cooling
profile of the shock itself. In this physical model, observations
require that the width of the shocked region is of the order of a few
hundred AU. This limits pre-shock densities to <105 cm-3. In
order to achieve a brightness in the S(1) v=1-0 line in excess of
10-5 Wm-2 sr-1, this turns out to require velocities of
40-50 km s-1. Computed excitation temperature profiles however
show
![]() remaining roughly constant, at 2600 K to 2800 K,
throughout the emitting zone. Hence excitation temperature profiles do
not resemble those observed (Figs. 5a, b) and we
conclude that this edgeways-view model is not correct.
remaining roughly constant, at 2600 K to 2800 K,
throughout the emitting zone. Hence excitation temperature profiles do
not resemble those observed (Figs. 5a, b) and we
conclude that this edgeways-view model is not correct.
Turning first to a suitable model for the high
![]() zones, a large range of C- and J-type shocks has been
explored in order to try to reproduce the high observed excitation
temperatures. For C-type shocks, the only group which yield
zones, a large range of C- and J-type shocks has been
explored in order to try to reproduce the high observed excitation
temperatures. For C-type shocks, the only group which yield
![]() of 3500-4000 K are those which involve shock velocities of 25 to 30 km s-1
impinging on gas at a pre-shock density of
of 3500-4000 K are those which involve shock velocities of 25 to 30 km s-1
impinging on gas at a pre-shock density of
![]() cm-3 (or higher, but with correspondingly lower
shock velocities). For example, a shock velocity of 28 km s-1 in
gas of pre-shock density
cm-3 (or higher, but with correspondingly lower
shock velocities). For example, a shock velocity of 28 km s-1 in
gas of pre-shock density
![]() cm-3 yields
cm-3 yields
![]() K and a post-shock density of
K and a post-shock density of
![]() cm-3 at 10 K. However the calculated brightness
in the v=1-0 S(1) line is
cm-3 at 10 K. However the calculated brightness
in the v=1-0 S(1) line is
![]() Wm-2 sr-1,
whereas the observed average brightness is
Wm-2 sr-1,
whereas the observed average brightness is ![]() 10 times
lower. We find no C-type shocks which yield a high excitation
temperature accompanied by the observed lower brightness, that is,
lower brightness than in low
10 times
lower. We find no C-type shocks which yield a high excitation
temperature accompanied by the observed lower brightness, that is,
lower brightness than in low
![]() zones.
zones.
Slower J-type shocks turn out to be better candidates to describe high excitation temperature zones. It is possible to identify a limited range of J-shock
velocities and pre-shock densities which yields the observed
excitation temperature and a suitable H2 emission brightness. For
example a J-type shock of velocity 15 km s-1, impinging on
pre-shock gas at a density of 106 cm-3, yields a brightness in
the v=1-0 S(1) line of
![]() Wm-2 sr-1 and in
v=2-1 S(1) of
Wm-2 sr-1 and in
v=2-1 S(1) of
![]() Wm-2 sr-1. This corresponds
to
Wm-2 sr-1. This corresponds
to
![]() K, representative of hot zones. The post-shock density
at 50 K is estimated to be
K, representative of hot zones. The post-shock density
at 50 K is estimated to be
![]() cm-3. This and similar
shock models provide a brightness between 2 and 3 times less than the
observed average value of
cm-3. This and similar
shock models provide a brightness between 2 and 3 times less than the
observed average value of
![]() Wm-2 sr-1 in
the 1-0 S(1) line. A higher preshock density may be chosen to yield
the observed figure. However, as we describe in section 3.2, there is
a PDR contribution to the emission of comparable magnitude to that
provided by the shock and the uncertainties in both the shock and PDR
models do not warrant more detailed estimates of shock speeds and
densities. Despite this complexity, the v=2-1/1-0 S(1) line ratio appears to be a good
diagnostic of the physical conditions in the sense that high
Wm-2 sr-1 in
the 1-0 S(1) line. A higher preshock density may be chosen to yield
the observed figure. However, as we describe in section 3.2, there is
a PDR contribution to the emission of comparable magnitude to that
provided by the shock and the uncertainties in both the shock and PDR
models do not warrant more detailed estimates of shock speeds and
densities. Despite this complexity, the v=2-1/1-0 S(1) line ratio appears to be a good
diagnostic of the physical conditions in the sense that high
![]() clearly implies high pre- and post-shock gas densities. The model width of the J-shocks mentioned above is a small
fraction of 1 AU. Thus we postulate that the medium is under
continuous shock excitation and is subject to a large number of small
scale shocks, since these features together would yield the extended emission observed.
clearly implies high pre- and post-shock gas densities. The model width of the J-shocks mentioned above is a small
fraction of 1 AU. Thus we postulate that the medium is under
continuous shock excitation and is subject to a large number of small
scale shocks, since these features together would yield the extended emission observed.
As described in V2001, which used the models described in Wilgenbus et al. (2000), C-type shocks are essential to reproduce the
level of v=1-0 S(1) emission in the brightest regions. Thus the
brightly emitting zones of low excitation temperature, where the
greatest v=1 -0 S(1) emission is found, can be modelled as C-type
shocks involving pre-shock densities of the order of 106 cm-3,
post shock densities of a few
![]() cm-3 at 10 K, with
accompanying shock velocities of 25-30 km s-1. The observed
1-0/2-1 line ratio in cooler parts of region 1, for example, is
cm-3 at 10 K, with
accompanying shock velocities of 25-30 km s-1. The observed
1-0/2-1 line ratio in cooler parts of region 1, for example, is
![]() around the peak of emission. The C-type shock models mentioned yield results which span this range, running from 9.6 to 5.0 or
around the peak of emission. The C-type shock models mentioned yield results which span this range, running from 9.6 to 5.0 or
![]() to 2900 K. Models predict a brightness in the v=1-0 S(1)
line of 3 to
to 2900 K. Models predict a brightness in the v=1-0 S(1)
line of 3 to
![]() Wm-2 sr-1 and are therefore
also consistent with or a little brighter than values recorded in our
observations.
Wm-2 sr-1 and are therefore
also consistent with or a little brighter than values recorded in our
observations.
In the shock interpretation outlined above, the excitation image is seen
effectively to trace gas density and we conclude that clumps of
material possess very dense regions. Using the scale size of
![]() pc derived in V2001, it was shown in
V2001 on the basis of the Jeans length that gravitational instability
may set in for number densities in excess of
pc derived in V2001, it was shown in
V2001 on the basis of the Jeans length that gravitational instability
may set in for number densities in excess of ![]() 107 cm-3,
for the largest of the clumps (region 1 in Fig. 2). It now
appears that parts of this and other objects possess albeit small
regions with number density of several times 108 cm-3 and
therefore that the total mass contained within these clumps is
somewhat larger than previous estimates of
107 cm-3,
for the largest of the clumps (region 1 in Fig. 2). It now
appears that parts of this and other objects possess albeit small
regions with number density of several times 108 cm-3 and
therefore that the total mass contained within these clumps is
somewhat larger than previous estimates of ![]() 0.1
0.1 ![]() .
This strengthens the conclusion of V2001 that region 1,
for example, may contain sufficient material for low mass star
formation.
.
This strengthens the conclusion of V2001 that region 1,
for example, may contain sufficient material for low mass star
formation.
In this connection, a new element in our interpretation arises from spatially and velocity resolved GriF data for H2 emission in OMC1 (see Sect. 2; Gustafsson et al. 2003). We interpret these data as showing evidence that some of the OMC1 clumps may already possess protostars buried within them. Since outflow is characteristic of protostars (André et al. 1993; Evans 1999; Eislöffel et al. 2000), these clumps therefore suffer shocks originating from flows within the clumps rather than from an external source alone, such as the well characterised outflow from the BN-IRc2 zone (Doi et al. 2002). If a clump contains a protostar, H2 emission then represents a later post-collapse stage of star formation, rather than the hastening of star formation through shock accumulation of dense material prior to gravitational collapse.
The region observed is exposed to the far-UV radiation field of the
Trapezium stars, of which the dominant contributor is the O-star
![]() 1C Ori,
1C Ori, ![]() 0.09 pc distant from the H2 emitting
clumps. We initially set aside the high densities that arise in the
shock model of Sect. 3.1 and consider purely PDR excitation.
0.09 pc distant from the H2 emitting
clumps. We initially set aside the high densities that arise in the
shock model of Sect. 3.1 and consider purely PDR excitation.
![]() 1C Ori generates a radiation field of 2-
1C Ori generates a radiation field of 2-
![]() times
the standard interstellar field (
times
the standard interstellar field (
![]() ),
including appropriate attenuation by dust in the HII outflow, as
discussed in SH99. We note that estimates of G0 could be too low by
an order of magnitude (Ferland 2001), but that predictions
of PDR models are insensitive to variation of G0 over this range
(SH99). With
),
including appropriate attenuation by dust in the HII outflow, as
discussed in SH99. We note that estimates of G0 could be too low by
an order of magnitude (Ferland 2001), but that predictions
of PDR models are insensitive to variation of G0 over this range
(SH99). With
![]() ,
,
![]() cm-3,
including 2.6 km s-1 of advective heating, SH99 reports a
brightness of
cm-3,
including 2.6 km s-1 of advective heating, SH99 reports a
brightness of
![]() Wm-2 sr-1 in the v=1 -0 S(1)
line. This is
Wm-2 sr-1 in the v=1 -0 S(1)
line. This is ![]() 7 times lower than the brightness of the central
0
7 times lower than the brightness of the central
0
![]() 8 of region 1, for example (V2001). With the same model
parameters, the v=2 -1 line brightness predicted in SH99 is
8 of region 1, for example (V2001). With the same model
parameters, the v=2 -1 line brightness predicted in SH99 is
![]() Wm-2 sr-1, whereas the observed is
Wm-2 sr-1, whereas the observed is
![]()
![]() Wm-2 sr-1. Results in SH99
correspond to an excitation temperature of
Wm-2 sr-1. Results in SH99
correspond to an excitation temperature of ![]() 2000 K. Data in SH99
represent the most extreme PDR conditions which have been explored and
thus no known PDR model can account for the present
observations. There must nevertheless be a PDR contribution to the
H2 emission, as subsequently discussed.
2000 K. Data in SH99
represent the most extreme PDR conditions which have been explored and
thus no known PDR model can account for the present
observations. There must nevertheless be a PDR contribution to the
H2 emission, as subsequently discussed.
In addition, ![]() 1C Ori can also generate a shock in the zone
of interest. The mass loss rate of
1C Ori can also generate a shock in the zone
of interest. The mass loss rate of ![]() 1C Ori is
1C Ori is
![]()
![]() yr-1 with a velocity of 1000 km s-1
(Howarth & Prinja 1989; O'Dell 2001). This corresponds however to an energy flux of
material in the region of H2 emission which is 2 to 3 orders of
magnitude too small to drive the shocks described in Sect. 3.1. Thus
shocks from
yr-1 with a velocity of 1000 km s-1
(Howarth & Prinja 1989; O'Dell 2001). This corresponds however to an energy flux of
material in the region of H2 emission which is 2 to 3 orders of
magnitude too small to drive the shocks described in Sect. 3.1. Thus
shocks from ![]() 1C Ori cannot account for the structure
observed in the excitation temperature image. Rather the
form of this image arises because the H2
emission zones represent dense clouds within an HII region, subject both to shocks and PDR excitation, as we now describe.
1C Ori cannot account for the structure
observed in the excitation temperature image. Rather the
form of this image arises because the H2
emission zones represent dense clouds within an HII region, subject both to shocks and PDR excitation, as we now describe.
We combine the effects of shocks, discussed in Sect. 3.1, with the
environment generated by ![]() 1C Ori. The general nature of this
environment in the zone of interest has been extensively studied. The
HII region associated with the Trapezium cluster is very
well-documented and its morphology is known in detail
(Ferland 2001; O'Dell 2001; Wen &
O'Dell 1995). Following Wen & O'Dell (1995), the main wall
of the HII region lies 0.15 to 0.2 pc beyond the region observed. This
is corroborated, for example, by recent data in Takami et al. (2002), who describe the morphology of the HII zone around
the Trapezium stars, using [FeII], HeI and Pa
1C Ori. The general nature of this
environment in the zone of interest has been extensively studied. The
HII region associated with the Trapezium cluster is very
well-documented and its morphology is known in detail
(Ferland 2001; O'Dell 2001; Wen &
O'Dell 1995). Following Wen & O'Dell (1995), the main wall
of the HII region lies 0.15 to 0.2 pc beyond the region observed. This
is corroborated, for example, by recent data in Takami et al. (2002), who describe the morphology of the HII zone around
the Trapezium stars, using [FeII], HeI and Pa![]() lines as
diagnostic of the presence of the HII region. These data show that the
present region is overrun by the HII zone and thus that the clumps
observed are dense fragments, surviving in the HII region around the
Trapezium stars (O'Dell 2001). This is supported by the fact
that high
lines as
diagnostic of the presence of the HII region. These data show that the
present region is overrun by the HII zone and thus that the clumps
observed are dense fragments, surviving in the HII region around the
Trapezium stars (O'Dell 2001). This is supported by the fact
that high
![]() regions are generally sharp-edged, where the expansion of the
HII zone is effectively inhibited by the high density. Thus we
interpret the form of the excitation temperature images in terms of a
combination of shocks, which build high density, and an intense far-UV
photon field from the south, largely from
regions are generally sharp-edged, where the expansion of the
HII zone is effectively inhibited by the high density. Thus we
interpret the form of the excitation temperature images in terms of a
combination of shocks, which build high density, and an intense far-UV
photon field from the south, largely from ![]() 1C Ori, which
scours away less dense material through photoevaporation. This latter
aspect is analogous to the photoevaporation model of circumstellar
disks, so-called "proplyds'' (Henney & O'Dell 1999). Only
dense gas survives when unshielded from
1C Ori, which
scours away less dense material through photoevaporation. This latter
aspect is analogous to the photoevaporation model of circumstellar
disks, so-called "proplyds'' (Henney & O'Dell 1999). Only
dense gas survives when unshielded from ![]() 1C Ori - providing
the mass reservoir is large enough. This gives a qualitative
explanation for the generally southern facing morphology of the hot
dense zones, pointing towards the Trapezium cluster.
1C Ori - providing
the mass reservoir is large enough. This gives a qualitative
explanation for the generally southern facing morphology of the hot
dense zones, pointing towards the Trapezium cluster.
In this combined photoevaporation-shock description, the radiation
field of ![]() 1C Ori falls upon very dense material, with
1C Ori falls upon very dense material, with
![]() cm-3, 2 orders of magnitude denser than in proplyd
photoevaporation models of SH99. In
order to estimate the brightness generated in the H2 lines for such
a dense region, a PDR model has been run using
cm-3, 2 orders of magnitude denser than in proplyd
photoevaporation models of SH99. In
order to estimate the brightness generated in the H2 lines for such
a dense region, a PDR model has been run using
![]() and number densities between 108 cm-3 and
and number densities between 108 cm-3 and
![]() cm-3.
This model, based on a code described in Abgrall et al. (1992),
involves purely the fluorescence mechanism of
excitation of H2. We find that the model generates a surface
brightness of 1.5 to
cm-3.
This model, based on a code described in Abgrall et al. (1992),
involves purely the fluorescence mechanism of
excitation of H2. We find that the model generates a surface
brightness of 1.5 to
![]() Wm-2 sr-1 in the v=1-0S(1) line and 6 to
Wm-2 sr-1 in the v=1-0S(1) line and 6 to
![]() Wm-2 sr-1 in the v=2-1S(1) line. Thus photon excitation makes a significant contribution to
the H2 emission brightness, very comparable with the J-type shocks
discussed in Sect. 3.1 and yielding the same excitation
temperature. Moreover since this PDR model does not include advective
flow, which should be present, the true emission brightness due to the
FUV field of
Wm-2 sr-1 in the v=2-1S(1) line. Thus photon excitation makes a significant contribution to
the H2 emission brightness, very comparable with the J-type shocks
discussed in Sect. 3.1 and yielding the same excitation
temperature. Moreover since this PDR model does not include advective
flow, which should be present, the true emission brightness due to the
FUV field of ![]() 1C Ori will be greater than the estimates
mentioned. These considerations largely remove the discrepancy between
observation and calculated brightness, found for the J-shock alone, as
discussed in 3.1.
1C Ori will be greater than the estimates
mentioned. These considerations largely remove the discrepancy between
observation and calculated brightness, found for the J-shock alone, as
discussed in 3.1.
The photoevaporation model proposed in SH99 may also provide some
basis for our inference, drawn from shock models, that shocks are both
C-type and J-type within closely lying regions. C-type shocks require
the presence of transverse magnetic induction, whereas J-type assume
that this is absent or that the degree of ionization in the region is
negligible. SH99 (and references therein) show that the effects of an
intense FUV field falling upon dense material is to generate a neutral
outflow. One may speculate that neutral outflowing material may drag
ions and electrons away with it, creating a zone of low ionization,
relatively devoid of magnetic induction, in which J-type shocks may
propagate. A further possibility is that shocks in high
![]() zones
do not achieve a steady state and we are observing the J-type region
which accompanies the developing C-type shock.
zones
do not achieve a steady state and we are observing the J-type region
which accompanies the developing C-type shock.
A further point arises which may stimulate new observations.
The combination of shocks and a PDR as above would yield a velocity spectrum
of H2 showing a narrow line for the PDR, superposed on broader shock emission.
Thus high spectral resolution spectro-imaging of these regions, with a spatial
resolution of ![]() 0
0
![]() 2, would yield data which provide a useful test of
the model proposed. Existing data in Chrysostomou et al. (1997)
or Salas et al. (1999) is of sufficient spectral resolution but has a spatial resolution of no better than
2, would yield data which provide a useful test of
the model proposed. Existing data in Chrysostomou et al. (1997)
or Salas et al. (1999) is of sufficient spectral resolution but has a spatial resolution of no better than ![]() 1
1
![]() 6.
6.
The observational data presented here for v=2-1 S(1) H2 emission
provide evidence for highly structured excitation temperatures and
densities in clumps of gas in Orion. In a fraction of the volume of
these clumps, densities deduced from shock models are an order of
magnitude higher than previous estimates in V2001, where the latter
were based solely upon v=1-0 S(1) emission. We propose that the density structure of the clumps, a few times 107 cm-3in the bulk, but in excess of 108 cm-3 at the high excitation
temperature south-facing edges, is dictated by a combination of
energetic shock compression and radiative evaporation. The emission of
H2 is formed in the body of the clumps by C-type shocks. However at
the edges, facing ![]() 1C Ori, emission is generated through
roughly equal contributions from J-type shocks and the PDR created by
the intense FUV field of
1C Ori, emission is generated through
roughly equal contributions from J-type shocks and the PDR created by
the intense FUV field of ![]() 1C Ori. The radiation field
competes with the shock-induced process of accumulation of material,
stripping away less dense matter at the fringes of the clumps and
leaving behind only very dense regions facing in the direction of the
Trapezium stars.
1C Ori. The radiation field
competes with the shock-induced process of accumulation of material,
stripping away less dense matter at the fringes of the clumps and
leaving behind only very dense regions facing in the direction of the
Trapezium stars.
Acknowledgements
DF, LEK and MG would like to acknowledge the support of the Aarhus Centre for Atomic Physics (ACAP), funded by the Danish Basic Research Foundation. DF would also like to acknowledge support received from the Observatoire de Paris Meudon during the period of this work. JLL and GC would like to acknowledge the support of the PCMI National Program, funded by the CNRS in cooperation with the CEA and IN2P3. We also wish to thank the Directors and Staff of ESO and of the CFHT for making possible observations reported in this paper. Thanks are also due to F.P. Pijpers (Aarhus) for his help in implementing the deconvolution techniques used here and to C.Nehme (Observatoire de Paris-Meudon) for running the PDR codes mentioned in the text.