A&A 412, 837-848 (2003)
DOI: 10.1051/0004-6361:20031307
J. Madej1 - M. Pietrachowicz1 - P. C. Joss2 - A. Majczyna3 - A. Rózanska3 - M. Nalezyty1
1 - Astronomical Observatory, University of Warsaw,
Al. Ujazdowskie 4, 00-478 Warsaw, Poland
2 -
Department of Physics, Center for Theoretical Physics and Center
for Space Research, Massachusetts Institute of Technology,
Cambridge, MA 02139, USA
3 -
Copernicus Astronomical Center, Polish Academy of Sciences,
Bartycka 18, 00-716 Warsaw, Poland
Received 31 October 2002 / Accepted 30 July 2003
Abstract
We explore photometric properties of hypothetical iron core
white dwarfs and compute their expected colors in UBVRI Johnson
broadband system. Atmospheres of iron core WDs in this paper
consist of pure iron covered by a pure hydrogen layer of an arbitrary
column mass. LTE model atmospheres and theoretical spectra are calculated
on the basis of Los Alamos TOPS opacities and the equation of state
from the OPAL project, suitable for nonideal Fe and H gases.
We have also computed UBVRI colors of the models and
determined an area on the B-V vs. U-B and B-V vs. V-I planes,
occupied by both pure Fe,
and pure H model atmospheres of WD stars.
Finally, we search for iron core white dwarf candidates in the available
literature.
Key words: stars: atmospheres - stars: white dwarfs - stars: fundamental parameters
The chemical composition of white dwarf stars cores has not yet been convincingly determined. While most white dwarfs are believed to have pure carbon or mixed carbon-oxygen interiors, there are suggestions that cores of some WDs are built of heavier elements, and pure iron cores represent the extreme case.
An idea that some white dwarfs have cores built of heavier elements
was put forward by Provencal et al. (1998) and Provencal & Shipman (1999).
In particular, they noted that the nearby white dwarf Procyon B has
the relatively normal white dwarf mass of 0.594 ![]() ,
but has a
very small radius (cf. also Girard et al. 2000). This would imply that
Procyon B has a very heavy core, perhaps of iron. They found that radii of
other WD stars EG 50 and GD 140 are also located significantly below
the mass-radius relation predicted for typical carbon interior compositions.
Only recently, Provencal et al. (2002) on the basis of
precise Hubble spectral measurements recognized that Procyon B
is a normal white dwarf, belonging to the DQZ spectral class.
,
but has a
very small radius (cf. also Girard et al. 2000). This would imply that
Procyon B has a very heavy core, perhaps of iron. They found that radii of
other WD stars EG 50 and GD 140 are also located significantly below
the mass-radius relation predicted for typical carbon interior compositions.
Only recently, Provencal et al. (2002) on the basis of
precise Hubble spectral measurements recognized that Procyon B
is a normal white dwarf, belonging to the DQZ spectral class.
Panei et al. (2000) have obtained thorough theoretical mass-radius relations for iron-dominated cores. They show that EG 50, GD 140 and 40 Eri B satisfy these relations for iron cores, contrary to mass-radius relations for carbon and oxygen cores. Their result convinced us that the existence of the iron core white dwarfs is possible. The above hypothesis is sufficient for us to perform and publish this research paper.
Atmospheres of these stars are probably built from pure iron gas covered by a hydrogen (and/or helium) layer, since stratified atmospheres are common among the known white dwarfs. We expect that most likely iron and hydrogen are not perfect gases, at least in cooler WDs.
In the following sections we describe model atmosphere calculations
in the local thermodynamical equilibrium (LTE), which are based on a frequently
used equation of state computed by the OPAL Project for nonideal hydrogen
(Rogers et al. 1996) and iron gas (Rogers 2002).
Our calculations use exclusively the Los Alamos TOPS monochromatic
absorption and scattering opacities, consistent with the
nonideal EOS for both gases (Magee et al. 1995). Model atmosphere
and spectrum calculations are restricted to atmospheres in radiative
equilibrium, corresponding to effective temperatures
![]() K.
K.
Los Alamos opacity tables were originally designed to study physics and pulsational instabilities in stellar envelopes by means of Rosseland mean opacities. Therefore the tables do not have a spectral resolution adequate to study details of stellar atmospheric spectra. This is the reason that our paper presents and discusses mostly spectral indices U-B, B-V, V-R, and V-I of the broadband Johnson photometric system. We attempt to find a prescription for differentiating most common DA white dwarfs with pure hydrogen atmospheres from iron core white dwarfs with pure iron or stratified hydrogen-iron atmospheres.
Model atmosphere equations are based on the following equation
of radiative transfer, suitable for planar geometry
Computer code used here has been derived from the code ATM21 adapted to coherent scattering in stellar atmosphere (exact description in Madej 1991, 1994, 1998; Madej & Rózanska 2000; Stage et al. 2002).
The foregoing papers explain in detail the equations of hydrostatic and radiative equilibrium, which are imposed on the model atmospheres, as well as two boundary conditions associated with the equation of transfer. The equation of transfer and the radiation field was solved with the method of variable Eddington factors (Mihalas 1978).
Model atmosphere equations were expressed in a discrete form on
frequency grid ![]() ,
,
![]() and standard optical
depth grid
and standard optical
depth grid
![]() ,
,
![]() .
Here, in our models,
the monochromatic optical depth at the fixed wavelength of 1500 Å is used. For each model we set I=749 and started computations from a very small
standard optical depth point
.
Here, in our models,
the monochromatic optical depth at the fixed wavelength of 1500 Å is used. For each model we set I=749 and started computations from a very small
standard optical depth point
![]() .
We have assumed a value for D equal to D=150 for pure hydrogen models,
while for pure iron and stratified H-Fe models D=155 was set.
Both the monochromatic absorption and scattering coefficiens, and hence
the
.
We have assumed a value for D equal to D=150 for pure hydrogen models,
while for pure iron and stratified H-Fe models D=155 was set.
Both the monochromatic absorption and scattering coefficiens, and hence
the
![]() ,
were determined at each frequency
,
were determined at each frequency ![]() and depth
points
and depth
points
![]() by direct interpolation of extensive TOPS opacity
tables. The equation of state for nonideal gas, i.e. the values of gas
density for a given temperature and gas pressure, were similarly
determined by interpolation of the OPAL EOS tables either for H or
pure Fe gas.
by direct interpolation of extensive TOPS opacity
tables. The equation of state for nonideal gas, i.e. the values of gas
density for a given temperature and gas pressure, were similarly
determined by interpolation of the OPAL EOS tables either for H or
pure Fe gas.
The nonideal equation of state for partially ionized plasma, which was used in our research, has been extensively described by Rogers (1994), Rogers et al. (1996), cf. also references therein. These authors refer to their derivation as to the activity expansion of the grand canonical partition function of plasma, the latter being basic function in statistical thermodynamics. The method includes quantum mechanical two-body and many-body interactions, and electron degeneracy along with other effects. We feel not enough competent to present and discuss details of their method in the present paper. However, we mention after Rogers et al. (1996) that their derivation of the EOS for various plasmas basically differs from common methods which are based on minimization of free energy in plasma.
This research uses EOS data which is available for the general user. EOS tables for pure hydrogen plasma were taken from the Lawrence Livermore National Laboratory www site (http://www-phys.llnl.gov/Research/OPAL/index.html). With EOS tables for pure iron gas we were kindly provided by Dr. F.J. Rogers (2002).
Extensive TOPS monochromatic opacity tables have been prepared at the Los Alamos National Laboratory (Magee et al. 1995). We have collected hydrogen and iron data from their web page at http://www.t4.lanl.gov/opacity/tops.html See that www site for more details on the TOPS opacity calculations.
![\begin{figure}
\par\resizebox{11.7cm}{!}{\includegraphics[clip]{aa3245f1.eps}} \hspace*{4mm}
\parbox[b]{50mm}{}
\end{figure}](/articles/aa/full/2003/49/aa3245/Timg31.gif) |
Figure 1: Comparison of theoretical colors, B-V vs. U-B, for two grids of pure hydrogen, hot DA atmospheres. Models are computed either with the TLUSTY195 and SYNSPEC42 NLTE codes, or with our ATM21 code based on the nonideal EOS and Los Alamos opacities. Consistency of both families of broadband B-V and U-B indices is not perfect but is satisfactory. |
| Open with DEXTER | |
Having calculated the models, we acquired their broadband Johnson UBVRI colors using a color synthesis procedure described by Bergeron et al. (1995); see also detailed review of photometric systems by Girardi et al. (2002).
At first, stellar magnitudes of a theoretical spectrum are computed according
to the standard formula
We used the Johnson UBVRI transmission functions defined by Bessell (1990),
and restricted our research to analysis of colors, i.e. differences of the
respective magnitudes. Then the definition of the respective colors, e.g. B-V color, is as follows:
Note that plane-parallel model atmosphere codes
compute theoretical spectra of radiation ![]() which are emitted by unit
surface on the star, this is 1 cm2 in case of the ATM21 code.
Therefore theoretical flux
which are emitted by unit
surface on the star, this is 1 cm2 in case of the ATM21 code.
Therefore theoretical flux ![]() in Eq. (3) is never directly
comparable with e.g. the flux measured on Earth or absolute flux in that
filter, which would be measured at 10 pc distance.
in Eq. (3) is never directly
comparable with e.g. the flux measured on Earth or absolute flux in that
filter, which would be measured at 10 pc distance.
Equation (3) can be applied to Vega, which is the fundamental
spectrophotometric standard. In our research each color of Vega is equal to
zero by assumption. Setting ![]() to the flux of Vega allowed us
to determine constants CU-B, CB-V, CV-R and CV-Ifor all theoretical colors presented in the following sections.
to the flux of Vega allowed us
to determine constants CU-B, CB-V, CV-R and CV-Ifor all theoretical colors presented in the following sections.
For the above calibration purposes we adapted absolute fluxes of Vega
observed by Hayes (1985), for
![]() Å. His paper gives
values of the Vega flux in equidistant intervals of 25 Å and
therefore gives a poor description of the flux in the near ultraviolet, where
prominent higher Balmer lines merge and the wavelength dependence of Vega
flux is very complex. Therefore for
Å. His paper gives
values of the Vega flux in equidistant intervals of 25 Å and
therefore gives a poor description of the flux in the near ultraviolet, where
prominent higher Balmer lines merge and the wavelength dependence of Vega
flux is very complex. Therefore for
![]() Å we have taken
theoretical fluxes from Castelli & Kurucz (1994). They have computed
ATLAS12 model atmosphere and spectrum of Vega with a high spectral
resolution, normalised in the same way as Hayes' (1985) observations.
Å we have taken
theoretical fluxes from Castelli & Kurucz (1994). They have computed
ATLAS12 model atmosphere and spectrum of Vega with a high spectral
resolution, normalised in the same way as Hayes' (1985) observations.
We have taken this approach to reference spectra of Vega from Bergeron et al. (1995), in order to make our color indices for hydrogen and iron atmospheres fully compatible with their tables of Johnson photometry colors computed for DA and DB white dwarfs.
In this section we construct and discuss two different series of pure hydrogen model atmospheres of white dwarfs. This is done in order to compare and measure the discrepancies between each model and assess the uncertainty of colors of atmospheres computed with the following two basically different numerical methods. By doing this, we also test the compatibility of both OPAL and TOPS data with the existing model atmosphere codes. We draw a conclusion that our pure Fe model atmospheres, based on those data, are consistent with pure H atmospheres.
For calculating models of hot WD atmospheres consisting of pure hydrogen, the following approaches were taken: (1) We assumed that plasma of hot hydrogen atmospheres is described by the EOS of an ideal gas. Under this assumption, thorough models were calculated in the NLTE regime. Models and spectra computations were performed using TLUSTY195 and SYNSPEC42 codes (Hubeny 1988; Hubeny & Lanz 1992, 1995). Three spectral series of hydrogen (Lyman, Balmer, and Paschen) were considered as we computed outgoing flux spectra and color indices. Since Paschen lines are not present in the standard versions of both codes, we have adopted the opacities of thermally & pressure-broadened Paschen lines from Lemke (1997). (2) Alternatively, we assumed more factual, nonideal EOS for gas and derived a number of models in LTE. Tables for nonideal EOS were taken from the OPAL project, while the Los Alamos TOPS monochromatic opacity tables were used.
In the present work we are concerned about isolated hot WD atmospheres with effective temperatures
![]() in the
range of 20 000 to 100 000 K and surface gravities ranging from
in the
range of 20 000 to 100 000 K and surface gravities ranging from
![]() to 10.0 (cgs units). White dwarfs of as high
surface gravity as
to 10.0 (cgs units). White dwarfs of as high
surface gravity as
![]() are not yet known, however, one can
expect that iron core white dwarfs of a given mass have a particularly
small radius and therefore high surface gravity. Consequently, we
appended high gravity hydrogen model atmospheres to obtain grid
consistent with pure iron high gravity atmospheres.
The radiative and hydrostatic equilibria are implied in all models.
are not yet known, however, one can
expect that iron core white dwarfs of a given mass have a particularly
small radius and therefore high surface gravity. Consequently, we
appended high gravity hydrogen model atmospheres to obtain grid
consistent with pure iron high gravity atmospheres.
The radiative and hydrostatic equilibria are implied in all models.
Grids of color indices for both NLTE ( TLUSTY195) and LTE (Los Alamos)
series of models were plotted on two-index plane, U-B vs. B-V,
and are displayed in Fig. 1. Colors of the TOPS-based LTE
models are in a reasonable agreement
with the corresponding colors of the NLTE models, especially for highest
effective temperatures
![]() .
The largest difference in the
U-B index is equal to almost 0.1 mag (for
.
The largest difference in the
U-B index is equal to almost 0.1 mag (for
![]() K and
K and
![]() );
in the B-V it is mere 0.034 mag (for
);
in the B-V it is mere 0.034 mag (for
![]() K and
K and
![]() ). The differences in V-I color are smaller still.
). The differences in V-I color are smaller still.
We conclude that the models, based on TOPS and OPAL tables,
are in satisfactory agreement with the NLTE TLUSTY195 models,
as long as pure hydrogen models are concerned. Therefore we
believe that pure iron or stratified hydrogen-iron models with nonideal
EOS would be consistent with NLTE ideal gas models at the high
![]() limit.
limit.
It is interesting to note that colors of pure H model atmospheres
computed either with the EOS of ideal gas or with the OPAL nonideal EOS exhibit systhematic differences for lower effective temperatures
![]() of our grid. Only at the highest
of our grid. Only at the highest
![]() both series of models converge
on the U-B vs. B-V plane. Such systhematic differences are not present
in the B-V vs. V-I diagram and hence are not displayed here.
both series of models converge
on the U-B vs. B-V plane. Such systhematic differences are not present
in the B-V vs. V-I diagram and hence are not displayed here.
Furthermore, our synthetic NLTE colors of pure hydrogen white dwarfs are nearly identical to both our LTE colors of these stars (computed with other option to the TLUSTY195 code and still using ideal EOS) and the LTE colors obtained by Bergeron et al. (1995) in their intensive study on ages, luminosities, and other photometric parameters of DA white dwarfs.
The above-mentioned systhematic differences could be caused by the effects
of deviations from the ideal EOS for hydrogen gas, since they vanish at
the highest
![]() .
In order to verify such a hypothesis, we have
chosen several temperature T and gas pressure
.
In order to verify such a hypothesis, we have
chosen several temperature T and gas pressure ![]() points across our
sample pure H model atmosphere,
points across our
sample pure H model atmosphere,
![]() K and
K and
![]() ,
computed
with the nonideal EOS and TOPS opacity data, see Table 3.
,
computed
with the nonideal EOS and TOPS opacity data, see Table 3.
We compared two different densities corresponding to the same pair of T, ![]() :
density
:
density
![]() ,
obtained by direct interpolation of
the OPAL tables, and
,
obtained by direct interpolation of
the OPAL tables, and
![]() corresponding to an ideal H gas, obtained
from the relevant subroutines of the ATM21 code. One can see that
the difference between both densities reach 0.3% at the bottom of the
model, and it is much smaller in upper layers. Therefore we conclude
that the EOS of an ideal gas is well fulfilled in all our pure H atmospheres,
including also models of higher
corresponding to an ideal H gas, obtained
from the relevant subroutines of the ATM21 code. One can see that
the difference between both densities reach 0.3% at the bottom of the
model, and it is much smaller in upper layers. Therefore we conclude
that the EOS of an ideal gas is well fulfilled in all our pure H atmospheres,
including also models of higher
![]() ,
of course. This firmly suggests
that the impact of nonideal gas effects on the color discrepancies between
our H models and these obtained with TLUSTY195 is negligible.
,
of course. This firmly suggests
that the impact of nonideal gas effects on the color discrepancies between
our H models and these obtained with TLUSTY195 is negligible.
Such differences could be due to NLTE effects
considered by the code TLUSTY195, or other reasons. Earlier studies
on this subject have already predicted the nonideal EOS and NLTE effects in hydrogen atmospheres of white dwarfs. Wesemael et al. (1980)
in their extensive paper on WD model atmospheres and spectra have also
studied the influence of hydrogen line blanketing and NLTE effects on
both U-B and B-V color indices. They found, for a pure H model
atmosphere of
![]() K and
K and
![]() ,
that both
,
that both
![]() and
and
![]() line-blanketing corrections are of the order of 0.001 mag (at most).
line-blanketing corrections are of the order of 0.001 mag (at most).
Therefore NLTE corrections to UBV are negligible in the case of pure H
white dwarfs, for relatively hot objects of
![]() K. This
conclusion is also supported by our own computations, not
detailed in this paper.
K. This
conclusion is also supported by our own computations, not
detailed in this paper.
The influence of blanketing by Balmer and Lyman lines is much more
important. Wesemael et al. (1980) have determined that both
![]() and
and
![]() corrections, LTE minus NLTE, are equal to -0.017 mag and +0.043 mag, respectively, for a model of
corrections, LTE minus NLTE, are equal to -0.017 mag and +0.043 mag, respectively, for a model of
![]() K and
K and
![]() .
Both corrections should increase in their absolute value with decreasing
.
Both corrections should increase in their absolute value with decreasing
![]() (see p. 300 of that paper). The quantity of both corrections, when
extrapolated down to the
(see p. 300 of that paper). The quantity of both corrections, when
extrapolated down to the
![]() K, seems comparable with both differences
K, seems comparable with both differences
![]() and
and
![]() ,
cf. Fig. 1.
,
cf. Fig. 1.
Note that both series of pure H model atmospheres displayed in Fig. 1
take into account the blanketing by Balmer and Lyman lines. However, one can
expect that perhaps TOPS hydrogen opacity tables do not include the most
sophisticated theories of H line broadening, thus causing
![]() and
and
![]() errors seen in Fig. 1. The difference strongly decreases
in V-I color, since in both V and I filters there are only single
Balmer lines, and their broadening becomes unimportant for the wide-band
photometry.
errors seen in Fig. 1. The difference strongly decreases
in V-I color, since in both V and I filters there are only single
Balmer lines, and their broadening becomes unimportant for the wide-band
photometry.
At this point we turn the reader's attention to the paper by Hubeny et al. (1994), who discuss the theory of NLTE model atmospheres with line blanketing also near the series limit (the occupation probability formalism). The latter implies dissolving of merging lines, which is the effect of nonideal gas in a stellar atmosphere (see also Lanz & Hubeny, who applied the theory of dissolving levels in hydrogen dominated DA atmospheres with carbon or iron in trace abundances). Such a nonideal gas effect has been included also in our TLUSTY195 hydrogen atmosphere calculations, see Table 2 and Fig. 1.
A recent paper by Rohrmann et al. (2002) presents the theory and derivation of the nonideal EOS for H and He gas, including their molecules. Rohrmann et al. (2002) concentrate on the theory of He core white dwarfs, which are much colder than WDs discussed in this paper.
We have computed and present here extensive set of pure iron
model atmospheres and synthetic UBVRI broadband colors for models of
![]() K and
K and
![]() and 10 (cgs).
We have extended our
computations to an extremely large
and 10 (cgs).
We have extended our
computations to an extremely large ![]() .
In fact we are not aware of
the existence of any white dwarf star with
.
In fact we are not aware of
the existence of any white dwarf star with
![]() but assume that iron cores of a given mass M would have much
smaller radius R, and therefore
but assume that iron cores of a given mass M would have much
smaller radius R, and therefore ![]() ,
than common carbon-oxygen cores.
Pure H model atmospheres discussed in the previous section were
also extended to such a large surface gravity due to the same reason.
,
than common carbon-oxygen cores.
Pure H model atmospheres discussed in the previous section were
also extended to such a large surface gravity due to the same reason.
Pure Fe model atmospheres were computed using nonideal EOS by Rogers (2002)
and Los Alamos TOPS monochromatic opacities. Iron models were computed also
on the grid of 155 discrete standard optical depth points, starting from
the extremely high layer
![]() and with 901 discrete
frequencies. Computations were very difficult and sometimes unstable due to
complicated monochromatic opacities in the Los Alamos tables and due to
high gradients of opacities (with respect both to temperature and
gas density) at higher densities of this exotic chemical composition.
Moreover, a pure iron model of
and with 901 discrete
frequencies. Computations were very difficult and sometimes unstable due to
complicated monochromatic opacities in the Los Alamos tables and due to
high gradients of opacities (with respect both to temperature and
gas density) at higher densities of this exotic chemical composition.
Moreover, a pure iron model of
![]() K and
K and ![]() was not in
hydrostatic equilibrium, since the model exceeded the Eddington limit
in its deeper layers. In other words, the acceleration of gas, exerted by
the integrated
radiative flux and directed upwards, exceeded gravitational acceleration g in those layers.
was not in
hydrostatic equilibrium, since the model exceeded the Eddington limit
in its deeper layers. In other words, the acceleration of gas, exerted by
the integrated
radiative flux and directed upwards, exceeded gravitational acceleration g in those layers.
Physical properties of pure Fe white dwarf atmospheres do not differ
substantially from pure H atmospheres, at least for relatively high
effective temperatures
![]() K which were investigated in this
paper. Table 3 presents concisely values of a few most important
thermodynamical variables across the sample pure Fe model atmosphere
with
K which were investigated in this
paper. Table 3 presents concisely values of a few most important
thermodynamical variables across the sample pure Fe model atmosphere
with
![]() K and
K and
![]() ,
organized in the same way as it was
described in Sect. 3.1.
,
organized in the same way as it was
described in Sect. 3.1.
After each temperature iteration (and also after the final one), gas
pressures ![]() in the model are determined by integrating the equation
of hydrostatic equilibrium
in the model are determined by integrating the equation
of hydrostatic equilibrium
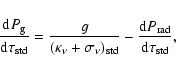 |
(4) |
Column No. 6 in Table 3 shows that TOPS opacities (for 1 gram of gas) are only ![]() 4 times higher for iron than for hydrogen.
This implies that the resulting gas pressures
4 times higher for iron than for hydrogen.
This implies that the resulting gas pressures ![]() on a fixed
on a fixed
![]() are a few times smaller in a pure Fe sample atmosphere than in a pure H
atmosphere of the same
are a few times smaller in a pure Fe sample atmosphere than in a pure H
atmosphere of the same
![]() K. Iron and hydrogen atmospheres do not
differ substantially in the physical variables T,
K. Iron and hydrogen atmospheres do not
differ substantially in the physical variables T, ![]() ,
and the density
,
and the density ![]() .
.
Unlike the pure H model, Cols. 4 and 5 of Table 3
show that the realistic nonideal Fe gas density
![]() (Rogers 2002)
differs
from the density
(Rogers 2002)
differs
from the density
![]() ,
computed by our ATM21 code according
to the ideal gas EOS. The difference of both densities reaches one order of
magnitude in that model, which clearly demonstrates that the ideal EOS of iron
would be of no use in WDs of
,
computed by our ATM21 code according
to the ideal gas EOS. The difference of both densities reaches one order of
magnitude in that model, which clearly demonstrates that the ideal EOS of iron
would be of no use in WDs of
![]() K.
We have checked that an iron gas of density
K.
We have checked that an iron gas of density
![]() (cgs) behaves
like an ideal gas in temperature T as high as 106 K or higher.
(cgs) behaves
like an ideal gas in temperature T as high as 106 K or higher.
Column 7 in Table 3 presents geometrical depths of various standard
optical depth levels
![]() ,
assuming that the zero (reference)
level of geometrical height is fixed at the upper boundary of the model
atmosphere. The depth of a fixed level
,
assuming that the zero (reference)
level of geometrical height is fixed at the upper boundary of the model
atmosphere. The depth of a fixed level
![]() is given by
is given by
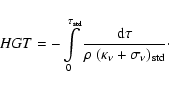 |
(5) |
![\begin{figure}
\par\resizebox{8.8cm}{!}{{\includegraphics[clip]{aa3245f2.eps}}}
\end{figure}](/articles/aa/full/2003/49/aa3245/Timg66.gif) |
Figure 2:
Pure iron and hydrogen LTE white dwarf synthetic spectra
of
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{{\includegraphics[clip]{aa3245f3.eps}}}
\end{figure}](/articles/aa/full/2003/49/aa3245/Timg67.gif) |
Figure 3:
The LTE theoretical spectra of iron and hydrogen
atmospheres of Fig. 1 are displayed here on narrower range of wavelengths, with higher
resolution, from near
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{{\includegraphics[clip]{aa3245f4.eps}}}
\end{figure}](/articles/aa/full/2003/49/aa3245/Timg69.gif) |
Figure 4:
Same as Fig. 2 for
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{{\includegraphics[clip]{aa3245f5.eps}}}
\end{figure}](/articles/aa/full/2003/49/aa3245/Timg71.gif) |
Figure 5:
Same as Fig. 2 for
|
| Open with DEXTER | |
Sample spectra of both pure iron and pure hydrogen model atmospheres are
plotted in Figs. 2-7. They are arranged in order of increasing effective
temperatures
![]() to demonstrate quantitatively the evolution of both Fe and H spectra with increasing
to demonstrate quantitatively the evolution of both Fe and H spectra with increasing
![]() in the wide spectral region where
most radiative energy is emitted. Effective temperatures
in the wide spectral region where
most radiative energy is emitted. Effective temperatures
![]() chosen
for this presentation range from 20 000 K up to 100 000 K and
chosen
for this presentation range from 20 000 K up to 100 000 K and
![]() or 9.0 in hotter models.
or 9.0 in hotter models.
Both series of model atmospheres were computed with the nonideal EOS from the OPAL Project to ensure consistency. One can see that the pure Fe spectrum is entirely different from the H spectrum, both in the visual (Fig. 3) and in far and extreme UV (Figs. 2 and 4-7). The Los Alamos TOPS monochromatic opacities suitable for a nonideal EOS allowed us to reproduce strongly broadened hydrogen Lyman and Balmer lines (Fig. 3). The appearance of the theoretical optical and near UV spectrum of the iron atmospheres is completely different and also exhibits strongly broadened iron features, but their identification is beyond the scope of this paper.
Figure 3 shows that the sample pure Fe atmosphere of
![]() K is
much brighter than a pure H atmosphere in the visual and also in
the far UV region beyond the Lyman edge
(wavelengths
K is
much brighter than a pure H atmosphere in the visual and also in
the far UV region beyond the Lyman edge
(wavelengths
![]() Å). In the near UV,
for
Å). In the near UV,
for
![]() Å, a pure Fe atmosphere is fainter that its
pure H (i.e. the DA type) counterpart. Figures 4-7 demonstrate that Fe atmospheres are very bright for
Å, a pure Fe atmosphere is fainter that its
pure H (i.e. the DA type) counterpart. Figures 4-7 demonstrate that Fe atmospheres are very bright for
![]() Å also in higher
Å also in higher
![]() .
Only in the extreme UV, for
.
Only in the extreme UV, for
![]() Å,
Fe atmospheres are extremely faint apparently due to increasing iron
monochromatic absorption.
Å,
Fe atmospheres are extremely faint apparently due to increasing iron
monochromatic absorption.
![\begin{figure}
\par\resizebox{8.8cm}{!}{{\includegraphics[clip]{aa3245f6.eps}}}
\par\end{figure}](/articles/aa/full/2003/49/aa3245/Timg76.gif) |
Figure 6:
Same as Fig. 2 for
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{{\includegraphics[clip]{aa3245f7.eps}}}
\end{figure}](/articles/aa/full/2003/49/aa3245/Timg77.gif) |
Figure 7:
Same as Fig. 2 for
|
| Open with DEXTER | |
The latter effect, i.e. an increase of iron absorption in EUV and X-rays,
is clearly seen in TOPS tables at any fixed temperature Tand gas density ![]() .
In general, iron gas is much more opaque than
hydrogen at any wavelength. This implies also that our pure Fe model
atmospheres are geometrically thinner, as compared with pure H atmospheres
of the same
.
In general, iron gas is much more opaque than
hydrogen at any wavelength. This implies also that our pure Fe model
atmospheres are geometrically thinner, as compared with pure H atmospheres
of the same
![]() and
and ![]() ,
see also Table 3.
,
see also Table 3.
Theoretical broadband UBVRI colors of our pure iron models are
displayed in Table 3. Comparison of Tables 1 and 3 shows that U-B
and B-V colors of iron models are significantly lower than the same
color indices of hydrogen model atmospheres. Therefore, a pure iron
atmosphere of a given
![]() and
and ![]() appears as if it was much
hotter than a pure H atmosphere with the same parameters
(an iron WD appears more blue to an observer).
appears as if it was much
hotter than a pure H atmosphere with the same parameters
(an iron WD appears more blue to an observer).
Table 1:
Broadband colors in stellar magnitudes for pure hydrogen
atmospheres. Models are computed with nonideal EOS and Los Alamos
(TOPS) opacities. Temperatures
![]() are given in thousands K and
are given in thousands K and ![]() are in cgs units.
are in cgs units.
Table 2: Broadband colors in stellar magnitudes for pure hydrogen NLTE atmospheres (results of TLUSTY195). Units are the same as in Table 1.
We have also computed model atmospheres of a more complex structure,
in which pure iron gas is covered by a pure hydrogen layer of arbitrary
thickness. Table 4 presents color indices of such stratified atmospheres,
in which we have arbitrarily assumed that the transition depth between
hydrogen and iron layers is located at the standard optical depth
![]() .
This assumption precisely determines the column mass
of a hydrogen layer in each model atmosphere
.
This assumption precisely determines the column mass
of a hydrogen layer in each model atmosphere
It would be very interesting to convert H column masses to the total
mass of a hydrogen envelope covering the iron core of a white dwarf. Such
a rescaling requires the knowledge of the radius R, whereas our models
are parametrized by the gravity,
![]() .
We have arbitrarily assumed
the mass of a white dwarf to be
.
We have arbitrarily assumed
the mass of a white dwarf to be ![]() ,
and used M-R relations for
iron core
white dwarfs (Panei et al. 2000; Althaus 2003).
Respectively, the total mass of a hydrogen envelope in the two above sample
models is less than
,
and used M-R relations for
iron core
white dwarfs (Panei et al. 2000; Althaus 2003).
Respectively, the total mass of a hydrogen envelope in the two above sample
models is less than
![]() for
for
![]() K and
K and
![]() ,
and is approximately equal to
,
and is approximately equal to
![]() for the hottest model of
for the hottest model of
![]() K and
K and
![]() .
.
One can note that the estimated masses of a hydrogen layer are rather
small, as compared with H masses arbitrarily assumed in published grids
of theoretical M-R relations (
M = 10-16 up to
![]() .
This is because H-Fe stratified models in the present paper require
a H layer of the moderate optical depth
.
This is because H-Fe stratified models in the present paper require
a H layer of the moderate optical depth
![]() in frequencies
corresponding to the UBVRI filters, which do not cover completely the
iron core.
in frequencies
corresponding to the UBVRI filters, which do not cover completely the
iron core.
Table 3:
Model atmospheres of
![]() K, and
K, and
![]() (cgs units),
with pure hydrogen or pure iron composition.
(cgs units),
with pure hydrogen or pure iron composition.
Figures 8 and 10 show positions of various model atmospheres on the theoretical B-V vs. U-B diagram, whereas Figs. 9 and 11 display colors of the
models on the B-V vs. V-I diagram. The figures present colors of
both pure and stratified atmospheres.
For these models, we obtained U-B, B-V and V-I colors which depend on
changes of
![]() and
and ![]() in a rather complex way (cf. Tables 3-4).
One can clearly see that the colors of iron-containing
models may overlap, causing them to be a non-unique function
of the set of parameters
in a rather complex way (cf. Tables 3-4).
One can clearly see that the colors of iron-containing
models may overlap, causing them to be a non-unique function
of the set of parameters
![]() ,
,
![]() .
Pure hydrogen models are also
subject to this (at least on the B-V vs. V-I diagram),
but the complexity for the iron models is much higher. This complicated
dependence
of the colors is due to a noisy structure of the TOPS grids of iron monochromatic opacities.
Consequently, all these figures present shaded areas, where atmospheres
containing pure iron are located. We do not highlight lines of constant
.
Pure hydrogen models are also
subject to this (at least on the B-V vs. V-I diagram),
but the complexity for the iron models is much higher. This complicated
dependence
of the colors is due to a noisy structure of the TOPS grids of iron monochromatic opacities.
Consequently, all these figures present shaded areas, where atmospheres
containing pure iron are located. We do not highlight lines of constant
![]() or
or ![]() for those models. One can see that the region occupied
by pure iron model atmospheres significantly differs from the region
corresponding to pure hydrogen models in all the analysed cases.
for those models. One can see that the region occupied
by pure iron model atmospheres significantly differs from the region
corresponding to pure hydrogen models in all the analysed cases.
The latter observation shows that it would be possible to distinguish pure
iron WD atmospheres from pure hydrogen DA atmospheres with
![]() K by means of broadband Johnson UBV photometry, at least in principle.
Our analysis and figures include neither the possible admixture of
helium or other heavier elements in DA white dwarf atmospheres, nor
the influence of their opacities on spectra and theoretical colors of mostly
hydrogen white dwarf atmospheres. Admixture of heavier elements in hot
WD atmospheres seems very common in real stars. For example, Barstow et al.
(1993) showed that most of the hot DA white dwarfs with effective temperatures
K by means of broadband Johnson UBV photometry, at least in principle.
Our analysis and figures include neither the possible admixture of
helium or other heavier elements in DA white dwarf atmospheres, nor
the influence of their opacities on spectra and theoretical colors of mostly
hydrogen white dwarf atmospheres. Admixture of heavier elements in hot
WD atmospheres seems very common in real stars. For example, Barstow et al.
(1993) showed that most of the hot DA white dwarfs with effective temperatures
![]() K have some abundance of elements heavier than He in their
atmospheres. This can explain their generally low X-ray luminosity, as
it is found in the ROSAT all-sky catalog of white dwarfs.
K have some abundance of elements heavier than He in their
atmospheres. This can explain their generally low X-ray luminosity, as
it is found in the ROSAT all-sky catalog of white dwarfs.
There exist many U-B and B-V color measurements available for isolated white dwarfs, which were published in the catalogue by McCook & Sion (1999). Therefore we have plotted colors for individual white dwarfs in both Figs. 8 and 10 as asterisks, in order to search for possible white dwarfs with pure or stratified Fe atmospheres. Unfortunately, one can note that the observed stars generally do not fall into shaded areas of each figure, but rather avoid them. Most of the observed U-B and B-V colors mostly overlap the area of pure hydrogen atmospheres.
The above observation proves that the set of white dwarfs with color indices predicted for iron atmospheres is almost empty, except for a few cases of marginal significance.
Figures 9 and 11 do not include observed colors of real WDs. Measurements of near infrared luminosity I (and therefore V-I color) are extremely rare for hotter isolated white dwarfs. Also the newest catalogs of B-V and V-I of hot objects, which are known to us (Renzini 2001; Zoccali et al. 2001) do not distinguish hydrogen DA and other types of white dwarfs. Existing surveys of V-I colors of white dwarfs concentrate on the search for infrared excess presumably in binary stars, and are not useful in this research.
Table 4:
Broadband colors in stellar magnitudes for pure iron atmospheres.
Models are computed with nonideal EOS and Los Alamos (TOPS) opacities.
Units of
![]() and
and ![]() are the same as in Table 1.
are the same as in Table 1.
![\begin{figure}
\par\includegraphics[clip]{aa3245f8.eps} \end{figure}](/articles/aa/full/2003/49/aa3245/Timg91.gif) |
Figure 8:
Plot of U-B vs. B-V for hot white dwarf stars.
The shaded area denotes the region occupied by colors
of pure iron
model atmospheres computed in this paper. Numbers put in
this area denote effective temperatures
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[clip]{aa3245f9.eps}
\end{figure}](/articles/aa/full/2003/49/aa3245/Timg92.gif) |
Figure 9: Plot of B-V vs. V-I for hot white dwarf stars. Also here, shaded area and the adjacent numbers correspond to the colors of pure Fe model atmospheres. The transparent grid of sections corresponds to pure H models (nonideal EOS). Unfortunately, there are no observed color indices available. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[clip]{aa3245f10.eps}
\end{figure}](/articles/aa/full/2003/49/aa3245/Timg93.gif) |
Figure 10:
Plot of U-B vs. B-V for hot stratified Fe/H model
atmospheres. In these models, pure Fe atmosphere is
covered by a pure H layer, reaching from the standard
optical depth
|
| Open with DEXTER | |
Based on the first quoted paper we have selected 7 white dwarfs, for which the best determined masses and radii place them closest to the theoretical mass-radius relation for iron core white dwarf stars (cf. Fig. 3 in Provencal et al. 1998). Neglecting possible errors of M and R determinations we suggest that these stars are promising candidates for a comparison with our theoretical UBVRI color indices (see Table 5). Some of these stars were also indicated by Panei et al. (2000), who placed them on their theoretical mass-radius relation for iron core white dwarfs.
Unfortunately, the stars listed in our Table 6 are rather cold. The hottest of
them, EG 50 (
![]() K) and GD 140 (
K) and GD 140 (
![]() K), are located
practically at the border of the grid presented in this paper.
Color indices and the positions of both stars in our two-color diagrams
places them far from the region occupied by pure iron atmospheres.
Moreover, they are located in the region occupied by
pure hydrogen atmospheres. Therefore we conclude that even if those
stars have iron cores, they are covered by a thick hydrogen layer of a
large optical depth. This conclusion is supported by the fact that
McCook & Sion (1999) classified all the stars from Table 5 as pure hydrogen DA white dwarfs.
K), are located
practically at the border of the grid presented in this paper.
Color indices and the positions of both stars in our two-color diagrams
places them far from the region occupied by pure iron atmospheres.
Moreover, they are located in the region occupied by
pure hydrogen atmospheres. Therefore we conclude that even if those
stars have iron cores, they are covered by a thick hydrogen layer of a
large optical depth. This conclusion is supported by the fact that
McCook & Sion (1999) classified all the stars from Table 5 as pure hydrogen DA white dwarfs.
In order to search for candidate iron core stars we have performed a search of papers listing mass and surface gravity determinations of white dwarfs carried out in recent surveys (Vennes et al. 1997; Finley et al. 1997; Homeier et al. 1998; Napiwotzki et al. 1999; Vennes 1999; Bergeron et al. 2001).
The above papers discuss mostly DA white dwarfs,
i.e. those with hydrogen-rich atmospheres and therefore strong Balmer
lines (cf. Figs. 2-3). Grids of theoretical UBVRI colors of Fe-abundant
atmospheres given in Tables 3-4 are not useful here. Therefore we attempted
to identify stars of exceptionally high ![]() (and hence a small
radius) in those papers.
Unfortunately, several trial figures displaying M vs.
(and hence a small
radius) in those papers.
Unfortunately, several trial figures displaying M vs. ![]() relations have shown that there are no stars that
exhibit large
relations have shown that there are no stars that
exhibit large ![]() for a given mass compared to the general trend.
for a given mass compared to the general trend.
As an example, we plot two such relations in Fig. 12, based on the data from Finley et al. (1997) and Homeier et al. (1998). The former paper presents a table with mass and surface gravity determinations for 90 hot DA white dwarfs from the Extreme Ultraviolet Explorer (EUVE) all-sky survey.
Table 5:
Broadband colors in stellar magnitudes for stratified
hydrogen/iron models with nonideal EOS and Los Alamos (TOPS) opacities.
Units of
![]() and
and ![]() are the same as in Table 1.
Transition depth is located at
are the same as in Table 1.
Transition depth is located at
![]() .
.
Table 6: List of iron core candidate stars selected from the data by Provencal et al. (1998). Procyon B has been excluded already from their data.
![\begin{figure}
\par\includegraphics[clip]{aa3245f11.eps}
\end{figure}](/articles/aa/full/2003/49/aa3245/Timg97.gif) |
Figure 11: Plot of B-V vs. V-I for Fe/H stratified atmospheres. Again, no observations of real white dwarfs are available here. |
| Open with DEXTER | |
The surface gravity ![]() and
and
![]() are usually determined by fitting of
the observed Balmer line profiles and therefore this method makes direct
the observable quantities. One should note, however, that in
all the above papers, masses of DA white dwarfs were obtained using the
theoretical mass-radius relations for carbon-core stars with a hydrogen or
helium envelope (see Wood 1995). We are aware that if masses were
determined with the most recent mass-radius relations for iron-core WDs by
Panei et al. (2000), then the above figure would change significantly.
are usually determined by fitting of
the observed Balmer line profiles and therefore this method makes direct
the observable quantities. One should note, however, that in
all the above papers, masses of DA white dwarfs were obtained using the
theoretical mass-radius relations for carbon-core stars with a hydrogen or
helium envelope (see Wood 1995). We are aware that if masses were
determined with the most recent mass-radius relations for iron-core WDs by
Panei et al. (2000), then the above figure would change significantly.
The most important areas of concern of our paper can be summarized as follows.
1. We have computed and presented here LTE model atmosphere computations of hot white dwarfs, whose atmospheres consist either of pure iron, stratified iron/hydrogen layers, or pure hydrogen. Model atmospheres are in both radiative and hydrostatic equilibrium. Computations use exclusively the equation of state for nonideal Fe and H gases, obtained by the OPAL project, and the extensive tables of the TOPS monochromatic opacities from the Los Alamos National Laboratory. The latter opacities are fully compatible with the nonideal EOS for both gases.
2. This paper presents calibration of colors in U-B, B-V, V-R and V-Iof the broadband Johnson UBVRI photometry, for pure Fe, pure H and stratified Fe/H atmospheres. These colors were computed from theoretical spectra of our model atmospheres with a nonideal EOS.
3. The paper investigates the influence of a nonideal equation of state on the photometric UBVRI colors of the broadband Johnson system, both in pure H and pure Fe model atmospheres. We showed that effects of a nonideal EOS for pure iron model atmospheres are substantial in the investigated models, contrary to pure H WD atmospheres.
4. We have also computed UBVRI colors of the models and determined the area on the B-V vs. U-B and B-V vs. V-I planes, occupied by both pure Fe and pure H model atmospheres of WD stars.
The importance of our paper is that we have determined the area on
two-color diagrams in which colors of the hypothetical pure iron
or stratified H/Fe atmospheres should be located. Colors of the above
hypothetical atmospheres are distinctly different from colors of pure
hydrogen DA WDs with
![]() K. We are aware, however, that
our paper does not predict colors of iron core WDs in the case, where the
core is covered by a hydrogen layer of significant optical thickness.
K. We are aware, however, that
our paper does not predict colors of iron core WDs in the case, where the
core is covered by a hydrogen layer of significant optical thickness.
![\begin{figure}
\par\resizebox{8.8cm}{!}{{\includegraphics[clip]{aa3245f12.eps}}}
\end{figure}](/articles/aa/full/2003/49/aa3245/Timg98.gif) |
Figure 12:
Catalog of
|
| Open with DEXTER | |
Acknowledgements
We thank I. Hubeny for his permission to use the TLUSTY195 code and related discussions. We appreciate also comments by P. Bergeron and A. Renzini regarding photometric properties of DA white dwarfs. Our thanks are also due to L.G. Althaus for providing us with his theoretical M - R relations for various white dwarfs. This work has been supported by the Polish Committee for Scientific Research grant No. 2 P03D 021 22.