A&A 412, 903-904 (2003)
DOI: 10.1051/0004-6361:20034401
Research Note
On Maximum Likelihood Estimation of averaged power spectra
T. Appourchaux
European Space Agency, Research and Science Support
Department, Science Payload and Advanced
Concept Office, PO Box 299, 2200Ag Noordwijk, The Netherlands
Received 25 September 2003 / Accepted 7 October 2003
Abstract
It is custom in helioseismology to assume that the power
spectra of time series of solar radial velocity or of solar
intensity have a 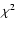 with 2 degrees of freedom statistics.
This assumption is regularly used in helioseismology for using
Maximum Likelihood Estimators for single power spectra
with that assumed statistics. When
independent power spectra are added, it is also custom to assume
that the resulting power spectra can be approximated by a Gaussian
distribution. Here we show that this approximation is irrelevant,
and that the software code developed for fitting single power spectra
can be used without any approximation after proper normalization
of the added power spectra.
with 2 degrees of freedom statistics.
This assumption is regularly used in helioseismology for using
Maximum Likelihood Estimators for single power spectra
with that assumed statistics. When
independent power spectra are added, it is also custom to assume
that the resulting power spectra can be approximated by a Gaussian
distribution. Here we show that this approximation is irrelevant,
and that the software code developed for fitting single power spectra
can be used without any approximation after proper normalization
of the added power spectra.
Key words: methods: data analysis - methods: statistical - methods: analytical - Sun:
helioseismology
In helioseismology, the statistics of time series of various
observables is assumed to be a 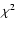 with 2 degrees of
freedom (d.o.f.). This assumption leads to the fitting of a power
spectrum using
Maximum Likelihood Estimators (MLE) with the aforementioned statistics (Appourchaux et al. 1998; Anderson et al. 1990; Duvall & Harvey 1986).
When dealing with long duration time series, it is sometimes custom
to split the observations into many independent data sets. It is
thought to be somewhat convenient to average the power spectra of the
independent time series in order to have better statistics.
Provided that the number n of independent time series is large
(say n>2), the statistics of the resulting power spectra is often
approximated to be close to Gaussian statistics as in Jiménez et al. (1994).
This approximation is not needed, and we show
hereafter that the software code used for ML estimation of a power spectrum having a
with 2 degrees of
freedom (d.o.f.). This assumption leads to the fitting of a power
spectrum using
Maximum Likelihood Estimators (MLE) with the aforementioned statistics (Appourchaux et al. 1998; Anderson et al. 1990; Duvall & Harvey 1986).
When dealing with long duration time series, it is sometimes custom
to split the observations into many independent data sets. It is
thought to be somewhat convenient to average the power spectra of the
independent time series in order to have better statistics.
Provided that the number n of independent time series is large
(say n>2), the statistics of the resulting power spectra is often
approximated to be close to Gaussian statistics as in Jiménez et al. (1994).
This approximation is not needed, and we show
hereafter that the software code used for ML estimation of a power spectrum having a 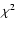 with 2 d.o.f. can be
used for a power spectrum having a
with 2 d.o.f. can be
used for a power spectrum having a 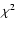 with n d.o.f., where
n>2.
with n d.o.f., where
n>2.
Let xi (i=1, ..., n) be independent and identically distributed
random variables with mean zero and unit variance following a Gaussian
distribution. Then according to
Abramowitz & Stegun (1970), the probability density for the sum of the
square (
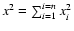 ), a normalized random variable, is written as:
), a normalized random variable, is written as:
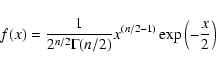 |
(1) |
where n is the d.o.f., and 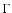 is the Gamma function. From this general
formulation we can extract the probability density for u being the
sum of the square of non-normalized random variables having a Gaussian
distribution. This is done using a change of variable:
is the Gamma function. From this general
formulation we can extract the probability density for u being the
sum of the square of non-normalized random variables having a Gaussian
distribution. This is done using a change of variable:
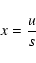 |
(2) |
where s is the rms value of the individual random variable making
the distribution. The probability density
is then written as
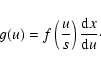 |
(3) |
Then we obtain the following probability density for u:
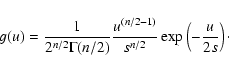 |
(4) |
Since we deal not with individual Fourier components
distributed as 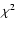 with one d.o.f. but with a power spectrum, here we change parameter. We write:
with one d.o.f. but with a power spectrum, here we change parameter. We write:
where S is the mean of the power spectrum that we usually utilize in the
model of the 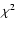 with 2 d.o.f. statistics. With this minor
change we now have:
with 2 d.o.f. statistics. With this minor
change we now have:
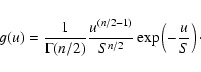 |
(6) |
Finally, we change variable. What we observe is
really u, i.e. the random variable associated with the sum of the power spectra (there are p=n/2 summed
power spectra). By doing a simple normalization, we can greatly
simplify the statistics:
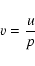 |
(7) |
where v is the random variable associated with the observed spectrum
u divided by the number of summed spectra p; when p=1, we get back the original
power spectrum as only one spectrum is used. Then the probability density is written as:
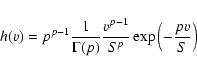 |
(8) |
the associated pseudo log likelihood can be written as:
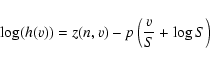 |
(9) |
where z(n,v) is a function of v and n. When the minimization of
the log likelihood l is performed on the data, we have:
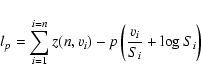 |
(10) |
where vi and Si are respectively the data and the model at
the ith bin; all bins are assumed independent. It is now clear that minimization of the likelihood for
the mean of the sum of p power spectra is the same as minimizing the
following function:
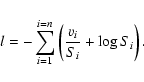 |
(11) |
The terms in parentheses is the usual expression for a 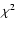 with
2 d.o.f. When p=1, this is exactly what we minimize. The curvature
of the minimized function providing the error bars is increased by
p; this should be taken into account when computing the
error bars (divide by
with
2 d.o.f. When p=1, this is exactly what we minimize. The curvature
of the minimized function providing the error bars is increased by
p; this should be taken into account when computing the
error bars (divide by 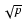 as it can be derived from
Appourchaux et al. 1998).
as it can be derived from
Appourchaux et al. 1998).
Here we give a practical procedure for fitting the sum of p spectra
using the regular MLE code used for spectra with a 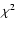 with 2 d.o.f.:
with 2 d.o.f.:
- compute the sum of the p power spectra;
- divide the sum by p;
- fit the model to the mean spectrum using the
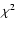 with 2 d.o.f. statistics;
with 2 d.o.f. statistics;
- normalize error bars provided by the routines by dividing them by
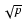 .
.
There is no approximation performed here. The procedure only applies to independent power
spectra having independent frequency bins.
This technique has been implemented by Jiménez et al. (2002) at the request
of the author. It has been proven to be effective and should be used in
helioseismology (or other fields) whenever deemed necessary.
Acknowledgements
Thanks to Frederic Baudin for suggesting the writing of this
Research Note, and to Antonio Jiménez for triggering the
scientific mind of a referee.
-
Abramowitz, M., & Stegun, I. A. 1970, Handbook of mathematical functions,
9th edition (New York: Dover Publication, Inc.)
In the text
-
Anderson, E. R., Duvall, T. L. J., & Jefferies, S. M. 1990, ApJ, 364, 699
In the text
NASA ADS
-
Appourchaux, T., Gizon, L., & Rabello-Soares, M. C. 1998, A&AS, 132, 107
In the text
NASA ADS
-
Duvall, T. L. J., & Harvey, J. W. 1986, in Seismology of the Sun and the
Distant Stars, 105
In the text
-
Jiménez, A., Perez Hernandez, F., Claret, A., et al. 1994, ApJ, 435, 874
In the text
NASA ADS
-
Jiménez, A., Roca Cortés, T., & Jiménez-Reyes, S. J. 2002,
Sol. Phys., 209, 247
In the text
NASA ADS
Copyright ESO 2003
![]() with 2 degrees of freedom statistics.
This assumption is regularly used in helioseismology for using
Maximum Likelihood Estimators for single power spectra
with that assumed statistics. When
independent power spectra are added, it is also custom to assume
that the resulting power spectra can be approximated by a Gaussian
distribution. Here we show that this approximation is irrelevant,
and that the software code developed for fitting single power spectra
can be used without any approximation after proper normalization
of the added power spectra.
with 2 degrees of freedom statistics.
This assumption is regularly used in helioseismology for using
Maximum Likelihood Estimators for single power spectra
with that assumed statistics. When
independent power spectra are added, it is also custom to assume
that the resulting power spectra can be approximated by a Gaussian
distribution. Here we show that this approximation is irrelevant,
and that the software code developed for fitting single power spectra
can be used without any approximation after proper normalization
of the added power spectra.
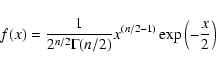
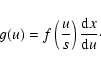
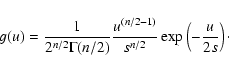
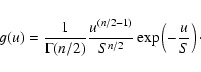
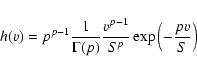
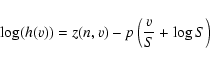
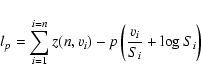
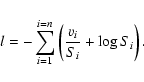
![]() with
2 d.o.f. When p=1, this is exactly what we minimize. The curvature
of the minimized function providing the error bars is increased by
p; this should be taken into account when computing the
error bars (divide by
with
2 d.o.f. When p=1, this is exactly what we minimize. The curvature
of the minimized function providing the error bars is increased by
p; this should be taken into account when computing the
error bars (divide by ![]() as it can be derived from
Appourchaux et al. 1998).
as it can be derived from
Appourchaux et al. 1998).
![]() with 2 d.o.f.:
with 2 d.o.f.: