A&A 412, 349-371 (2003)
DOI: 10.1051/0004-6361:20031427
J. Patris 1,2,![]() - M. Dennefeld 1,2,
- M. Dennefeld 1,2,![]() - G. Lagache 3 - H. Dole 4
- G. Lagache 3 - H. Dole 4
1 - Institut d'Astrophysique de Paris (IAP), 98 bis Bd. Arago,
75014 Paris, France
2 -
Université Pierre et Marie Curie (Paris VI), 4 place
Jussieu 75005 Paris, France
3 -
Institut d'Astrophysique Spatiale, Bât. 121, Université
Paris XI, 91405 Orsay Cedex, France
4 -
Steward Observatory, University of Arizona, 933 N Cherry
Ave Tucson AZ 85721, USA
Received 23 September 2002 / Accepted 2 September 2003
Abstract
We have performed optical spectroscopy of the brightest 170 ![]() m
sources
in the FIRBACK South Marano (FSM) field.
The spectroscopic sample is
m
sources
in the FIRBACK South Marano (FSM) field.
The spectroscopic sample is ![]() complete at the 4
complete at the 4![]() level.
Analysis of spectra and comparison with spectra of a faint
IRAS (60
level.
Analysis of spectra and comparison with spectra of a faint
IRAS (60 ![]() m selected) reference sample is conducted simultaneously.
The sources in both samples are characterized by a predominance of
emission-line spectra and moderate IR luminosities (
m selected) reference sample is conducted simultaneously.
The sources in both samples are characterized by a predominance of
emission-line spectra and moderate IR luminosities (
![]() )
The fraction of AGN's is low (about
)
The fraction of AGN's is low (about ![]() )
and the majority of sources
are nearby (z<0.3), dusty, star forming
galaxies, with moderate star formation rates (a few 10
)
and the majority of sources
are nearby (z<0.3), dusty, star forming
galaxies, with moderate star formation rates (a few 10 ![]() per year). The infrared emission of the FSM galaxies shows a colder
spectral energy distribution than was expected.
The galaxies in both samples (IRAS faint sources and FSM) are essentially
undistinguishable with the available data, and
seem to represent a population of closeby, cold, star forming
galaxies rather neglected up to now. Although their contribution to
the far-IR background seems to be low, they deserve a more detailed
study on their own to assess their importance in the chemical
evolution of the local universe. The contribution of fainter,
presumably more distant, galaxies to the far-IR background will be
discussed when we will have completed the follow-up of the fainter part of
this 170
per year). The infrared emission of the FSM galaxies shows a colder
spectral energy distribution than was expected.
The galaxies in both samples (IRAS faint sources and FSM) are essentially
undistinguishable with the available data, and
seem to represent a population of closeby, cold, star forming
galaxies rather neglected up to now. Although their contribution to
the far-IR background seems to be low, they deserve a more detailed
study on their own to assess their importance in the chemical
evolution of the local universe. The contribution of fainter,
presumably more distant, galaxies to the far-IR background will be
discussed when we will have completed the follow-up of the fainter part of
this 170 ![]() m survey.
m survey.
Key words: galaxies: infrared - galaxies: evolution - cosmology: observations
FIRBACK (Far InfraRed BACKground) is a ![]() m survey carried out by
ISO and designed to study the nature of the CIB (Cosmic Infrared
Background). It comprises a northern field (FIRBACK N1 and N2; thereafter FN1 and FN2)
and a southern one (the FIRBACK Marano field, FSM). Dole et al. (2001) have
presented the
global results of the survey and concluded that a fraction of the CIB can be
resolved into individual sources
brighter than 135 mJy (the 3
m survey carried out by
ISO and designed to study the nature of the CIB (Cosmic Infrared
Background). It comprises a northern field (FIRBACK N1 and N2; thereafter FN1 and FN2)
and a southern one (the FIRBACK Marano field, FSM). Dole et al. (2001) have
presented the
global results of the survey and concluded that a fraction of the CIB can be
resolved into individual sources
brighter than 135 mJy (the 3 ![]() limit of the survey).
A preliminary analysis by Puget et al. (1999) proposes that
these sources are a mix of preferentially
distant galaxies (at typical
redshifts of 1 to 2), whose detection is favoured in the far-IR by the
negative K-correction, and which would best reproduce the evolution of the
number counts (far in excess over those expected from the local FIR population
discovered by IRAS), and of a nearby population of very cold galaxies.
This lead naturally to attempts to observe these sources in the sub-mm range,
and several
of them have been detected with SCUBA in the FN1 field (Scott et al. 2000;
Sajina et al. 2003).
But until recently, only two redshifts were available, in the FN1 field, two
optically faint sources (I=24 & 22)
observed with the Keck telescope, giving z=0.5 and 0.9, respectively
(Chapman et al. 2002).
These two sources are identified as ULIRG class galaxies, with merger morphologies
and relatively cold dust temperatures.
Pending more redshifts, Sajina et al. (2003) used their sub-mm data and
spectral energy distributions (SED's) to show,
but on a statistical basis only, that FN1 sources appear
to show a bimodal galaxy distribution, with normal star-forming galaxies
at z
limit of the survey).
A preliminary analysis by Puget et al. (1999) proposes that
these sources are a mix of preferentially
distant galaxies (at typical
redshifts of 1 to 2), whose detection is favoured in the far-IR by the
negative K-correction, and which would best reproduce the evolution of the
number counts (far in excess over those expected from the local FIR population
discovered by IRAS), and of a nearby population of very cold galaxies.
This lead naturally to attempts to observe these sources in the sub-mm range,
and several
of them have been detected with SCUBA in the FN1 field (Scott et al. 2000;
Sajina et al. 2003).
But until recently, only two redshifts were available, in the FN1 field, two
optically faint sources (I=24 & 22)
observed with the Keck telescope, giving z=0.5 and 0.9, respectively
(Chapman et al. 2002).
These two sources are identified as ULIRG class galaxies, with merger morphologies
and relatively cold dust temperatures.
Pending more redshifts, Sajina et al. (2003) used their sub-mm data and
spectral energy distributions (SED's) to show,
but on a statistical basis only, that FN1 sources appear
to show a bimodal galaxy distribution, with normal star-forming galaxies
at z ![]() 0
and a
0
and a ![]() 0.4-0.9 population of much more luminous objects.
The existence of local, cold galaxies is known from the ISOPHOT serendipity survey
(Stickel et al. 2000) which detected a cold (
0.4-0.9 population of much more luminous objects.
The existence of local, cold galaxies is known from the ISOPHOT serendipity survey
(Stickel et al. 2000) which detected a cold (![]() 20 K) dust component in many galaxies,
but their
sample is not complete in any sense and cannot be used for a statistical analysis.
The FIRBACK sample is therefore the best sample to study the respective importance
of these two populations and its systematic optical follow-up
remains to be done.
20 K) dust component in many galaxies,
but their
sample is not complete in any sense and cannot be used for a statistical analysis.
The FIRBACK sample is therefore the best sample to study the respective importance
of these two populations and its systematic optical follow-up
remains to be done.
The aim of this paper is to present a first appraisal of the optical counterparts of the FIRBACK population (more specifically the brighter sources in the southern FSM field) and to derive their nature and distance by spectroscopy. Spectra in the optical range can provide, in addition to redshifts, an analysis of the ionizing source, and an estimate of the extinction. In order to compare the FIRBACK objects with well-studied populations of IR-selected galaxies, we observed also, with the same ESO facilities, a series of IRAS very faint sources selected from the sample of Bertin et al. (1997). The IRAS "Bright Galaxy Sample'' of Soifer et al. (1987), observed in the optical by Kim et al. (1995) and analyzed by Veilleux et al. (1995), will also be used as a reference on bright IR galaxies.
After analyzing all information that can be extracted from the spectra, and comparing these objects with other populations, we come to the conclusion that the Marano brightest objects are part of a very important population of star forming, dusty, closeby galaxies, that has been essentially neglected up to now. The question is still open for the fainter sources of the FSM survey, which are under study with the ESO VLT.
The paper is organized as follow: the next three sections describe the various data sets and how they were reduced, while Sect. 5 presents and discusses the results. The nature of FIRBACK bright galaxies is summarized in Sect. 6 and the conclusions are presented in the last section.
The FIRBACK survey consists of three separate
high galactic latitude
regions which have been observed at 170 ![]() m using
the ISOPHOT instrument (Lemke et al. 1996) on board ISO (Kessler et al. 1996).
Two of these areas are in the northern sky
(FN1 and FN2), while the one we are interested in
throughout this paper is the southern area, the FIRBACK South Marano or FSM
field (Dole et al. 2001).
m using
the ISOPHOT instrument (Lemke et al. 1996) on board ISO (Kessler et al. 1996).
Two of these areas are in the northern sky
(FN1 and FN2), while the one we are interested in
throughout this paper is the southern area, the FIRBACK South Marano or FSM
field (Dole et al. 2001).
The FSM region is itself composed of four individual fields,
summing up about 22 sources detected at 4 ![]() and 13 more at a 3
and 13 more at a 3 ![]() detection level (Dole et al. 2001), for a total area of 0.95 square degree.
detection level (Dole et al. 2001), for a total area of 0.95 square degree.
From this source list, we selected the
21 brightest objects (FSM_000 to FSM_020) for spectroscopic
follow-up, in order to be complete down
to the 4 ![]() flux limit (200 mJy at 170
flux limit (200 mJy at 170 ![]() m) in a first phase.
Three more objects at lower IR fluxes (FSM_026,
FSM_035, FSM_039) have been
observed also during this run, as a first exploration
of the possible nature of fainter sources.
m) in a first phase.
Three more objects at lower IR fluxes (FSM_026,
FSM_035, FSM_039) have been
observed also during this run, as a first exploration
of the possible nature of fainter sources.
The coordinates and IR fluxes of those objects are presented in
Table 1. The 170 ![]() m fluxes are from the FSM catalog (Dole et al. 2001) while the IRAS fluxes have been obtained from the
SCANPI
m fluxes are from the FSM catalog (Dole et al. 2001) while the IRAS fluxes have been obtained from the
SCANPI![]() procedure.
procedure.
Table 1: List of observed FIRBACK South Marano infrared sources.
In addition to the FSM objects, another set of IR selected
galaxies was analyzed for comparison. These are objects extracted from
the IRAS Very Faint Source catalog, in the fields studied
by Bertin et al. (1997) and selected
for their very low 60 ![]() m fluxes (in fact the faintest IRAS detections outside the north
ecliptic pole). The
sample observed is not complete in any sense, but contains a random
selection essentially in the
110 mJy
m fluxes (in fact the faintest IRAS detections outside the north
ecliptic pole). The
sample observed is not complete in any sense, but contains a random
selection essentially in the
110 mJy
![]() m)
m) ![]() 200 mJy
flux range (only a few have stronger fluxes). No particular selection has
been made, contrary to other samples where only
ULIRG objects where searched for.
The technique used to identify those sources is similar to the
one used for the FSM sources (see Sect. 3) and the spectroscopic
follow-up has been done with the same telescope and similar instruments
as for the FSM sources.
The absolute flux accuracy of the reduced optical
spectra in this sample is at the 10% level.
The follow-up
of this reference sample is not complete yet and the final results will be
published later (Dennefeld et al., in prep).
Due to their faintness, and to the relative sensitivity
of the various IRAS channels, in most cases the 100
200 mJy
flux range (only a few have stronger fluxes). No particular selection has
been made, contrary to other samples where only
ULIRG objects where searched for.
The technique used to identify those sources is similar to the
one used for the FSM sources (see Sect. 3) and the spectroscopic
follow-up has been done with the same telescope and similar instruments
as for the FSM sources.
The absolute flux accuracy of the reduced optical
spectra in this sample is at the 10% level.
The follow-up
of this reference sample is not complete yet and the final results will be
published later (Dennefeld et al., in prep).
Due to their faintness, and to the relative sensitivity
of the various IRAS channels, in most cases the 100 ![]() m fluxes are not
available.
m fluxes are not
available.
A deep continuum 1.4 GHz radio survey (Dole et al., in prep.) of the ISO FIRBACK field has been performed using the Australia Telescope Compact Array.
A total of 102 hours of observations took place between May 14th and 22nd, 1999, using the 6A configuration, at 1432 MHz and with a correlator bandwidth of 128 MHz. Twelve pointings cover the ISO field with an uniform sensitivity in the center. Data were reduced and mosaiced using the Miriad package (Sault et al. 1995).
The non-symmetric synthesized beam has a FWHM of approximatively
![]() (in RA, Dec), resulting in a source position accuracy of
at worst
(in RA, Dec), resulting in a source position accuracy of
at worst
![]() ;
with a similar observational strategy, Hopkins et al. (1998, 2003) and Gruppioni et al. (1999) showed that the
astrometry is better than 2 arcsec.
The 5
;
with a similar observational strategy, Hopkins et al. (1998, 2003) and Gruppioni et al. (1999) showed that the
astrometry is better than 2 arcsec.
The 5 ![]() sensitivity is of the order of 0.27 mJy.
The Miriad task
sensitivity is of the order of 0.27 mJy.
The Miriad task SFind, using the False Discovery Rate method
(Hopkins et al. 2002) was used to extract the sources in the mosaiced
image.
The position of the radio sources is marked by dark squares on the finding charts (see Fig. 8). Only the positional information has been used, when necessary, for the FSM source identification, as the flux calibration of this radio sample has still to be completed.
The optical follow-up described here consists of long slit spectroscopy of the galaxies in 23 fields, corresponding essentially to the brighter FSM sources. Imaging and photometry of the whole area is also under way, but the final data are not yet available.
The long slit spectra were obtained on the nights 26-29 November 2000 using
EFOSC 2 on the 3.6 m telescope of ESO in La Silla, Chile. For all
spectra, a 1.2
![]() slit was used with grism #13.
This setting gives
a resolution of 2.77 Å per pixel and 20 Å per slit width, with
a wavelength coverage from 3680 Å to 9340 Å. It
allows the identification of many features
in the spectra of low z galaxies: in particular the
slit was used with grism #13.
This setting gives
a resolution of 2.77 Å per pixel and 20 Å per slit width, with
a wavelength coverage from 3680 Å to 9340 Å. It
allows the identification of many features
in the spectra of low z galaxies: in particular the
![]() emission lines should be detectable for galaxies
in the redshift range z=0-1.5, while the H
emission lines should be detectable for galaxies
in the redshift range z=0-1.5, while the H![]() Balmer line
remains in the range for galaxies closer
than z=0.4. The spectral resolution is sufficient to separate
H
Balmer line
remains in the range for galaxies closer
than z=0.4. The spectral resolution is sufficient to separate
H![]() from
from
![]() with the help of fitting procedures.
with the help of fitting procedures.
The standard procedure with EFOSC2 is to first take an image of the field, and then select interactively the object(s) to be put in the slit. Rotation of the slit allows to obtain at least two spectra in a single exposure if necessary. The acquisition image was obtained with a red Bessel filter (ESO number 642), with an exposure time of at least one minute, to allow easy source identification and aperture correction if necessary.
The seeing was generally better than 1
![]() during this observing run
and all the nights were photometric.
during this observing run
and all the nights were photometric.
The spectra were reduced and calibrated using ESO's MIDAS
software in the interactive context "LONG''. Wavelength
calibration was performed using helium argon lamps spectra, and
fitting a three degree polynomial. The error on ![]() was found to
be less than 3 Å, essentially independent of the
telescope position.
was found to
be less than 3 Å, essentially independent of the
telescope position.
All the spectra were flux calibrated, after correction of atmospheric extinction, using three spectrophotometric standard stars: LTT 3218, LTT 3864 and LTT 1020 (Hamuy et al. 1992, 1994). The variation between the response curves (two observations for LTT 1020, one for LTT 3864 and one for LTT 3218) was found to be about 2% and we used an averaged response to calibrate all scientific spectra: we can thus estimate the error on absolute fluxes (apart from slit losses) to be less than 5%.
For each calibrated spectrum, the following procedure was employed, making use of ESO/MIDAS routines.
First, a noise spectrum is estimated by summing up the two first scales of a wavelet transform (automatic number of scales of 10 for a 2000 pixels spectrum). The two first scales are indeed below the resolution of the instrument (20 Å) and thus can be supposed to be pure noise component. This noise spectrum is used: i) to estimate the global S/N ratio of the spectrum and ii) to extract the high-frequency noise of the whole spectrum and thus make it more readable.
Then the cleaned spectrum is visually examined, and a hypothesis on z is made. The hypothesis is tested automatically by searching for
emission and absorption lines. If more than three separate features
are found with a ![]() lower than 0.001, the
redshift is considered a good guess.
The program then searches for all lines of a given list.
Each line found is fitted with a deblend MIDAS routine, with a continuum
interpolated between two "flat'' regions (pre-determined, the same for
all objects) around the line. The total flux, equivalent width and
measured redshift are given for each line. The final z is determined
by averaging over all detected features, and the error is given by
the dispersion - it is generally of the order of
lower than 0.001, the
redshift is considered a good guess.
The program then searches for all lines of a given list.
Each line found is fitted with a deblend MIDAS routine, with a continuum
interpolated between two "flat'' regions (pre-determined, the same for
all objects) around the line. The total flux, equivalent width and
measured redshift are given for each line. The final z is determined
by averaging over all detected features, and the error is given by
the dispersion - it is generally of the order of
![]() for
an average spectrum, and never worse than a few 10-3.
for
an average spectrum, and never worse than a few 10-3.
A rough spectral classification (reported
in Col. 8 of Table 2) is done according to the following
rules:
- a when no emission line has been detected, so that the only
measurable features are the H and K Ca II lines (at 3933 Å and 3968 Å) and possibly other absorption lines;
- e+a when emission lines have been detected (H![]() equivalent
width greater than one Å, other
non-Balmer emission lines), along with absorption features;
equivalent
width greater than one Å, other
non-Balmer emission lines), along with absorption features;
- agn when high excitation forbidden lines indicate an active nucleus.
Table 2: Flux measurements for the FIRBACK South Marano sample.
In about half the cases, only one optical galaxy was found (although sometimes
more than one spectrum was taken, to check other optical candidates, which
then proved to be stars). If more than one optical galaxy is found inside
the error circle, we then used the following criteria to pursue the
identification further:
- the spectrum should look similar to a "standard" starburst galaxy, i.e. have
emission lines (particularly [OII] or H![]() ), a reddened continuum, etc.;
), a reddened continuum, etc.;
- the radio emission in the ATCA data at 1.4 GHz (Dole et al., in preparation), if available in the field, should correspond to this
galaxy. The better angular resolution (at the
arc-second level) of the radio
observations allows in most cases to identify without ambiguity the
optical candidate associated with the radio source.
This general procedure relies on the assumption that the IR PHOT source
is of a similar nature
than the standard IRAS galaxies, powered by star-formation or an AGN, and
where the
well known radio/IR correlation holds over a large range of fluxes. This
"bias" would, at this early stage, prevent identification of sources of
different nature, should they exist in this sample. However, the
"radio emission'' criterion was decisive only for a few objects (four IR sources) and we have found no case (in this bright sample) where there
was only one radio source, corresponding to a non-emission lines galaxy.
If several optical objects have similar properties (same redshift, emission lines, radio emission) and all lie inside the error circle, we assume they all contribute to the IR emission and thus we sum all the optical contributions. The redshift attributed to the IR object is then the average of the optical redshifts. This is the case for four objects: FSM_005, FSM_010, FSM_013 and FSM_018.
More difficult is the case when two galaxies with different redshifts
but otherwise similar properties (emission lines, radio emission...) lie
in the error circle. Both candidates probably contribute to the final
infrared flux, and, since there is no perfect criterion to chose
one candidate or the other, we chose to distribute the IR flux
proportionnaly to
the H![]() line intensity (this assumes a linear relation
between IR and emission line fluxes, which holds only roughly).
These problematic
cases are fortunately rare enough here (1 case out of 28 for the IRAS
sample, 2 out of 24 for the FSM sample) that they will not affect our
general conclusions. We found only one case where none of this criteria
could be used: in FSM_018, there is no detected radio emission, and none
of the observed galaxies does show emission lines (see discussion of individual
sources).
line intensity (this assumes a linear relation
between IR and emission line fluxes, which holds only roughly).
These problematic
cases are fortunately rare enough here (1 case out of 28 for the IRAS
sample, 2 out of 24 for the FSM sample) that they will not affect our
general conclusions. We found only one case where none of this criteria
could be used: in FSM_018, there is no detected radio emission, and none
of the observed galaxies does show emission lines (see discussion of individual
sources).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{h3999.fig1.ps}\end{figure}](/articles/aa/full/2003/48/aah3999/Timg80.gif) |
Figure 1: R-band image of FSM_005 infrared source, showing galaxy number 1 (left) & 2, taken with the ESO 3.6 m telescope in La Silla. This picture shows clearly the two merging galaxies. The field is rotated (the star is due north of the galaxies) in order to place the slit across both galaxies). |
| Open with DEXTER | |
Figure 8 presents the DSS images with a superposed infrared error circle, radio identifications (when available), spectrograph slit position and final identification(s) (the optical galaxy finally associated with the IR emission is indicated by an asterisk, see also Table 2). In the following, we discuss each identification separatly.
Main catalog:
![]() FSM_000: Two large galaxies have been placed on the
slit. The infrared source is associated with the
large galaxy inside the error circle, witch is also a radio source.
The second galaxy (also a radio source, but outside the
circle) has not a starburst spectrum and is therefore assumed to
contribute little or nothing to the IR emission.
FSM_000: Two large galaxies have been placed on the
slit. The infrared source is associated with the
large galaxy inside the error circle, witch is also a radio source.
The second galaxy (also a radio source, but outside the
circle) has not a starburst spectrum and is therefore assumed to
contribute little or nothing to the IR emission. ![]() FSM_001: The infrared source is associated with the
large galaxy inside the error circle, which is also a radio source,
object #2 being out of the error circle and with no radio emission.
FSM_001: The infrared source is associated with the
large galaxy inside the error circle, which is also a radio source,
object #2 being out of the error circle and with no radio emission.![]() FSM_002: Only one large galaxy is in the error circle,
but there is no radio emission.
FSM_002: Only one large galaxy is in the error circle,
but there is no radio emission.![]() FSM_003: Among the numerous stars of the nearby globular
cluster lies a large galaxy, which is also a radio source.
FSM_003: Among the numerous stars of the nearby globular
cluster lies a large galaxy, which is also a radio source.![]() FSM_004: One large radio bright galaxy.
FSM_004: One large radio bright galaxy.![]() FSM_005: On close examination (see Fig. 1),
the central optical source is in fact a couple of merging galaxies (of whom
one at least is a radio source). We associated the infrared flux with
both optical galaxies (and thus added the emission line intensities).
FSM_005: On close examination (see Fig. 1),
the central optical source is in fact a couple of merging galaxies (of whom
one at least is a radio source). We associated the infrared flux with
both optical galaxies (and thus added the emission line intensities).![]() FSM_006: The galaxy associated with the infrared flux
(#2) is inside the error circle, and is associated with radio
emission. A contribution from galaxy #1 is possible too.
FSM_006: The galaxy associated with the infrared flux
(#2) is inside the error circle, and is associated with radio
emission. A contribution from galaxy #1 is possible too. ![]() FSM_007: This large galaxy,
close to the globular cluster, is also a radio source.
FSM_007: This large galaxy,
close to the globular cluster, is also a radio source.![]() FSM_008: One galaxy is in the error circle, which is
also a radio source.
FSM_008: One galaxy is in the error circle, which is
also a radio source.![]() FSM_009: There are two galaxies but galaxy #2 is on the border of the error circle, has weak emission lines and no radio
counterpart. We thus attribute the IR flux to galaxy #1 only.
FSM_009: There are two galaxies but galaxy #2 is on the border of the error circle, has weak emission lines and no radio
counterpart. We thus attribute the IR flux to galaxy #1 only.![]() FSM_010: Two faint galaxies have been observed
spectroscopically. One is well inside the error circle but has no
radio counterpart, the other is on the limit of the error circle and
is associated with a radio source. Since both galaxies are at the same
redshift (though separated by about 250 kpc with a standard, H0= 65 km/h/Mpc cosmology) we added the optical fluxes. A much fainter object (not
observed spectroscopically) and coinciding with a radio source could
contribute also.
FSM_010: Two faint galaxies have been observed
spectroscopically. One is well inside the error circle but has no
radio counterpart, the other is on the limit of the error circle and
is associated with a radio source. Since both galaxies are at the same
redshift (though separated by about 250 kpc with a standard, H0= 65 km/h/Mpc cosmology) we added the optical fluxes. A much fainter object (not
observed spectroscopically) and coinciding with a radio source could
contribute also. ![]() FSM_011: No bright galaxy was visible inside the
error circle, so we placed two slits to check various faint optical
sources. We found a few stars, two very weak galaxies with no emission
line, and a point-like active galaxy with bright emission lines and
rather high redshift (z=0.66). The infrared flux was attributed to this
object. Note that this object has the highest IR luminosity
of the whole sample, by far.
FSM_011: No bright galaxy was visible inside the
error circle, so we placed two slits to check various faint optical
sources. We found a few stars, two very weak galaxies with no emission
line, and a point-like active galaxy with bright emission lines and
rather high redshift (z=0.66). The infrared flux was attributed to this
object. Note that this object has the highest IR luminosity
of the whole sample, by far.
![]() FSM_012: One of the few cases where radio emission
was decisive: galaxy #1 was chosen because of it (although galaxy #2 has
week emission too).
FSM_012: One of the few cases where radio emission
was decisive: galaxy #1 was chosen because of it (although galaxy #2 has
week emission too).
![]() FSM_013: Two of the three galaxies in the slit are
well inside the error circle, with similar redshifts. They are
probably interacting, and thus we considered that both contributed to
the infrared flux (optical fluxes were added).
FSM_013: Two of the three galaxies in the slit are
well inside the error circle, with similar redshifts. They are
probably interacting, and thus we considered that both contributed to
the infrared flux (optical fluxes were added).![]() FSM_014: All galaxies lie within the error circle,
with no radio identification available. Without further information
available,
we divided the infrared flux in two parts, proportionnally to the
H
FSM_014: All galaxies lie within the error circle,
with no radio identification available. Without further information
available,
we divided the infrared flux in two parts, proportionnally to the
H![]() emission line strength: one part (infrared object FSM_014 A)
is attributed to galaxies #1 and #2 (two galaxies probably
interacting at z=0.16, optical fluxes added), and the other part
(infrared object FSM_014 B) to galaxy #3
(z=0.3).
emission line strength: one part (infrared object FSM_014 A)
is attributed to galaxies #1 and #2 (two galaxies probably
interacting at z=0.16, optical fluxes added), and the other part
(infrared object FSM_014 B) to galaxy #3
(z=0.3).
![]() FSM_015: One large galaxy at the center of the error
circle, no radio emission.
FSM_015: One large galaxy at the center of the error
circle, no radio emission.![]() FSM_016: One large galaxy at the error
circle's center, with radio emission.
FSM_016: One large galaxy at the error
circle's center, with radio emission.
![]() FSM_017: Two galaxies are inside the error circle, we
chose #1 because it has radio emission.
FSM_017: Two galaxies are inside the error circle, we
chose #1 because it has radio emission.![]() FSM_018: We observed spectroscopically both
galaxies inside the error circle, however, none of them shows any
emission line. There is no radio emission. This would be the only case where
the optical counterpart has no emission line. The identification here is
still unsecure.
FSM_018: We observed spectroscopically both
galaxies inside the error circle, however, none of them shows any
emission line. There is no radio emission. This would be the only case where
the optical counterpart has no emission line. The identification here is
still unsecure. ![]() FSM_019: Only one galaxy lies inside the error
circle, has emission lines but no radio emission: we consider it as the IR counterpart. Note however that another faint source lies on the borderline,
with radio emission (which was not known at the time of our observations),
and could contribute to the IR flux also.
FSM_019: Only one galaxy lies inside the error
circle, has emission lines but no radio emission: we consider it as the IR counterpart. Note however that another faint source lies on the borderline,
with radio emission (which was not known at the time of our observations),
and could contribute to the IR flux also. ![]() FSM_020: One large galaxy inside the error
circle, with optical emission and radio emission.
FSM_020: One large galaxy inside the error
circle, with optical emission and radio emission.
Complementary catalog:
![]() FSM_026: One large galaxy at the center of the error
circle. Weak optical emission but no radio emission.
FSM_026: One large galaxy at the center of the error
circle. Weak optical emission but no radio emission.
![]() FSM_035: From the two radio sources, one seems to be a quiet
galaxy (no redshift determined) and the other a bright point-like radio-loud
QSO at z=0.6. We thus
provisionnally attribute the infrared flux to the AGN alone.
FSM_035: From the two radio sources, one seems to be a quiet
galaxy (no redshift determined) and the other a bright point-like radio-loud
QSO at z=0.6. We thus
provisionnally attribute the infrared flux to the AGN alone.
![]() FSM_039: Two galaxies with no radio detection lie in
the error circle, #1 at z=0.14, rather bright but off-centered, #2
at z=0.27, fainter, centered. We divided the IR flux proportionnally
to the H
FSM_039: Two galaxies with no radio detection lie in
the error circle, #1 at z=0.14, rather bright but off-centered, #2
at z=0.27, fainter, centered. We divided the IR flux proportionnally
to the H![]() emission line intensity.
emission line intensity.
We have used a 1.2
![]() slit for the observations, wider than the seeing
during the whole run. While for point-like source, we may then
consider that most of the object's flux is transmitted,
for extended galaxies, on the contrary, a fraction of the flux is lost at
the entrance, and should be evaluated.
The question of aperture correction is however difficult, and
different solutions have been used in the literature:
slit for the observations, wider than the seeing
during the whole run. While for point-like source, we may then
consider that most of the object's flux is transmitted,
for extended galaxies, on the contrary, a fraction of the flux is lost at
the entrance, and should be evaluated.
The question of aperture correction is however difficult, and
different solutions have been used in the literature:
- correction using photometry: the total
spectrophotometric flux can be corrected by comparing it to the
photometric flux (magnitude)
(solution used for instance in the CFRS,
Tresse et al. 1996). However, this procedure assumes a regular
distribution of the surface brightness over the galaxy,
and when emission lines are concerned
(our main interest here) is far from being satisfactory. If (as is
probably the case for our objects)
the star forming region is essentially circumnuclear,
such a correction would grossly overestimate
the total emission.
- no correction at all, if the slit is considered wide enough
(e.g. in Sullivan et al. 2000 for the
FOCA UV-galaxies follow-up).
Our case is intermediate between these two extremes, but because the
emission is mostly circumnuclear in IRAS galaxies, we decided not
to correct the spectra for this effect. In doing this, the measured
fluxes are certainly lower limits, but should not greatly
underestimate the real values for absolute fluxes. It does not affect,
of course, equivalent widths and flux ratios.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{h3999.fig2a.ps}\...
...m}
\par\includegraphics[angle=270,width=8.8cm,clip]{h3999.fig2c.ps}
\end{figure}](/articles/aa/full/2003/48/aah3999/Timg82.gif) |
Figure 2:
Correction for stellar absorption. First panel: test,
correction of a pure absorption H |
| Open with DEXTER | |
The Balmer emission lines have a particular importance in the
spectrum: the "Balmer decrement'' is the main
indicator of dust reddening (see next section); the diagnostic
diagrams use H![]() and/or H
and/or H![]() with forbidden
lines to assess the nature of the ionizing source;
H
with forbidden
lines to assess the nature of the ionizing source;
H![]() is one of the best star formation indicators. Yet,
atmospheres of A and B stars, generally present in the underlying stellar
populations of galaxies, absorb in the same lines, thus altering
the resulting spectrum significantly.
It is then of particular importance to
correct for this underlying absorption by stars. Several solutions have
been applied in the past, depending on the quality of the spectra
and the available information:
is one of the best star formation indicators. Yet,
atmospheres of A and B stars, generally present in the underlying stellar
populations of galaxies, absorb in the same lines, thus altering
the resulting spectrum significantly.
It is then of particular importance to
correct for this underlying absorption by stars. Several solutions have
been applied in the past, depending on the quality of the spectra
and the available information:
- A constant correction applied to the equivalent width of the emission line.
The value applied is usually around 2 Å for HII regions,
and can go up to 5 Å (Kennicutt 1992). This is an average value, not well
calibrated on galactic objects. This type of correction is usually
used for large samples where individual properties are
neglected and when no other solution is available.
- Fit the wings of the absorption lines. These wings are
usually seen on both sides of the emission line. This technique has been
used for instance by Sullivan et al. (2000)
or Kim et al. (1995) to reconstruct both the absorption and the emission
features. However, this method requires a very good spectral resolution and is
very sensitive to noise. Fitting a deep absorption line on very faint wings can
lead to large errors in the final flux determination.
Furthermore, if other emission lines lie close to the Balmer line (like
for instance [NII]6548 and [NII]6583) the absorption wings
will be completely lost, reducing the accuracy of the method.
- Use of the higher order Balmer lines. This is the most efficient method,
which makes use of the
H![]() and H
and H![]() lines: the emission decreases rapidly with the order of
the line whereas the absorption increases.
One can compute (e.g.
Osterbrock 1989) that the ratio of the H
lines: the emission decreases rapidly with the order of
the line whereas the absorption increases.
One can compute (e.g.
Osterbrock 1989) that the ratio of the H![]() and H
and H![]() emission lines is (case B approximation):
emission lines is (case B approximation):
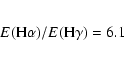
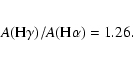
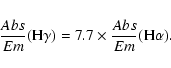
In the FSM field we have enough spectral resolution and wavelength coverage
to measure Balmer absorption lines of higher order in all the spectra. In
the IRAS sample on the contrary, due to a slightly different instrumental
setting (further red), for many spectra only H![]() is in the observed range: for those spectra we
therefore applied the average
global correction obtained for the sample (see below).
is in the observed range: for those spectra we
therefore applied the average
global correction obtained for the sample (see below).
In practice, to correct the H![]() emission line from underlying absorption, we
fitted the H
emission line from underlying absorption, we
fitted the H![]() and H
and H![]() absorption lines and derived
from them the absorption lines at 4961 Å and 6563 Å
respectively. The original spectrum is then divided by this absorption
feature, reconstructing the "original'' emission line. In Fig. 2 we
show the efficiency of this method: the first image shows the results
of the method on a pure absorption spectrum, and the two others
illustrate how the H
absorption lines and derived
from them the absorption lines at 4961 Å and 6563 Å
respectively. The original spectrum is then divided by this absorption
feature, reconstructing the "original'' emission line. In Fig. 2 we
show the efficiency of this method: the first image shows the results
of the method on a pure absorption spectrum, and the two others
illustrate how the H![]() line is recovered, even when it was too low
(due to the presence of stellar absorption) to be distinguished from the noise.
line is recovered, even when it was too low
(due to the presence of stellar absorption) to be distinguished from the noise.
H![]() is usually blended with a large Mg absorption band, so we
prefer to use H
is usually blended with a large Mg absorption band, so we
prefer to use H![]() when available. When both lines are clearly
detected, we check that the results are consistent (given the error
bars) and correct H
when available. When both lines are clearly
detected, we check that the results are consistent (given the error
bars) and correct H![]() and H
and H![]() from the average result.
from the average result.
If none of these two lines is detectable in absorption, (or if they are in
emission only), we consider that the absorption by stars is negligible and make
no correction. In several spectra, the correction makes H![]() pop
out of the noise. When H
pop
out of the noise. When H![]() doesn't appear even after the
correction (whereas H
doesn't appear even after the
correction (whereas H![]() is visible in emission) we deduce that H
is visible in emission) we deduce that H![]() is completely absorbed by dust, and we then use the noise in the continuum
to estimate an upper value for H
is completely absorbed by dust, and we then use the noise in the continuum
to estimate an upper value for H![]() .
.
We find an average correction of 3 Å for the FSM sample and 3.35 Å for the IRAS sample (average over the corrected spectra -not including the non-corrected ones).
For the FSM sample, we can neglect the foreground galactic
extinction because of the high galactic latitude of the field (
![]() ).
In most FSM galaxies, both H
).
In most FSM galaxies, both H![]() and H
and H![]() are available in emission, so we can use the Balmer decrement to estimate the
extinction. This method relies on several assumptions:
are available in emission, so we can use the Balmer decrement to estimate the
extinction. This method relies on several assumptions:
- the intrinsic
![]() ratio has to be known. Indeed
theoretical
calculations have shown that for a case B recombination this ratio is
almost independent of density and temperature. We will use
ratio has to be known. Indeed
theoretical
calculations have shown that for a case B recombination this ratio is
almost independent of density and temperature. We will use
![]() ,
the value given by Osterbrock (1989) for a density
of 100 cm-1 and a temperature of 10 000 K.
,
the value given by Osterbrock (1989) for a density
of 100 cm-1 and a temperature of 10 000 K.
- the general form of the extinction curve with wavelength is supposed to
be known. We used
the Howarth (1983) extension of Seaton's (1979) extinction law for the
Milky Way. Other extinction curves
used in the literature do not differ widely, at least for the optical range of the
spectrum.
We can thus compute the amount of absorption in the visible, AV, for
each object, using R=3.2 (Seaton 1979) and
![]() as
described in Howarth (1983).
The AV value is included in Table 2.
as
described in Howarth (1983).
The AV value is included in Table 2.
Table 3: Summary of the two observational samples.
We try here to characterize the galaxies selected by the
![]() survey, and compare them to the IRAS sample.
All luminosities were computed with a standard cosmology:
survey, and compare them to the IRAS sample.
All luminosities were computed with a standard cosmology:
![]() ,
,
![]() and we took a Hubble constant of H0 = 65 km s-1 Mpc-1.
Due to the small distance of the detected objects, the derived parameters
are rather insensitive to the adopted cosmology.
and we took a Hubble constant of H0 = 65 km s-1 Mpc-1.
Due to the small distance of the detected objects, the derived parameters
are rather insensitive to the adopted cosmology.
The results of the spectral analysis are presented in Table 2 for the main emission lines used in the discussion.
![\begin{figure}
\par\includegraphics[angle=270,width=8cm,clip]{h3999.fig3a.ps}\vs...
...*{3mm}
\includegraphics[angle=270,width=8cm,clip]{h3999.fig3b.ps}
\end{figure}](/articles/aa/full/2003/48/aah3999/Timg94.gif) |
Figure 3: Distribution of absorption by dust. Top: histograms of the Av values, with median hashing corresponding to FSM galaxies and inclined hashing to the IRAS sample. Bottom: cumulative function of Av for: i) FSM sample (solid curve) and ii) IRAS reference sample (dotted curve). |
| Open with DEXTER | |
Figure 3 presents the histograms of AV (after correction from underlying stellar absorption) for both samples, and Table 4 presents the statistics of the distribution for all spectra observed (excluding occasional stars). The reason to use for the statistics all the observed spectra is because when several galaxies are associated to one IR source, an "average'' extinction factor would have no real meaning. The result of a Kolmogorov-Smirnov test on the cumulative functions shows that the two samples have a reasonable chance of coming from the same initial distribution (a D parameter of less than 0.4, with n=17, leads to a p(D)=25%, that is to say that two samples drawn from the same distribution have 25% chances of being farther apart than these two samples; see Miller 1956).
We conclude that the two samples are remarquably alike as far as
extinction is concerned (![]() for both samples).
They are also very similar to the "Bright galaxies sample'' (Veilleux
et al. 1995, thereafter BGS), where AV has an average value of 3.6 (with our adopted value of R=3.2), but rather far from
UV-selected samples (
for both samples).
They are also very similar to the "Bright galaxies sample'' (Veilleux
et al. 1995, thereafter BGS), where AV has an average value of 3.6 (with our adopted value of R=3.2), but rather far from
UV-selected samples (
![]() ;
Sullivan et al. 2000 for the
FOCA galaxies). The extinction is also significantly higher than in
the CFRS z<0.3 sample, where
AV=1.52 for objects selected in the I band (and is an upper limit, as no correction has been applied there for underlying
stellar absorption).
This effect is not surprising: it is
quite clear that
;
Sullivan et al. 2000 for the
FOCA galaxies). The extinction is also significantly higher than in
the CFRS z<0.3 sample, where
AV=1.52 for objects selected in the I band (and is an upper limit, as no correction has been applied there for underlying
stellar absorption).
This effect is not surprising: it is
quite clear that ![]() m and
m and ![]() m observations both select
heavily obscured objects.
m observations both select
heavily obscured objects.
Table 4: Extinction parameter for individual galaxies in both samples. The two distributions are similar, given the small statistics, and cover the same range.
We want to stress that an extinction of AV = 2.9 mag (average value) results in a reduction of a factor 9 (or an optical
depth of
![]() )
in the H
)
in the H![]() line intensity, and a
factor of 50 (
line intensity, and a
factor of 50 (
![]() )
for the [OII] blend, as compared to
a factor of 2 in H
)
for the [OII] blend, as compared to
a factor of 2 in H![]() and 4 in [OII] when we take the usual
prescription of AV = 1 only. It is thus important to characterize
the type of object selected , in order to apply the appropriate
correction.
and 4 in [OII] when we take the usual
prescription of AV = 1 only. It is thus important to characterize
the type of object selected , in order to apply the appropriate
correction.
![\begin{figure}
\par\includegraphics[angle=270,width=8cm,clip]{h3999.fig4a.ps}\vs...
...*{3mm}
\includegraphics[angle=270,width=8cm,clip]{h3999.fig4b.ps}
\end{figure}](/articles/aa/full/2003/48/aah3999/Timg100.gif) |
Figure 4: Distribution of the redshifts of the IR sources. |
| Open with DEXTER | |
We show in Fig. 4 and Table 5 the statistics of the obtained redshift distributions. It is quite obvious that the repartitions are similar. The Kolmogorov-Smirnov test tells us that two stochastic samples taken from the same parent distribution have a probability of more than 70% to be more different than these two.
The only two objects at larger redshift (z>0.3) in the FSM
sample are Seyfert galaxies. The brighter sources in the 170 ![]() m selection are thus rather close by.
m selection are thus rather close by.
Table 5: Statistics on z for both samples. The two distributions are obviously very alike.
We will use classical diagnostic diagrams to derive the nature of those galaxies.
In the FSM sample, we usually have secure measurement for (at least) the
following lines: [OII] (3727 Å), H![]() ,
[OIII] (4959 Å,
5007 Å), H
,
[OIII] (4959 Å,
5007 Å), H![]() ,
[NII] (6548 Å, 6583 Å).
There is no broad emission
line object in the FSM sample. Although our statistics is small (only 20 objects in the brighter part studied here), this is consistent with the
results of the BGS where Veilleux et al. (1995) found only two
Seyfert 1 galaxies out of the 140 spectra analyzed, and they are very
bright IR objects.
,
[NII] (6548 Å, 6583 Å).
There is no broad emission
line object in the FSM sample. Although our statistics is small (only 20 objects in the brighter part studied here), this is consistent with the
results of the BGS where Veilleux et al. (1995) found only two
Seyfert 1 galaxies out of the 140 spectra analyzed, and they are very
bright IR objects.
The fraction of emission-line galaxies in our sample is very
high, confirming the pertinence of an IR-selected
sample to find star forming objects. To all but one (FSM_18) 170 ![]() m
sources, the optical corresponding object is one (or several)
emission-line galaxy.
Except for this single case, all spectra can be classified "emission +
absorption'' (all spectra have Balmer
emission, most have Balmer absorption and metallic absorption lines),
see Fig. 9.
m
sources, the optical corresponding object is one (or several)
emission-line galaxy.
Except for this single case, all spectra can be classified "emission +
absorption'' (all spectra have Balmer
emission, most have Balmer absorption and metallic absorption lines),
see Fig. 9.
Figure 5 presents one of the most classical diagnostic diagrams (Baldwin et al. 1981) to separate HII region-type galaxies (bottom left of the diagram) from Seyfert 2 (upper right of the diagram) and LINER (Low Ionisation Nuclear Emission Line Regions, bottom right). The frontiers are from Dessauges-Zavadsky et al. (2000), but a variety of empirical separations can be found in the literature, and the definition of the regions is rather approximative.
This diagram is well adapted to our data. The
signal to noise ratio of our spectra does not allow us to use [OI] or [NeIII] lines (usually not detected), or the [SII] often affected by atmospheric features.
For objects at z>0.3,
![]() is out of the observed range, so we use also the "R23'' criterion from Dessauges-Zavadsky et al. (2000):
is out of the observed range, so we use also the "R23'' criterion from Dessauges-Zavadsky et al. (2000):
![\begin{eqnarray*}R23 = \frac{[{\rm OII}]_{3727}+[{\rm OIII}]_{4959} + [{\rm OIII}]_{5007}}{{\rm H}\beta}
\end{eqnarray*}](/articles/aa/full/2003/48/aah3999/img101.gif)
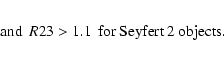
Two FSM objects are classified as "LINER'' on the diagram, FSM_013 and FSM_003 (though this last one is not secure, given the error bars). Unfortunately, the classical test for LINER is not applicable here since the [OI] 6300 Å line has not been detected in our spectra.
We thus get 3 to 5 active objects out of 29 in the FSM sample, that is 11% to 19% of the objects. The IRAS reference sample shows similar results, though the statistic is much smaller due to the smaller observed range and spectral resolution.
These values are similar to the CFRS results (between 8%
and 18% when including the effects of stellar absorption), but
rather far from the high number of AGN found in the IRAS bright
galaxy sample. If this effect is confirmed (by larger
samples) it tends to show that the faint IR galaxies are indeed a
population different from the bright IR objects: heavily obscured, but
with a majority of star forming objects and only few AGN. This is consistent
with the finding (e.g. Lutz et al. 1998; Veilleux et al. 1999) that
the fraction of AGN increases strongly when going to ULIRG objects.
Indeed, as shown in Sect. 5.5, the IR luminosities of the bright FSM objects
are rather modest (
![]() )
and, at those
luminosities, the fraction of
AGN's is smaller than 20% in the 1 Jy sample studied
by Veilleux et al., for instance. It increases abruptly to 50% only at
)
and, at those
luminosities, the fraction of
AGN's is smaller than 20% in the 1 Jy sample studied
by Veilleux et al., for instance. It increases abruptly to 50% only at
![]() .
.
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{h3999.fig5.ps}
\end{figure}](/articles/aa/full/2003/48/aah3999/Timg106.gif) |
Figure 5:
Diagnostic diagram for both our samples. +, FSM sample; *, IRAS reference sample. All emission-line measurements are corrected
for dust extinction and absorption lines. Only spectra with H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=10.8cm,width=8.2cm,clip]{h3999.fig6.ps}
\end{figure}](/articles/aa/full/2003/48/aah3999/Timg107.gif) |
Figure 6: SED modelisation compared to five observed cases. Solid line: starburst template, dashed line: Cold template. Both templates are from Lagache et al. (2003). Also shown for comparison is the spectrum of M82 (dashed-dotted). |
| Open with DEXTER | |
One of the main characteristic of our galaxies is their cool IR temperature, which can be determined when we have more than one
observational point. As indicated in Table 1, for 5
out of 29 objects, we have, in addition to
the 170 ![]() m fluxes, also the 60 and 100
m fluxes, also the 60 and 100 ![]() m IRAS measurements,
obtained from the SCANPI procedure.
For another 13 galaxies, this
method gives only upper limits for 60 and/or 100
m IRAS measurements,
obtained from the SCANPI procedure.
For another 13 galaxies, this
method gives only upper limits for 60 and/or 100 ![]() m fluxes.
m fluxes.
To characterise the dust emissivity of these galaxies, we studied three quantities: the greybody temperature T, the infrared colors and the spectral energy distribution.
The greybody temperature T was computed for direct comparison with other
galaxies from the literature. We use a spectral index of
![]() ,
and fit a modified blackbody to the infrared measurements at 60
and 170
,
and fit a modified blackbody to the infrared measurements at 60
and 170 ![]() m for 5 galaxies, and use the upper limits at 60
m for 5 galaxies, and use the upper limits at 60 ![]() m for 13 other galaxies. We find an average temperature of 22.7 K, with values
ranging from 20.9 K (FSM_002) to 24.7 (FSM_001) for the first
5 galaxies, and a somewhat wider distribution when we work also with upper
limits: average temperature of 23.5 K with values ranging from 19.5
(FSM_005) to 32.7 K (FSM_011). This results indicate a rather
cold population.
m for 13 other galaxies. We find an average temperature of 22.7 K, with values
ranging from 20.9 K (FSM_002) to 24.7 (FSM_001) for the first
5 galaxies, and a somewhat wider distribution when we work also with upper
limits: average temperature of 23.5 K with values ranging from 19.5
(FSM_005) to 32.7 K (FSM_011). This results indicate a rather
cold population.
In addition to the greybody temperature, we computed
the IR color
![]() m
m
![]() m)), as usually done for IRAS
galaxies. We find a mean ratio of -0.32, with a dispersion of 0.2 dex. This is highly compatible with the "normal'' IRAS galaxies:
Soifer et al. (1989; their Fig. 1) show that the histogram of the color
distribution of all the BGS galaxies is centered at -0.3. A similar
value is obtained with our own small IRAS sample.
m)), as usually done for IRAS
galaxies. We find a mean ratio of -0.32, with a dispersion of 0.2 dex. This is highly compatible with the "normal'' IRAS galaxies:
Soifer et al. (1989; their Fig. 1) show that the histogram of the color
distribution of all the BGS galaxies is centered at -0.3. A similar
value is obtained with our own small IRAS sample.
Thus the FSM galaxies have the same average color as normal IRAS 60 ![]() m selected galaxies, but the observations at 170
m selected galaxies, but the observations at 170 ![]() m show a
cooler dust temperature. This is generally the result whenever a longer
wavelength point is added to IRAS measurements, as a single temperature
blackbody is probably too crude an approximation to reproduce the SED of
those objects.
m show a
cooler dust temperature. This is generally the result whenever a longer
wavelength point is added to IRAS measurements, as a single temperature
blackbody is probably too crude an approximation to reproduce the SED of
those objects.
To investigate further the IR spectral energy distribution
of these galaxies, we fit our observational data points
with the "starburst'' and "normal'' galaxy templates from
Lagache et al. (2003). The "normal'' galaxy template
is colder than the "starburst'' template, with a peak
at around 180 ![]() m. Results of the fit are shown in Fig. 6 and detailed below:
m. Results of the fit are shown in Fig. 6 and detailed below:
As for most objects in our sample, we do not have the IRAS (60 ![]() m, 100
m, 100 ![]() m) flux measurements,
we cannot use the classical formula (Helou
et al. 1988) to derive the total IR luminosity (
m) flux measurements,
we cannot use the classical formula (Helou
et al. 1988) to derive the total IR luminosity (
![]() ).
We are thus obliged to use models or template SED to derive it in a
homogeneous way for all objects in the sample.
).
We are thus obliged to use models or template SED to derive it in a
homogeneous way for all objects in the sample.
We first performed a series of tests to determine the best way to
compute the total luminosity. Three different methods are compared
(we note the disadvantages of each method in italics):
1 - take in the grid of spectra proposed by Lagache et al. the
one that is closest to the observed points. This supposes a
universal relationship between luminosity and color.
2 - use the normal template SED from Lagache (built from a number
of FIRBACK objects).
This supposes a universal shape for
all objects.
3 - fit only the shape of the model of Lagache et al., regardless of
its intrinsic absolute value at peak, and then compute the total
luminosity. This method is correct only for those objects were we have
more than one observational point (9 for the FSM
sample, 3 for the IRAS reference sample).
Though the three methods lead to very different colors for a given object,
the computed total luminosities do not differ by more than 20%
(and 10% on average), which is also the value of the error bars of
the ISO and IRAS data.
We conclude that any of the two first methods can be used to
derive the total luminosity for all objects in a homogeneous way, with
a resulting uncertainty of less than 20%. The third method can be
used as a check of
this uncertainty for the 6 objects where more than one measured point is
available. Note that this "total" IR luminosity is about 2 times larger than
the FIR usually derived from the IRAS data alone (40-200 ![]() m;
Helou et al. 1988).
m;
Helou et al. 1988).
![]() has in the end been determined using the first method, and
the error is then of the order of 0.1 dex.
has in the end been determined using the first method, and
the error is then of the order of 0.1 dex.
Most of the FIR selected galaxies are LIRGs (Luminous Infrared Galaxies)
with
![]() ,
and many of them have lower
luminosities, down to
,
and many of them have lower
luminosities, down to
![]() .
Very few are ULIRGs:
the only two objects belonging to this category are the higher
redshift AGN's found here in the FSM.
Figure 7 shows the distribution of
.
Very few are ULIRGs:
the only two objects belonging to this category are the higher
redshift AGN's found here in the FSM.
Figure 7 shows the distribution of
![]() and Table 6
gives the statistics on
and Table 6
gives the statistics on
![]() .
.
We finally derived the IR to optical luminosity ratio as follows:
-
![]() computed with the first method;
computed with the first method;
- optical luminosity computed by integrating the continuum from 4000 to 7000 Å in the rest frame (range directly accessible with our spectra).
We find ratios between 10 and 100, with an average of 65. These are
rather high values, indicative of high extinction and/or strong activity.
On the two higher redshift FIRBACK source identifications
(z=0.45 and z=0.91) found in FN1, Chapman et al. (2002) derived these ratios
between 10 and 15; but correcting for the different definition they used
(standard IRAS FIR, and a 4 times broader range for the optical
luminosity), it appears that their values are entirely compatible with
those we find here in this larger sample.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{h3999.fig7.eps}
\end{figure}](/articles/aa/full/2003/48/aah3999/Timg116.gif) |
Figure 7:
Distribution of IR luminosities (from 0.4 to 1000 |
| Open with DEXTER | |
Table 6:
Statistics on total IR luminosities (from 0.4 to 1000 ![]() m, in units of solar luminosity) for both samples.
m, in units of solar luminosity) for both samples.
Several indicators are generally used to determine the star formation rate of
galaxies, the two most useful ones in our sample being the H![]() emission line and the IR luminosity.
emission line and the IR luminosity.
The H![]() emission line fluxes used to derive the star formation rate
are corrected
for extinction: this is indispensable as our objects are heavily obscured.
For the conversion factor, we use the values from Kennicutt (1983):
emission line fluxes used to derive the star formation rate
are corrected
for extinction: this is indispensable as our objects are heavily obscured.
For the conversion factor, we use the values from Kennicutt (1983):
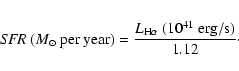
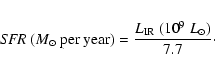
Table 7:
Distribution of the star formation rate for the FSM and
the IRAS sample (computed from the corrected H![]() emission
flux and from the total IR luminosity;
only objects classified as "HII region-like'' in Sect. 4.3 have been used). For comparison, the SFR inferred from the IR is also shown for
the sub-samples with a measurable H
emission
flux and from the total IR luminosity;
only objects classified as "HII region-like'' in Sect. 4.3 have been used). For comparison, the SFR inferred from the IR is also shown for
the sub-samples with a measurable H![]() line.
line.
We observed the brightest objects in the FIRBACK South Marano sample,
and were almost
complete in our follow-up of the brightest sources (20 out of 22 IR sources in the 4 ![]() catalog). Pending the follow-up of
the faintest objects in the FSM complementary catalog (15 objects with
catalog). Pending the follow-up of
the faintest objects in the FSM complementary catalog (15 objects with
![]() ), and the study of similar sources in the
northern FIRBACK fields, we have already here with this sample a
fairly good picture of the nature of the brightest 170
), and the study of similar sources in the
northern FIRBACK fields, we have already here with this sample a
fairly good picture of the nature of the brightest 170 ![]() m sources.
m sources.
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{iFSM_000.ps}\inc...
...SM_004.ps}\includegraphics[angle=270,width=7.5cm,clip]{iFSM_005.ps}
\end{figure}](/articles/aa/full/2003/48/aah3999/Timg122.gif) |
Figure 8: Identification charts for FIRBACK South Marano field. DSS optical image superimposed to the error circle of infrared ISO source and radio emission (black mark). The straight line shows the position of the slit (1.2'' large and 5' long), and an arrow indicates a galaxy with an available spectrum. The number associated to each arrow corresponds to the number in Table 2, with an asterisk indicating that the galaxy is associated to the infrared emission. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{iFSM_006.ps}\inc...
...[angle=270,width=7.5cm,clip]{iFSM_011.ps}\addtocounter{figure}{-1}\end{figure}](/articles/aa/full/2003/48/aah3999/Timg123.gif) |
Figure 8: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{iFSM_012.ps}\inc...
...angle=270,width=7.5cm,clip]{iFSM_017.ps}\addtocounter{figure}{-1}\end{figure}](/articles/aa/full/2003/48/aah3999/Timg124.gif) |
Figure 8: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{iFSM_018.ps}\inc...
...[angle=270,width=7.5cm,clip]{iFSM_039.ps}\addtocounter{figure}{-1}\end{figure}](/articles/aa/full/2003/48/aah3999/Timg125.gif) |
Figure 8: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.9cm,angle=270]{im0001.ps}\includegra...
...raphics[width=5.9cm,angle=270]{im0036.ps}
\addtocounter{figure}{-1}
\end{figure}](/articles/aa/full/2003/48/aah3999/Timg126.gif) |
Figure 9: Spectra. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.9cm,angle=270]{im0037.ps}\includegra...
...raphics[width=5.9cm,angle=270]{im0044.ps}
\addtocounter{figure}{-1}
\end{figure}](/articles/aa/full/2003/48/aah3999/Timg127.gif) |
Figure 9: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.9cm,angle=270]{im0003.ps}\includegra...
...raphics[width=5.9cm,angle=270]{im0010.ps}
\addtocounter{figure}{-1}
\end{figure}](/articles/aa/full/2003/48/aah3999/Timg128.gif) |
Figure 9: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.9cm,angle=270]{im0011.ps}\includegra...
...aphics[width=5.9cm,angle=270]{im0018.ps}
\addtocounter{figure}{-1}
\end{figure}](/articles/aa/full/2003/48/aah3999/Timg129.gif) |
Figure 9: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.9cm,angle=270]{im0019.ps}\includegra...
...raphics[width=5.9cm,angle=270]{im0028.ps}
\addtocounter{figure}{-1}
\end{figure}](/articles/aa/full/2003/48/aah3999/Timg130.gif) |
Figure 9: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6cm,angle=270]{im0029.ps}\includegraph...
...70]{im0032.ps}\par\includegraphics[width=6cm,angle=270]{im0033.ps}
\end{figure}](/articles/aa/full/2003/48/aah3999/Timg131.gif) |
Figure 9: continued. |
| Open with DEXTER | |
Because of the so-called "negative K-correction effect" (e.g. Dole
et al. 2001), a deep flux limited survey in a far-IR band like
FIRBACK is expected to be biased towards distant galaxies.
Our results however point to a population of galaxies much nearer
than expected. Sajina et al. (2003) described the
T/(1 + z) degeneracy in imaging infrared surveys such as
FIRBACK. The results of our follow-up shows that the 170 ![]() m luminosity is more an effect of low temperature than one of high redshift, at
least for the brightest objects. This has also been seen by
Chapman et al. (2002), who, upon selecting just two FIRBACK objects
supposed to be at very
high redshift, found in fact redshifts much lower than expected.
We show that this property is more general and that we systematically
overestimated the sources's redshifts.
m luminosity is more an effect of low temperature than one of high redshift, at
least for the brightest objects. This has also been seen by
Chapman et al. (2002), who, upon selecting just two FIRBACK objects
supposed to be at very
high redshift, found in fact redshifts much lower than expected.
We show that this property is more general and that we systematically
overestimated the sources's redshifts.
The physical properties of the galaxies in this sample can be summarized as follows.
First, as expected, they are heavily extincted. Measurements of AV give an average value of about 3, with extreme cases up to 7,
consistent with classical IRAS galaxies (Sanders & Mirabel 1996).
A very high proportion (more than 80%) of the galaxies shows narrow
emission lines. The origin of the IR emission at 170
![]() is therefore likely to be a central/circumnuclear engine heating
the dust, just as in IRAS galaxies. The total infrared luminosity
produced by this source is moderate in both our IRAS faint galaxies and in the
FIRBACK galaxies: they can be classified as "luminous infrared
galaxies'', with
is therefore likely to be a central/circumnuclear engine heating
the dust, just as in IRAS galaxies. The total infrared luminosity
produced by this source is moderate in both our IRAS faint galaxies and in the
FIRBACK galaxies: they can be classified as "luminous infrared
galaxies'', with
![]()
![]()
![]() ,
but not ULIRG's.
The dominant energy source is star formation in most
cases (
,
but not ULIRG's.
The dominant energy source is star formation in most
cases (![]() 85% of the galaxies), as indicated by the analysis
of the emission spectrum.
Among the 15% of objects possibly dominated by an AGN, two are the
most luminous and farthest objects of the sample; only one is
dominated by an active nucleus in the
85% of the galaxies), as indicated by the analysis
of the emission spectrum.
Among the 15% of objects possibly dominated by an AGN, two are the
most luminous and farthest objects of the sample; only one is
dominated by an active nucleus in the ![]() sample consisting of
nearby, bright objects.
Consistently with the properties of IRAS galaxies, we find that: i) nearby
luminous infrared galaxies are mainly powered by star formation
and ii) the proportion of AGN increases with the IR luminosity.
sample consisting of
nearby, bright objects.
Consistently with the properties of IRAS galaxies, we find that: i) nearby
luminous infrared galaxies are mainly powered by star formation
and ii) the proportion of AGN increases with the IR luminosity.
The homogeneity of the properties of 80% of the FIRBACK galaxies
analyzed so far allows us to consider them as a population in itself,
characterized by
the following properties: a small redshift (
![]() ), a moderate
IR luminosity (
), a moderate
IR luminosity (
![]() ), a peak
of infrared emission between 100 and 200
), a peak
of infrared emission between 100 and 200 ![]() m, and a main energy source due
to star formation with moderate SF rates (
m, and a main energy source due
to star formation with moderate SF rates (
![]() ). Is this
population "new'' or is it part of another, already known, class of
galaxies? To answer this question, we can compare this FSM sample
to three other samples of infrared galaxies: the 15
). Is this
population "new'' or is it part of another, already known, class of
galaxies? To answer this question, we can compare this FSM sample
to three other samples of infrared galaxies: the 15 ![]() m-selected sample
of Elbaz et al. (2002), our sample of faint IRAS galaxies, and the
classical IRAS galaxies in the BGS (Soifer et al. 1987; Kim et al. 1995; Veilleux et al. 1995, under others).
m-selected sample
of Elbaz et al. (2002), our sample of faint IRAS galaxies, and the
classical IRAS galaxies in the BGS (Soifer et al. 1987; Kim et al. 1995; Veilleux et al. 1995, under others).
The comparison with the galaxies of Elbaz et al. (2002) in the ISOCAM
15 ![]() m survey shows that the
two population differ rather widely. Elbaz et al. found a higher density of objects in the HDF-N (40 galaxies at
S15 >
0.1 mJy over a field of 26'2), but their survey is also deeper:
0.1 mJy at
m survey shows that the
two population differ rather widely. Elbaz et al. found a higher density of objects in the HDF-N (40 galaxies at
S15 >
0.1 mJy over a field of 26'2), but their survey is also deeper:
0.1 mJy at
![]() m corresponds to 4.5 mJy at
m corresponds to 4.5 mJy at
![]() m with our template SED, and this leads to galaxies
more luminous on the average, and at higher redshift (<z> = 0.8).
But the FSM galaxies cannot be simply interpreted as corresponding to the
closest and coldest tail of the distribution of Elbaz's objects:
those have a very low
infrared luminosity and usually no emission line, contrary to the FSM galaxies.
The FSM galaxies resemble in fact much more to their
highest redshift objects. The two populations are therefore quite different.
The comparison can however not be pushed much further, in particular
the comparison of the SED's, as no far-IR measurements are available
for Elbaz's sample.
m with our template SED, and this leads to galaxies
more luminous on the average, and at higher redshift (<z> = 0.8).
But the FSM galaxies cannot be simply interpreted as corresponding to the
closest and coldest tail of the distribution of Elbaz's objects:
those have a very low
infrared luminosity and usually no emission line, contrary to the FSM galaxies.
The FSM galaxies resemble in fact much more to their
highest redshift objects. The two populations are therefore quite different.
The comparison can however not be pushed much further, in particular
the comparison of the SED's, as no far-IR measurements are available
for Elbaz's sample.
On the contrary, the comparison of the FSM galaxies with the very faint IRAS
galaxies selected at 60 ![]() m
shows that the two populations are very similar. All the
properties we were able to measure on both samples are close to identical:
z distribution, average IR luminosity, nature of the
powering source, and star formation rates. With the
available data, it is impossible to distinguish statistically
between the two samples. Unfortunately, because this IRAS sample corresponds
to the faintest detectable galaxies (Bertin et al. 1997) at
m
shows that the two populations are very similar. All the
properties we were able to measure on both samples are close to identical:
z distribution, average IR luminosity, nature of the
powering source, and star formation rates. With the
available data, it is impossible to distinguish statistically
between the two samples. Unfortunately, because this IRAS sample corresponds
to the faintest detectable galaxies (Bertin et al. 1997) at ![]() m,
which is the most sensitive band in the IRAS survey, no
m,
which is the most sensitive band in the IRAS survey, no ![]() m data
are available for them and therefore no dust temperature
estimate can be made, nor a SED derived.
Further measurements with SIRTF will be desirable to better characterize
those objects.
m data
are available for them and therefore no dust temperature
estimate can be made, nor a SED derived.
Further measurements with SIRTF will be desirable to better characterize
those objects.
If we now compare the FSM galaxies with the more classical IRAS galaxies
like the BGS for example, we find many similarities (spectral properties, IR luminosities) but one significant difference: the shape of the infrared SED.
Other deep
samples of IRAS galaxies have focused on the search for ULIRG's and therefore
selected, by definition, objects much warmer than the FSM galaxies. It is
therefore
quite plausible that the majority of faint, unstudied, IRAS galaxies have on
average a colder IR emission than assumed up to now (and than measured in
the few
![]() m selected samples).
Although we cannot exclude at this stage of analysis that the
galaxies picked up here at
m selected samples).
Although we cannot exclude at this stage of analysis that the
galaxies picked up here at ![]() m and the very faint IRAS galaxies
have in fact an even colder infrared emission than
the main IRAS sample, it has been shown in the ISOPHOT serendipity sample by
Stickel et al. (2000) that a cold dust component was present in many
galaxies, so that all these objects could be similar, but
only a detailed analysis of SED's will definitely answer this question.
m and the very faint IRAS galaxies
have in fact an even colder infrared emission than
the main IRAS sample, it has been shown in the ISOPHOT serendipity sample by
Stickel et al. (2000) that a cold dust component was present in many
galaxies, so that all these objects could be similar, but
only a detailed analysis of SED's will definitely answer this question.
The brightest objects of the FIRBACK South Marano survey sample
the same population as the IRAS faint survey: a numerous population of cold,
dusty, nearby galaxies. These galaxies are characterized by:
i) a high density of sources (about 20 per square degree) in
a small volume of the universe, since all these sources lie at
![]() ;
;
ii) a cold IR emission, with a peak of the emission closer to ![]() m
than to
m
than to ![]() m;
m;
iii) a moderate IR luminosity in the LIRG range
(
![]() ), quite similar to the
"average'' IRAS galaxies;
), quite similar to the
"average'' IRAS galaxies;
iv) a high proportion of star forming objects, though with moderate
SF rates (around ten solar masses per year), and a very small fraction
of active galactic nuclei.
The importance of this "quiet" population of IR galaxies was clearly underestimated in the analysis of the IRAS survey and has to be taken into account in the calculations of the far-IR background. It is now clear that the far-IR background cannot be reproduced only by high-zgalaxies (Lagache et al. 2003), but that closer and colder galaxies are contributing also. Even if their contribution is probably rather low, they will form an important foreground for future infrared deep field observations. The relative contributions of nearby galaxies and of distant objects in the far-IR selected samples in particular, and in the far-IR background in general, will be estimated more precisely when we have completed the survey of fainter objects in the FSM and in the northern fields of the FIRBACK survey.