A&A 412, 271-280 (2003)
DOI: 10.1051/0004-6361:20031407

Effect of anisotropic velocity distribution on the linear polarization of coronal lines

Does the ion cyclotron exist in the inner corona?

N.-E. Raouafi[*] - S. K. Solanki

Max-Planck-Institut für Aeronomie, Max-Planck-Str. 2, 37191 Katlenburg-Lindau, Germany

Received 16 September 2002 / Accepted 3 September 2003

Abstract
The effect of an anisotropic velocity field distribution of scattering ions on the polarization parameters of a spectral line emitted by resonance scattering is considered. The anisotropy of the velocity field distribution can be interpreted in terms of the ion-cyclotron effect that is believed to influence some heavy ions in the solar corona. We present a theoretical study of the Stokes parameters of a spectral line emitted by atoms or ions in the presence of a bi-Maxwellian velocity field distribution. It is found from test calculations that such a distribution measurably changes the polarization properties of the $O {\sc vi}$ D2 coronal line. Consequently, measurements of the linear polarization of this line may serve as a new diagnostic of a possible bi-Maxwellian velocity distribution. As a preliminary application, the obtained theoretical results are used to interpret the polarization parameters of the $O {\sc vi}$ D2 coronal line ( $\lambda1031.92$) measured using SUMER/SoHO observations. The obtained results are compatible with SUMER's observations for more reasonable solar wind parameters than for an isotropic velocity field distribution of the scattering ions. Thus, the outflow velocity field vector of the emitting ions is less inclined with respect to the polar axis of the Sun (the minimal value of the polar angle $\eta $ is $8^{\circ}$ for an anisotropic velocity distribution versus  $17^{\circ}$ for an isotropic velocity field distribution). These results are obtained assuming that the re-emitted photons come from a small area in the center of the coronal polar hole, with zero magnetic field. Since SUMER/SoHO observations integrate over the line of sight, the results of the current analysis must be considered preliminary pending computations including an integration along the line of sight.

Key words: polarization - scattering - line: profiles - Sun: corona - Sun: solar wind - Sun: UV radiation

1 Introduction

Spectropolarimetry of coronal ultraviolet lines which are sensitive to the effect of the Doppler redistribution due to ion motion and/or to the effect of the coronal magnetic field (Hanle effect, see Mitchell & Zemansky 1934) could yield more accurate information about the physical conditions of the coronal plasma. In fact, spectropolarimetry provides access to the magnetic field vector as well as the velocity field vector (see Raouafi et al. 2002a; Sahal-Bréchot et al. 1998). In contrast, without polarimetric information the spectroscopy of lines only provides partial information on the vectorial quantities, basically through Doppler shifts.

The $O {\sc vi}$  $\lambda1031.92$ line (hereafter D2 line) is one of the strongest emitted by the solar corona up to high altitudes, as demonstrated by Vial et al. (1980); Kohl et al. (1998); Xing Li et al. (1998); and other papers related to UVCS (Ultraviolet Coronagraph Spectrometer: Kohl et al. 1995 & 1997) aboard of SoHO (the Solar and Heliospheric Observatory: Domingo et al. 1995). The $O {\sc vi}$ D2 line (and also the $O {\sc vi}$  $\lambda1037.61$ line, hereafter $O {\sc vi}$ D1) is formed in the chromosphere-corona transition region. In the corona, the O5+ ions are excited by isotropic electronic collisions (which do not create polarization in the Zeeman sub-levels of the excited ions) and by the unpolarized photons with a somewhat anisotropic distribution (due to the center-to-limb brightening) coming from the underlying transition region. The partial anisotropy of the radiation coming from the chromosphere-corona transition region creates the partial linear polarization of the $O {\sc vi}$ D2 coronal line detected for the first time by Raouafi et al. (1999a) in observations performed by the SUMER spectrometer (Solar Ultraviolet Measurements of Emitted Radiation; Wilhelm et al. 1995, 1997; Lemaire et al. 1997) on SoHO. These observations are raster sequences performed at different angles with respect to the polar axis of the Sun by rotating the SoHO spacecraft and moving SUMER's slit laterally. The area common to all the rasters is centered on the polar axis. The observations are described in detail by Raouafi et al. (1999).

The present paper is the third of a series of papers on the interpretation of the linear polarization parameters of the $O {\sc vi}$ D2 line. The goal is the determination of the velocity field vector in the solar corona, which is dominated by the solar wind at increasing distance from the Sun. Raouafi et al. (2002a) showed that the Doppler redistribution effect (due to the ions' motion with an isotropic velocity distribution and a drift velocity vector) on the linear polarization of the $O {\sc vi}$ D2 coronal line gives results in agreement with SUMER/SoHO observations. However, the obtained solutions correspond to velocity field vectors (solar wind velocity field vectors) with relatively high inclinations with respect to the polar axis. Thus the minimal value of the polar angle $\eta $ of the velocity field vector of the solar wind with respect to the polar axis (Pz) is $17\hbox {$^\circ $ }$ (see Fig. 1). This is unsatisfactory because although the expansion of the coronal structures in the polar holes is non-radial, these latter are quasi-radial at the altitudes where SUMER/SoHO observations were carried out (1.29 $R_{\odot}$ from the center of the Sun) (see Fig. 1 in Wilhelm et al. 1998). Raouafi et al. (2002b) showed also that the combination of the Doppler redistribution effect with the Hanle effect due to the coronal magnetic field gives better results than those obtained for the case of the Doppler redistribution alone. In the present paper, we consider the influence of an anisotropic coronal velocity field on the polarization of the $O {\sc vi}$ D2. The effect of the magnetic field is not taken into account in the present paper. In fact the expected range of the coronal magnetic strength is at the lower edge of the interval of the $O {\sc vi}$ D2 line's sensitivity to the Hanle effect. For such field strengths the effect of Doppler redistribution is more important than that of the coronal magnetic field. The combined effect of a magnetic field and of anisotropic velocity distribution of the scattering ions will be the subject of a future investigation, together with the effect of the integration along the line of sight.

Observations performed by UVCS/SoHO (Kohl et al. 1995) show that line profiles of some of the minor ions (O5+ and Mg9+) of the solar corona indicate the presence of two components. One is a very broad component with a Doppler width corresponding to temperatures of many million Kelvin. This component provides the dominant contribution to the spectral line at high altitudes where evidence of anisotropic velocity field distribution is obtained from the observed line profiles combined with the intensity ratio of the D1 and D2 lines of the O5+ doublet (e.g. Kohl et al. 1998; Cranmer et al. 1999; Cranmer 2001). The outflow speeds of O5+ ions are also found to be higher than expected for most of the coronal ions. A promising interpretation of these unexpected observational results proposes the transport of energy by magnetohydrodynamic waves at the cyclotron frequencies of the heavy particles in the local magnetic field (e.g. Kohl et al. 1999; Cranmer 2000; Markovskii 2001; Gary et al. 2001; Isenberg 2001; Axford & McKenzie 2002).

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS3088_Fig1.eps} \end{figure} Figure 1: Definition of the different axes and angles used for the calculation of the effect of an anisotropy of the velocity field distribution on the polarization parameters of a spectral line. The scattering atoms or ions are located in a small volume around P. They interact with electrons with an isotropic velocity distribution and with the radiation coming from the transition region located in the spherical cap (shaded area on the solar disk). $\alpha $ and $\beta $ are the angular coordinates of the unitary vector ${\textbf {\textit {n}}}$ that is directed along a radiation beam coming from a small area centered on M. The velocity field distribution of the atoms and ions is considered to be a bi-Maxwellian with a drift velocity field vector ${\textbf {\textit {V}}}$. The angular coordinates $(\eta,~\psi)$ of ${\textbf {\textit {V}}}$ in the frame (Pxyz) are given in the panel in the top-right of the present figure. The line of sight (PZ) is in the scattering plane (yPz) and makes an angle $\theta $ with the polar axis (Pz).
Open with DEXTER

The paper is structured as follows. In Sect. 2, we present theoretical results concerning the Stokes parameters of spectral lines emitted by resonance scattering by atoms or ions in the presence of an anisotropic velocity field distribution. In Sect. 3, we present numerical calculations showing the effect of the anisotropy of the velocity field distribution on the polarization parameters of the re-emitted line. In Sect. 4, as an application of the obtained results, we apply the theory developed in this paper to the interpretation of the polarimetric measurements made by SUMER/SoHO (Wilhelm et al. 1995) of the linear polarization parameters of the $O {\sc vi}$ D2 coronal line and the intensity ratio of the $O {\sc vi}$ doublet. Finally, in Sect. 5 the results are discussed.

2 Basic theory

The equations presented by Raouafi (2000, 2002) describing the Stokes parameters of a resonantly scattering spectral line sensitive to the Hanle and Doppler redistribution effects are general. They give the Stokes parameters as a function of the velocity vector of the scattering atoms (or ions) and the local magnetic field vector (the coronal magnetic field vector in the solar case) they are immersed in. However, the relevant equations show that both effects are decoupled. In the limit of zero magnetic field, the results of Sahal-Bréchot et al. (1998) are recovered which were derived considering only the effect of the velocity field. To obtain the magnetic field effect alone it is sufficient to eliminate the dimming term by cancelling the macroscopic velocity field vector of the scattering ions, and we obtain the results of Sahal-Bréchot et al. (1986).

Raouafi (2000 & 2002) derived the general expressions giving the linear polarization of a spectral line created by resonance scattering that is sensitive to the Doppler redistribution due to the motion of the scattering atoms (or ions) and/or to the Hanle effect caused by a local magnetic field. A particular case is that of coronal lines scattered by lithium-like ions (O5+, N4+, C3+, ...). The general form of the Stokes parameters of the re-emitted radiation (here we only take into account the linear polarization) is given by (Eq. (20) in Raouafi 2002)

\begin{displaymath}{\cal{S}}_i({{\vec{v}}},{\textbf{\textit{B}}})= {\displaystyl... ...ul}~{\cal{A}}_{{\cal{S}}_{i}} \right] } \hspace{.5cm} i=0,1,2. \end{displaymath} (1)

${\cal{S}}_i$ represents the Stokes parameters ${\cal{I}}$, ${\cal{Q}}$ and ${\cal{U}}$ describing emissivity and linear polarization of the scattered spectral line. ${{\vec{v}}}$ and ${\textbf{\textit{B}}}$ denote the velocity and magnetic vectors, respectively. ${\textbf{\textit{B}}}$ enters through the phase matrix, but here we consider B=0. $\delta_{0i}$ is the Dirac function and $\left[\delta_{0i} + c_{ul}~{\cal{A}}_{{\cal{S}}_{i}}\right]$ is the phase-matrix, with cul being equal to the coefficient $W_2(J,J^\prime)$ in Landi Degl'Innocenti (1984) (see also Landi Degl'Innocenti & Landi Degl'Innocenti 1988; Stenflo 1994). ${\cal{I}}_{\rm {inc}}(\alpha,\beta,\nu)$ is the emissivity profile of the incident spectral line as a function of the frequency $\nu$ and the direction of incidence given by the angles $\alpha $ and $\beta $ (illustrated in Fig. 1). $N_{\rm {i}}$ is the number of scattering ions per unit volume, ${N_{\rm {e}}}$ is the electron density (cm-3) and $T_{\rm {e}}$ is the electron temperature. ${\alpha}_{lu}(T_{\rm {e}})$ is the coefficient of electronic collisions and Blu is the Einstein coefficient for absorption. $F({{\vec{v}}})$ is the velocity field distribution of the scattering ions. The quantities ${\cal{A}}_{{\cal{S}}_{i}}$ are the elements of the phase-matrix and are given by Sahal-Bréchot et al. (1998) for spectral lines sensitive only to the Doppler redistribution (the effect of the macroscopic velocity field of the scattering ions) and by Raouafi (2002) for spectral lines sensitive to the effects of the Doppler redistribution and the magnetic field (Hanle effect) acting simultaneously. In the present paper, we will limit ourselves hereafter to the effect of the Doppler redistribution alone (zero magnetic field limit).

In order to obtain the Stokes profiles as a function of the scattered radiation frequency $\nu$, one needs to average the previous expression over all the atoms or ions having $v_{\scriptscriptstyle{Z}}$ along the line of sight. This could be achieved by a double integration over the velocity field components $v_{\scriptscriptstyle{X}}$ and $v_{\scriptscriptstyle{Y}}$ in the plane perpendicular to the line of sight (inset of Fig. 1). They are given (in photons s-1 cm-3 Hz-1 str-1) by

 
$\displaystyle {\cal{S}}_i(\nu)~ {\rm {d}}\nu = {\rm {d}}v_{\scriptscriptstyle{Z... ...c{v}}})~ {\rm {d}}v_{\scriptscriptstyle{X}}~{\rm {d}}v_{\scriptscriptstyle{Y}}.$     (2)

The expressions of the Stokes parameters of the scattered radiation given by Eq. (2) are general. In particular, there is no assumption about the incident line profile nor about the solar wind velocity field distribution of the scattering ions. If we assume that the incident line profile is Gaussian, as given by
 
$\displaystyle \begin{array}{ll} {\displaystyle{\cal{I}}_{\rm {inc}}(\alpha,\bet... ...tit{n}}} }} {{\displaystyle \alpha_{\rm {inc}}}}\right)^2\right] }, \end{array}$     (3)

where $\alpha_{\rm {inc}}$ is the width of the incident line profile, $I_{\rm C}$ is the specific intensity emitted from the center of the solar disk (integrated over the whole line profile), $f(\alpha,\beta)$ is the variation of the emissivity of different parts of the solar disk. In the case where the scattering ions are illuminated by a homogeneous area (such as a spherical cap that is part of the transition region, as illustrated in Fig. 1) this function is reduced to a limb-brightening function that depends only on the angle $\alpha $. We make use of this simplification in the rest of the paper. We further assume that the scattering ions have an anisotropic velocity field distribution given by a bi-Maxwellian of the form

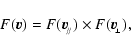\begin{displaymath}F({{\vec{v}}})=F({{\vec{v}}}_{\!_{/\!/}})\times F({{\vec{v}}}_{\!_\perp}), \end{displaymath} (4)

where ${{\vec{v}}}_{\!_{/\!/}}$ and ${{\vec{v}}}_{{\!_\perp}}$ are the components of the atomic velocity field vectors in the directions parallel and perpendicular to the coronal magnetic field vector, respectively. This velocity field distribution can be interpreted by the ion cyclotron effect observed by UVCS/SoHO at heliocentric latitudes greater than 1.5 $R_{\odot}$ in the polar coronal holes (Kohl et al. 1999). $F({{\vec{v}}}_{\!_{/\!/}})$ and $F({{\vec{v}}}_{{\!_\perp}})$ are the distributions of the velocity field parallel and perpendicular to the direction of the magnetic field and are given by

\begin{displaymath}F({{\vec{v}}}_{\!_{/\!/}})=\frac{1}{\sqrt{\pi}~\alpha_{\!_{/\... ...}}-{\textbf{\textit{V}}}}{\alpha_{\!_{/\!/}}}\right)^2\right], \end{displaymath}


\begin{displaymath}F({{\vec{v}}}_{\!_\perp})=\frac{1}{\pi~\alpha_{\!_\perp}^2}~\... ...{\vec{v}}}_{\!_\perp}}{\alpha_{\!_\perp}}\right)^2\right]\cdot \end{displaymath} (5)

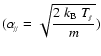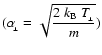${\displaystyle (\alpha_{\!_{/\!/}}=\sqrt{\frac{2~k_{\rm B}~T_{\!_{/\!/}}}{m}})}$ and ${\displaystyle(\alpha_{\!_\perp}=\sqrt{\frac{2~k_{\rm B}~T_{\!_\perp}}{m}})}$ are, respectively, the widths in the directions parallel and perpendicular to the magnetic field vector. $k_{\rm B}$ is the Boltzmann constant and m is the atomic (or ionic) mass. $T_{\!_{/\!/}}$ and $T_{\!_\perp}$ are the ionic temperatures in the directions parallel and perpendicular to the magnetic field, respectively.

For the radiative term in Eq. (2), the integration over the velocity field components perpendicular to the line of sight is achieved by integrating the velocity field distribution $F({{\vec{v}}})$ multiplied by the Gaussian term in the incident line profile of Eq. (3)

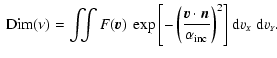$\displaystyle \begin{array}{l} {\displaystyle {\rm {Dim}}(\nu)= \int\!\!\!\int ... ...m {d}}v_{\scriptscriptstyle{X}}~{\rm {d}}v_{\scriptscriptstyle{Y}}. \end{array}$     (6)

For the electronic term, the contribution to the Stokes parameters is given by an integration of the velocity field distribution over the velocity components on the plane perpendicular to the line of sight ( $v_{\scriptscriptstyle{X}}$ and $v_{\scriptscriptstyle{Y}}$). This comes from the fact that electrons are much faster than protons and heavy ions, so that the atomic motion can be neglected when an electron interacts with a scattering ion. In fact, electrons see ions at rest when they interact with them. Equation (6) can be integrated analytically, giving
$\displaystyle \begin{array}{l} {\displaystyle{\rm {Dim}}(\nu)= \frac{1}{~\pi~\a... ...lpha_{\!_{/\!/}}}~\frac{\Delta_3}{\Delta_1}\right)^2\right] } \cdot \end{array}$     (7)

The full expressions for $\Delta_1$, $\Delta_2$, $\Delta_3$ and $\Delta_4$ are given in Appendix A. Then the Stokes profiles of the re-emitted radiation as a function of the frequency of the scattered photons are given by
 
$\displaystyle \begin{array}{l} {\cal{S}}_i(\nu)= {\displaystyle\frac{N_{\rm {i}... ...{\cal{S}}_{i}} \right] }, \vspace{0.25cm}\\ \hspace{3.cm} i=0,1,2. \end{array}$     (8)

Here $v_{\scriptscriptstyle{Z}}$ is the component of the macroscopic velocity field vector of the scattering ions along the line of sight. It is related to the frequency of the scattered photons by
$\displaystyle \nu=\frac{\nu_0}{c}~v_{\scriptscriptstyle{Z}}.$     (9)

$\nu_0$ is the rest frequency of the emitted line (central frequency of the line emitted by ions at rest) and c is the light speed.

In order to obtain the Stokes parameters integrated over the line profile of the scattered radiation, we need to integrate Eq. (8) over the frequency $\nu$. This is equivalent to integrating over $v_{\scriptscriptstyle{Z}}$ and could be also done analytically. For the collisional part of Eq. (8), the integration gives

 
$\displaystyle \begin{array}{l} {\cal{S}}_{i,{\rm {col}}}= {\displaystyle\frac{N... ..._{lu}(T_{\rm {e}})}{4~\pi}~ ~ \delta_{0i} } \hspace{1.5cm} i=0,1,2. \end{array}$     (10)

For the radiative part, we obtain the so-called dimming term that is given by
$\displaystyle \displaystyle {\rm {Dim}}=\frac{1}{\sqrt\pi~\alpha_{\rm {inc}}~\a... ...\!_{/\!/}}}\bigg)^2 \frac{\Delta_2+\Delta_3^2}{\Delta_1~\Delta_4} }\right]\cdot$     (11)

Finally, we obtain
                               $\displaystyle {\cal{S}}_i$ = $\displaystyle \frac{N_{\rm {i}}~{N_{\rm e}}~{\alpha}_{lu}(T_{\rm {e}})}{4~\pi}~... ...i\right)^2~\sqrt\pi~\alpha_{\rm {inc}}~\alpha _{\!_{/\!/}}~\alpha_{\!_\perp}^2}$  
    $\displaystyle \times \int_{\alpha}\!{\rm {d}}\alpha~\sin\alpha \int_{\beta}\!{\rm {d}}\beta~f(\alpha,\beta) \frac{1}{\sqrt{\Delta_1}}~$  
    $\displaystyle \times\exp\left[{\bigg(\frac{V}{\alpha_{\!_{/\!/}}}\bigg)^2 \frac{\Delta_2+\Delta_3^2}{\Delta_1~\Delta_4} }\right]$  
    $\displaystyle \times\left[\delta_{0i} + c_{ul}~{\cal{A}}_{{\cal{S}}_{i}} \right] , \hspace{1.5cm} i=0,1,2.$ (12)

For $\alpha_{\!_{/\!/}}=\alpha_{\!_\perp}$, i.e. for an isotropic velocity field distribution with a drift velocity field vector, we recover results given by Raouafi (2002). Note that the system is Markovian and that we adopt the same approximations as in Raouafi (2002), which basically are the impact approximation and the "no-back reaction'' approximation.

3 Numerical results


  \begin{figure} \par\includegraphics[width=18cm,clip]{MS3088_Fig2.eps} \end{figure} Figure 2: Top panels give the degree of linear polarization as a function of the azimuthal angle $\psi $ (of the macroscopic velocity field vector ${\textbf {\textit {V}}}$) for different values of the polar angle $\eta $ (see lower right panel for a legend) and for outflow speeds of 10, 20 and 27 km s-1 (left, middle and right panels, respectively). The bottom panels exhibit the rotation angle of the direction of linear polarization with respect to the tangent to the solar limb. The ratio of the widths of the velocity field distribution in the directions parallel and perpendicular to the magnetic field ( $\alpha_{\!_{/\!/}}$ and $\alpha_{\!_\perp}$, respectively) is set to 2 in the present case, which corresponds roughly to $\alpha_{\!_\perp}\sim54$ km s-1. These curves are obtained for the case of right-angle scattering $(\theta =-\pi /2)$.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=17.4cm,clip]{MS3088_Fig3.eps} \end{figure} Figure 3: The same as Fig. 2, but for outflow speeds of 35, 40 and 50 km s-1 (left, middle and right panels, respectively).
Open with DEXTER

In the present section, we calculate numerically by using the theoretical results obtained in the previous section, the polarization parameters (degree and rotation angle of the direction of linear polarization with respect to the tangent to the solar limb) of the D2 line scattered by the $O {\sc vi}$ coronal ions. For simplicity and in order to compare the present results to those obtained for an isotropic velocity distribution (see Raouafi et al. 2002a), we consider the same system as by Raouafi et al. (2002a). However, we consider a bi-Maxwellian velocity distribution instead of a simple Maxwellian one.

This means that the Doppler width parallel to the magnetic field vector differs from the Doppler width perpendicular to the field. In a first approximation, the Doppler width of the re-emitted line is in this case given by

 
$\displaystyle \begin{array}{l} \displaystyle\alpha_{\mbox{obs}}\approx\alpha_{\... ...\left(\frac{\alpha _{\!_\perp}}{\alpha_{\!_{/\!/}}}\right)^4 }\cdot \end{array}$     (13)

The quantities $A_{\scriptscriptstyle{Z}},B_{\scriptscriptstyle{Z}},C_{\scriptscriptstyle{Z}}$ are defined in the Appendix. The second term of Eq. (13) is the Doppler width of the profile of the electronic contribution within a volume element. At $1.3~R_{\odot}$, the measured width of the D2 coronal line of the O5+ ion is equal to $\sim $55 km s-1. We have chosen in a next step to numerically test how changing the ratio $\displaystyle{(\alpha _{\!_\perp}}/{\alpha_{\!_{/\!/}})}$ between values of 1 and 5 affects the consistency with the observations. In order to remain consistent with $\alpha_{\rm obs}$ we allow, for a given $\displaystyle{(\alpha _{\!_\perp}}/{\alpha_{\!_{/\!/}})}$, the values of  $\alpha_{\!_\perp}$ and $\alpha_{\!_{/\!/}}$ to vary, with the additional constraint that Eq. (13) must be satisfied. Since $\alpha_{\!_{/\!/}}$ and $\alpha_{\!_\perp}$ are functions of $\eta, \psi$ (the angular coordinates of the outflow velocity vector) and the scattering angle $\theta $ (we have chosen values ranging from 1 to 5) this is only possible iteratively.

We consider scattering ions that are located in an infinitesimal volume around the point P on the polar axis at $1.29~R_{\odot}$ from the solar center. They are illuminated by the partially anisotropic radiation coming from a spherical cap that contains a polar hole with axial symmetry. The polar hole has a radius of $0.5~R_{\odot}$. The emitting ions interact also with electrons with an isotropic distribution. The considered electron density[*]  ${N_{\rm {e}}}$ is $3.5 \times 10^6$ cm-3 and the collision coefficient ${\alpha}_{lu}(T_{\rm {e}})$ is $1.9\times10^{-8}$ cm-3 s-1 (Sahal-Bréchot et al. 1986). We take into account also the limb-brightening function given by Raouafi et al. (2002a). The re-emitted photons are observed at a scattering angle $\theta $ equal to $-83\hbox{$^\circ$ }$. The Einstein coefficient Blu is determined from the atomic data given by Sahal-Bréchot et al. (1986) and the specific intensity $I_{\rm C}$ is determined from SUMER/SoHO observations and is equal to $386\pm15$ erg s-1 cm-2 str-1.

For weak values of the outflow speed (V<27 km s-1), the Doppler redistribution effect is depolarizing for the re-emitted radiation. The depolarization increases with the outflow speed (compare left and middle top panels of Fig. 2, note the small decrease in the y-axis numbers) and with the polar angle $\eta $ (compare different lines in the top left or middle panels of Fig. 2 which range from $\eta=0\hbox{$^\circ$ }$ for the topmost line to $\eta=30\hbox{$^\circ$ }$ for the lowest). This is until a given limit of around 27 km s-1 where the velocity effect becomes polarizing for some ranges of the azimuthal angle $\psi $ (see top-right panel in Fig. 2). Beyond this limit, the depolarization of the scattered radiation due to the Doppler redistribution increases with the outflow speed and decreases with the polar angle $\eta $ (see top panels of Fig. 3). For this range of outflow speeds (beyond the limit of 27 km s-1), the shapes of the curves giving the polarization parameters as a function of the azimuthal angle $\psi $ are similar to those obtained with an isotropic velocity distribution. Curves given by speeds around 27 km s-1 are between those obtained for the two ranges of outflow speed (see top-right panel of Fig. 2; for V=27 km s-1).

The curves giving the rotation angle of the direction of linear polarization with respect to the tangent to the solar limb (Px) are quasi-sinusoidal for outflow speeds far away from the limit of V=27 km s-1. The amplitude of these curves has the same behavior as that obtained for the polarization degree (see bottom panels of Figs. 2 and 3). The variation of the amplitude of the curves of the rotation angle of the polarization direction with the outflow speed and the polar angle is clearer than for the polarization degree. The curves giving the polarization parameters as a function of the azimuthal angle $\psi $ for the low speeds are shifted by $\pi$ with respect to those given by values greater than $\sim $20 km s-1 of the outflow speed (see Figs. 2 and 3).

Note that the amplitudes of the different curves increases with the ratio $\displaystyle{(\alpha _{\!_\perp}}/{\alpha_{\!_{/\!/}})}$. The position of the critical limit between weak and strong outflow speeds does not change very much with this ratio ($\sim $24 km s-1 for $\displaystyle({\alpha _{\!_\perp}}/{\alpha_{\!_{/\!/}}}=1.5)$, 27 km s-1 for $\displaystyle({\alpha _{\!_\perp}}/{\alpha_{\!_{/\!/}}}=2)$ and 28 km s-1 for $\displaystyle({\alpha _{\!_\perp}}/{\alpha_{\!_{/\!/}}}=3)$).

Compared to the effect of an isotropic velocity field distribution (a Maxwellian with a drift velocity field vector, for more details see Raouafi et al. 2002a), an anisotropic velocity field distribution has an important effect on the direction of linear polarization. The effect on the degree of linear polarization is less important (see Figs. 2 and 3 and compare with Figs. 8-10 of Raouafi et al. 2002a). In fact, with an anisotropic velocity field distribution we obtain more rotation of the direction of linear polarization for all the polar angle values. Significant values of the rotation angle of the linear polarization are obtained for high outflow speeds beyond the second limit.

4 Application: Interpretation of the linear polarization of the O VI D2 coronal line measured by SUMER/SoHO

The SUMER spectrometer operating on board the SoHO spacecraft is sensitive to the linear polarization of the observed light due to oblique reflections in the instrument, which have different reflection coefficients for orthogonal linear polarizations ($\sim $37% at $\sim $1000 Å) (Wilhelm et al. 1995; Hassler et al. 1997). It has been used to analyze the linear polarization of the $O {\sc vi}$ D2 coronal line. The net linear polarization is obtained by subtracting two intensity measurements from each other, one obtained before, the other after rotating the whole SoHO spacecraft by $90\hbox{$^\circ$ }$ around its optical axis. The observations recorded by SUMER/SoHO on March 19 1996 are described by Raouafi et al. (1999 & 2002a). The obtained degree of linear polarization integrated over the line profile is found to be equal to $p= 9\% \pm2\%$. The rotation angle of the direction of linear polarization with respect to the tangent to the solar limb is found to be equal to $+9\hbox{$^\circ$ }\pm 6\hbox{$^\circ$ }$. The mean intensity ratio of the $O {\sc vi}$ doublet $\left({\cal{I}}_{{\rm {D}}_2}/{\cal{I}}_{{\rm {D}}_1}\right)$ is found to be $2.88\pm0.05$ (for more details, see Raouafi et al. 2002a).

Raouafi et al. (2002a) found that the Doppler redistribution effect due to the scattering ions' motion, together with an isotropic velocity field distribution (Maxwellian with a drift velocity field that could be equated to the outflow velocity field vector of the solar wind) reproduces very well the measured values. It provides strong constraints on the outflow speed of the solar wind in the polar holes. However, the velocity field vectors corresponding to the obtained solutions have a relatively high inclination angle with respect to the polar axis of the Sun (minimal value of the inclination angle $\eta $ is $17\hbox {$^\circ $ }$ with respect to the polar axis (Pz) in Fig. 1). In the polar hole of the solar corona, one expects that velocity field vectors are more or less radial directly above the pole (neglecting contributions from fore- or background material). Raouafi et al. (2002b) showed also that the combination of the Doppler redistribution effect with the Hanle effect due to the coronal magnetic field gives better results. It sets constraints on the solar wind velocity field and on the coronal magnetic field vectors in the polar holes at a heliocentric distance of $1.29~R_{\odot}$. Nonetheless the inclination angles with respect to the polar axis of the vectors corresponding to the numerical solutions remain relatively high.

In the present section, we apply the theoretical results obtained above to the case of the $O {\sc vi}$ D2 coronal line. We consider an anisotropic bi-Maxwellian velocity field distribution. The outflow speed of the solar wind is given by the drift velocity field vector parallel to the coronal magnetic field. Both the strength and direction of the velocity vector are allowed to vary.

As in Raouafi et al. (2002a & 2002b), we calculate the degree and rotation angle of the direction of linear polarization with respect to the tangent to the solar limb ((Px) in Fig. 1). We calculate also the intensity ratio $\left({\cal{I}}_{{\rm {D}}_2}/{\cal{I}}_{{\rm {D}}_1}\right)$ of the $O {\sc vi}$ doublet D1 and D2. After comparison of the obtained results with the measured values, we keep only velocity field vectors which give linear polarization degree in the observed range $\left[7\%,~11\%\right]$, rotation angle of the direction of linear polarization in the range $\left[3\hbox{$^\circ$ },~15\hbox{$^\circ$ }\right]$ and an intensity ratio of the $O {\sc vi}$ doublet within the range $\left[2.83,~2.93\right]$. We first carry out the calculations for the case $\alpha_{\!_{/\!/}}<\alpha_{\!_\perp}$ which is consistent with the UVCS/SoHO measurements.

In the present case, we consider $O {\sc vi}$ ions to be contained in an infinitesimal volume on the polar axis at a heliocentric distance of $1.29~R_{\odot}$. The influence of an extended distribution of the gas along the line-of-sight will be studied in a forthcoming paper. They re-emit by resonant scattering the partially anisotropic and unpolarized radiation coming from the underlying chromosphere-corona transition region. They are also excited by isotropic electron collisions that do not create polarization in the Zeeman levels of the excited ions. The electron density is taken to be equal to $3.5 \times 10^6$ cm-3. The re-emitted photons are observed under a scattering angle of $-83\hbox{$^\circ$ }$. These are the same conditions considered by Raouafi et al. (2002a,b) to study the effect of the Doppler redistribution on the polarization of the $O {\sc vi}$ D2 line and the intensity ratio of the D2 and D1 lines of the  $O {\sc vi}$ ion.

4.1 The case of $\alpha_{\!_{/\!/}}<\alpha_{\!_\perp}$

We consider a bi-Maxwellian velocity distribution with widths  $\alpha_{\!_{/\!/}}$ in the direction parallel to the coronal magnetic field and  $\alpha_{\!_\perp}$ in the direction perpendicular to the coronal magnetic field vector that correspond to different values of the ratio $(\alpha_{\!_\perp}/\alpha_{\!_{/\!/})}$ and satisfy Eq. (13). These parameters are qualitatively consistent with the results obtained from UVCS/SoHO, although the latter refer to larger radial distances from the Sun's surface. For the numerical calculations, the outflow speed varies from 0 to 100 km s-1, the polar angle $\eta $ varies from $0\hbox{$^\circ$ }$ to $90\hbox{$^\circ$ }$ and the azimuth angle varies from  $0\hbox{$^\circ$ }$ to $2~\pi$. For the interpretation of the numerical results, we adopt the polar angle ranges considered by Raouafi et al. (2002a,b):

$\bullet$
weak inclinations $(0\hbox{$^\circ$ }\le\eta\le20\hbox{$^\circ$ })$;
$\bullet$
weak + medium inclinations ( $0\hbox{$^\circ$ }\le\eta\le30\hbox{$^\circ$ }$);
$\bullet$
weak + medium + strong inclinations ( $0\hbox{$^\circ$ }\le\eta\le90\hbox{$^\circ$ }$).
The range of the outflow velocity values that give numerical results compatible with the observation depends on the polar angle range (direction of the velocity vector) and also on the rratio $(\alpha_{\!_\perp}/\alpha_{\!_{/\!/})}$. For $(\alpha_{\!_\perp}/\alpha_{\!_{/\!/}})>1$, the lowest outflow velocity that gives numerical results in agreement with the observations is equal to $\sim $34 km s-1 with polar angles greater than  $20\hbox{$^\circ$ }$ (see Table 1). By increasing the macroscopic speed of the scattering ions, good agreement with the measurements is obtained for velocity vectors with lower inclinations with respect to the polar axis. This is demonstrated in Fig. 4. The lowest value of the achieved polar angle is  $8\hbox {$^\circ $ }$ and corresponds to speeds of around 41 km s-1 (lower panel of Fig. 4). Velocity field vectors with weak inclinations give results consistent with the SUMER/SoHO data only for strengths within the range of $\sim $35 and 42 km s-1 (within the limitations of the present analysis). If we also consider vectors with medium polar angle values, then flow speeds between 34 and $\sim $43 km s-1 give results in agreement with the measurements. If one also allows for vectors with strong inclinations, we obtain good results between 34 to $\sim $48 km s-1. However, inclinations > $30\hbox{$^\circ$ }$ are too large for a location just at the solar pole, when overlying a coronal hole.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS3088_Fig4.eps} \end{figure} Figure 4: $(\eta,~\psi)$ diagrams giving the angular coordinates of velocity field vectors with strengths of 41 km s-1 that correspond to numerical solutions in agreement with SUMER/SoHO measurements of the polarization and width of the D2 line and of the intensity ratio of the  $O {\sc vi}$ doublet. The top panel corresponds to $\displaystyle({\alpha _{\!_\perp}}/{\alpha_{\!_{/\!/}}}=1.5)$ and the bottom one corresponds to $\displaystyle({\alpha _{\!_\perp}}/{\alpha_{\!_{/\!/}}}=3)$. The velocity field distribution underlying the shaded areas is considered to be a bi-Maxwellian with a drift velocity field parallel to the magnetic field vector. Velocity field vectors with weak inclinations that reproduce the data lie within the range $\sim $36-42 km s-1. The lowest value of the polar angle of the velocity field vector giving good results is equal to $8\hbox {$^\circ $ }$ and corresponds to a speed of 41 km s-1. It is lower than for an isotropic velocity field distribution where the lowest value of $\eta $ was found equal to $17\hbox {$^\circ $ }$. For comparison, the valid solutions obtained for speeds of 41 km s-1 for an isotropic velocity field distribution lie inside the contours overplotted on each panel (see Raouafi et al. 2002a).
Open with DEXTER

In Fig. 5 we summarize the minimum angle $\eta $ obtained for different values of the ratio $(\alpha_{\!_\perp}/\alpha_{\!_{/\!/})}$. Clearly, $\eta_{\rm min}$ drops rapidly from its value at $(\alpha_{\!_\perp}/\alpha_{\!_{/\!/}})=1$ ( $17\hbox {$^\circ $ }$) before reaching an asymptotic value of close to $7\hbox{$^\circ$ }$ for $(\alpha_{\!_\perp}/\alpha_{\!_{/\!/}})\ge4$. Due to the unrealistically narrow $\alpha_{\!_{/\!/}}$ profiles resulting from the requirement of simultaneously also satisfying Eq. (13) we consider only $(\alpha_{\!_\perp}/\alpha_{\!_{/\!/}})\le3$ to be realistic.

The observations are thus reproduced for more reasonable parameters in the case of $\alpha_{\!_\perp}>\alpha_{\!_{/\!/}}$ than for $\alpha_{\!_\perp}=\alpha_{\!_{/\!/}}$. Are the Stokes measurements of the $O {\sc vi}$ lines thus providing support for an anisotropic temperature and eventually for ion-cyclotron waves? To test the uniqueness of the result obtained in this section we consider, for comparison, the opposite case, namely $\alpha_{\!_\perp}<\alpha_{\!_{/\!/}}$ in the following section.

4.2 The case of $\alpha_{\!_{/\!/}}>\alpha_{\!_\perp}$

For values of the ratio $(\alpha_{\!_\perp}/\alpha_{\!_{/\!/})}$ smaller than 1, we also obtain results compatible with the observations. The obtained results are similar to those obtained for the case of an isotropic velocity distribution. The minimal value of the polar angle is $16\hbox{$^\circ$ }$ and corresponds to $(\alpha_{\!_\perp}/\alpha_{\!_{/\!/}})=0.85$. We are aware that in the coronal case, one expects that the ion temperature in the direction perpendicular to the magnetic field be higher than that in the parallel direction. These calculations are just for purposes of comparison. They demonstrate that the sign of the difference  $(\alpha_{\!_{/\!/}}-\alpha_{\!_\perp})$ cannot be determined with sufficient accuracy from current SUMER/SoHO observations.

5 Discussion

Table 1: Limits of the outflow speeds providing results in agreement with the observations and corresponding to different values of the ratio $(\alpha_{\!_\perp}/\alpha_{\!_{/\!/})}$ and to different ranges of the polar angle $\eta $ (weak inclinations, weak + medium inclinations and weak + medium+ strong inclinations, respectively). The outflow speed V is in km s-1.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS3088_Fig5.eps} \end{figure} Figure 5: Minimal values of the polar angle $\eta $ of the outflow velocity vector plotted as a function of the ratio $(\alpha_{\!_\perp}/\alpha_{\!_{/\!/})}$.
Open with DEXTER

We have considered the effect of an anisotropic velocity distribution on the intensity and polarization properties of optically thin spectral lines. We have then applied the general theory to the specific case of the D1 and D2 lines of O VI. Evidence for an anisotropic velocity distribution in the solar corona has been provided by observations made by the UVCS instrument on SoHO (Kohl et al. 1998, 1999). The anisotropy of the velocity field distribution can be interpreted in terms of ion cyclotron waves which, according to theoretical models, could exist everywhere in the solar corona (Marsch 1999; Marsch & Tu 2001; Tu & Marsch 2001; Vocks & Marsch 2001, 2002).

We find that the velocity field anisotropy has a significant effect on the direction of linear polarization. It also influences the degree of linear polarization and the intensity ratio, but these effects are less important for the velocities we consider here. In fact, the polar angle of velocity field vectors giving results compatible with the observations goes down to  $8\hbox {$^\circ $ }$; while for an isotropic velocity field distribution the lowest value of the polar angle is  $17\hbox {$^\circ $ }$. Since the SUMER/SoHO data we compare with were recorded directly above the pole in a coronal hole, the results obtained by taking into account a bi-Maxwellian velocity field distribution are more apropriate than those obtained with a simple Maxwellian velocity field distribution.

In both cases $\alpha_{\!_{/\!/}}<\alpha_{\!_\perp}$ and $\alpha_{\!_{/\!/}}>\alpha_{\!_\perp}$ (independently of the physical significance of these two cases, particularly the second one), the obtained results fit very well the measured values. Note that up until this date at very low altitudes in the corona (< $1.35~R_{\odot}$ from the center of the Sun) there is no observational proof of an anisotropic temperature distribution of the scattering ions. The UVCS/SoHO data refer to $r>1.7~R_{\odot}$, while SUMER/SoHO data, which we compare to our calculations, were obtained at $1.29~R_{\odot}$. The relevant UVCS/SoHO observations at high altitudes (> $1.7~R_{\odot}$ from solar center) are interpreted such that the ion temperature in the direction perpendicular to the coronal magnetic field is much higher than that in the direction parallel to the magnetic field vector.

In summary, we have shown that the linear polarization measured in coronal holes above the solar limb can serve as a diagnostic of an anisotropic velocity distribution. A simple analysis provides results that favor the presence of an anisotropic velocity distribution. However, there remains a need to find more concrete evidence of an anisotropic temperature at the heights considered here. To enhance the reliability of the current results we need to study the simultaneous influence of a magnetic field and an anisotropic velocity distribution, as well as the effect of the 3D geometry of the coronal magnetic field on the observations (e.g., influence of the presence of inhomogeneities on the radiation integrated along the line of sight).

Acknowledgements
The authors gratefully acknowledge an anonymous referee for constractive critics and E. Marsch for helpful discussions.

  
Appendix A: Stokes parameters

The quantities $\Delta_1$, $\Delta_2$, $\Delta_3$ and $\Delta_4$ first appearing in Eq. (7) are given by

                                 $\displaystyle \Delta_1$ = $\displaystyle (S_{\scriptscriptstyle{X}}~S_{\scriptscriptstyle{Y}}~S_{\scriptsc... ...iptscriptstyle{YZ}})^2-(S_{\scriptscriptstyle{Y}}~S_{\scriptscriptstyle{XZ}})^2$  
    $\displaystyle -(S_{\scriptscriptstyle{Z}}~S_{\scriptscriptstyle{XY}})^2+2~S_{\scriptscriptstyle{XY}}~S_{\scriptscriptstyle{XZ}}~S_{\scriptscriptstyle{YZ}} ,$  
                             $\displaystyle \Delta_2$ = $\displaystyle \big((A_{\scriptscriptstyle{X}}~S_{\scriptscriptstyle{Y}})^2+(A_{... ...criptscriptstyle{X}})^2-(S_{\scriptscriptstyle{X}}~S_{\scriptscriptstyle{Y}})^2$  
    $\displaystyle -2~A_{\scriptscriptstyle{X}}~A_{\scriptscriptstyle{Y}}~S_{\scriptscriptstyle{XY}}+S_{\scriptscriptstyle{XY}}^2\big)~\Delta_1 ,$  
                                          $\displaystyle \Delta_3$ = $\displaystyle A_{\scriptscriptstyle{X}}~\big(S_{\scriptscriptstyle{XY}}~S_{\scr... ...iptscriptstyle{XZ}}-S_{\scriptscriptstyle{X}}^2~S_{\scriptscriptstyle{YZ}}\big)$  
    $\displaystyle + A_{\scriptscriptstyle{Z}}~\big((S_{\scriptscriptstyle{X}}~S_{\scriptscriptstyle{Y}})^2-S_{\scriptscriptstyle{XY}}^2\big) ,$  
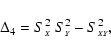\begin{displaymath}\Delta_4= S_{\scriptscriptstyle{X}}^2~S_{\scriptscriptstyle{Y}}^2-S_{\scriptscriptstyle{XY}}^2 , \end{displaymath} (A.1)

where
                                    $\displaystyle S_{\scriptscriptstyle{X}} = \left(A_{\scriptscriptstyle{X}}^2+B_{... ...le{X}}^2+C_{\scriptscriptstyle{X}}^2+D_{\scriptscriptstyle{X}}^2\right)^{1/2} ,$  
    $\displaystyle S_{\scriptscriptstyle{Y}} = \left(A_{\scriptscriptstyle{Y}}^2+B_{... ...le{Y}}^2+C_{\scriptscriptstyle{Y}}^2+D_{\scriptscriptstyle{Y}}^2\right)^{1/2} ,$  
    $\displaystyle S_{\scriptscriptstyle{Z}} = \left(A_{\scriptscriptstyle{Z}}^2+B_{... ...le{Z}}^2+C_{\scriptscriptstyle{Z}}^2+D_{\scriptscriptstyle{Z}}^2\right)^{1/2} ,$  
    $\displaystyle S_{\scriptscriptstyle{XY}}= A_{\scriptscriptstyle{X}}~A_{\scripts... ...C_{\scriptscriptstyle{Y}}+D_{\scriptscriptstyle{X}}~D_{\scriptscriptstyle{Y}} ,$  
    $\displaystyle S_{\scriptscriptstyle{XZ}}= A_{\scriptscriptstyle{X}}~A_{\scripts... ...C_{\scriptscriptstyle{Z}}+D_{\scriptscriptstyle{X}}~D_{\scriptscriptstyle{Z}} ,$  
    $\displaystyle S_{\scriptscriptstyle{YZ}}= A_{\scriptscriptstyle{Y}}~A_{\scripts... ...C_{\scriptscriptstyle{Z}}+D_{\scriptscriptstyle{Y}}~D_{\scriptscriptstyle{Z}} .$ (A.2)

The coefficients $A_{\scriptscriptstyle{X}}$, $A_{\scriptscriptstyle{Y}}$ and $A_{\scriptscriptstyle{Z}}$ are the angular coordinates of  ${{\vec{v}}}_{\!_{/\!/}}/\alpha_{\!_{/\!/}}$ in the frame of the line of sight (PXYZ); Bi and Ci (i=X,Y,Z) are those of ${{\vec{v}}}_{\!_\perp}/\alpha_{\!_\perp}$; and Di are the coordinates of ${\textbf{\textit{n}}}/\alpha_{\rm {inc}}$. They are given by
                                        $\displaystyle A_{\scriptscriptstyle{X}}=\cos\psi~\sin\eta/\alpha_{\!_{/\!/}} ,$  
    $\displaystyle A_{\scriptscriptstyle{Y}}=(\cos\eta~\sin\theta+\cos\theta~\sin\eta~\sin\psi)/\alpha_{\!_{/\!/}} ,$  
    $\displaystyle A_{\scriptscriptstyle{Z}}=(\cos\eta~\cos\theta-\sin\eta~\sin\theta~\sin\psi)/\alpha_{\!_{/\!/}} ,$  
    $\displaystyle B_{\scriptscriptstyle{X}}=(\cos\eta~\cos\psi)/\alpha_{\!_\perp} ,$  
    $\displaystyle B_{\scriptscriptstyle{Y}}=(-\sin\eta~\sin\theta+\cos\eta~\cos\theta~\sin\psi)/\alpha_{\!_\perp} ,$  
    $\displaystyle B_{\scriptscriptstyle{Z}}=(-\cos\theta~\sin\eta-\cos\eta~\sin\theta~\sin\psi)/\alpha_{\!_\perp} ,$  
    $\displaystyle C_{\scriptscriptstyle{X}}=-\sin\psi/\alpha_{\!_\perp} ,$  
    $\displaystyle C_{\scriptscriptstyle{Y}}=\cos\theta~\cos\psi/\alpha_{\!_\perp} ,$  
    $\displaystyle C_{\scriptscriptstyle{Z}}=-\cos\psi~\sin\theta/\alpha_{\!_\perp} ,$  
    $\displaystyle D_{\scriptscriptstyle{X}}=n_{\scriptscriptstyle{X}}/\alpha_{\rm {inc}} ,$  
    $\displaystyle D_{\scriptscriptstyle{Y}}=n_{\scriptscriptstyle{Y}}/\alpha_{\rm {inc}} ,$  
    $\displaystyle D_{\scriptscriptstyle{Z}}=n_{\scriptscriptstyle{Z}}/\alpha_{\rm {inc}}.$ (A.3)

$\theta $ is the scattering angle; $\eta $ and $\psi $ are, respectively, the polar angle and the azimuthal angle of the vector ${\textbf{\textit{n}}}_{\!_{/\!/}}/\alpha_{\rm {inc}}$ (see Fig. 1), while ${\textbf{\textit{n}}}_{\!_{/\!/}}$ is the unit vector along the direction of ${{\vec{v}}}_{\!_{/\!/}}$ $\displaystyle\left({\textbf{\textit{n}}}_{\!_{/\!/}}=\frac{{{\vec{v}}}_{\!_{/\!... ...rac{{\textbf{\textit{V}}}}{\parallel{\textbf{\textit{V}}}\parallel}\right)\cdot$

References


Copyright ESO 2003