A&A 412, 257-265 (2003)
DOI: 10.1051/0004-6361:20031361
J. M. Jensen1,2 - F. P. Pijpers1
1 - Theoretical Astrophysics Center, Institute for Physics and
Astronomy, Aarhus University, 8000 Aarhus C, Denmark
2 -
Department of Earth Sciences, University of Aarhus, Denmark
Received 22 December 2000 / Accepted 19 August 2003
Abstract
The study of the solar convection zone has been given a new impetus
with what
promises to be a very powerful new tool in time-distance
helioseismology (Duvall et al. 1993). Using data obtained with
this technique, it has become possible to do a tomographic
reconstruction of structures in the convection zone. Most of the
work done on inversion of these data has relied on the ray
approximation to deliver sensitivity kernels for the inversion
procedures (Kosovichev 1996).
Inversions using non ray-theoretical kernels were shown by
Jensen et al. (2001).
In this paper we go beyond the ray
approximation and derive sensitivity kernels based on the Rytov
approximation and Green's function theory. We derive an expression
for the sensitivity kernel using ray-based Green's functions and
show how further approximations can be done to increase the
computational efficiency.
Key words: Sun: helioseismology - Sun: general
For more than a decade helioseismology has been unraveling the secrets of the solar interior by inferring the solar properties from measurements of eigenmode frequencies. From these measurements it has been possible to obtain very detailed knowledge about the global structure of the sun through the use of inversion techniques. Since this method uses the eigenmodes of the entire sun it is difficult to obtain information about very localized structures. A further problem is the inability of the global helioseismic method to resolve any azimuthal variations. Using the newly developed technique of time-distance helioseismology (Duvall et al. 1993) it has become possible to measure travel times of acoustic waves between different points on the solar surface. From these measurements it is possible to obtain information about very localized structures such as sun spots (Kosovichev 1996), convection cells (Kosovichev & Duvall 1997) and meridional flows (Giles et al. 1997). This information is obtained using inversion techniques which are very similar to those used in terrestrial seismology. To use these inversion techniques it is necessary to obtain sensitivity kernels that describe the forward problem. Previous inversion studies of helioseismic time-distance data used sensitivity kernels obtained in the ray approximation (Kosovichev 1996; Kosovichev & Duvall 1997; Giles et al. 1997). This high-frequency approximation has also been widely used in terrestrial seismology with great success even though its validity can be questioned in many cases. The approximation is even more questionable in the solar case as the ratio of wavelength to ray length is larger than in the terrestrial case. The fact that the ray approximation is not strictly applicable for the Sun was pointed out by Bogdan (1997), who showed that a wave packet propagating in a solar-like atmosphere is not confined to the ray path but samples a large volume of the surrounding medium. Spetzler & Snieder (2001) examined the regimes of validity for ray theory and scattering theory. They found that the scattering theory is superior when the inhomogenieties are smaller than the widths of the first Fresnel zone. This is often the case in time-distance helioseismology. The problem with the ray approximation is well known in geophysics and several suggestions about how to calculate sensitivity kernels for sound-speed perturbations without the ray approximation have been made (e.g. Woodward 1992; Snieder & Lomax; 1996; Marquering et al. 1999). Such sensitivity kernels have also been calculated for the helioseismic case (Birch & Kosovichev 2000; Jensen et al. 2000b). Jensen et al. (2000a) applied these to synthetic data to test the inversion procedure while Jensen et al. (2001) used such kernels on solar data.
This paper aims to develop these techniques from geophysics to the helioseismic case and to show the theoretical foundation for the approximate sensitivity kernels which were proposed in Jensen et al. (2000b) and applied to data by Jensen et al. (2001) to study sun-spot structures.
We wish to study the propagation and scattering of sound waves in the solar convection zone using diffraction tomography. An early analysis of a similar problem is found in Slaney et al. (1984) for the case of micro-wave tomography.
In Appendix A we derive a wave equation for acoustic waves traveling
in the solar convection zone in the presence of flows.
The wave equation can be written in Fourier domain as
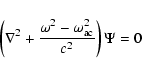 |
(1) |
We now wish to write the wave-propagation problem as a scattering problem
where
sound-speed variations are considered small deviations
from a reference model.
The sound-speed perturbations are
given as
![]() ,
where c0 is the reference
sound-speed model.
The wave equation can be rewritten as
,
where c0 is the reference
sound-speed model.
The wave equation can be rewritten as
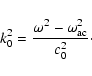 |
(3) |
The wave equation given by Eq. (2) is non linear and in order to solve it one has to apply some approximation. The most widely used approximation is the Born approximation which Birch & Kosovichev (2002) and Gizon & Birch 2002 have used in helioseismology. In the Born approximation one obtains a linear relation between the slowness perturbations of the medium and the scattered wavefield, but it is not straightforward to separate the effects of the perturbation on the phase and amplitude of the scattered waves. This separation occurs naturally in the Rytov approximation which we will use in this paper (for further details on the Rytov approximation see e.g. Ishimaru 1978; Slaney et al. 1984 or Snieder & Lomax 1996). In the helioseismic literature the Rytov approximation has previously been used by Brüggen 2000 to investigate the effect of solar convection of the eigen-mode frequencies.
The Rytov approximation is derived from the wavefield expressed
as
Inserting Eq. (4) into the wave equation yields
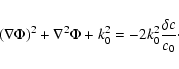 |
(12) |
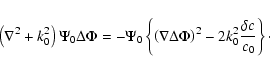 |
(13) |
Inserting the expression for the object function
into Eq. (15) and introducing the Rytov
wave path,
![]() ,
we get
,
we get
![\begin{figure}
\par\includegraphics[clip,width=8.4cm]{Fig1a.eps}\\
\includegraphics[clip,width=8.4cm]{Fig1b.eps}\end{figure}](/articles/aa/full/2003/47/aa10610/Timg58.gif) |
Figure 1: Horizontal and vertical cross section of the imaginary part of a Rytov wave path in a homogeneous medium. The reference velocity is 20 km s-1 and the period is 5 min. Light areas corresponds to positive sensitivity and dark areas to negative sensitivity |
| Open with DEXTER | |
In time-distance helioseismology the wavefield is not directly measured.
The (processed) data are usually in the
form of a correlation C between the radial velocity measured at two
areas on the solar surface (cf. Duvall 1993; D'Silva 1996a):
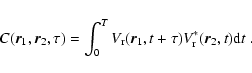 |
(21) |
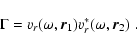 |
(22) |
| |
= | ||
| = | |||
| = | |||
| (23) |
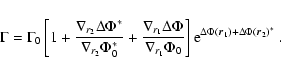 |
(24) |
When evaluating
![]() and
and
![]() one has to remember that the source of the waves is the
turbulence generated by convection. Thus the source is a
distributed source rather than a localized one.
For a distributed noise source,
one has to remember that the source of the waves is the
turbulence generated by convection. Thus the source is a
distributed source rather than a localized one.
For a distributed noise source,
![]() ,
the background wave field is given as
,
the background wave field is given as
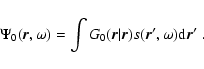 |
(25) |
In practice time-distance helioseismology has worked with arrival times obtained in a way described in Appendix C, for which one can work with either the wavefield or the correlation function. Since the wavefield and correlation function behave in much the same way the differences between the arrival times extracted from them should be small. The theory in this paper has been applied to the wavefield but could just as well be applied to the correlation function. For full waveform analysis one should use the correlation function as described here.
Since the imaginary part of the complex phase-function perturbation is
sensitive to the phase perturbation it is sensitive to the travel-time delays.
In Appendix C we show how to obtain information about the travel-time
perturbation from the imaginary part of the phase-function perturbation.
For a monochromatic wavefield the travel-time perturbation is
given by
![]() ,
where the subscript i denotes the measurement configuration.
Together with Eq. (18) this gives the travel-time perturbation as
,
where the subscript i denotes the measurement configuration.
Together with Eq. (18) this gives the travel-time perturbation as
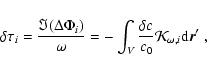 |
(26) |
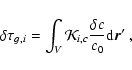 |
(30) |
In the case of the phase travel time the perturbations are shown in
Appendix C to be given as
The equations of this section show how to calculate sensitivity kernels from knowledge of the Green's function for the reference medium and the power spectrum. These equations are a general result which is independent of the way the Green's functions are calculated. In the following sections we will show one way of calculating Green's function and examples of sensitivity kernels obtained using these Green's functions. The kernels given here are a generalized form of what Woodward (1992) called the bandlimited ray path, and Snieder & Lomax (1996) proved a similar result for the travel time of narrow-band signals.
We assume the reference medium is sufficiently smooth for the ray
approximation to be valid thus we can solve Eq. (16) using
the ray approximation and thereby obtain an expression for
![]() .
In the following we will consider a source
at
.
In the following we will consider a source
at
![]() .
To find the solution we
write G0 as a function of a slowly varying amplitude and
a phase as
.
To find the solution we
write G0 as a function of a slowly varying amplitude and
a phase as
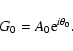 |
(33) |
In the regions where the acoustic cut-off frequency is small
the group- and phase travel times become identical.
The travel-time perturbations corresponds to the group travel-time
perturbations given by Eq. (29).
In this case the Green's functions are given as
Another way of obtaining Green's functions is from the global eigenmodes. If
we have the complete set of eigenfunctions (![]() )
and the corresponding
eigenvalues (
)
and the corresponding
eigenvalues (
![]() )
then the Green's function is given by (Zwillinger 1989)
)
then the Green's function is given by (Zwillinger 1989)
To obtain a sensitivity kernel for the travel time we insert
Eq. (34)
into Eq. (20).
This gives an expression for the
Rytov wave path as
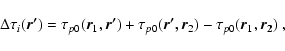 |
(41) |
The spectrum of the solar oscillation spans a range of frequencies with a peak around periods of five minutes. To obtain a frequency-integrated sensitivity kernel for the solar case we use a Gaussian power spectrum with a central frequency of 3.15 mHz and a FWHM of 1.5 mHz. Figure 3 shows a frequency-integrated sensitivity kernel obtained, using this power spectrum along with Eqs. (31), and (42). Here we see that the sensitivity kernel has the shape of a hollow banana. The shape of the kernel, with the property that the sensitivity is zero along the ray path, gave rise to what is called the banana-doughnut paradox by Marquering et al. (1999). We see in Fig. 3 that the single-frequency sensitivity kernels interfere destructively in the outer Fresnel zones and constructively in the first Fresnel zone. This illustrates the finding of Snieder & Lomax (1996) that the travel-time perturbations can be written as an averaging integral over the first Fresnel zone. Similar effects were also noted by Woodward (1992).
In the preceding section we calculated frequency-integrated sensitivity kernels using the ray-based Green's functions. In this section we show how examples of approximation which can be made to simplify the amplitude terms or the frequency integration. We then investigate the effects of these approximations on the kernels. The point of this section is twofold. First we wish to shown how to efficiently calculte approximate kernels which are an improvement over the Fresnel volumes or "fat rays'' suggested in terrestrial seismology (e.g. Cervený & Soares 1992; Husen & Kissling 2001) Secondly we wish to show how the sensitivity kernels suggested and used by Jensen et al. (2000a, 2000b, 2001) are related to the frequency integrated kernels.
![\begin{figure}
\par\includegraphics[clip,width=8.4cm]{Fig2a.eps}\\
\includegraphics[clip,width=8.4cm]{Fig2b.eps}\end{figure}](/articles/aa/full/2003/47/aa10610/Timg110.gif) |
Figure 2: Cross sections along and perpendicular to the ray path of single frequency sensitivity kernel obtained from ray based Green's functions for a frequency of 3.2 mHz. The kernels are normalized by c02. The solid line in the upper panel shows the ray path. |
| Open with DEXTER | |
As shown in Appendix D the amplitude can be approximated in terms
of the travel time as
![]() which corresponds
to the amplitude in the homogeneous case.
If we use these approximate amplitudes
we find that the sensitivity kernel is given by
which corresponds
to the amplitude in the homogeneous case.
If we use these approximate amplitudes
we find that the sensitivity kernel is given by
In order to emulate the effect of cancellation outside the first
Fresnel zone
Jensen et al. (2000b) used a Gaussian envelope to restrict the sensitivity to
the first few Fresnel zones for the two dimensional problem.
In three dimensions an approximate kernel obtained from this approach
is given by:
![\begin{figure}
\par\includegraphics[clip,width=8.4cm]{Fig3a.eps}\\
\includegraphics[clip,width=8.4cm]{Fig3b.eps}\end{figure}](/articles/aa/full/2003/47/aa10610/Timg117.gif) |
Figure 3: Cross sections along and perpendicular to the ray path of sensitivity kernel obtained from ray based Green's functions for a Gaussian frequency profile (see text). The kernels are normalized by c02. The solid line in the upper panel shows the ray path. |
| Open with DEXTER | |
If we take Eq. (42) as the central frequency kernel and
use a Gaussian to emulate the cancellation outside the first
Fresnel zone as in Eq. (44) we obtain for the
approximate sensitivity kernel for sound-speed perturbations:
![\begin{figure}
\par\includegraphics[clip,width=8.3cm]{Fig4a.eps}\\
\includegraphics[clip,width=8.3cm]{Fig4b.eps}\end{figure}](/articles/aa/full/2003/47/aa10610/Timg125.gif) |
Figure 4:
Sensitivity variation with depth across the ray path
at a distance of 3 Mm (top) and 20 Mm (bottom)
from the source. Shown are
|
| Open with DEXTER | |
Figure 4 shows two cross sections through the different kernels.
One cross section is taken halfway between ![]() and
and
![]() at a distance of 20 Mm
right where the ray has its turning point. The
other is taken much closer to
at a distance of 20 Mm
right where the ray has its turning point. The
other is taken much closer to ![]() at a distance of 3 Mm from it.
First of all we can see that the use of a Gaussian to emulate
the frequency integration works well as the two kernels,
at a distance of 3 Mm from it.
First of all we can see that the use of a Gaussian to emulate
the frequency integration works well as the two kernels,
![]() and
and
![]() ,
are very similar.
One difference between the two kernels is that the approximate
kernel is a bit wider than the frequency-integrated kernel. This
is due to the factor
,
are very similar.
One difference between the two kernels is that the approximate
kernel is a bit wider than the frequency-integrated kernel. This
is due to the factor ![]() in the expression for
in the expression for
![]() (Eq. (31)). This factor
increases the influence of the high-frequency single-frequency
kernels and since these kernels have smaller first Fresnel zones
than the kernel at the central frequency we see this shrinking of
the frequency-integrated kernel.
(Eq. (31)). This factor
increases the influence of the high-frequency single-frequency
kernels and since these kernels have smaller first Fresnel zones
than the kernel at the central frequency we see this shrinking of
the frequency-integrated kernel.
The last kernel,
![]() ,
has the same
overall shape as the other kernels but the amplitude is more off.
It is lower than the other kernels in the cross section close to
,
has the same
overall shape as the other kernels but the amplitude is more off.
It is lower than the other kernels in the cross section close to
![]() and higher in the other cross section. This is because
the amplitudes were approximated using just knowledge of the travel times.
Thus although
and higher in the other cross section. This is because
the amplitudes were approximated using just knowledge of the travel times.
Thus although
![]() is not in as good
agreement with
is not in as good
agreement with
![]() as
as
![]() it gives
a very efficient way of calculating a kernel which is in reasonable
good agreement with the frequency-integrated sensitivity kernel.
it gives
a very efficient way of calculating a kernel which is in reasonable
good agreement with the frequency-integrated sensitivity kernel.
Jensen et al. (2001) showed the first inversion results obtained using
non-ray sensitivity kernels. The kernels they used were similar to
![]() ,
except for a factor of 1/c0which unfortunately was obmitted in the earlier kernels.
Inversions using the new kernels show that the same overall structures
can be recovered although some of the details change.
Use of the more correct kernels in the inversion procedures should increase
the reliability of the results.
,
except for a factor of 1/c0which unfortunately was obmitted in the earlier kernels.
Inversions using the new kernels show that the same overall structures
can be recovered although some of the details change.
Use of the more correct kernels in the inversion procedures should increase
the reliability of the results.
Figure 5 shows a comparison between our frequency-integrated sensitivity kernels, Born kernels obtained from global modes and ray-theoretical kernels. The kernels shown are one-dimensional kernels for a sound-speed perturbation which is spherical or planar depending on the geometry of the kernels. The Born kernels are described in Birch & Kosovichev (2000a) and are obtained in a spherical geometry whereas the frequency-integrated kernels are calculated for a planar geometry. Both kernels use the Gaussian power spectrum described in Sect. 8. Two different ray-theoretical kernels are shown; one obtained in a spherical geometry which includes the effect of the acoustic cut-off frequency and one obtained in a planar geometry neglecting the acoustic cut-off frequency. All kernels are for an offset of 10 heliospheric degrees.
We here see that the shape of the frequency-integrated kernel and the Born kernel are very similar although there are some differences. The amplitude of the frequency-integrated kernel is larger near the ray turning point than the amplitude of the Born kernel. The right panel of Fig. 5 shows a close up of the kernels near the surface. Here the Born kernel shows some oscillations which the frequency-integrated kernel lacks. We can also see that the frequency-integrated kernel and the Born kernel follow the ray path from the same geometry close to the surface. For the ray kernels the differences near the surface are due to the effect of the acoustic cut-off frequency while the differences near the turning point are due to geometrical effects. The differences between the frequency-integrated kernel and the Born kernel can be due to geometrical effects, the neglecting of the acoustic-cut-off frequency, different filtering and the use of different approximations (Rytov and Born approximations). The exact causes of the discrepancies are not yet fully understood.
Birch & Kosovichev (2001) showed a comparison between one-dimensional sensitivity kernels obtained from a global-mode approach in the Born approximation (Birch & Kosovichev 2000a) and ray theoretical sensitivity kernels. Their Fig. 1 shows the sensitivity kernels for an offset of 22.5 degrees. By comparing this figure with our Fig. 5 we can see that since the ratio of wavelength to ray length is smaller for the larger offset the kernel is closer to the ray kernel although there still are larger discrepancies near the upper and lower turning point.
![\begin{figure}
\par\includegraphics[clip,width=8.4cm]{Fig5.eps}\\
\end{figure}](/articles/aa/full/2003/47/aa10610/Timg128.gif) |
Figure 5: Comparison of 1D sensitivity kernels for an offset of 10 heliospheric degrees. Shown are a frequency-integrated sensitivity kernel (solid) and a ray-approximation kernel (dashed) both obtained in a planar geometry and without inclusion of the acoustic cut-off frequency These are shown together with a sensitivity kernel obtained from global-mode summation (dash-dotted) and a ray-approximation kernel (dotted), both from a spherical geometry with inclusion of the acoustic cut-off frequency. To the right is shown a close up of the kernels near the surface. |
| Open with DEXTER | |
The theory presented in this paper show how to calculate sensitivity kernels for a point to point measurement geometry. In time-distance helioseismology normal practice has been to correlate a central pont with an surrounding annulus or quadrants of such an annulus (e.g. Duvall et al. 1996). D'Silva (2001) showed that the travel time obtained from this procedure is the average of the point to point travel times weighted with the wave field amplitude. The frequency-integrated kernels presented in this paper are an weighted average over frequency. It is straight forward to expand this weighted average to also include the spatial averaging.
The Green's functions used to calculate the sensitivity kernels have been calculated without inclusion of the acoustic cut-off frequency. The equations for the frequency-integrated kernels presented in Sect. 7 are independent of the approximations made in calculation of the Green's functions and the same expressions for the sensitivity kernels can be used to calculate kernels taking the acoustic cut-off frequency into account The same holds true for the expressions for approximate sensitivity kernels except where noted in the text.
In time-distance helioseismology measurements are made for waves traveling in opposite directions. The differences and averages of these measurements are then taken in order to isolate the effects of sound-speed perturbations from flows (see e.g. Kosovichev & Duvall 1997). In this paper only kernels concerning sound-speed perturbations have been calculated and a future goal is to extend the theory to include flows. Another goal for future work is to derive a wave theoretical treatment of wave propagation in the presence of magnetic structures in the solar convection zone. This will be necessary in order to fully investigate sunspots and other magnetic features in the Sun.
In this paper we show how to compute sensitivity kernels for helioseismic time-distance tomography using the Rytov approximation and the Green's function approach.
The use of non ray-theoretical kernels in the inversion of helioseismic time-distance data increases the accuracy of the inversion results. Preliminary tests using similar two-dimensional kernels (Jensen et al. 2000a) demonstrate this. These kernels along with rapid inversion techniques such as the MultiChannelDeconvolution technique (Jacobsen et al. 1999) provides a powerful tool which would allow reliable fast inversion of helioseismic time-distance data.
Expressions for both the group- and phase travel-time perturbations are given in this paper. Using these expressions the differences between the group- and phase travel-time perturbations could be used to improve the inversions.
It is also shown that the full correlation function can be directly related to the slowness perturbations through a linear inverse equation for which the kernels are derived. This opens the way for full waveform inversion on the time-distance data.
Acknowledgements
The authors wish to thank Aaron Birch for providing the one dimensional Born kernels and ray kernels for the spherical geometry and for fruitfull discussions. JMJ especially wishes to acknowledge Aaron Birchs help regarding sensitivity kernels for flows. This research was supported by the Danish National Research Foundation through the establishment of the Theoretical Astrophysics Center. The authors also wish to thank an anonymous referee for helping improve the original manuscript.
In this Appendix we derive a wave equation for acoustic waves traveling in the solar convection zone in the presence of subsurface flows and magnetic fields. The derivation for stratified media follows work done by Gough (1993), while Christensen-Dalsgaard (1997) treat flows. Here we present a treatment which include both effects and derive a wave equation for this case.
| (A.1) | |||
| (A.2) | |||
| (A.3) |
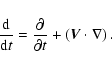 |
(A.4) |
| (A.5) | |||
| (A.6) | |||
| (A.7) |
| (A.8) |
We now consider the effect of density stratification.
Here the perturbed equations are
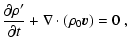 |
(A.9) | ||
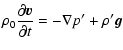 |
(A.10) | ||
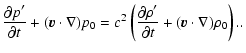 |
(A.11) | ||
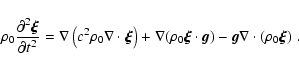 |
(A.12) |
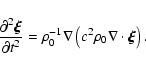 |
(A.13) |
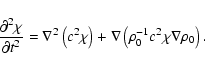 |
(A.14) |
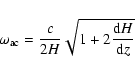 |
(A.16) |
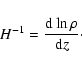 |
(A.17) |
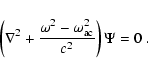 |
(A.18) |
We wish to obtain a wave equation for the complex phase
perturbation
![]() .
One way of doing this was demonstrated by Slaney et al. (1984)
and we follow their approach here.
Inserting Eq. (4) into the wave equation
and using that
.
One way of doing this was demonstrated by Slaney et al. (1984)
and we follow their approach here.
Inserting Eq. (4) into the wave equation
and using that
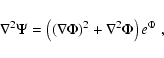 |
(B.1) |
We wish to determine travel-time differences
by fitting the perturbed wavefield to the
unperturbed wavefield. The method described here is a generalisation
of the method employed by Snieder & Lomax (1996).
We assume that the wave field (or correlation function) can be described
by a Gabor wavelet which is a cosine modulated with a Gaussian envelope.
D'Silva (1996a) and Kosovichev & Duvall (1997) both showed that the
correlation function can be written in this way using a ray theoretical
approach and a global mode approach respectively.
This gives the wave field or correlation function as
![\begin{displaymath}\Psi_0(t) =
A \exp \left [- \frac{\delta \omega ^2}{4} (t - \...
... \right ]
\exp \left [ i \omega _0 ( t -\tau_{\rm p}) \right ]
\end{displaymath}](/articles/aa/full/2003/47/aa10610/img166.gif) |
(C.1) |
![\begin{displaymath}\Psi_0(\omega) = A \exp \left [- \frac{(\omega - \omega_0)^2}...
... \left [ - i \omega _0 ( \tau_{\rm g} -\tau_{\rm p}) \right ].
\end{displaymath}](/articles/aa/full/2003/47/aa10610/img170.gif) |
(C.2) |
![\begin{displaymath}\Psi(\omega) = a \Psi_0
\exp \left ( i \omega \delta \tau_{\r...
...mega _0 ( \delta \tau_{\rm g} - \delta \tau_{\rm p}) \right ].
\end{displaymath}](/articles/aa/full/2003/47/aa10610/img173.gif) |
(C.3) |
| M | = | (C.4) | |
| = | (C.5) |
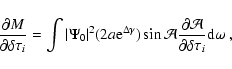 |
(C.7) |
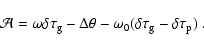 |
(C.8) |
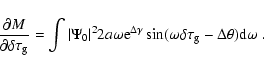 |
(C.9) |
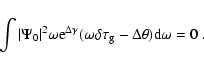 |
(C.10) |
We note that if one used only one travel-time parameter the equation obtained would be identical to this.
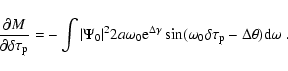 |
(C.12) |
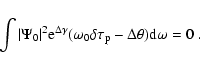 |
(C.13) |
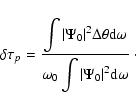 |
(C.14) |
In this appendix we wish to solve the wave equation using
the ray approximations. This will allow us to derive
ray-based Green's functions for the reference medium which can be used
to calculate sensitivity kernels for the perturbed medium
which takes diffraction into account.
All quantities in this appendix are related to the reference model
thus the subscript 0 has been obmitted for ease of notation.
For a more detailed treatment see e.g. Gough (1993).
First we start by writing the wave field in terms of
a slowly varying amplitude and a phase component as
| (D.1) |
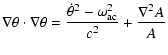 |
(D.2) | ||
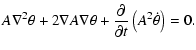 |
(D.3) |
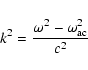 |
(D.5) |
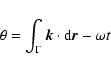 |
(D.6) |
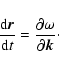 |
(D.7) |
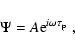 |
(D.8) |
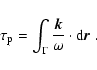 |
(D.9) |
The travel-time perturbation can be calculated using Fermats Principle
which states that to first order a perturbation to ![]() does not perturb the ray path (see e.g. Gough 1993).
The the travel-time perturbation is then given as
does not perturb the ray path (see e.g. Gough 1993).
The the travel-time perturbation is then given as
In a stationary medium the amplitude is also independent of time,
thus the last term in the transport equation is zero.
The remaining terms can with the help of
Eq. (D.4) be rewritten as
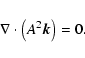 |
(D.11) |
| (D.12) |
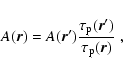 |
(D.14) |
To describe the geometrical behavior of a ray tube in a more
quantitative way one can use the Jacobian of the problem (Jensen
et al. 1994). In three dimensions we have the Jacobian given by:
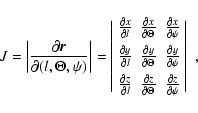 |
(D.16) |
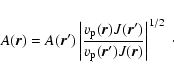 |
(D.17) |