A&A 411, L473-L476 (2003)
DOI: 10.1051/0004-6361:20031299
A new model for brown dwarf spectra including accurate unified line
shape theory for the Na I and K I resonance line profiles
N. F. Allard1,2 - F. Allard3
- P. H. Hauschildt4
- J. F. Kielkopf5 - L. Machin1,3
1 - Institut d'Astrophysique de Paris, CNRS, 98bis boulevard
Arago, 75014 Paris, France
2 -
Observatoire de Paris-Meudon, LERMA, 92195 Meudon Principal
Cedex, France
3 - Centre de Recherche Astronomique de Lyon,
École Normale Supérieure, 69364 Lyon Cedex 07, France
4 - Hamburger Sternwarte, Gojenbergsweg 112, 21029 Hamburg, Germany
5 -
Department of Physics, University of Louisville,
Louisville, KY 40292, USA
Received 28 July 2003 / Accepted 26 August 2003
Abstract
We present the first brown dwarf atmosphere models based
on theoretical calculations of absorption profiles of sodium and
potassium perturbed by helium and molecular hydrogen. The synthetic
spectra have been compared to previous calculations with Lorentz
profiles and the classic van der Waals approximation, and to the
observed spectrum of the T dwarf SDSS 1624. The new
profiles provide increased opacities in the optical spectra of methane
brown dwarfs. However, the potassium and sodium far
wings alone cannot explain the missing opacity in the 0.85 to 1.1 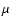 m range.
m range.
Key words: brown dwarfs - line: profiles -
radiation mechanisms: general -
stars: atmospheres
Evolved methane brown dwarfs are hydrogen-rich substellar mass objects
which show methane bands in their spectra. Their atmosphere is
depleted of refractory elements due to grain sedimentation. Resonance
lines of alkali elements can form in deep regions of the atmosphere,
and are the rare remaining sensitive spectral type and atmospheric
parameter indicators. The importance of the far wings of the
potassium doublet, centered at 0.77 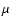 m in spectra of methane brown
dwarfs, has been demonstrated by Burrows et al. (2000). With these
wings defining a pseudo-continuum out to more than 2500 Å from the
line center, it became clear that the classical approximations that
were widely used in main sequence star and brown dwarf model
atmospheres (see e.g. Allard et al. 2001) - Lorentz profiles using
van der Waals damping constants, such as described by Schweitzer et al. (1996) for example - were not appropriate to handle this
situation. This motivated Burrows et al. (2002) to modify Lorentz
profiles, introducing cutoffs and parameters.
m in spectra of methane brown
dwarfs, has been demonstrated by Burrows et al. (2000). With these
wings defining a pseudo-continuum out to more than 2500 Å from the
line center, it became clear that the classical approximations that
were widely used in main sequence star and brown dwarf model
atmospheres (see e.g. Allard et al. 2001) - Lorentz profiles using
van der Waals damping constants, such as described by Schweitzer et al. (1996) for example - were not appropriate to handle this
situation. This motivated Burrows et al. (2002) to modify Lorentz
profiles, introducing cutoffs and parameters.
Fortunately, the broadening of alkali lines by rare gases is a problem
which has been extensively investigated in experimental and
theoretical work (Allard & Kielkopf 1982). Interatomic interactions
are the main physical quantities needed for a good understanding of
collisional processes. The theoretical potentials for the binary
interactions of alkali atoms perturbed by He or H2 were computed
for the lower states to an accuracy suitable for line shape
calculations by Pascale (1983, 2003) and Rossi & Pascale (1985).
This allows us to solve the radiative collision problem given an
appropriate theoretical framework for the line shape. In a recent
paper, Burrows & Volobuyev (2003, hereafter BV), using their
evaluations of multiconfiguration self-consistent field Hartree-Fock
potentials, have calculated the far wing line profiles of the
0.589 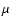 m sodium D and 0.77
m sodium D and 0.77 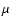 m potassium doublets using the uniform approximation to the wing profile (Szudy & Baylis 1975;
1996). This is a major improvement compared to the unrealistic use of
a Lorentzian so far in the wings. Also, in contrast to a simple
quasistatic model, this formula has no singularity and should in
principle predict the satellite shapes. However, profiles in the
satellite regions were poorly determined by BV, and no applications to
brown dwarfs model atmospheres and synthetic spectra have been
published to this day.
m potassium doublets using the uniform approximation to the wing profile (Szudy & Baylis 1975;
1996). This is a major improvement compared to the unrealistic use of
a Lorentzian so far in the wings. Also, in contrast to a simple
quasistatic model, this formula has no singularity and should in
principle predict the satellite shapes. However, profiles in the
satellite regions were poorly determined by BV, and no applications to
brown dwarfs model atmospheres and synthetic spectra have been
published to this day.
In this paper, we present the first application of accurate
alkali profiles of sodium and potassium doublets to the model
atmospheres and synthetic spectra of brown dwarfs, and we compare the
results and the depth of satellite bands to the observed spectrum of
the T dwarf SDSS 1624.
A theory of spectral line broadening has been developed to calculate
neutral atom spectra given the interaction and transition moments for
relevant states of the radiating atom with other atoms in its
environment. Within this framework it is possible to compute the
complete spectrum with a unified approach. Unlike impact theories of
line broadening which predict a lorentzian line, the classical static
theories that may apply in regions of the near wing, or the
approximation methods of Szudy & Baylis (1975, 1996) used by BV, our
unified theory provides an accurate spectrum from the line center to
the extreme wing. Complete details and the derivation of the theory
are given by Allard et al. (1999). Our approach is based on quantum
theory of spectral line shapes by Baranger (1958a,b) with an adiabatic
representation to include the degeneracy of atomic levels.
![\begin{figure}
\par {\resizebox{8.8cm}{!}{ \includegraphics[clip]{letter_allard_fig1.eps}} }\end{figure}](/articles/aa/full/2003/46/aafg281/Timg8.gif) |
Figure 1:
Variation of the Na and K line profiles perturbed by He with
density
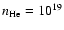 cm-3. The temperatures (top
to bottom) are 3000, 2000, 1000, and 500 K. cm-3. The temperatures (top
to bottom) are 3000, 2000, 1000, and 500 K. |
| Open with DEXTER |
The spectrum can be written as the Fourier transform
of the autocorrelation function of the dipole moment
in the Heisenberg representation
(Allard & Kielkopf 1982)
![\begin{displaymath}F_\nu(\Delta \nu) = {\bf FT} \left[\exp\left(ng(s)\right)\right].
\end{displaymath}](/articles/aa/full/2003/46/aafg281/img9.gif) |
(1) |
For a transition
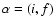 from
initial state i to final state f, we have
from
initial state i to final state f, we have
The e and e' label the energy surfaces on which the interacting
atoms approach the initial and final atomic states of the transition as
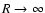 (here R denotes the internuclear distance between
the radiator and the perturber).
The total line strength of the transition is
(here R denotes the internuclear distance between
the radiator and the perturber).
The total line strength of the transition is
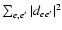 .
The radiative dipole transition moment of each component of the
line depends on R, and changes during the collision. At time t from the point of closest approach for a rectilinear classical path
.
The radiative dipole transition moment of each component of the
line depends on R, and changes during the collision. At time t from the point of closest approach for a rectilinear classical path
![\begin{displaymath}R(t) = \left[\rho^2 + (x + vt)^2 \right]^{1/2} \; , \;
\end{displaymath}](/articles/aa/full/2003/46/aafg281/img17.gif) |
(3) |
where 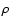 is the impact parameter of the perturber trajectory, and x is the position of the perturber along its trajectory.
We define
is the impact parameter of the perturber trajectory, and x is the position of the perturber along its trajectory.
We define
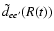 as a modulated dipole
(Allard et al. 1999)
as a modulated dipole
(Allard et al. 1999)
![\begin{displaymath}\tilde{d}_{ee'}[R(t)] =
d_{ee'}[R(t)]{\rm e}^{-\frac{\beta}{2}V_{e}[R(t)] } \; , \;
\end{displaymath}](/articles/aa/full/2003/46/aafg281/img20.gif) |
(4) |
where 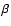 is the inverse temperature (1/kT).
is the inverse temperature (1/kT).
The alkali line profiles and satellites are calculated for physical
conditions encountered in the atmospheres of brown dwarfs. Although
our theory takes into account the effects of multiple close
collisions, for use here we computed the line profile in the low
density limit as described by Allard et al. (1994). This
method uses the expansion of the autocorrelation function in
powers of density. We assume that interactions of an absorbing atom with
more than one perturber do not contribute to the far line wing profile
under conditions in brown dwarf atmospheres.
We used the molecular potentials and dipole moments of Pascale (1983)
for the alkalis perturbed by He.
The shape of the line wing is sensitive to the
difference between the ground and excited state interaction
potentials, and satellites appear corresponding to
extrema in  .
The difference potential energy surfaces
as shown in Figs. 2a and 2b give rise to satellites
in the far wings
positioned at
.
The difference potential energy surfaces
as shown in Figs. 2a and 2b give rise to satellites
in the far wings
positioned at
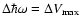 (Allard 1978).
Another important factor is the variation of the radiative dipole
moment during
the collision once modulated by the Boltzmann factor e
-Ve (r)/2kT (Figs. 2a and 2b).
(Allard 1978).
Another important factor is the variation of the radiative dipole
moment during
the collision once modulated by the Boltzmann factor e
-Ve (r)/2kT (Figs. 2a and 2b).
The maxima in the difference potentials 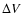 lead to far blue
satellites. Their presence is very sensitive to the temperature due to
the fast variation of the modulated dipole moment with temperature in
the internuclear region where the line satellite is formed
(Figs. 2a and 2b). We present in Fig. 1
the absorption cross section for the resonance lines of Na and K for a
He density of 1019 cm-3 and temperatures from 500 to 3000 K.
The strength of the satellites increases with temperature. For Na,
the satellite due to interactions with He is at 0.52
lead to far blue
satellites. Their presence is very sensitive to the temperature due to
the fast variation of the modulated dipole moment with temperature in
the internuclear region where the line satellite is formed
(Figs. 2a and 2b). We present in Fig. 1
the absorption cross section for the resonance lines of Na and K for a
He density of 1019 cm-3 and temperatures from 500 to 3000 K.
The strength of the satellites increases with temperature. For Na,
the satellite due to interactions with He is at 0.52 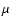 m with
oscillatory structure between the satellite and the line center. For K, the He satellite is at 0.69
m with
oscillatory structure between the satellite and the line center. For K, the He satellite is at 0.69 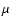 m. At lower temperatures the
satellites are manifested as a distinct break in the line wing
continuum, but at 1000 K and above, there is a broad line-like
maximum, often referred to as a "satellite band.''
m. At lower temperatures the
satellites are manifested as a distinct break in the line wing
continuum, but at 1000 K and above, there is a broad line-like
maximum, often referred to as a "satellite band.''
The alkali-H2 molecular potentials have been calculated by Rossi
& Pascale (1985), but only for the C2v and C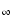 symmetries. We also had to assume that the dipole moment for the
transitions is constant and equal to its asymptotic value, but
modulated by the Boltzmann factor to take into account temperature
effects.
symmetries. We also had to assume that the dipole moment for the
transitions is constant and equal to its asymptotic value, but
modulated by the Boltzmann factor to take into account temperature
effects.
We note the presence of far blue satellites of Na-H2 between 0.49
and 0.508 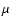 m shown in Fig. 3a. The satellites arising
from potentials with C2v symmetry are more sharply defined and
intense at a given temperature, and closer to the resonance line
center. In Fig. 3b, the blue satellites of K-H2 appear
from 0.67 to 0.69
m shown in Fig. 3a. The satellites arising
from potentials with C2v symmetry are more sharply defined and
intense at a given temperature, and closer to the resonance line
center. In Fig. 3b, the blue satellites of K-H2 appear
from 0.67 to 0.69 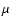 m. These satellite features increase in
strength with temperature over the range of our calculations from 500
to 3000 K. An extended red wing with no satellite structure also
increases with temperature. This is due to contributions from the
difference potentials which do not present extrema.
m. These satellite features increase in
strength with temperature over the range of our calculations from 500
to 3000 K. An extended red wing with no satellite structure also
increases with temperature. This is due to contributions from the
difference potentials which do not present extrema.
![\begin{figure}
\par\mbox{\subfigure[K-He]{\resizebox{8cm}{!}{\includegraphics[cl...
...izebox{8cm}{!}{\includegraphics[clip]{letter_allard_fig2b.eps}} }}\end{figure}](/articles/aa/full/2003/46/aafg281/Timg23.gif) |
Figure 2:
Variation with temperatures of the K-He and K-H2modulated dipole at 3000, 2000, 1000, and 500 K (top to bottom), and
the difference of upper and lower state potentials for the resonance
lines. For K-H2, difference potentials 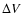 are shown for the C2v (--) and C
are shown for the C2v (--) and C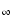 (- - -) symmetries. (- - -) symmetries. |
| Open with DEXTER |
![\begin{figure}
\par\mbox{\subfigure[Na-H$_2$\space profiles.]{\resizebox{8cm}{!}...
...zebox{8cm}{!}{ \includegraphics[clip]{letter_allard_fig3b.eps}} }}\end{figure}](/articles/aa/full/2003/46/aafg281/Timg24.gif) |
Figure 3:
Variation with temperature of the Na and K line profiles
perturbed by H2 for the C2v (--) and
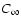 (- - -)
symmetries. The density of perturbers is
(- - -)
symmetries. The density of perturbers is
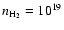 cm-3. The temperatures (top to bottom) are 3000,
2000, 1000, and 500 K. cm-3. The temperatures (top to bottom) are 3000,
2000, 1000, and 500 K. |
| Open with DEXTER |
![\begin{figure}
\par {\resizebox{8.8cm}{!}{
\includegraphics[clip]{letter_allard_fig4.eps}} }\end{figure}](/articles/aa/full/2003/46/aafg281/Timg26.gif) |
Figure 4:
Synthetic spectra obtained with the van der Waals
approximation (dot-dashed line), and with the detailed profiles of Fig. 3 (dotted line) are compared for an effective temperature of 1000 K, surface gravity of
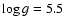 ,
and solar composition. The
observed spectrum of SDSS 1624 (Strauss et al. 1999, full line) is
also shown. The synthetic spectra have been degraded to a 10 Å
resolution thoughout, and the models are converged. ,
and solar composition. The
observed spectrum of SDSS 1624 (Strauss et al. 1999, full line) is
also shown. The synthetic spectra have been degraded to a 10 Å
resolution thoughout, and the models are converged. |
| Open with DEXTER |
We have computed model atmospheres and synthetic spectra using the
Allard et al. (2001) atmosphere program PHOENIX and the new
theoretical Na I D and K I profiles. The results are compared to previous models in
Fig. 4, and demonstrate that these improvements are of
fundamental importance for obtaining a better quantitative
interpretation of the spectra. The new profiles carry significantly
more opacity within the first 1800 Å from the line centers, while
providing less opacity further in the red wings. The optical-to-red
pseudo-continuum is therefore depressed, while raised at the flux
maximum near 1.1 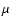 m, compared to models based upon the van der Waals approximation. Figure 4 also shows the observed spectrum
of the T6 methane brown dwarf SDSS 1624. The changes provided by the
new profiles correspond more closely to the strongly depressed red
spectrum of the T dwarf.
m, compared to models based upon the van der Waals approximation. Figure 4 also shows the observed spectrum
of the T6 methane brown dwarf SDSS 1624. The changes provided by the
new profiles correspond more closely to the strongly depressed red
spectrum of the T dwarf.
BV stated that satellites would provide only negligible additional
opacity for these two transitions. Indeed, these features, located
around 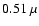 m and
m and 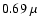 m for the
Na I D and K I
m for the
Na I D and K I 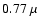 m
doublets respectively, occur in a regime of low emitted flux for such
cool brown dwarfs, and do not affect significantly the balance of
energy and the thermal profile. However, the K I
m
doublets respectively, occur in a regime of low emitted flux for such
cool brown dwarfs, and do not affect significantly the balance of
energy and the thermal profile. However, the K I 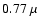 m satellite forms a broad but weak feature in the vicinity of
the Li I transition at 6708 Å, which could be
observable with a resolution better than 10 Å and low noise. This
is not the case of the Keck LRIS
m satellite forms a broad but weak feature in the vicinity of
the Li I transition at 6708 Å, which could be
observable with a resolution better than 10 Å and low noise. This
is not the case of the Keck LRIS
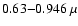 m spectra of SDSS1624 shown in Fig. 4. We have therefore removed the observed
spectrum in Fig. 4 for wavelengths below
m spectra of SDSS1624 shown in Fig. 4. We have therefore removed the observed
spectrum in Fig. 4 for wavelengths below 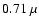 m for
clarity.
m for
clarity.
However we find that the far wings of the potassium and sodium
doublets cannot alone explain the missing opacities between 0.85 and 1.1 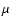 m. Perhaps allowing for contributions of other alkalis such as Rb I and Cs I can resolve this problem. For the systems Rb-He and Cs-He the
line satellites are much closer to the line core, and their effect is
important in the near wing. However, the relative abundances of these
elements are small, and their effect may be negligible.
m. Perhaps allowing for contributions of other alkalis such as Rb I and Cs I can resolve this problem. For the systems Rb-He and Cs-He the
line satellites are much closer to the line core, and their effect is
important in the near wing. However, the relative abundances of these
elements are small, and their effect may be negligible.
Another important point is the use of the low-density limit
for the wing. We have restricted our expansion of the autocorrelation
function to the first order, assuming that interactions with more than
one perturber do not contribute to the profile. This is acceptable if
the density of perturbers at the depth of formation of the wings is
less than 1019 cm-3 for Na I and K I,but it is not correct for higher densities, or when
the line satellites of the alkali-perturber system are closer to the
main line (Allard et al. 2003). This cannot be taken into account in
the uniform approximation of the Frank-Condon theory, and will be included
in future work.
In conclusion we have presented the first application of detailed alkali
profiles in the construction of synthetic spectra for brown dwarf
atmospheres. While the results are encouraging and account for the
observed opacity in the visible spectrum, the
source of additional opacity in the 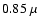 m to
m to 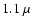 m
region remains a mystery.
m
region remains a mystery.
Acknowledgements
We are grateful to J. Pascale for kindly providing the molecular
potentials and dipole moments, and to S. K. Leggett for providing an
up-to-date observed spectrum of the T6 brown dwarf SDSS 1624.
- Allard, F., Hauschildt, P. H., Alexander, D. R., Tamanai, A.,
& Schweitzer, A. 2001, ApJ, 556, 357
In the text
NASA ADS
- Allard, N. F. 1978, J. Phys. B, 11, 8, 1383
In the text
NASA ADS
- Allard, N. F., & Kielkopf, J. F. 1982, Rev. Mod. Phys., 54, 1103
In the text
NASA ADS
- Allard, N. F., Koester, D., Feautrier, N., & Spielfiedel, A.
1994, A&A, 108, 417
In the text
- Allard, N. F., Royer, A., Kielkopf, J. F., & Feautrier, N.
1999, Phys. Rev. A, 60, 1021
In the text
NASA ADS
- Allard, N. F., Kielkopf, J. F., Hébrard, G., & Peek, J. M. 2003, Eur. Phys. J. D,
submitted
In the text
- Baranger, M. 1958a, Phys. Rev., 111, 481
In the text
NASA ADS
- Baranger, M. 1958b, Phys. Rev., 111, 494
NASA ADS
- Burrows, A., Marley, M. S., & Sharp, C. M. 2000, ApJ, 531, 438
In the text
NASA ADS
- Burrows, A., Burgasser, A. J., Kirkpatrick, J. D., et al. 2002, ApJ, 573, 394
In the text
NASA ADS
- Burrows, A., & Volobuyev, M. 2003, ApJ, 583, 985
In the text
NASA ADS
- Pascale, J. 1983, Phys. Rev. A, 28, 632
In the text
NASA ADS
- Pascale, J. 2003, Private communication
In the text
- Rossi, F., & Pascale, J. 1985, Phys. Rev. A, 32, 2657
In the text
NASA ADS
- Schweitzer, A., Hauschildt, P. H., Allard, F., & Basri, G.
1996, MNRAS, 283, 821
In the text
NASA ADS
- Strauss, M. A., Fan, X., Gunn, J. E., et al. 1999, ApJ, 522, L61
In the text
NASA ADS
- Szudy, J., & Baylis, W. 1975, J.
Quant. Spectrosc. Radiat. Transfer., 15, 641
In the text
- Szudy, J., & Baylis, W. 1996, Phys. Rep., 266, 127
In the text
Copyright ESO 2003
![\begin{figure}
\par {\resizebox{8.8cm}{!}{ \includegraphics[clip]{letter_allard_fig1.eps}} }\end{figure}](/articles/aa/full/2003/46/aafg281/Timg8.gif)
![\begin{displaymath}F_\nu(\Delta \nu) = {\bf FT} \left[\exp\left(ng(s)\right)\right].
\end{displaymath}](/articles/aa/full/2003/46/aafg281/img9.gif)
![$\displaystyle \times \int^{+\infty}_{0}\!\!2\pi\rho {\rm d}\rho
\int^{+\infty}_{-\infty}\!\! {\rm d}x \;
\tilde{d}_{ee'}[ ~ R(0) ~ ] ~$](/articles/aa/full/2003/46/aafg281/img13.gif)
![\begin{displaymath}R(t) = \left[\rho^2 + (x + vt)^2 \right]^{1/2} \; , \;
\end{displaymath}](/articles/aa/full/2003/46/aafg281/img17.gif)
![\begin{displaymath}\tilde{d}_{ee'}[R(t)] =
d_{ee'}[R(t)]{\rm e}^{-\frac{\beta}{2}V_{e}[R(t)] } \; , \;
\end{displaymath}](/articles/aa/full/2003/46/aafg281/img20.gif)
![\begin{figure}
\par\mbox{\subfigure[K-He]{\resizebox{8cm}{!}{\includegraphics[cl...
...izebox{8cm}{!}{\includegraphics[clip]{letter_allard_fig2b.eps}} }}\end{figure}](/articles/aa/full/2003/46/aafg281/Timg23.gif)
![\begin{figure}
\par\mbox{\subfigure[Na-H$_2$\space profiles.]{\resizebox{8cm}{!}...
...zebox{8cm}{!}{ \includegraphics[clip]{letter_allard_fig3b.eps}} }}\end{figure}](/articles/aa/full/2003/46/aafg281/Timg24.gif)
![\begin{figure}
\par {\resizebox{8.8cm}{!}{
\includegraphics[clip]{letter_allard_fig4.eps}} }\end{figure}](/articles/aa/full/2003/46/aafg281/Timg26.gif)