A&A 411, L481-L485 (2003)
DOI: 10.1051/0004-6361:20031587
Heating the magnetically open ambient background corona of the Sun
by Alfvén waves
H. Peter1 - C. Vocks2
1 - Kiepenheuer-Institut für Sonnenphysik,
79104 Freiburg, Germany
2 -
Astrophysikalisches Institut Potsdam,
14482 Potsdam, Germany
Received 6 June 2003 / Accepted 9 October 2003
Abstract
Observations of UVCS/SOHO of very high emission line widths in
the outer corona suggest that the open field regions there
are heated by ion-cyclotron resonance absorption of Alfvén waves
resulting in the ions being much hotter than the electrons.
In the lower corona it is usually assumed that the effective
Coulomb-interactions ensure equal temperatures of ions and electrons.
However, recent models have shown that in regions of strong magnetic field
gradients the ion-cyclotron absorption can be so efficient that the
ion temperature overcomes the electron temperature.
In this paper we will present new observational results from SUMER/SOHO
showing that the lines of O 5 and S 6 have very large line
widths just above the limb.
The peak line width occurs at about 10
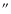 above the limb and corresponds to ion temperatures of more than
above the limb and corresponds to ion temperatures of more than
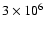 K.
We compare these observational results to new models in which plasma in
coronal funnels is heated and accelerated by means of ion-cyclotron
absorption of high-frequency waves.
As our model is in good qualitative agreement with the observations we come
to the conclusion that the open corona in coronal funnels could well be
heated by an ion-cyclotron absorption mechanism, even close to the Sun in
the low corona.
K.
We compare these observational results to new models in which plasma in
coronal funnels is heated and accelerated by means of ion-cyclotron
absorption of high-frequency waves.
As our model is in good qualitative agreement with the observations we come
to the conclusion that the open corona in coronal funnels could well be
heated by an ion-cyclotron absorption mechanism, even close to the Sun in
the low corona.
Key words: Sun: corona - Sun: solar wind
Images of the solar corona are dominated by loop-like structures which are
concentrated above active regions with strong magnetic fields.
Outside these active regions, in the "quiet Sun'', the emission formed
in the upper atmosphere at temperatures up to 300 000 K is enhanced
above lanes outlining super-granular convection cells, where the
photospheric magnetic field is accumulated.
At higher temperatures, i.e., into the corona, this network with a typical
cell size of 20 to 30 Mm is vanishing (Reeves 1976).
Rooted in the network, magnetic funnels are rapidly widening to fill the
whole space in the corona (Gabriel 1976).
Below these magnetically open funnels small magnetically closed loop-like
structures have to exist if one is to understand the emissivity observed in
emission lines formed below
100 000 K (Peter 2001; Dowdy et al. 1986).
Initially bright loop systems as seen in EUV or X-ray wavelengths by
the TRACE
or Yohkoh
satellites seem to be the most rewarding
objects representing the magnetically closed corona.
However, these active regions fill only a fraction of the space available.
To investigate the major part of the corona and also the acceleration of
the solar wind near the solar surface we have to study the darker
ambient background corona, even though this seems, but only at first
glance, less exciting.
Coronal holes, regions of significantly reduced emission from the
corona, are mainly magnetically open and dominated by coronal
funnels.
When observing quiet solar regions above the limb with no high arching
loops the emission some 1000 km above the limb should be dominated by
open coronal funnels as well (cf. Fig. 1).
In this paper we will investigate the properties of these open
structures above the limb and for the first time present evidence for
heating of the lowest open corona by high-frequency Alfvén waves.
This conclusion is based on a comparison of spectroscopic observations
with a kinetic model for coronal heating in a coronal funnel, the basic
constituent of the open background corona.
2 Line width observations across the limb
The observations presented here have been obtained on 13 June 2000 using
the SUMER spectrometer (Solar Ultraviolet Measurements of Emitted
Radiation; Wilhelm et al. 1995) on-board the SOHO spacecraft (Solar and
Heliospheric Observatory; Fleck et al. 1996).
The
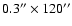 spectrograph slit (# 7) was used to
observe the south-east limb (Fig. 1) from 15:58 to 17:48 UT with
detector A with exposure times of 100 s.
We will concentrate on profiles of the emission lines of O 5 at
62.9 nm formed at about 240 000 K and of S 6 at 93.3 nm formed
at 190 000 K, while we have analysed a much larger number of lines from
higher and lower temperatures.
For each profile a single Gaussian fit was calculated using a Genetic
Algorithm based optimisation method from Charbonneau (1995).
To enhance the signal-to-noise ratio and to ensure better fits we applied
a spatial running mean with a box width of five 1
spectrograph slit (# 7) was used to
observe the south-east limb (Fig. 1) from 15:58 to 17:48 UT with
detector A with exposure times of 100 s.
We will concentrate on profiles of the emission lines of O 5 at
62.9 nm formed at about 240 000 K and of S 6 at 93.3 nm formed
at 190 000 K, while we have analysed a much larger number of lines from
higher and lower temperatures.
For each profile a single Gaussian fit was calculated using a Genetic
Algorithm based optimisation method from Charbonneau (1995).
To enhance the signal-to-noise ratio and to ensure better fits we applied
a spatial running mean with a box width of five 1
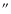 pixels.
A sample spectral frame covering the O 5 line at 62.9 nm
is shown in Fig. 2.
The distance along the slit has been converted into a distance above the
white light limb (the location of the limb was determined from the continuum
near the respective line; 1
pixels.
A sample spectral frame covering the O 5 line at 62.9 nm
is shown in Fig. 2.
The distance along the slit has been converted into a distance above the
white light limb (the location of the limb was determined from the continuum
near the respective line; 1
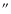 corresponds to 720 km on the Sun).
The fits to the spectra are quite good even far above the limb, where the
count rates are rather low.
corresponds to 720 km on the Sun).
The fits to the spectra are quite good even far above the limb, where the
count rates are rather low.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Ff061_f1.ps}\par
\end{figure}](/articles/aa/full/2003/46/aaff061/Timg4.gif) |
Figure 1:
The area on the Sun under study here seen in light from the
million Kelvin corona (Fe 9/ 10 lines) and from the
cool chromosphere (He 2).
The vertical line shows the position of the slit of the SUMER spectrograph
used to acquire the emission line profiles.
The slit was positioned well outside regions of coronal activity, i.e. in
the ambient background corona.
(Images from SOHO/EIT.) |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,height=7.2cm,clip]{Ff061_f2.ps}
\end{figure}](/articles/aa/full/2003/46/aaff061/Timg5.gif) |
Figure 2:
Spectrum in the line of O 5 at 62.9 nm (left panel) at the
approximate slit location shown in Fig. 1.
Note that the emission of this line formed at about 240 000 K extends
well above the white light limb of the Sun.
The right panels show individual spectra as bars (Poisson statistics;
spatially binned) at the location along the slit indicated at the left
panel.
The solid lines are single Gaussian fits to the line profiles. |
| Open with DEXTER |
In Fig. 3 we plot the line intensity (dotted-dashed) and the line
width (solid) of the O 5 and S 6 lines as a function of
height above the white light limb.
The intensity gradually increases towards the limb,
which is a simple line-of-sight effect for optically thin emission lines.
It then decreases roughly exponentially reflecting the stratification of
the atmosphere.
For O 5 and S 6 beyond about 15
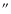 (dotted lines) the
instrumental stray-light is dominating and thus the intensity gradient
becomes more shallow.
(dotted lines) the
instrumental stray-light is dominating and thus the intensity gradient
becomes more shallow.
The most interesting part is how the line width is changing across the
limb.
The line width (Gaussian half width at 1/e) starts rising just at the
limb reaching a maximum well outside the intensity maximum before it
starts decreasing again.
In the stray-light domain the width is close to the on-disk value again,
of course.
It should be stressed here that the intensity starts decreasing already well
before the stray-light dominates.
The line widths well exceed the thermal line widths expected for a
temperature equilibrium of ions and electrons, which are about 11 km s-1and 7 km s-1 for O 5 and S 6.
One possibility to interpret the line width is for it to be due to a (kinetic)
ion temperature well exceeding the electron temperature (this will be used
in the following discussion of the Alfvén wave heating).
Then the line width w is related to the ion temperature
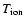 by
by
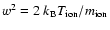 ,
with the
ion mass
,
with the
ion mass
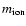 and Boltzmann's constant
and Boltzmann's constant
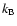 .
We added these
.
We added these
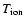 -scales to Fig. 3.
-scales to Fig. 3.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Ff061_f3.ps}
\end{figure}](/articles/aa/full/2003/46/aaff061/Timg10.gif) |
Figure 3:
Variation of line intensity (dotted-dashed, left axis) and line width
(solid, right axis) as a function of distance above the limb for the
lines of O 5 at 62.9 nm (see also Fig. 2) and S 6
at 93.3 nm.
The shaded areas indicate the error estimates for the line width.
The dashed curves show the variation of line width for Mg 10 as
published by Hassler et al. (1990) (scaled to match
O 5 and S 6 on disk values respectively).
The vertical dashed lines show the position of the limb, the dotted lines
indicate the location where the stray-light becomes important
(outside about 15
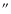 ).
The axis to the far right shows a scale of the line width converted into
an ion temperature. ).
The axis to the far right shows a scale of the line width converted into
an ion temperature. |
| Open with DEXTER |
The effect of an increasing width above the limb is not observable with
lines formed at lower temperatures such as C 2 simply because
of the small intensity scale height of these lines.
For higher temperature lines such as Mg 10 we do not expect to see
this effect because of the very large spatial extend of the line
contribution function smearing out the effect.
Ionisation equilibrium calculations from Mazzotta et al. (1998) show that
O 5 and S 6 are the only lines having a
contribution sharply concentrated from 150 000 K to 300 000 K
in electron temperature and which are suitable for this study.
Emission lines from ions with similar formation temperature have also
either a strong contribution from higher temperatures (e.g. N 5) or
are not strong enough above the limb (e.g. Ne 5).
Summarising these observations we find for the first time that exclusively the O 5 and S 6 lines show a strong increase of
line width above the solar limb outside the maximum intensity
of the respective line, with a peak line width at about 10
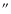 or
7500 km above the limb followed by a strong decrease further outwards.
Even though we concentrated on one particular observation here, we found this
effect also in other data sets.
or
7500 km above the limb followed by a strong decrease further outwards.
Even though we concentrated on one particular observation here, we found this
effect also in other data sets.
Interpreting the peak line width as an ion temperature, we find maximum
values of 7 and 5 million K for S 6 and O 5
(Fig. 3), corresponding to an ion temperature ratio of 1.4.
This corresponds quite well to the ratios of the mass-to-charge ratios of
the two ions,
(32/5)/(16/4)=1.6, i.e. the ion temperatures are
proportional to mass-to-charge ratios.
This outcome implies that a kinetic process of wave-particle
interaction could be involved.
To interpret these results we turn to a discussion of heating the open
corona in funnels by high-frequency Alfvén waves.
One successful mechanism of coronal heating and solar wind acceleration in
funnels is based on absorption of high-frequency Alfvén waves close to
the ion-cyclotron
frequency (Marsch & Tu 1997; Tu & Marsch 1997; Hackenberg et al. 2000).
These high-frequency disturbances of the magnetic field are a natural
consequence of small-scale reconnection in the chromospheric
plasma (Axford & McKenzie 1997), and they can propagate up through the
steep temperature gradient into the
corona (Vocks & Marsch 2002; Vocks 2002).
Alternatively they could be produced by a turbulent cascade in
the corona (Li et al. 1999).
This ion-cyclotron heating mechanism has two major consequences for the
temperature:
(1) The ions are heated preferentially perpendicular to the magnetic
field.
This leads to non-isotropic velocity distributions of the ions that can be
characterized by two ion temperatures, one parallel and one perpendicular to
the magnetic field,
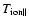 and
and
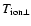 ,
with
,
with
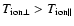 .
(2) The other major consequence is that the ion temperatures are higher than
the electron temperature
.
(2) The other major consequence is that the ion temperatures are higher than
the electron temperature
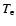 .
Both consequences were observed in-situ with HELIOS in the inner
heliosphere and are in good agreement with model calculations
(Marsch 1991; Marsch et al. 1982).
.
Both consequences were observed in-situ with HELIOS in the inner
heliosphere and are in good agreement with model calculations
(Marsch 1991; Marsch et al. 1982).
Other than in the in-situ observations, spectroscopic investigations give
directly information only on
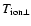 when observing above the
limb and assuming that the magnetic field is predominantly vertical.
To derive the parallel temperature model assumptions have to be made.
when observing above the
limb and assuming that the magnetic field is predominantly vertical.
To derive the parallel temperature model assumptions have to be made.
In the outer corona, some solar radii above the surface, observations of
UVCS indeed show extreme line broadening indicating high perpendicular ion
temperatures (Kohl et al. 1998).
Some evidence has been presented that the perpendicular temperature
exceeds the parallel one (Cranmer et al. 1999), but as just mentioned
this latter conclusion is model dependent.
Nevertheless, as with the in-situ observations in the inner heliosphere,
the temperature of the ions largely exceeds the one of the electrons, at
least perpendicular to the magnetic field.
In the lower corona, where the densities are higher, it is usually
assumed that the Coulomb interaction will ensure equal and isotropic
temperatures of ions and electrons.
However, using the following model we will show that it is still possible
that the heating of the ions by ion-cyclotron resonances can overcome the
equilibrating effect of the Coulomb collisions, even in the low corona,
i.e.
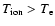 .
.
![\begin{figure}
\par\includegraphics[width=17.6cm]{Ff061_f4.ps}
\end{figure}](/articles/aa/full/2003/46/aaff061/Timg16.gif) |
Figure 4:
Schematic representation of the ion-cyclotron heating at the base of a
coronal funnel.
The left panel ( a)) indicates the magnetic field geometry of the coronal funnel.
Where the funnel expands the magnetic field drops rapidly ( a), b); dark
shaded area).
Thus in that region a large range of gyrofrequencies is covered ( b)).
As the incident Alfvén wave spectrum is (roughly) a power law ( c)), the
power absorbed in the small region of rapid field expansion is very large
(dark shaded area).
That is why the heating rate is highest in the region of strong magnetic
field gradients ( d)). |
| Open with DEXTER |
We have performed new computations of ion-cyclotron absorption of
high-frequency Alfvén waves in a coronal funnel in order to
interpret our observations (for details of the model
see Vocks & Marsch 2002; Vocks 2002).
The funnel geometry is prescribed as in the analytical model of
Hackenberg et al. (2000) and a simple single fluid model is used to
provide the initial conditions.
The model plasma consists of protons, alphas, and the ions O 5,
O 6, S 6, and Mg 10.
Electrons are treated as a neutralizing fluid only and their temperature is
taken from the initial single fluid model.
The velocity distribution functions of the ions are calculated
self-consistently by a kinetic method
(see Vocks & Marsch 2002; Vocks 2002) solving the Boltzmann-Vlasov
equations in one spatial dimension along the centre of the funnel.
This includes Coulomb collisions and especially resonant interaction
between ion-cyclotron waves and the ions.
The latter process leads to the heating of the ions and is treated
self-consistently.
The simulation box extends from the transition region to over 60 Mm
into the corona.
The ion cyclotron waves enter the box at its lower boundary with a given
power-law spectrum and propagate upwards.
Inside the box, the wave spectrum evolves due to the absorption by the
ions and according to the plasma conditions changing with height.
Ion-cyclotron heating is most efficient if a wide range of
frequencies are absorbed in a rather small volume, i.e. if the
gyro-frequencies available in the given volume match a large part of the
incident Alfvén wave spectrum.
Therefore in regions of strong magnetic field gradients, i.e., of a wide
range of gyro-frequencies over a small distance, the heating can be very
efficient.
Such a region can be found at the base of coronal funnels where these are
rapidly expanding, i.e. some 2 to 10 Mm above the solar surface
(Hackenberg et al. 2000; Gabriel 1976).
In fact, this heating can be so strong there that the temperatures of the
ions exceed those of the electrons and are not equilibrated by Coulomb
collisions as usually assumed for high densities as found in the low
corona
(cf. Fig. 4)
.
This effect is restricted to a rather small volume, where the magnetic
field gradient is large.
Thus the resulting profile of the ion temperatures perpendicular to the
magnetic field
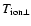 has a bump just where the magnetic
field gradient is largest.
This is clearly evident from Fig. 5, where
has a bump just where the magnetic
field gradient is largest.
This is clearly evident from Fig. 5, where
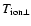 as
following from the model is plotted as a function of altitude.
as
following from the model is plotted as a function of altitude.
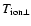 can reach more than 106 K well in excess of the
electron temperature.
The parallel temperatures
can reach more than 106 K well in excess of the
electron temperature.
The parallel temperatures
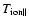 are close to the electron
temperature.
are close to the electron
temperature.
![\begin{figure}
\par\includegraphics[width=8.8cm,height=6.2cm,clip]{Ff061_f5.ps}
\end{figure}](/articles/aa/full/2003/46/aaff061/Timg17.gif) |
Figure 5:
Ion temperatures perpendicular to the magnetic field computed using the
model of ion-cyclotron absorption of high-frequency Alfvén waves in a
coronal funnel.
The electron temperature is basically the same as for the protons. |
| Open with DEXTER |
The model shows that very high ion temperatures can be produced at the
very base of the corona and so demonstrated that the large line widths we
have reported in Sect. 2 could be a signature of the heating
mechanism.
The high
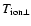 are expected where the magnetic field rapidly
expands.
As the flow will follow the magnetic field at the base of the funnel (low
plasma-
are expected where the magnetic field rapidly
expands.
As the flow will follow the magnetic field at the base of the funnel (low
plasma-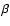 ), the flow will not be strictly vertical, but will
be quite inclined especially at the edges of the funnel (cf. left panel
of Fig. 4).
Thus we will see not only the perpendicular temperature, but
also (partly) the parallel temperature of the ions when observing above
the limb - the observations will show some mixture of
), the flow will not be strictly vertical, but will
be quite inclined especially at the edges of the funnel (cf. left panel
of Fig. 4).
Thus we will see not only the perpendicular temperature, but
also (partly) the parallel temperature of the ions when observing above
the limb - the observations will show some mixture of
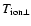 and
and
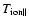 .
Especially, we will not be able to distinguish between
.
Especially, we will not be able to distinguish between
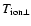 and
and
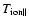 from spectroscopic observations.
from spectroscopic observations.
Nevertheless we can list a number of properties predicted by the model:
(1) Even though we see a mixture of
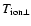 and
and
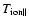 we should observe a line width of the emission lines
corresponding to an ion temperature well in excess of the electron (or
line formation) temperature.
(2) As the effect is quite restricted in height, and consequently in
electron temperature, we can expect to see this effect only in a limited
number of lines, namely those that are formed in just the temperature
range where the funnels expand most rapidly.
According to Gabriel (1976) this is the case at about 200 000 K.
(3) Furthermore the high line width should be quite restricted in
geometrical height, as the effect mentioned above will occur only at the
base of the funnels, i.e. some 2-10 Mm above the photosphere.
we should observe a line width of the emission lines
corresponding to an ion temperature well in excess of the electron (or
line formation) temperature.
(2) As the effect is quite restricted in height, and consequently in
electron temperature, we can expect to see this effect only in a limited
number of lines, namely those that are formed in just the temperature
range where the funnels expand most rapidly.
According to Gabriel (1976) this is the case at about 200 000 K.
(3) Furthermore the high line width should be quite restricted in
geometrical height, as the effect mentioned above will occur only at the
base of the funnels, i.e. some 2-10 Mm above the photosphere.
All these predictions are observed:
The effect is observed only in S 6 and O 5 formed at
190 000 and 240 000 K respectively, the widths of these lines show a
sharp peak about 7 Mm above the limb reaching well above 106 K.
We did not fine-tune the model to match the observed ion temperatures, as
this would have required specific assumptions on, e.g., the poorly known
expansion of the funnel.
We would still like to stress that the model and the observations nicely
fit qualitatively.
Especially the peak ion temperatures occur at roughly the same altitude as
the observed line widths peak.
But as the observations cannot tell about the ratio of
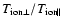 ,
the observations do not provide a
final proof that what we see is a signature of ion-cyclotron heating.
The agreement is in many other properties strongly supporting this
interpretation, though.
,
the observations do not provide a
final proof that what we see is a signature of ion-cyclotron heating.
The agreement is in many other properties strongly supporting this
interpretation, though.
Hassler et al. (1990) studied the coronal lines of Mg 10 at 609 and 625 Å and found increasing line widths above the limb.
Their increase of line width though was shallow compared to our results
for the transition region lines O 5 and O 6, and can be
attributed to an upward propagating wave (cf. Fig. 3).
A similar result for Mg 10 has been found more recently by
Harrison et al. (2002).
We would like to stress that these Mg 10 results are not comparable
to our results, as we see a pronounced peak in O 5 and S 6
widths close to the Sun and decreasing width above this, while the coronal
Mg 10 width increases much slower and does not reach a maximum line
width within some 200
 .
A more elaborate comparison of transition region and coronal lines is on
the way.
.
A more elaborate comparison of transition region and coronal lines is on
the way.
As the line broadening for O 5 and O 6 is of the order of the
sound speed or more it is hard to imagine that not resolved flows can
account for the effect.
It would especially demand clarification why the effect should be so
restricted in line formation temperature.
Opacity effects can also be excluded, as the maximum of the line width
would then be expected near or inside the maximum of the intensity, which
is contrary to the observations (an opacity effect can be found for other
lines like C 4 (Mariska 1992).
As we think the peak of the line width as presented in Sect. 2 cannot
be understood in terms of the effects we have just discussed, i.e. waves,
flows and opacity, we are left with concluding that this effect should be
caused by direct heating of the ions.
Considering these arguments and the good agreement of model predictions and
observations, we conclude that the ion cyclotron absorption
is a valuable candidate for the interpretation our observations.
It would be of interest to extend the model calculations presented here
further out into the corona and by that to link the present observations
with the UVCS results.
Such a numerical effort is beyond the scope of this paper, however.
We have presented observations which reveal for the first time a strong
increase of the width of emission lines from the lower solar corona just
above the limb.
The comparison with new model results of ion-cyclotron absorption of
high-frequency Alfvén waves by six ion species showed that this effect
can be attributed to an increase in ion temperature.
Thus the presented investigation strongly suggests that heating
by ion-cyclotron absorption of high-frequency Alfvén waves is present
even in the lowermost corona and plays an important role in the heating of
the low corona and the initial acceleration of the solar wind.
Acknowledgements
We would like to thank the SUMER team and especially Werner Curdt at MPAe in
Lindau/Germany for their goodsupport on technical problems and especially
for the open data policy.
Sincere thanks are due to Eckart Marsch and Reiner Hammer for comments and
suggestions.
The SUMER project is supported by DARA, CNES, NASA and
the ESA PRODEX programme (Swiss contribution).
-
Axford, W. I., & McKenzie, J. F. 1997, in Cosmic winds and the heliosphere, ed.
J. R. Jokipii, C. P. Sonett, & M. S. Giampapa (Tucson: Univ. of Arizona Press), 31
In the text
-
Charbonneau, P. 1995, ApJS, 101, 309
In the text
NASA ADS
-
Cranmer, S. R., Kohl, J. L., Noci, G., et al. 1999, ApJ, 511, 481
In the text
NASA ADS
-
Dowdy, J. F., Rabin, D., & Moore, R. L. 1986, Sol. Phys., 105, 35
In the text
NASA ADS
-
Fleck, B., Domingo, V., & Poland, A. I. (ed.) 1996, The SOHO mission, Sol.
Phys., 162) (Dordrecht: Kluwer Academic Publishers)
In the text
-
Gabriel, A. H. 1976, Phil. Trans. Roy. Soc. Lond., A 281, 339
In the text
NASA ADS
-
Hackenberg, P., Marsch, E., & Mann, G. 2000, A&A, 360, 1139
In the text
NASA ADS
-
Harrison, R., Hood, A. W., & Pike, C. D. 2002, A&A, 392, 319
In the text
NASA ADS
-
Hassler, D. M., Rottman, G. J., Shoub, E. C., & Holzer, T. E. 1990, ApJ, 348,
L77
In the text
NASA ADS
-
Kohl, J. L., Noci, G., Antonucci, E., et al. 1998, ApJ, 501, L127
In the text
NASA ADS
-
Li, X., Habbal, S. R., Hollweg, J. V., & Esser, R. 1999, J. Geophys. Res., 104, 2521
In the text
NASA ADS
-
Mariska, J. T. 1992, The solar transition region
(Cambridge: Cambridge Univ. Press)
In the text
-
Marsch, E. 1991, in Physics of the inner heliosphere, Vol. 2, ed.
R. Schwenn, & E. Marsch (Berlin: Springer-Verlag), 45
In the text
-
Marsch, E., & Tu, C.-Y. 1997, A&A, 319, L17
In the text
NASA ADS
-
Marsch, E., Goertz, C. K., & Richter, K. 1982, J. Geophys. Res., 87, 5030
In the text
NASA ADS
-
Mazzotta, P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998, A&AS,
133, 403
In the text
NASA ADS
-
Peter, H. 2001, A&A, 374, 1108
In the text
NASA ADS
-
Reeves, E. M. 1976, Sol. Phys., 46, 53
In the text
NASA ADS
-
Tu, C.-Y., & Marsch, E. 1997, Sol. Phys., 171, 363
In the text
NASA ADS
-
Vocks, C. 2002, ApJ, 568, 1017
In the text
NASA ADS
-
Vocks, C., & Marsch, E. 2002, ApJ, 568, 1030
In the text
NASA ADS
-
Wilhelm, K., Curdt, W., Marsch, E., et al. 1995, Sol. Phys., 162, 189
In the text
NASA ADS
Copyright ESO 2003
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Ff061_f1.ps}\par
\end{figure}](/articles/aa/full/2003/46/aaff061/Timg4.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,height=7.2cm,clip]{Ff061_f2.ps}
\end{figure}](/articles/aa/full/2003/46/aaff061/Timg5.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Ff061_f3.ps}
\end{figure}](/articles/aa/full/2003/46/aaff061/Timg10.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,height=6.2cm,clip]{Ff061_f5.ps}
\end{figure}](/articles/aa/full/2003/46/aaff061/Timg17.gif)