C. Neiner1,2,3 - H. F. Henrichs1 - M. Floquet2 - Y. Frémat2 - O. Preuss4 - A.-M. Hubert2 - V. C. Geers1 - A. H. Tijani1 - J. S. Nichols5 - S. Jankov6,7
1 - Sterrenkundig Instituut "Anton Pannekoek'', Universiteit van Amsterdam, The Netherlands
2 - GEPI/UMR 8111 du CNRS, Observatoire de Paris-Meudon, France
3 - Current affiliation: RSSD, Estec / ESA, Keplerlaan 1, 2201 AZ,
Noordwijk ZH, The Netherlands
4 - Max Planck Institut für Aeronomie, Lindau, Germany
5 - Harvard/Smithsonian Center for Astrophysics, Cambridge, MA, USA
6 - Observatoire de la Côte d'Azur, France
7 - Astronomical Observatory Beograd, Yugoslavia
Received 13 August 2002 / Accepted 19 August 2003
Abstract
V 2052 Oph is a ![]() Cep star with
Cep star with
![]() km s-1.
The behavior of its stellar wind was studied in the ultraviolet wavelength region
with the IUE satellite. It revealed periodic variations in the equivalent
widths (EW)
of the resonance lines of wind-sensitive ions with a period of 3.638833 d, which is
identified as the rotational period. These variations are typical of magnetic stars.
Therefore time-resolved circular spectropolarimetric observations were
obtained with the Musicos échelle spectropolarimeter at the 2-m Télescope Bernard
Lyot (TBL) to search for a magnetic field in the star. Stokes V patterns were
observed, the inclination and magnetic
angles were derived and a value was determined for the polar magnetic field
(
km s-1.
The behavior of its stellar wind was studied in the ultraviolet wavelength region
with the IUE satellite. It revealed periodic variations in the equivalent
widths (EW)
of the resonance lines of wind-sensitive ions with a period of 3.638833 d, which is
identified as the rotational period. These variations are typical of magnetic stars.
Therefore time-resolved circular spectropolarimetric observations were
obtained with the Musicos échelle spectropolarimeter at the 2-m Télescope Bernard
Lyot (TBL) to search for a magnetic field in the star. Stokes V patterns were
observed, the inclination and magnetic
angles were derived and a value was determined for the polar magnetic field
(
![]() G)
using an oblique rotator dipole model.
The spectroscopic information was used to search for periodicity in line-profile
variations (lpv), radial velocity and minimum intensity curves. Multiperiodicity was
found, corresponding to radial (f1=7.15 c d-1) and non-radial
(f2=6.82 c d-1, l=3 or 4) pulsation modes. The rotation period is also
detected in rotationally modulated observables because of the magnetic poles
passing through the observer's line of sight.
We determined the stellar parameters of the star, which was found to be chemically
peculiar, in particular He-enriched. This makes V 2052 Oph the first
magnetic He-strong early B star with known pulsational properties.
G)
using an oblique rotator dipole model.
The spectroscopic information was used to search for periodicity in line-profile
variations (lpv), radial velocity and minimum intensity curves. Multiperiodicity was
found, corresponding to radial (f1=7.15 c d-1) and non-radial
(f2=6.82 c d-1, l=3 or 4) pulsation modes. The rotation period is also
detected in rotationally modulated observables because of the magnetic poles
passing through the observer's line of sight.
We determined the stellar parameters of the star, which was found to be chemically
peculiar, in particular He-enriched. This makes V 2052 Oph the first
magnetic He-strong early B star with known pulsational properties.
Key words: stars: magnetic fields - stars: winds, outflows - stars: chemically peculiar - stars: early-type - stars: oscillations
Rountree & Sonneborn (1991) classified the star from the photospheric lines in the UV spectrum as B2 IVw, where the w-designation signifies anomalous wind lines.
They also noted
that the single spectrum they considered looked very similar to that of ![]() Cas, a
star being known for its variable C IV wind lines
(Sonneborn et al. 1987), and which was
recently found to be magnetic (Neiner et al. 2003).
Cas, a
star being known for its variable C IV wind lines
(Sonneborn et al. 1987), and which was
recently found to be magnetic (Neiner et al. 2003).
Inspection of the three available spectra in the microfiche atlas of all
high-resolution spectra of OB stars taken during the first 10 years of IUE (Bohlin et al. 1994)
showed clearly variable wind lines, similar to what is observed in known
magnetic B stars,
i.e. showing periodic absorption modulations, but very
much unlike the variability found in O stars, i.e. discrete absorption components (DACs).
This specific type of wind variations appeared a reliable signature of the presence
of a weak stellar magnetic field, such as in the case of ![]() Cep (Henrichs et al. 2003),
and enables an accurate determination of the rotational period.
Henrichs et al. (1998) estimated a 3.75 day period and predicted a minimum field of a few
hundred Gauss.
Cep (Henrichs et al. 2003),
and enables an accurate determination of the rotational period.
Henrichs et al. (1998) estimated a 3.75 day period and predicted a minimum field of a few
hundred Gauss.
In addition, studying the pulsation properties of a rotating magnetic star gives strong constraints on its stellar parameters and its evolutionary stage, which is of high asteroseismological importance.
These considerations motivated us to undertake a detailed time-resolved UV study of V 2052 Oph which was intensively monitored with the IUE satellite (March 1994-August 1995), to attempt to measure the expected magnetic field (June 2000 and 2001) with the Musicos spectropolarimeter at TBL (Pic du Midi, France), and to analyze the pulsational properties of the star.
In Sect. 2 we present the UV and spectropolarimetric observations. We analyze
the UV stellar wind changes and extract the rotational period of V 2052 Oph in Sect. 3. We determine an improved
value for the ![]() of the star, review its stellar parameters and determine
its chemical composition in Sect. 4. In Sect. 5 we study the pulsations in the
line profiles and radial velocities. In Sect. 6 we
report on the measurements of the longitudinal component of the magnetic field, in
the context of an oblique magnetic dipole. We discuss the results and present conclusions in
Sect. 7.
of the star, review its stellar parameters and determine
its chemical composition in Sect. 4. In Sect. 5 we study the pulsations in the
line profiles and radial velocities. In Sect. 6 we
report on the measurements of the longitudinal component of the magnetic field, in
the context of an oblique magnetic dipole. We discuss the results and present conclusions in
Sect. 7.
High-dispersion ultraviolet spectra (
![]() )
were obtained with the Short
Wavelength Prime (SWP) camera onboard the IUE satellite. Table 1 presents
the journal of the 41 obtained spectra of V 2052 Oph. 3 spectra taken
during 1981 and 1982 were extracted from the IUE archive, whereas 38 spectra
were taken in 1994 and during 11-31 August 1995 by one of us (JN).
All reduced data were retrieved from the INES database for homogeneity.
The spectra were mapped on a uniform wavelength
grid of 0.1 Å, which effectively degraded the resolving
power to 12 000-15 000. The signal-to-noise ratio of the spectra is about 25
(see Henrichs et al. 1994).
)
were obtained with the Short
Wavelength Prime (SWP) camera onboard the IUE satellite. Table 1 presents
the journal of the 41 obtained spectra of V 2052 Oph. 3 spectra taken
during 1981 and 1982 were extracted from the IUE archive, whereas 38 spectra
were taken in 1994 and during 11-31 August 1995 by one of us (JN).
All reduced data were retrieved from the INES database for homogeneity.
The spectra were mapped on a uniform wavelength
grid of 0.1 Å, which effectively degraded the resolving
power to 12 000-15 000. The signal-to-noise ratio of the spectra is about 25
(see Henrichs et al. 1994).
Table 1: Journal of IUE observations of V 2052 Oph (programs PHCAL and BEPJN). Column 1 indicates the number in the IUE archives. Column 2 gives the exposure time in seconds. The Heliocentric Julian Date (HJD) at mid-exposure minus 2 440 000 is given in the last column.
The fiber-fed Musicos échelle spectropolarimeter (
![]() )
is mounted at the
Cassegrain focus of the 2-m Télescope Bernard Lyot (TBL) at Pic du Midi in
France (see Donati et al. 1999). Stellar light is collected in a 2'' entrance aperture in the spectral
range 4500-6600 Å. Linear/circular sheet polarisers can be inserted in
the beam. One half-wave and one quarter-wave retarder can also be inserted and
rotated to achieve a linear or circular analysis of the stellar light.
)
is mounted at the
Cassegrain focus of the 2-m Télescope Bernard Lyot (TBL) at Pic du Midi in
France (see Donati et al. 1999). Stellar light is collected in a 2'' entrance aperture in the spectral
range 4500-6600 Å. Linear/circular sheet polarisers can be inserted in
the beam. One half-wave and one quarter-wave retarder can also be inserted and
rotated to achieve a linear or circular analysis of the stellar light.
Table 2: Journal of TBL observations of V 2052 Oph obtained in 2000 and 2001. Column 1 indicates the number of the polarimetric set. Columns 2 and 3 show the date and time of the beginning of observations. Column 4 indicates the number of obtained polarimetric sets or individual subexposures. Column 5 gives the exposure time in seconds of each individual subexposure.
To detect stellar magnetic fields, one analyses the circular polarisation
of the light. The light is split into two beams, fed to the
spectrograph through a double optical fiber and simultaneously recorded onto the
![]() 24
24 ![]() m square pixel SITe CCD detector. The observing strategy is
to set the quarter-wave plate and
take 4 subexposures: one at azimuth -45
m square pixel SITe CCD detector. The observing strategy is
to set the quarter-wave plate and
take 4 subexposures: one at azimuth -45![]() ,
two at azimuth 45
,
two at azimuth 45![]() ,
and one more at azimuth -45
,
and one more at azimuth -45![]() .
In principle only 2 exposures are
needed (one at each azimuth) but with 4 exposures the path of the two beams are
mutually exchanged through the instrument during one complete Stokes V
measurement. With this procedure, systematic spurious circular polarisation
signals are removed down to an accuracy of 0.002%.
.
In principle only 2 exposures are
needed (one at each azimuth) but with 4 exposures the path of the two beams are
mutually exchanged through the instrument during one complete Stokes V
measurement. With this procedure, systematic spurious circular polarisation
signals are removed down to an accuracy of 0.002%.
25 Stokes V measurements were obtained in June-July 2000 (observers CN, HH, AT) and 88 Stokes V measurements in June-July 2001 (observers CN, HH, VG), i.e. 113 measurements in total (see Table 2). The individual subexposures can also be used as normal spectroscopic data, including subexposures which do not form a complete set for a magnetic measurement. Therefore we have 518 individual spectra available for pulsation analysis. Their average S/N in the intensity continuum is about 120.
A dedicated software package, ESpRIT (see Donati et al. 1997), is available at TBL to
reduce and analyze the data.
We implemented an improved version of ESpRIT, using two series of flat-fields taken
in the two positions of the quarter-wave plate, which optimizes the extraction of the échelle
orders. Fringes were present in the spectra taken in 2001. They were removed using a fringe
template extracted from the Stokes V spectrum of a non-magnetic star (![]() Oph)
taken and reduced in the same way as V 2052 Oph. Fringes are probably also
present in the data taken in 2000, but due to the lower quality of these data they could not be
identified. Tests on the 2001 data showed, however, that when the S/N ratio is low, application
of the fringe correction makes no difference in the value derived for the magnetic
field.
Oph)
taken and reduced in the same way as V 2052 Oph. Fringes are probably also
present in the data taken in 2000, but due to the lower quality of these data they could not be
identified. Tests on the 2001 data showed, however, that when the S/N ratio is low, application
of the fringe correction makes no difference in the value derived for the magnetic
field.
After applying the Least-Squares Deconvolution (LSD), a cross-correlation technique developed by Donati et al. (1997), one can detect a stellar magnetic field through the Zeeman signatures generated in the shape and polarization state of spectral line profiles. The LSD method combines the very small circularly polarized signatures, properly weighted, of all available line profiles in the spectrum to increase the signal to noise ratio. For V 2052 Oph, a line template of 159 spectral lines was created and used to provide a mean Stokes V profile. These photospheric lines correspond to ions of He I, C II, C III, N II, O II, Ne I, Mg II, Al III, Si II, Si III, S II, Ar II, Fe III, with line depths from 0.01 to 0.46 and Landé factors from 0.5 to 2.7. The line depths and Landé factors are extracted from Kurucz models provided in the ESpRIT Package. The method assumes that the intrinsic broadening is similar for all lines. When a magnetic field is present, the Stokes V profile indicates a Zeeman signature.
One single VLT/UVES spectrum was obtained on September 25th 2001 (courtesy of L.
Kaper and his colleagues). The resolution is about
![]() with a
signal to
noise ratio of
with a
signal to
noise ratio of
![]() .
The spectrum covers three wavelength domains:
[3250-4500], [4580-5555] and [5600-6580] Å. The reduction was not performed with the
dedicated UVES pipeline in MIDAS
.
The spectrum covers three wavelength domains:
[3250-4500], [4580-5555] and [5600-6580] Å. The reduction was not performed with the
dedicated UVES pipeline in MIDAS![]() , as this pipeline is optimized for spectra with
S/N < 100. The usual bias and flat-field correction, order extraction and
wavelength calibration was done with the IRAF
, as this pipeline is optimized for spectra with
S/N < 100. The usual bias and flat-field correction, order extraction and
wavelength calibration was done with the IRAF![]() software package.
software package.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3013f1.eps}}
\end{figure}](/articles/aa/full/2003/46/aa3013/Timg21.gif) |
Figure 1: Mean spectrum of 40 IUE spectra ( top panels), together with the detected variability ( lower panels). The repetitive pattern in the variability signature is due to imperfect correction of the échelle-order overlap regions. |
| Open with DEXTER | |
Figure 1 shows a mean spectrum of 40 (out of 41) available
high-resolution IUE spectra (top panels), along with the ratio of the measured
to expected variability (lower panels).
A ratio higher than unity signals statistically significant variability.
Image SWP 14514 was omitted in the average spectrum due to overexposure
especially at longer wavelengths.
The expected variability was obtained using a noise model for such IUE spectra
![]() as derived by Henrichs et al. (1994), where F is
the flux, A=26 and
as derived by Henrichs et al. (1994), where F is
the flux, A=26 and
![]() .
The wind-sensitive doublet resonance lines of C IV 1550, Si IV 1400, N V 1240 and Al III 1860 are strongly variable and are
analysed for periodicity below. The highly instrumentally contaminated
Si III 1206 line and probably the C III complex at 1175 Å are
also variable, but are not considered further.
.
The wind-sensitive doublet resonance lines of C IV 1550, Si IV 1400, N V 1240 and Al III 1860 are strongly variable and are
analysed for periodicity below. The highly instrumentally contaminated
Si III 1206 line and probably the C III complex at 1175 Å are
also variable, but are not considered further.
The top panels of Fig. 2 show an overplot of the IUE C IV, Si IV, N V and Al III line profiles, respectively, along with their variability signatures in the bottom panels. The variability occurs mainly in the strength of the line over a given range in velocity space, extending from -300 to +300 km s-1 for each of the lines. Note that the C IV doublet is in emission as observed in other similar stars.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3013f2a.eps}}\par...
....eps}}\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3013f2d.eps}}
\end{figure}](/articles/aa/full/2003/46/aa3013/Timg24.gif) |
Figure 2: Variations of the line profiles in the UV data of the C IV, Si IV, N V and Al III lines. Fluxes are normalized to the average profile. |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3013f3.eps}}
\end{figure}](/articles/aa/full/2003/46/aa3013/Timg25.gif) |
Figure 3:
Variations of the equivalent width (in Å) from the UV data of the Si IV,
C IV, N V and Al III lines, folded in phase with the
rotational period. The EW were measured in the following intervals: C IV in [-450, 750] km s-1 at 10-10 erg cm-2 s-1 Å-1,
Si IV in [-400, 2200] km s-1 at 10-10 erg cm-2 s-1 Å-1,
N V in [-250, 200] km s-1 at
|
| Open with DEXTER | |
We search for periodicity in the equivalent widths of the UV data of the
C IV, Si IV, N V and Al III lines in
intervals with variability signature exceeding unity.
The final result is obtained with a least-square method which uses weights
equal to the inverse of the error bars assigned to each datapoint.
With user-supplied initial starting values for the free parameters a steepest
descent technique then searches for the lowest mimimum of the ![]() .
The
variance matrix provides the formal
errors in the parameters. A single sinusoid does not fit the data. Therefore
we use the following function:
.
The
variance matrix provides the formal
errors in the parameters. A single sinusoid does not fit the data. Therefore
we use the following function:
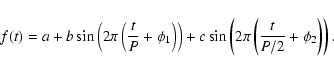 |
(1) |
The equivalent width measurements (in Å) of the C IV, Si IV,
N V and Al III lines folded in phase with the
rotational period are shown in Fig. 3.
Like in ![]() Cep, the EW of these lines folded in phase shows two unequal
minima, the deeper corresponding to maximum emission, and two equal maxima,
corresponding to maximum absorption.
Cep, the EW of these lines folded in phase shows two unequal
minima, the deeper corresponding to maximum emission, and two equal maxima,
corresponding to maximum absorption.
The ![]() value usually quoted for V 2052 Oph is 120 km s-1
(Jerzykiewicz 1972) but it has been estimated with poor accuracy from low-resolution
spectra in 1972. Wolff et al. (1982) found
value usually quoted for V 2052 Oph is 120 km s-1
(Jerzykiewicz 1972) but it has been estimated with poor accuracy from low-resolution
spectra in 1972. Wolff et al. (1982) found
![]() km s-1 from visual comparison
with a rotational standard. More recently Smith & Groote (2001) derive 100 km s-1
from a comparison of models.
km s-1 from visual comparison
with a rotational standard. More recently Smith & Groote (2001) derive 100 km s-1
from a comparison of models.
We determine the value of ![]() by applying a Fourier transform analysis
(Gray 1976) to the mean line profile of the He I 4713, 4921, 5016
and 5876 and Si III 4553 and 4568 lines obtained at TBL. A
limb darkening coefficient
by applying a Fourier transform analysis
(Gray 1976) to the mean line profile of the He I 4713, 4921, 5016
and 5876 and Si III 4553 and 4568 lines obtained at TBL. A
limb darkening coefficient
![]() is adopted. The results are reported
in Table 3. We obtain
is adopted. The results are reported
in Table 3. We obtain
![]() km s-1.
km s-1.
Table 3:
![]() determination using a Fourier transform analysis.
determination using a Fourier transform analysis.
The star V 2052 Oph is a V=5.85
star with a spectral type B2 IV-V (Rountree Lesh 1968). UV classification gives B2 IV
(Rountree & Sonneborn 1991) by comparison with the star ![]() Cas.
Cas.
Two previous studies indicate rather different fundamental
parameters. An equivalent width study performed
by Wolff & Heasley (1985) led to an effective
temperature of about
![]() K, for a gravity of
K, for a gravity of
![]() and a He/H ratio of 0.085. However, Smith & Groote (2001) found that the flux of the UV IUE spectra
implies a higher effective temperature
and a He/H ratio of 0.085. However, Smith & Groote (2001) found that the flux of the UV IUE spectra
implies a higher effective temperature
![]() K for a gravity
fixed at
K for a gravity
fixed at
![]() .
.
In our first attempt we determined the stellar effective temperature and
superficial gravity assuming a solar He/H ratio (0.1) by fitting
several He I lines (4026, 4387, 4921 Å), observed with the VLT.
We built up line profile grids
using NLTE model atmospheres computed with TLUSTY
(Hubeny & Lanz 1995, and references therein) for different values of effective
temperature and gravity. In these calculations H, He, C, N, O and Si
were treated in NLTE. Except for O I which was treated with the MODION IDL package, the atomic models we used are those proposed by Hubeny & Lanz on
TLUSTY's web site![]() .
.
![\begin{figure}
\par\resizebox{18cm}{!}{\includegraphics[clip]{3013f4.ps}}
\end{figure}](/articles/aa/full/2003/46/aa3013/Timg43.gif) |
Figure 4: Model fit result for the lines used to determine the stellar parameters. The dots representing the synthetic spectra are overplotted on the observations (solid lines). |
| Open with DEXTER | |
For the solar He/H case, we are able to model simultaneously all the
He I line profiles with
![]() K,
K,
![]() and
and
![]() km s-1.
This is very close to the results obtained by Wolff & Heasley (1985).
In this configuration, nitrogen and oxygen have solar abundances (Grevesse & Sauval 1998)
while carbon and silicon are depleted. Although the computed line
wings are not as extended as the observations, a good agreement is obtained
for the H
km s-1.
This is very close to the results obtained by Wolff & Heasley (1985).
In this configuration, nitrogen and oxygen have solar abundances (Grevesse & Sauval 1998)
while carbon and silicon are depleted. Although the computed line
wings are not as extended as the observations, a good agreement is obtained
for the H![]() line, but the Si II 4128 and 4132 (VLT) and Si III 4553,
4568 and 4575 (TBL) lines could not be fitted using the same silicon abundances.
We find that, in order to fit all the silicon and neutral helium lines
simultaneously with the same abundance, we need to increase the effective
temperature and, consequently, increase the He/H ratio.
line, but the Si II 4128 and 4132 (VLT) and Si III 4553,
4568 and 4575 (TBL) lines could not be fitted using the same silicon abundances.
We find that, in order to fit all the silicon and neutral helium lines
simultaneously with the same abundance, we need to increase the effective
temperature and, consequently, increase the He/H ratio.
To estimate the helium abundance, we extend our flux grids using
computations made by Zboril (2000) with TLUSTY for different values of
the He/H ratio and available at the CDS. The most consistent model, according
to the helium and silicon line profiles, is obtained for
![]() K,
K,
![]() ,
,
![]() km s-1and
km s-1and
![]() .
These values are much closer
to the ones proposed by Smith & Groote (2001). They allow us to fit the
Si II and Si III lines simultaneously. Moreover they also allow
to fit the
continuum slope of the short wavelength IUE spectra adopting the mean reddening law
derived by Cardelli et al. (1989) and
E(B-V)=0.30,
derived from Papaj et al. (1990) and consistent with the determination
E(B-V)=0.33 from
Diplas & Savage (1994).
As far as the red He I and H
.
These values are much closer
to the ones proposed by Smith & Groote (2001). They allow us to fit the
Si II and Si III lines simultaneously. Moreover they also allow
to fit the
continuum slope of the short wavelength IUE spectra adopting the mean reddening law
derived by Cardelli et al. (1989) and
E(B-V)=0.30,
derived from Papaj et al. (1990) and consistent with the determination
E(B-V)=0.33 from
Diplas & Savage (1994).
As far as the red He I and H![]() lines are concerned, the agreement
between observations and theory are better than with the solar value (Fig. 4).
The value of
lines are concerned, the agreement
between observations and theory are better than with the solar value (Fig. 4).
The value of ![]() is compatible with the one derived in the
previous Sect. 4.1.
With this effective temperature, V 2052 Oph would be a B1 V star
rather than a B2 IV-V star. The mismatch with the
MK classification is probably due to the unusual strength of the He I lines.
is compatible with the one derived in the
previous Sect. 4.1.
With this effective temperature, V 2052 Oph would be a B1 V star
rather than a B2 IV-V star. The mismatch with the
MK classification is probably due to the unusual strength of the He I lines.
Table 4: Stellar parameters of the star V 2052 Oph (HD 163472, HR 6684).
Using the evolutionary tracks of Schaller et al. (1992), we derive
![]() for the mass and
for the mass and
![]() for the radius.
For a star with such a mass, the critical break-up rotational velocity is about 580 km s-1. The critical radius
for the radius.
For a star with such a mass, the critical break-up rotational velocity is about 580 km s-1. The critical radius
![]() is
obtained using Roche's model. The angular velocity
is
obtained using Roche's model. The angular velocity ![]() is about 15%
of the angular critical velocity. The effects of gravity
darkening are therefore negligible.
Using
is about 15%
of the angular critical velocity. The effects of gravity
darkening are therefore negligible.
Using
![]() and R, we also obtain the luminosity of the star
and R, we also obtain the luminosity of the star
![]() .
.
Using the above parameters,
E(B-V)=0.30 (Papaj et al. 1990) and comparing the flux
of the IUE spectra to the flux of the models, we obtain a distance
![]() pc, which is compatible with the distance derived from the Hipparcos
parallax of 254
+83-50 pc.
In Sect. 3 we showed that the rotational period is
pc, which is compatible with the distance derived from the Hipparcos
parallax of 254
+83-50 pc.
In Sect. 3 we showed that the rotational period is
![]() d.
With
d.
With
![]() km s-1, we obtain
km s-1, we obtain
![]() and v=63 km s-1.
The stellar parameters are summarized in Table 4.
and v=63 km s-1.
The stellar parameters are summarized in Table 4.
With the model presented above we can also determine the chemical composition of the star by fitting individual lines with Tlusty (Hubeny & Lanz 1995, and references therein). The H, He, C, N and O ions are treated in NLTE, while the other ions are treated in LTE. Again, the atomic models are those proposed on Tlusty's web site, except for O I.
Table 5: Chemical composition of V 2052 Oph. Column 2 gives the number N of lines for each ion, used to determine the chemical abundance.
To determine the abundances of carbon, nitrogen, oxygen and silicon, we
select from the
NIST compilation database the transitions with the most accurate oscillator strengths
(10% or better). We update Kurucz line lists with these new values and fit the
selected observed spectral range (Fig. 4) using the least squares method.
We adopt a 2 km s-1 microturbulence velocity, as proposed in Andrievsky et al. (1999),
which allows to fit simultaneously the different studied transitions.
The results of our fits are given in Table 5 where
![]() denotes the abundance in the star relative to the abundance in
the Sun as compiled by Grevesse & Sauval (1998).
denotes the abundance in the star relative to the abundance in
the Sun as compiled by Grevesse & Sauval (1998).
We found that V 2052 Oph is He-strong and O-weak. The relative C, N and O abundances we derive follow the same pattern as the one described by Zboril & North (2000) in their LTE spectral analysis for a sample of 21 He-strong stars. The carbon abundance is twice lower than their mean value for this kind of objects, probably due to strong departures from LTE for the C II 4267 line they used, as noted by the authors.
We performed two methods to search for periodicity in the data used in this paper: the Restricted Local Cleanest (RLC, based on Foster 1995,1996, developed by Emilio 1997 and Domiciano de Souza Jr. 1999 and applied in Domiciano de Souza et al. 2000) and a Least-Squares (LS) fitting methods.
In each wavelength bin, the RLC method searches for 20 frequencies in a predefined range and computes all possible models with 4 frequencies. Comparing the power of each of these models, it selects 7 optimal frequencies while suppressing the aliases. A Local Cleanest (Foster 1995) is then applied to these 7 values to finetune the final frequencies (for more details see Neiner et al. 2002).
With the LS method, we look at the whole line at the same time, i.e. all wavelength bins at once, to determine which frequencies describe the variations in the best way. After a first frequency is found, the data are prewhitened, and the program looks for the next frequency in the residual spectra. This procedure is repeated several times.
Table 6: Frequencies detected from the analysis of different lines using the RLC method for the 2001 data. The frequencies obtained with the LS method are shown in boldface.
![\begin{figure}
\par\resizebox{18cm}{!}{\includegraphics[clip]{3013f5.ps}}
\end{figure}](/articles/aa/full/2003/46/aa3013/Timg76.gif) |
Figure 5: For each studied line, the upper panel shows the periodogram obtained with the RLC method, together with the mean line profile in the lower panel. |
| Open with DEXTER | |
The 111 individual spectra obtained at TBL in 2000 and the 407 ones obtained in 2001 are used to search for periodicity in the line profile variations of the He I 4713, 4921, 5016 and 5876 and Si III 4553 line. We use the two methods described above. The search is separately performed on both sets of data and on the combined dataset 2000+2001. As the data taken in 2000 are of lower quality and badly sampled in time because of bad weather conditions, including them does not improve the results obtained with the data taken in 2001 only. Therefore we will present here the results obtained with the 2001 data only. Due to the timebase of the observations, frequencies lower than 0.05 c d-1cannot be detected. For the same reason, two frequencies closer than 0.025 c d-1cannot be distinguished.
For all the studied lines, three frequencies are detected:
(i) a very strong frequency stands out at
![]() c d-1,
corresponding to the well-known pulsation period P1=3h21min;
c d-1,
corresponding to the well-known pulsation period P1=3h21min;
(ii) a second frequency is detected at
![]() c d-1 corresponding to a period P2=3h31min;
c d-1 corresponding to a period P2=3h31min;
(iii) a third frequency is present at
![]() c d-1. This corresponds
to twice the rotational frequency
c d-1. This corresponds
to twice the rotational frequency
![]() c d-1.
c d-1.
This is the first detection of multiperiodicity in V 2052 Oph.
The detected frequencies for each line with the two methods of analysis are
summarized in Table 6.
Periodograms, together with the mean line
profile, are shown in Fig. 5. Other frequencies also appear in the
periodograms and are due either to the window spectrum or to the combination of
the real frequencies (f1, f2, f3 and
![]() )
with each other
and with the window spectrum.
)
with each other
and with the window spectrum.
The power spectrum obtained for the He I 5016 line profile, showing the three frequencies and
![]() ,
is plotted in Fig. 6. In
the top panel, the power spectrum of the He I 4921 line profile,
which is slightly different in this frequency region, is overplotted.
,
is plotted in Fig. 6. In
the top panel, the power spectrum of the He I 4921 line profile,
which is slightly different in this frequency region, is overplotted.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3013f6.eps}}
\end{figure}](/articles/aa/full/2003/46/aa3013/Timg82.gif) |
Figure 6: Example of a power spectrum obtained for the He I 5016 line profile. In the top panel the power spectrum of the He I 4921 line profile is overplotted with a dashed line. |
| Open with DEXTER | |
A very strong frequency is detected at f1 = 7.145 c d-1. This frequency was already known in the literature (e.g. Jerzykiewicz 1972) and was also detected by the Hipparcos satellite. Cugier et al. (1994) proposed that this belongs to a radial pulsation mode.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3013f7.ps}}
\end{figure}](/articles/aa/full/2003/46/aa3013/Timg83.gif) |
Figure 7: Power and phase of the frequency f1 =7.145 c d-1 along the line profiles of the Si III 4553 and the He I 4713, 4921, 5016 and 5876 lines. |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3013f8.ps}}
\end{figure}](/articles/aa/full/2003/46/aa3013/Timg84.gif) |
Figure 8: Greyscale plot of the spectra taken in 2001, folded in phase with the frequency f1=7.145 c d-1. |
| Open with DEXTER | |
Looking at the phase and power of this frequency along the line profile (Fig. 7), we can confirm that f1 is due to a pulsation mode with l=0, as the phase shows no significant slope (see Schrijvers et al. 1997). The phase is also coherent outside the line in some cases, due to the presence of other weak lines (e.g. blue side of the He I 4921 line) which also pulsate with f1.
A greyscale plot of the spectra for several lines, from which the mean line profile has been subtracted, is presented in Fig. 8 in phase with the frequency f1.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3013f9.ps}}
\end{figure}](/articles/aa/full/2003/46/aa3013/Timg85.gif) |
Figure 9: Power and phase of the frequency f2 = 6.82 c d-1 along the line profiles of the Si III 4553 and the He I 4713, 4921, 5016 and 5876 lines. |
| Open with DEXTER | |
Although it is about 20 times less powerful than f1, a frequency is detected at f2 = 6.82 c d-1. Looking at the slope of the phase and power of this frequency (Fig. 9), we can derive the pulsation degree l (see Schrijvers et al. 1997). We obtain that f2 corresponds to a non-radial pulsation mode with l=3 or 4.
A greyscale plot of the He I 4713, 4921, 5016 and 5876 and Si III 4553 lines, obtained after prewhitening the frequency f1, is presented in Fig. 10 in phase with the frequency f2. The prewhitening was done by computing the phase and power of the frequency f1 with a least squares fit for all wavelength bins simultaneously (see LS description in Sect. 5.1) at each time. The spectra, minus the mean line profile, were then corrected from this two-dimensional sine curve, in wavelength and time.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3013f10.ps}}
\end{figure}](/articles/aa/full/2003/46/aa3013/Timg86.gif) |
Figure 10: Greyscale plot of the spectra taken in 2001, prewhitened from the frequency f1, folded in phase with the frequency f2 = 6.82 c d-1. |
| Open with DEXTER | |
A frequency is detected at f3=0.55 c d-1. This frequency cannot be due to a
window effect, as it does not appear in the window power spectrum. Interestingly, the
frequency f3
corresponds to twice the rotational frequency
![]() c d-1 derived from the UV analysis. The rotational frequency itself,
c d-1 derived from the UV analysis. The rotational frequency itself,
![]() ,
is also detected but with a weaker
power. See Sect. 7 for further discussion.
,
is also detected but with a weaker
power. See Sect. 7 for further discussion.
Radial velocities are measured using a centroid set at the intensity 0.8. We study the radial velocity variations of the He I 4921 and 5876 lines. They are dominated by the frequency f1 as shown in Fig. 11 for the He I 4921 line. In this figure we overplotted parts of the best fit sine wave imposing the frequency f1. The same behavior is observed for the He I 5876 line. The semi-amplitude of the fit is about 9 km s-1 for He I 4921 and 5876 (see also Fig. 13).
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3013f11.eps}}
\end{figure}](/articles/aa/full/2003/46/aa3013/Timg87.gif) |
Figure 11: Radial velocity measurements of the He I 4921 line. Best fit sine waves with the frequency f1, determined for each night, are overplotted. |
| Open with DEXTER | |
Folding the data in phase with f1 (Fig. 12)
shows that the scatter of points (![]() 2 km s-1) is higher
than the precision of the measurements compared to the individual best-fit sine
curves (Fig. 11) and implies the presence of at least one other
frequency.
2 km s-1) is higher
than the precision of the measurements compared to the individual best-fit sine
curves (Fig. 11) and implies the presence of at least one other
frequency.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3013f12.eps}}
\end{figure}](/articles/aa/full/2003/46/aa3013/Timg88.gif) |
Figure 12: Radial velocity measurements of the He I 4921 and 5876 lines, folded in phase with the frequency f1 = 7.145 c d-1. |
| Open with DEXTER | |
We measure the mean value and amplitude of the variations for each night of observations and investigate the variations of these measurements. Although it is difficult to extract a frequency with any method we tried, due to the small amount of points and small amplitude of variations, folding the data in phase with f3=0.55 c d-1 shows that this frequency is present in the radial velocity measurements (e.g. Fig. 13 for the He I 4921 line).
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3013f13.eps}}
\end{figure}](/articles/aa/full/2003/46/aa3013/Timg89.gif) |
Figure 13: Mean radial velocity and semi-amplitude for each night of the He I 4921 line, folded in phase with the frequency f3 = 0.55 c d-1. |
| Open with DEXTER | |
We study the minimum intensity variations of the He I 4921 and 5876 lines. The
minimum intensity
![]() ,
normalized to the continuum intensity
,
normalized to the continuum intensity
![]() ,
is obtained
for each spectrum by taking the point P of minimum intensity and fitting a parabola to the
21 points around this minimum (
,
is obtained
for each spectrum by taking the point P of minimum intensity and fitting a parabola to the
21 points around this minimum (![]() points).
Using a LS method to search for periodicity, we detect the
frequencies
points).
Using a LS method to search for periodicity, we detect the
frequencies
![]() ,
f1, f2 and f3 for almost all the studied lines.
,
f1, f2 and f3 for almost all the studied lines.
Folding the minimum intensity measurements of the He I lines in phase with the rotational frequency (Fig. 14) reveals two minima and two maxima, similar to the equivalent width measurements of the UV stellar wind lines. Interestingly, the Si III 4553 line varies in the opposite way compared to the He I lines. Note that the He I 5876 line also seems to show a different behavior, probably due to saturation.
Due to the relative faintness of the star the magnetic measurements have relatively large error
bars. Table 7 (only available in electronic form) shows the longitudinal magnetic field value B, its error bar ![]() ,
the null polarisation N and its error
,
the null polarisation N and its error ![]() .
The null polarisation N gives an
indication of the pollution by non-stellar effects and should be zero for a
perfect measurement. It is produced by associating the four subexposures of one
magnetic measurement in the same way as for creating the Stokes V profile, except
that the two last subexposures are exchanged.
In the following, only measurements for which
.
The null polarisation N gives an
indication of the pollution by non-stellar effects and should be zero for a
perfect measurement. It is produced by associating the four subexposures of one
magnetic measurement in the same way as for creating the Stokes V profile, except
that the two last subexposures are exchanged.
In the following, only measurements for which
![]() are
used.
Moreover, for the data taken in 2000, bad weather conditions and fringes also
decrease the quality of the data, making them less reliable than the 2001 data.
Exposure times were chosen between 7 and 12 min, i.e. much shorter than the pulsation period, to
avoid smearing of the magnetic signal because of the pulsational effect.
are
used.
Moreover, for the data taken in 2000, bad weather conditions and fringes also
decrease the quality of the data, making them less reliable than the 2001 data.
Exposure times were chosen between 7 and 12 min, i.e. much shorter than the pulsation period, to
avoid smearing of the magnetic signal because of the pulsational effect.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3013f14.eps}}
\end{figure}](/articles/aa/full/2003/46/aa3013/Timg96.gif) |
Figure 14:
Minimum intensity measurements of the Si III 4553, He I 4713,
4921, 5016 and 5876 lines, folded in phase with therotational period
|
| Open with DEXTER | |
Although no strong signatures appear in the individual Stokes V profiles,
the coherent variation of the magnetic measurement in phase is an
indication of the presence
of a weak longitudinal field in V 2052 Oph.
In the frame of the magnetic rotator model (see Shore 1987) the UV period corresponds
to the rotational period of the star (see next section).
The magnetic field should then vary in phase with the
equivalent width of the UV resonance lines, i.e with ![]() d
(see Fig. 15).
d
(see Fig. 15).
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3013f15.eps}}
\end{figure}](/articles/aa/full/2003/46/aa3013/Timg98.gif) |
Figure 15: Top panel: variations of the equivalent width of the UV C IV line; middle panels: variations of the minimum intensity of the He I 5016 and Si III 4553 lines; lower panel: variations of the longitudinal magnetic field; the best sine fit (dashed line) and the dipole model (solid line) are overplotted. All the plots are folded with the rotation period. |
| Open with DEXTER | |
Assuming that V 2052 Oph hosts a magnetic field and folding the
magnetic data with
![]() ,
we calculate a best-fit sine wave through
the magnetic data. This gives an amplitude
of the longitudinal component of
,
we calculate a best-fit sine wave through
the magnetic data. This gives an amplitude
of the longitudinal component of
![]() G, around the average value of
G, around the average value of
![]() G with a reduced
G with a reduced
![]() .
This fit is shown as a dashed line in Fig. 15.
.
This fit is shown as a dashed line in Fig. 15.
With the derived phase we find for the ephemeris of the maximum value of the field
strength: HJD(
![]() .
Comparison with the observed EW minimum of the
C IV UV data, which were taken
.
Comparison with the observed EW minimum of the
C IV UV data, which were taken ![]() 1200 rotational cycles prior to the
magnetic data, shows that a deep EW minimum is predicted at HJD
1200 rotational cycles prior to the
magnetic data, shows that a deep EW minimum is predicted at HJD
![]() ,
which is within the uncertainties identical to the phase of maximum magnetic
field.
Note the striking resemblance in phase correlation with the
,
which is within the uncertainties identical to the phase of maximum magnetic
field.
Note the striking resemblance in phase correlation with the ![]() Cep results (Donati et al. 2001; Henrichs et al. 2000).
Cep results (Donati et al. 2001; Henrichs et al. 2000).
We have found evidence for a weak varying longitudinal field in V 2052 Oph, consistent
with an oblique magnetic dipole with a rotational period of about 3.64 d.
In the oblique magnetic dipole model (Stibbs 1950) the axis of the dipole and the
axis of rotation do not coincide. The observed stellar configuration can then be
characterised by the inclination angle i and by the angle ![]() between the magnetic axis and the rotation axis.
Therefore, as the star rotates, the aspect of its visible hemisphere changes (e.g. Fig. 16). This leads to variations in various observables with the stellar rotation
period, such as the shape and equivalent width of wind-sensitive UV resonance
lines (see Sects. 3 and 5) and the value of the longitudinal magnetic field.
See Shore (1987) for more details on the following Eqs. (2)-(4).
between the magnetic axis and the rotation axis.
Therefore, as the star rotates, the aspect of its visible hemisphere changes (e.g. Fig. 16). This leads to variations in various observables with the stellar rotation
period, such as the shape and equivalent width of wind-sensitive UV resonance
lines (see Sects. 3 and 5) and the value of the longitudinal magnetic field.
See Shore (1987) for more details on the following Eqs. (2)-(4).
For a dipolar field, the ratio of the magnetic extremes
![]() is related to the inclination angle i and the angle between the magnetic and the
rotation axis
is related to the inclination angle i and the angle between the magnetic and the
rotation axis ![]() via
via
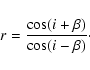 |
(2) |
The observed phase difference
![]() between the two UV maxima is also
related to the angles i and
between the two UV maxima is also
related to the angles i and ![]() through
through
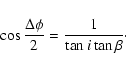 |
(3) |
When two maxima are observed in the UV equivalent width variations, it is
expected that
| (4) |
With the known angles i and ![]() in the oblique dipolar model, the strength
of the magnetic field at the poles, i.e the maximum field, can be determined.
in the oblique dipolar model, the strength
of the magnetic field at the poles, i.e the maximum field, can be determined.
The oblique dipolar rotator model we used was described by
Stift (1975).
Starting with the observer's system where the z-axis is defined
by the line-of-sight, a surface point on the visible hemisphere
of the star is given by a vector.
This vector is transformed into the corotating system of the star,
followed by a rotation around the rotational z-axis.
The position of the dipole system relative to the rotational system
is uniquely described by three Eulerian angles.
The effect of the three Eulerian rotations
can be summarized without loss of generality by a rotation with ![]() around the x-axis.
Given the offset coordinates of the dipole in the rotation system,
we obtain the coordinates of the surface point relative to the dipole system
and the field strength in the dipole system.
From this we get the field strength in the observer's system.
around the x-axis.
Given the offset coordinates of the dipole in the rotation system,
we obtain the coordinates of the surface point relative to the dipole system
and the field strength in the dipole system.
From this we get the field strength in the observer's system.
![\begin{figure}
\par\resizebox{18cm}{!}{\includegraphics[bb=25 40 677 350, clip]{3013f16.ps}}
\end{figure}](/articles/aa/full/2003/46/aa3013/Timg116.gif) |
Figure 16:
Greyscale representation of the relative contribution of the magnetic
dipole to the integrated longitudinal magnetic field on the visible
hemisphere of V 2052 Oph, at different rotational phases with step
of
|
| Open with DEXTER | |
To reproduce the measured longitudinal field values, we use a limb darkening
law as described in Stift (1975), with k = 0.4 as established by
Claret (2000) for this kind of star in the optical.
With
![]() derived in Sect. 4.2 and
derived in Sect. 4.2 and
![]() derived
in Sect. 6.2, we
model a centered oblique magnetic rotator and fit it to the longitudinal magnetic
field data. The best fit is obtained with
derived
in Sect. 6.2, we
model a centered oblique magnetic rotator and fit it to the longitudinal magnetic
field data. The best fit is obtained with
![]() G,
G,
![]() G and a polar field
G and a polar field
![]() G, with a reduced
G, with a reduced
![]() .
The values obtained for B0 and
.
The values obtained for B0 and ![]() are compatible with the ones obtained
from the best sine fit in Sect. 6.1, with a similar
are compatible with the ones obtained
from the best sine fit in Sect. 6.1, with a similar ![]() value.
Note that the angles i and
value.
Note that the angles i and ![]() are anticorrelated, i.e. to keep B0 and
are anticorrelated, i.e. to keep B0 and ![]() constant when increasing
constant when increasing ![]() ,
i and
,
i and
![]() have to be
decreased.
have to be
decreased.
A greyscale representation of the relative contribution of the magnetic dipole to the integrated longitudinal field on the visible hemisphere of the star, at different rotational phases, is shown in Fig. 16. Although the strongest magnetic field is at the magnetic poles, the positions on the stellar surface that contribute the most to the longitudinal field are not at the poles, due to a geometrical effect and to the limb darkening effect.
We determined the 3.638833 d stellar rotation period from the variations in equivalent
width of the UV stellar wind lines. We found that the minimum intensity of optical
photospheric lines (He I and Si III lines) also varies with the
rotation period. The strength of the absorption in the UV resonance lines varies
in phase with the optical Si III line, but in antiphase with the optical
He I lines: when the highly ionized lines are deep, the He I lines are
weak, and vice versa.
The equivalent widths of the Si III lines increase with higher
temperature for stars with
![]() K (Becker & Butler 1990). The
equivalent widths of the He I lines vary in the opposite way for stars with
K (Becker & Butler 1990). The
equivalent widths of the He I lines vary in the opposite way for stars with
![]() K (Leone & Lanzafame 1998).
Thus the behaviour observed in V2052 Oph could be easily explained
by temperature variations.
K (Leone & Lanzafame 1998).
Thus the behaviour observed in V2052 Oph could be easily explained
by temperature variations.
In the context of a magnetic star, these variations could also be explained by a temperature difference between the magnetic poles and the rest of the stellar surface. The deepest profile of the He I line corresponds to the minimum temperature. We can estimate the temperature variations from the visual magnitude changes measured by Hipparcos. The frequency detected by Hipparcos (Perryman et al. 1997) corresponds to f1 (radial mode, see Sect. 7.2). However, an analysis of the Hipparcos data with the LS method shows that the second detected frequency is f3, i.e. twice the rotational frequency. It is therefore possible that the star undergoes temperature variations due to its radial mode, as was already found by Morton & Hansen (1974), plus apparent temperature variations due to the magnetic poles passing through the line of sight of the observer.
However, it appears that the amplitude of these additional temperature variations needed to explain the rotationally modulated line depths of V 2052 Oph is of the same order as the one produced by the pulsations, i.e. about 2000 K, which is higher than the temperature variation observed for Ap stars (e.g. 600 K for 41 Tau, Sokolov 1999) with a ten times stronger field than the one of V 2052 Oph. We conclude that the weak magnetic field of V 2052 Oph is unlikely to produce such strong additional temperature effects and that it is mainly an abundance effect (see Sect. 7.4).
In the case of Ap and roAp magnetic oblique rotators, the oblique pulsator model also applies (Kurtz 1982), i.e. the pulsation axis is aligned with the magnetic axis, being oblique to the rotation axis. As the star rotates, the angle between the observer and the pulsational axis changes. Therefore one expects to see rotational modulation of the amplitude and phase of oscillations. This seems to also be the case in V 2052 Oph (see Fig. 13).
Although the S/N of the direct measurements of the longitudinal component of the
magnetic field of V 2052 Oph is weak due to the faintness of the star, a
magnetic field is likely detected by combining all measurements and folding them
with the known rotation period. The angles derived for the oblique dipole,
![]() and
and
![]() are such that the magnetic poles pass through the observer's line of sight.
This is confirmed by the detection of f3 in the optical photospheric lines,
with one pole appearing stronger than the other one, as expected from the difference
in strength of the two absorption minima observed in the lines.
The dipole model gives then
are such that the magnetic poles pass through the observer's line of sight.
This is confirmed by the detection of f3 in the optical photospheric lines,
with one pole appearing stronger than the other one, as expected from the difference
in strength of the two absorption minima observed in the lines.
The dipole model gives then
![]() G.
G.
Other evidence for the presence of a magnetic field in this
star is the fact that the extremum field occurs within the uncertainty limits at
the same
epoch as the predicted mimimum EW of the stellar wind lines, i.e. identical to
what is
observed in other magnetic stars, such as ![]() Cep.
Cep.
Our analysis shows that the star is chemically peculiar: it is He-strong and O-weak. It is known that the oxygen abundance in a star forming region is often 3/4 of the solar abundance. However, the oxygen in V 2052 Oph is even less abundant than that fraction and therefore cannot be attributed to an underabundance in the star forming region. In addition, Smith & Groote (2001) found that V 2052 Oph has a low metal abundance.
Peculiar chemical compositions are usually found in magnetic stars, in which microscopic diffusion effects allow elements with a high atomic mass to sink in the atmosphere under the dominant influence of gravity, while elements which can absorb photons of many wavelengths from the outward flow of radiation through the star are lifted towards the surface. The first element with a peculiar abundance is then helium (Michaud et al. 1987). In most of the stars this process is usually cancelled by mixing processes (e.g. convection in cool stars). However, the presence of a magnetic field inhibits mixing motions in the outer layers, and hence produces chemical peculiarities.
The line profile modulation can rather be attributed to inhomogeneous surface distribution
of chemical abundances. This effect is well-known in Ap stars.
Michaud et al. (1987) showed that in the presence of mass loss, the He abundances in the
line-forming depths may be modified by chemical separation that takes place not
only
in the atmosphere but also in the wind and in the envelope of the star. At
![]() K this leads to differential winds. Groote & Hunger (1997) found that the
magnetic He-strong B star
K this leads to differential winds. Groote & Hunger (1997) found that the
magnetic He-strong B star ![]() Ori E, which presents many similarities
with V 2052 Oph, has surface patches of
He-enrichment related to fractionation of the wind. Smith & Groote (2001) extended this
model by proposing the presence of co-rotating torus-shaped clouds between the
magnetic poles and equator. Hunger & Groote (1999) found that
He-fractionation occurs for stars with
Ori E, which presents many similarities
with V 2052 Oph, has surface patches of
He-enrichment related to fractionation of the wind. Smith & Groote (2001) extended this
model by proposing the presence of co-rotating torus-shaped clouds between the
magnetic poles and equator. Hunger & Groote (1999) found that
He-fractionation occurs for stars with
![]() K. They
also stated that a fraction of hydrogen or helium is forced to fall back to
the star by gravity, because it was not yet coupled at the critical point
or because it did not attain the escape velocity and was decoupled further out.
If a magnetic field is present this
reaccreation proceeds along the same trajectories as those of the ascending
particles. Thus the abundance anomalies should show up at the wind bases, i.e the
magnetic poles. They conclude that all He-strong main sequence stars are also magnetic stars,
otherwise the turbulence would suppress the inhomogeneities.
K. They
also stated that a fraction of hydrogen or helium is forced to fall back to
the star by gravity, because it was not yet coupled at the critical point
or because it did not attain the escape velocity and was decoupled further out.
If a magnetic field is present this
reaccreation proceeds along the same trajectories as those of the ascending
particles. Thus the abundance anomalies should show up at the wind bases, i.e the
magnetic poles. They conclude that all He-strong main sequence stars are also magnetic stars,
otherwise the turbulence would suppress the inhomogeneities.
The influence of the inhomogeneous abundance distribution on the shape of the line profiles could be studied in more detail with Doppler imaging techniques.
V 2052 Oph is very similar to ![]() Cep, which hosts a magnetic
field. The parameters are very similar, except that
Cep, which hosts a magnetic
field. The parameters are very similar, except that ![]() Cep has
its magnetic axis almost perpendicular to its rotational axis (
Cep has
its magnetic axis almost perpendicular to its rotational axis (
![]() ), whereas for V 2052 Oph
), whereas for V 2052 Oph
![]() .
.
![]() Cep has a magnetically confined wind (Donati et al. 2001),
i.e. the stellar-wind streams from both magnetic hemispheres collide with each
other in the magnetic equatorial plane, producing a strong shock, an extended post-shock
region and a high-density cooling disc (for more details see Babel & Montmerle 1997).
This is
consistent with the magnetic measurements and wind UV data, i.e.
Cep has a magnetically confined wind (Donati et al. 2001),
i.e. the stellar-wind streams from both magnetic hemispheres collide with each
other in the magnetic equatorial plane, producing a strong shock, an extended post-shock
region and a high-density cooling disc (for more details see Babel & Montmerle 1997).
This is
consistent with the magnetic measurements and wind UV data, i.e.
![]() when
the UV absorption is at maximum. We find that
the same model would apply for V 2052 Oph (see Fig. 15), with the same agreement
in phase, i.e. the wind is
magnetically confined.
The magnetic field strength of the two stars and their wind are very similar.
when
the UV absorption is at maximum. We find that
the same model would apply for V 2052 Oph (see Fig. 15), with the same agreement
in phase, i.e. the wind is
magnetically confined.
The magnetic field strength of the two stars and their wind are very similar.
Moreover ![]() Cep pulsates radially and non-radially, similar to V 2052 Oph.
From ROSAT observations (Berghoefer et al. 1996) a non-detection,
i.e. an upper limit, of X-rays was
obtained with log
Cep pulsates radially and non-radially, similar to V 2052 Oph.
From ROSAT observations (Berghoefer et al. 1996) a non-detection,
i.e. an upper limit, of X-rays was
obtained with log
![]() .
Using the luminosity determined
in this paper
leads to log (
.
Using the luminosity determined
in this paper
leads to log (
![]() for V 2052 Oph, which is
similar to the detection with log (
for V 2052 Oph, which is
similar to the detection with log (
![]() obtained for the
nearer star
obtained for the
nearer star ![]() Cep.
This is consistent with both stars having the same intrinsic X-ray emission.
Similarly, if V 2052 Oph would have the same IR excess as
Cep.
This is consistent with both stars having the same intrinsic X-ray emission.
Similarly, if V 2052 Oph would have the same IR excess as ![]() Cep the lack of detection of an IR excess from IRAS data
is compatible with the difference in distance (A. Lenorzer, private
communication).
Thus, from all these aspects, these two stars resemble each other.
Cep the lack of detection of an IR excess from IRAS data
is compatible with the difference in distance (A. Lenorzer, private
communication).
Thus, from all these aspects, these two stars resemble each other.
However, the slowly rotating Be star ![]() Cep sometimes exhibits
H
Cep sometimes exhibits
H![]() line emission (Neiner et al. 2001; Kaper & Mathias 1995). The H
line emission (Neiner et al. 2001; Kaper & Mathias 1995). The H![]() line of V 2052 Oph has never been observed in emission, and this star is
therefore not classified as a Be star, but given the many specific
similarities, it is tempting to suggest a H
line of V 2052 Oph has never been observed in emission, and this star is
therefore not classified as a Be star, but given the many specific
similarities, it is tempting to suggest a H![]() line-emission phase in
the future.
line-emission phase in
the future.
V 2052 Oph is the second discovered magnetic pulsating B star, after ![]() Cep. Such stars are apparently rather rare, but will provide the most
massive examples of stars useful for asteroseismological (and hence evolutionary)
tests. We hope to be able to confirm the direct detection of a magnetic field in V 2052 Oph, and other similar stars, and analyze the rotational modulation
of the field, using
the new spectropolarimeter ESPaDOnS, which will be installed at CFHT in
January 2004 and is
expected to be at least 10 times more efficient than Musicos.
Cep. Such stars are apparently rather rare, but will provide the most
massive examples of stars useful for asteroseismological (and hence evolutionary)
tests. We hope to be able to confirm the direct detection of a magnetic field in V 2052 Oph, and other similar stars, and analyze the rotational modulation
of the field, using
the new spectropolarimeter ESPaDOnS, which will be installed at CFHT in
January 2004 and is
expected to be at least 10 times more efficient than Musicos.
Acknowledgements
We are grateful to J. Cami, P. Ehrenfreud, L. Kaper and A. van den Meer for providing the VLT spectrum and J. Jimenez for reducing it. CN wish to thank J.-F. Donati and E. Verdugo for useful discussions concerning the TBL fringe correction, S. Solanki for his help on the dipole model and A. de Koter for interesting discussions on winds. Thanks also goes to E. Verdugo for her contribution to the determination of the rotation period and to the referee D. Gies.
Table 7: Table of longitudinal magnetic field measurements. Columns 1, 2 and 3 indicate the number, HJD and phase (with P = 3.638833 d) of each measurement respectively. Columns 4 and 5 give the longitudinal field measurement and its error bar. Columns 6 and 7 give the null polarisation and its error bar.