A. Olech1 -
P. Kedzierski2 - K. Z![]() oczewski2 -
K. Mularczyk2 - M. Wisniewski1
oczewski2 -
K. Mularczyk2 - M. Wisniewski1
1 - Nicolaus Copernicus Astronomical Center, ul. Bartycka 18,
00-716 Warszawa, Poland
2 -
Warsaw University Observatory, Al. Ujazdowskie 4, 00-478 Warszawa, Poland
Received 15 July 2003 / Accepted 8 August 2003
Abstract
We report extensive photometry of the dwarf nova QW Ser throughout its
February 2003 superoutburst untill quiescence. During the superoutburst
the star displayed clear superhumps with a mean period of
![]() days. In the quiescence we observed a double humped wave
characterized by a period of
P=0.07457(2) days. As both periods obey
the Stolz-Schoembs relation with a period excess equal to
days. In the quiescence we observed a double humped wave
characterized by a period of
P=0.07457(2) days. As both periods obey
the Stolz-Schoembs relation with a period excess equal to
![]() %, the latter period is interpreted as the orbital period
of the binary system
%, the latter period is interpreted as the orbital period
of the binary system
Key words: stars: individual: QW Ser - stars: binaries: close - stars: novae, cataclysmic variables
QW Ser (TmzV46, USNO-A2.0 0975-07829422) was discovered by Takamizawa
(1998), who detected three significant brightenings of the star on
JD 2 449 620, 2 449 716 and 2 450 906. Photometric behavior and color of QW Ser
suggested that it was a dwarf nova. In October 1999, Schmeer (1999)
reported another outburst of QW Ser. Subsequent observations were made
by Kato & Uemura (1999). According to them, the initial decline of
![]() mag observed during the first seven days of the outburst
was followed by a much slower decrease of the brightness. The reported
rate of mean decline of 0.1 mag per day was neither consistent with
those of superoutbursts in SU UMa-type stars nor long outbursts of SS
Cyg-type dwarf novae, thus the definitive classification of QW Ser
remained an open question.
mag observed during the first seven days of the outburst
was followed by a much slower decrease of the brightness. The reported
rate of mean decline of 0.1 mag per day was neither consistent with
those of superoutbursts in SU UMa-type stars nor long outbursts of SS
Cyg-type dwarf novae, thus the definitive classification of QW Ser
remained an open question.
The February 2003 outburst of QW Ser was reported by Muyllaert (2003), who caught the star at a magnitude of 12.5 on 2003 Feb. 23.715 UT. Observations of Schmeer (2003) reported at a later date indicated that the star reached 12.5 mag on Feb. 21.199 UT.
Observations of QW Ser reported in the present paper were obtained during
14 nights between February 23, 2003 and May 04, 2003 at the
Ostrowik station of the Warsaw University Observatory. The data was
collected using the 60-cm Cassegrain telescope equipped with a
Tektronics TK512CB back-illuminated CCD camera. The scale of the camera
was 0.76
![]() /pixel providing a
/pixel providing a
![]() field of view. The full
description of the telescope and camera was given by Udalski & Pych
(1992).
field of view. The full
description of the telescope and camera was given by Udalski & Pych
(1992).
We monitored the star in "white light''. This was due to the lack of an autoguiding system, not yet implemented after a recent telescope renovation. Thus we did not use any filters to shorten the exposures in order to minimize guiding errors.
The exposure times were from 60 to 90 s during the bright state and from 200 to 350 s in the minimum light.
A full journal of our CCD observations of QW Ser is given in Table 1. In total, we monitored the star during 36.47 hours and obtained 896 exposures.
Table 1: Journal of the CCD observations of QW Ser.
All the data reductions were performed using a standard procedure
based on the IRAF![]() package and
the profile photometry has been derived using the DAOphotII package
(Stetson 1987).
package and
the profile photometry has been derived using the DAOphotII package
(Stetson 1987).
Relative unfiltered magnitudes of QW Ser were determined as the
difference between the magnitude of the variable and the magnitude of
the comparison star GSC 0927:464 (
![]() ,
,
![]() )
located 1.1 arcmin to the east of the variable. This
comparison star is marked in the chart displayed in Fig. 1.
)
located 1.1 arcmin to the east of the variable. This
comparison star is marked in the chart displayed in Fig. 1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig1.eps}
\end{figure}](/articles/aa/full/2003/46/aa0080/Timg10.gif) |
Figure 1:
Finding chart for QW Ser covering a region of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{fig2.eps}
\end{figure}](/articles/aa/full/2003/46/aa0080/Timg11.gif) |
Figure 2: The general photometric behavior of QW Ser during its 2003 superoutburst. Visual estimates collected in the VSNET archive are shown as open circles and CCD observations described in this paper as dots. |
| Open with DEXTER | |
The typical accuracy of our measurements varied between 0.001 and 0.009 mag in the bright state and between 0.009 and 0.091 mag in the minimum light. The median value of the photometry errors was 0.004 and 0.031 mag, respectively.
Figure 2 presents the photometric behavior of QW Ser as observed between
February and May 2003. Relative magnitudes of the variable were
transformed to the visual scale using the photographic magnitude of our
comparison star equal to
![]() mag and taken from the GSC
Catalog (Lasker et al. 1999). Additionally, open circles denote the
visual and CCD estimates made by amateur astronomers and published in
the VSNET mailing list. Our transformation of "white light'' observations
is based on the photographic magnitude of the comparison star and it is
a rough estimate, which is used only to show the general behavior of the
star. The true brightness of the QW Ser may differ even by about 0.5 mag from that shown in Fig. 2.
mag and taken from the GSC
Catalog (Lasker et al. 1999). Additionally, open circles denote the
visual and CCD estimates made by amateur astronomers and published in
the VSNET mailing list. Our transformation of "white light'' observations
is based on the photographic magnitude of the comparison star and it is
a rough estimate, which is used only to show the general behavior of the
star. The true brightness of the QW Ser may differ even by about 0.5 mag from that shown in Fig. 2.
It is difficult to determine the exact time of the beginning of the
superoutburst. The maximal brightness of 12.5 mag was reported by
Schmeer (2003) on Feb. 21.199 UT. Previous estimates of the brightness
of QW Ser were made a week earlier and found the star in quiescence.
Presence of the clear superhumps with an amplitude as high as 0.23 mag
during our first run on Feb. 23/24 may suggest that Schmeer's
observations correspond to the real beginning of the superoutburst. Thus
our first observing run is most probably the fourth night of the superoutburst.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{fig3.eps}
\end{figure}](/articles/aa/full/2003/46/aa0080/Timg13.gif) |
Figure 3: The light curves of QW Ser observed during four consecutive nights in February 2003. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig4.eps}
\end{figure}](/articles/aa/full/2003/46/aa0080/Timg14.gif) |
Figure 4: The light curves of QW Ser observed during the eight longest runs from period Mar. 07/08-May 04/05. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig5.eps}
\end{figure}](/articles/aa/full/2003/46/aa0080/Timg15.gif) |
Figure 5: ANOVA power spectrum of the light curve of QW Ser. The inset shows the magnification of the power spectrum around main frequency. |
| Open with DEXTER | |
Our observations from Mar. 07/08 catch the star around minimum light. Observations by Dubovsky (2003) made on Mar. 7.099 UT indicate that the brightness of QW Ser was then at a magnitude of 15.1 i.e. about two magnitudes brighter than our determination from the subsequent night. Thus we conclude that the superoutburst of QW Ser lasted until Mar. 07/08 i.e. 15 days.
Figure 3 shows the light curves of QW Ser during four consecutive nights of the February 2003 superoutburst. The superhumps are clearly visible in each run. Their amplitude is 0.23, 0.21, 0.18 and 0.16 mag from the first to fourth night, respectively.
The lights curves of the eight longest runs from the period Mar. 07/08 - May 04/05 are displayed in Fig. 4. The magnitude of the star varied during this interval with an amplitude sometimes exceeding 0.5 mag, thus suggesting the presence of a periodic signal in the data (see Sect. 5).
From each light curve of QW Ser in superoutburst we removed the first or
second order polynomial and analyzed them using ANOVA
statistics and two harmonic Fourier series (Schwarzenberg-Czerny 1996).
The resulting periodogram is shown in Fig. 5. The most prominent peak is
found at a frequency of
![]() c/d, which corresponds to the
period
c/d, which corresponds to the
period
![]() days (
days (
![]() min). The peak visible
at 6.5 c/d is a ghost of the main frequency arising due to the use of
two harmonics. The harmonic peak at 26 c/d appears to be real. The inset
in Fig. 5 shows the magnification of the power spectrum around the main
frequency. Apart from this main peak and its aliases the inset shows no
other significant periodicities.
min). The peak visible
at 6.5 c/d is a ghost of the main frequency arising due to the use of
two harmonics. The harmonic peak at 26 c/d appears to be real. The inset
in Fig. 5 shows the magnification of the power spectrum around the main
frequency. Apart from this main peak and its aliases the inset shows no
other significant periodicities.
The light curves of QW Ser in superoutburst were prewhitened with the main period and its first harmonic. The power spectrum of the resulting light curve shows no clear peaks except second, third and fourth harmonics of the main frequency.
For nights from the superoutburst we determined six times of maxima and
nine times of minima of the superhumps. They are shown in Table 2
together with their cycle numbers E. The least squares linear fit to
the data from Table 2 gives the following ephemeris for the maxima:
| (1) |
| (2) |
Table 2: Times of extrema in the light curve of QW Ser in February 2003.
Combination of both O-C determinations of the period with its value derived from the power spectrum analysis gives the mean value of the superhump period as equal toThe O-C departures from the ephemeris (1) and (2) are given also in Table 2. They show no clear trend, thus we conclude that our observational coverage of the superoutburst was too weak for a valuable determination of the superhump period derivative.
During the period Mar 07/08-May 04/05 QW Ser was observed in a minimum light of around 17 mag. The ANOVA power spectrum for this period is shown in Fig. 6. Before calculation, the light curves were prewhitened using the first order polynomial.
The resulting periodogram yields a clear peak at a frequency of
![]() c/d, which corresponds to a period of
P=0.07457(2) days (
c/d, which corresponds to a period of
P=0.07457(2) days (
![]() min).
min).
A significant group of high peaks is also visible close to the first harmonic of the main period at a frequency around 26.8 c/d. It is due to the shape of the light curve, which often displayed a double wave structure (see Fig. 4 and nights Mar. 26/27, Apr. 5/26 and May 04/05, for example).
We have prewhitened our original light curve of QW Ser using the main
periodicity and its first harmonic. The power spectrum of the resulting
light curve shows no significant peaks in the period range of 0-50 c/d
indicating that in quiescence QW Ser is a monoperiodic object.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig6.eps}
\end{figure}](/articles/aa/full/2003/46/aa0080/Timg24.gif) |
Figure 6: ANOVA power spectrum of the light curve of QW Ser from the period Mar. 07/08 - May 04/05. |
| Open with DEXTER | |
The first detection of superhumps with a period of
![]() during the 2003 superoutburst of QW Ser unambiguously proves that this
star belongs to the group of SU UMa-type dwarf novae.
during the 2003 superoutburst of QW Ser unambiguously proves that this
star belongs to the group of SU UMa-type dwarf novae.
Superhumps occur at a period slightly longer than the orbital period of
the binary system. They are most probably a result of the accretion disc
precession caused by the gravitational perturbations from the secondary.
These perturbations are most effective when the disc particles moving on
eccentric orbits enter the 3:1 resonance. Then the superhump period is
simply the beat period between orbital and precession rate periods:
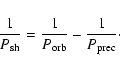 |
(3) |
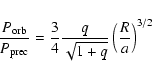 |
(4) |
where a is the binary separation, R is the disc radius and q is the mass ratio
M2/M1. At the 3:1 resonance we can assume
that
![]() and hence:
and hence:
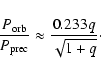 |
(5) |
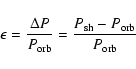 |
(6) |
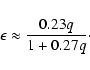 |
(7) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig7.eps}
\end{figure}](/articles/aa/full/2003/46/aa0080/Timg33.gif) |
Figure 7: Stolz & Schoembs relation for 44 ordinary SU UMa stars (open circles) and 10 stars other than dwarf novae (filled circles). The position of QW Ser is denoted by the solid triangle. |
| Open with DEXTER | |
Figure 7 shows the Stolz & Schoembs relation for 44 ordinary SU UMa-type stars (open circles) and 10 stars other than dwarf novae (filled circles). Data for this graph are taken from Patterson (1998) and the newest alerts published in the VSNET archive.
The double wave structure of brightness modulations observed in QW Ser
during quiescence and the period of these modulations, which is slightly
shorter than the superhump period, strongly suggests that we have
detected the orbital period of the binary system. Double humped waves
characterized by the orbital period of the binary are observed in some
SU UMa stars with high inclinations of orbit (see for example WZ Sge,
AL Com and V485 Cen - Patterson et al. 1996, 1998; Olech 1997). The
period excess for QW Ser is then
![]() .
According
to the Eq. (7) this corresponds to the mass ratio q=0.15.
.
According
to the Eq. (7) this corresponds to the mass ratio q=0.15.
In Fig. 7 QW Ser is plotted using a filled triangle. Error bars are of the same size as the symbol. It is clear that both periods observed in the light curve of this star conform to the Stolz & Schoembs relationship. This is a strong argument for our interpretation that modulations observed in quiescence are connected to the orbital period of the binary system.
Acknowledgements
We gratefully acknowledge the generous allocation of the Warsaw Observatory 0.6-m telescope time. This work was partially supported by KBN grant number 2 P03D 024 22 to A. Olech and used the on-line service of the VSNET. We would like to thank Chris O'Connor for reading and commenting on the manuscript.