1 - Astrophysics Division, Max-Planck-Institut für Kernphysik, Saupfercheckweg 1, 69117 Heidelberg, Germany
2 - ISO Data Centre, Astrophysics Division, ESA, Villafranca del Castillo, PO Box 50727, 28080 Madrid, Spain

Abstract
The "P32'' Astronomical Observation Template (AOT) provided a means to map large areas of sky (up to $45\times 45$ arcmin) in the far-infrared (FIR) at high redundancy and with sampling close to the Nyquist limit using the ISOPHOT C100 ( $3 \times 3$ ) and C200 ( $2\times 2$ ) detector arrays on board the Infrared Space Observatory (ISO). However, the transient response behaviour of the Ga:Ge detectors, if uncorrected, can lead to severe systematic photometric errors and distortions of source morphology on maps. We describe the basic concepts of an algorithm which can successfully correct for transient response artifacts in P32 observations. Examples are given to demonstrate the photometric and imaging performance of ISOPHOT P32 observations of point and extended sources corrected using the algorithm. For extended sources we give the integrated flux densities of the nearby galaxies NGC 6946, M 51 and M 101. and an image of M 101 at 100 $~\rm\mu m$ .

Key words: methods: data analysis - techniques: photometric - infrared: general

From the point of view of signal processing and photometry, diffraction-limited mapping in the FIR with cryogenic space observatories equipped with photoconductor detectors poses a particular challenge. In this wavelength regime the number of pixels in detector arrays is limited in comparison with that in mid- and near-IR detectors. This means that more repointings are needed to map structures spanning a given number of resolution elements. Due to the logistical constraints imposed by the limited operational lifetime of a cryogenic mission, this inevitably leads to the problem that the time scale for modulation of illumination on the detector pixels becomes smaller than the characteristic transient response timescale of the detectors to steps in illumination. The latter timescale can reach minutes for the low levels of illumination encountered on board a space observatory. The result is that the signals from the detectors can depend as much on the illumination history as on the instantaneous illumination. Unless corrected for, the transient response behaviour of the detectors lead to distortions in images, as well as to systematic errors in the photometry, especially for discrete sources appearing on the maps. In general, these artifacts become more long lived and more difficult to correct for at fainter levels of illumination, since the transient response timescales increase with decreasing illumination.

For mapping observations in the FIR, the Infrared Space Observatory (ISO; Kessler et al. 1996) was equipped with two Gallium-doped Germanium photoconductor detectors which comprised part of the ISOPHOT instrument (Lemke et al. 1996). The ISOPHOT C200 detector was a $2\times 2$ (stressed) pixel array operating in the 100-200 $~\rm\mu m$ range, and the ISOPHOT C100 detector was a $3 \times 3$ pixel array operating in the 50-100 $~\rm\mu m$ range. Compared to the IRAS survey detectors, the ISOPHOT-C detectors had relatively small pixels designed to provide near diffraction limiting imaging. ISOPHOT thus generally encountered larger contrasts in illumination between source and background than IRAS did, making the artifacts from the transient response more prominent, particularly for fields with bright compact sources and faint backgrounds.

A further difficulty specific to mapping in the FIR with ISO was that, unlike IRAS, the satellite had no possibility to cover a target field in a controlled raster slew mode. This limited the field size that could be mapped using the spacecraft raster pointing mode alone, since the minimum time interval between the satellite fine pointings used in this mode was around 8 s. This often greatly exceeded the nominal exposure time needed to reach a required level of sensitivity (or even for many fields the confusion limit). Furthermore, the angular sampling and redundancy achievable using the fine pointing mode in the available time was often quite limited, so that compromises sometimes had to be made to adequately extend the map onto the background.

A specific operational mode for ISO - the "P32'' Astronomical Observation Template (AOT) - was developed for the ISOPHOT instrument to alleviate these effects (Heinrichsen et al. 1997). This mode employed a combination of standard spacecraft repointings and rapid oversampled scans using the focal plane chopper. The technique could achieve a Nyquist sampling on map areas of sky ranging up to $45\times 45$ arcmin in extent (ca. $70\times 70$ FWHM resolution elements) on timescales of no more than a few hours. In addition to mapping large sources, the P32 AOT was extensively used to observe very faint compact sources where the improved sky sampling and redundancy alleviated the effects of confusion and glitching.

In all, over 6% of the observing time of ISO was devoted to P32 observations during the 1995-1998 mission, but the mode could not until now be fully exploited scientifically due to the lack of a means of correcting for the complex non-linear response behaviour of the Ge:Ga detectors. Here we describe the basic concept of an algorithm which can successfully correct for the transient response artifacts in P32 observations. This algorithm forms the kernel of the "P32Tools'' package, which is now publically available as part of the ISOPHOT Interactive Analysis package PIA (Gabriel et al. 1997; Gabriel & Acosta-Pulido 1999). Information on the algorithm, as well as the first scientific applications, can also be found in Tuffs et al. (2002a,b) and Tuffs & Gabriel (2002). The user interface of P32Tools that connects the P32 algorithm to PIA is described by Lu et al. (2002). After a brief overview of relevant aspects of the P32 AOT in Sect. 2, we describe the semi-empirical model used to reproduce the transient response behaviour of the PHT-C detectors in Sect. 3. Section 4 describes the algorithms used to correct data. Examples demonstrating the photometric and imaging performance of ISOPHOT P32 observations are given in Sect. 5, based on maps corrected using the P32 algorithm.

$\begin{figure} \par\includegraphics[scale=0.45,angle=0.,clip]{h4471f1.eps} \end{figure}$

Figure 1: A schematic representation of the P32 observing technique. The sky is sampled using a combination of a coarse spacecraft raster in the satellite Y and Z coordinates (horizontal and vertical directions on the figure) and finely sampled sweeps of the focal plane chopper in the Y coordinate. The spacecraft raster (in this example a $4\times 3$ raster) starts at the maximum value of Z and the minimum value of Y and proceeds as shown by the arrows. The position angle $\beta$ of the first scan leg in Y according to normal astronomical convention (taken positive E from N) is related to the satellite roll angle $\alpha$ by $\beta = \alpha +90^\circ$ . At each spacecraft pointing direction a chopper sweep of length 180 arcsec (the diameter of the unvignetted field of view of ISO) is made with a sampling of 1/3 of the detector pixel separation. This results in chopper sweeps of 13 positions separated by 15 arcsec for observations using the C100 detector array (as depicted in this example), and chopper sweeps of 7 positions sampled at 31 arcsec for the C200 detector array. The spacecraft raster sampling interval in Y is set to be a multiple of the chopper sampling interval (in the example depicted it is set to 6 chopper sampling intervals). A series of uniformly sampled linear scans for each detector pixel in Y is obtained in this fashion, built up from a sequence of registered and overlapping chopper sweeps obtained on each spacecraft scan leg in Y. The sampling of the target field in Z is controlled entirely by the spacecraft raster sampling interval in Z. In the example depicted the C100 detector detector array is stepped in intervals of 1.5 times the detector pixel separation in Z. For this particular case, the linear scans from different C100 detector pixels can be combined to sample the sky at half the detector pixel separation in Z, resulting in an overall sampling of $15\times 23$ arcsec over the target field.

Open with DEXTER

2 The P32 AOT

The basic concept of the P32 AOT, in which imaging was achieved using a combination of standard spacecraft repointings and rapid oversampled scans using ISOPHOT's focal plane chopper, is summarised in Fig. 1. There were two basic requirements, outlined in the original proposal for the AOT (Tuffs & Chini 1990) which led to the final design: the first goal was to give ISOPHOT the capability of achieving a Nyquist sky sampling ( $\rm\Delta\Theta = \lambda/2D=17$ arcsec at 100 $~\rm\mu m$ ) on extended sources subtending up to 50 resolution elements in a tractable observation time. As well as providing a unique representation of any arbitrary sky brightnesss distribution, this also improved the effective confusion limit in deep observations, which, in directions of low background was $\sim$ 100 and 20 mJy rms at 200 and 100 $~\rm\mu m$ , respectively, for ISOPHOT-C.

The second requirement was to achieve a redundancy in the observed data. This led to the sampling of each of a given set of sky directions by each detector pixel at different times. The redundancy was achieved in part by making several (at least 4) chopper sweeps at each spacecraft pointing direction. Further redundancy was achieved by having an overlap in sky coverage of at least half the chopper sweep amplitude between chopper sweeps made at successive spacecraft pointing directions in the Y spacecraft coordinate. Thus, a given sky direction was sampled on three different time scales by each detector pixel: on intervals of the detector non-destructive read interval, on intervals of the chopper sweep, and on intervals of the spacecraft raster pointings. Although the redundancy requirement was originally made to help follow the long term trends in detector responsivity during an observation, in practice it also proved very useful in removing effects caused by cosmic particle impacts (Gabriel & Acosta-Pulido 2000), the so-called "glitches'', from the data. This was especially important to optimise the sensitivity of deep observations using the C100 detector, which are generally limited by glitching rather than by confusion.

Both these requirements led to dwell times per chopper plateau which could be as low as 0.1 s. For a given sky brightness, this also had the consequence that the detector was generally read faster than in the other AOTs using the PHT-C detectors, which allows a higher time resolution in the deglitching procedures. A further beneficial side effect of the P32 AOT was that because the transient response timescale of the detectors is longer than the dwell time of the chopper, even for bright sources, the effective limiting source brightness that could be observed without saturating the detector was higher than for the other AOTs.

2.1 The P32 "natural grid''

The fact that the spacecraft pointing increment in Y was constrained to be a multiple of the chopper step interval means that a rectangular grid of directions on the sky can be defined such that all data taken during P32 measurement fine pointings will, to within the precision of the fine pointings, exactly fall onto the directions of the grid. This so-called P32 "natural grid'' allows maps to be made without any gridding function, thus optimising angular resolution. The P32 natural grid is also a basic building block of the algorithm to correct for the transient response behaviour of the detector, as the algorithm solves for the intrinsic sky brightness in $M\times N$ independent variables for a grid dimension of $M\times N$ . Here M and N are the number of columns and rows on the P32 natural grid. An example of the almost perfect registration of data onto the grid is shown in Fig. 2.

All the example maps shown in this paper will be sampled without a gridding function on the P32 natural grid. This means that the data in each of the map pixels is independent. This is unlike the situation for most other maps calculated using PIA, where a gridding function is employed and so raw data can contribute to more than one map pixel.

$\begin{figure} \par\includegraphics[scale=0.55,angle=90.,clip]{h4471f2.eps} \end{figure}$

Figure 2: Pointing directions observed towards Ceres at 105 $~{\mu}$ m. The spacecraft raster dimension was $3 \times 3$ in the spacecraft coordinates $Y \times Z$ . Sky sampling in Y is achieved through a combination of chopper scans in Y and repointings of the spacecraft. In Z the sky sampling is determined alone by the spacecraft repointing interval. Each pointing direction for 11 833 individual data samples for the central pixel of the C100 detector array is plotted as a cross. The rectangular grid is the "P32 natural grid'' (see text) for this observation, on which the sky brightness distribution is to be solved. The grid sampling is $14.99\times 45.98$ arcsec. Only points with the on target flag set (i.e. notincluding slews) are plotted. The pointings typically lie within1 arcsec of the centre of each pixel of the P32 natural grid.

Open with DEXTER

3 Transient response of the PHT-C detectors

Gallium doped germanium photoconductor detectors exhibit a number of effects under low background conditions which create severe calibration uncertainties. The ISOPHOT C200 (Ge:Ga stressed) and especially the C100 (Ge:Ga) detectors have a complex non-linear response as a function of illumination history on timescales of $\sim$ 0.1-100 s, which depends on the absolute illumination as well as the changes in illumination. The following behaviour is seen in response to illumination steps (see also Fouks 1992; Acosta-Pulido et al. 2000 and Laureijs et al. 2000, Sect. 4.2.2.):

3.1 Semi-empirical detector model

Unlike the ISOCAM and ISOPHOT-S Si:Ge detectors on board ISO, which operate in the mid-IR, the transient response behaviour of the Ge:Ga detectors of ISOPHOT-C are not described by the analytical Fouks Schubert model (Fouks & Schubert 1995; Schubert et al. 1995; Acosta-Pulido 1998; see Coulais & Abergel 2000 for its application to ISOCAM). Although numerical simulations of the transient behaviour of Ge:Ga detectors have been made (Hagel et al. 1996), these do not cover the wide range of operating conditions experienced by the ISOPHOT detectors. However, the effects observed in ISOPHOT-C can to some extent be qualitatively understood in terms of the build up of charge on the contacts between semiconductor and readout circuit, as analytically modelled by Sclar (1984). Sclar's model can be formulated as the superposition of three exponentials to describe the response of the detector to a step in illumination. A superposition of three exponentials has also been proposed by Fujiwara et al. (1995) and Church et al. (1996) to represent the transient behaviour. The three timescales involved are a minimum requirement to reproduce the hook response and the long term approach to the asymptotic response. However, no theory exists to predict values for the constants in this representation, and thus they must be found empirically.

In practice it is a formidable and unsolved problem to extract the constants from in flight data for as many as three temporal components to the transient response behaviour. In this paper we describe an approximate solution involving a superposition of two exponentials, each with illumination-dependent constants. This was found to adequately represent the detector response on timescales greater than a few seconds, though it only approximately model the hook response (see also Blomme & Runacres 2002). Our model can be viewed as a generalisation of the single exponential model developed for correction of longer stares by Acosta-Pulido et al. (2000).

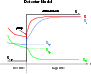$\begin{figure} \par\epsfig{file=h4471f4.eps, width=8cm,clip=} \end{figure}$

Figure 4: A schematic representation of the response of the semi-empirical detector model used in the P32 algorithm to an upwards step in illumination from $S_{\rm\infty p}$ to $S_{\rm\infty }$ . The overall response S is the sum of a "slow'' signal response S₁ and a "fast'' signal response S₂ (see Sect. 3.1). $S_{\rm 1p}$ and $S_{\rm 2p}$ respectively denote the signal response of these two components immediately prior to the step in illumination.

Open with DEXTER

In the model considered here, schematically illustrated in Fig. 4, the basic detector response Sto an instantaneous step in illumination from $S_{\rm\infty p}$ to $S_{\rm\infty }$ is given by the sum of a "slow'' signal response S₁ and a "fast'' signal response S₂ as:

3.2 Determination of model parameters

The parameterisation of the illumination dependence of the primary parameters $\tau _{\rm 1}$ , $\beta _{\rm 1}$ , $\tau _{\rm 2}$ and $\beta _{\rm 2}$ was made in engineering units (V/s), rather than in astrophysical units such as MJy/sr. Thus, it was assumed that there is no dependence of the detector response on the wavelength of the IR photons reaching the detector. Since the individual pixels of the C100 and the C200 arrays behave as independent detectors, each of the 12 parameters of the detector model had to be separately determined for each detector pixel.

The "slow'' primary parameters $\tau _{\rm 1}$ and $\beta _{\rm 1}$ were found from fits to the detector response to fine calibration source (FCS) exposures. To make this determination independent of the determination of the "fast'' parameters, only data points corresponding to times of 5 s or longer after the switch-on of the FCS was used. An example of a fit to the signal from an FCS exposure is given in Fig. 5. The model fit to the signal response on time scales ranging from a few seconds up to the duration of the FCS exposure depends mainly on the values of $\tau _{\rm 1}$ and $\beta _{\rm 1}$ .

A database of values for $\tau _{\rm 1}$ and $\beta _{\rm 1}$ was built up for a sample of FCS measurements, selected so as to correspond to the complete range of sky and source illuminations encountered by ISOPHOT during the ISO mission. These allowed the dependence of $\tau _{\rm 1}$ and $\beta _{\rm 1}$ on illumination to be determined according to Eqs. (6) and (7). An example showing the illumination dependence of $\beta _{\rm 1}$ for pixel 8 of the C100 array is given in Fig. 6a. The solid line is the fitted illumination dependence of $\beta _{\rm 1}$ used to find the values of the parameters $\beta_{\rm 10}$ , $\beta_{\rm 11}$ and $\beta_{\rm 12}$ used in the model. A corresponding plot for the illumination dependence of $\tau _{\rm 1}$ is given in Fig. 6b.

$\begin{figure} \par\includegraphics[scale=0.52,clip]{h4471f5.eps} \end{figure}$	Figure 5: Example of a model fit (curve) to the response of the central pixel of the C100 array to a constant FCS illumination starting at t=0 s. Prior to the FCS illumination the detector was viewing blank sky. The horizontal line indicates the fitted value of the illumination. No data was recorded in the first two seconds following FCS switch-on.
Open with DEXTER

At shorter timescales the response is primarily determined by the "fast'' primary parameters $\tau _{\rm 2}$ and $\beta _{\rm 2}$ . However, the FCS exposures could not be used to find $\tau _{\rm 2}$ and $\beta _{\rm 2}$ since no data was recorded in the first two seconds following the detector switch-on. This is also the reason why the hook response is not seen in Fig. 5. Furthermore, there is very probably a non-negligible timescale needed by the FCS to reach its final operating temperature. Therefore, the "fast'' parameters (with timescales $\sim$ $0.1\le \tau \le \sim 5$ s) were found using a self calibration technique (described in Sect. 4.2), operating on co-added repeated chopper sweeps crossing standard point source calibrators. During the self calibration the "slow'' parameters were fixed to the values determined in the fits to the FCS exposures. Observations of standard point source calibrators (12 source-wavelength combinations for both the C100 and C200 arrays) were analysed using the self-calibration technique. Each observation of a source provided several points for the determination of the "fast'' detector constants, since individual subscans through the source could be processed independently. In all, self calibrations were performed on data spanning a range in detector illumination of about 100. This allowed the dependence of $\tau _{\rm 2}$ and $\beta _{\rm 2}$ on illumination to be determined according to the parameterisation of Eqs. (8) and (9). Examples showing the illumination dependence of $\beta _{\rm 2}$ and $\tau _{\rm 2}$ for pixel 8 of the C100 array are given in Figs. 6c and 6d, respectively. The values of the 12 parameters determined for each pixel of the C100 and C200 detectors are given in Tables 1 and 2, respectively.

$\begin{figure} \par\mbox{\subfigure[]{ \includegraphics[scale=0.67,clip]{h4471f6... ...} \subfigure[]{ \includegraphics[scale=0.67,clip]{h4471f6d.eps} }}\end{figure}$

Figure 6: a) Values of the parameter $\beta _{\rm 1}$ for pixel 8 of the C100 array found from fits to the detector response to FCS exposures, plotted versus FCS illumination. The solid line is a fit of the function $\beta _{\rm 1}=\beta _{\rm 10}+\beta _{\rm 11}S_{\rm\infty }^{\beta _{\rm 12}}$ with $\beta _{\rm 10}=0.96$ , $\beta _{\rm 11}=-0.28$ , and $\beta _{\rm 12}=0.075$ . These are the parameters adopted for the model giving the default illumination dependence of $\beta _{\rm 1}$ for this pixel. b) As a), but for the parameter $\tau _{\rm 1}$ (in seconds). The solid line is a fit of the function $\tau _{\rm 1}=\tau _{\rm 10}+\tau _{\rm 11}S_{\rm\infty }^{-\tau _{\rm 12}}$ with $\tau _{\rm 10}=7.73$ s, $\tau _{\rm 11}=11.60$ , and $\tau _{\rm 12}=-1.28$ . These are the parameters adopted for the model giving the default illumination dependence of $\tau _{\rm 1}$ for this pixel. c) Values of the parameter $\beta _{\rm 2}$ for the central pixel of the C100 array found from self calibration optimisation of the model on observations of standard point source calibrators, plotted versus illumination. The solid line is a fit of the function $\beta _{\rm 2}=\beta _{\rm 20}+\beta _{\rm 21}S_{\rm illum}^{\beta _{\rm 22}}$ with $\beta _{\rm 20}=1.171$ , $\beta _{\rm 21}=-0.870$ , and $\beta _{\rm 22}=-0.0145$ , where $S_{\rm illum}$ is the known illumination of the detector pixel due to the point source calibrator. These are the parameters adopted for the model giving the default illumination dependence of $\beta _{\rm 2}$ for this pixel. d) As c), but for the parameter $\tau _{\rm 2}$ (in seconds). The solid line is a fit of the function $\tau _{\rm 2}=\tau _{\rm 20}+\tau _{\rm 21}S_{\rm illum}^{-\tau _{\rm 22}}$ with $\tau_{\rm 20}=0.333~$ s, $\tau _{\rm 21}=0.381$ , and $\tau _{\rm 22}=0.584$ . These are the parameters adopted for the model giving the default illumination dependence of $\tau _{\rm 2}$ for this pixel.

Open with DEXTER

4 The P32 algorithm

In a standard reduction of ISOPHOT data using the interactive analysis procedures of PIA, the analysis is made in several irreversible steps, starting with input "edited raw data'' at the full time resolution, and finishing with the final calibrated map. To correct for responsivity drift effects, however, it is necessary to iterate between a sky map and the input data at full time resolution. This different concept required a completely new data reduction package. In its development phase, and for the determination of the detector model parameters, this data reduction package was run as a set of IDL scripts. Running in the PIA environment, P32Tools provides access to the main functionality of this data reduction package via a GUI interface (Lu et al. 2002).

There are three basic elements to the concept of the P32 algorithm. The first step is signal conditioning, which aims to provide a stream of signal values, each with an attached time, from which artifacts such as glitches, dark current, and non-linearity effects have been removed, but which retains the full imprint of the transient response of the detector to the illumination history at the sharpest available time resolution. We will refer to such a stream of signals as the "signal timeline''.

The second step is the transient correction itself, which is an iterative process to determine the most likely sky brightness distribution giving rise to the observed signals. This is a non-linear optimisation problem with the values of sky brightness as variables. For large maps several hundred independent variables are involved.

Lastly, there is the calculation of calibrated transient corrected maps. This entails the conversion from V/s to MJy/sr, flat fielding, and the coaddition of data from different detectors pixels. Using P32Tools, this third stage requires the exporting of the transient corrected signal timeline into PIA at the SCP level, followed by the application of standard PIA processing. Here we just describe the new procedures for signal conditioning and transient correction.

4.1 Signal conditioning

4.2 Transient correction

A data flow diagram summarising the iterative non-linear optimisation process to solve for the sky brightnesses sampled on the P32 natural grid is summarised in Fig. 7. The calculation to correct for the transient response behaviour is made separately for each detector pixel. The kernel of the procedure is to solve for the illumination corresponding to the signal on each chopper plateau. This is done in a constrained optimisation using a binary chop scheme for set values of the 12 detector parameters. The constraints set for the solution in illumination define the search range for illumination. They are set such that the solution for illumination should be positive, and less than 10 times the value of the highest uncorrected signal. In practice the illuminations found on bright sources are never more than a factor of 5 higher than the uncorrected signal, so the determined photometry is not sensitive to the exact value of the upper limit in the search range. The values for $S_{\rm 1p}$ and $S_{\rm 2p}$ needed to solve for illumination on each chopper plateau are calculated from the response of the model to the preceding illumination history. After solving for the illumination on the current chopper plateau (in the representation in Fig. 7, to give the kth value I_K of the sequence of illuminations in the "signal timeline''), the found value I_K is divided by the vignetting corresponding to the chopper phase to obtain a new estimate of the sky brightess for the viewed direction on the P32 natural grid. This sky brightness estimate is then combined with any previous solutions for the same P32 natural grid pixel obtained with the same detector pixel from previous chopper plateaus, and the trial sky map (sampled on the P32 natural grid) is updated for this improved knowledge. The response of the detector pixel to the illumination history is then recalculated and a solution is found for the illumination viewed on the next chopper plateau. This procedure is continued until all the signal timeline has been processed. Then a second pass through the data can be made (the "second major iteration'' loop in Fig. 7), and so on, until the overall solution for the sky brightness distribution no longer changes between successive major iterations. Any sky directions for which no solution can be found are flagged in an output mask, sampled on the P32 natural grid.

The goodness of the solution is quantified through a value for $\chi^{\rm 2}$ , calculated from a comparison between the model fit and the signal timeline. The random uncertainties assigned to each signal sample in the timeline can optionally be recalculated from the self consistency of solutions for the illumination found in a given sky direction. Examples of model fits to the signal timeline are shown in Fig. 8 for the C100 detector and in Fig. 9 for the C200 detector.

The algorithm can also be used for datasets for which the readout rate was too rapid to allow all the data to be transmitted to the ground. In such cases the illumination history can still be determined at all times on fine pointings, even where there are gaps in the signal timeline. On slews, the illumination history during the gaps are either interpolated in time, or taken from the nearest previously solved direction on the P32 natural grid.

$\begin{figure} \par\includegraphics[width=15.0cm,clip]{h4471f8.eps} \end{figure}$

Figure 8: Detail from a signal timeline from an observation of the standard calibrator Ceres, observed in the C105 filter. The green line shows the fit to the observed signal (shown in red) from pixel 1 of the C100 array, as found by the P32 algorithm for correction of the transient response behaviour of this pixel. 5 chopper sweeps, each comprising 13 pointing directions ("chopper plateaus'') are shown, divided by vertical dotted lines separated in time by a duration of 6.1 s for each sweep. The upper line in the figure shows the fine pointing flag; whereas the first chopper sweep shown was made while the spacecraft was slewing between fine pointings (flag value 0), the subsequent chopper sweeps were made on a single fine pointing (flag value 1). The remaining horizontal lines denote masks at the full time resolution of the data denoting glitches, readout status and whether or not a solution for the illumination could be found by the algorithm. The overall solution for the sky illumination for this detector pixel is given by the histogram in black. As described in the text, this overall solution is calculated from a combination of individual solutions for illumination on each successive chopper plateau, which are shown here as purple bars. For the very brightest sources, as shown in this example, the derived illuminations can be up to a factor of 6 brighter than the raw data for pixels in the C100 array. In this example the hook response is well seen in each chopper sweep at the 9th and 10th chopper plateaus.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=15.0cm,clip]{h4471f9.eps} \end{figure}$

Figure 9: Detail from a timeline of signal versus time from another observation of Ceres, this time observed in the C160 filter using the C200 detector array. The key to the plot is as given in the caption to Fig. 8. This example shows the transition from a spacecraft fine pointing for which the chopper is sweeping through beam sidelobes to a fine pointing where the chopper samples the beam kernel. In this case the red line corresponding to the data is not seen during the intervening spacecraft slew, as it is exactly overplotted by the green line showing the fit to the data (see text). The chopper sweeps on the second fine pointing encompassing the beam kernel show a typical enhancement of the source-background contrast induced by the algorithm for correction of the transient response.

Open with DEXTER

For most observations using the C200 detector, and observations of moderate intensity sources made using the C100 detector, good fits to the entire unbroken signal timeline can be obtained for each detector pixel. For observations of bright sources using the C100 detector, however, it is often necessary to break up the solutions into smaller segments, according to the distribution of the sources in the field mapped. This is best achieved by solving separately for the portions of the signal timeline passing through the bright sources. The most conservative processing strategy, appropriate for observations using the C100 detector of complex brightness distributions with high source to background contrast, is to break up the calculation into time intervals corresponding to individual spacecraft fine pointings. In this latter case, no processing of the slews is required.

Several processing options are available for the interactive processing, to optimise solutions for the particular characteristics of each dataset:

The default operation of the program is to assume that the detector is in equilibrium at the start of the observation, viewing the sky direction corresponding to the first detector plateau. This corresponds to the case $S_{\rm 1p} = S_{\rm01} = S_{\rm\infty}$ and $S_{\rm 1p} = 0$ . This will very rarely be the case, however, since an FCS measurement which may not be perfectly matched to the sky brightness will have been made just seconds prior to the start of the spacecraft raster. Therefore, the algorithm can optionally find a solution for the detector starting state, as characterised by the values of $S_{\rm 1p}$ and $S_{\rm 2p}$ immediately prior to the start of the first chopper plateau. This is done by solving for $S_{\rm 1p}$ and $S_{\rm 2p}$ for a fixed $S_{\rm\infty }$ on the first plateau, where $S_{\rm\infty }$ is determined from the last chopper plateau in the first spacecraft pointing to view the same sky direction. The timeline for the first spacecraft pointing is then repeatedly processed until a stable solution for $S_{\rm 1p}$ and $S_{\rm 2p}$ prior to the first plateau is found. This option was found to be particularly useful for data taken with the C200 detector.

In order to determine the primary detector parameters $\beta _{\rm 2}$ and $\tau _{\rm 2}$ in the first instance, "a self calibration'' processing technique was used by which any of the 12 detector parameters (Sect. 3.1) could be determined from observations of bright sources. The self calibration functionality has also been implemented in the publically available P32Tools. This is because, even though the standard parameters of the detector model given in Tables 1 and 2 generally give good results, some fine tuning of the parameters may still yield improved fits to the signal timeline for some astronomical targets, particularly for targets with a high contrast to the background.

Sources of any arbitrary brightness distribution and position can be used for the self calibration. However, in the initial determination of the detector parameters for the "fast'' response of the detector, point source calibrators of known brightness were used, and the solutions for $\tau _{\rm 2}$ and $\beta _{\rm 2}$ were additionally constrained by the requirement that the solutions for illumination were consistent with the known flux densities of the calibrators.

The self calibration procedure works by simply repeating the optimisation process for different subsets of the 12 detector parameters, specified by the user. Each combination of detector parameters produces an individual solution for the sky brightness distribution, as well as a value for $\chi^{\rm 2}$ . A search is made in the parameter space of the detector parameters until a minimum is found in $\chi^{\rm 2}$ . This is a lengthy process, however, making it advisable to perform self calibrations on limited portions of the timeline. This is often chosen to correspond to a single spacecraft pointing where the chopper sweeps for the detector pixel being investigated pass through bright structure. The process can be further accelerated in cases that the repeated chopper sweeps through a source give the same repeated signal pattern. Then, the optimisation can be performed on an average of the coadded chopper sweeps performed on a single spacecraft pointing. This latter technique is referred to in P32Tools as a "composite self calibration''. Some examples of the useage of the self calibration procedure are given by Schulz et al. (2002a).

The calculation of the illumination history for data taken during the slews is less straightforward than for data taken during the spacecraft fine pointings. This is because the instantaneous pointing directions during slews are effectively at random positions with respect to the P32 natural grid. Therefore, the use of solutions for the sky brightness distribution on the P32 natural grid found from analysis of previous fine pointings will in general lead to inaccuracies in the determination of the illumination history during the slews. There are two main approaches which can be adopted to counter this problem.

The first is to solve for the illumination not over a chopper plateau, but for individual readouts in the signal timeline during the slew. This automatically provides a solution in which the model fit exactly matches the data, as there is only one fitted data point for each determined illumination. An example is given in the fit to the signal timeline for the C200 detector shown in Fig. 9. This approach is useful for observations of bright structured sources in which the variations in illumination with position on the slew on timescales of a chopper plateau exceed the signal to noise on individual data samples. It is the default processing option for the C200 detector.

In cases of low signal to noise, and for all instances where not all data are transmitted to the ground, solving for the average illumination on each chopper plateau is a preferable technique. Otherwise, the values of $S_{\rm 1p}$ and $S_{\rm 2p}$ calculated just prior to the first chopper plateau on the next fine pointing can be wildly inaccurate, which can corrupt the solutions for the remainder of the signal timeline of the observation. Processing on a plateau by plateau basis is the default processing option to calculate the illumination history during slews for observations with the C100 detector. Another reason for processing slews on a plateau-by-plateau basis for the C100 detector is that the procedure to solve for illumination for individual readouts is very susceptible to any residual glitches, and the C100 detector is more prone to glitching than the C200 detector.

5 Photometric performance

In this section we give examples of the photometric performance achieved from maps made using the P32 algorithm. In all cases the standard calibration parameters used in the signal conditioning step prior to the correction of the transient response behaviour and the subsequent conversion from engineering units (V/s) to astronomical units (MJy/str and Jy) were taken from version 8.1 of PIA. To illustrate the quantitative effect of the transient correction we give results for datasets processed by the P32 algorithm both with and without the transient correction. In all cases, the corrections for the transient response behaviour were made using the standard detector model parameters given in Tables 1 and 2. In Sect. 5.1 we give examples of the effects of the transient correction on the derived spatially integrated flux densities. Where possible these integrated flux densities are also compared with flux densities from IRAS or from source models for the standard calibrators. In Sect. 5.2 we give examples of the imaging performance.

5.1 Integrated flux densities

In general the corrections in integrated flux densities made by the algorithm depend on the source brightness, structure, size, the source/background ratio, and the dwell time on each chopper plateau. The largest corrections are for bright point sources on faint backgrounds observed with the C100 detector.

In Fig. 10 we plot the measured integrated and colour-corrected flux densities of standard ISOPHOT calibrators (the asteroids Ceres and Vesta, and the planet Neptune) versus the nominal flux densities of these sources (determined as described by Schulz et al. 2002b). Since these same sources were used to derived the detector model, one expects a good statistical match between the nominal and the derived flux densities. Indeed, the integrated flux densities found after correction for the transient behaviour of the detector lie reasonably close to the solid line indicating an equality between the measured and nominal flux densities, though with some scatter (of around 15 percent). It can be seen that the flux densities derived from data uncorrected for the transient effects have been raised by factors ranging from $\sim$ 2 for the fainter standards to $\sim$ 5 for the brighter ones.

$\begin{figure} \par\includegraphics[scale=0.6,clip]{h4471f10.eps} \end{figure}$

Figure 10: The measured integrated and colour-corrected flux densities of the standard calibrators Ceres, Vesta and Neptune plotted against the nominal flux densities. The observations were done in various filters using the C100 detector. The photometry derived with and without correction for the transient response behaviour is shown with crosses and diamonds, respectively. The solid line shows the expected trend for equality between the measured and nominal flux densities.

Open with DEXTER

$\begin{figure} \par\includegraphics[scale=0.5,clip]{h4471f11.eps} \end{figure}$

Figure 11: The measured integrated flux densities of the faint standard star HR 1654 plotted against the predicted flux densities from a stellar model. The observations were done in various filters using the C100 detector. The photometry derived with and without correction for the transient response behaviour is shown with crosses and stars, respectively. The solid line shows the expected trend for equality between the measured flux densities and those predicted from the stellar model.

Open with DEXTER

As an example of the photometric performance for fainter point sources we give results achieved for the faint standard star HR 1654. This source was not used in the determination of the detector model parameters, so it constitutes a test of the photometric performance of ISOPHOT in its P32 observing mode. The derived integrated flux densities, with and without correction for the transient response behaviour of the C100 detector, were compared in Fig. 11 with predicted flux densities from a stellar model. The corrected photometry is in reasonable agreement with the theoretical predictions. As expected, there is again a trend for observations with larger detector illuminations to have larger corrections in integrated photometry.

$\begin{figure} \par\includegraphics[scale=0.5,clip]{h4471f12.eps} \end{figure}$	Figure 12: Integrated and colour-corrected flux densities of Virgo cluster galaxies measured in the ISO C100 filter versus the corresponding flux densities measured by IRAS in its 100 $~\rm\mu m$ band (taken from Fig. 7 of Tuffs et al. 2002a). The dotted line represents the relation $\rm ISO/IRAS=0.82$ . The star symbols are used for galaxies not fully covered by the spacecraft raster.
Open with DEXTER

A good linear correlation is also seen between integrated flux densities of Virgo cluster galaxies (Tuffs et al. 2002a), derived from P32 ISOPHOT observations processed using the P32 algorithm, and flux densities from the IRAS survey (Fig. 12). The interpretation of these measurements constituted the first science application (Popescu et al. 2002) of the P32 algorithm. The ISOPHOT observations of Virgo cluster galaxies were furthermore used to derive the ratios of fluxes measured by ISO to those measured by IRAS. The ISO/IRAS ratios were found to be 0.95 and 0.82 at 60 and 100 $~\rm\mu m$ , respectively, after scaling the ISOPHOT measurements onto the COBE-DIRBE flux scale (Tuffs et al. 2002a).

The effect of the transient response behaviour on the integrated flux densities of very extended sources is illustrated by the photometry of a few bright extended nearby galaxies. Thus, in Table 3, Col. 5, we give the integrated flux densities of NGC 6946, M 51 and M 101 taken from Tuffs et al. (2003; in preparation). For NGC 6946 the integrated flux densities are given here for the first time; those for M 51 and M 101 supercede the values given by Hippelein et al. (1996). The standard values for the detector parameters (as given in Tables 1 and 2) were used for the correction of the transient response. Table 3 also gives a comparison with the IRAS flux densities at 60 and 100 $~\rm\mu m$ . In general, the ISOPHOT photometry yields somewhat lower integrated flux densities than the corresponding IRAS photometry, similar to the ISO/IRAS ratios found for the Virgo cluster galaxies (Tuffs et al. 2002a). As for the point sources, we also reduced the maps of these nearby galaxies without correcting for the transient response of the detectors. We were thus able to derive the "correction factor'' (Col. 6) indicating the ratio between the integrated flux densities with and without correcting for the transient. In comparison to the point sources of similar integrated flux densities, these corrections factors are moderate, varying between 1.07 and 1.45. This is because the timescale for the detector to traverse these extended sources becomes comparable to the time constants for the transient behaviour. The result therefore is a redistribution of flux density within the area of the galaxies along the scan direction, which goes some way to offset the loss of signal. We emphasise however that the remaining corrections are systematic, rather than random effects, and that the precise value of the correction factor for integrated flux density depends on the extent and morphology of the target. Furthermore, the correction factors for any point-like sources within extended sources, such as galactic nucleii or HII regions, will be much larger, comparable to those found for the point source calibrators.

5.2 Imaging performance

$\begin{figure} \par\epsfig{file=h4471f13.eps, width=8.0cm,clip=} \end{figure}$	Figure 13: Brightness profiles (in MJy/str) along the Y spacecraftdirection through the standard star HR 1654 at 100 $~\rm\mu m$ . The solid line represents the brightness profile obtained after processing with the P32 algorithm, while the dotted line shows the profile derived from identically processed data, but without correction for the transientresponse of the detector.
Open with DEXTER

Another effect of the inability to model the hook response is that the beam profile becomes somewhat distorted. This also has the consequence, that for observations of bright sources, the measured FWHM can become narrower than for the true point spread function, as predicted from the telescope optics and pixel footprint. We emphasise that, because of the beam distortion, the flux density of bright point sources cannot be found from the peak surface brightness, but instead should be determined by integrating the map. An example of an extremely bright point source reduced using the P32 algorithm is given in Fig. 14, depicting maps of Ceres in the C105 filter, made with and without the correction for the transient response of the C100 detector.

$\begin{figure} \par\includegraphics[scale=0.72,clip=]{h4471f14a.eps}\par\includegraphics[scale=0.72,clip=]{h4471f14b.eps} \end{figure}$

Figure 14: Top: contour map of Ceres in the C105 filter after responsivity drift correction. The contour levels are 5 . 2ⁿ MJy/sr for all integers n with $1 \le n \le 10$ . The measured integrated flux density after background subtraction is 98.4 Jy $\pm~0.2$ Jy (random) $\pm$ 6% (systematic). The actual flux density of this standard calibrator (from a stellar model) is 109 Jy. As in Fig. 2, the the map pixels of the P32 natural grid have been overlaid. Bottom: contour map of Ceres in the C105 filter without correction for the transient response behaviour of the detector. The contour levels are 5 . 2ⁿ MJy/sr for all integers n with $1~\le~n~\le~7$ . The The measured integrated flux density after background subtraction is 28.0 Jy $\pm~0.07$ Jy (random) $\pm$ $4\%$ (systematic).

Open with DEXTER

$\begin{figure} \par\includegraphics[scale=0.72]{h4471f15a.eps}\par\includegraphics[scale=0.72]{h4471f15b.eps} \end{figure}$

Figure 15: The interacting galaxy pair KPG 347 observed in the C160filter. Top: after processing with the P32 algorithm. Bottom: with identical processing, except that the correction for the transient response behaviour of the detector has been omitted. The map pixels corresponding to the P32 natural grid (see Sect. 2.1) have been overlaid. In both maps, contours are logarithmic, at levels 1, 2, 4, 8, 16, 32, 64 MJy/sr. The peak brightnesses are 126 and 109 MJy/str for the maps with and without processing with the P32 algorithm, respectively.

Open with DEXTER

Despite the limitations due to the lack of a proper modelling of the hook response, the algorithm can effectively correct for artifacts associated with the transient response on timescales from a few seconds to a few minutes. This is illustrated in Fig. 15 by the maps of the interacting galaxy pair KPG 347 in the C200 filter (again, after and before correction for the transient response of the detector, respectively). The uncorrected map shows a spurious elongation in the direction of the spacecraft Y coordinate, which is almost completely absent in the corrected map. If uncorrected, such artifacts could lead to false conclusions about the brightness of FIR emission in the outer regions of resolved sources. Also visible are artifacts at $Y=\pm310$ arcsec. Similar artifacts are also seen at the same offset in other P32 observations made with the C200 detector, with position and amplitude relative to the central source independent of the filter used. These features are attributable to optical effects peculiar to the P32 mode, in which a small fraction of the light from a centrally positioned compact source is deflected away from the main beam into the vignetted part of the field of view for a certain combination of the offset in spacecraft fine pointing and chopper phase. Although these artifacts have nothing to do with the transient response behaviour of the detector, they are alleviated by the application of the P32 algorithm when solutions for detector illumination are converted into sky brightnesses, due to the vignetting correction made in this processing step.

The image of M 101 in Fig. 16, made using the C100 detector with the C100 filter, is given as a state of the art example of what can be achieved with a careful interactive processing of P32 data using the P32 algorithm. In addition to the transient response corrections and a masking of residual hook response artifacts, a time dependent flat field has been applied. The spiral structure of the galaxy, with embedded HII region complexes and a component of diffuse interarm emission can clearly be seen.

		$\displaystyle S =S_{\rm 1} + S_{\rm 2}$	(1)
		$\displaystyle S_{\rm 1} = (1 - \beta_{\rm 2})~S_{\rm\infty}~ (1 - {\rm exp}[-t/\tau_{\rm 1}])~+~S_{\rm01}~{\rm exp}[-t/\tau_{\rm 1}]$	(2)
		$\displaystyle S_{\rm 2} = \beta_{\rm 2}~S_{\rm\infty}~ (1 - {\rm exp}[-t/\tau_{\rm 2}])~+~S_{\rm02}~{\rm exp}[-t/\tau_{\rm 2}]$	(3)

$\displaystyle S_{\rm01}$	=	$\displaystyle \beta_{\rm 1}~(S_{\rm\infty} - S_{\rm\infty p}) + S_{\rm 1p}$	(4)
$\displaystyle S_{\rm02}$	=	$\displaystyle S_{\rm 2p}.$	(5)

Photometric mapping with ISOPHOT using the "P32'' Astronomical Observation Template

1 Introduction

2 The P32 AOT

2.1 The P32 "natural grid''

3 Transient response of the PHT-C detectors

3.1 Semi-empirical detector model

3.2 Determination of model parameters

4 The P32 algorithm

4.1 Signal conditioning

4.2 Transient correction

5 Photometric performance

5.1 Integrated flux densities

5.2 Imaging performance

References

$\begin{figure} \par\includegraphics[scale=0.52,clip]{h4471f3.eps} \end{figure}$	Figure 3: Example of the transient response of a Ge:Ga detector following an upwards step to a constant level of illumination at 100 $~\rm\mu m$ . The hook response is shown in the inset.
Open with DEXTER

		$\displaystyle \beta_{\rm 1} = \beta_{\rm 10}~+~\beta_{\rm 11}~*~S_{\rm\infty}^{\beta_{\rm 12}}$	(6)
		$\displaystyle \tau_{\rm 1} = \tau_{\rm 10}~+~\tau_{\rm 11}~*~S_{\rm\infty}^{-\tau_{\rm 12}}$	(7)
		$\displaystyle \beta_{\rm 2} = \beta_{\rm 20}~+~\beta_{\rm 21}~*~S_{\rm\infty}^{\beta_{\rm 22}}$	(8)
		$\displaystyle \tau_{\rm 2} = \tau_{\rm 20}~+~\tau_{\rm 21}~*~S_{\rm\infty}^{-\tau_{\rm 22}}.$	(9)

$\begin{figure} \par\includegraphics[scale=0.8,clip]{h4471f7.eps} \end{figure}$	Figure 7: Iterative scheme for transient correction (see Sect. 4.2).
Open with DEXTER

$\begin{figure} \par\includegraphics[scale=0.65,clip]{h4471f16.eps} \end{figure}$	Figure 16: A $27\times 27$ arcmin field containing the galaxy M 101, as mapped in the C100 filter, after processing with the P32 algorithm. The map sampling is $15\times 23$ arcsec.
Open with DEXTER