A&A 410, 639-648 (2003)
DOI: 10.1051/0004-6361:20031212
Testing the "strong'' PAHs hypothesis
II. A quantitative link between DIBs and far-IR emission features
G. Mulas1 -
G. Malloci1,2 -
P. Benvenuti2,3
1 - INAF - Osservatorio Astronomico di Cagliari - AstroChemistry Group,
Strada n.54, Loc. Poggio dei Pini, 09012 Capoterra (CA), Italy
2 -
Dipartimento di Fisica, Università degli Studi di Cagliari,
S.P. Monserrato-Sestu Km 0.7, 09042 Cagliari, Italy
3 -
Space Telescope-European Coordinating Facility, ESA,
Karl-Schwarzschild-Strasse 2, 85748 Garching bei Munchen, Germany
Received 15 April 2003 / Accepted 5 August 2003
Abstract
In Paper I (Malloci et al. 2003) we proved the profile invariance of the
first permitted electronic transition of the typical Polycyclic Aromatic
Hydrocarbon cation C32H14+ as a first necessary check for the
"strong'' PAHs hypothesis. In this paper we derive a quantitative
relation between the intensities of the former band, which ought to be
observable in absorption in the visible range, and those of the far-IR
bands, which are predicted by the PAH model to be simultaneously present in
emission.
Contrary to the mid-IR bands, collectively known as "Unidentified Infrared
Bands'' (UIBs), which do not discriminate specific molecules, the far IR,
skeletal bands can be expected to be a fingerprint of each single species.
This fact provides a number of independent constraints which must be
simultaneously fulfilled for a successful PAH identification. Our approach
thus offers a powerful criterion for the identification of specific PAHs, both
in the presently available ISO data and in those of the forthcoming SIRTF and
Herschel missions.
As an interesting by-product, we quantitatively evaluate the impact of
isotopic substitutions ( 13C 12C and D
12C and D
 H) on the resulting infrared emission bands.
H) on the resulting infrared emission bands.
Key words: astrochemistry - line: identification - molecular processes -
ISM: lines and bands - ISM: molecules - infrared: ISM
The so called "Unidentified Infrared Bands'' (UIBs) are emission bands seen
in the infrared near 3030, 1610, 1280, 1150 and 885 cm-1 (3.3, 6.2, 7.7,
8.6 and 11.3  m), in numerous galactic objects as well as in external
galaxies. First detected in two planetary nebulae by Gillett et al. (1973), UIBs have
since been ubiquitously observed in dusty environments along a large number of
interstellar sight-lines covering a wide range of excitation conditions
(see e.g. Allamandola et al. 1989).
m), in numerous galactic objects as well as in external
galaxies. First detected in two planetary nebulae by Gillett et al. (1973), UIBs have
since been ubiquitously observed in dusty environments along a large number of
interstellar sight-lines covering a wide range of excitation conditions
(see e.g. Allamandola et al. 1989).
UIBs are commonly believed to arise from the vibration of CH and CC bonds in
aromatic groups, hence their other common name of "Aromatic Infrared Bands''
(see e.g. Pech et al. 2002). Their most natural interpretation is in terms
of free gas phase polycyclic aromatic hydrocarbons (PAHs) which are thought to
be ubiquitous in the interstellar medium thanks to their high photostability
and the fact that they are carbon-based (Allamandola et al. 1985; Léger & Puget 1984). The physical
mechanism invoked for the production of the UIBs is the IR-cooling of PAHs
transiently heated by the absorption of a single UV/visible photon
(see e.g. Allamandola et al. 1985; Léger & Puget 1984; Puget & Léger 1989; Allamandola et al. 1989).
In order to understand the role of PAH compounds in the chemistry of the
interstellar medium (ISM) it is necessary to identify individual members in
this class. This task is far from trivial on the sole basis of the oserved
UIBs, because the near and mid infrared region contains most of the normal
vibrational modes which are a common, shared feature of the whole class of
PAHs (Langhoff 1996); this is supposed to be the reason why these features
are so strong, since a whole population of different PAH-like molecules may
contribute to them. Indeed, in order to match to the observational constraint
of smooth profiles of the observed bands, a mixture of radicals, neutrals and
ionized molecules is required, rather than a single such species. Along these
lines, recent laboratory IR spectra of neutral and positively charged PAHs,
have been successfully used by Allamandola et al. (1999) to model the observed UIBs. For
this same reason therefore these same near and mid infrared bands do not
permit an unambiguous identification of any single molecular species
(Salama 1999; Langhoff 1996). However, on the other hand, every single such molecule
ought to show its spectral fingerprint both in the far infrared spectral
regions, which contains the vibrational frequencies associated with the
bending of the skeletal structure (Joblin et al. 2002; Zhang et al. 1996; Langhoff 1996), and
UV/visible electronic transitions. Hence UIBs ought to be strongly related to
the diffuse interstellar bands (DIBs), and their possible common root
represents the so-called PAHs-DIBs hypothesis in its most ambitious form
(see e.g. Salama 1999, and references therein). Indeed, as shown by
Rouan et al. (1992) and quantitatively studied in Mulas (1998) and Malloci et al. (2003), infrared
emission is supposed to be the dominant mechanism driving the rotation of an
isolated PAH in the ISM, hence suggesting a direct link between DIB spectral
profiles and IR emission bands.
Following the above line of reasoning to its extremes, it is clear that if
PAHs account for the UIBs, their electronic transitions must also show
up in the form of a large number of DIBs (van der Zwet & Allamandola 1985; Léger & D'Hendecourt 1985). Therefore the
failure to find their absorption bands in the visible would cast strong
doubts on the applicability of the PAHs model for the UIBs and on their
alleged presence in the ISM at all: the two hypotheses are not unrelated and
independent but, instead, they either stand together or fail together.
As a matter of fact, despite many observational, experimental and theoretical
efforts which led to infer upper limits on the abundance of some PAHs
(see e.g. Salama & Allamandola 1992a; Ehrenfreund et al. 1995; Salama & Allamandola 1992b), no definitive spectral
identification of any specific interstellar PAH exists to date. The
identification of DIBs-UIBs would thus yield an important improvement in our
knowledge of the physics and chemistry of the ISM. First of all, since the
abundances of dust forming elements, such as carbon, required by any dust model
seem to be larger than those available in the ISM, the identification of some
large, carbon-bearing molecule, and the resulting measure of its column
density, would place direct constraints on the well-known problem of the
"carbon-crisis'' (Cardelli et al. 1996). More broadly, it would have an impact on our
understanding of the origin of life on the early Earth through the exogenous
delivery (cometary encounters and meteoritic bombardments) of prebiotic
organic molecules (see e.g. Bernstein et al. 1999).
In Malloci et al. (2003), henceforth mal03c, we modelled the photophysics
of a prototypical medium sized PAH cation, namely C32H14+, and showed
that its vibronic bands can easily match the observational constraint
of spectral profile stability of DIBs in a wide variety of interstellar
environments. Here we used the same model to obtain its expected IR emission
spectra in the same environments, providing a quantitative estimate of the
ratio of the equivalent width of the modelled "DIB'' and the intensities of
the infrared emission bands which ought to be simultaneously produced by the
same molecules.
Ovalene (C32H14) is a good representative of middle
sized, compact PAHs, hence many of the results which we obtained can be
expected to apply to other, similar molecules. We can trivially tailor our
model to many other large molecules under relatively weak assumptions, so that
the present implementation should be regarded as a "proof of concept''
for its validity as a diagnostic tool. For this reason, we restricted the
present work to neutral ovalene and its singly charged cation, although
middle sized PAHs are expected to be significantly present in a wider variety
of charge states in many interstellar environments (see e.g. Bakes et al. 2001a,b, and
references therein). This does not affect the validity of the
results presented here, since infrared emission by free-flying interstellar
PAHs is expected to be pumped by single-photon absorption and is thus utterly
independent of the history of the molecule considered. We do plan to apply this
same approach to a wide range of molecules in this class, including e.g. larger
molecules, different hydrogenation and ionisation states, possibly nitrogen
substituted species, in forthcoming works.
The general assumptions of the Monte-Carlo model, the parameters it needs
and the different ambient interstellar conditions assumed, are fully detailed
in mal03c. The present work concentrates on the quantitative link
between the modelled "DIB'' at about 9700 Å (Ruiterkamp et al. 2002), and the expected
infrared emission bands, with particular regard to the skeletal vibrational
modes, peculiar of the specific molecule considered (Joblin et al. 2002; Zhang et al. 1996; Langhoff 1996).
Moreover, using the vibrational analysis obtained through ab initio
density functional theory calculations, we quantitatively studied the impact of
the most likely isotopic substitutions ( 13C 12C and
D
12C and
D H) on the infrared emission bands.
H) on the infrared emission bands.
In the following Sect. 2 we present the results of our
Monte-Carlo/ab initio approach. We discuss them in
Sect. 3 with special emphasis to the new quantitative
constraint provided for PAHs identification in the ISM. Our main conclusions
are presented in the final Sect. 4.
2 Results
In mal03c we used a compendium of calculated and experimental data
about C32H14 and C32H14+ to run our Monte-Carlo model
(Mulas 1998) for a grid of molecular parameters and exciting radiation
fields. In particular, the four different radiation fields considered are shown
in Fig. 1.
All our ab initio calculations were performed using the NWChem computer
code (Harrison et al. 2001). Following Bauschlicher & Langhoff (1997); Langhoff (1996), and Hudgins et al. (2001) we
obtained the full vibrational analysis using density functional theory,
specifically with the exchange-correlation functional B3LYP (Becke 1993; Stephens et al. 1994)
and the 4-31G Gaussian basis set (Frish et al. 1984) to expand the molecular
orbitals. According to the table of characters of the D2h point group, the
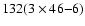 normal modes of vibration of C32H14 and C32H14+
span the following irreducible representation
(see e.g. Wilson Jr. et al. 1955, p. 327):
normal modes of vibration of C32H14 and C32H14+
span the following irreducible representation
(see e.g. Wilson Jr. et al. 1955, p. 327):
 |
= |
23 Ag + 10 Au + 22 B1g + 12 B1u |
(1) |
| |
|
+ 9 B2g + 22 B2u + 12 B3g + 22 B3u, |
|
where the molecule is assumed to lie in the x-y plane.
We obtained all of the 132 vibrational frequencies for both the neutral and
ovalene cation at the ground state optimised geometry using the usual
projection operator technique (Wilson Jr. et al. 1955) implemented within NWChem.
They are all used within the Monte-Carlo model to compute the density of
vibrational states as a function of energy. The complete list of the 56
IR-active modes (symmetries B1u, B2u and B3u), the corresponding
symmetries, the vibrational type (CC stretch, CH bend etc.) and the absolute
intensities of the corresponding 0-1 transitions of C32H14 and
C32H14+ can be found in Malloci (2003). The vibrational frequencies
obtained through quantum-chemical calculations at the B3LYP/4-31G level
of theory are well known to slightly overestimate the real values for this
class of molecules, and are usually scaled with an empirical factor of
 0.958, which accounts for anharmonicity (Bauschlicher & Langhoff 1997; Hudgins et al. 2001; Langhoff 1996) and
brings them into near coincidence with experimental data. Our calculated
vibrational frequencies are in good agreement with the results previously
published by Langhoff (1996). However, to avoid introducing empirical
parameters, we chose to use the vibrational frequencies exactly as obtained
by our quantum-chemical calculations, with no scaling; this is consistent
with our long-term aim to build a complete theoretical computational machine,
capable to run with as few free parameters as possible.
0.958, which accounts for anharmonicity (Bauschlicher & Langhoff 1997; Hudgins et al. 2001; Langhoff 1996) and
brings them into near coincidence with experimental data. Our calculated
vibrational frequencies are in good agreement with the results previously
published by Langhoff (1996). However, to avoid introducing empirical
parameters, we chose to use the vibrational frequencies exactly as obtained
by our quantum-chemical calculations, with no scaling; this is consistent
with our long-term aim to build a complete theoretical computational machine,
capable to run with as few free parameters as possible.
For more details on the grid of adopted parameters which we ran our
Monte-Carlo model on, we again refer the reader to mal03c,
while the algorithm of the model is fully described in Mulas (1998).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4463F1.eps}\end{figure}](/articles/aa/full/2003/41/aah4463/Timg14.gif) |
Figure 1:
Two average interstellar radiation fields of Mathis et al. (1983), 5 kpc and
13 kpc away from the galactic centre are compared to the radiation fields of
the stars illuminating the specific reflection and planetary nebulae
considered in this work; both of them were obtained from stellar atmospheric
models of Kurucz (1992) scaled by the blackbody dilution factor corresponding
to the geometry of the source (cf. mal03c). |
| Open with DEXTER |
Our Monte-Carlo model yields the IR emission bands produced by the IR-cooling
cascades following the absorption of a sequence of UV/Vis photons
[see][]mal03c. More specifically, the model outputs the total
power
 isotropically radiated in each IR-active vibrational mode
by one molecule embedded in a given radiation field. The dimensions of this
quantity are energy per unit time per unit solid angle. We obtained the
expected absolute IR emission spectra of both C32H14 and C32H14+. In particular, we present here only the results obtained using
the approximation (a) of the absorption cross section of the cation in the
vacuum ultraviolet, as defined in mal03c following Robinson et al. (1997);
the results we obtained using approximation (b) from the same reference are
virtually undistinguishable in the present context.
isotropically radiated in each IR-active vibrational mode
by one molecule embedded in a given radiation field. The dimensions of this
quantity are energy per unit time per unit solid angle. We obtained the
expected absolute IR emission spectra of both C32H14 and C32H14+. In particular, we present here only the results obtained using
the approximation (a) of the absorption cross section of the cation in the
vacuum ultraviolet, as defined in mal03c following Robinson et al. (1997);
the results we obtained using approximation (b) from the same reference are
virtually undistinguishable in the present context.
Tables 3 and 4 list the predicted
 values respectively for the neutral and cation molecule in all of
the different interstellar radiation fields considered here. Band positions are
given in
values respectively for the neutral and cation molecule in all of
the different interstellar radiation fields considered here. Band positions are
given in  m, and the results of simulations are given in terms of flux,
integrated over the given band, per unit column density of the emitting
species, in units of W sr-1. Band positions are reported as calculated by
the NWChem ab initio quantum chemistry package, with no empirical
scaling. They are estimated to be accurate within a few percent. Their
relative positions are expected to be more accurate, hence we list them with
enough significant digits to distinguish close bands.
m, and the results of simulations are given in terms of flux,
integrated over the given band, per unit column density of the emitting
species, in units of W sr-1. Band positions are reported as calculated by
the NWChem ab initio quantum chemistry package, with no empirical
scaling. They are estimated to be accurate within a few percent. Their
relative positions are expected to be more accurate, hence we list them with
enough significant digits to distinguish close bands.
For readability, we also depict the resulting emission spectra respectively in
Figs. 3 and 4, where we used a fixed band
width of  m in order to make sure that peak heights be proportional to
band fluxes. We stress that our results are the absolute integrated fluxes
(i.e. the Tables 3 and 4), since we have
no new information about band-widths, which were arbitrarily chosen in order to
maximize readability of the synthetic spectra (i.e. the
Figs. 3 and 4), which are meant to be
nothing more than a concise and convenient representation.
m in order to make sure that peak heights be proportional to
band fluxes. We stress that our results are the absolute integrated fluxes
(i.e. the Tables 3 and 4), since we have
no new information about band-widths, which were arbitrarily chosen in order to
maximize readability of the synthetic spectra (i.e. the
Figs. 3 and 4), which are meant to be
nothing more than a concise and convenient representation.
Thanks to the fact that our computational approach uses ab initio
calculations to perform the vibrational analysis of the species under study,
we could easily estimate the effects of isotopic substitutions on the
resulting IR emission spectra.
The vibrational analysis in the case of isotopic substitutions can be
obtained with no additional computational costs, reusing the hessian
previously computed for the unsubstituted case.
In C32H14 there are respectively 9 inequivalent C atoms and 4
inequivalent H atoms; they are labelled in Fig. 2.
Table 1 lists the multiplicity of each inequivalent atom and the
corresponding statistical weight, i.e. the estimated probability of it being
singly replaced respectively by 13C or D, as obtained
for the abundances given by Wilson & Rood (1994) and assuming no isotopic
fractionation. We evaluated the overall probabilities considering substitutions
as cumulative independent binomial events. More specifically, assuming the
probability of each single substitution to be proportional to the isotopic
abundances, p1 = 13C/ 12C
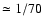 and
p2 = D/ H
and
p2 = D/ H
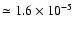 ,
we obtained:
,
we obtained:

We considered only single isotopic substitutions, and not multiple
simultaneous ones, since their probabilities turn out to be much smaller.
Table 1:
Multiplicities  of the 13 inequivalent atoms of C32H14
labelled in Fig. 2 and corresponding statistical weigth,
evaluated from the probabilities of p*=0.631 and q*=0.002 for
12C and H to be replaced by their most aboundant
isotopes 13C and D, respectively.
of the 13 inequivalent atoms of C32H14
labelled in Fig. 2 and corresponding statistical weigth,
evaluated from the probabilities of p*=0.631 and q*=0.002 for
12C and H to be replaced by their most aboundant
isotopes 13C and D, respectively.
Of course, since isotopic substitutions lower the symmetry of the molecule, a
large number of bands which are IR-inactive in the unsubstituted molecule
become weakly active. However, these single isotopic substitutions produce a
negligible effect on the overall predicted band intensities. The
lengthy, complete list of the estimated
 in every IR-active band,
for all the radiation fields considered and each of the inequivalent single
isotopic susbtitutions is presented in Malloci (2003), and it is not reproduced
here.
in every IR-active band,
for all the radiation fields considered and each of the inequivalent single
isotopic susbtitutions is presented in Malloci (2003), and it is not reproduced
here.
On the other hand, these substitutions may affect in a possibly detectable way
the predicted spectral profiles of some single bands. Figures 5-7 show details of selected
spectral regions around the strongest bands. In each figure, the top box
presents respectively the IR spectrum for no isotopic substitutions and
for each of the 13 inequivalent isotopic substitutions labelled in
Fig. 2; the bottom box shows the overall expected spectrum,
obtained as a weighted sum of the above spectra with statistical weights
according to Table 1, along with the spectrum obtained with no
isotopic substitutions, for comparison.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{H4463F2.eps}\end{figure}](/articles/aa/full/2003/41/aah4463/Timg24.gif) |
Figure 2:
Ground state geometry of C32H14 showing the 9 inequivalent C
atoms (labelled by 1, 3, 7, 11, 15, 19, 23, 27 and 29) and the 4 inequivalent
H atoms (labelled by 33, 35, 39 and 43); the molecule lies in the xy-plane,
the y-axis being the longer one. |
| Open with DEXTER |
Note that we did not model the intrinsic profile of specific bands, which
has been studied in detail in the literature (see, e.g. Pech et al. 2002; Verstraete et al. 2001)
but just arbitrarily assumed sensible values for their widths, with the aim to
emphasize the effect of isotopic substitutions alone on the resulting overall
profile.
![\begin{figure}
\par\includegraphics[width=17.8cm,clip]{H4463F3.eps}\end{figure}](/articles/aa/full/2003/41/aah4463/Timg26.gif) |
Figure 3:
IR emission spectrum of C32H14 in all the radiation fields
considered, expressed in terms of flux per unit column density of the emitting
species in units of W sr m-1. We arbitrarily assumed a fixed
band width of m-1. We arbitrarily assumed a fixed
band width of  m in order to make sure that peak heights be
proportional to band fluxes. m in order to make sure that peak heights be
proportional to band fluxes. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=17.8cm,clip]{H4463F4.eps}\end{figure}](/articles/aa/full/2003/41/aah4463/Timg27.gif) |
Figure 4:
IR emission spectrum of C32H14+ in all the radiation fields
considered, expressed in terms of flux per unit column density of the emitting
species in units of W sr m-1. We arbitrarily assumed a fixed
band width of m-1. We arbitrarily assumed a fixed
band width of  m in order to make sure that peak heights be
proportional to band fluxes. m in order to make sure that peak heights be
proportional to band fluxes. |
| Open with DEXTER |
3 Discussion
Our results bring out a quantitative link between the visible absorption bands
and the IR emission features.
Under optically thin conditions, the observed integrated flux
 in a given IR band, per unit solid angle
on the sky, is given by
in a given IR band, per unit solid angle
on the sky, is given by
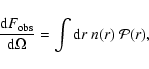 |
(2) |
where n(r) is the number density of the emitting species. If the emitting
molecules along the line of sight can be assumed to be illuminated by the
same radiation field,
 does not depend on r and can be taken
out of the integral, hence the above equation simplifies to
does not depend on r and can be taken
out of the integral, hence the above equation simplifies to
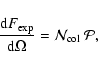 |
(3) |
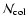 being the column density of the emitting species.
With
being the column density of the emitting species.
With
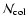 expressed in cm-2 and
expressed in cm-2 and
 in
W sr-1,
in
W sr-1,
 results expressed in
units of W cm-2 sr-1.
results expressed in
units of W cm-2 sr-1.
Analogously, the equivalent width
 of an optically
thin vibronic absorption band of central wavelength
of an optically
thin vibronic absorption band of central wavelength
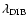 ,
a
possible DIB, is related to the total column density of absorbers
,
a
possible DIB, is related to the total column density of absorbers
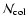 by the well-known formula
(see e.g. van der Zwet & Allamandola 1985):
by the well-known formula
(see e.g. van der Zwet & Allamandola 1985):
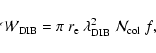 |
(4) |
where
 cm is the classical electron radius and f is the
oscillator strength of the specific transition considered. Therefore, dividing
Eq. (3) by Eq. (4) we obtain the relation
cm is the classical electron radius and f is the
oscillator strength of the specific transition considered. Therefore, dividing
Eq. (3) by Eq. (4) we obtain the relation
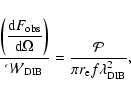 |
(5) |
where all the quantities on the left side are observables, while the right hand
side can be evaluated using our model for any "DIB-like'' vibronic band
of any known molecule and radiation field for which it is applicable.
The best way to fully exploit the discriminating power of
Eq. (5) is to apply it to spectral features which are
peculiar of a single, specific molecular species. While this is certainly the
case for the electronic transition of a PAH cation, it is not necessarily
so for its near and middle infrared bands, which are typically very similar
for the whole class of molecules. The infrared bands which can most safely
be expected to be different for each specific molecule are the ones
corresponding to the lowest energy normal vibrational modes, which involve the
molecular skeleton in its entirety (Joblin et al. 2002; Zhang et al. 1996; Langhoff 1996).
Table 2 shows some numerical values of the right hand side
of Eq. (5) obtained considering respectively the two
far-infrared skeletal vibrational modes of C32H14+ at about 85 and
150  m and the "DIB'' at a wavelength of about 9701 Å, as obtained through
our simulation in the four different radiation fields considered, assuming
m and the "DIB'' at a wavelength of about 9701 Å, as obtained through
our simulation in the four different radiation fields considered, assuming
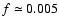 (Ehrenfreund et al. 1995).
(Ehrenfreund et al. 1995).
Table 2:
Numerical values of the predicted ratios between
 (for the two far-infrared skeletal
vibrational modes at about 85 and 150
(for the two far-infrared skeletal
vibrational modes at about 85 and 150  m) and
m) and
 of the electronic transition near 9701 Å of C32H14+, as obtained through our simulation in the four different
radiation fields considered. The ratios in the table are expressed in
units of W cm-2 sr-1 mÅ-1.
of the electronic transition near 9701 Å of C32H14+, as obtained through our simulation in the four different
radiation fields considered. The ratios in the table are expressed in
units of W cm-2 sr-1 mÅ-1.
Apart from the relation we derived above between the relative intensities of
IR emission bands and DIBs, it might be tempting to consider intensity ratios
between different skeletal far-IR bands as possible diagnostics of the
radiation field exciting their emission. However, despite the extremely
wide variation in the spectra of the radiation fields considered, e.g.
between the Red Rectangle and IRAS 21282+5050, and the relatively large
frequency difference between the band at  85 and
85 and  150
150  m, the
predicted intensity ratios remain almost constant, differences being of the
order of 1% or less.
m, the
predicted intensity ratios remain almost constant, differences being of the
order of 1% or less.
Concerning isotopic substitutions, our results show that the resulting isotopic
shifts are too small to be resolved in the near and mid infrared bands,
with the bandwidths commonly assumed for these bands
(see e.g. Pech et al. 2002). Figure 5, for example, shows
the expected infrared spectrum of C32H14+ in the radiation field of the
Red Rectangle, in the wavelength range between about 5 and 9  m, this time
assuming educated guesses for the bandwidths, following Pech et al. (2002).
While each single spectrum of the isotopically substituted molecules shows
quite apparent differences, their weighted sum according to the expected
statistical weights (see Table 1) is virtually undistinguishable
from the spectrum of the unsubstituted molecule. Moreover, in the case of
near and mid infrared bands it would be very difficult to disentangle the
contribution of any specific molecule (see e.g. Pech et al. 2002)
possibly present in many ionisation states (Bakes et al. 2001a,b) and finally,
within this contribution, further disentangle the effects
of different
isotopic substitutions from those of anharmonicity. The situation is more promising for far infrared, skeletal bands, since they
are more likely to be able to distinguish different species. However, very
little is known on the intrinsic bandwidth of such far-IR bands in PAHs, hence
it is difficult to assess whether isotopic substitutions might produce a
detectable effect in their profiles. Figures 6 and 7 display again the expected spectrum of C32H14+ in
the radiation field of the Red Rectangle, this time in the wavelength range
around
m, this time
assuming educated guesses for the bandwidths, following Pech et al. (2002).
While each single spectrum of the isotopically substituted molecules shows
quite apparent differences, their weighted sum according to the expected
statistical weights (see Table 1) is virtually undistinguishable
from the spectrum of the unsubstituted molecule. Moreover, in the case of
near and mid infrared bands it would be very difficult to disentangle the
contribution of any specific molecule (see e.g. Pech et al. 2002)
possibly present in many ionisation states (Bakes et al. 2001a,b) and finally,
within this contribution, further disentangle the effects
of different
isotopic substitutions from those of anharmonicity. The situation is more promising for far infrared, skeletal bands, since they
are more likely to be able to distinguish different species. However, very
little is known on the intrinsic bandwidth of such far-IR bands in PAHs, hence
it is difficult to assess whether isotopic substitutions might produce a
detectable effect in their profiles. Figures 6 and 7 display again the expected spectrum of C32H14+ in
the radiation field of the Red Rectangle, this time in the wavelength range
around  80
80  m, for two arbitrarily assumed bandwidths. The comparison
between these two figures shows the effect of isotopic substitutions to be
definitely visible for a bandwidth of
m, for two arbitrarily assumed bandwidths. The comparison
between these two figures shows the effect of isotopic substitutions to be
definitely visible for a bandwidth of  0.1
0.1  m, while it is completely
washed out with a bandwidth of
m, while it is completely
washed out with a bandwidth of  1
1  m.
More detailed experimental measures of far-IR bands in large PAHs are badly
needed for a definitive assessment of the importance of isotopic substitutions
in this respect.
m.
More detailed experimental measures of far-IR bands in large PAHs are badly
needed for a definitive assessment of the importance of isotopic substitutions
in this respect.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4463F5.eps}\end{figure}](/articles/aa/full/2003/41/aah4463/Timg47.gif) |
Figure 5:
Expected emission spectrum of C32H14+ in
the radiation field of the Red Rectangle in the wavelength range between
 5 and 5 and  9 9  m, assuming educated guesses for the bandwidth following
Pech et al. (2002). The top box shows individual spectra for each isotopic
substitution, the bottom box compares the spectrum for the unsubstituted
molecule with the weighted average assuming standard interstellar isotopic
abundances and no fractionation. m, assuming educated guesses for the bandwidth following
Pech et al. (2002). The top box shows individual spectra for each isotopic
substitution, the bottom box compares the spectrum for the unsubstituted
molecule with the weighted average assuming standard interstellar isotopic
abundances and no fractionation. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4463F6.eps}\end{figure}](/articles/aa/full/2003/41/aah4463/Timg48.gif) |
Figure 6:
Expected emission spectrum of C32H14+ in
the radiation field of the Red Rectangle in the wavelength range around
its strongest far infrared skeletal band, near  80 80  m, assuming a
bandwidth of m, assuming a
bandwidth of  1 1  m. The top box shows individual spectra for each
isotopic substitution, the bottom box compares the spectrum for the
unsubstituted molecule with the weighted average assuming standard
interstellar isotopic abundances and no fractionation. m. The top box shows individual spectra for each
isotopic substitution, the bottom box compares the spectrum for the
unsubstituted molecule with the weighted average assuming standard
interstellar isotopic abundances and no fractionation. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4463F7.eps}\end{figure}](/articles/aa/full/2003/41/aah4463/Timg49.gif) |
Figure 7:
Expected emission spectrum of C32H14+ in
the radiation field of the Red Rectangle in the wavelength range around
its strongest far infrared skeletal band, near  80 80  m, assuming a
bandwidth of m, assuming a
bandwidth of  0.1 0.1  m. The top box shows individual spectra for each
isotopic substitution, the bottom box compares the spectrum for the
unsubstituted molecule with the weighted average assuming standard
interstellar isotopic abundances and no fractionation. m. The top box shows individual spectra for each
isotopic substitution, the bottom box compares the spectrum for the
unsubstituted molecule with the weighted average assuming standard
interstellar isotopic abundances and no fractionation. |
| Open with DEXTER |
4 Conclusions and future work
Using ab initio calculations, available experimental data and
our Monte-Carlo model, we modelled the photophysics of C32H14 and
C32H14+, obtaining their IR emission bands in a grid of interstellar
environments. These results will be useful for a definitive assessment on the
presence of such specific molecules in interstellar space.
Table 3:
Values of
 ,
as defined in Sect. 3, for
C32H14 without isotopic substitutions; bands with a fraction of emitted
photons below 0.1% were omitted, leaving 52 out of the 56 IR-active modes of
C32H14 (cf. Table 5 in mal03c).
,
as defined in Sect. 3, for
C32H14 without isotopic substitutions; bands with a fraction of emitted
photons below 0.1% were omitted, leaving 52 out of the 56 IR-active modes of
C32H14 (cf. Table 5 in mal03c).
Table 4:
Values of
 ,
as defined in Sect. 3, for
C32H14+ without isotopic substitutions; bands with a fraction of
emitted photons below 0.1% were omitted, leaving 53 out of the 56 IR-active
modes of C32H14+ (cf. Table 6 in mal03c).
,
as defined in Sect. 3, for
C32H14+ without isotopic substitutions; bands with a fraction of
emitted photons below 0.1% were omitted, leaving 53 out of the 56 IR-active
modes of C32H14+ (cf. Table 6 in mal03c).
More generally, we showed this approach to be feasible, at least, for the
whole class of PAH molecules and their cations, and demonstrated its potential
in providing a number of independent identification criteria for potential
DIB-UIBs carriers. In particular, Eq. (5)
provides an independent, very powerful criterion for molecule identification,
especially with the presently available ISO data and the forthcoming SIRTF
and Herschel missions, which are expected to provide the scientific
community with observations of unprecedented sensitivity in the wavelength
range where far-IR skeletal vibrations of large PAHs are expected to occur.
The importance of such calculations for future astronomical
observations is underlined in the recent paper by Joblin et al. (2002) where
band profiles and intensities of the low-frequency vibrational modes of the
neutral coronene molecule (C24H12) are presented.
Our long term aim will be to systematically apply the above analysis to a
large sample of astrophysically relevant molecules, with particular
emphasis on larger PAHs, in a wide range of ionisation and hydrogenation
states, possibly nitrogen substituted. With more computational tools providing
Time Dependent DFT becoming more reliable and commonly available (see e.g. Weisman et al. 2003),
we expect to be able to obtain ab initio electronic excitation energies and
absorption spectra of PAHs, at least up to excitation energies of a few eVs
(Hirata et al. 1999; Weisman et al. 2001, 2003). This will provide a completely self-contained computational tool
which will be a valuable guide for targeted experiments and observations.
Acknowledgements
The authors thank the referee who helped improve the paper with useful
comments. G. Malloci gratefully acknowledges the financial support by
INAF - Osservatorio Astronomico di Cagliari. The authors are thankful to
Prof. G. Cappellini and Dr. G. Satta for their help with ab-initio
methodologies. We acknowledge the High Performance Computational Chemistry
Group for using their code: "NWChem, A Computational Chemistry Package for
Parallel Computers, version 4.0.1'' (2001), Pacific Northwest National
Laboratory, Richland, Washington, USA.
-
Allamandola, L. J., Hudgins, D. M., & Sandford, S. A. 1999, ApJ, 511,
L115
In the text
NASA ADS
-
Allamandola, L. J., Tielens, A. G. G. M., & Barker, J. R. 1985, ApJ,
290, L25
In the text
NASA ADS
-
Allamandola, L. J., Tielens, G. G. M., & Barker, J. R. 1989, ApJS, 71,
733
In the text
NASA ADS
-
Bakes, E. L. O., Tielens, A. G. G. M., & Bauschlicher, C. W.
2001a, ApJ, 556, 501
In the text
NASA ADS
-
Bakes, E. L. O., Tielens, A. G. G. M., Bauschlicher, C. W., Hudgins,
D. M., & Allamandola, L. J. 2001b, ApJ, 560, 261
In the text
NASA ADS
-
Bauschlicher, C. W., & Langhoff, S. R. 1997, Spectrochim. Acta Part A, 53,
1225
In the text
-
Becke, A. D. 1993, J. Chem. Phys., 98, 5648
In the text
NASA ADS
-
Bernstein, M. P., Sandford, S. A., Allamandola, L. J., et al. 1999,
Science, 283, 1135
In the text
NASA ADS
-
Cardelli, J. A., Meyer, D. M., Jura, M., & Savage, B. D. 1996, ApJ,
467, 334
In the text
NASA ADS
-
Ehrenfreund, P., Foing, B. H., D'Hendecourt, L., Jenniskens, P., &
Désert, F. X. 1995, A&A, 299, 213
In the text
NASA ADS
-
Frish, M. J., Pople, J. A., & Binkley, J. S. 1984, J. Chem. Phys., 80, 3265
In the text
NASA ADS
-
Gillett, F. C., Forrest, W. J., & Merrill, K. M. 1973, ApJ, 183, 87
In the text
NASA ADS
-
Harrison, R. J., Nichols, J. A., Straatsma, T. P., et al. 2001, NWChem, A
Computational Chemistry Package for Parallel Computers, Version 4.0.1
In the text
-
Hirata, S., Lee, T., & Head-Gordon, M. 1999, J. Chem. Phys., 111, 8904
In the text
NASA ADS
-
Hudgins, D. M., Bauschlicher, C. W., & Allamandola, L. J. 2001,
Spectrochim. Acta Part A, 57, 907
In the text
NASA ADS
-
Joblin, C., Toublanc, D., Boissel, P., & Tielens, A. G. G. M. 2002,
Mol. Phys., 100, 3595
In the text
-
Kurucz, R. 1992, in The Stellar Populations of Galaxies, ed. B. Barbuy, &
A. Renzini, Proc. 149th Symp. IAU (Dordrecht: Kluwer Academic Publishers), 225
In the text
-
Langhoff, S. R. 1996, J. Phys. Chem., 100, 2819
In the text
-
Léger, A., & D'Hendecourt, L. 1985, A&A, 146, 81
In the text
NASA ADS
-
Léger, A., & Puget, J. L. 1984, A&A, 137, L5
In the text
NASA ADS
-
Malloci, G. 2003, Ph.D. Thesis, Università degli Studi di Cagliari
In the text
-
Malloci, G., Mulas, G., & Benvenuti, P. 2003, A&A, 410, 623 (Paper I)
In the text
-
Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212
In the text
NASA ADS
-
Mulas, G. 1998, A&A, 338, 243
In the text
NASA ADS
-
Pech, C., Joblin, C., & Boissel, P. 2002, A&A, 388, 639
In the text
NASA ADS
-
Puget, J. L., & Léger, A. 1989, ARA&A, 27, 161
In the text
NASA ADS
-
Robinson, M. S., Beegle, L. W., & Wdowiak, T. J. 1997, ApJ, 474, 474
In the text
NASA ADS
-
Rouan, D., Léger, A., Omont, A., & Giard, M. 1992, A&A, 253,
498
In the text
NASA ADS
-
Ruiterkamp, R., Halasinski, T., Salama, F., et al. 2002, A&A, 390,
1153
In the text
NASA ADS
-
Salama, F. 1999, in Solid Interstellar Matter: The ISO Revolution, Les
Houches Workshop, February 2-6, 1998, ed. L. d'Hendecourt, C. Joblin,
& A. Jones (EDP Sciences and Springer-Verlag), 65
In the text
-
Salama, F., & Allamandola, L. J. 1992a, Nature, 358, 42
In the text
NASA ADS
-
Salama, F., & Allamandola, L. J. 1992b, ApJ, 395, 301
In the text
NASA ADS
-
Stephens, P. J., Devlin, F. J., Chabalowski C. F., & Frisch, M. 1994,
J. Phys. Chem., 98, 11623
In the text
-
van der Zwet, G. P., & Allamandola, L. 1985, A&A, 146, 76
In the text
NASA ADS
-
Verstraete, L., Pech, C., Moutou, C., et al. 2001, A&A, 372, 981
In the text
NASA ADS
-
Weisman, J. L., Lee, T. J., & Head-Gordon, M. 2001, Spectrochim. Acta Part
A, 57, 931
In the text
NASA ADS
-
Weisman, J. L., Lee, T. J., Salama, F., & Head-Gordon, M. 2003, ApJ,
587, 256
In the text
NASA ADS
-
Wilson, T. L., & Rood, R. T. 1994, ARA&A, 32, 191
In the text
NASA ADS
-
Wilson Jr., B., Decius, J. C., & Cross, P. C. 1955, Molecular Vibrations - The
theory of Infrared and Raman Vibrational Spectra (New York: McGraw-Hill)
In the text
-
Zhang, K., Guo, B., Colarusso, P., & Bernath, P. F. 1996, Science,
274, 582
In the text
NASA ADS
Copyright ESO 2003
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4463F1.eps}\end{figure}](/articles/aa/full/2003/41/aah4463/Timg14.gif)

![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{H4463F2.eps}\end{figure}](/articles/aa/full/2003/41/aah4463/Timg24.gif)
![\begin{figure}
\par\includegraphics[width=17.8cm,clip]{H4463F3.eps}\end{figure}](/articles/aa/full/2003/41/aah4463/Timg26.gif)
![\begin{figure}
\par\includegraphics[width=17.8cm,clip]{H4463F4.eps}\end{figure}](/articles/aa/full/2003/41/aah4463/Timg27.gif)
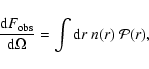
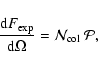
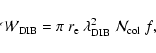
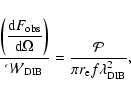
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4463F5.eps}\end{figure}](/articles/aa/full/2003/41/aah4463/Timg47.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4463F6.eps}\end{figure}](/articles/aa/full/2003/41/aah4463/Timg48.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4463F7.eps}\end{figure}](/articles/aa/full/2003/41/aah4463/Timg49.gif)