A&A 410, 671-684 (2003)
DOI: 10.1051/0004-6361:20031203

Dependence of coronal X-ray emission on spot-induced brightness variations in cool main sequence stars[*]

S. Messina1,[*] - N. Pizzolato2 - E. F. Guinan3 - M. Rodonò4


1 - Catania Astrophysical Observatory, National Institute for Astrophysics, Via S. Sofia 78, 95123 Catania, Italy
2 - Palermo Astronomical Observatory, National Institute for Astrophysics, Piazza del Parlamento 1, 90134 Palermo, Italy
3 - Department of Astronomy and Astrophysics, Villanova University, Villanova 19085, PA, USA
4 - Department of Physics and Astronomy, University of Catania, Via S. Sofia 78, 95123 Catania, Italy

Received 7 February 2003 / Accepted 5 August 2003

Abstract
The maximum amplitude ( $A_{{\rm max}}$) of spot-induced brightness variations from long-term V-band photometry and the ratio $L_{\rm X}$/ $L_{\rm bol}$between X-ray and bolometric luminosities are suitable indicators of the level of magnetic activity in the photosphere and in the corona of late-type stars, respectively. By using these activity indicators we investigate the dependence of coronal X-ray emission on the level of photospheric starspot activity in a homogeneous sample of low mass main sequence field and cluster stars of different ages (IC 2602, IC 4665, IC 2391, $\alpha$ Persei, Pleiades and Hyades). First, the activity-rotation connection at the photospheric level is re-analysed, as well as its dependence on spectral type and age. The upper envelope of  $A_{{\rm max}}$ increases monotonically with decreasing rotational period (P) and Rossby number (R0) showing a break around 1.1 d that separates two rotation regimes where the starspot activity shows different behaviours. The $A_{{\rm max}}$-P and $A_{{\rm max}}$-R0 relations are fitted with linear, exponential and power laws to look for the function which best represents the trend of the data. The highest values of $A_{{\rm max}}$ are found among K-type stars and at the ages of $\alpha$ Persei and Pleiades. We also analyse the activity-rotation connection at the coronal level as well as its dependence on spectral type. The level of X-ray emission increases with increasing rotation rate up to a saturation level. The rotational period at which saturation occurs is colour-dependent and increases with advancing spectral type. Also the $L_{\rm X}$/ $L_{\rm bol}$-P and $L_{\rm X}$/ $L_{\rm bol}$-R0relations are fitted with linear, exponential and power laws to look for the best fitting function. Among the fastest rotating stars ($P\le 0.3$ d) there is evidence of super-saturation. Also the highest values of $L_{\rm X}$/ $L_{\rm bol}$ are found among K-type stars. Finally, the photospheric-coronal activity connection is investigated by using for the first time the largest ever sample of light curve amplitudes as indicators of the magnetic filling factor. The activity parameters $L_{\rm X}$/ $L_{\rm bol}$ and $A_{{\rm max}}$ are found to be correlated with each other, thus confirming the dependence of coronal activity on photospheric magnetic fields. More precisely, the $L_{\rm X}$/ $L_{\rm bol}$- $A_{{\rm max}}$ distribution shows the presence of an upper envelope, which is constant at the $L_{\rm X}$/ $L_{\rm bol} \simeq -3.0$ saturation level, and of a lower envelope. The best fit to the lower envelope is given by a power law with steepness decreasing from F-G to M spectral types. However, it is considered a tentative result, since the fit reduced chi-squares are large. Such spectral-type dependence may be related to a colour dependence of $A_{{\rm max}}$ on the total starspot filling factor, as well as to the coronal emission being possibly more sensitive to starspot activity variations in F- and G-type than in M-type stars. The $L_{\rm X}$/ $L_{\rm bol}$- $A_{{\rm max}}$ mean values for each cluster in our sample decrease monotonically with increasing age, showing that the levels of photospheric and coronal activity evolve in time according to a single power law till the Sun's age.

Key words: stars: activity - stars: late-type - stars: magnetic fields - stars: starspots - X-rays: stars

1 Introduction

Late-type stars of F-M spectral types with deep convection zones and high angular velocities (comparable to or higher than the solar value) can modify and intensify, by orders of magnitude, weak magnetic fields by means of magnetohydrodynamic processes (Parker 1979; Schüssler 1983). Once intensified, the magnetic fields determine the structure, the energetic balance and the evolution of stellar atmospheres, inducing a complex of phenomena known as activity (Catalano et al. 1999; Rodonò 2000). Brightness variations originating from the photosphere, line emission fluxes originating from the chromosphere and the Transition Region (TR), and coronal X-ray fluxes are among the well-studied manifestations of magnetic activity. Observational studies have shown that these activity manifestations are all correlated with the axial rotational period and, less sensitively, with the convective zone depth (e.g., Messina et al. 2001; Marilli & Catalano 1984; Pizzolato et al. 2003). The chromospheric, TR and coronal fluxes are found to be correlated with each other with increasing slope when increasingly high temperature diagnostics are plotted versus the coolest ones (Ayres et al. 1995; Marilli & Catalano 1984). However, the direct correlation of these activity diagnostics with the quantity of photospheric magnetic fields has not been so extensively investigated, the direct measurements of magnetic fields in late-type stars being not trivial (Landstreet 1992) and the measurements of parameters such as filling factor and field strength being very sparse and limited to small stellar samples (Saar 1990a; Saar & Schrijver 1987; Saar 1991).

The main aim of this paper is to investigate if a correlation exists between the level of coronal X-ray emission and the amplitude of the spot-induced brightness variations, more precisely, the light curve amplitude which is used as a tracer of the starspot filling factor. The use of light curve amplitudes will allow us to analyse a very large stellar sample, overcoming the paucity of direct measurements. A preliminary investigation was carried out by Messina et al. (2001) who used the maximum light curve amplitude ( $A_{{\rm max}}$) as a lower limit to the value of the starspot filling factor ( $f_{\rm spot}$), that is the fraction ( $f_{\rm spot} \le 1$) of the stellar photosphere covered by spots. They derived relations between X-ray, CIV and MgII luminosities and $A_{{\rm max}}$. However, as they pointed out, such relations were derived by simply folding empirical relations of X-ray, CIV and MgII luminosities and $A_{{\rm max}}$ with the rotational period. In the present paper for the first time we compare directly X-ray luminosities and brightness variation amplitudes and derive empirical relations. These are expected to help in testing and improving the current models of coronal heating, as it will be addressed in a following paper.

In Sects. 2 and 3 we present the photometric data on which our analysis is based and updated relations between $A_{{\rm max}}$, rotational period and spectral type. In Sects. 4 and 5 we present the X-ray data and how the luminosity depends on rotation and spectral type. In Sect. 6 we investigate the correlation between the ratio $L_{\rm X}$/ $L_{\rm bol}$ of X-ray on bolometric luminosities and $A_{{\rm max}}$. Discussion and conclusions are presented in Sects. 7 and 8.

2 Photometric data

In order to secure a stellar sample as homogeneous as possible, the following selection criteria were adopted: a) single main-sequence stars, because it is not clear yet how both binarity and evolution of the internal structure outside of the main sequence influence magnetic activity; b) stars belonging to clusters of known age (IC 2602, IC 4665, IC 2391, $\alpha$ Persei, Pleiades and Hyades) as well as field stars, in order to study age effects on magnetic activity; c) stars with known rotational periods; d) stars with well-determined light curves (in the V-band of Johnson's UBV system); e) stars with measurements of the X-ray flux.

Photometric data were collected mainly from the literature. For six stars we used additional unpublished photometric data obtained at Villanova University[*]. The analysis presented in this paper is based on a sample totalling 264 stars and 861 light curves that are distributed as reported in Table 1.

Table 1: Number of stars, light curves and age of the open clusters used in the present analysis.

This sample has 15% more stars and 72% more light curves than the sample previously analysed by Messina et al. (2001, hereafter referred to as Paper I). More precisely, it contains 39 additional stars, 10 of which belong to the IC 4665 cluster which was not present in the previous analysis, and 362 additional light curves.

A few field stars were subsequently discarded from the initial sample because they did not meet all the above quoted selection criteria: HD 21845, HD 25893, HD 52452, HD 64096, HD 78644 turned out to be spectroscopic binaries, HD 98712 a visual binary, HD 31993 a giant and EXO 052707-3329.32 a Pre-Main-Sequence (PMS) star.

The photometric data of our star sample and their references are presented in electronic form Tables. The typical error of the light curve maximum amplitudes ( $A_{{\rm max}}$) used in the following analysis is of the order of 0.015 mag.


  \begin{figure} \par\includegraphics[angle=90,width=14.1cm,clip]{H4295F1.ps}\end{figure} Figure 1: $A_{{\rm max}}$ versus rotational period (P). In the fast rotation regime the upper envelopes for F- and K-type stars are best fitted by an exponential law (dashed lines); whereas for G- and M-type stars (upper envelope 1) they are best fitted by a linear law (continuous lines). The best fit for M-type stars (upper envelope 2) is given by a power law (dotted line). In the ultra fast rotation regime the upper envelopes are best fitted by a linear law (continuous lines). The downward arrow indicates HD 111395 (see text). Note that the abscissa is logarithmic.
Open with DEXTER

3 Analysis of photometric data

3.1 Activity-rotation relation

Considering that the stars and light curves we newly retrieved for the present study enlarge by almost 70% the total sample of Paper I, it is interesting to re-investigate the dependence of the historical maximum V-band light curve amplitude ( $A_{{\rm max}}$) on the rotational period, to check the validity of previous results and to determine updated values of the empirical relation parameters. In order to investigate the mass and, therefore, the convective zone depth dependence of the activity-rotation relation, the stellar sample was studied in four different colour ranges:

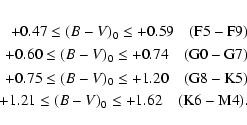
\begin{eqnarray*}+0.47 \leq (B-V)_0 \leq +0.59 \quad ({\rm F5-F9})\\ +0.60 \leq... ...rm G8-K5})\\ +1.21 \leq (B-V)_0 \leq +1.62 \quad ({\rm K6-M4}). \end{eqnarray*}


Each star was assigned to one of the four spectral ranges only on the basis of the dereddened (B-V)0 colour index. The following interstellar reddening corrections E(B-V) were applied to cluster stars: 0.04 mag for IC 2602 (Randich et al. 1995), 0.18 mag for IC 4665 (Giampapa et al. 1998), 0.006 mag for IC 2391 (Patten & Simon 1996), 0.10 mag for $\alpha$ Persei (Randich et al. 1996), 0.04 mag for Pleiades (Stauffer et al. 1994) and no correction for Hyades stars (Pinsonneault et al. 1998).

Figure 1 shows $A_{\max}$ vs. rotational period. Different symbols are used to distinguish field stars and stars in different clusters. $A_{{\rm max}}$ is an activity parameter directly related to the starspot component unevenly distributed on the stellar photosphere (cf. Sect. 2 of Paper I) and it is proportional to the total starspot filling factor ( $f_{\rm spot}$). Since starspots are the dominant photospheric magnetic pattern in fast rotating stars (Radick et al. 1989, 1998), $A_{{\rm max}}$ turns out to be a suitable indicator of the total magnetic filling factor. Actually, $A_{{\rm max}}$ represents a lower limit to $f_{\rm spot}$ and only the $A_{{\rm max}}$ upper envelope values most reliably trace the way $f_{\rm spot}$ depends on P and B-V. This envelope (circled symbols in Figs. 1 and 2) was defined by dividing the sample into bins of rotational period and by selecting the stars having the highest $A_{{\rm max}}$ values (more precisely, differing by less that 0.02 mag from the maximum within each bin). The stars used to define the upper envelope are listed in the electronic form Tables marked with the label fit.

In all the spectral ranges the $A_{\max}$ upper envelope is a decreasing function of the rotational period. However, as evident in the G and K spectral ranges, the activity-rotation relation shows a break at $P\sim 1.1$ d, i.e., ultra fast ($P \la 1.1$ d) and fast ($P \ga 1.1$ d) rotators behave differently. Such a behaviour for F- and M-type stars may be only supposed, their data in the ultra fast rotation regime being currently too sparse. Figure 2 shows $A_{\max}$ vs. Rossby number ($R_{\rm0}$). Symbols and circled symbols have the same meaning as in Fig. 1. The Rossby number ( $R_{\rm0}=P/\tau_{\rm c}$) was computed adopting the empirical turnover time $\tau_{\rm c}$ given by Noyes et al. (1984). The results of the following analysis are qualitatively unchanged when Gilliland (1985), Kim & Demarque (1996) or Stepien's (1989) turnover times are used. Ultra fast G-, K- and M-type stars have $A_{\max}$ maximum values at about $P \simeq 0.35$ d, which are never exceeded even among the fastest rotators ( $P \la 0.35$ d), as shown in Fig. 2.


  \begin{figure} \par\includegraphics[angle=90,width=14.3cm,clip]{H4295F2.ps}\end{figure} Figure 2: $A_{{\rm max}}$ versus Rossby number ($R_{\rm0}$). In the fast rotation regime the upper envelopes for F- and K-type stars are best fitted by an exponential law (dashed lines); whereas for G- and M-type stars (upper envelope 1) are best fitted by a linear law (continuous lines). The best fit for M-type stars (upper envelope 2) is given by a power law (dotted line). In the ultra fast rotation regime the upper envelopes are best fitted by a linear law (continuous lines). The downward arrow indicates HD 111395 (see text). Note that the abscissa is logarithmic.
Open with DEXTER

Table 2: Correlation coefficients (r), number of stars used to define the upper envelope (N), parameters of the linear, exponential and power law weighted fits to the data upper envelope of $A_{\max}-P$ and $A_{\max}-R_{\rm 0}$ relations and reduced chi-squares ( $\chi ^2_{\rm\nu }$).

$A_{{\rm max}}$ upper envelope data were fitted by linear, exponential and power law relations. A different weight was assigned to the upper envelope data according to the number of light curves used to derive them (see the electronic form tables). Correlation coefficients (r), fit parameters (a and b) and reduced chi-squares ( $\chi ^2_{\rm\nu }$) are given in Table 2.

In the fast rotation regime the $A_{{\rm max}}$-P and $A_{{\rm max}}$-$R_{\rm0}$ upper envelopes for F- and K-type stars are best fitted by an exponential law (dashed lines in Figs. 1 and 2); whereas for G-type stars it is best fitted by a linear law (continuous lines in Figs. 1 and 2). In the case of M-type stars (upper envelope 1), the  $A_{{\rm max}}$-P upper envelope is best fitted by a linear law (continuous lines in Fig. 1), while exponential and linear laws give similar best fits to the $A_{{\rm max}}$-$R_{\rm0}$upper envelope, their reduced chi-squares differing by less than 5% (continuous lines in Fig. 2). The best fit for M-type stars (upper envelope 2) is given by a power law (dotted line in Figs. 1 and 2). In the ultra fast rotation regime the $A_{{\rm max}}$-P and $A_{{\rm max}}$-$R_{\rm0}$ upper envelopes are best fitted by a linear law (continuous lines in Figs. 1 and 2).

We feel that the fits in Table 2 can be trusted since we have used rather simple functions to fit the trend of the data and since an additional analysis based on non-reduced chi-squares values gave the same results.

According to the quoted selection criteria, the IC 2602, IC 2391 and IC 4665 members of spectral type later than G8 were excluded from the fit, because they are pre-main-sequence stars. Since most of the K6-M4 stars in our sample have not arrived yet on the zero-age main-sequence (D'Antona & Mazzitelli 1994), this subsample is not as homogeneous as the others and the $A_{{\rm max}}$ upper envelope in this spectral range must be considered as tentative. For this reason we did not define an upper envelope for K6-M4 ultra fast rotating stars nor the presence of a break.

For K6-M4 fast rotating stars two different upper envelopes seem to exist (see bottom panels of Figs. 1 and 2): the lower envelope (labelled as upper envelope 1) has a similar behaviour as in the other spectral ranges; the upper one (labelled as upper envelope 2) seems to diverge as the rotational period decreases.

The only star with an $A_{{\rm max}}$ value unusually high, given the P=15.8-d rotational period, is the G5V star HD 111395 (marked by a downward arrow in Figs. 1 and 2). The periodogram from which Strassmeier et al. (1999) determined this rotational period presents a relatively high noise level and several secondary peaks. Therefore, we suspect that the detected period is an alias of a shorter, e.g. P=7.9 d, rotational period. If this is the case, the light curve amplitude would be perfectly consistent with the $A_{{\rm max}}$-P relation.

As a result of this analysis we found that while the exponential law best describes the way $A_{{\rm max}}$ decreases with increasing rotational period and Rossby number in a few data subsets, in others the best fit is given by a linear law. However, the linear law is physically less supportable, since we expect convergence of $A_{{\rm max}}$ toward a saturation value when the starspot filling approaches unity at the highest rotation regimes. The presence of linear best fits may only result from the still limited sample of stars available to define the upper envelope.

With regard to this, it is interesting to note that by using the direct measurements of the magnetic filling factor collected by Saar (1990a, 1991), Stepien (1991) found that an exponential relation between filling factor ( $f_{\rm mag}$) and Rossby number is preferred. More precisely he found

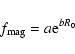\begin{displaymath}% f_{\rm mag} = a {\rm e}^{b R_0} \end{displaymath} (1)

with $b=-1.75\pm 0.33$. The upper value of this coefficient differs by $\sim$10% from the lower value of the coefficient $b=-2.75\pm 0.4$, found by us for the G8-K5 spectral range, by using Stepien's turnover times. For instance, this agreement gives us some confidence about the reliability of the activity indicator $A_{{\rm max}}$ used in this analysis. Nonetheless, the values of the exponential coefficients have to be compared with great caution, because Stepien's sample consists of only 24 stars, six of which being in visual binary systems, five in close binary systems and $\sim$25% being G-type stars. But more important, while we fitted only the data upper envelope, they fit all data, which are a snapshot of the level of activity at the time of the measurements. A similar agreement is also found with the results presented by Hempelmann (1995) who found

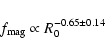\begin{displaymath}% f_{\rm mag} \propto R_0^{-0.65\pm 0.14} \end{displaymath} (2)

the power law coefficient found by us (averaged over all spectral types) being b= -0.72 $\pm$ 0.13. Also in a more recent study on the chromospheric emission-magnetic filling factor relation, Fawzy et al. (2002) found that an exponential law best fits the dependence of the theoretical filling factor on the rotational period, at least in the rotation range they analysed (10 $\leq$ P $\leq$ 40 d). We refer the reader to Paper I for a detailed discussion about the existence of the break at P $\sim$ 1.1 d in the $A_{{\rm max}}$-P and $A_{{\rm max}}$-$R_{\rm0}$ relations and about differences with respect to previous studies.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{H4295F3.ps}\end{figure} Figure 3: $A_{{\rm max}}$ versus B-V. Symbols have same meaning as in the previous figures except that circled symbols denote fast rotating stars. The dotted and the continuous lines are plotted just to better show how the largest $A_{{\rm max}}$ values vary with B-V colour in the ultra fast and fast rotation regimes, respectively.
Open with DEXTER

3.2 Colour and age dependence

Figure 3 shows the dependence of $A_{{\rm max}}$ on the star's B-V colour index. Symbols have the same meaning as in Fig. 1, except that fast rotating stars are distinguished from ultra fast rotating stars by circled symbols. Vertical bars separate the four spectral ranges. Dotted and continuous lines are plotted to show how the largest $A_{{\rm max}}$ values vary with B-Vin the ultra fast and fast rotation regimes, respectively. In the ultra fast rotation regime the starspot activity level monotonically increases up to a maximum value of $A_{\rm max}\simeq 0.30$ mag at B-V $\simeq$ 1.1 in the G8-K5 spectral range, then it monotonically decreases towards later spectral types. In the fast rotation regime the starspot activity level shows a more complex behaviour. $A_{{\rm max}}$ is largest in the same G8-K5 spectral range but with two maxima of comparable height of $A_{\rm max}\simeq 0.20$ mag at B-V $\simeq$ 0.9 and B-V $\simeq$ 1.2. It decreases down to a minimum at about B-V $\simeq$ 1.5, then it starts increasing towards the coolest stars of the sample. Different dynamo actions operating in the two rotation regimes, as already highlighted by the presence of a break in the activity-rotation relation, may determine such different colour dependence in the starspot activity level.

The presence in our sample of cluster stars of known age allows us to assess the influence of stellar age on the starspot activity level. The stellar clusters at our disposal have ages (see Table 1) in the range from 0.03 Gyr (IC 2602 and IC 4665) to 0.6 Gyr (Hyades). The subsample of field stars, although it contains objects of different ages, is mainly composed of stars belonging to the Pleiades cluster moving group having a similar average age. As shown in Figs. 1-3, since the upper envelope is mainly determined by the Pleiades, $\alpha$ Persei and field stars, the starspot activity level around the Pleiades age (0.115 Gyr) seems to be higher than in the zero-age main sequence.

In the K6-M4 spectral range, where most of the stars are in the pre-main sequence evolutionary stage, the spot activity level appears to be comparable to G-type stars. The coolest M-type stars have a slightly higher activity level.

Models of stellar evolution predict that stars have a minimum radius and a maximum rotation rate, provided that the angular momentum is conserved, as soon as they arrive on the zero-age main sequence. As the stars age, they spin down due to magnetic braking and their level of magnetic activity decreases (Skumanich 1972). The increase in the starspot activity level of F- and G-type stars from ZAMS to the Pleiades age may be an artifact, since the fraction of very young stars in our sample (and of corresponding light curves) is smaller than the fraction of older stars. More data may show the highest activity level to be effectively at the beginning of the ZAMS.

4 X-ray data

4.1 Field stars

All of the field stars we selected for this study, but one (HD 77191), were detected as X-ray sources during the ROSAT All Sky Survey (RASS). Count rates H and S in the hard (0.4-2.0 KeV) and soft (0.1-0.4 KeV) ROSAT-PSPC pulse height channels, respectively, hardness ratio HR= (H-S)/(H+S) and associated errors have been retrieved from the RASS Bright Sources Catalog (Voges et al. 1999) for all the selected stars except for HD 234601, whose X-ray data are listed in the RASS Faint Source Catalog (Voges et al. 2000). Stellar distances were derived from Hipparcos parallaxes. For 8 stars only, which were not in the Hipparcos catalogue, previously known values of parallaxes were used. For these stars we adopted the constant value 0.4, as the most appropriate ratio between the parallax error and its estimate. This number was chosen as the most appropriate taking into account the errors associated with the stellar parallaxes published in the fourth edition of the Yale Trigonometric Parallaxes (Van Altena 1995) available before Hipparcos.

In order to calculate the X-ray luminosity ($L_{\rm X}$) of these stars we have estimated a count rate-to-energy flux conversion factor (CF) following the linear regression curve published by Schmitt et al. (1995) of CF as a function of the Hardness Ratio. The uncertainty on the X-ray luminosities was estimated by taking into account the errors on the stellar parallax, count rate and hardness ratio.

For all the stars with B-V <1.34, the bolometric luminosity was calculated by using the bolometric correction (BC) derived from the B-V colour via the transformations of Flower (1996); for redder stars, whose B-V color less reliably indicates the stellar effective temperature (e.g., see Amado & Byrne 1997 and references therein) we have adopted the calibration of Delfosse et al. (1998) by using the BC vs. (R-I)Ccolour relationship. The uncertainty on the X-ray to bolometric luminosity ratio ( $L_{\rm X}/L_{\rm bol}$) was assumed to be the same as that calculated for the X-ray luminosity, the error on bolometric luminosity being negligible compared to that on X-ray luminosity.

4.2 Cluster stars

We have searched the literature in order to get the X-ray emission data available for the previous cluster studies. We have retrieved the X-ray luminosities and the $L_{\rm X}/L_{\rm bol}$ ratios of all the cluster members from the original papers (see the reference list in the electronic form Tables). X-ray data of all cluster stars were obtained by the ROSAT-PSPC, except for IC 4665 whose X-ray data were obtained by the ROSAT-HRI High Resolution Imager. X-ray luminosities (L$_{\rm X}$) were computed in the same 0.1-2.0 KeV energy band as done for the field stars. We have also estimated the uncertainty on X-ray luminosity by retrieving the published error on $L_{\rm X}$, where available, or by considering both errors on the count rate and stellar distance, deriving the latter from Hipparcos data (Robichon et al. 1999). Following Pizzolato et al. (2003), we verified that the bolometric luminosities of such cluster stars, mainly derived by using the BC from Johnson (1966) for stars with B-V <1.34 and Monet et al. (1992) relationship for later-type stars, resulted to be consistent with the bolometric luminosities as computed for field stars.

X-ray luminosities, X-ray to bolometric luminosity ratios, their uncertainties and references are listed in the electronic form tables.


  \begin{figure} \par\includegraphics[angle=90,width=14.3cm,clip]{H4295F4.ps}\end{figure} Figure 4: $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) versus rotational period (P). Dashed line represents the power law fit to F-type stars. Continuous lines represent exponential fits to G-, K- and M-type stars. Dotted lines represent the range of rotational period where the saturation starts. Stars within this range were excluded from the fits. Downward arrows are upper limits, while the leftward arrow indicates the G-type star HD111395 (see text).
Open with DEXTER

5 Analysis of X-ray data

5.1 Activity-rotation relation

Several observational studies have shown the existence of a dependence of the level of X-ray emission on rotation rate in late-type stars (Walter 1981, 1982; Stauffer et al. 1994; Hempelmann et al. 1995; Randich et al. 1995, 1996; Patten & Simon 1996). However, the use of different pairs of parameters such as surface flux ($F_{\rm X}$), X-ray luminosity ($L_{\rm X}$) or its ratio to bolometric luminosity ($L_{\rm X}$/ $L_{\rm bol}$), and the projected equatorial velocity ($v\sin~i$) or the axial rotational period, but especially the use of stellar samples differing in size and containing stars of quite different spectral type, luminosity class, binarity and age has resulted in different relations regarding the X-ray emission-rotation distribution or different values of their coefficients.

In this section we analyse the X-ray emission-rotation relation for one of the most numerous and homogeneous (cf. Sect. 1) stellar samples currently available and characterized by accurate determination of rotational periods and of V-band light curve amplitudes. Moreover, we use the dimensionless $L_{\rm X}$/ $L_{\rm bol}$ quantity, where bolometric luminosities of field and cluster stars have been computed consistently (see Pizzolato et al. 2003).

The whole stellar sample is studied in four different spectral ranges to investigate the mass dependence. $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) is plotted vs. rotational period in Fig. 4 and vs. Rossby number in Fig. 5, where symbols have same meaning as in Fig. 1 and circled symbols denote the stars used to define the data upper envelope in the $A_{{\rm max}}$-P and $A_{{\rm max}}$-$R_{\rm0}$ relations (Sect. 3). The correlation coefficients and the relation parameters of the linear, exponential and power law weighted fits are listed in Table 3.


  \begin{figure} \par\includegraphics[angle=90,width=14.1cm,clip]{H4295F5.ps}\end{figure} Figure 5: $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) versus Rossby number. Continuous lines represent exponential fits. Dotted lines represent the range of the rotational period were the saturation starts. Stars within this range were excluded from the fits. Downward arrows are upper limits, while the rightward arrow indicates the G-type star HD111395 (see text).
Open with DEXTER

The level of X-ray emission increases with increasing rotation rate up to a saturation level. The rotational period where saturation starts is colour dependent and increases with advancing spectral type (see Pizzolato et al. 2003). The dotted lines in Fig. 4 indicate the rotational period range within which the saturation starts. The continuous and dashed lines in Figs. 4 and 5 represent the exponential and power law fits to the data. Stars in the saturation regime (more precisely those with a rotational period shorter than that indicated by the dotted line) were excluded from the fit. By fitting $\log$  $(L_{\rm X}$/ $L_{\rm bol}$)-P and $\log$ ($L_{\rm X}$/ $L_{\rm bol}$)-R0 relations of G-, K- and M-type stars, the smallest reduced chi-squares values were obtained with linear and exponential laws, the last with larger chi-squares values, and with linear and power laws in the case of F-type stars. As noted in Sect. 3.1, the linear law is physically less supportable, since $L_{\rm X}$/ $L_{\rm bol}$ tends to saturate toward highest rotation rates. However, it must be pointed out that also the exponential law for G-, K- and M-type stars, and the power law for F-type stars might not give the most appropriate description of the trend in the data, since the reduced chi-squares values are large (from 6.5 to 24.4 in Table 3).

As already noted in the study carried out by Patten & Simon (1996) we find that in our sample of K-type stars a discontinuous jump appears in the relation around P $\simeq$ 8-10 d ( $R_0 \simeq$ 0.3-0.4).

At the highest rotation rates ( $P \la 0.40$ d, $R_0 \la 0.018$) in the K and M spectral ranges, it is possible to see evidence of the supersaturation regime (Prosser et al. 1996; Randich 1998; James et al. 2000), where the level of the X-ray emission tends to decrease with increasing rotation rate. We also note that the $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) ratio of HD 111395 is higher than expected. A rotational period smaller than the known value would reduce its scatter from the $\log$ ($L_{\rm X}$/ $L_{\rm bol}$)-P fit.

Table 3: Correlation coefficients (r), number of stars used to define the upper envelope (N), parameters of the linear, exponential and power law weighted fits to the upper data envelope of the $L_{\rm X}$/ $L_{\rm bol}$-P and $L_{\rm X}$/ $L_{\rm bol}$-$R_{\rm0}$ relations and reduced chi-squares ( $\chi ^2_{\rm\nu }$).

5.2 Colour dependence

In Fig. 6 we plot $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) vs. B-V colour. Symbols have the same meaning as in the previous figures, except that circled symbols refer to stars in the fast rotation regime. The continuous segments are plotted to better show the behaviour of the upper envelope of fast rotating stars. It is interesting to note that such an envelope has a dependence on B-V colour, similar to the trend shown by the $A_{{\rm max}}$ upper envelope (cf. Fig. 3). The luminosity ratio $\log$($L_{\rm X}$/ $L_{\rm bol}$) monotonically increases in the F-G spectral ranges, then reaches the maximum value of  $\simeq-2.9$ in the K spectral range at B-V $\simeq$ 0.85. It decreases to a minimum of  $\simeq-3.3$ at B-V $\simeq$ 1.00 and it shows a secondary maximum of $\log$ ($L_{\rm X}$/ $L_{\rm bol})\simeq -2.8$ at B-V $\simeq$ 1.10. Then, $L_{\rm X}$/ $L_{\rm bol}$ decreases towards later spectral types, with evidence of a slight increase among the coolest stars. Differently than observed for the $A_{{\rm max}}$ upper envelope, the ultra fast F-, G- and M-type stars (around B-V $\simeq$ 1.4) have an X-ray luminosity level only slightly higher than fast stars. The spread of values of $\log$ ($L_{\rm X}$/ $L_{\rm bol}$), which is constant in the F-K spectral ranges, is considerably smaller among M-type stars. According to Stauffer et al. (1994), such a spread is mainly attributable to the large range of rotational periods. More precisely, the spread decreases towards later spectral types since M stars have longer braking time scales and are mostly rotating very rapidly (Stauffer 1990; Barnes 2003).

6 $L_{\rm X}/L_{\rm bol}$-$A_{\max}$ correlation

In the panels of Fig. 7 we note a significant increase (from 2 up to 3 orders of magnitude) in the minimum values of $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) with increasing $A_{{\rm max}}$, but with decreasing steepness from F and G to the later spectral types. Such a behaviour is expected from both the $\log$ ($L_{\rm X}$/ $L_{\rm bol}$)-P and  $A_{{\rm max}}$-P relations. In fact, most of the stars (plotted with circled symbols) in the lower envelope, which is defined by the minimum values of $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) for any $A_{{\rm max}}$ value, are the same stars determining the $A_{{\rm max}}$-P upper envelope. Since they have the slowest rotational period for any given $A_{{\rm max}}$ value (see Fig. 1), they also have the lowest $\log$  $(L_{\rm X}$/ $L_{\rm bol})$ values, given the decrease of X-ray emission on rotational period (see Fig. 4). The scatter within the lower envelope is larger than within the upper envelope in the $A_{{\rm max}}$-P relation. In fact, while $A_{{\rm max}}$ values are derived from long-term studies and represent the maximum photospheric activity level, on the contrary, the X-ray data represent a snapshot of the coronal activity level at the time of observation, that is at a given phase of rotation and long-term activity. Therefore, the relatively high scatter is mainly attributable to the short- and long-term variations of the X-ray emission level, the first due to rotational modulation and flare-like activity and the second due to intrinsic time changes of coronal structures (e.g., Schmitt 1992; Marino et al. 2002). We would expect to observe a reduced scatter if long-term X-ray studies were also available. The stars on the left of the lower envelopes in Fig. 7 have few determinations of $A_{{\rm max}}$ (see electronic form Tables). When long-term photometric studies will also be available for these stars, their location in the graph is expected to approach the lower data envelope, appreciably reducing the observed spread, apart from that deriving from the X-ray variability.

The $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) vs. $A_{{\rm max}}$ distribution also presents evidence of an upper envelope which is constant at the saturation level of $\log$ ($L_{\rm X}$/ $L_{\rm bol}$)  $\simeq -3.0$. The range of $A_{{\rm max}}$ values in such an envelope increases from F5-F9, where actually it is not clearly detectable, to K6-M4 spectral ranges. The stars in the upper envelope (plotted with open diamonds) are the same ultra fast rotating stars (0.3 < P < 1.1 d) determining the upper envelope in the $A_{{\rm max}}$-P relation. The stars below the upper envelope (plotted with open squares) are in the super-saturation regime (P < 0.3 d). In these regimes the $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) depends neither on the rotational period nor on $A_{{\rm max}}$.

The coefficients of correlation r as well as the parameters a and b and the reduced chi-squares ( $\chi^2_{\nu}$) of the linear, exponential and power law weighted fits to the lower envelope of the $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) vs. $A_{{\rm max}}$ distribution are listed in Table 4. The smallest reduced chi-squares values for F-, G-, K- and M-type stars (upper fit) are obtained when power and exponential laws are used, the chi-squares values of the power law fits being smaller on average by less than 20% than the chi-squares values from the exponential law fit. The smallest reduced chi-squares values for M-type stars (lower fit) are given by an exponential law. However, at least for F-, G- and K-type stars the power law might not be the most appropriate function to describe the trend of the $L_{\rm X}/L_{\rm bol}{-}A_{\rm max}$ data, since the reduced chi-squares values are large (see Table 4). Nontheless, in order to compare the results of this analysis with those from previous studies let us consider the power law fits (continuous lines in Fig. 7) which we write in the form of

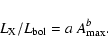\begin{displaymath}% L_{\rm X}/L_{\rm bol}=a~A_{\rm max}^b. \end{displaymath} (3)

The power exponent $b=2.39\pm 0.10$ we found for K-type stars is in good agreement with the value of 1.96 $\pm$ 0.25 and 2.22 $\pm$ 0.36 found by Stepien (1991) by analysing, respectively, Saar (1990b, 1991) and Schrijver et al. (1989) stellar samples. Such agreement makes us confident about the reliability of the activity indicator $A_{{\rm max}}$ we adopted for this analysis as tracer of the magnetic filling factor.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{H4295F6.ps}\end{figure} Figure 6: $\log$($L_{\rm X}$/ $L_{\rm bol}$) versus B-V. Symbols have same meaning as in the previous figures. Circled symbols denote fast rotating stars. Continuous segments are plotted to better show the upper envelope of fast rotating stars.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{H4295F7a.ps}\hspa... ...space*{2mm} \includegraphics[angle=90,width=8.8cm,clip]{H4295F7d.ps}\end{figure} Figure 7: $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) vs. $A_{{\rm max}}$ for F- ( top left panel), G- ( top right panel), K- ( bottom left panel) and M-type stars ( bottom right panel). Circled symbols (and also open triangles for M-type stars) represent the stars defining the upper envelope of the $A_{{\rm max}}$-P relation for fast rotating stars. Open diamonds represent the stars defining the upper envelope of the $A_{{\rm max}}$-P relation for ultra fast rotating stars. Open squares represent the stars in the super-saturation regime ($P\le 0.3$ d). Continuous and dotted lines are the power law fits to the lower and upper envelope data, respectively. The leftward arrow in the top right panel indicates the G-type star HD 111395, while capital letters (A, B, C and D) indicate the stars appreciably below the lower envelope.
Open with DEXTER

We note that HD 111395, even assuming a shorter rotational period, lies far from the fit shown in Fig. 7, the level of its coronal and photospheric activity not being consistent with one another. This star certainly deserves attention in future studies. Also the K-type stars VB 43, VB 91 and AP 72 (labels A, B and C, respectively, in Fig. 7) are appreciably below the $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) lower envelope. In the case of VB 43 and VB 91 it is due to a $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) ratio smaller than expected for their rotational period (see Fig. 4), while in the case of AP 72 it may also due to the relatively large uncertainty on the luminosity ratio.

In the case of M-type stars two power law fits are plotted (bottom right panel of Fig. 7): the lower envelope 1 (continuous line) refers to the $A_{{\rm max}}$ upper envelope 1 in Fig. 1 and the lower envelope 2 (dashed line) refers to the $A_{{\rm max}}$ upper envelope 2 in the same figure. Dotted lines (bottom right panel of Fig. 7) represent power law fits to the upper envelope data in the saturation regime (marked with open diamonds). Apart from HII 250 (label D in Fig. 7), which is the only G-type star with a $\log$  $(L_{\rm X}$/ $L_{\rm bol})$ appreciably lower than in the other stars, in the saturation regime there is no apparent correlation between $\log$  $(L_{\rm X}$/ $L_{\rm bol})$ and $A_{{\rm max}}$. In the case of M-type stars there is a slight tendency for $\log$  $(L_{\rm X}$/ $L_{\rm bol})$ to decrease with increasing  $A_{{\rm max}}$. Also in the super-saturation regime no correlation apparently exists between $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) and $A_{{\rm max}}$.

7 Discussion

The $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) vs. $A_{{\rm max}}$ distributions plotted in Fig. 7 are consistent with current models of stellar angular momentum evolution. These models assume that the rate of angular momentum loss, due to braking by a magnetized wind, depends basically on angular velocity and spectral type (e.g., Pinsonneault et al. 1990; Chaboyer et al. 1995; Barnes & Sofia 1996). The angular velocity determines the braking strength according to a power law, but only up to a threshold angular velocity beyond which loss rate saturation occurs and the braking strength becomes almost constant (e.g., Kawaler 1988; Chaboyer et al. 1995). The spectral type, more precisely the depth of the convective zone, determines the braking time scale which increases with advancing spectral type (Stauffer 1990; Barnes 2003). We expect to find evidence of such spectral-type dependent time evolution in the normalized distributions of rotational periods of our stellar sample. Actually, in Fig. 8 we see that the fraction of faster rotating stars significantly increases with advancing spectral type, except for F-type stars because of a selection effect. In fact, our sample of F-type stars lacks slow rotators, since their activity level is very low and it is difficult to detect the photometric variability. Such spectral-type dependent evolution of the rotational period distribution is also seen in the $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) vs. $A_{{\rm max}}$ relationship.


  \begin{figure} \par\includegraphics[angle=90,width=8.3cm,clip]{H4295F8.ps}\end{figure} Figure 8: Normalized distributions of rotational periods in F, G, K and M spectral ranges. Continuous and dotted lines represents cubic fit to the histogram obtained using a three-day binning.
Open with DEXTER

The M-type stars in our sample are mostly PMS or just arrived on the zero-age-main sequence. They have not undergone magnetic braking and are in the activity saturation regime. Moreover, the onset of the saturation regime occurs at longer rotational periods ($P\le 5$ d) for M-type stars than for other spectral types (see Fig. 4 and Pizzolato et al. 2003). Consistently, in the bottom right panel of Fig. 7 most stars are located in the upper envelope. Lower envelopes (1 and 2), which are determined by the fraction of slower rotating stars, have a relatively small range (-4< $\log$  $(L_{\rm X}$/ $L_{\rm bol})$ <-3) of values. Lower envelopes 1 and 2 reflect the different dependence of upper envelopes 1 and 2 on rotational period (see Fig. 1).

The K-type stars of the youngest clusters (IC 2602, IC 4665, IC 2391 and $\alpha$ Persei) are also rapid rotators, while the older-age K-type stars (Pleiades, Field and Hyades) have already left the saturation regime due to magnetic braking. Consistently, in the bottom left panel of Fig. 7 the upper envelope is still well populated by stars in the saturation (diamonds) and super-saturation (squares) regimes, and the lower envelope has a range of values (-5< $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) <-3) much larger than the M-type stars, the fraction of slower rotators being increased.


  \begin{figure} \par\includegraphics[angle=90,width=8.2cm,clip]{H4295F9.ps}\end{figure} Figure 9: Power law fits to the $\log$ ($L_{\rm X}$/ $L_{\rm bol}$)- $A_{{\rm max}}$ relation. Different line-styles and symbols are used to distinguish different spectral ranges and clusters, respectively. The different symbols represent the mean $\log$ $L_{\rm X}$/ $L_{\rm bol}$ for each cluster, computed using the values plotted in Fig. 4 for $P\ge $ 1.1 d. Data for K-type stars have been circled to better distinguish them from G-type star data.
Open with DEXTER

Table 4: Coefficients of correlation (r), number of stars used in the fit (N), parameters (a and b) of the linear, exponential and power law weighted fits to the lower envelope of the $L_{\rm X}$/ $L_{\rm bol}$- $A_{{\rm max}}$ distribution in the fast rotation regime ($P \ge 1.1$ d) and reduced chi-squares ( $\chi ^2_{\rm\nu }$).

In the G0-G7 spectral range only the stars of the youngest clusters (IC 2602, IC 4665, IC 2391) are rapid rotators. All the older cluster stars have been already slowed by magnetic braking. Consistently, in the top right panel of Fig. 7 the upper envelope is poorly populated, most stars having moved towards the lower envelope, which has a similar range of values (-5< $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) <-3) as the K-type stars, the fraction of slower rotators ($P \ge 10$ d) being similar in the G and K spectral ranges (see Fig. 8).

All F-type stars are expected to have been slowed by magnetic braking (Stauffer 1990; Barnes 2003) and, consistently, in the top left panel of Fig. 7 we observe them to be located only in the lower envelope. Apparently, the level of photospheric as well as coronal activity of F-type stars is low enough to overcome the excess of F-type rapid rotators.

New information on the time evolution of magnetic activity can be inferred from the $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) vs. $A_{{\rm max}}$ distributions.

In Fig. 9 we plot the lower envelope power law fits from Fig. 7 (see also Table 4). The spectral types are distinguished by different line styles and the cluster stars $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) mean values by different symbols. We focus on fast rotating stars ($P \ge 1.1$ d), since ultra fast rotating stars are in a saturation or super-saturation regime and do not show a correlation between $\log$  $(L_{\rm X}$/ $L_{\rm bol})$ and $A_{{\rm max}}$. Field stars are less active than the Pleiades, being older on average. Also F-type $\alpha$ Persei stars seem to be less active than the Pleiades, the number of stars from which the average is computed being small. Finally, among M-type stars the mean values of $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) and $A_{{\rm max}}$ seem to vary quite independently of the cluster ages. It is interesting to note that in the case of G-type stars the power law relation (dotted line) we derive from our data provides a good fit to solar $L_{\rm X}$/ $L_{\rm bol}$ value. We see that the $\log$ ($L_{\rm X}$/ $L_{\rm bol}$) and $A_{{\rm max}}$ values for all but M spectral types evolve in time according to a single power law, the youngest clusters being the most active and the oldest one (Hyades) the least active. This is a first remarkable result because it may indicate that the way coronal heating is linked to photospheric activity is constant in time, the strength or efficiency of the coronal heating mechanism being basically the main variable.

The distributions plotted in Fig. 7 are also consistent with the theoretical scenario according to which the section of flux tubes, as well as their total filling factor, increase with height from the photosphere towards the upper atmospheric layers (e.g., Spruit 1981). Since the total amount of magnetic fields emerging at photospheric level primarily depends on the rotational period, then the filling by magnetic fields increases with increasing rotational period at all atmospheric layers and more rapidly in the upper layers. This is clearly seen in the activity-rotation and flux-flux relations, where the activity diagnostics are correlated to rotational period and with each other with increasing slope when increasingly high temperature diagnostics, such as the X-ray ($L_{\rm X}$) luminosity, are plotted versus the coolest ones such as the CIV ( $L_{\rm CIV}$) or the MgII ( $L_{\rm MgII}$) luminosity (e.g., Dorren et al. 1994; Pizzolato et al. 2003). The values of the power law coefficients of the lower envelope fits in Fig. 7 are consistent with this scenario. In fact, if we compare the relations between X-ray, Mg II h&k and CIV luminosities for G-type stars, e.g. those derived from Dorren et al. (1994)

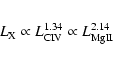
\begin{eqnarray*}L_{\rm X} \propto L_{{\rm CIV}}^{1.34} \propto L_{{\rm MgII}}^{2.14} \end{eqnarray*}


and the new relation derived in this study

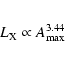
\begin{eqnarray*}L_{\rm X} \propto A_{{\rm max}}^{3.44} \end{eqnarray*}


we see that coefficient b=3.44 is larger than the coefficients of the flux-flux relations between upper layer diagnostics. We point out that the power law fit to the lower envelope of G-type stars of Fig. 7 was recomputed by using $L_{\rm X}$ instead of $L_{\rm X}$/ $L_{\rm bol}$ to be consistent with the Dorren et al. relations.

The distributions plotted in Fig. 7 also add new information on the colour dependence of the coronal activity on the photospheric one. F-type stars, which have a shallow convective zone, apparently have coronae most sensitive to variations of the starspot activity level. A small increase in the quantity of photospheric spots, e.g. $\Delta A_{\rm max}=+ 0.05$ mag, produces an increase in the level of coronal emission up to an order of magnitude. On the contrary, M-type stars, which have a very deep convective zone, apparently have coronae less sensitive to variations of the starspot activity level. The same increase in the quantity of photospheric spots determines an increase in the coronal emission level of only one tenth that of the F-type star's value. Such different sensitivity to the variations of the starspot activity level may origin in the corona as well as in the photosphere and can be related to the use of $A_{{\rm max}}$ as tracer of the total starspot filling factor. We know that in G-type stars the quantity of spots unevenly ( $A_{{\rm max}}$) and evenly ($A_{\rm u}$) distributed in longitude are similar (see Paper I). If we assume that in K- and M-type stars $A_{\rm u} \gg$ $A_{{\rm max}}$, even with small $A_{{\rm max}}$ the total starspot filling factor would be high. That would explain the high level of X-ray emission in the later spectral types for small values of $A_{{\rm max}}$and the apparently lower sensitivity of coronal emission to the variation of photospheric activity. The sensitivity might be found to be comparable among different spectral types, when $f_{\rm tot}$ would be used in place of $A_{{\rm max}}$. As soon as the current photometric monitorings (e.g. Rodonò et al. 2002; Messina & Guinan 2002) make available the more numerous and longer-term photometric data sets for F-, K- and M-type stars, we will be in the position to check the validity of our assumption. However, at present we cannot say if the dependence of the efficiency of the coronal heating mechanism on the spectral type is effective or if it depends on the prevailing type (uniform or asymmetric) of distribution of spotted regions in the photosphere, which may as well be spectral-type dependent.

Finally, the existence of a $\log$  $(L_{\rm X}$/ $L_{\rm bol})$- $A_{{\rm max}}$ relation is remarkable because photometric determinations of $A_{{\rm max}}$ allow us to put a lower limit on the X-ray luminosity for those stars for which X-ray measurements are not yet available.

8 Conclusions

Observational studies have confirmed that the presence of hot coronae in late-type stars and the level of their X-ray luminosity depend ultimately on the strength and total amount of surface magnetic fields, as expected on the basis of theoretical arguments and of the solar analogy. However, direct measurements of surface magnetic fields are currently very difficult to be obtained and limited to small and inhomogeneous stellar samples. Thus, such measurements are not suitable to infer the accurate empirical relations between magnetic field and global stellar parameters needed to test and improve the current models of coronal heating.

To overcome the paucity of direct measurements, in the present paper we propose the use of the maximum light curve amplitude ( $A_{{\rm max}}$) as the closest, although indirect, indicator of magnetic filling factor. By handling a very large and homogeneous sample of field and cluster main-sequence stars the following results are presented:

1.
In the ultra fast rotation regime $A_{{\rm max}}$ decreases with increasing P and R$_{\rm0}$ preferentially according to a linear law. In the fast rotation regime the $A_{{\rm max}}$-P and $A_{{\rm max}}$-$R_{\rm0}$ upper envelopes for F- and K-type stars are best fitted by an exponential law, for G-type stars by a linear law, for M-type stars (upper envelope 2) by a power law. In the case of M-type stars (upper envelope 1) the $A_{{\rm max}}$-Pupper envelope is best fitted by a linear law, while the $A_{{\rm max}}$-$R_{\rm0}$ upper envelope by exponential and linear laws with similar chi-squares values. The value of the exponential coefficient for K-type stars is consistent with the results of studies based on direct measurements of the magnetic filling factor. This makes us confident about the reliability of the activity indicator $A_{{\rm max}}$ used in this analysis. A break in the relation around 1.1 d as well as a different colour dependence of  $A_{{\rm max}}$ on P between ultra fast and fast rotating stars suggest the possible existence of two different dynamo regimes. $\alpha$ Persei and Pleiades K-type stars show the highest level of starspot activity.
2.
The ratio $L_{\rm X}$/ $L_{\rm bol}$ between X-ray and bolometric luminosities increases with increasing rotation rate and decreasing $R_{\rm0}$ up to a saturation level. The rotational period at which saturation starts is colour dependent and increases with advancing spectral type. The smallest chi-squares values are given by linear and exponential law fits for G-, K- and M-type stars (the exponential law with larger $\chi_{\nu}^2$ values), and by linear and power law fits for F-type stars. However, these might not be the most appropriate functions describing the $L_{\rm X}$/ $L_{\rm bol}$-P and $L_{\rm X}$/ $L_{\rm bol}$-R0 relations, since the reduced chi-squares values are rather large. Among the fastest rotating stars ($P\le 0.3$ d) there is evidence of super-saturation. K-type stars show the highest values of $L_{\rm X}$/ $L_{\rm bol}$.
3.
The $L_{\rm X}$/ $L_{\rm bol}$- $A_{{\rm max}}$ distribution shows the presence of a lower envelope whose steepness decreases from F-G to M-type stars. The existence of such a lower envelope confirms the dependence of the level of coronal activity on the quantity of photospheric magnetic fields. The power law gives the smallest chi-squares values for F-, G-, and K-type stars. However, it might not be the most appropriate function describing the $L_{\rm X}$/ $L_{\rm bol}$- $A_{{\rm max}}$ lower envelopes, since the reduced chi-squares values are rather large. For M-type stars the lower envelopes (upper and lower fits) are best fitted by exponential and power laws, respectively. The power law exponent has a value consistent with those derived from studies based on direct measurements of the magnetic filling factor. This result makes us confident on the reliability of $A_{{\rm max}}$ as an indicator of the magnetic filling factor. The colour dependence of the $L_{\rm X}$/ $L_{\rm bol}$- $A_{{\rm max}}$ lower envelope may indicate that F-type stars have coronae more sensitive to variations in the starspot activity level than M-type stars. However, we cannot rule out a colour dependence of $A_{{\rm max}}$ on the total starspot filling factor. That is, the dynamo may preferentially produce uniformly distributed spotted regions ( $A_{\rm u} \gg$ $A_{{\rm max}}$) as the spectral type advances, small values of $A_{{\rm max}}$ being consistent with a large starspot filling factor. The $L_{\rm X}$/ $L_{\rm bol}$- $A_{{\rm max}}$ distribution also shows the presence of a constant upper envelope at the X-ray saturation level of $\log$ ($L_{\rm X}$/ $L_{\rm bol}$)  $\simeq -3.0$.
4.
The mean values of $L_{\rm X}$/ $L_{\rm bol}$ and $A_{{\rm max}}$ of each cluster decrease monotonically with increasing age according to a single power law. This may indicate that the way coronal heating is linked to photospheric activity is constant in time, the strength or efficiency of the coronal heating mechanism being basically the main variable. The solar $L_{\rm X}$/ $L_{\rm bol}$ value is well fitted by the power law relation derived for G-type stars.
5.
We found that $L_{\rm X}$ depends on $A_{{\rm max}}$ according to the same power law as the other upper layer activity diagnostics. Moreover, consistently with other flux-flux relations whose slopes increase when increasingly high temperaturediagnostics are plotted versus the cooler ones, the $L_{\rm X}$- $A_{{\rm max}}$ relashionship has the largest value of the power law exponent.

Acknowledgements
Active star research at the Catania and Palermo Astrophysical Observatories, INAF, is funded by MIUR (Ministero dell'Istruzione, dell'Università e della Ricerca) and the Regione Siciliana, whose financial support is gratefully acknowledged. This research is also supported by the US National Science Foundation for Research whose financial support is gratefully acknowledged. The extensive use of the SIMBAD database, operated by the CDS center, Strasbourg, France, is gratefully acknowledged. We thank the referee, Dr. N.A. Webb, for careful reading of the manuscript and valuable comments.

References


Copyright ESO 2003