S. L. Schuh1,14,![]() -
G. Handler2,3 -
H. Drechsel4 -
P. Hauschildt5 -
S. Dreizler1,14,
-
G. Handler2,3 -
H. Drechsel4 -
P. Hauschildt5 -
S. Dreizler1,14,![]() -
R. Medupe3,6 -
C. Karl4,
-
R. Medupe3,6 -
C. Karl4,![]() -
R. Napiwotzki4,
-
R. Napiwotzki4,![]() -
S.-L. Kim7 -
B.-G. Park7 -
M. A. Wood8 -
M. Paparó9 -
B. Szeidl9 -
G. Virághalmy9 -
D. Zsuffa9 -
O. Hashimoto10 -
K. Kinugasa10 -
H. Taguchi10 -
E. Kambe11 -
E. Leibowitz12 -
P. Ibbetson12 -
-
S.-L. Kim7 -
B.-G. Park7 -
M. A. Wood8 -
M. Paparó9 -
B. Szeidl9 -
G. Virághalmy9 -
D. Zsuffa9 -
O. Hashimoto10 -
K. Kinugasa10 -
H. Taguchi10 -
E. Kambe11 -
E. Leibowitz12 -
P. Ibbetson12 -
Y. Lipkin12 -
T. Nagel1,![]() -
E. Göhler1,
-
E. Göhler1,![]() -
M. L. Pretorius13
-
M. L. Pretorius13
1 - Institut für Astronomie und Astrophysik, Universität
Tübingen, Sand 1, 72076, Tübingen, Germany
2 -
Institut für Astronomie, Universität Wien, Türkenschanzstraße
17, 1180 Wien, Austria
3 -
South African Astronomical Observatory, PO Box 9, Observatory 7935, Cape, South Africa
4 -
Dr.-Remeis-Sternwarte, Astronomisches Institut der
Universität Erlangen-Nürnberg, Sternwartstr. 7, 96049 Bamberg, Germany
5 -
Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112,
21029 Hamburg, Germany
6 -
Department of Physics, University of the North-West,
Private Bag X2046, Mmabatho 2735, South Africa
7 -
Korea Astronomy Observatory, 61-1, Whaam, Yuseong, Daejeon, 305-348,
Korea
8 -
Department of Physics and Space Sciences and SARA Observatory,
Florida Institute of Technology, 150 West University Boulevard, Melbourne,
FL 32901-6975, USA
9 -
Konkoly Observatory, Box 67, 1525 Budapest XII, Hungary
10 -
Gunma Astronomical Observatory, 6860-86 Nakayama Takayama-mura
Agatsuma-gun Gunma-ken, Postal Code: 377-0702, Japan
11 -
Department of Earth and Ocean Sciences, National Defense Academy,
Yokosuka, Kanagawa 239-8686, Japan
12 -
Wise Observatory, Sackler Faculty of Exact Sciences, Tel Aviv
University, Tel Aviv 69978, Israel
13 -
Department of Astronomy, University of Cape Town, Rondebosch 7700, South
Africa
14 -
Universitätssternwarte Göttingen, Geismar Landstraße 11,
37083 Göttingen, Germany
Received 8 April 2003 / Accepted 4 August 2003
Abstract
We report the discovery of a new eclipsing system less than
one arcminute south of the pulsating DB white dwarf KUV 05134+2605. The
object could be identified with the point source 2MASS J0516288+260738
published by the Two Micron All Sky Survey. We present and discuss the
first light curves as well as some additional colour and spectral
information. The eclipse period of the system is 1.29 d, and,
assuming this to be identical to the orbital period, the
best light curve solution yields a mass ratio of
m2/m1=0.11, a
radius ratio of
![]() and an inclination of 74
and an inclination of 74![]() .
The spectral anaylsis results in a
.
The spectral anaylsis results in a
![]() K
for the primary. On this basis, we suggest that the new system
probably consists of a late K + Brown dwarf (which would imply a
system considerably younger than
K
for the primary. On this basis, we suggest that the new system
probably consists of a late K + Brown dwarf (which would imply a
system considerably younger than ![]() 0.01 Gyr to have
0.01 Gyr to have
![]() ), and outline possible future observations.
), and outline possible future observations.
Key words: ephemerides - stars: variables: general - stars: binaries: eclipsing - stars: low-mass, brown dwarfs - stars: individual: 2MASS J0516288+260738
Future improvements of the theoretical mass-radius relation for the lower main sequence would strongly benefit from a larger empirical database through an increased sample of eclipsing binaries. Recently, 137 eclipsing low-luminosity candidates were announced by the OGLE (Optical Gravitational Lensing Experiment) consortium (Udalski et al. 2002a,b,2003), of which several of the secondaries turned out to be M-type stars (Dreizler et al. 2002). In this paper we report the discovery of another interesting eclipsing binary system, 2MASS J0516288+260738, whose components appear to bracket the M-star range, with the potential of extending the empirical mass-radius relation into the sub-stellar range.
The new eclipsing system has been discovered in observational data taken during a coordinated photometric monitoring campaign in December 2001. This dataset has been obtained to monitor the light variations of the DB variable white dwarf KUV 05134+2605 (Grauer et al. 1989; Handler et al. in prep.). It consists of many individual light curves taken by either photomultiplier (PMT) or CCD instruments; the newly discovered object is included in 48 individual time series of images obtained with CCD cameras. While analysing field stars for photometric stability to check whether they could be used as references, an object located a little less than one arcminute south of the DB was found to show the signature of an eclipse in the Calar Alto 2.2 m data set of 2001 Dec. 07 (see Table 1, only available in electronic form at http://www.edpsciences.org). Subsequent searches in the other data sets revealed that eight more eclipses had partly or fully been observed. A year later, 5 additional data sets were obtained, two of which covered the eclipse. The full time-resolved photometric data are compiled in Sect. 3. Archive searches contributed an identification of the object as well as additional colour information (Sects. 2 and 4). Two months after the initial observations, an optical spectrum could be obtained, and in the following observing season, an infrared spectrum was taken (see Sect. 4).
In the following, we compile the information that is currently available on the object, report our results from the light curve solution and the spectral analysis, and propose a possible configuration for this system.
| |
Figure 1:
Finding charts for 2MASS J0516288+260738 (DSS-2
red: left, DSS-2 blue: right). The side length is
|
| Site | Telescope | Observers | |
| CAHA | Calar Alto Observatory, Centro Astronómico Hispano Alemán, Almería, Spain | 2.2 m | SD, SLS |
| CAHA II | Calar Alto Observatory, Centro Astronómico Hispano Alemán, Almería, Spain | 1.2 m | TN, EG |
| BOAO | Bohyunsan Optical Astronomy Observatory, Korea | 1.8 m | SLK, BGP |
| SAAO | South African Astronomical Observatory, Sutherland, South Africa | 1.0 m | GH, TM |
| SARA | Kitt Peak National Observatory, Tucson, Arizona, United States of America | 0.9 m | MW |
| GAO | Gunma Astronomical Observatory, Japan | 1.5 m | OH, KK, HT, EK |
| WISE | The Florence and George Wise Observatory, Tel-Aviv University, Israel | 1.0 m | EL, PI, YL |
| Piszkésteto | Piszkésteto, the mountain station of Konkoly Observatory, Mátra Mountains, Hungary | 1.0 m | MP, BS, GV, DZ |
The light curve shows a clear periodicity of 1.29 days. All observed eclipses are similar to each other, have a duration of about 0.10 days and exhibit a decrease in flux of 15% (or 0.17 mag) at the deepest point. There is no indication of a secondary eclipse in any of the eight 2001 data sets that partly or fully cover the phase where such an event would be expected. Furthermore, the three 2002 data sets covering that phase put a clear upper limit to the depth of any secondary eclipse: 0.49% (or 5.4 mmag) in white light and 0.70% (or 7.6 mmag) in the Johnson I filter.
Primary minima times were determined by fitting parabolas to the
eclipses. The results for the epochs 0 (two independent data sets), 3,
9, 10, 11, 12 (concatenated from two different non-overlapping data
sets), 259 and 262 are given in Table 1; no fits
could be obtained for epochs 5 and 7
since only parts of either ingress or egress had been observed there. A
linear regression for the measured minima times then gives the linear
elements and their 1![]() errors for the primary minima as
errors for the primary minima as
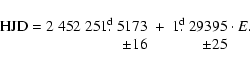
The folded profile has also been carefully inspected to verify that no
secondary eclipse is apparent in the data. The profile remains at the same
relative flux level outside of the primary eclipse with no significant
indication of ellipsoidal light variations or reflection effects. It
was then used to obtain a light curve solution as discussed in
Sect. 6.
Photographic B, R and I magnitudes are published in the
USNO-B catalogue (Monet et al. 2003), and
infrared J, H and K magnitudes are available from the 2MASS
catalog. They are compiled in Table 3.
The USNO-B and 2MASS magnitudes m have been converted to
![]() using the relation
using the relation
| B | V | R | I | J | H | K | |
| Magnitude | 19.47 | 18.1 | 16.8 | 15.84 | 14.247 | 13.346 | 13.115 |
| Error | | | | | | |
|
|
|
0.43 | 0.55 | 0.70 | 0.90 | 1.25 | 1.65 | 2.17 |
|
|
4440 | 3810 | 2880 | 2240 | 1593 | 1089 | 713 |
|
|
1.17 | 2.17 | 3.36 | 3.83 | 6.12 | 5.51 | 2.58 |
|
*
| ||||||||||
![\begin{displaymath}F_{\lambda} {\rm\left[erg~s^{-1} cm^{-2} \AA^{-1}\right]} = F...
...10^{-0.4 m}\cdot3\times 10^{-13} / \lambda_{0}{\rm [\mu m]}^2.
\end{displaymath}](/articles/aa/full/2003/41/aa3829/img30.gif)
The Sloan Digital Sky Survey (SDSS) does not cover the field in its EDR (Early Data
Release, Stoughton et al. 2002)
so that no further photometric information is available. Since the object,
according to its infrared colours, is very red, we also checked the VLA
FIRST survey at 20 cm, which currently does not cover this field either,
and the NRAO/VLA Sky Survey (NVSS) at 1.4 GHz (Condon et al. 1998),
which covers the field but does not show a radio source in the vicinity.
For completeness, we finally note that neither the ROSAT Bright Source
Catalogue as compiled from the WFC All Sky Survey (Pounds et al. 1993) nor the
ROSAT XUV Pointed Phase Source Catalogue as compiled from WFC observations
during pointed phase (Kreysing et al. 1995) list sources at or near the object's position.
| Object | Instrument | Start time (UT) | Exp. time | HJD | ||
| 2MASS J0516288+260738 | TWIN | 3900-5000, 6000-7090 | 2002 Feb. 23 | 21:34 | 1800 s | 2 452 329.411 |
| G191-B2B | TWIN | 3900-5000, 6000-7090 | 2002 Feb. 25 | 18:40 | 300 s | 2 452 331.281 |
| 2MASS J0516288+260738 | TWIN | 3900-5000, 6000-7090 | 2002 Feb. 25 | 20:49 | 1800 s | 2 452 331.380 |
| 2MASS J0516288+260738 | OMEGA-Cass | HK: 14 000-25 000 | 2002 Oct. 27 | 23:31 | 24 |
2 452 575.484 |
| GD 71 | OMEGA-Cass | HK: 14000-25000 | 2002 Oct. 28 | 02:21 | 10 |
2 452 575.602 |
| 2MASS J0516288+260738 | OMEGA-Cass | JH: 10 000-18 000 | 2003 Feb. 03 | 21:49 | 24 |
2 452 674.412 |
| GD 71 | OMEGA-Cass | JH: 10 000 - 18 000 | 2003 Feb. 03 | 23:12 | 24 |
2 452 674.470 |
Each time, a set of 24 spectra was obtained using the OMEGA-Cass instrument mounted on the 3.5 m telescope (see Table 4), well off both primary and secondary eclipse. Since the background is high for infrared observations, the set of 24 spectra was obtained in such a way that alternating exposures contain the source on two different locations on the chip. After bias and flatfield correction of the individual exposures, this allows to determine a mean background at the (dispersed) location of the source for both types of images from the respective subset of the complementary frames. These two measures of the mean background can then be used to subtract the appropriate background from all frames of the two subsets. To do this, the shift for each background row was first determined by cross-correlating it along the dispersion direction with the corresponding image row, and the overall run of the shift along the chip obtained by fitting these row-by-row measurements with a low-order polynomial. To achieve the best possible subtraction in the vicinity of the source location on the chip, this fit with sub-pixel accuracy was then used to shift the background onto the image before subtracting it. For the wavelength dispersions at the two source locations, no shifts could be detected during the course of the exposure series. Therefore, next these bias subtracted, flatfield corrected and background subtracted frames of each of the two sets were added to yield two summed images. The spectra were extracted from these two images using standard procedures for extraction, sky correction, cosmic filtering, illumination correction, and wavelength calibration. The same procedure was used for the set of 10 and 24 exposures of the standard star GD 71. For each observation, the two spectra for the standard star were then combined and compared to tabulated flux values to obtain the factor for absolute flux calibration, which was then applied to both the two object spectra and the two individual standard star spectra.
Comparing the results for the individual spectra for both stars leads to the conclusion that the error bars in the resulting combined spectra must be considered to be of the same magnitude as any "features'' that one might be tempted to spot. The same conclusion results from a comparison of the H band parts of the spectra from the two different observing dates, where most "features'' are not reproduced. Furthermore, a flux difference by a factor of about 1.5 between those two independent observations gives an estimate for the errors in the flux calibration. The rescaled infrared spectra for 14 000-25 000 Å and 10 000-18 000 Å are displayed in Fig. 3.
The uncertainty in the optical spectrum results since both object and
flux standard star were observed under non-photometric conditions.
The same argument applies to the infrared spectral observations, where
observations from different nights, although both nominally flux
calibrated, result in different flux levels for the overlapping H band. A consistent adjustment therefore seems justified. Residual
errors may result from the transformation of magnitudes to ![]() .
.
In the following, it will be assumed that the observed spectral energy distribution consists of light from the primary only; furthermore, for reasons detailed in Sect. 7.2, the primary will be presumed to be a late main sequence star. Since 2MASS J0516288+260738 is located close to the galactic plane, the effect of interstellar reddening is not negligible even for low-luminosity and close-by objects.
For the initial analysis of the observed data we use a grid
of model atmospheres and synthetic spectra that is based on
the models of Allard et al. (2001). We have extended the
model grid to effective temperatures of 10 000 K for gravities
from
![]() using spherical symmetry. The
mixing length was set to twice the pressure scale height, this
choice of the mixing length was calibrated on early M dwarfs
(Ludwig et al. 2002).
using spherical symmetry. The
mixing length was set to twice the pressure scale height, this
choice of the mixing length was calibrated on early M dwarfs
(Ludwig et al. 2002).
Synthetic spectra generated from the models were compared to the observed spectra
using an IDL program. This step was restricted to the infrared spectra.
First, the resolution of the synthetic spectra was
degraded to that of each observed spectrum by convolution with
a Gaussian of the appropriate width, and the spectra were normalized to unit
area for scaling. Next, for each observed spectrum the program calculated a
quality function q, similar to a ![]() value, for the comparison with all
synthetic spectra in the grid. The quality function is calculated by first
scaling the model spectrum to the observed fluxes and then by mapping
the synthetic spectrum (reduced to the resolution of the observed data) onto
the grid of observed wavelength points and then calculating
value, for the comparison with all
synthetic spectra in the grid. The quality function is calculated by first
scaling the model spectrum to the observed fluxes and then by mapping
the synthetic spectrum (reduced to the resolution of the observed data) onto
the grid of observed wavelength points and then calculating
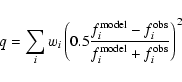
The best fitting model has an effective temperature
![]() K
and a reddening of
E(B-V)=0.9. The low resolution of the data and
the relative insensitivity of the spectral energy distribution to gravity
prevent us from determining a value of
K
and a reddening of
E(B-V)=0.9. The low resolution of the data and
the relative insensitivity of the spectral energy distribution to gravity
prevent us from determining a value of ![]() ,
it is clear, however, that
the object is a dwarf rather than a giant. The formal error in effective
temperature is about
,
it is clear, however, that
the object is a dwarf rather than a giant. The formal error in effective
temperature is about ![]() 200 K and about
200 K and about ![]() 0.2 for the extinction.
The low resolution data also prevent detailed metallicity determinations,
and so far only solar metallicities were considered. Overall, the
spectral analysis results suggest a spectral type of about K7 V
(
0.2 for the extinction.
The low resolution data also prevent detailed metallicity determinations,
and so far only solar metallicities were considered. Overall, the
spectral analysis results suggest a spectral type of about K7 V
(![]() 2 subclasses).
2 subclasses).
The resulting fit is shown in Fig. 3. We have applied the reddening to the synthetic spectrum (dotted line) in order to facilitate the comparison without modifying the data themselves. All available spectral and colour information is included in the figure. The fit is in general acceptable, unfortunately data are missing in spectral regions where they would be extremely useful to test the resulting model parameters.
A consistency check of our solution can be performed by comparing our
measured reddening with the model of the Galactic interstellar
extinction constructed by Arenou et al. (1992). First we
estimate the distance from the spectral type - absolute magnitude
calibration of Schmidt-Kaler (1982). From their Table 13 we get an absolute
magnitude of MV=8.1 for spectral type K7 V. With
E(B-V)=0.9 as
derived above, the dereddened V magnitude is 15.3 (adopting
R=3.1). Thus the resulting distance module is 7.2, corresponding to
a distance of 280 pc. The reddening predicted from the Arenou et al.
model and the position of
2MASS J0516288+260738 (l=178.8, b=-6.9) amounts to
![]() .
The scatter results mostly from the
patchiness of the interstellar medium in this region. Although this
value is somewhat smaller than our measured reddening both values
agree within the error limits. Note that the model of Galactic
extinction provides an upper limit of
.
The scatter results mostly from the
patchiness of the interstellar medium in this region. Although this
value is somewhat smaller than our measured reddening both values
agree within the error limits. Note that the model of Galactic
extinction provides an upper limit of
![]() for the
reddening at the position of 2MASS J0516288+260738. This
limit results from the fact that stars exceeding a certain distance
are above the absorbing dust layers of the Galaxy. This allows us to
rule out highly reddened early type stars (cf. also the independent
discussion of this aspect in Sect. 7.2 which leads to the
same result).
for the
reddening at the position of 2MASS J0516288+260738. This
limit results from the fact that stars exceeding a certain distance
are above the absorbing dust layers of the Galaxy. This allows us to
rule out highly reddened early type stars (cf. also the independent
discussion of this aspect in Sect. 7.2 which leads to the
same result).
This light curve, formed of 187 normal points (in intensity units), normalized to unity outside eclipse, was subjected to a numerical solution by the application of the MORO code (Drechsel et al. 1995). The code is based on the Wilson-Devinney (1971) logistical approach, but incorporates a modified Roche model to account for radiative interaction between the components and uses the SIMPLEX method as parameter optimization algorithm.
The solution mode was chosen such that no a priori restriction of the
system configuration was imposed (equivalent to the original
Wilson-Devinney mode 2). The total number
of light curve parameters for a single passband curve amounts to
17. Since the observed eclipse minimum depth is only moderate
(![]() 16% of maximum light), as no signature of the secondary
except its light blocking effect is evident, and because no colour information
follows from the white light curve, solutions tend to be
underdetermined, especially if the adjustable parameter set is too
large. Hence it was important to use any available secondary
information from spectroscopy or stellar atmospheres' theory to reduce
the number of free light curve parameters and keep some of them at
fixed values.
16% of maximum light), as no signature of the secondary
except its light blocking effect is evident, and because no colour information
follows from the white light curve, solutions tend to be
underdetermined, especially if the adjustable parameter set is too
large. Hence it was important to use any available secondary
information from spectroscopy or stellar atmospheres' theory to reduce
the number of free light curve parameters and keep some of them at
fixed values.
| Parameter | a | b | c | d | e | f | g | h |
| q (=M2/M1) | 0.085 | 0.094 | 0.110 | 0.122 | 0.156 | 0.181 | 0.182 | 0.184 |
| i | ||||||||
| T1/T2 | 1.67 | 1.72 | 1.74 | 1.73 | 1.77 | 1.63 | 1.83 | 1.88 |
| r1/r2 a | 1.11 | 0.89 | 0.85 | 0.87 | 0.85 | 0.67 | 0.73 | 0.64 |
| 5.138 | 5.350 | 5.510 | 5.520 | 5.598 | 6.123 | 6.001 | 6.220 | |
| 1.961 | 1.943 | 1.997 | 2.055 | 2.182 | 2.197 | 2.236 | 2.198 | |
| L1b | 0.998 | 0.998 | 0.999 | 0.998 | 0.999 | 0.993 | 0.999 | 0.999 |
| x1c | 0.60* | 0.60* | 0.50* | 0.50* | 0.60* | 0.60* | 0.488 | 0.60* |
| x2 c | 0.50* | 0.50* | 0.50* | 0.50* | 0.50* | 0.50* | 0.527 | 0.50* |
| l3d | 0%* | 0%* | 0%* | 0%* | 0%* | 0%* | 1.5% | 0%* |
|
|
0.00750 | 0.00750 | 0.00749 | 0.00749 | 0.00749 | 0.00755 | 0.00750 | 0.00749 |
| a Ratio of mean Roche radii. |
| b Relative luminosity L1/(L1 + L2); L2 is not independently adjusted, but recomputed from r2 and T2. |
| d Fraction of third light at maximum. |
| * Fixed. |
No information at all is available for a possible eccentricity of the orbit, since the position of the unobserved secondary eclipse cannot be determined, and radial velocity measurements do not exist so far. Therefore circular orbits (e = 0) and synchronously rotating components were assumed - as is mostly the case in close binary systems due to their very short synchronization time scales. According to the late spectral type, bolometric albedos A1 and A2 were fixed at their usually expected values of 0.5 for convective outer layers, and gravity darkening exponents g1 and g2 were set to 0.32 as predicted by Lucy's law (1967). Linear limb darkening coefficients are poorly known for very late spectral types. From an extrapolation of the grids of Wade & Rucinski (1985) and Díaz-Cordovés et al. (1995) at their cool ends one obtains approximate values of x1 = 0.5 - 0.6, which were used in the solutions. Values of x2 (and g2) are irrelevant due to the absence of any measurable secondary light.
The primary effective temperature was always fixed at T1=3000 K,
typical for spectral type M5 V, since the result of
![]() K from the spectral analysis has only become available
recently, following the February 2003 OMEGA-Cass observations.
This choice is however not critical,
because the light curve solution only allows to derive the temperature
ratio T1/T2, and from a single unfiltered curve no colour information
can be extracted. The remaining set of adjustable parameters therefore
comprised inclination i, mass ratio q=M2/M1, secondary temperature T2, surface potentials
K from the spectral analysis has only become available
recently, following the February 2003 OMEGA-Cass observations.
This choice is however not critical,
because the light curve solution only allows to derive the temperature
ratio T1/T2, and from a single unfiltered curve no colour information
can be extracted. The remaining set of adjustable parameters therefore
comprised inclination i, mass ratio q=M2/M1, secondary temperature T2, surface potentials ![]() and
and ![]() ,
primary luminosity L1, and third light l3. L2 was not independently adjusted, but
recomputed from T2 and the secondary surface area over the Planck law.
Trial runs showed that the percentage of third light l3 attributable to
a possible unresolved field star tended toward zero (except for solution g,
see Table 5), so that this parameter was subsequently fixed at l3 = 0
in the iterations of all other solutions.
,
primary luminosity L1, and third light l3. L2 was not independently adjusted, but
recomputed from T2 and the secondary surface area over the Planck law.
Trial runs showed that the percentage of third light l3 attributable to
a possible unresolved field star tended toward zero (except for solution g,
see Table 5), so that this parameter was subsequently fixed at l3 = 0
in the iterations of all other solutions.
Convergent solutions were achieved after numerous trial runs with a variety
of start parameter sets (start simplices) and different parameter
increments as starting points of the automatic iteration process, which
covered essentially the whole range of physically reasonable parameter
values. For reasons discussed earlier the numerical process could not be
expected to yield a single best and unique solution. Instead,
for a couple of comparably good solutions,
there was no obvious way to qualify one of these as definitely best representation,
as judged from the final standard deviations of normal points from the synthetic
curves.
To give an impression of the typical scatter of final parameters we
present a subsample of 8 different solutions with the relatively best
sigma standard deviations in Table 5. These are sorted in a
sequence of increasing q values. It is obvious that
one can identify two groups of solutions according to the value of the
mass ratio: solutions a-d cluster around
![]() ,
while cases e-h yielded
,
while cases e-h yielded
![]() .
.
A common feature of all solutions are consistent values of
inclination (
![]() ), temperature ratio (
), temperature ratio (
![]() ), ratio of radii (r1/r2 around 0.9), extremely low secondary luminosity
(
), ratio of radii (r1/r2 around 0.9), extremely low secondary luminosity
(
![]() ), and similar system configuration.
As shown for solution c in
Fig. 4, which can be
considered as representative for the group of solutions with
), and similar system configuration.
As shown for solution c in
Fig. 4, which can be
considered as representative for the group of solutions with
![]() ,
the secondary is of about the same size as the primary, and nearly fills
its Roche lobe in a close to semi-detached configuration. The photometric
determination of T2 and hence the temperature ratio must be considered very
uncertain, because of the
missing secondary eclipse and the extreme luminosity ratio.
,
the secondary is of about the same size as the primary, and nearly fills
its Roche lobe in a close to semi-detached configuration. The photometric
determination of T2 and hence the temperature ratio must be considered very
uncertain, because of the
missing secondary eclipse and the extreme luminosity ratio.
The overall representation of the observations by the theoretical light
curve is very good. Figure 5
(top) displays the normal points in comparison with
the synthetic curve (solid line). Especially the eclipse minimum is matched
in detail. The standard deviation amounts to only 7.5 mmag, which
corresponds to the typical scatter of measurements binned to normal points.
As shown in the bottom part of Fig. 5,
most observations lie in a ![]() band, and all within a
band, and all within a ![]() belt, with no apparent systematic
deviations.
Figure 6
gives a 3-dimensional impression of the aspects of the system at
different phase angles as viewed under an inclination of
belt, with no apparent systematic
deviations.
Figure 6
gives a 3-dimensional impression of the aspects of the system at
different phase angles as viewed under an inclination of
![]() ;
the
configuration corresponds to the parameters of solution c.
;
the
configuration corresponds to the parameters of solution c.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{aa3829f4.eps}
\end{figure}](/articles/aa/full/2003/41/aa3829/Timg66.gif) |
Figure 4: Meridional intersection of surface and inner critical Roche equipotentials corresponding to the nearly semi-detached system configuration of solution c (see Table 5); the substellar secondary component is close to contact with its Roche lobe. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa3829f5.eps}
\end{figure}](/articles/aa/full/2003/41/aa3829/Timg67.gif) |
Figure 5:
Top part shows the observed light curve in white light
(dots are normal points formed by binning individual observations to phase
intervals of width 0.005) together with the theoretical curve
(solid line) corresponding to solution c of Table 5; maximum light
(intensity) was normalized to unity, and phases were computed
according to the ephemeris of Sect. 3.2; bottom part shows
residuals of observations (in intensity units) with |
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{aa3829f6.eps}
\end{figure}](/articles/aa/full/2003/41/aa3829/Timg68.gif) |
Figure 6:
Aspects of the system at three different phases; viewing
angle is
|
In a naïve consideration, the early type giants could fit within the orbital separation, even if it is clear that most of the time they would reach well over half of the total distance. But although these earlier types could just about fit into the system, it can easily be shown that their deformation within the Roche potential would in all cases result in large ellipsoidal light variations, which are not observed in the actual light curve. In addition, the width of the observed eclipse minimum would cover a much broader phase range. For these estimates, the binary eclipse simulation program nightfall (R. Wichmann, Landessternware Heidelberg, Germany) which calculates synthetic light curves taking into account the distortion of the stars in Roche geometry was used.
Since these considerations equally apply to luminosity classes II and I, and even in a much stricter form there, the luminosity class for the more luminous object in the system must be V or higher.
The light curve solutions constrain the mass ratio, the radius ratio and the ratio of the effective temperatures almost regardless of the absolute value of T1. Using tabulated values for the masses, radii and effective temperatures of stellar and substellar objects, the possible components making up the system can be constrained by requiring that both of them have parameters reasonably close to those of isolated main sequence stars or substellar objects. The stellar parameters used in the following were taken from Cox (2000), those for substellar objects (for ages ranging from 1 M yrs to 10 G yrs) from Chabrier et al. (2000) and Baraffe et al. (2002).
The ratios of effective temperatures and masses of the binary
components for the light curve solutions c and g from
Table 5, which can be considered representative for the two
bulges of solutions clustering around q = 0.10 and 0.18,
are used to find the corresponding effective
temperatures and masses of the secondary as a function of primary mass.
For all main sequence stars, their effective temperatures and those
required by the two representative solutions for the secondary are plotted in
Fig. 8. The zero-age main sequence objects and the
youngest substellar objects (1 M yrs old) are marked by plus signs
and are connected by a thick solid line; higher age substellar
models are also represented by plus signs, which remain, however, isolated for
clarity. For both solutions a row of squares connected by a solid line
is shown. The squares correspond to the locations of the secondary in the
![]() diagram, which follow from the temperature and mass of a
main sequence primary using the temperature and mass ratios of the
respective photometric solutions c and g. For each square
plotted, the corresponding error estimates from the typical
dispersion within each of the two groups are indicated by small dots which
represent the end points of the associated error bars (not drawn as
full lines to preserve more clarity in this complex representation).
For the primary a variety of spectral
types between O5 V and M8 V were considered to cover the full zero-age main
sequence (plus signs).
When inspecting this figure and the following graph, note that the
plot scale is logarithmic so that
offsets between curves can be much larger in regions of the plot that
correspond to the upper main sequence than they might intuitively seem.
diagram, which follow from the temperature and mass of a
main sequence primary using the temperature and mass ratios of the
respective photometric solutions c and g. For each square
plotted, the corresponding error estimates from the typical
dispersion within each of the two groups are indicated by small dots which
represent the end points of the associated error bars (not drawn as
full lines to preserve more clarity in this complex representation).
For the primary a variety of spectral
types between O5 V and M8 V were considered to cover the full zero-age main
sequence (plus signs).
When inspecting this figure and the following graph, note that the
plot scale is logarithmic so that
offsets between curves can be much larger in regions of the plot that
correspond to the upper main sequence than they might intuitively seem.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms3829.f7.ps}
\end{figure}](/articles/aa/full/2003/41/aa3829/Timg71.gif) |
Figure 7: Orbital separation a as a function of the mass sum M1+M2 of the system at the 1.29 d period. Overplotted are radii for type III giants; explanation see text (Sect. 7.1). |
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{ms3829.f8.ps}
\end{figure}](/articles/aa/full/2003/41/aa3829/Timg72.gif) |
Figure 8: Effective temperature as a function of the stellar mass for zero-age main sequence stars and substellar objects (plus signs) and their secondaries according to Table 5 (squares); further explanations see text (Sect. 7.2). |
| Possible primary spectral types for solution | Group a-d | Group e-h |
| From mass-temperature relation (Fig. 8) | upper limit G5 | region G0-K0, or upper limit M2 |
| From mass-radius relation (Fig. 9) | upper limit G5 | upper limit M0 |
| Combined constraints | upper limit G5 | upper limit M2 |
| Consistency with spectroscopy (
|
fully consistent | marginally consistent at most |
|
Resulting secondary mass [
|
upper limit 0.11 | upper limit 0.076 |
| Resulting secondary mass [
|
|
|
The curve for the secondary corresponding to solution c only approaches and intersects the main sequence at its lower end and therefore excludes highly reddened hotter main sequence stars as a possible primary, since the corresponding secondaries cannot exist. The other line corresponding to solution g starts off close to the main sequence and comes back to it earlier than the other one. As stated above, the combination of two upper main sequence stars as a possible solution can be ruled out, because such extended stars could only reside within the given orbit if an appreciable distortion of the primary is allowed for, which would inevitably result in an easily observable ellipsoidal light variation. Apart from this special case for g on the upper main sequence, solutions (discretised in, on average, 5-subclass steps!) were elected possible whenever the error range for such a discrete secondary location intersected the stellar or substellar regime. Errors in parameter ratios are regularly smaller than the discretisation in spectral classes used, so the limits given can be regarded to be accurate to within roughly two subclasses.
On the lower main sequence, the earliest possible spectral types for the primary in the two cases are as listed in the first line of Table 6. In case g, K5 and M0 primaries must be excluded. When the mass-radius relation is taken into account in addition to the just invoked mass-temperature correlation, these upper limits can be even further constrained, as will be shown next.
The ratios of radius and mass for the binary components (also taken from Table 5) together with tabulated mass-radius relations from the same sources as above can be subjected to the same procedure. The designations in Fig. 9 are analogous to those in Fig. 8. The results are also compiled in Table 6. The primary can be constrained to be of spectral type G5 or later for solution c, or of spectral type M0 for solution g. The second line in Table 6 lists these limits without any additional age constraints that migth be present (see this discussion later).
Combining the constraints from both Figs. 8 and 9 yields an overall upper limit for each solution as listed in Table 6, line 3. Solution c allows for a primary no earlier than G5, while solution g restricts possible primaries to spectral types no earlier than M2. Spectroscopic results strongly favour the group a-d solution, since the overall constraint of G5 for the primary spectral class is entirely consistent with the conclusion in Sect. 5. For an upper limit of M2, on the other hand, it would be hard to claim consistency with the spectroscopy results. Table 6 nevertheless explores the mass range for the secondary in different scenarios (entries in lines 5 and 6).
An additional constraint not taken into account so far is the age of
the system, which for the more likely solutions a-d is restricted to
below 0.01 Gyr by the mass-radius relation. A young system is also
allowed for by the mass-temperature relation. However, this
corresponds to a lifetime of the system in which the K star will not
have had enough time to attain the zero-age main sequence yet, and
will hence not necessarily have the ZAMS parameters assumed to deduce
these constraints in the first place. This might well limit the
overall usefulness of this discussion, and is a point that will have
to be re-addressed once better data has become available for this
object.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{ms3829.f9.ps}
\end{figure}](/articles/aa/full/2003/41/aa3829/Timg76.gif) |
Figure 9: Mass-radius relation for zero-age main sequence stars and substellar objects (plus signs) and their secondaries according to Table 5 (squares); further explanations see text (Sect. 7.2). |
This interpretation should now be checked by trying to confirm the spectral classification via the detection of spectral lines in new high resolution, high signal-to-noise optical and/or infrared spectra. These lines could then also be used to obtain radial velocity measurements for the system which should eventually provide absolute masses.
Together with the extensive light curve available, the system has the potential to provide a new high-quality point for the mass-radius relation of the lower main sequence (or for pre-main sequence evolutionary tracks), and the first one obtained from eclipse measurements for a sub-stellar object.
Acknowledgements
The authors would like to thank K. Werner and H. Mauder for helpful discussions and friendly support, and P. A. Woudt for his assistance in obtaining a V magnitude for 2MASS J0516288+260738. We also would like to thank R. Gredel for allocating Director's discretionary time and U. Thiele for carrying out the OMEGA-Cass observation at Calar Alto observatory in service mode. We acknowledge the use of the nightfall program for light-curve synthesis of eclipsing binaries (http://www.lsw.uni-heidelberg.de/~rwichman/Nightfall.html), written by R. Wichmann. Part of this work was supported by the German Deutsche Forschungsgemeinschaft under project grants DR 281/13-1 and DR 281/13-2, as well as under travel grants DR 281/16-1, DR 281/18-1, and NA 365/6-1. The Wise Observatory contribution to this work is supported by the Israel Science Foundation. This research has made use of the USNOFS Image and Catalogue Archive operated by the United States Naval Observatory, Flagstaff Station (http://www.nofs.navy.mil/data/fchpix/).