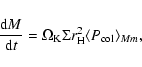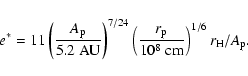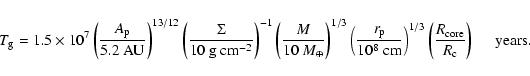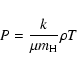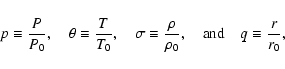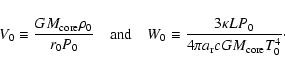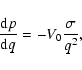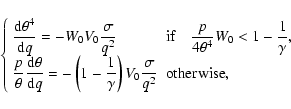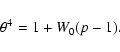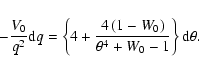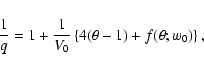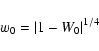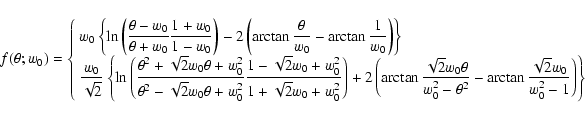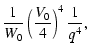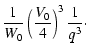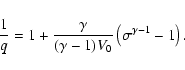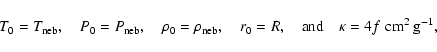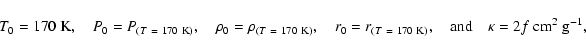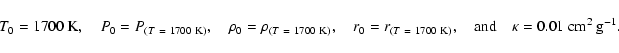A&A 410, 711-723 (2003)
DOI: 10.1051/0004-6361:20031248
Enhanced collisional growth of a protoplanet that has an atmosphere
S. Inaba1 - M. Ikoma2
1 - Department of Earth and Planetary Sciences,
Tokyo Institute of Technology,
2-12-1 Oookayama, Meguro-ku, Tokyo 152-8551, Japan
2 -
Interactive Research Center of Science, Tokyo Institute of Technology, 2-12-1 Oookayama,
Meguro-ku, Tokyo 152-8551, Japan
Received 14 February 2003 / Accepted 12 May 2003
Abstract
Once a protoplanet becomes larger than about lunar size,
it accumulates a significant atmosphere that surrounds the solid core.
When a planetesimal approaches the protoplanet, it interacts with
the atmosphere.
If enough energy of the planetesimal
is lost by gas drag of the atmosphere,
it is captured in the atmosphere
even if its original trajectory would not lead to a direct
collision with the solid core of the protoplanet.
This increases the collision rate,
resulting in faster growth of the protoplanet.
We have derived the analytical calculations for the
collision rate, and
calculated the structure of the atmosphere and the trajectories of
the planetesimals in the atmosphere.
As a result of their large gas drag,
small planetesimals are easily captured,
resulting in a large rate of collision with the protoplanet.
A collision rate of a protoplanet of Earth size
with a planetesimal of 100 m radius is, for example,
enhanced by a factor of 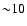 .
These effects play an essential role in
the study of formation of solid cores
of gas giant planets by the core accretion model.
.
These effects play an essential role in
the study of formation of solid cores
of gas giant planets by the core accretion model.
Key words: solar system: formation
Planets form in a circumstellar disk
composed of gas and dust.
A gas giant planet in particular has to be born in such a disk
to acquire a large amount of gas.
We are assuming the standard core accretion model in which
formation of gas giant planets
proceeds as follows. A number of
planetesimals of 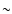 km radius form by
collisions and sticking of small dust particles
(Weidenschilling 1997a),
or gravitational instability of a dust disk (Goldreich & Ward 1973;
Goodamn & Pindor 2000).
Runaway growth of planetesimals occurs in the course of accumulation
of gravitationally interacting planetesimals, resulting
in a bimodal mass distribution of planetesimals,
where a small number of protoplanets
and a large number of small planetesimals coexist
(Wetherill & Stewart 1989).
Protoplanets larger than about the size of the moon
can attract gas gravitationally and can have
atmospheres.
The solid part of the protoplanet is often called the core.
The atmospheric mass increases with the mass of the core.
When the atmospheric mass is comparable to the mass of the core,
runaway gas accretion occurs, and the protoplanet
acquires a large amount of gas from a circumstellar disk to
become a gas giant planet (Mizuno 1980;
Bodenheimer & Pollack 1986).
km radius form by
collisions and sticking of small dust particles
(Weidenschilling 1997a),
or gravitational instability of a dust disk (Goldreich & Ward 1973;
Goodamn & Pindor 2000).
Runaway growth of planetesimals occurs in the course of accumulation
of gravitationally interacting planetesimals, resulting
in a bimodal mass distribution of planetesimals,
where a small number of protoplanets
and a large number of small planetesimals coexist
(Wetherill & Stewart 1989).
Protoplanets larger than about the size of the moon
can attract gas gravitationally and can have
atmospheres.
The solid part of the protoplanet is often called the core.
The atmospheric mass increases with the mass of the core.
When the atmospheric mass is comparable to the mass of the core,
runaway gas accretion occurs, and the protoplanet
acquires a large amount of gas from a circumstellar disk to
become a gas giant planet (Mizuno 1980;
Bodenheimer & Pollack 1986).
One of the challenging problems in the core accretion model
is the timescale-problem for the formation of
Jupiter and Saturn.
In a pioneering contribution, Pollack et al. (1996) simulated
the formation of gas giant planets
calculating the gas and planetesimal accretion rates
in a self-consistent manner and
constructed one plausible pathway by which
Jupiter and Saturn
could have formed in their current positions before
the disappearance of the disk gas.
They adopted a simple model
of planetesimal accretion, where a single core grows
by accumulation of planetesimals whose velocities are constant,
and the effects of fragmentation of planetesimals was not considered.
Weidenschilling (1997b)
reexamined the accretion process of the solid core
under the same initial condition except that
velocities of planetesimals are not constant.
The core could not grow to sufficiently large mass
to acquire a large amount of gas within the
probable lifetime of the disk gas.
In the early stage of the planetesimal accumulation,
the velocities of the planetesimals are determined by the
gravitational interactions with other planetesimals
and are so small that fragmentation does not occur
when they collide with each other.
On the other hand,
in the late stage of the planetesimal accumulation,
protoplanets
enhance the velocities of the planetesimals (Ida & Makino 1993).
Collisions of the planetesimals in the high velocities
lead to their fragmentation.
The created fragments are vulnerable
to radial migration to the central star by gas drag
of the disk gas (Wetherill & Stewart 1993).
A portion of the mass of solid is removed as fragments.
As a result, the growth rates of the cores decrease.
Inaba & Wetherill (2001) calculated planetesimal accumulation
with fragmentation and realized that even the largest core
could not reach the so-called critical core mass,
beyond which the runaway gas accretion occurs,
and thus failed to become a gas giant planet .
Inaba & Wetherill (2001)
assumed that the planetesimals were captured by
the protoplanet only when they collided with the core of
the protoplanet.
The rate of these collisions
has been examined in detail by many researchers
(e.g., Ida & Nakazawa 1989; Greenzweig & Lissauer 1992).
However, this collision rate is not useful
if the protoplanet has an atmosphere.
Because the atmosphere surrounds the core,
planetesimals interact with the atmosphere first.
Planetesimal
energies are reduced by gas drag of the atmosphere, and
if enough energy is lost, they can be captured in the
atmosphere.
The gas drag depends
not only on the gas density of the atmosphere but also the size
of the planetesimal.
As mentioned above,
many small fragments are produced by collisions of planetesimals.
The small fragments have large gas drags
and are easily captured in the atmosphere.
As a result, fragments that would not be captured by base cores
can be captured in the atmosphere.
Because the radius of the atmosphere can become much larger than
that of the core, a large increase in the collision rate
is expected. In this paper we will calculate this collision rate.
Previously, Podolak et al. (1988) studied the interaction
of planetesimals with atmospheres, including detailed
physics of gas drag and ablation of the planetesimals.
They calculated the trajectories of the planetesimals
and obtained the range of the impact parameters with which
the planetesimals are captured in the atmosphere.
The range of the impact parameter is strongly
dependent on the radius of the planetesimal.
Their choice of parameters is so limited that it is difficult
to use their result in the simulation of planetesimal
accumulation. In this study we will derive an analytical
expression of the collision rate, which is useful for a wide range
of the parameters.
The effects of the atmospheric gas drag on the accumulation of planetesimals
are also important to explain the present compositions of
the envelopes of Jupiter and Saturn.
They are known to be
enriched in heavy elements
(at least by a factor of 5 for Saturn) compared with the solar value
(Wuchterl et al. 2000).
Some captured planetesimals would be ablated and produce small
particles that are vaporized in an inner part of the atmosphere
(i.e., the proto-envelope).
This would increase the amount of
heavy elements in Jupiter's and Saturn's envelopes.
In the present paper,
we will investigate what size of planetesimals
are captured in what location of the atmosphere of the protoplanet.
If the planetesimals are captured far away from the surface of the core,
it helps the growth of the protoplanet and enhances the total mass
of heavy elements in the atmosphere.
In Sect. 2, we first describe the calculation methods of
the atmospheric structure and motion of planetesimals in the atmosphere.
Next, we find that the effective radius of a planet capturing a planetesimal
is much larger than the radius of the solid core.
After that, we derive an approximate expression of the effective radius,
which gives us insight into its dependence on
several parameters concerning the structure of the atmosphere
as well as the dynamics of planetesimals.
In Sect. 3,
we obtain the enhanced collision rate of
a protoplanet that has an atmosphere.
The gas density of the atmosphere
is much larger close to the center
of the protoplanet (see Fig. 1).
A planetesimal is more easily captured
in the close region because of the large gas drag.
If the distance between the planetesimal and the protoplanet
is smaller than a critical distance, the planetesimal is captured
in the atmosphere.
Otherwise, the planetesimal passes through the atmosphere
with a loss of energy.
In this subsection, we will define the critical distance.
![\begin{figure}
\par\resizebox{11cm}{!}{\includegraphics[clip]{MS3608f1.eps}}\end{figure}](/articles/aa/full/2003/41/aa3608/Timg17.gif) |
Figure 1:
Gas density of the atmosphere is plotted as a function of distance
from the center of the planet. The solid and dashed lines are
the numerical and analytical solutions, respectively.
The detail of the former is described in the Sect. 2.2 and
that of the latter in Appendix. a) The dependence on the core mass,
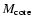 ,
and b) the dependences on the luminosity, L and
the grain depletion factor, f, are shown. ,
and b) the dependences on the luminosity, L and
the grain depletion factor, f, are shown.
|
| Open with DEXTER |
Before the planetesimal enters the atmosphere, the energy
of the planetesimal is constant and
determined by
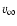 where
where
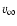 is
the relative velocity between the planetesimal
and the protoplanet when their distance is infinite.
We assume that the mass of the planetesimal,
is
the relative velocity between the planetesimal
and the protoplanet when their distance is infinite.
We assume that the mass of the planetesimal,
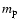 ,
is much smaller than that of the protoplanet,
,
is much smaller than that of the protoplanet,
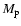 .
Then the impact energy is given by
.
Then the impact energy is given by
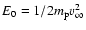 .
Once the planetesimal gets into the atmosphere, the gas drag
starts removing the energy,
.
Once the planetesimal gets into the atmosphere, the gas drag
starts removing the energy,
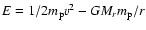 ,
where v is the relative velocity,
r is the relative distance between the planetesimal and
the protoplanet, and
Mr is the total mass contained within r.
In the two body system composed of the planetesimal and the protoplanet,
the planetesimal is captured by
the protoplanet if E<0.
,
where v is the relative velocity,
r is the relative distance between the planetesimal and
the protoplanet, and
Mr is the total mass contained within r.
In the two body system composed of the planetesimal and the protoplanet,
the planetesimal is captured by
the protoplanet if E<0.
In order to include the effect of a central star
approximately in this two body system,
we introduce the Hill radius of the protoplanet,
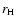 ,
within which the gravity of the protoplanet is larger than that of
the central star, defined by
(Ida & Nakazawa 1989)
,
within which the gravity of the protoplanet is larger than that of
the central star, defined by
(Ida & Nakazawa 1989)
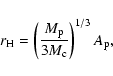 |
(1) |
where
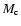 is the mass of the central star and
is the mass of the central star and
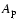 is the semimajor axis of the protoplanet.
In this system,
the planetesimal is captured by the protoplanet if
the apocentre of the planetesimal that orbits
the protoplanet is within the Hill radius.
Otherwise, the planetesimal is not captured by the protoplanet but
orbits the central star.
The largest energy of the captured planetesimal is given by
is the semimajor axis of the protoplanet.
In this system,
the planetesimal is captured by the protoplanet if
the apocentre of the planetesimal that orbits
the protoplanet is within the Hill radius.
Otherwise, the planetesimal is not captured by the protoplanet but
orbits the central star.
The largest energy of the captured planetesimal is given by
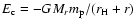 .
In general, r is much smaller than
.
In general, r is much smaller than
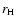 ,
,
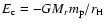 .
If E becomes
smaller than
.
If E becomes
smaller than
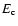 by the gas drag,
the planetesimal is captured by the protoplanet.
The critical distance,
by the gas drag,
the planetesimal is captured by the protoplanet.
The critical distance,
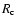 ,
is defined by the value of r when
,
is defined by the value of r when
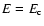 ,
that is,
,
that is,
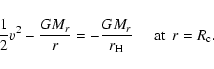 |
(2) |
Because the planetesimal is captured by the protoplanet
if r is smaller than
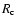 ,
,
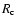 reduces to the radius
of the core,
reduces to the radius
of the core,
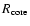 ,
if the protoplanet does not have the atmosphere.
As shown later,
,
if the protoplanet does not have the atmosphere.
As shown later,
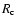 is much larger than
is much larger than
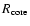 .
It is adequate to call
.
It is adequate to call
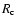 the enhanced radius of the protoplanet.
In Sect. 3,
we will show that the discussion for the two body system
approximately hold true for
the three body system that includes the central star.
the enhanced radius of the protoplanet.
In Sect. 3,
we will show that the discussion for the two body system
approximately hold true for
the three body system that includes the central star.
As mentioned above, the density of the atmospheric gas is
one of the key factors for the enhanced radius,
because the gas drag is dependent on it.
Thus, we should know the density profile of the atmosphere
as accurately as reasonable.
In this study, we calculate the structure of the atmosphere.
We consider a spherically-symmetric protoplanet
composed of a rigid core and a chemically-uniform atmosphere.
The mass fractions of hydrogen, helium, and the other heavy elements are
0.740, 0.243, and 0.017, respectively,
that are the same to those used by Pollack et al. (1996).
The atmosphere is assumed to be in purely hydrostatic equilibrium.
The outer boundary of the atmosphere
(i.e., the radius of the protoplanet, R)
is assumed to be the smaller of
the Hill radius, 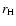 ,
defined by Eq. (1) and
the Bondi radius,
,
defined by Eq. (1) and
the Bondi radius, 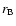 ,
defined by
,
defined by
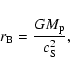 |
(3) |
where 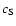 is the sound velocity of the disk gas.
The atmosphere is assumed to connect smoothly with the disk
at radius R.
These assumptions are basically the same as those of Mizuno (1980).
is the sound velocity of the disk gas.
The atmosphere is assumed to connect smoothly with the disk
at radius R.
These assumptions are basically the same as those of Mizuno (1980).
The basic equations are the usual set of equations
for study of stellar structure
(e.g., Kippenhahn & Weigert 1990):
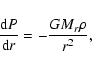 |
(4) |
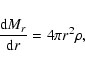 |
(5) |
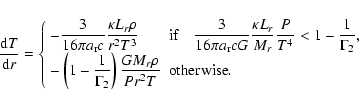 |
(6) |
Here P is the pressure,
r is the distance from the center of the core,
Mr is the mass inside a sphere of radius r,
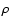 is the density,
T is the temperature,
is the density,
T is the temperature,
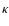 is the opacity,
is the opacity,
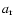 is the radiation density constant,
c is the light velocity,
is the radiation density constant,
c is the light velocity,
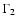 is the second adiabatic exponent,
and Lr is the energy per unit time passing
through a sphere of radius r.
In this study, we assume
is the second adiabatic exponent,
and Lr is the energy per unit time passing
through a sphere of radius r.
In this study, we assume
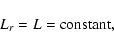 |
(7) |
where L is called the luminosity.
This assumption might be oversimplification,
because it is likely that energy sources
are distributed by planetesimals throughout the atmosphere.
As for the situation under consideration, the energy deposition can occur
at various positions, depending on planetesimal size.
However, the dependence of the enhanced radius on the luminosity is small,
as will be found later.
The opacity is given by
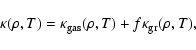 |
(8) |
where
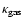 is the gas opacity given by
Alexander & Ferguson (1994),
is the gas opacity given by
Alexander & Ferguson (1994),
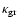 is the grain opacity
with an interstellar size distribution given by Pollack et al. (1985),
and f is the so-called grain depletion factor introduced by
Mizuno (1980).
We treat L and f as parameters.
The equation of state used here is one including
non-ideal effects given by Saumon et al. (1995).
is the grain opacity
with an interstellar size distribution given by Pollack et al. (1985),
and f is the so-called grain depletion factor introduced by
Mizuno (1980).
We treat L and f as parameters.
The equation of state used here is one including
non-ideal effects given by Saumon et al. (1995).
The inner boundary condition is
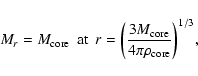 |
(9) |
where
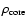 is the mean density of the core.
The outer boundary conditions are
is the mean density of the core.
The outer boundary conditions are
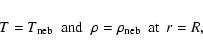 |
(10) |
where
 and
and
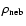 are the temperature and the density
of the disk gas, respectively.
The values of
are the temperature and the density
of the disk gas, respectively.
The values of
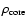 ,
,
 ,
and
,
and
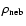 adopted in this study are
adopted in this study are
 ,
,
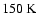 ,
and
,
and
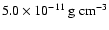 ,
respectively,
that are the same used by Pollack et al. (1996).
,
respectively,
that are the same used by Pollack et al. (1996).
In Fig. 1,
we show examples of the density profiles for some different
values of
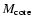 ,
L, and f.
In this figure,
we also compare the results of our numerical calculations
with the analytical solutions derived in Appendix.
The density increases with decreasing distance from the planet's center:
its dependence being expressed as
,
L, and f.
In this figure,
we also compare the results of our numerical calculations
with the analytical solutions derived in Appendix.
The density increases with decreasing distance from the planet's center:
its dependence being expressed as
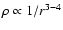 .
The density at a given radius increases rapidly
with the mass of the core (see Fig. 1a), because
the gravity becomes strong.
On the other hand,
the larger the luminosity Land/or the grain depletion factor f (i.e., the opacity) becomes,
the smaller the density becomes
especially in deep regions of the atmosphere (see Fig. 1b).
All of this behavior can be understood by the help of
the analytical solutions obtained in Appendix.
.
The density at a given radius increases rapidly
with the mass of the core (see Fig. 1a), because
the gravity becomes strong.
On the other hand,
the larger the luminosity Land/or the grain depletion factor f (i.e., the opacity) becomes,
the smaller the density becomes
especially in deep regions of the atmosphere (see Fig. 1b).
All of this behavior can be understood by the help of
the analytical solutions obtained in Appendix.
In the numerical simulation, we consider the gravity of
the core and the atmosphere,
the gas drag of the atmosphere, and ablation.
We assume that the planetesimal has no atmosphere.
The equations that describe the time evolution of
the position and mass of the planetesimal
are given by the following two equations
(Borovicka & Spurný 1996):
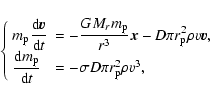 |
(11) |
where 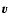 and
and 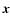 are the relative velocity
and position vectors, respectively,
Mr is the total mass of the core
and the atmosphere within the orbit of the planetesimal,
D is the gas drag coefficient, and
are the relative velocity
and position vectors, respectively,
Mr is the total mass of the core
and the atmosphere within the orbit of the planetesimal,
D is the gas drag coefficient, and
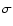 is the ablation coefficient.
We adopt the gas drag coefficient given by Podolak et al. (1988).
Their gas coefficient is similar to that obtained
by Adachi et al. (1976).
We calculate Eq. (11) using a 4th order Runge-Kutta
scheme.
The gas density of the atmosphere is obtained
numerically as described in the Sect. 2.2.
is the ablation coefficient.
We adopt the gas drag coefficient given by Podolak et al. (1988).
Their gas coefficient is similar to that obtained
by Adachi et al. (1976).
We calculate Eq. (11) using a 4th order Runge-Kutta
scheme.
The gas density of the atmosphere is obtained
numerically as described in the Sect. 2.2.
We study the two cases with and without ablation.
When we consider the effect of ablation, we use
the ablation coefficient,
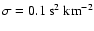 even though the
theoretical value of
even though the
theoretical value of
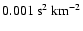 (Field & Ferrara 1995) is much smaller
(Borovicka & Spurný 1996).
In the next subsection, we will show that the effect of ablation is small
to obtain the enhanced radius of the protoplanet.
(Field & Ferrara 1995) is much smaller
(Borovicka & Spurný 1996).
In the next subsection, we will show that the effect of ablation is small
to obtain the enhanced radius of the protoplanet.
The energy and mass of the planetesimal are constant before entry into
the atmosphere.
The outer boundary of the atmosphere
is determined by
Eq. (1) or (3).
Because we have the analytical solution to the motion of the planetesimal
before the planetesimal gets into the atmosphere,
we carry out the simulation after
the distance between the planetesimal and the protoplanet
is equal to the radius of the atmosphere, R.
The parameters used in the simulation
are shown in Table 1.
Table 1:
Parameters used in the simulations.
![\begin{figure}
\par\resizebox{11cm}{!}{\includegraphics[clip]{MS3608f2.eps}}\end{figure}](/articles/aa/full/2003/41/aa3608/Timg74.gif) |
Figure 2:
a) The enhanced radii of the protoplanet
with
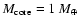 , ,
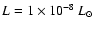 ,
and f=0.01 when
the velocities of planetesimals are ,
and f=0.01 when
the velocities of planetesimals are
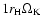 and b) the dynamical pressure the planetesimals take.
The cases without and with ablation are shown
by the solid lines and the filled circles.
The strength of the planetesimal given by Benz & Asphaug (1999)
is shown by the dashed curve as well.
Planetesimals with the radii larger than and b) the dynamical pressure the planetesimals take.
The cases without and with ablation are shown
by the solid lines and the filled circles.
The strength of the planetesimal given by Benz & Asphaug (1999)
is shown by the dashed curve as well.
Planetesimals with the radii larger than
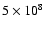 cm
cannot be captured in the atmosphere. cm
cannot be captured in the atmosphere.
|
| Open with DEXTER |
In Fig. 2a, we show the enhanced radii
normalized by the radius of the core
as a function of the radius
of the planetesimal
for the case of
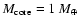 ,
,
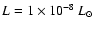 ,
f=0.01,
and
,
f=0.01,
and
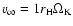 ,
where
,
where
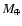 is Earth mass, and
is Earth mass, and
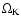 is Keplerian angular velocity
and given by
is Keplerian angular velocity
and given by
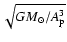 .
With an increase in the radius of the planetesimal,
the enhanced radius decreases.
The large planetesimals have to get into
a deep region of the atmosphere to be captured.
The planetesimal with the radius
larger than
.
With an increase in the radius of the planetesimal,
the enhanced radius decreases.
The large planetesimals have to get into
a deep region of the atmosphere to be captured.
The planetesimal with the radius
larger than
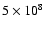 cm cannot be
captured in the atmosphere even if it takes the largest
gas drag produced in the deepest region of the atmosphere.
A planetesimal of this size can only be
captured by the protoplanet by colliding with the core.
The enhanced radii for the small planetesimals are larger than the
radius of the core.
A planetesimal with radius of
cm cannot be
captured in the atmosphere even if it takes the largest
gas drag produced in the deepest region of the atmosphere.
A planetesimal of this size can only be
captured by the protoplanet by colliding with the core.
The enhanced radii for the small planetesimals are larger than the
radius of the core.
A planetesimal with radius of
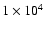 cm is captured
at
cm is captured
at
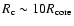 .
This increases the collisional cross section between
the protoplanet and the planetesimal and, as a result,
the growth rate of the protoplanet increases.
The mass loss of planetesimals by ablation is small.
We have nearly the same results
for the cases with and without ablation.
.
This increases the collisional cross section between
the protoplanet and the planetesimal and, as a result,
the growth rate of the protoplanet increases.
The mass loss of planetesimals by ablation is small.
We have nearly the same results
for the cases with and without ablation.
Planetesimals might lose mass by fragmentation.
If dynamical pressure (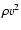 )
exceeds the strength
of the planetesimal, fragmentation of the planetesimal occurs.
The largest dynamical pressure that the planetesimal experiences
is shown in Fig. 2b. An increase in the dynamical
pressure is caused
by a sharp increase in the gas density
of a deep region of the atmosphere.
It is still smaller than the strength of the planetesimal
that was obtained by Benz & Asphaug (1999) with use of a
smooth particle hydrodynamics method.
When the planetesimals are captured,
they are not fragmented by the dynamical pressure.
)
exceeds the strength
of the planetesimal, fragmentation of the planetesimal occurs.
The largest dynamical pressure that the planetesimal experiences
is shown in Fig. 2b. An increase in the dynamical
pressure is caused
by a sharp increase in the gas density
of a deep region of the atmosphere.
It is still smaller than the strength of the planetesimal
that was obtained by Benz & Asphaug (1999) with use of a
smooth particle hydrodynamics method.
When the planetesimals are captured,
they are not fragmented by the dynamical pressure.
![\begin{figure}
\par\resizebox{11cm}{!}{\includegraphics[clip]{MS3608f3.eps}}\end{figure}](/articles/aa/full/2003/41/aa3608/Timg85.gif) |
Figure 3:
The enhanced radii of protoplanets with various parameters.
a) The enhanced radii of the protoplanets for the case with
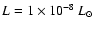 , ,
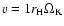 ,
and ,
and
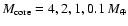 .
b) Those for the cases
with .
b) Those for the cases
with
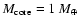 , ,
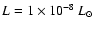 ,
and ,
and
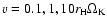 ,
c) those
for the cases with ,
c) those
for the cases with
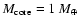 , ,
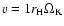 ,
and ,
and
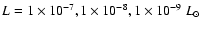 .
In every cases, the grain depletion factor is f=0.01.
Comparison between the enhanced radii obtained from the numerical
simulation (solid lines) and the analytical formula (dashed lines)
is shown as well. .
In every cases, the grain depletion factor is f=0.01.
Comparison between the enhanced radii obtained from the numerical
simulation (solid lines) and the analytical formula (dashed lines)
is shown as well.
|
| Open with DEXTER |
We show the enhanced radii of the protoplanets with the different
parameters (the mass of the core,
the luminosity, the initial velocity)
in Fig. 3 by the solid lines.
The atmosphere of the protoplanet with a massive core is dense
because of the large gravity of the core.
The large gas drag due to the dense atmosphere increases
the enhanced radius (Fig. 3a).
Planetesimals with the large initial velocities have
more energy to be captured.
By getting into a deep region of the atmosphere, they take
large gas drag and are captured (Fig. 3b).
The dependence of the initial velocity on the enhanced radius
is small specially for
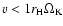 because the velocity is
determined by
because the velocity is
determined by
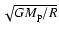 just before
the planetesimal enters the atmosphere.
With a decrease in the luminosity of the atmosphere,
the gas density of the atmosphere increases as shown in the Sect. 2.2.
The gas drag becomes more effective and
the enhanced radii increase (Fig. 3c).
just before
the planetesimal enters the atmosphere.
With a decrease in the luminosity of the atmosphere,
the gas density of the atmosphere increases as shown in the Sect. 2.2.
The gas drag becomes more effective and
the enhanced radii increase (Fig. 3c).
In this subsection, we derive an approximate solution for
the enhanced radius,
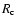 .
Because the effect of the ablation is shown to be small in
the last subsection, we consider only the gas drag.
The gas drag of the atmosphere decrease the relative velocity
from v to
.
Because the effect of the ablation is shown to be small in
the last subsection, we consider only the gas drag.
The gas drag of the atmosphere decrease the relative velocity
from v to
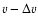 ,
which results in the decrease in the energy as
,
which results in the decrease in the energy as
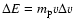 .
The decrease in the velocity is
given approximately by
.
The decrease in the velocity is
given approximately by
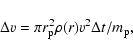 |
(12) |
where
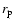 is the radius of the planetesimal,
is the radius of the planetesimal,
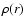 is the gas density of the atmosphere at r,
and
is the gas density of the atmosphere at r,
and 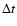 is the period while
the planetesimal passes the atmosphere.
We assume that the velocity of
the planetesimal decreases only at
is the period while
the planetesimal passes the atmosphere.
We assume that the velocity of
the planetesimal decreases only at
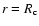 .
This assumption is reasonable because the gas drag is effective
in a deep region
by a sharp increase in
the gas density of the atmosphere.
Then the velocity is given by the sum of the relative velocity
at infinity and the escape velocity:
.
This assumption is reasonable because the gas drag is effective
in a deep region
by a sharp increase in
the gas density of the atmosphere.
Then the velocity is given by the sum of the relative velocity
at infinity and the escape velocity:
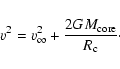 |
(13) |
Because the mass of the atmosphere is much smaller than
that of the core, we replace the total mass
of the core and the atmosphere
with the mass of the core.
The gas density is given approximately by
that at
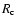 as
as
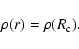 |
(14) |
Because the planetesimal orbits the protoplanet at
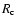 while the gas drag is effective, we assume that
the period,
while the gas drag is effective, we assume that
the period, 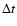 ,
is given by
,
is given by
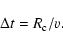 |
(15) |
It will be shown that
the approximate solutions can reproduce
the numerical results well.
With the use of the above equations, we have
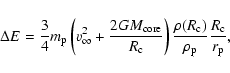 |
(16) |
where
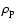 is
the material density of the planetesimal.
is
the material density of the planetesimal.
For the planetesimal to be captured by the protoplanet,
the energy of the planetesimal have to be smaller than
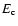 (see Sect. 2.1).
If
(see Sect. 2.1).
If 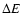 is equal to
is equal to
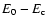 ,
the planetesimal
is captured by the protoplanet.
Using Eq. (16),
we have the radius of the captured planetesimal
as a function of the gas density of the atmosphere and
,
the planetesimal
is captured by the protoplanet.
Using Eq. (16),
we have the radius of the captured planetesimal
as a function of the gas density of the atmosphere and
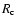 :
:
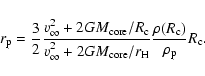 |
(17) |
If
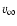 is much smaller than the escape velocity
of the core,
is much smaller than the escape velocity
of the core,
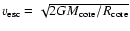 ,
,
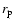 is independent of
is independent of
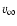 and given by
and given by
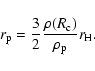 |
(18) |
As seen in Sect. 2.2, the gas density increases with proximity
to the center of the protoplanet.
Equation (18) shows that large planetesimals
can be captured in a deep region of the atmosphere, while
small ones in an outer region.
We show the comparison between the numerical results (solid lines)
and the approximate solution given by Eq. (17)
with the approximate solution of the atmospheric structure
given in the Appendix (dashed lines)
in Fig. 3 as well.
The enhanced radii for the planetesimal
with radius larger than
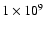 cm are different from
each other (a factor of less than two).
This is caused by
the difference of the gas density obtained analytically
and numerically. However, for the wide range of the size of the planetesimal,
both numerical and analytical results are consistent with each other.
cm are different from
each other (a factor of less than two).
This is caused by
the difference of the gas density obtained analytically
and numerically. However, for the wide range of the size of the planetesimal,
both numerical and analytical results are consistent with each other.
Pollack et al. (1996) simulated formation of
Jovian planets, including the effects of the enhanced radius.
In their simulation, the core of the protoplanet
grew by accumulation
of a specific size of planetesimals (100 km radius).
In Fig. 4, we show
the enhanced radius given by Pollack et al. (1996)
as a function of the core mass (dashed curve).
With an increase in the core mass, the enhanced radius increases as well.
The enhanced radius
becomes larger than the radius of the core
after the core mass increases to
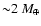 .
That is, the planetesimal of 100 km radius
was captured in the atmosphere
of the protoplanet by the gas drag.
For the protoplanet with the core mass of
.
That is, the planetesimal of 100 km radius
was captured in the atmosphere
of the protoplanet by the gas drag.
For the protoplanet with the core mass of
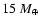 ,
the enhanced radius became about 10 times larger than
the radius of the core.
,
the enhanced radius became about 10 times larger than
the radius of the core.
It is valuable
to compare their result with that obtained in this study.
By the use of the derived analytical solution (Eq. (17)),
we have the enhanced radius of a protoplanet, given
the core mass, the luminosity, and the radius of a planetesimal.
For the comparison, we adopt the same core mass and luminosity
to those of Pollack et al. (1996).
The enhanced radius given by this study is shown by
the solid curve in Fig. 4.
The difference of the enhanced radii for the core mass larger
than
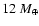 comes from the fact that
the contribution of the mass of the atmosphere to the total mass
becomes large. In Pollack et al. (1996),
for example, the total mass of the protoplanet is
comes from the fact that
the contribution of the mass of the atmosphere to the total mass
becomes large. In Pollack et al. (1996),
for example, the total mass of the protoplanet is
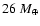 when the core mass is
when the core mass is
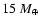 .
On the other hand, we assume the protoplanet has a negligible
atmosphere.
However,
we obtain the similar enhanced radius to that
of Pollack et al. (1996) for the wide range of the core mass.
.
On the other hand, we assume the protoplanet has a negligible
atmosphere.
However,
we obtain the similar enhanced radius to that
of Pollack et al. (1996) for the wide range of the core mass.
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics*[clip]{MS3608f5.eps}}\end{figure}](/articles/aa/full/2003/41/aa3608/Timg110.gif) |
Figure 4:
The enhanced radii of the protoplanet
normalized by the core radius
given by case J1 of Pollack et al. (1996) (dashed curve)
and this study (solid curve).
The radius of the planetesimal is 100 km.
|
| Open with DEXTER |
In this section, we will show the relationship of
the enhanced radius to the collision rate.
A collision rate of a protoplanet without an atmosphere (a core)
and a planetesimal under the gravity of the sun was studied
(Ida & Nakazawa 1989; Greenzweig & Lissauer 1992).
If the distance between the protoplanet and the planetesimal
is smaller than the radius of the core of the protoplanet,
they will collide. Using the analytical and numerical
methods, the collision rate as a function
of the relative velocity and the radius of the core of
the protoplanet was obtained.
Inaba et al. (2001) compiled their data and used the collision
rate for the simulation of planetesimal accumulation.
For simplicity, we consider the case that
the eccentricities and inclinations of
a protoplanet and a planetesimal are zero, i.e., circular and non-inclined
orbits. The semimajor axis is the only parameter.
The initial relative position is determined by the difference
between the two semimajor axes,
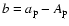 ,
where
,
where
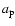 and
and
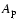 are the semimajor axes of the planetesimal
and the protoplanet, respectively.
Because the orbit with
are the semimajor axes of the planetesimal
and the protoplanet, respectively.
Because the orbit with
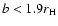 corresponds to the horseshoe
orbit, the planetesimal cannot approach the protoplanet
(Ida & Nakazawa 1989).
A planetesimal with
corresponds to the horseshoe
orbit, the planetesimal cannot approach the protoplanet
(Ida & Nakazawa 1989).
A planetesimal with
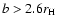 ,
is not influenced by the gravity of the protoplanet.
The planetesimal with
,
is not influenced by the gravity of the protoplanet.
The planetesimal with
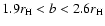 can get to the close place to the center of the
protoplanet.
Ida & Nakazawa (1989) summed the orbits, of which
the closest distance is smaller than the radius of the core,
and obtained the collision rate of the core and the planetesimal.
can get to the close place to the center of the
protoplanet.
Ida & Nakazawa (1989) summed the orbits, of which
the closest distance is smaller than the radius of the core,
and obtained the collision rate of the core and the planetesimal.
![\begin{figure}
\par\resizebox{11cm}{!}{\includegraphics[clip]{MS3608f4.eps}}\end{figure}](/articles/aa/full/2003/41/aa3608/Timg116.gif) |
Figure 5:
The closest distances of the planetesimals with radius of 100 m
from the protoplanet with
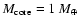 , ,
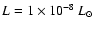 ,
and f=0.01for the
cases without the atmosphere (the dashed line)
and with the atmosphere (the solid line).
The enhanced radius, ,
and f=0.01for the
cases without the atmosphere (the dashed line)
and with the atmosphere (the solid line).
The enhanced radius,
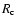 ,
obtained from Fig. 2
and the radius of the core, ,
obtained from Fig. 2
and the radius of the core,
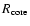 ,
are shown by the horizontal dotted lines. ,
are shown by the horizontal dotted lines.
|
| Open with DEXTER |
If the protoplanet has an atmosphere, the situation is different.
Even if the closest distance is larger than the radius of the core,
it can be smaller than the enhanced radius.
Then we expect the planetesimal is captured in the atmosphere
even if it does not collide with the core.
We carry out two simulations of protoplanet-planetesimal interaction,
one for a protoplanet with an atmosphere and the other for
a no-atmosphere condition.
The latter case is similar to the previous studies
(Ida & Nakazawa 1989).
Gravity of the sun was included in both cases.
The mass of the core of the protoplanet
is
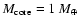 and the radius of the planetesimal is 100 m.
When we consider the atmosphere of the protoplanet,
the luminosity of the atmosphere is
and the radius of the planetesimal is 100 m.
When we consider the atmosphere of the protoplanet,
the luminosity of the atmosphere is
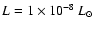 and the grain depletion factor is f=0.01.
In Fig. 5, the closest distances between the protoplanet
and the planetesimal are shown.
The solid horizontal line corresponds to the initial distance,
and the grain depletion factor is f=0.01.
In Fig. 5, the closest distances between the protoplanet
and the planetesimal are shown.
The solid horizontal line corresponds to the initial distance,
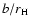 ,
of the planetesimal from the protoplanet that is at the origin.
The planetesimal with
the small (<1.9) and large (>2.6) initial
distances are not considered because they
cannot interact with the atmosphere.
The dashed line corresponds to
the closest distances between the planetesimal and the protoplanet
that does not have the atmosphere, while the solid line gives
the closest distances of the planetesimal from the protoplanet that has
the atmosphere.
If the closest distance is equal to the radius of the core that is
given by the dotted line with
,
of the planetesimal from the protoplanet that is at the origin.
The planetesimal with
the small (<1.9) and large (>2.6) initial
distances are not considered because they
cannot interact with the atmosphere.
The dashed line corresponds to
the closest distances between the planetesimal and the protoplanet
that does not have the atmosphere, while the solid line gives
the closest distances of the planetesimal from the protoplanet that has
the atmosphere.
If the closest distance is equal to the radius of the core that is
given by the dotted line with
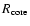 ,
the planetesimal
collides with the core.
Because of the gas drag of the atmosphere,
the planetesimal lose the energy.
The closest distances of some planetesimals
from the center of the protoplanet become small
for the case that the protoplanet has an atmosphere.
When the protoplanet has an atmosphere,
the planetesimals that have
initial distances
in the ranges of
,
the planetesimal
collides with the core.
Because of the gas drag of the atmosphere,
the planetesimal lose the energy.
The closest distances of some planetesimals
from the center of the protoplanet become small
for the case that the protoplanet has an atmosphere.
When the protoplanet has an atmosphere,
the planetesimals that have
initial distances
in the ranges of
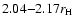 and
and
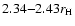 lose energy and collide with the core.
The boundaries of the two ranges are approximately determined
by
the closest distance for the case that the protoplanet does not have the
atmosphere and the enhanced radius.
Once the planetesimal approaches the protoplanet within the
enhanced radius, it loses energy and is captured by
the effective gas drag.
Therefore,
it is a good approximation to replace
the radius of the core,
lose energy and collide with the core.
The boundaries of the two ranges are approximately determined
by
the closest distance for the case that the protoplanet does not have the
atmosphere and the enhanced radius.
Once the planetesimal approaches the protoplanet within the
enhanced radius, it loses energy and is captured by
the effective gas drag.
Therefore,
it is a good approximation to replace
the radius of the core,
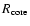 ,
with the enhanced radius,
,
with the enhanced radius,
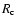 ,
in order to obtain a collision rate
between a protoplanet that has the atmosphere and a planetesimal.
,
in order to obtain a collision rate
between a protoplanet that has the atmosphere and a planetesimal.
The average number of collisions
between a protoplanet and planetesimals
per unit time,
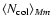 ,
is given by
Nakazawa et al. (1989) as
,
is given by
Nakazawa et al. (1989) as
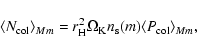 |
(19) |
where
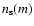 is the surface number
density of planetesimals with mass of m, and
is the surface number
density of planetesimals with mass of m, and
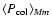 is the non-dimensional mean collision rate.
Inaba et al. (2001) obtained an approximate formula
of
is the non-dimensional mean collision rate.
Inaba et al. (2001) obtained an approximate formula
of
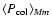 for the case without an atmosphere.
In Fig. 5, it is shown that
the replacement of
for the case without an atmosphere.
In Fig. 5, it is shown that
the replacement of
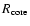 with
with
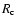 is a good
approximation. According to Inaba et al. (2001),
we propose a new formula of the mean collision rate
when we consider the atmosphere of the protoplanet.
For the high velocity regime
(
is a good
approximation. According to Inaba et al. (2001),
we propose a new formula of the mean collision rate
when we consider the atmosphere of the protoplanet.
For the high velocity regime
(
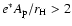 ), where
e* is the dispersion of the eccentricity of the planetesimals,
the mean collision rate is expressed as
), where
e* is the dispersion of the eccentricity of the planetesimals,
the mean collision rate is expressed as
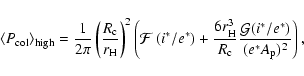 |
(20) |
where i* is the dispersion of the inclination
of the planetesimals.
The functions
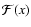 and
and
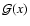 are given, respectively, by
are given, respectively, by
![\begin{displaymath}{\cal F}(x) \equiv
8 \int^{1}_{0} {\rm d}\lambda
\frac{x^{2}E...
.../2\right]}
{\left[x^{2}+\left(1-x^{2}\right)\lambda^2\right]},
\end{displaymath}](/articles/aa/full/2003/41/aa3608/img128.gif) |
(21) |
where K and E are the complete elliptic integrals
of the first and second kinds, respectively.
While for the low velocity regime,
(
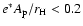 ),
),
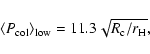 |
(22) |
and for the medium regime
(
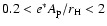 ),
),
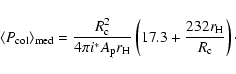 |
(23) |
With the use of the above equations, the mean collision rate is
given by
![\begin{displaymath}\langle P_{\mbox{\scriptsize col}} \rangle_{Mm}
=\min\left[\l...
...}} \rangle_{\mbox{\scriptsize low}}^{-2}\right)^{-1/2}\right].
\end{displaymath}](/articles/aa/full/2003/41/aa3608/img133.gif) |
(24) |
The presence of an atmosphere surrounding a protoplanet
increases the radial distance over which planetesimals
are captured by the protoplanet.
Planetesimals approaching the protoplanet interact with the atmosphere.
Their velocities are reduced by the gas drag.
If they lose enough energy, they are captured in the atmosphere.
The enhanced radius of the protoplanet
is much larger than the radius of the core of the protoplanet.
This distance reduces to the radius of
the core if the protoplanet does not have the atmosphere.
We call this distance the enhanced radius
of the protoplanet.
The enhanced radius depends on the gas density of the atmosphere.
The gas density increases with an increase in
the mass of the core because of the large gravity.
With increases in the luminosity of the atmosphere and/or
the grain opacity of the atmosphere, the gas density decreases.
Approximate solutions to
the gas density of the atmosphere have been derived as a function of
mass of the core, luminosity, and
grain opacity of the atmosphere.
The solutions reproduce the gas density obtained by
the numerical simulations well.
The enhanced radius also depends on the size of a planetesimal and
increases with a decrease in
the size of the planetesimal because
gas drag is more effective for small planetesimals.
We have derived the approximate solutions to
the enhanced radius of a protoplanet as a function
of the size of the planetesimal and the gas density.
With the use of the approximate solutions, we have
derived the collision rate between the protoplanet that has an atmosphere
and the planetesimal.
We study the effect of ablation on the enhanced radius.
By ablation,
planetesimals lose their mass in the atmosphere.
If the planetesimal lose mass,
gas drag becomes more effective so that
the protoplanet can capture the planetesimal.
Even if we adopt the relatively large value
of the ablation constant (
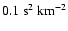 ),
only small amount of mass is lost and, as a result,
the enhanced radius does not change.
Furthermore,
we examine if fragmentation by the dynamical pressure
occurs while
planetesimals are captured in the atmosphere.
The dynamical pressure that the planetesimal experiences is smaller
than the strength of planetesimals
and the planetesimals are not fragmented.
),
only small amount of mass is lost and, as a result,
the enhanced radius does not change.
Furthermore,
we examine if fragmentation by the dynamical pressure
occurs while
planetesimals are captured in the atmosphere.
The dynamical pressure that the planetesimal experiences is smaller
than the strength of planetesimals
and the planetesimals are not fragmented.
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[clip]{MS3608f6.eps}}\end{figure}](/articles/aa/full/2003/41/aa3608/Timg137.gif) |
Figure 6:
The growth time,
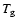 ,
of the protoplanet with ,
of the protoplanet with
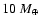 by accumulation of uniform planetesimals
with radius of by accumulation of uniform planetesimals
with radius of
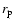 without (dashed curve) and with (solid curve) the effect of enhanced radius. without (dashed curve) and with (solid curve) the effect of enhanced radius.
|
| Open with DEXTER |
Based on the results obtained in this study, we simply estimate
the growth time of the protoplanet with
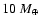 .
With the use of Eq. (19), we have
the growth rate of the protoplanet as
.
With the use of Eq. (19), we have
the growth rate of the protoplanet as
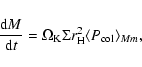 |
(25) |
where 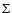 is the surface density of solid.
As shown in Eq. (20),
the collision rate,
is the surface density of solid.
As shown in Eq. (20),
the collision rate,
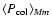 ,
is dependent on the random
velocities (i.e., eccentricities) of planetesimals.
When the protoplanet is large, its gravitational interactions
with planetesimals determine
the eccentricities of the planetesimals
(Ida & Makino 1993):
,
is dependent on the random
velocities (i.e., eccentricities) of planetesimals.
When the protoplanet is large, its gravitational interactions
with planetesimals determine
the eccentricities of the planetesimals
(Ida & Makino 1993):
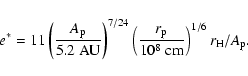 |
(26) |
Using Eqs. (20), (25), and (26),
the growth time of the protoplanet
(
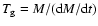 )
is approximately given by
)
is approximately given by
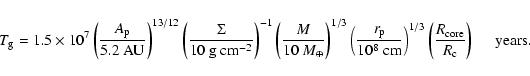 |
(27) |
The growth time is dependent on the enhanced radius.
The protoplanet with a large enhanced radius has a short growth time.
As seen in Fig. 3c, the enhanced radius decreases with an increase
in the luminosity.
Assuming that the luminosity is given by the gravitational energy
released by the incoming planetesimals, that is
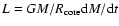 ,
we have
,
we have
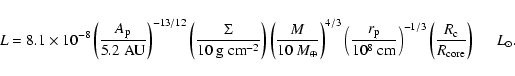 |
(28) |
Therefore,
the luminosity and the enhanced radius
are dependent on each other.
After several trials, we find the enhanced radius that does not
contradict the luminosity.
Using the obtained enhanced radius and Eq. (27),
we have the growth time
of the protoplanet with
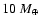 ,
as shown in Fig. 6.
By the inclusion of the enhanced radius, the growth time reduces
by factors of 3 and 10 when planetesimals with radii of
,
as shown in Fig. 6.
By the inclusion of the enhanced radius, the growth time reduces
by factors of 3 and 10 when planetesimals with radii of
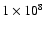 cm and
cm and
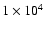 cm, respectively, are accumulated by the protoplanet.
If we consider that the protoplanet grows by accumulating
planetesimals of
cm, respectively, are accumulated by the protoplanet.
If we consider that the protoplanet grows by accumulating
planetesimals of
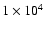 cm radius,
the growth time of the protoplanet becomes
less than 105 years.
This growth time is much smaller than the probable lifetime
of a disk and might explain the formation of Jovian planets.
However,
we have to be very careful to have the conclusion
because this estimate is too simple.
This estimate does not include
the size distribution of planetesimals or the decrease of the
surface density of solid due to
migration of planetesimals toward the central star by the gas drag of
a circumstellar disk.
The detailed calculations of formation of Jovian planets
including the above effects
will be studied in Inaba et al. (2003).
cm radius,
the growth time of the protoplanet becomes
less than 105 years.
This growth time is much smaller than the probable lifetime
of a disk and might explain the formation of Jovian planets.
However,
we have to be very careful to have the conclusion
because this estimate is too simple.
This estimate does not include
the size distribution of planetesimals or the decrease of the
surface density of solid due to
migration of planetesimals toward the central star by the gas drag of
a circumstellar disk.
The detailed calculations of formation of Jovian planets
including the above effects
will be studied in Inaba et al. (2003).
Acknowledgements
We would like to express our gratitude to G. W. Wetherill
for extremely helpful discussions.
We also thank M. Podolak for motivating this study,
T. Fagan for a comment on this paper and
H. Tanaka for discussion.
S. Inaba and M. Ikoma received financial support
from Research Fellowships of the Japan Society for Promotion of Science
for Young Scientists (Nos. 06423 and 06405).
We make additional assumptions to derive an approximate solution.
First, we assume
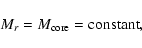 |
(A.1) |
since the atmospheric mass is much smaller than the mass of the core
before the critical core mass.
From this assumption, Eq. (5) can be eliminated.
Next, we use the equation of state for ideal gas given by
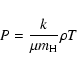 |
(A.2) |
with assumption of constant mean molecular weight, 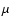 (k: Boltzmann constant;
(k: Boltzmann constant; 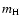 :
mass of a hydrogen atom).
Finally, we assume that the opacity is constant in radiative zones
and the second adiabatic exponent is constant in convective zones;
:
mass of a hydrogen atom).
Finally, we assume that the opacity is constant in radiative zones
and the second adiabatic exponent is constant in convective zones;
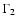 is equal to the usual adiabatic exponent
is equal to the usual adiabatic exponent 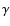 in the ideal approximation.
in the ideal approximation.
For convenience, we introduce the following dimensionless quantities:
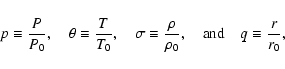 |
(A.3) |
where the quantities with suffices 0 are some reference values.
Furthermore, we define two non-dimensional numbers such as
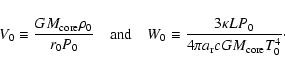 |
(A.4) |
Using these,
we can rewrite Eq. (4) as
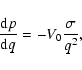 |
(A.5) |
Eq. (6) as
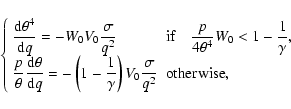 |
(A.6) |
and Eq. (A.2) as
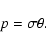 |
(A.7) |
First, we derive an analytical solution for a radiative atmosphere.
Dividing the first equation of Eq. (A.6) by
Eq. (A.5) and integrating the obtained equation,
we have
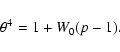 |
(A.8) |
Inserting Eq. (A.7) into
Eq. (A.5) and
using Eq. (A.8) leads to
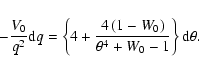 |
(A.9) |
This equation can be integrated analytically to be
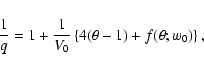 |
(A.10) |
where
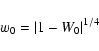 |
(A.11) |
and
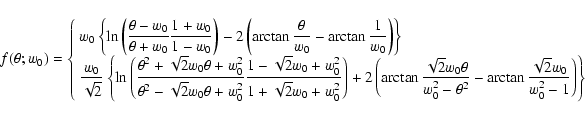 |
(A.12) |
(the upper and the lower equations for W0 < 1 and W0 > 1, respectively).
It should be noted that
this solution reduces to that derived by Mizuno (1980)
and Stevenson (1982)
for
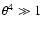 and
and 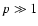 ,
that is,
,
that is,
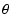 |
= |
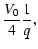 |
(A.13) |
| p |
= |
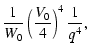 |
(A.14) |
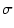 |
= |
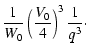 |
(A.15) |
Next, we consider convective cases.
From Eq. (A.5) and
the second equation of Eq. (A.6),
we obtain the familiar adiabatic relation such as
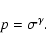 |
(A.16) |
Substituting this in Eq. (A.5) and
integrating the obtained differential equation,
we have
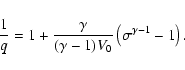 |
(A.17) |
In summary, we use Eqs. (A.7), (A.8),
and (A.10) for radiative zones;
we use Eqs. (A.7), (A.16), and
(A.17) for convective zones.
We divide the atmosphere into three layers in order to reproduce
the numerical solutions as accurately as possible using our
approximate solutions.
This requirement arises from the fact that the grain opacity drops
abruptly because of evaporation (typically of ice and silicate),
so that we cannot replace 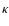 with a constant value throughout
the atmosphere. From our experience, we decide to calculate in the
following way.
with a constant value throughout
the atmosphere. From our experience, we decide to calculate in the
following way.
We choose the normalized temperature 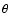 as the independent variable.
The two boundaries are the points at which
as the independent variable.
The two boundaries are the points at which
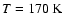 and
and
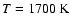 .
These temperatures are typical evaporation temperatures of
ice and silicate. We calculate our approximate solutions inward
from the outer boundary and change the reference values at the boundaries.
That is,
.
These temperatures are typical evaporation temperatures of
ice and silicate. We calculate our approximate solutions inward
from the outer boundary and change the reference values at the boundaries.
That is,
- 1.
- for
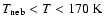 ,
we choose
,
we choose
- 2.
- for
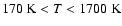 ,
,
- 3.
- for
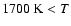 ,
,
Only at each boundary,
we judge whether radiative or convective solutions should be used.
If
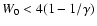 (
(
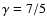 here),
then we use the radiative solution; otherwise,
the convective solution.
here),
then we use the radiative solution; otherwise,
the convective solution.
In Fig. 1, we compare the above-obtained solutions with
our numerical solutions described in the Sect. 2.2.
As seen from these figures, our analytical solutions reproduce
the numerical solutions well,
except for the model with
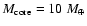 in Fig. 1a.
The difference between the analytical and
numerical solutions for the model of
in Fig. 1a.
The difference between the analytical and
numerical solutions for the model of
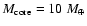 originates mainly from neglecting the contribution of the atmospheric mass
to the planetary radius R (see Eq. (3));
the atmospheric mass is about 1/3 times as large as the core mass
at the critical core mass (see Stevenson 1982).
However, this deviation is not important in this study, because
the information required here is not the density at a given radius,
but the radius for a given density.
In this sense, our analytical solutions coincide with the numerical ones
within the accuracy of 50%.
originates mainly from neglecting the contribution of the atmospheric mass
to the planetary radius R (see Eq. (3));
the atmospheric mass is about 1/3 times as large as the core mass
at the critical core mass (see Stevenson 1982).
However, this deviation is not important in this study, because
the information required here is not the density at a given radius,
but the radius for a given density.
In this sense, our analytical solutions coincide with the numerical ones
within the accuracy of 50%.
-
Adachi, I., Hayashi, C., & Nakazawa, K. 1976, Prog. Theor. Phys., 56, 1756
In the text
NASA ADS
-
Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879
In the text
NASA ADS
-
Benz, W., & Asphaug, E. 1999, Icarus, 142, 5
In the text
NASA ADS
-
Bodenheimer, P., & Pollack, J. B. 1986, Icarus, 67, 391
In the text
NASA ADS
-
Borovicka, J., & Spurný, P. 1996, Icarus, 121, 484
In the text
NASA ADS
-
Field, G. B., & Ferrara, A. 1995, ApJ, 438, 957
In the text
NASA ADS
-
Goldreich, P., & Ward, W. R. 1973, ApJ, 183, 1051
In the text
NASA ADS
-
Goodman, J., & Pindor, B. 2000, Icarus, 148, 537
In the text
NASA ADS
-
Greenzweig, Y., & Lissauer, J. J. 1992, Icarus, 100, 440
In the text
NASA ADS
-
Ida, S., & Makino, J. 1993, Icarus, 106, 210
In the text
NASA ADS
-
Ida, S., & Nakazawa, K. 1989, A&A, 224, 303
In the text
NASA ADS
-
Inaba, S., & Wetherill, G. W. 2001, Proc. LPSC 32nd, 1384
In the text
-
Inaba, S., Tanaka, H., Nakazawa, K., et al. 2001, Icarus, 149, 235
In the text
NASA ADS
-
Inaba, S., Wetherill, G. W., & Ikoma, M. 2003, Icarus, in press
In the text
-
Kippenhahn, R., & Weigert, A. 1990, in Stellar Structure and Evolution (Berlin: Springer-Verlag)
In the text
-
Mizuno, H. 1980, Prog. Theor. Phys., 64, 544
In the text
NASA ADS
-
Nakazawa, K., Ida, S., & Nakagawa, Y. 1989, A&A, 220, 293
In the text
NASA ADS
-
Podolak, M., Pollack, J. B., & Reynolds, R. 1988, Icarus, 73, 163
In the text
NASA ADS
-
Pollack, J. B., McKay, C., & Christofferson, B. 1985, Icarus, 64, 471
In the text
NASA ADS
-
Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62
In the text
NASA ADS
-
Saumon, D., Chabrier, G., & Van Horn, H. M. 1995, ApJS, 99, 713
In the text
NASA ADS
-
Stevenson, D. J. 1982, Planet. Space Sci., 30, 755
In the text
NASA ADS
-
Weidenschilling, S. J. 1997a, Icarus, 127, 290
In the text
NASA ADS
-
Weidenschilling, S. J. 1997b, Proc. LPSC 28th, 1513
In the text
-
Wetherill, G. W., & Stewart, G. R. 1989, Icarus, 77, 330
In the text
NASA ADS
-
Wetherill, G. W., & Stewart, G. R. 1993, Icarus, 106, 190
In the text
NASA ADS
-
Wuchterl, G., Guillot, T., & Lissauer, J. J. 2000, in Protostars and Planets IV, ed. V. Mannings, A. P. Boss, & S. S. Russell (Tucson: Univ. Arizona Press), 1081
In the text
Copyright ESO 2003
![\begin{figure}
\par\resizebox{11cm}{!}{\includegraphics[clip]{MS3608f1.eps}}\end{figure}](/articles/aa/full/2003/41/aa3608/Timg17.gif)
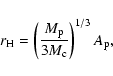
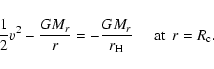
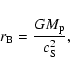
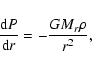
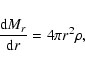
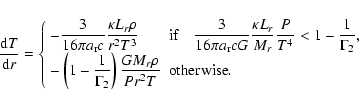
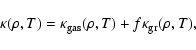
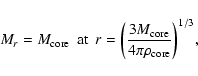
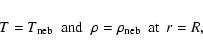
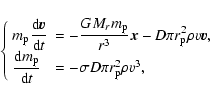
![\begin{figure}
\par\resizebox{11cm}{!}{\includegraphics[clip]{MS3608f2.eps}}\end{figure}](/articles/aa/full/2003/41/aa3608/Timg74.gif)
![\begin{figure}
\par\resizebox{11cm}{!}{\includegraphics[clip]{MS3608f3.eps}}\end{figure}](/articles/aa/full/2003/41/aa3608/Timg85.gif)
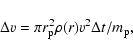
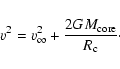
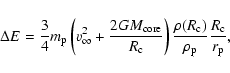
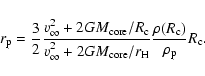
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics*[clip]{MS3608f5.eps}}\end{figure}](/articles/aa/full/2003/41/aa3608/Timg110.gif)
![\begin{figure}
\par\resizebox{11cm}{!}{\includegraphics[clip]{MS3608f4.eps}}\end{figure}](/articles/aa/full/2003/41/aa3608/Timg116.gif)
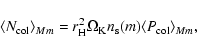
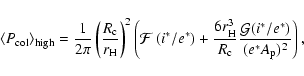
![\begin{displaymath}{\cal F}(x) \equiv
8 \int^{1}_{0} {\rm d}\lambda
\frac{x^{2}E...
.../2\right]}
{\left[x^{2}+\left(1-x^{2}\right)\lambda^2\right]},
\end{displaymath}](/articles/aa/full/2003/41/aa3608/img128.gif)
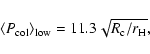
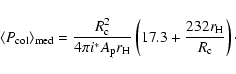
![\begin{displaymath}\langle P_{\mbox{\scriptsize col}} \rangle_{Mm}
=\min\left[\l...
...}} \rangle_{\mbox{\scriptsize low}}^{-2}\right)^{-1/2}\right].
\end{displaymath}](/articles/aa/full/2003/41/aa3608/img133.gif)
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[clip]{MS3608f6.eps}}\end{figure}](/articles/aa/full/2003/41/aa3608/Timg137.gif)