A&A 410, 389-396 (2003)
DOI: 10.1051/0004-6361:20031194

A new template background estimate for source searching in TeV $\gamma $-ray astronomy

G. P. Rowell

Max Planck Institut für Kernphysik, Postfach 103980, 69029 Heidelberg, Germany

Received 21 May 2003 / Accepted 30 July 2003

Abstract
A new method is described that permits quickly and easily, a 2-dimensional search for TeV $\gamma $-ray sources over large fields of view ($\sim$$6^\circ$) with instruments utilising the imaging atmospheric Cerenkov technique. It employs as a background estimate, events normally rejected according to a cosmic-ray background rejection criterion based on image shape, but with reconstructed directions overlapping the source of interest. This so-called template background model is demonstrated using example data taken with the stereoscopic HEGRA System of Cerenkov Telescopes. Discussion includes comparisons with a conventional background estimate and limitations of the model. The template model is well suited to the search for point-like, moderately extended sources and combinations thereof, and compensates well for localised systematic changes in cosmic-ray background response.

Key words: methods: data analysis - gamma rays: observations

1 Motivation and introduction

The search for new astrophysical sources of TeV $\gamma $-ray emission today is well motivated by the multi-wavelength picture of candidate sources, and also by the high performance offered by present and future instruments. Many of the >150 unidentified EGRET sources (MeV-GeV energies) have positional uncertainties approaching several degrees (Hartman et al. 1999), presenting exciting opportunities for TeV instruments to identify possible counterparts over the coming years. The ground-based imaging atmospheric Cerenkov technique presently offers on-axis flux sensitivities better than (for energies >1 TeV) $\sim$10-12 erg cm-2 s-1 for 50 hrs exposure, and can achieve arc-minute scale angular resolution over fields of view approaching 5$^\circ $ diameter (see e.g. Konopelko et al. 2002). Rather wide surveys for new TeV sources are therefore possible even from singly pointed observations. Techniques to generate 2D skymaps of event excess significance for such surveys have therefore become more important in recent years. Critically important, for such skymap generation is an estimate of the cosmic ray background over the field of view (FoV). Many expected, and known sites of TeV $\gamma $-ray production, such as supernova remnants, pulsars/plerions, microquasars, and nearby extragalactic sources will likely present complicated morphology for future instruments as sensitivities improve. Particularly in cases where combinations of such sources might be expected in the FoV, it is vital that the background estimate is not contaminated by other TeV sources and various systematic biases are well understood.

Described here is the template background model (an earlier version is described in Rowell 2000), designed to provide a background estimate for sources of interest at all positions in the FoV. The model is demonstrated on archival data from the HEGRA System of Cerenkov telescopes (HEGRA CT-System). For detailed descriptions of this instrument and its performance see Daum et al. (1997) and Pühlhofer et al. (2003). Comparisons are made between results of the template model and those taken from a conventional background model presently in use in HEGRA CT-System data analysis. Some features and limitations of the template model are described.

2 Conventional background estimates and 2D skymap generation

Present ground-based instruments utilising the imaging atmospheric Cerenkov technique (100 GeV to $\sim$30 TeV), must detect $\gamma $-ray initiated events against a background of vastly outnumbering isotropic cosmic-ray (CR) initiated events. First, a set of so-called $\gamma $-ray cuts are employed to preferentially select events conforming to a $\gamma $-ray hypothesis. These are a priori chosen, and based primarily on Cerenkov image shape parameters, for example width, length (Hillas 1985), and mean-scaled-width ($\bar{w}$) (Konopelko 1995; Daum et al. 1997). Second, event arrival directions are also reconstructed based on the orientation of recorded Cerenkov images (see e.g. Buckley et al. 1998; Hofmann et al. 1999) and a so-called directional cut made on the distance $\theta$ (or analogous parameters) between the reconstructed and assumed arrival directions. To assess the statistical significance of any region in the FoV, an estimate of the CR background surviving both $\gamma $-ray and directional cuts must be made. This background estimate can be derived from separate observations of different OFF tracking positions (ON/OFF tracking), or control regions displaced within the same FoV containing the source region. The latter types of background models are termed here displacement backgrounds, and a number of different displacement background geometries are available. Background regions are chosen so that their CR response matches as closely as possible, that of the source region (see Fig. 1).

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{backgrounds3_AAS.epsi}\par\end{figure} Figure 1: Illustration of some conventional background estimation methods. (1) Separate OFF source observations are taken at matching zenith angles to those of ON source data. (2) Discrete background regions within the same FoV at a common source-to-tracking distance so as to match background response. (3) A continuous version of (2), ring or ring segments may be used instead. Regions adjacent to the source (shaded) may be preferred to avoid global systematic changes in response. (4) A ring region completely surrounding the source. Methods 2, 3 and 4 are termed displacement background models. Method 4 is used when the source is too close to the tracking position to implement methods 2 and 3, or over the entire FoV.
Open with DEXTER

In ON/OFF tracking this is achieved by choosing background regions with the same relative displacement from respective tracking positions as that for the source. For displacement backgrounds, such regions are mirrored through the tracking position (methods 2 and 3), except for sources very close to the tracking position in which a region surrounding completely the source can be implemented (method 4). In this latter case an extra correction is applied to account for differences in CR response. Provided the FoV is large compared to the angular resolution and source size, and global systematic changes in CR response are minimal or can be alleviated, displacement backgrounds may be implemented. Displacement backgrounds are favoured over the ON/OFF method since they do not require extra time taking dedicated OFF source observations. A recent modification of the ON/OFF method, however, is proposed by Petry 2003. The large cameras ($\sim$4.3$^\circ $ diameter) and stereoscopic trigger employed by the HEGRA CT-System achieves a quite flat FoV ( ${\textit FWHM} \sim3^\circ$) that is amenable to displacement background models over the entire FoV. In this paper, using example data from the HEGRA CT-System, results from a combination of displacement methods 3 and 4 (termed here the displacement background model) are used to compare with the template model. For source to tracking distances larger than $\sim$$0.4^\circ$, a ring segment or arc (method 3) adjacent to the source region (within position angles 135$^\circ $ to 165$^\circ $) is used, otherwise, method 4 is chosen. Ring background regions rather adjacent to the source are often preferred to avoid global systematic changes (of $\sim$few percent) in CR response across the FoV.

For a given region in the FoV, the source events s are derived from within a nominal source region according to some directional cut $\theta <\theta _{\rm cut}$ and $\gamma $-ray cuts on image shape parameters. The number of background events b are derived according to the above-described displacement background methods, after also applying the same $\gamma $-ray cuts. The statistical significance S of excess counts $s-\alpha b$ is then estimated from Eq. (17) of Li & Ma (1983):

 \begin{displaymath}S = \sqrt{2} \left( s~{\rm ln}\left[\frac{s(1+\alpha)}{\alpha... ... ln}\left[\frac{b(1+\alpha)}{s+b}\right] \right)^{\frac{1}{2}} \end{displaymath} (1)

where a normalisation $\alpha $ accounts for the solid angle ratio between the source and background regions when displaced backgrounds are used, or different observation times if ON/OFF tracking is used. Under the displaced background models applied to HEGRA CT-System data, typical normalisation values of 0.05 to 0.3 are achieved, thereby considerably improving the background estimate compared to an $\alpha=1.0$ situation usually achieved in ON/OFF tracking.

In 2D skymap generation, the above procedure is repeated over the FoV at a series of grid positions. Directional parameters such as $\theta$ and those necessary to form the background estimate are then re-calculated with respect to each grid position, and excesses and significances are calculated accordingly.

   
3 The template background model

The template background model invokes a different philosophy to that of displacement background models. Instead of selecting spatially different regions in the FoV for background estimates, template model background events are comprised of those with their arrival directions reconstructed in the same region as that for the source, yet separated in image shape parameter space. Such events can form a suitable template of response for $\gamma $-ray-like CR events over the FoV.

As applied to data of the HEGRA CT-System, the shape parameter mean-scaled-width ($\bar{w}$ ) is used to construct the template background estimate. $\bar{w}$ is the image scaled-width, averaged over all images accepted for analysis. The scaled-width is the image width scaled according to a $\gamma $-ray hypothesis. This scaling is dependent upon the total photoelectron yield of the image, the zenith angle of observations, and the impact parameter or distance to the air-shower core. By design (see Fig. 2), true $\gamma $-ray events have $\bar{w}$ values centred at unity, leaving the generally broader CR events to fill higher values.

  \begin{figure} \par\includegraphics[width=7.5cm]{typ_msw.epsi}\par\end{figure} Figure 2: Normalised distributions of $\bar{w}$ for $\gamma $-ray and cosmic-ray (CR) events, based on Monte Carlo simulations (solid histograms) and real data (error bars). Adapted from Konopelko (2002).
Open with DEXTER

In the search for weak, background-dominated sources in CT-System data, the cut $\hbox{$\bar{w}$ } <1.1$ has been found optimal. Template background events should be derived from a $\bar{w}$ regime containing little or no true $\gamma $-rays, i.e. $\hbox{$\bar{w}$ } >1.1$. Experience has found that events within the regime $1.3<\hbox{$\bar{w}$ } <1.5$ work well, although regimes containing higher $\bar{w}$ values have proved adequate. To apply the template model practically however, two dominant systematic effects must be corrected: For a nominal region in the FoV defined by a cut $\theta <\theta _{\rm cut}$, $\gamma $-ray-like events s are selected according to $\bar{w}$  < 1.1. Similarly after applying the same cut on $\theta$, template background events b are defined as those satisfying the condition 1.3< $\bar{w}$  <1.5. In summary template background events are assigned a weight $\omega_i$:
 
$\displaystyle s = \sum_{i} \omega_i$         $\textstyle \omega_i = 1.0$                           $\displaystyle ~~ (\bar{w}<1.1)$ (2)
         $\displaystyle b = \sum_{i} \omega_i$      $\textstyle ~~ \omega_i = \frac{\textstyle p_s(\theta^2_{{\rm track},i})}{\textstyle p_b(\theta^2_{{\rm track},i})} ~ f(\Delta {z_{i}})$       $\displaystyle ~~ (1.3<\bar{w}<1.5)$ (3)

for events i in the source region. The correction terms applied to b can be described with suitable parametrisations as follows. The radial acceptance of the $\gamma $-ray-like ( $\hbox{$\bar{w}$ } <1.1$) and template ( $1.3<\hbox{$\bar{w}$ } <1.5$) regimes over the entire FoV are sufficiently fitted out to radius R, with 8th-order polynomials, ps and pb respectively and normalised. Both polynomials are functions of the event distance to tracking position $\theta_{\rm track}$. A strong increase or pile-up of reconstructed event directions due to camera edge effects is normally seen at the FoV edge. Ignoring Cerenkov images whose centroid distance from the camera centre dis exceeds $1.7^\circ$ effectively suppresses this pile-up, and allows fitting of the FoV response to the physical camera limits. The choice of R is limited by event statistics, and practically, can reach values up to $3^\circ$. Fitting such polynomials assumes that the radial response is azimuthally symmetric. However, a second systematic effect, a gradient $f(\Delta z)$ correlating with the difference in zenith angle $\Delta z$ between the event and tracking position, is also generally present. This can be described by a linear function vs. $\Delta z$, of the ratio of FoV responses between the $\gamma $-ray-like and template $\bar{w}$ regimes. This linear fit is made after first correcting for the radial profiles. Thus the template correction functions are generated in a two-step process (Appendix A summarises these corrections for a particular example discussed shortly). The radius R also defines the FoV used in determining the overall normalisation ratio $\alpha $ when estimating event excess and significance (e.g. according to Eq. (1)). If the total number of events in each $\bar{w}$ regime out to a radius R is given by Ps and Pb respectively, the template normalisation $\alpha $ is given by:

 \begin{displaymath}\alpha = P_s / P_b. \end{displaymath} (4)


  \begin{figure} \par\includegraphics[width=8.0cm]{fov2.epsi}\par\end{figure} Figure 3: Illustration of the template background geometry with the FoV and normalisation region (defined by radius R) in relation to various source positions. The template background and "$\gamma $-ray-like'' events are defined by the $\bar{w}$ (MSW) regimes $1.3<\hbox{$\bar{w}$ } <1.5$ and $\hbox{$\bar{w}$ } <1.1$ respectively. Shown here un-normalised, the template regime contains a factor $3\sim 4$ more events than that of the $\gamma $-ray-like regime. Source regions of interest are defined by a cut on some directional parameter, e.g. $\theta <\theta _{\rm cut}$, and are spatially coincident in both $\bar{w}$ regimes. The normalisation region should be sufficiently large to encompass all such source regions.
Open with DEXTER

Alternatively, one may also integrate out to R, the polynomial functions (un-normalised) ps and pb, to obtain a similar result. Typical $\alpha $ values achieved are quite similar to that of the displacement background model. The template model philosophy is illustrated in Fig. 3. A caveat is that the normalisation region must encompass all source regions. This will set a natural limit on the size of any source region, although systematic effects (Sect. 5) usually dominate for large source sizes. Note that the template model correction terms generated from a given dataset should strictly be applied only to these same data.

   
4 Template model performance on real data

2D skymaps of excess significance are shown in Fig. 4, illustrating the template model performance at various stages of correction. About 50 hours of CT-System exposure on Tycho's SNR out to a radius $R=2.24^\circ$ ( $\sqrt{5.0}^\circ$) were used in generating these skymaps. Previous analysis of these data are described in Aharonian et.al (2001b).

  \begin{figure} \par\includegraphics[width=13.0cm]{tychomap_cr.epsi}\par\includeg... ..._crc.epsi}\par\includegraphics[width=13.0cm]{tychomap_crcz.epsi}\par\end{figure} Figure 4: 2D Skymaps and 1D distributions of significance Susing the template background estimate after various correction levels. a) no correction, wi=1.0 b) radial correction only, $f(\Delta {z_i})=1.0$ c) full correction as per Eq. (3). White star: nominal position (SIMBAD) of Tycho's SNR, White dots: tracking positions, Dashed line: Gaussian ($\mu =0.0$, $\sigma =1.0$), Solid line: fitted Gaussian. Events are summed within a circle of radius 0.12$^\circ $ at each grid position ( $120\times 120$ grid), in $0.05^\circ \times 0.05^\circ $ steps.
Open with DEXTER

Table 1: Event excesses $s-\alpha b$ and significances S derived using the template and displacement background models for a number of established TeV $\gamma $-ray sources. The source region is defined by the cut $\theta <\theta _{\rm cut}$. s: $\gamma $-ray-like events; b: background estimate; $\alpha $: normalisation. Datasets are from the HEGRA CT-System archive; Cas A (212 hours), H1426+428 (42 hours, 1999/2000), 1ES1959+650 (94 hours, 2000/2001), Crab (33 hours).

At each grid point in $0.05^\circ$ steps, a $\theta<0.12^\circ$cut defines both the source (which is applicable for point-like sources) and template background regions. The significance S is estimated using Eq. (1). It is apparent the Tycho skymap statistics approach that of a Gaussian distribution only after correcting for both the radial and zenith-correlated systematics. A quite strong zenith-correlated gradient of 9% per degree is present, which if not corrected, leads to biases in the excess significance peaking at the declination edges of the FoV (Appendix A summarises these template correction terms in more detail). The bin statistics in these skymaps are somewhat correlated, and lead to a slight overestimate in the width $\sigma$ of the 1D distribution of significances. The level of this overestimate is taken from a 2D skymap of significances from bins that have no overlap with neighbouring bins. The 1D distributions of significances for this skymap is $\sigma=0.93\pm0.03$, implying that the template background is slightly over-corrected, effectively underestimating slightly the significance in the FoV. Overall one may conclude however that the template model is quite suitable for point source searches over the FoV in these data. In this example, the minimum number of telescopes required for stereoscopic direction reconstruction and $\bar{w}$ calculation has been chosen at $n_{\rm tel}\ge 2$, and the stereo reconstruction algorithm #1 of Hofmann et al. (1999) was used. The template model performs equally well however under higher choices of $n_{\rm tel}$ (up to 5), varying choices of FoV/normalisation radius R, and various reconstruction algorithms.

The template model was also tested with a number of a priori chosen positions in the FoV corresponding to established $\gamma $-ray sources. Presented in Table 1 are the excess significances for a representative sample of TeV $\gamma $-ray sources with a variety of signal to CR background ratios. Results using background estimates from both the template and displacement background models are given for comparison. In all cases a normalisation radius for the template background model of $R=2.24^\circ$ and minimum number of images $n_{\rm tel}\ge 2$ have been used. The template model provides derived excesses $s-\alpha b$ quite consistent with those obtained from the displacement model. Since the example sources of Table 1 lie quite close to their respective tracking positions, the zenith-correlated correction term of the template background has little effect, and hence results only for the fully corrected template background are shown. For the Crab, a slight modification regarding the template correction is made to the fit limits of the polynomials ps and pb, to exclude regions containing this strong source. The polynomial fits are affected by strong sources near (<$0.5^\circ$) the tracking position and these should be avoided. It should be stressed that the derived excesses and significances for the Cas A and H1426+428 and 1ES1959+650 here are generally lower than those of presently published analyses (Aharonian et al. 2001a,2002; Horns et al. 2002), which employed the more sensitive reconstruction algorithms #2 and #3 (Hofmann et al. 1999), and in some cases a higher minimum $n_{\rm tel}$. The template model does reproduce published results when employing the corresponding analyses.

Finally, a particularly useful feature of the template model is demonstrated against a problematic systematic effect arising when camera pixels view bright stars in the FoV. Increased noise fluctuations (and corresponding anode currents) in camera pixels viewing bright stars can distort derived image parameters. Affected pixels, usually the same for all five cameras, are therefore removed from a camera trigger dynamically during data taking and also from image analysis at a software level. Any pixel with anode current $\geq$$3~\mu$A is not considered in estimation of image parameters and consequent event direction reconstruction (Bulian et al. 1998; Daum et al. 1997). A residual effect of this latter step is to leave a systematic deficit of reconstructed event directions in a region broadly centred on the offending star. This effect was verified by artificially removing certain pixels before image parametrisation. In practise, up to two to three pixels may be removed during data taking at any given time depending on the star brightness. The Crab field, with $\zeta $-Taurii (mB=2.9) and the Cas-A field with AR-Cas (mB=4.8), are ideal examples to illustrate such star deficits. Quantitatively, star deficits amount to a reduction in CR events up to $\sim$20% over a diameter $\sim$$0.2^\circ$. Table 2 summarises the template (after full correction only) and displacement background model performance at the $\zeta $-Taurii and AR-Cas positions. Since the template background closely follows the CR background response of gamma-ray-like events, star deficits are considerably reduced when using the template model. The displacement background however, which does not include the star region, produces a strong negative bias. Conversely, if displacement background regions (applied to another source region) were to overlap star deficit(s), some positive biases could be introduced. A large number of bright stars in the FoV would in general render application of displacement background models problematic.

Table 2: Event excesses $s-\alpha b$ and significances S at star positions within the Crab ($\zeta $-Taurii, 161 hrs) and Cas-A (AR-Cas, 212 hrs) fields of view. Compared are results using the template and displacement background models.

Overall the template model appears able to match localised systematic changes in response of $\gamma $-ray-like CR events in the FoV.

   
5 Limitations

The template model as designed here employs corrections only for large-scale systematic changes in CR response, correlating radially from the tracking position and with event zenith angle. Higher-order systematics (correlating with alternate system parameters) arising from, say, differences in telescope camera response can also reasonably be expected, despite long-term efforts to maintain a homogeneous response in the HEGRA CT-System (see Pühlhofer et al. 2003). Since systematic effects will grow in proportion to the size of the source region and also exposure, these are better revealed in deep exposure datasets. For the Tycho's SNR dataset however, significance skymaps generated with larger source sizes in mind (e.g. $\theta_{\rm cut}$ up to 0.6$^\circ $) do not show behaviour significantly differing from a Gaussian distribution. An upper limit to the systematic error in the derived excess $s-\alpha b$ across the Tycho FoV can be estimated by using subjectively-chosen "hot'' and "cold'' regions (of size $\sim$$1.0^\circ$) of the fully corrected skymap. In this way a systematic error of $\sim$$\pm4$% in units of the normalised background $\alpha b$ is calculated.

The Tycho's SNR dataset is representative of many in the CT-System archive of order 50 hrs exposure, with $\geq$4 telescopes of the CT-System in operation. Such an exposure is generally found not sufficient to reveal higher-order systematic effects. The Cas A dataset comprises a deeper exposure (>200 hrs). The fully corrected template model skymap of these data (Fig. 5) shows a strong deviation from Gaussian behaviour (1D $\sigma=1.126\pm0.008$) already when searching for point sources ( $\theta_{\rm cut} < 0.12^\circ$). A "hotter'' group of bins is seen at ${\rm RA}>23.5$ h, Dec 58$^\circ $ to $59^\circ$, representing an additional systematic excess of order few percent in units of normalised background. The source of this systematic is as yet not fully understood. It may be linked to a "missing'' telescope (CT2 is not present in large fraction of these data) which is uncovering inhomogeneities in trigger response correlating with certain telescopes, although this gradient does not align with the CT-System geometry. It is seen in these data that artificial removal of other telescopes for example, can also introduce further similar-scale effects which may or may not be related. Changes in average skynoise across the FoV may also contribute. Care should therefore be taken when searching for sources in affected regions, employing alternative background estimates such as displacement backgrounds as a check. All background methods will of course also be affected by large-scale systematics of various types and so the above-mentioned problem is not particular to the template model.

  \begin{figure} \par\includegraphics[width=14.5cm,clip]{cas-a_map_crcz.epsi}\par\end{figure} Figure 5: Skymap (2D and 1D) of significance S using the fully corrected template background estimate for Cas-A data. White star: Nominal position (SIMBAD) of Cas-A, White dots: tracking positions. Dashed line: Gaussian ($\mu =0.0$, $\sigma =1.0$). Details for skymap construction are the same as for Fig. 4.
Open with DEXTER

Extra correction terms could be added to the template model to accommodate such higher order effects but this has not yet been explored in detail. Experience has shown that for large exposures, higher order systematic effects can be averaged out or considerably reduced by employing a variety of tracking positions, for example in a mosaic fashion. All of the example datasets presented here employed the so-called wobble mode in which only two tracking positions were alternated $\pm$$0.5^\circ$ in declination with respect to the primary source of interest. Investigation of higher order effects and their origin is presently continuing, in the context of a search for TeV sources from the entire CT-System archive (Pühlhofer et al. 2002; Aharonian et al. 2003).

The estimation of energy spectra from source excesses requires that the background estimate be comprised of events with a similar distribution of estimated energies to that of events from the source region. The template background estimate however does not meet this criterion since the $\bar{w}$ values comprising the background estimate will differ in estimated energy from those in the $\gamma $-ray-like $\bar{w}$ regime. Thus alternative background models should be used for spectral analysis.

6 Conclusions

Described in this paper is a new method to estimate the CR background in 2D searches for sources of TeV $\gamma $-ray emission with ground-based detectors. This so-called template background estimate, demonstrated here with HEGRA CT-System data, employs a subset of CR events normally rejected according to the Cerenkov image shape parameter mean-scaled-width $\bar{w}$ . These template events spatially and temporally overlap with CR events considered "gamma-ray-like'', and thus no dedicated OFF source observations are required. Applying the template model successfully to HEGRA CT-System data involves correction over of the field of view for: (1) differences in radial response and (2) differences in a zenith-correlated gradient, both between the CR events of the two $\bar{w}$ regimes. A particularly useful feature of the template model is its ability to compensate well for localised systematic changes in CR event density due to the presence of stars in the field of view. It is well suited to cases where many stars and TeV sources are present. The template model applicability is limited by the presence of systematic gradients in CR event density which are presently not corrected. All background models will however suffer to various extent from weak, large scale systematics. Further investigation of these aspects is ongoing. Systematic uncertainties in the derived event excess of less than 4% of the normalised background are achieved when searching for sources of size less than $\sim$$0.6^\circ$ radius in many datasets.

It should be possible to extend the template model philosophy to analyses which use other means to reject CR background, for example maximum likelihood methods, multi-dimensional cluster analyses, applied to either single or multi-telescope systems. Issues relating to systematic gradients over the FoV and star deficits will be important for the next generation IACTs such as H.E.S.S., VERITAS, CANGAROO III and MAGIC. In these new systems, CR event rates of order 500 Hz are expected, likely revealing higher-order systematic gradients in response after observation times significantly shorter than that required in HEGRA CT-System data. Furthermore, the larger mirror areas of these future experiments will also increase considerably the number of stars that could cause detrimental systematics in the FoV response. The template background model could therefore be quite useful in 2D skymap construction, in future searches for TeV $\gamma $-ray sources.

Acknowledgements
HEGRA colleagues are thanked for advice with CT-System data analysis and valuable discussions on this topic (in particular Niels Götting, Dieter Horns and Gerd Pühlhofer). GPR acknowledges receipt of a von Humboldt Fellowship.

   
Appendix A: Template background corrections

Summarised here are the two template background correction terms calculated specifically for the HEGRA CT-System Tycho's SNR dataset (Fig. 4).
1.
Radial Correction: The radial event density for the entire dataset, centred on the various tracking positions may be fitted with 8th-order polynomials out to a radius $R=2.24^\circ$: (1) ps for the "gamma-ray-like'' ( $\hbox{$\bar{w}$ } <1.1$), and (2) pb for the template regime ( $1.3<\hbox{$\bar{w}$ } <1.5$):

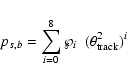\begin{displaymath}p_{s,b} = \sum_{i=0}^{8} \wp_i ~~ (\theta^2_{\rm track})^i \end{displaymath} (A.1)

where for Tycho's SNR data one fits:


  ps pb
$\wp_0 $ $215.3\pm0.7$ $815.3\pm0.9$
$\wp_1 $ $ 17.0\pm0.8$ $160.8\pm1.9$
$\wp_2 $ $-148.7\pm0.1$ $-606.2\pm0.8$
$\wp_3 $ $ 148.00\pm0.02$ $576.80\pm0.19$
$\wp_4 $ $ -62.340\pm{\rm O}(10^{-3}$) $-243.60\pm0.04$
$\wp_5 $ $ 7.987\pm{\rm O}(10^{-3}$) $31.95\pm0.01$
$\wp_6 $ $ 1.661\pm{\rm O}(10^{-4}$) $6.117\pm{\rm O}(10^{-3}$)
$\wp_7 $ $ -0.5548\pm{\rm O}(10^{-5}$) $-2.103\pm{\rm O}(10^{-4}$)
$\wp_8 $ $ 0.0418\pm{\rm O}(10^{-4}$) $0.158\pm{\rm O}(10^{-3}$)


2.
Zenith-Correlated Correction: A linear function is used to describe the ratio of event densities, as a function of the zenith angle difference $(\Delta z)$ between the event and tracking positions, of the gamma-ray-like and template $\bar{w}$ regimes,:

\begin{displaymath}f(\Delta z) = (0.998~\pm 0.006)~~ +~~ (0.898~\pm 0.006)~ \Delta z . \end{displaymath} (A.2)

A linear gradient of order 9% per degree along the zenith axis is therefore present in the Tycho's SNR data. Separately, one can also fit functions to each $\bar{w}$ regime; $f(\Delta z)_s$ and $f(\Delta z)_b$, and note that the function $f(\Delta z)=f(\Delta z)_s / f(\Delta z)_b$:
$\displaystyle f(\Delta z)_s = (0.999~\pm 0.006)~~ +~~ (0.107~\pm 0.006)~ \Delta z$      
$\displaystyle f(\Delta z)_b = (1.000~\pm 0.006)~~ +~~ (0.015~\pm 0.006)~ \Delta z .$      

The zenith-correlated gradient therefore arises predominantly from CR events in the gamma-ray-like $\bar{w}$ regime.

This gradient actually comprises two components: (1) the naturally expected event rate dependence upon zenith angle for a Cerenkov detection instrument, and (2) using in the construction of the $\bar{w}$ parameter which employs a zenith-dependent scaling, the tracking zenith angle instead of that for each individual event. Here, the template model is demonstrated for a type of worst-case-scenario, without removing component (2). Component (1) is usually of order few percent per degree for data taken at zenith angles such in the Tycho's SNR dataset.

It should also be noted that Eq. (1) takes no account of statistical errors in the normalisation $\alpha $, and the template correction terms. These errors are however generally less than one percent (for obs. time >10 h) and can be neglected given the high significance levels to which these parameters are estimated.

References


Copyright ESO 2003