P. Gurfil - N. J. Kasdin
Mechanical and Aerospace Engineering Department, Princeton University, Princeton NJ 08544, USA
Received 3 June 2003 / Accepted 23 June 2003
Abstract
This paper presents a Hamiltonian approach to modelling
relative coorbital motion based on derivation of canonical
coordinates for the relative coorbital dynamics. The Hamiltonian
formulation facilitates the modelling of high-order terms and
orbital perturbations while allowing us to obtain closed-form
solutions to the relative coorbital motion in Hill's restricted
three-body problem. First, the Hamiltonian is partitioned into a
linear term and a high-order term. The Hamilton-Jacobi equations
are solved for the linear part by separation, and new constants
for the relative motions are obtained, called epicyclic orbital
elements. The influence of the gravitational interaction between
the coorbiting satellites is incorporated into the analysis by a
variation of parameters procedure.
Key words: celestial mechanics - planets and satellites: general - reference systems
The motion of any number of mutually gravitating satellites, confined to follow the same mean orbit about a massive primary, is usually referred to as coorbital motion. The coorbital motion problem can be modelled by using either a restricted-three body approach, in which one of the coorbiting objects is assumed to have an infinitesimal mass (Libre & Ollè 2001), or a more general treatment in which the coorbital satellies are assumed to have small, but nonzero, mass (Hénon 1969; Hénon & Petit 1986). The latter approach was originally developed by Hill (1878) and is known as Hill's restricted three-body problem. Applications of Hill's problem are ubiquitous (see e.g. Vilac & Scheers 2003; Scheeres et al. 2003, and the references therein). It has been shown that Hill's problem is characterized by the same generality as that of the restricted three-body problem, in the sense that the mass ration of the coorbiting objects is arbitrary (Hénon 1986).
The restricted three-body problem yields a very rich dynamical structure. In this work, we shall be primarily interested, however, in the 1:1 mean motion commensurability. For this problem, there are a few topologically distinct orbits: Tadpole orbits, taking place about the triangular Lagrangian equilibrium points L4 and L5 (e.g. Trojan asteroids); Horseshoe orbits about the Lagrangian points L3-L4-L5 (e.g. the Saturnian satellites Epimetheus and Janus); and retrograde/prograde coorbital motion (e.g. rings of Saturn).
A number of authors have addressed the coorbital motion problem. Libre & Ollé (2001) have utilized the restricted three-body problem framework to characterize the coorbital motion of Saturnian satellites. Yoder et al. (1983) have offered a simplified qualitative framework for modelling coorbital motion. In a later work, Salo & Yoder (1988) gave sufficiency conditions for the stability of a system of Ncoorbital objects. Namouni (1999) performed an extensive study of coorbital motion using Hill's three-body problem and an orbital elements-based generating solution, an approach reminiscent to that of Winter & Murray (1997), who utilized orbital elements coupled with Lagrange's planetary equations in order to study resonant motion. Broucke (1999) derived a Lagrangian formulation for the study of the 1:1 motion commensurability in the restricted three-body problem. However, thus far, the literature has not presented a canonical modelling methodology for the coorbital relative motion problem.
This paper is aimed at developing canonical orbital elements for modelling the relative coorbital motion problem using Hill's equations. In other words, we attempt to find Delaunay-like canonical elements for the relative motion.
In order to solve the problem, we first write the Lagrangian for the coorbital motion, and then perform a Legendre transformation to find the Hamiltonian. We solve the Hamilton-Jacobi equations and treat the gravitational interaction of the coorbiting objects as a perturbation. The new orbital elements, which we termed epicyclic orbital elements, are constants of the relative motion. Due to the fact that the epicyclic orbital elements are canonical, any given perturbation can be modelled using Hamilton's equation. This methodology offers a simple and general framework for modelling coorbital motion. We illustrate the use of the newly developed methodology by characterizing a few periodic orbits using a numerical search procedure.
We consider the coorbital motion of two bodies of masses m1 and
m2 about a primary of mass M, with
![]() .
The
coorbital motion can be described by any number of possible
coordinate systems. The best coordinate system for our purposes
is the one in which the Hamilton-Jacobi equation most easily
separates. To this end, Cartesian coordinates turn out to be the
most convenient. The work in this paper will be thus confined to a
rotating Cartesian Hill frame. This coordinate system, denoted by
.
The
coorbital motion can be described by any number of possible
coordinate systems. The best coordinate system for our purposes
is the one in which the Hamilton-Jacobi equation most easily
separates. To this end, Cartesian coordinates turn out to be the
most convenient. The work in this paper will be thus confined to a
rotating Cartesian Hill frame. This coordinate system, denoted by
![]() ,
is defined by the unit vectors
,
is defined by the unit vectors
![]() .
The origin of this coordinate
system is set on a circular reference orbit of radius a about
the primary. It is rotating with mean motion
.
The origin of this coordinate
system is set on a circular reference orbit of radius a about
the primary. It is rotating with mean motion
![]() .
The reference orbit plane is the fundamental plane, the positive
.
The reference orbit plane is the fundamental plane, the positive
![]() -axis points radially outward, the
-axis points radially outward, the ![]() -axis is
rotated
-axis is
rotated ![]() in the direction of motion and lies in the
fundamental plane, and the
in the direction of motion and lies in the
fundamental plane, and the ![]() -axis completes the setup to
yield a Cartesian dextral system.
-axis completes the setup to
yield a Cartesian dextral system.
For simplicity, we first treat the case of coorbital motion with respect to a circular reference orbit. This is the most common problem and should easily reduce to Hill's equations. We start with this case because of its simplicity, allowing us to focus attention on the details of the method. Nevertheless, we find that the resulting canonical perturbation equations still provide new and meaningful results. In future work we will present the more involved case of arbitrary elliptical orbits.
We initially assume zero gravitational interaction between the coorbital bodies. We then introduce the gravitational interaction as generalized forces in the Lagrangian formulation and an interaction potential in the Hamiltonian formulation.
The first step is to develop the Lagrangian of the coorbital relative motion in the
rotating frame
![]() .
The velocities of the coorbiting
objects in
.
The velocities of the coorbiting
objects in
![]() is given by the usual equation:
is given by the usual equation:
![\begin{displaymath}\vec{v}_i=\left [ \begin{array}{c}
\dot{x}_i-ny_i \\
\dot{y}_i+nx_i+na \\
\dot{z}_i
\end{array} \right ].
\end{displaymath}](/articles/aa/full/2003/39/aah4571/img16.gif) |
(2) |
| |
= | ![$\displaystyle -\frac{GM}{\Vert\vec{R}_i\Vert}=-\frac{GM}{\Vert
\vec{r}+\mbox{\b...
...\left ( \frac{\displaystyle \rho_i}{\displaystyle a} \right
)^2 \right ]^{1/2}}$](/articles/aa/full/2003/39/aah4571/img21.gif) |
|
| = | 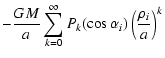 |
(4) |
The Lagrangian
![]() is now easily found by subtracting the
total potential energy from the total kinetic energy,
is now easily found by subtracting the
total potential energy from the total kinetic energy,
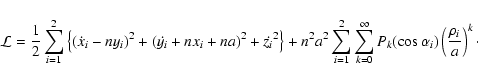 |
(6) |
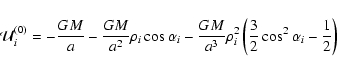 |
(7) |
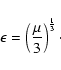 |
(15) |
Based on Eqs. (10)-(12), using the new
generalized coordinate
![]() ,
we can define
the relative motion Lagrangian
,
we can define
the relative motion Lagrangian
Our overall objective is to find the Hamiltonian of the relative
motion and divide it into a linear part and a perturbed part,
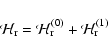
Finding the Hamiltonian for the system is straightforward. First,
we utilize the normalization n=a=1. The canonical momenta are
then found from the usual definition:
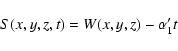
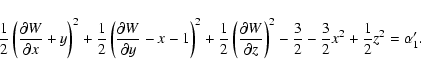 |
(19) |
| W'(x,y)=W1(x)+W2(y)-yx | (24) |
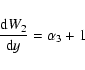
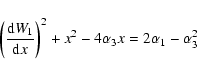 |
(25) |
We call the new constants of the motion
![]() epicyclic orbital elements for the relative motion. They
are defined on the manifold
epicyclic orbital elements for the relative motion. They
are defined on the manifold
![]() ,
where
,
where
![]() .
.
The epicyclic elements described above provide a convenient
parametrization of a first-order relative motion orbit in terms of
amplitude and phase. However, variational equations presented
later for these elements to account for the gravitational
interaction can become quite complicated and numerically
sensitive. This is particularly a concern when some of the
amplitudes approach zero, resulting in the phase terms becoming
ill-defined. For these situations it is convenient to introduce an
alternative set of constants in terms of amplitude variables only. We call these modified epicyclic orbital elements, label
them
![]() ,
and find them via the point transformation:
,
and find them via the point transformation:
| MJMT = J | (48) |
The primary value of the canonical approach is the ease with which
equations for the variations of parameters can be found. For
example, the variations of the epicyclic orbital elements are
given by Hamilton's equations on the perturbation Hamiltonian,
![]() :
:
We illustrate the use of the newly defined orbital elements by
implementing a numerical search procedure aimed at detecting
bounded planar solutions for the dynamical system ![]() .
To
this end, we express the modified epicyclic elements using Fourier
series expansions of the form
.
To
this end, we express the modified epicyclic elements using Fourier
series expansions of the form
Table 1: Initial conditions of modified epicyclic elements.
We emphasize that the optimization procedure described above is static. That is, the differential Eqs. (54)-(59) are transformed into algebraic equations using the pre-defined, periodic, topology of the (candidate) solutions given by Eqs. (61)-(64).
To illustrate the results obtained using the described
methodology, we chose
![]() ,
representing
the coorbital system of the Saturnian satellites Epimetheus and
Janus, and randomly selected initial guesses for
,
representing
the coorbital system of the Saturnian satellites Epimetheus and
Janus, and randomly selected initial guesses for ![]() .
A
number of retrograde quasiperiodic orbits were found. Figure 1
depicts some of these orbits. The top plots in this figure
describe the orbits in the x-y plane, i.e. the configuration
space, and the bottom plots describe the orbits in terms of the
guiding center, defined by
.
A
number of retrograde quasiperiodic orbits were found. Figure 1
depicts some of these orbits. The top plots in this figure
describe the orbits in the x-y plane, i.e. the configuration
space, and the bottom plots describe the orbits in terms of the
guiding center, defined by
![]() .
All
the axes are normalized by
.
All
the axes are normalized by ![]() .
The motion is coorbital if
the guiding center is contained within the annulus of the colinear
Lagrangian equilibrium points L1 and L2. In this case, the
dynamics are determined by the 1:1 mean motion commensurability.
.
The motion is coorbital if
the guiding center is contained within the annulus of the colinear
Lagrangian equilibrium points L1 and L2. In this case, the
dynamics are determined by the 1:1 mean motion commensurability.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{H4571.eps}}
\end{figure}](/articles/aa/full/2003/39/aah4571/Timg172.gif) |
Figure 1:
Quasiperiodic satellite orbits in the x-y plane (top
plots) and their guiding centers in the
|
| Open with DEXTER | |
Orbits (a) represents motion with small magnitude of the guiding
center (meaning small variation of the normalized coordinate
![]() ), orbit (b) represents motion with medium
magnitude, and orbits (c) and (d) represent motion with large
magnitude of the guiding center, which is still contained within
the annulus of the Lagrangian equilibrium points. Similar result
where obtained by Namouni (1999) using classical orbital
elements. The initial conditions used to integrate the equations
of motion (60) are given in Table 1. We emphasize that by
selecting suitable initial conditions, the center of mass of the
coorbital satellites will follow the reference
unit circle. The analysis of the relative motion is then carried out relative to the known motion of the center of mass.
), orbit (b) represents motion with medium
magnitude, and orbits (c) and (d) represent motion with large
magnitude of the guiding center, which is still contained within
the annulus of the Lagrangian equilibrium points. Similar result
where obtained by Namouni (1999) using classical orbital
elements. The initial conditions used to integrate the equations
of motion (60) are given in Table 1. We emphasize that by
selecting suitable initial conditions, the center of mass of the
coorbital satellites will follow the reference
unit circle. The analysis of the relative motion is then carried out relative to the known motion of the center of mass.
This paper developed a Hamiltonian framework for the analysis of coorbital motion in terms of canonical relative motion elements we termed "epicyclic'' orbital elements. The epicyclic elements are constants of the motion.
We conclude that the approach presented above is very useful for modelling coorbital motion. It renders an analytic insight to the coorbital motion problem and yields a convenient framework for numerical analysis of the coorbital motion problem.
There are many extensions to this approach. We are currently working on developing a solution for coorbital motion about elliptical orbits. We are also looking at the perturbations due to zonal and tesseral gravitational harmonics.