We present deep, high velocity resolution (
A. Begum - J. N. Chengalur
National Centre for Radio Astrophysics, Post Bag 3, Ganeshkhind, Pune 411 007, India
Received 15 May 2003 / Accepted 22 July 2003
Abstract
We present deep, high velocity resolution (![]() 1.6 km s-1)
Giant Meterwave Radio Telescope HI 21 cm synthesis images for the faint
(
1.6 km s-1)
Giant Meterwave Radio Telescope HI 21 cm synthesis images for the faint
(
![]() )
dwarf irregular galaxy GR8. We find that the velocity
field of the galaxy shows a clear systematic large scale pattern, with
a maximum amplitude
)
dwarf irregular galaxy GR8. We find that the velocity
field of the galaxy shows a clear systematic large scale pattern, with
a maximum amplitude ![]() 10 km s-1. Neither pure rotation, nor pure
radial motion alone can fit the observed velocity field; however a
combination of radial and circular motions can provide a reasonable
fit. The most natural interpretation is that the neutral ISM, in addition
to rotating about the center, is also expanding outwards, as a result of
energy input from the ongoing star formation in the galaxy. Support
for this interpretation comes from the fact that the pressure in the
HII regions in the galaxy is known to be substantially
(
10 km s-1. Neither pure rotation, nor pure
radial motion alone can fit the observed velocity field; however a
combination of radial and circular motions can provide a reasonable
fit. The most natural interpretation is that the neutral ISM, in addition
to rotating about the center, is also expanding outwards, as a result of
energy input from the ongoing star formation in the galaxy. Support
for this interpretation comes from the fact that the pressure in the
HII regions in the galaxy is known to be substantially
(![]() 55 times)
higher than the average pressure in the gas disk. It is, however, also
possible that the velocity field is the result of the gas swirling
inwards, in which case GR8 could be in the process of formation via
the merger of subgalactic clumps.
55 times)
higher than the average pressure in the gas disk. It is, however, also
possible that the velocity field is the result of the gas swirling
inwards, in which case GR8 could be in the process of formation via
the merger of subgalactic clumps.
Key words: galaxies: evolution - galaxies: dwarf - galaxies: kinematics and dynamics - galaxies: individual: GR8 radio lines: galaxies
Although bright irregular galaxies have rotating gas disks,
it is unclear whether the faintest dwarf irregular galaxies are
rotationally supported or not. Côté et al. (2000), based on a
study of the kinematics of eight dwarf irregular galaxies (with magnitudes
varying from
MB = -16.7 to
MB = -11.3) suggest that
normal rotation is seen only in dwarfs brighter than
![]() .
This is consistent with the earlier findings of Lo et al. (1993), who,
based on an interferometric study of faint dwarf galaxies (with
.
This is consistent with the earlier findings of Lo et al. (1993), who,
based on an interferometric study of faint dwarf galaxies (with
![]() to
to
![]() )
found that only two of their sample
of nine galaxies showed ordered velocity fields. However, this conclusion
has been questioned by Skillman (1996) who pointed out that the
interferometric observations of Lo et al. (1993) lacked sensitivity to
low extended HI distribution and could thus have been insensitive to
the large scale velocity field. Further, Begum et al. (2003) showed that
the dwarf irregular galaxy Camelopardalis B, despite being extremely
faint (
)
found that only two of their sample
of nine galaxies showed ordered velocity fields. However, this conclusion
has been questioned by Skillman (1996) who pointed out that the
interferometric observations of Lo et al. (1993) lacked sensitivity to
low extended HI distribution and could thus have been insensitive to
the large scale velocity field. Further, Begum et al. (2003) showed that
the dwarf irregular galaxy Camelopardalis B, despite being extremely
faint (
![]() )
nonetheless has a regular velocity field,
consistent with that expected from a rotating disk. So, some faint
galaxies at least, have rotating HI disks. What about the rest? If gas in
faint dwarf galaxies is not supported by rotation, what provides the energy
that keeps it from collapse? For very faint dwarf irregular galaxies, the
binding energy of the gas is not much larger than the energy output of a few
supernovae. Star formation in such galaxies could hence have a profound
effect on the kinematics of the ISM.
Indeed, the faintest dwarf galaxies are
expected to lose a substantial part of their gas due to the energy
deposited in the ISM by supernovae from the first burst of star formation
(e.g. Dekel & Silk 1986). Some observational support for such models
is provided by the large expanding HI supershells seen in the ISM of
some dwarf irregular galaxies with active star formation (e.g.
Ott et al. 2001). In this paper we discuss the issue of the kinematics
of faint dwarf galaxies, and its possible connections with energy
input from stellar processes, in the specific context of the
faint (
)
nonetheless has a regular velocity field,
consistent with that expected from a rotating disk. So, some faint
galaxies at least, have rotating HI disks. What about the rest? If gas in
faint dwarf galaxies is not supported by rotation, what provides the energy
that keeps it from collapse? For very faint dwarf irregular galaxies, the
binding energy of the gas is not much larger than the energy output of a few
supernovae. Star formation in such galaxies could hence have a profound
effect on the kinematics of the ISM.
Indeed, the faintest dwarf galaxies are
expected to lose a substantial part of their gas due to the energy
deposited in the ISM by supernovae from the first burst of star formation
(e.g. Dekel & Silk 1986). Some observational support for such models
is provided by the large expanding HI supershells seen in the ISM of
some dwarf irregular galaxies with active star formation (e.g.
Ott et al. 2001). In this paper we discuss the issue of the kinematics
of faint dwarf galaxies, and its possible connections with energy
input from stellar processes, in the specific context of the
faint (
![]() )
dwarf irregular galaxy GR8.
)
dwarf irregular galaxy GR8.
GR8 was first discovered by Reaves (1956) in the course of a survey for dwarf galaxies in the direction of the Virgo Cluster. It has also been cataloged as DDO 155 by van den Bergh (1959). The original distance estimates for GR8 were in the range 1.0-1.4 Mpc (Hodge 1967; De Vaucouleurs & Moss 1983; Hoessel & Danielson 1983), which would make GR8 a probable member of the local group. However, recent estimates give somewhat larger distances. Tolstoy et al. (1995) estimated a distance of 2.2 Mpc (based on observations of the only detected Cepheid variable). This estimate is in excellent agreement with that of Dohm-Palmer et al. (1998) which is based on the brightness of the tip of the red giant branch. From the location for the local group barycenter given by Courteau & van den Bergh (1999) one can compute that this distance places GR8 well outside the local group zero velocity surface. Consistent with this, van den Bergh (2000) does not classify GR8 as a member of the local group.
GR8 has a patchy appearance in optical images, with the emission
being dominated by bright blue knots. H-![]() imaging (Hodge 1967)
shows that these knots are sites of active star formation. However, in
addition to the bright blue knots, GR8 also possesses faint extended
emission (Hodge 1967; De Vaucouleurs & Moss 1983), indicative of earlier episodes
of star formation. Indeed, CM diagrams (based on HST imaging,
Dohm-Palmer et al. 1998), show that although the bright star forming knots in
GR8 have stars which are younger than
imaging (Hodge 1967)
shows that these knots are sites of active star formation. However, in
addition to the bright blue knots, GR8 also possesses faint extended
emission (Hodge 1967; De Vaucouleurs & Moss 1983), indicative of earlier episodes
of star formation. Indeed, CM diagrams (based on HST imaging,
Dohm-Palmer et al. 1998), show that although the bright star forming knots in
GR8 have stars which are younger than ![]() 10 Myr, the galaxy also
contains stars which are older than a few Gyr. Despite
this long history of star formation, the metallicity of the star
forming knots in GR8 is extremely low,
10 Myr, the galaxy also
contains stars which are older than a few Gyr. Despite
this long history of star formation, the metallicity of the star
forming knots in GR8 is extremely low, ![]() 3% solar (Skillman
et al. 1988b). This makes it one of the lowest metallicity galaxies known
(Kunth & Östlin 2000). In keeping with this low metallicity, despite
the fact that the star forming regions are expected to be associated with
molecular gas, CO has not been detected in the galaxy (Verter & Hodge 1995).
3% solar (Skillman
et al. 1988b). This makes it one of the lowest metallicity galaxies known
(Kunth & Östlin 2000). In keeping with this low metallicity, despite
the fact that the star forming regions are expected to be associated with
molecular gas, CO has not been detected in the galaxy (Verter & Hodge 1995).
There have been two independent studies of the kinematics of HI
in GR8, both using the VLA. However these two studies resulted in very
different interpretations of the galaxy's kinematics. Carignan et al. (1990)
assumed that the observed velocity field was produced by rotation
and used it to derive a rotation curve. On the other hand Lo et al. (1993)
interpreted the velocity field as being due to radial motions (i.e. either
expansion or contraction). Both of these studies were based on modest
(![]() 6 km s-1) velocity resolution observations. Further both observations
used the VLA C array, and hence were not sensitive to emission from the
extended low surface brightness portions of the HI disk. There has also
been a recent high velocity resolution VLA (Cs array) based study of
GR8 (Young et al. 2003). This study was focused on the local connections
between the ISM and star formation and not the large scale kinematics
of the gas. Although Young et al. (2003) noted that velocity field in GR8 does
show a large scale gradient, they chose to characterize the velocity
field as giving the overall impression of resulting from random
motions.
6 km s-1) velocity resolution observations. Further both observations
used the VLA C array, and hence were not sensitive to emission from the
extended low surface brightness portions of the HI disk. There has also
been a recent high velocity resolution VLA (Cs array) based study of
GR8 (Young et al. 2003). This study was focused on the local connections
between the ISM and star formation and not the large scale kinematics
of the gas. Although Young et al. (2003) noted that velocity field in GR8 does
show a large scale gradient, they chose to characterize the velocity
field as giving the overall impression of resulting from random
motions.
We present here deep, high velocity resolution (![]() 1.6 km s-1)
Giant Meterwave Radio Telescope (GMRT) observations of the HI emission
from GR8 and use them to study the kinematics of this galaxy.
The rest of the paper is divided as follows. The GMRT observations
are detailed in Sect. 2, while the results are presented
in discussed in Sect. 3. Throughout this paper we take
the distance to GR8 to be 2.2 Mpc, and hence its absolute magnitude to
be
1.6 km s-1)
Giant Meterwave Radio Telescope (GMRT) observations of the HI emission
from GR8 and use them to study the kinematics of this galaxy.
The rest of the paper is divided as follows. The GMRT observations
are detailed in Sect. 2, while the results are presented
in discussed in Sect. 3. Throughout this paper we take
the distance to GR8 to be 2.2 Mpc, and hence its absolute magnitude to
be
![]() .
.
The GMRT observations of GR8 were conducted from 16-18 November 2002. The setup for the observations is given in Table 1. Absolute flux calibration was done using scans on the standard calibrators 3C48 and 3C286, one of which was observed at the start and end of each observing run. Phase calibration was done using 1252+119 which was observed once every 30 min. Bandpass calibration was done in the standard way using 3C286.
The data were reduced using standard tasks in classic AIPS. For each run, bad visibility points were edited out, after which the data were calibrated. Calibrated data for all runs were combined using DBCON. The GMRT does not do online doppler tracking - any required doppler shifts have to be applied during the offline analysis. However since the differential doppler shift over our observing interval is much less than the channel width, there was no need to apply an offline correction.
The GMRT has a hybrid configuration (Swarup et al. 1991) with 14 of its
30 antennas located in a central compact array with size ![]() 1 km
(
1 km
(![]() 5 k
5 k![]() at 21cm) and the remaining antennas distributed
in a roughly "Y'' shaped configuration, giving a maximum baseline length
of
at 21cm) and the remaining antennas distributed
in a roughly "Y'' shaped configuration, giving a maximum baseline length
of ![]() 25 km (
25 km (![]() 120 k
120 k![]() at 21 cm). The baselines
obtained from antennas in the central square are similar in length to
those of the "D'' array of the VLA while the baselines between the arm
antennas are comparable in length to the "B'' array of the VLA. A single
observation with the GMRT hence yields information on both large and small
angular scales. Data cubes were therefore made at various (u,v) ranges,
including 0-5 k
at 21 cm). The baselines
obtained from antennas in the central square are similar in length to
those of the "D'' array of the VLA while the baselines between the arm
antennas are comparable in length to the "B'' array of the VLA. A single
observation with the GMRT hence yields information on both large and small
angular scales. Data cubes were therefore made at various (u,v) ranges,
including 0-5 k![]() ,
0-10 k
,
0-10 k![]() ,
0-15 k
,
0-15 k![]() and 0-80
k
and 0-80
k![]() using uniform weighting. At each (u,v) range, a circularly
symmetric Gaussian taper with a FWHM equal to 80% of the (u,v) range was
applied, in order to reduce the sidelobes of the synthesized beam. The
angular resolutions obtained for the various (u,v) ranges listed above
were
using uniform weighting. At each (u,v) range, a circularly
symmetric Gaussian taper with a FWHM equal to 80% of the (u,v) range was
applied, in order to reduce the sidelobes of the synthesized beam. The
angular resolutions obtained for the various (u,v) ranges listed above
were
![]() ,
,
![]() ,
,
![]() and 4
and 4
![]() respectively. All the three low resolution data cubes (i.e. up to 16
respectively. All the three low resolution data cubes (i.e. up to 16
![]() resolution)
were deconvolved using the the AIPS task IMAGR. For the highest resolution
data cube, the signal to noise ratio was too low for CLEAN to work
reliably and hence the 4
resolution)
were deconvolved using the the AIPS task IMAGR. For the highest resolution
data cube, the signal to noise ratio was too low for CLEAN to work
reliably and hence the 4
![]() resolution data cube could
not be deconvolved. Despite this, the low SNR of this image implies that
the inability to deconvolve it does not greatly degrade its dynamic range
or fidelity. The morphology of the emission should hence be accurately
traced, apart from an uncertainty in the scaling factor (this essentially
arises because the main effect of deconvolving weak emission at about the
noise level corresponds to multiplying by a scale factor;
Jörsäter & van Moorsel 1995; Rupen 1999).
resolution data cube could
not be deconvolved. Despite this, the low SNR of this image implies that
the inability to deconvolve it does not greatly degrade its dynamic range
or fidelity. The morphology of the emission should hence be accurately
traced, apart from an uncertainty in the scaling factor (this essentially
arises because the main effect of deconvolving weak emission at about the
noise level corresponds to multiplying by a scale factor;
Jörsäter & van Moorsel 1995; Rupen 1999).
The HI emission from GR8 spanned 28 channels of the spectral cube.
A continuum image was made using the average of remaining line free
channels. No continuum was detected from the disk of GR8 to a ![]() flux limit of 1.8 mJy/Bm (for a beam size of
flux limit of 1.8 mJy/Bm (for a beam size of
![]() ).
We also checked for the presence of any compact continuum sources in
the disk of GR8 by making a high resolution (
).
We also checked for the presence of any compact continuum sources in
the disk of GR8 by making a high resolution (
![]() )
map - no sources associated with the disk of GR8 were detected down
to a
)
map - no sources associated with the disk of GR8 were detected down
to a ![]() limit of 0.6 mJy/Bm.
limit of 0.6 mJy/Bm.
We examined the line profiles at various locations in the galaxy
and found that they were (to zeroth order) symmetric and single peaked.
In the very high column density regions, a double Gaussian and/or
a gauss-hermite fit does provide a somewhat better description of the data,
but even in these regions, the mean velocity produced by the moment
method agrees within the errors with the peak velocity of the profile.
Since we are interested here mainly in the systematic velocities, moment
maps provide an adequate description of the data. Moment maps (i.e.
maps of the total integrated flux (moment 0), the flux weighted velocity
(moment 1) and the flux weighted velocity dispersion (moment 2)) were
made from the data cubes using the AIPS task MOMNT. To obtain the moment
maps, lines of sight with a low signal to noise ratio were excluded by
applying a cutoff at the ![]() level, (
level, (![]() being the rms noise level
in a line free channel), after smoothing in velocity (using boxcar
smoothing three channels wide) and position (using a Gaussian with
FWHM
being the rms noise level
in a line free channel), after smoothing in velocity (using boxcar
smoothing three channels wide) and position (using a Gaussian with
FWHM ![]() times that of the synthesized beam). Maps of the velocity
field and the velocity dispersion were also made in GIPSY using single
Gaussian fits to the individual profiles. The velocities produced by
MOMNT in AIPS are in reasonable agreement with those obtained using a single
Gaussian fit. However the AIPS moment 2 map systematically underestimates
the velocity dispersion (as obtained from Gaussian fitting) particularly
near the edges where the signal to noise ratio is low. This can be
understood as the effect of the thresholding algorithm used by the MOMNT
task to identify the regions with signal. From the Gaussian fitting we find
that the velocity dispersion
times that of the synthesized beam). Maps of the velocity
field and the velocity dispersion were also made in GIPSY using single
Gaussian fits to the individual profiles. The velocities produced by
MOMNT in AIPS are in reasonable agreement with those obtained using a single
Gaussian fit. However the AIPS moment 2 map systematically underestimates
the velocity dispersion (as obtained from Gaussian fitting) particularly
near the edges where the signal to noise ratio is low. This can be
understood as the effect of the thresholding algorithm used by the MOMNT
task to identify the regions with signal. From the Gaussian fitting we find
that the velocity dispersion ![]() is
is ![]() 9.0 km s-1,
and shows only slight variation across the galaxy. This value of
9.0 km s-1,
and shows only slight variation across the galaxy. This value of
![]() and the lack of substantial variation of
and the lack of substantial variation of ![]() across the
galaxy is typical of dwarf galaxies (e.g. Lake et al. 1990; Skillman et al. 1988a).
across the
galaxy is typical of dwarf galaxies (e.g. Lake et al. 1990; Skillman et al. 1988a).
Table 1: Parameters of the GMRT observations.
The global HI emission profile of GR8, obtained from 40
![]() data cube, is shown in Fig. 1. A Gaussian fit to the
profile gives a central velocity (heliocentric) of
data cube, is shown in Fig. 1. A Gaussian fit to the
profile gives a central velocity (heliocentric) of ![]() km s-1.
The integrated flux is
km s-1.
The integrated flux is ![]() Jy km s-1. These are in good agreement
with the values of
Jy km s-1. These are in good agreement
with the values of ![]() km s-1 and 8.78 Jy km s-1 obtained
from single dish observations (Huchtmeier et al. 2000). The good agreement
between the GMRT flux and the single dish flux shows that no flux was
missed because of the missing short spacings in the interferometric
observation. The velocity width at the 50% level (
km s-1 and 8.78 Jy km s-1 obtained
from single dish observations (Huchtmeier et al. 2000). The good agreement
between the GMRT flux and the single dish flux shows that no flux was
missed because of the missing short spacings in the interferometric
observation. The velocity width at the 50% level (
![]() )
is
)
is
![]() km s-1, which again is in good agreement with the
km s-1, which again is in good agreement with the
![]() value of 27 km s-1 determined from the single dish
observations. The HI mass obtained from the integrated profile (taking
the distance to the galaxy to be 2.2 Mpc) is
value of 27 km s-1 determined from the single dish
observations. The HI mass obtained from the integrated profile (taking
the distance to the galaxy to be 2.2 Mpc) is
![]() ,
and the
,
and the
![]() ratio is found to be
ratio is found to be ![]() 1.0 in
solar units.
1.0 in
solar units.
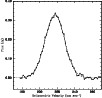 |
Figure 1:
The integrated spectrum for GR8 obtained from the 40
|
| Open with DEXTER | |
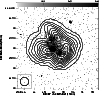 |
Figure 2:
The digitized Palomar Sky Survey image of GR8 (greyscales) with
the GMRT
|
| Open with DEXTER | |
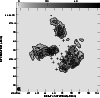 |
Figure 3:
Integrated HI emission at 4
|
| Open with DEXTER | |
Figure 2 shows the integrated HI emission from GR8 at
![]() resolution, overlayed on the digitized sky survey
(DSS) image. The HI distribution is clumpy and shows three major
clumps. This is highlighted in Fig. 3 which shows the integrated
HI emission at high resolution (
resolution, overlayed on the digitized sky survey
(DSS) image. The HI distribution is clumpy and shows three major
clumps. This is highlighted in Fig. 3 which shows the integrated
HI emission at high resolution (
![]() ). The faint
extended HI gas seen in the low resolution image is resolved out in this
image. One may suspect that the diffuse HI emission (particularly that
seen in between the three clumps in the low resolution map) is not real
but is the result of beam smearing. To check for this possibility,
the individual channel maps in the
). The faint
extended HI gas seen in the low resolution image is resolved out in this
image. One may suspect that the diffuse HI emission (particularly that
seen in between the three clumps in the low resolution map) is not real
but is the result of beam smearing. To check for this possibility,
the individual channel maps in the
![]() data cube were
inspected. In the channel maps, the peak of the diffuse emission in the
central region of the galaxy occurs at a different heliocentric velocity
than peak velocities of nearby HI clumps, contrary to what one would expect
from beam smearing. As a further confirmation of this, the clean components
from the
data cube were
inspected. In the channel maps, the peak of the diffuse emission in the
central region of the galaxy occurs at a different heliocentric velocity
than peak velocities of nearby HI clumps, contrary to what one would expect
from beam smearing. As a further confirmation of this, the clean components
from the
![]() resolution data cube were convolved with a
smaller restoring beam of
resolution data cube were convolved with a
smaller restoring beam of
![]() ,
to generate a new data
cube. The diffuse emission is visible in the channel maps in this cube,
contrary to what would have been expected in case the diffuse emission
was entirely due to beam smearing (in which case the clean components
would have been restricted to the three clumps).
,
to generate a new data
cube. The diffuse emission is visible in the channel maps in this cube,
contrary to what would have been expected in case the diffuse emission
was entirely due to beam smearing (in which case the clean components
would have been restricted to the three clumps).
As can be seen in Fig. 2, each HI clump
is associated with a clump of optical emission. However, for each clump,
the peak optical emission is generally offset from the peak of the HI emission. The H![]() image of Hodge et al. (1989) shows that
the optical clumps also emit copious amounts of H
image of Hodge et al. (1989) shows that
the optical clumps also emit copious amounts of H![]() and are
hence regions of ongoing star formation. In addition to the bright
clumps, diffuse optical emission is also seen in Fig. 2.
The optical emission has a much higher ellipticity than the HI emission
and the position angles of the optical and HI major axis can also be seen
to be different. Quantitatively, ellipse fitting to the outermost
contours of the 40
and are
hence regions of ongoing star formation. In addition to the bright
clumps, diffuse optical emission is also seen in Fig. 2.
The optical emission has a much higher ellipticity than the HI emission
and the position angles of the optical and HI major axis can also be seen
to be different. Quantitatively, ellipse fitting to the outermost
contours of the 40
![]() and 25
and 25
![]() resolution
HI moment maps (which are less distorted by the presence of the
HI clumps in the inner regions) gives a position angle of
resolution
HI moment maps (which are less distorted by the presence of the
HI clumps in the inner regions) gives a position angle of
![]() degrees and an inclination (assuming the intrinsic shape
of the HI disk to be circular) of 2
degrees and an inclination (assuming the intrinsic shape
of the HI disk to be circular) of 2![]() degrees. The values
obtained from the two different resolution maps agree to within the
error bars. On the other hand, these values are considerably different from
those obtained from ellipse fitting to the optical isophotes, which
yields a position angle of 38.4 degrees and an inclination of 57.7
degrees respectively (De Vaucouleurs & Moss 1983).
We return to this
issue in Sect. 3.3.
degrees. The values
obtained from the two different resolution maps agree to within the
error bars. On the other hand, these values are considerably different from
those obtained from ellipse fitting to the optical isophotes, which
yields a position angle of 38.4 degrees and an inclination of 57.7
degrees respectively (De Vaucouleurs & Moss 1983).
We return to this
issue in Sect. 3.3.
The velocity field derived from the
![]() resolution data cube is shown in Fig. 4. This velocity field
is in reasonable agreement (albeit of better quality) with that obtained
by Carignan et al. (1990). The velocity field shows closed contours and is,
to zeroth order, consistent with a velocity field that would be
produced by a rotating disk with an approximately north south kinematical
major axis. This would make the kinematical major axis roughly
perpendicular to the major axis obtained from ellipse fitting to
the HI disk. The kinematical major axis is also substantially misaligned
with the major axis obtained by ellipse fitting to the optical isophotes.
In addition to this misalignment, the kinematical center of the velocity
field is offset (to the north, as can be seen by comparing
Figs. 4 and 2) from the center (as determined by
ellipse fitting) of the HI disk.
resolution data cube is shown in Fig. 4. This velocity field
is in reasonable agreement (albeit of better quality) with that obtained
by Carignan et al. (1990). The velocity field shows closed contours and is,
to zeroth order, consistent with a velocity field that would be
produced by a rotating disk with an approximately north south kinematical
major axis. This would make the kinematical major axis roughly
perpendicular to the major axis obtained from ellipse fitting to
the HI disk. The kinematical major axis is also substantially misaligned
with the major axis obtained by ellipse fitting to the optical isophotes.
In addition to this misalignment, the kinematical center of the velocity
field is offset (to the north, as can be seen by comparing
Figs. 4 and 2) from the center (as determined by
ellipse fitting) of the HI disk.
Apart from the misalignments mentioned above, the velocity field of GR8 also shows clear departures from what would be expected from an axisymmetric rotating disk. The most important departure is that the isovelocity contours in the outer regions of the galaxy show large scale kinks. In addition, the velocity field shows several asymmetries. The most prominent asymmetry is between the northern and southern half of the galaxy. The closed isovelocity contours in the southern half are more elongated than those in the northern half. Further, the kinks noted above are much more prominent in the western part of the disk than in the eastern half. Since our velocity field is better sampled compared to the velocity fields derived by Lo et al. (1993) and Carignan et al. (1990) these kinematical peculiarities are more clearly seen. In particular, the offset between the morphological and kinematical center, which is apparent in our velocity field is not seen in velocity fields derived earlier. Further, because of the lower sensitivity, the kinks in the isovelocity contours seen towards the edges of the galaxy are not seen that clearly in the earlier velocity fields.
Following Carignan et al. (1990) we could try to fit GR8's velocity field to that expected from a rotating disk. In such a fit one can anticipate (based on the closed isovelocity contours) that the rotation curve would be falling and (based on the kinks in the isovelocity curves on the eastern and western edges of the disk) that either the rotation curve would need to rise again towards the edge of the disk, or the edges of the disk would need to be warped. We discuss rotation and other models for producing the observed velocity field in more detail in the next section.
 |
Figure 4:
The HI velocity field of GR8 at
|
| Open with DEXTER | |
As described in the last two sections, the morphology and kinematics
of GR8 are somewhat peculiar. If the HI gas and the stars in GR8 are both
in disks, then the stellar disk would have to be both more inclined and have
a different position angle than the gas disk. It is more likely that the
star formation in GR8 has occurred preferentially in a non axisymmetric
symmetric region in the center of the galaxy. In the extreme case, the
stars would have a more bar like distribution than the gas. A central
stellar bar could affect the gas dynamics, however
since the stellar mass is probably not dynamically dominant (from the
observed B-V color of 0.38 for GR8 and the low metallicity models
of Bell & de Jong (2001), the the stellar mass is
![]()
![]() ,
i.e. a factor of 2 less than the HI
mass) this effect may not be important.
,
i.e. a factor of 2 less than the HI
mass) this effect may not be important.
Apart from having a peculiar morphology, the kinematics of GR8 is
also unusual. The kinematical and HI major axis of this galaxy are
perpendicular to each other, the kinematical center is offset from
the morphological center and the observed velocity field is systematically
asymmetric. GR8 is not the only dwarf galaxy which shows misalignment
between kinematical and morphological axes, such misalignments have
also been seen in, for e.g. Sextans A (Skillman et al. 1988a), NGC 625
(Côté et al. 2000) and DDO 26 (Hunter & Wilcots 2002). However, the
misalignment and off-centered kinematics does imply that GR8 cannot be
modeled as a pure axisymmetric rotating disk (for which all axis
and centers would be aligned). Although, Carignan et al. (1990) had noted
some of these problems, they had nonetheless, modeled the kinematics of GR8
as an axisymmetric rotating disk. Their derived rotation curve had a
maximum amplitude of ![]() 8 km s-1, and fell sharply with increasing
galacto-centric distance.
8 km s-1, and fell sharply with increasing
galacto-centric distance.
Our attempts to derive a rotation curve from our velocity field
were not successful. The errors in the estimated parameters were large,
as were the residuals between the model and the observed velocity
field. Our failure to find a good fit
(as opposed to Carignan et al. 1990,
who were able to fit a rotation curve) is probably related to our
better sampling of the velocity field, which, as noted above,
makes the misalignments and asymmetries in the velocity field more
striking. To provide a feel for the velocity field that would be produced
by circular rotation, we show in Fig. 5B the model velocity
field that corresponds to the rotation curve of Carignan et al. (1990).
The disk has been taken to be intrinsically elliptical (with an
axis ratio of 2:1), so that despite having an inclination of ![]() (the inclination angle derived from the velocity field by
Carignan et al. 1990) the projected model HI disk matches the fairly
circular appearance of the observed HI disk. Essentially, the
foreshortening along the kinematical minor axis is offset by
the inherent ellipticity of the disk. As expected, although the model
produces closed isovelocity contours along the apparent morphological HI
minor axis, the asymmetries seen in the closed contours between
northern and southern half of the galaxy, the kinks in the isovelocity
contours towards the edges of the disk, as well as the offset between the
kinematical and morphological center are not reproduced. As discussed
in Sect. 3.2, kinks in the outer isovelocity contours
can be produced by requiring the rotation curve to rise again, or
by requiring the outer parts of the disk to be extremely warped.
Quantitatively, to reproduce the observed kinks, the inclination angle
is required to change by an amount sufficient to
cause the observed velocity at the edges to increase by a factor
of
(the inclination angle derived from the velocity field by
Carignan et al. 1990) the projected model HI disk matches the fairly
circular appearance of the observed HI disk. Essentially, the
foreshortening along the kinematical minor axis is offset by
the inherent ellipticity of the disk. As expected, although the model
produces closed isovelocity contours along the apparent morphological HI
minor axis, the asymmetries seen in the closed contours between
northern and southern half of the galaxy, the kinks in the isovelocity
contours towards the edges of the disk, as well as the offset between the
kinematical and morphological center are not reproduced. As discussed
in Sect. 3.2, kinks in the outer isovelocity contours
can be produced by requiring the rotation curve to rise again, or
by requiring the outer parts of the disk to be extremely warped.
Quantitatively, to reproduce the observed kinks, the inclination angle
is required to change by an amount sufficient to
cause the observed velocity at the edges to increase by a factor
of ![]() 2 compared to the unwarped model. Such extreme warps can,
in principle, lead to multiply peaked line profiles. However, because
of the low signal to noise ratio towards the edges, we cannot reliably
distinguish between single peaked and multiply peaked line profiles in
these regions. A more serious concern in modeling the velocity field of
GR8 as a rotating disk is the observed misalignment between the
kinematical and HI major axes. As noted above, this requires the HI
disk to be inherently elongated with an axis ratio of at least 2:1.
Such a highly non circular disk would be very unusual. Further,
the inner regions of the galaxy (i.e. the distance at which the
rotation curve of Carignan et al. 1990 peaks) will complete one rotation
in
2 compared to the unwarped model. Such extreme warps can,
in principle, lead to multiply peaked line profiles. However, because
of the low signal to noise ratio towards the edges, we cannot reliably
distinguish between single peaked and multiply peaked line profiles in
these regions. A more serious concern in modeling the velocity field of
GR8 as a rotating disk is the observed misalignment between the
kinematical and HI major axes. As noted above, this requires the HI
disk to be inherently elongated with an axis ratio of at least 2:1.
Such a highly non circular disk would be very unusual. Further,
the inner regions of the galaxy (i.e. the distance at which the
rotation curve of Carignan et al. 1990 peaks) will complete one rotation
in ![]() 80 Myr, while the rotation period at the edge of the disk
is
80 Myr, while the rotation period at the edge of the disk
is ![]() 1 Gyr. Hence, this differential rotation will wind up any
elongation in the disk on a timescale that is short compared to the
age of the galaxy.
1 Gyr. Hence, this differential rotation will wind up any
elongation in the disk on a timescale that is short compared to the
age of the galaxy.
 |
Figure 5:
A) The
|
| Open with DEXTER | |
Alternatively, as first proposed by Lo et al. (1993), the observed
velocity field of GR8 could also be the result of radial motions in
the gas i.e. expansion or contraction. Since the sign of the inclination
of the galaxy is unknown, it is not possible to distinguish between
inward and outward radial motions. Large scale bulk radial gas flows,
although difficult to understand in the context of normal spiral
galaxies, could nonetheless be plausible in small galaxies like GR8.
In models of dwarf galaxy formation and evolution, energy injected into
the ISM from stellar winds and supernova explosions could drive
significant expansive motions in the gas. In fact, in such models,
dwarf galaxies below a critical halo circular velocity of
![]() 100 km s-1 are expected to lose a significant fraction of their
ISM from the first burst of star formation (e.g. Dekel & Silk 1986;
Efstathiou 2000). Expulsion of the ISM because of the energy
input from supernovae is also postulated as a possible mechanism
for producing dwarf elliptical galaxies from gas rich progenitors
(e.g. Miralda-Escude & Rees 1997). Observationally, outflows of ionized
material have been seen in star bursting dwarf galaxies
(e.g. Marlowe et al. 1995). Of course, these models deal with the
expulsion of hot supernovae heated gas, where as, in this instance
we are dealing with cold neutral gas. For sufficiently small galaxies
however, model calculations (Ferrara & Tolstoy 2000) suggest that the ISM
could be "blown away'' i.e. that the ambient medium could be swept out
by the hot expanding supernovae superbubbles. This is in contrast to the
situation in slightly larger galaxies where there is instead a
"blow out'' i.e. the supernovae heated hot gas pierces the ambient
disk material and escapes into the intergalactic medium. Although
a situation where the entire ISM is expanding outwards has not
yet been observed, expansion of the neutral ISM on smaller scales
has been observed in a number of starbursting dwarf galaxies.
Such expanding HI supershells have been seen in, for example, Holmberg II
(Puche et al. 1992), IC 2574 (Walter & Brinks 1999) and Holmberg I
(Ott et al. 2001). One should note however, that while the observational
evidence for expanding shells in the ISM of these galaxies is
reasonably good, the mechanism by which these shells have been
created is less well established. Stewart & Walter (2000) find that the giant
supershell in IC 2574 is probably driven by energy input
from supernovae, while Rhode et al. (1999), despite deep optical
imaging, do not find the star clusters that would be expected to be
present in this scenario, at the centers of the HI holes in
Holmberg II.
100 km s-1 are expected to lose a significant fraction of their
ISM from the first burst of star formation (e.g. Dekel & Silk 1986;
Efstathiou 2000). Expulsion of the ISM because of the energy
input from supernovae is also postulated as a possible mechanism
for producing dwarf elliptical galaxies from gas rich progenitors
(e.g. Miralda-Escude & Rees 1997). Observationally, outflows of ionized
material have been seen in star bursting dwarf galaxies
(e.g. Marlowe et al. 1995). Of course, these models deal with the
expulsion of hot supernovae heated gas, where as, in this instance
we are dealing with cold neutral gas. For sufficiently small galaxies
however, model calculations (Ferrara & Tolstoy 2000) suggest that the ISM
could be "blown away'' i.e. that the ambient medium could be swept out
by the hot expanding supernovae superbubbles. This is in contrast to the
situation in slightly larger galaxies where there is instead a
"blow out'' i.e. the supernovae heated hot gas pierces the ambient
disk material and escapes into the intergalactic medium. Although
a situation where the entire ISM is expanding outwards has not
yet been observed, expansion of the neutral ISM on smaller scales
has been observed in a number of starbursting dwarf galaxies.
Such expanding HI supershells have been seen in, for example, Holmberg II
(Puche et al. 1992), IC 2574 (Walter & Brinks 1999) and Holmberg I
(Ott et al. 2001). One should note however, that while the observational
evidence for expanding shells in the ISM of these galaxies is
reasonably good, the mechanism by which these shells have been
created is less well established. Stewart & Walter (2000) find that the giant
supershell in IC 2574 is probably driven by energy input
from supernovae, while Rhode et al. (1999), despite deep optical
imaging, do not find the star clusters that would be expected to be
present in this scenario, at the centers of the HI holes in
Holmberg II.
In light of the above discussion, and the ongoing star formation
in GR8, it may be reasonable to assume that there are large scale radial
flows in the galaxy. If we make this assumption, then the line of sight
velocity
![]() is related to the circular velocity
is related to the circular velocity
![]() and the radial velocity
and the radial velocity
![]() by the relation
by the relation
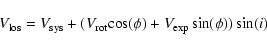 |
(1) |
While a pure expansion model does produce the closed
contours along the morphological minor axis, it does not produce the
asymmetries in the velocity field noted in Sect. 3.2.
The next most natural model to try is hence one in which there is
also some rotation. A velocity field with the same
![]() as
before, but with non zero
as
before, but with non zero
![]() is shown in Fig. 5D.
The rotation curve has been assumed to be linear; it
rises to a maximum of 6 km s-1 at the edge of the galaxy.
A linearly rising rotation curve was chosen because this
form of rotation curve is typical of dwarf galaxies.
Other types of rotation curves, i.e. a constant rotation curve,
a Brandt curve and an exponential curve (which are seldom observed for
dwarf galaxies) were also tried. While a constant rotation curve
gives a poor fit to the data, Brandt and exponential curves do
not provide a better fit to the observed velocity field than that
provided by a linear curve. Since these curves introduce many
more free parameters in the model without improving the fit quality
they were not explored further.
The rotation is assumed to be centered on the morphological center of the galaxy.
The inclination and position angle are the same as for the previous
model. As can be seen, this does reproduce the asymmetry in the kinks
in the isovelocity contours between the eastern and western
halves of the galaxy. However, it still does not reproduce the asymmetries in
the closed contours. A model which does reproduce most of the features
of the observed velocity field is shown in Fig. 5E.
This model is similar to that used to produce Fig. 5D,
the difference being that the expansion curve is no longer assumed
to be azimuthally symmetric. The positions of R1 and R2 in the
expansion curve (see Fig. 5F) were allowed to be different
at different azimuthal angles
in the southern half of the galaxy. However, the maximum amplitude of
the expansion curve was taken to be the same in all
azimuthal directions. The effect of this was to reproduce the
elongated closed contours in the southern half of the galaxy.
This asymmetry between the kinematics in the northern and southern
halves may be related to the corresponding asymmetry in the distribution
of HII regions (see Fig. 3, and also the discussion
below). The match can obviously
be improved by also allowing an azimuth angle dependent
scaling of the amplitude of the expansion curve, but in the absence of a
physically motivated prescription for the scaling factor, this would
not add much to our understanding of the galaxy's kinematics.
It should be noted that it has not been shown that our chosen
model provides a unique (or even "best'' in some rigorous statistical
sense) fit to the observed kinematics of the galaxy. It is possible
that one could find different forms for the expansion and rotation
curves which also provide adequate fits to the observed velocity field.
Strictly speaking, a more robust method would have been to determine a
least squares fit to the observed velocity field, allowing for both
expansion and rotation. This approach has however not been attempted
in this paper.
is shown in Fig. 5D.
The rotation curve has been assumed to be linear; it
rises to a maximum of 6 km s-1 at the edge of the galaxy.
A linearly rising rotation curve was chosen because this
form of rotation curve is typical of dwarf galaxies.
Other types of rotation curves, i.e. a constant rotation curve,
a Brandt curve and an exponential curve (which are seldom observed for
dwarf galaxies) were also tried. While a constant rotation curve
gives a poor fit to the data, Brandt and exponential curves do
not provide a better fit to the observed velocity field than that
provided by a linear curve. Since these curves introduce many
more free parameters in the model without improving the fit quality
they were not explored further.
The rotation is assumed to be centered on the morphological center of the galaxy.
The inclination and position angle are the same as for the previous
model. As can be seen, this does reproduce the asymmetry in the kinks
in the isovelocity contours between the eastern and western
halves of the galaxy. However, it still does not reproduce the asymmetries in
the closed contours. A model which does reproduce most of the features
of the observed velocity field is shown in Fig. 5E.
This model is similar to that used to produce Fig. 5D,
the difference being that the expansion curve is no longer assumed
to be azimuthally symmetric. The positions of R1 and R2 in the
expansion curve (see Fig. 5F) were allowed to be different
at different azimuthal angles
in the southern half of the galaxy. However, the maximum amplitude of
the expansion curve was taken to be the same in all
azimuthal directions. The effect of this was to reproduce the
elongated closed contours in the southern half of the galaxy.
This asymmetry between the kinematics in the northern and southern
halves may be related to the corresponding asymmetry in the distribution
of HII regions (see Fig. 3, and also the discussion
below). The match can obviously
be improved by also allowing an azimuth angle dependent
scaling of the amplitude of the expansion curve, but in the absence of a
physically motivated prescription for the scaling factor, this would
not add much to our understanding of the galaxy's kinematics.
It should be noted that it has not been shown that our chosen
model provides a unique (or even "best'' in some rigorous statistical
sense) fit to the observed kinematics of the galaxy. It is possible
that one could find different forms for the expansion and rotation
curves which also provide adequate fits to the observed velocity field.
Strictly speaking, a more robust method would have been to determine a
least squares fit to the observed velocity field, allowing for both
expansion and rotation. This approach has however not been attempted
in this paper.
Figure 5E shows that the observed velocity
field of GR8 can be quite well matched by a combination of rotational
and expansion motions. Assuming that this interpretation is correct,
the natural question that arises is, what drives the expansion
of the gas? Energy input from star formation is the obvious
suspect. For an expansion velocity of ![]() 10 km s-1 and an HI
mass of
10 km s-1 and an HI
mass of ![]()
![]() the corresponding kinetic energy is
the corresponding kinetic energy is
![]() 1052 erg. If we assume that the kinetic energy imparted
to the ISM by one supernova explosion is
1052 erg. If we assume that the kinetic energy imparted
to the ISM by one supernova explosion is ![]() 1051 erg
(e.g. Reynolds 1988), this implies that kinetic energy required for
the expansion motion is equivalent to the energy output of
1051 erg
(e.g. Reynolds 1988), this implies that kinetic energy required for
the expansion motion is equivalent to the energy output of ![]() 10
supernovae. It is plausible that this number of supernovae have occurred in
GR8 in the recent past. The lack of detection of radio continuum sources
(corresponding to the supernovae remnants) would then place a limit
on the magnetic field in the galaxy. On the other hand, no star
clusters are located at the center of expansion.
However, as can be seen from Fig. 3, the majority
of the HII regions associated with the three HI clumps lie
on the inner edges of the clumps (i.e. towards the center of
the galaxy). In a study of HII regions in dwarf galaxies Elmegreen & Hunter (2000)
found that the HII regions tend to have
a higher pressure than the average pressure in the disk. They
suggest that the HII regions could still be in pressure equilibrium
if they preferentially lie in dense HI clumps, where the ambient
pressure is higher than the average over the disk. Of the sample
of galaxies studied by Elmegreen & Hunter (2000) GR8 showed the largest
pressure anomaly; the pressure in the HII regions was found to
be at least a factor of
10
supernovae. It is plausible that this number of supernovae have occurred in
GR8 in the recent past. The lack of detection of radio continuum sources
(corresponding to the supernovae remnants) would then place a limit
on the magnetic field in the galaxy. On the other hand, no star
clusters are located at the center of expansion.
However, as can be seen from Fig. 3, the majority
of the HII regions associated with the three HI clumps lie
on the inner edges of the clumps (i.e. towards the center of
the galaxy). In a study of HII regions in dwarf galaxies Elmegreen & Hunter (2000)
found that the HII regions tend to have
a higher pressure than the average pressure in the disk. They
suggest that the HII regions could still be in pressure equilibrium
if they preferentially lie in dense HI clumps, where the ambient
pressure is higher than the average over the disk. Of the sample
of galaxies studied by Elmegreen & Hunter (2000) GR8 showed the largest
pressure anomaly; the pressure in the HII regions was found to
be at least a factor of ![]() 55 times larger than the average
disk pressure. Since these HII regions tend to lie at the inner
edges of the HI clumps, this over pressure could possibly drive
the clumps outwards. It is interesting to note in this regard,
that the star formation history of these clumps indicates that
they have been forming stars continuously over at least
last 500 Myr, i.e. the clumps themselves are gravitationally
bound (Dohm-Palmer et al. 1998). The measured expansion velocity
(
55 times larger than the average
disk pressure. Since these HII regions tend to lie at the inner
edges of the HI clumps, this over pressure could possibly drive
the clumps outwards. It is interesting to note in this regard,
that the star formation history of these clumps indicates that
they have been forming stars continuously over at least
last 500 Myr, i.e. the clumps themselves are gravitationally
bound (Dohm-Palmer et al. 1998). The measured expansion velocity
(![]() 10 km s-1) is also considerably smaller than the escape velocity
(which would be
10 km s-1) is also considerably smaller than the escape velocity
(which would be ![]() 30 km s-1, if we assume that GR8 is dark matter
dominated and has a dynamic mass to light ratio
30 km s-1, if we assume that GR8 is dark matter
dominated and has a dynamic mass to light ratio ![]() 10), which
means that the neutral ISM is still bound. This is consistent with the
models of dwarf galaxy evolution which include a clumpy ISM - in such
models the cold clumpy material does not escape from the galaxy
Andersen & Burkert (2000).
10), which
means that the neutral ISM is still bound. This is consistent with the
models of dwarf galaxy evolution which include a clumpy ISM - in such
models the cold clumpy material does not escape from the galaxy
Andersen & Burkert (2000).
So far we have been treating the radial motions as expansion. Since the sign of the radial motion is unconstrained, we should also note that the velocity field could instead arise from infall. In this case, gas is swirling inwards into the galaxy. The model would then be that GR8 is forming from the merger of the three clumps, and that the diffuse gas and stars are material that have been tidally stripped from the clumps and which are now settling down to form a disk. However, in this scenario, it is unclear if one would obtain the observed velocity field, which doesn't show any clear signature of tidal interaction. Another possible infall scenario is that the gas is now falling back towards the center of the potential after a previous expansion phase.
To conclude, we have presented deep, high velocity resolution
(![]() 1.6 km s-1) GMRT HI 21 cm synthesis images for the faint
(
1.6 km s-1) GMRT HI 21 cm synthesis images for the faint
(
![]() )
dwarf irregular galaxy GR8. We find that though the HI
distribution in the galaxy is very clumpy, there is nonetheless
substantial diffuse gas. The velocity field of the galaxy is not chaotic,
but shows a systematic large scale pattern. We are unable to fit this
pattern with either pure rotation or pure expansion. From an inspection
of the velocity field however, the following qualitative remarks can
be made. If this pattern is treated as arising because of rotation,
then (i) the rotation curve would have to be sharply falling, and the
disk would have to be extremely warped at the outer edges and (ii) the disk
has to inherently elliptical, with an axis ratio
)
dwarf irregular galaxy GR8. We find that though the HI
distribution in the galaxy is very clumpy, there is nonetheless
substantial diffuse gas. The velocity field of the galaxy is not chaotic,
but shows a systematic large scale pattern. We are unable to fit this
pattern with either pure rotation or pure expansion. From an inspection
of the velocity field however, the following qualitative remarks can
be made. If this pattern is treated as arising because of rotation,
then (i) the rotation curve would have to be sharply falling, and the
disk would have to be extremely warped at the outer edges and (ii) the disk
has to inherently elliptical, with an axis ratio
![]() 2. Such a
disk would get quickly wound up due to differential rotation. For these
reasons we regard it unlikely that GR8's velocity field is due to
pure rotation. A more likely model is one in which the kinematics
of GR8 can be described as a combination of radial and circular motions.
Such a model provides a reasonable fit to the observed velocity field.
In this interpretation, in case the radial motions are outwards, then
they could be driven by the star formation in GR8; a previous study
(Elmegreen & Hunter 2000) has shown that the pressure in the HII regions in
this galaxy is at least 55 times greater than the average pressure
in the disk. The measured expansion velocity is considerably less than
the estimated escape velocity, so even in this interpretation the cold
gas is still bound to the galaxy. Finally, the radial motions could
also be interpreted as infall, in which case GR8 is either in the
process of formation, or the ISM is falling back after a previous
phase of expansion.
2. Such a
disk would get quickly wound up due to differential rotation. For these
reasons we regard it unlikely that GR8's velocity field is due to
pure rotation. A more likely model is one in which the kinematics
of GR8 can be described as a combination of radial and circular motions.
Such a model provides a reasonable fit to the observed velocity field.
In this interpretation, in case the radial motions are outwards, then
they could be driven by the star formation in GR8; a previous study
(Elmegreen & Hunter 2000) has shown that the pressure in the HII regions in
this galaxy is at least 55 times greater than the average pressure
in the disk. The measured expansion velocity is considerably less than
the estimated escape velocity, so even in this interpretation the cold
gas is still bound to the galaxy. Finally, the radial motions could
also be interpreted as infall, in which case GR8 is either in the
process of formation, or the ISM is falling back after a previous
phase of expansion.
Acknowledgements
The observations presented in this paper would not have been possible without the many years of dedicated effort put in by the GMRT staff in order to build the telescope. The GMRT is operated by the National Centre for Radio Astrophysics of the Tata Institute of Fundamental Research. We are grateful to Rajaram Nityananda for many helpful conversations and valuable comments.