A&A 409, 851-856 (2003)
DOI: 10.1051/0004-6361:20031164

Weak lensing by high-redshift clusters of galaxies

II. Mean redshift of the faint background galaxy population

D. Clowe1,2,[*] - G. A. Luppino2 - N. Kaiser2


1 - Institut für Astrophysik und Extraterrestrische Forschung der Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
2 - Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI 96822, USA

Received 2 May 2003 / Accepted 21 July 2003

Abstract
We use weak lensing shear measurements of six z>0.5 clusters of galaxies to derive the mean lensing redshift of the background galaxies used to measure the shear. Five of these clusters are compared to X-ray mass models and verify a mean lensing redshift for a 23<R<26.3, R-I<0.9 background galaxy population in good agreement with photometric redshift surveys of the HDF-S. The lensing strength of the six clusters is also analyzed as a function of the magnitude of the background galaxies, and an increase in shear with increasing magnitude is detected at moderate significance. The change in the strength of the shear is presumed to be caused by an increase in the mean redshift of the background galaxies with increasing magnitude, and the degree of change detected is also in agreement with those in photometric redshift surveys of the HDF-S.

Key words: cosmology: observations - dark matter - gravitational lensing - galaxies: distances and redshifts - galaxies: clusters: general

1 Introduction

In recent years, spectroscopic surveys of faint galaxies on large aperture telescopes have been able to measure the redshift distribution of the galaxy population brighter than R=24 (e.g. Cohen et al. 2000). Obtaining spectroscopic redshifts for a large sample of galaxies to much fainter magnitudes is not feasible with the current generation of telescopes and spectrographs. Photometric redshifts (e.g. Bolzonella et al. 2000; Fernández-Soto et al. 2001) have been used on deep multi-color fields to obtain redshift estimates for galaxies to $R\sim 28$. These redshift estimates, however, are uncertain as the only tests on the photometric redshifts are from the brighter spectroscopically measured galaxies.

Weak gravitational lensing, where one measures the mass of a foreground object by detecting deviations from an isotropic background galaxy ellipticity distribution, can be used to obtain an independent estimate of the mean redshift of a galaxy population. Because the strength of the lensing signal varies with both the redshift of the background galaxies and the redshift of the lensing object, comparing the lensing strength of different populations of objects both within a given field and across different fields lensed by varying redshift foreground objects can be used to determine the mean redshift of the galaxy populations. This was attempted by Smail et al. (1994) using a set of three clusters at z=0.26, 0.55, and 0.89. Based primarily on the lack of lensing observed in the high redshift cluster, the data resulted in a best fit for a no evolution model where the majority of the I<25 galaxies were at z<1. It was later determined, however, that the z=0.89 cluster used had a very low X-ray luminosity (Castander et al. 1994). If the low X-ray luminosity is interpreted as a low mass, the lack of a weak lensing signal by this cluster would no longer constrain the faint galaxies to be at low redshift.

A weak lensing signal was detected in the high-redshift cluster MS 1054-0321, at z=0.826, by Luppino & Kaiser (1997), which implied that a large fraction of the $I\sim25$ galaxies must be at z>1. With the goals of determining the mass and dynamical state of X-ray selected, high-redshift clusters of galaxies and determining the mean redshift of the faint blue galaxy (FBG) population, we have undertaken a survey of six z>0.5 clusters. We selected as our sample of clusters the five EMSS high-redshift clusters (MS 0015.9+1609 at z=0.546, MS 0451.6-0305 at z=0.550, MS 1054.4-0321 at z=0.826, MS 1137.5+6625 at z=0.782, and MS 2053.7-0449 at z=0.583), which were the only z>0.5 clusters published from a serendipitous X-ray survey at the time, and one from the ROSAT North Ecliptic Pole survey (RXJ 1716.6+6708 at z=0.809) which was discovered shortly after we began our survey (Henry et al. 1997; Gioia et al. 1999). The weak lensing analysis of the clusters have been published (Clowe et al. 1998,2000). In this paper we present the results of our attempts to measure the mean redshift of the FBG population from their weak lensing signal.

In Sect. 2 we present the weak lensing techniques used in our analysis. Comparison of the weak lensing signal and X-ray mass estimates is given in Sect. 3. In Sect. 4 we present the results of direct comparison of the lensing signal of various galaxy populations. Section 5 contains our conclusions. Throughout this paper, unless otherwise stated, we assume an $\Omega _{{\rm m}}=0.3, \Lambda =0.7$ universe, parameterize our results in terms of H0 = 100 h km s-1Mpc-1 and give all errors as 1$\sigma $.

2 Weak lensing

Because the gravitational potential of a cluster of galaxies bends the trajectories of light rays which pass by it, the observed galaxies behind the cluster have been deflected away from the cluster center. In addition, the galaxies have been sheared in one dimension, which for a circularly symmetric cluster is tangential to the cluster center. This shearing results not only in a change of the ellipticity of the galaxy, as defined by the second moments of the surface brightness, but also, because the surface brightness of the galaxy is preserved, in a magnification of the observed flux. These effects are discussed in greater detail in Clowe et al. (2000), as well as in the reviews by Bartelmann & Schneider (2001) and Mellier (1999).

For a single thin lens, such as a cluster of galaxies, the strength of the lens is expressed in the dimensionless mass surface density $\kappa$, where

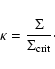\begin{displaymath}\kappa = {\Sigma \over \Sigma _{{\rm crit}}}\cdot \end{displaymath} (1)

$\Sigma $ is the surface density of the cluster, and $\Sigma _{{\rm crit}}$ is a scaling factor:

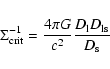\begin{displaymath}\Sigma _{{\rm crit}}^{-1} = {4 \pi G \over c^2}{ D_{{\rm l}} D_{{\rm ls}} \over D_{{\rm s}}} \end{displaymath} (2)

where $D_{{\rm s}}$ is the angular distance to the source (background) galaxy, $D_{{\rm l}}$ is the angular distance to the lens (cluster), and $D_{{\rm ls}}$ is the angular distance from the lens to the source galaxy. The variation of $\Sigma _{{\rm crit}}^{-1}$ with the redshift of the background galaxies and lens redshift is shown in Fig. 1. As can be seen, for low redshift $z\le 0.3$ clusters, $\Sigma _{{\rm crit}}^{-1}$quickly rises at redshifts slightly larger than the cluster, but by $z_{\rm bg} \sim 0.8$ changes very little with background galaxy redshift. For high redshift ($z\ge 0.5$) clusters, however, this is not the case, and $\Sigma _{{\rm crit}}^{-1}$ continues to increase with increasing background galaxy redshift throughout the region most background galaxies are likely to reside ( $0.8\le z_{{\rm bg}} \le 4$).
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H4502F1.ps} \end{figure} Figure 1: Plotted above are the values of $\Sigma _{{\rm crit}}^{-1}$as a function of background galaxy redshift for four lens redshifts. The redshifts of the lenses (0.1, 0.25, 0.5, and 0.8) can be determined from where $\Sigma _{{\rm crit}}^{-1}$ becomes 0. While the lower redshift lenses have $\Sigma _{{\rm crit}}^{-1}$ only slowing varying over the expected faint galaxy redshift distribution ($\sim $0.8-2), the higher redshift lenses still have $\Sigma _{{\rm crit}}^{-1}$ being a strong function of background galaxy redshift.
Open with DEXTER

Table 1: Summary of cluster data.

What is measured from the background galaxies, however, is not $\kappa$, but the reduced shear g, which is related to the gravitational shear $\gamma$by

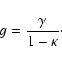\begin{displaymath}g = {\gamma \over 1 - \kappa}\cdot \end{displaymath} (3)

When measuring the shear around a circular aperture, one has the relation that

 \begin{displaymath}\langle \gamma (r)\rangle = \bar{\kappa }(<r) - \langle \kappa (r)\rangle \end{displaymath} (4)

where $\bar{\kappa }(<r)$ is the mean $\kappa$ inside radius r and the $\langle \rangle$ denote the average over the annulus. If $\kappa$ has a small variance along the azimuthally averaged circle,

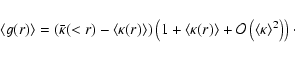\begin{displaymath}\langle g(r)\rangle = \left(\bar{\kappa }(<r) - \langle \kapp... ... \mathcal{O}\left(\langle \kappa \rangle ^2\right)\right)\cdot \end{displaymath} (5)

Thus, at large distances from the cluster, where $\kappa \ll 1$, the strength of the reduced shear signal is effectively linear with $\Sigma _{{\rm crit}}^{-1}$, and a mean background galaxy lensing redshift $\bar{z}_{\rm bg}$ can be defined for a sample of N galaxies with

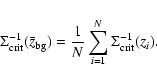\begin{displaymath}\Sigma _{{\rm crit}}^{-1}(\bar{z}_{\rm bg}) = {1\over N} \sum_{i=1}^N \Sigma _{{\rm crit}}^{-1}(z_i). \end{displaymath} (6)

By comparing the shears measured from different populations of galaxies having the same spatial distribution about the lenses, one can then measure directly a ratio in the mean lensing redshifts for the two populations.

A similar equation can be calculated for the non-weak lensing case, when $\kappa \sim 1$, however in this case the effective mean lensing redshift will be a function of the local mass surface density. Further, due to the competing effects of deflection and magnification of the background galaxies, the redshift distribution of a magnitude limited sample of the background galaxies will change with increasing $\kappa$ (e.g. Dye et al. 2001). As a result, accurately comparing the mean lensing redshifts of two galaxy populations near the cores of massive clusters is much harder than at large distances from the cores, and is near impossible without some pre-existing knowledge of the mass distribution of the clusters.

As can be seen in Eq. (4), in the weak lensing limit a sheet of constant density across the field can be added to the cluster surface density without affecting the measured shear. As a result, one cannot determine $\kappa$ or  $\bar{\kappa}$ at a given point uniquely, but can only determine them to within an unknown additive constant. As a result, a useful statistic to use as a mass estimate is aperture densitometry (Fahlman et al. 1994; Clowe et al. 2000),

 
                                     $\displaystyle \zeta _{\rm c}(r_1)$ = $\displaystyle \bar{\kappa }(<r_1) - \bar{\kappa }(r_2<r<r_{\rm max})$  
  = $\displaystyle 2\int_{r_1}^{r_2}{\rm d}\ln r \langle \gamma _{\rm T}\rangle + {2... ...^2\right)} \int_{r_2}^{r_{\rm max}}{\rm d}\ln r \langle \gamma _{\rm T}\rangle,$ (7)

in which the mean kappa in a constant annular region, $\bar{\kappa }(r_2<r<r_{\rm max})$, is subtracted from the  $\bar{\kappa}$ profile of the cluster. This statistic is also linear with $\Sigma _{{\rm crit}}^{-1}$and can therefore be combined with a cluster mass measurement at a given radius from another set of data (X-ray measurements, velocity dispersion, etc.) to determine the mean lensing redshift of the background galaxies. However, unless $\bar{\kappa }(r_2<r<r_{\rm max})$ can also be determined for the comparison mass measurement, then there will be a degeneracy between the assumed $\bar{\kappa }(r_2<r<r_{\rm max})$ and the derived mean lensing redshift.

Further, in the non-weak lensing limit, $\gamma_{\rm T}$in aperture densitometry is replaced by $g_{\rm T}$, and the resulting statistic is no longer measuring $\bar{\kappa }(<r_1) - \bar{\kappa }(r_2<r<r_{\rm max})$. The statistic is also no longer linear with $\Sigma _{{\rm crit}}^{-1}$, but can still be used to find a best fit $\bar{z}_{\rm bg}$ by converting a mass profile, which must cover the same range in r as  $\zeta _{\rm c}$, to a reduced shear profile and calculating the resulting  $\zeta _{\rm c}$statistic to compare with the measured value. If, however, one does have a mass profile determined from an independent data set, one will typically get a higher signal-to-noise measurement by fitting the observed reduced shear profile directly with the mass profile converted to reduced shear profile via the $\Sigma _{{\rm crit}}^{-1}(\bar{z}_{\rm bg})$ fit parameter. In both cases, the fitting for the mean lensing redshift can only be done in regions with a sufficiently low $\kappa$ and $\gamma$ that the magnification and displacement of the background galaxies do not significantly alter the background galaxy redshift distribution.

3 Comparison with X-ray data

All six clusters in the study were detected serendipitously in X-ray surveys, and at the time we created the sample they were the only six z>0.5 clusters discovered in X-ray surveys. As such, they have been targets of extensive studies in X-ray passbands and have published mass models derived from the measured X-ray luminosities and temperatures. In Table 1 are the X-ray temperatures and spherical $\beta $-model fits taken from the literature. The X-ray temperatures are from ASCA observations and $\beta $-model fits from ROSAT observations, except for MS 0451.6-0305, for which all the values are from Chandra observations, and MS 1054.4-0321, for which the temperature is from Chandra observations.
  \begin{figure} \par\includegraphics[width=17cm,clip]{H4502F2.ps} \end{figure} Figure 2: Shown above are the best fit values for the mean lensing redshift of the background galaxy population as a function of $\bar{\Sigma}_{{\rm ann}}$, which is the mean surface mass density in the negative annular region for $\zeta _{\rm c}$ (Eq. (7)), for the five clusters with complete X-ray data. The solid lines are the best fit, and the dashed, dot-dashed, and dotted lines are the 1, 2, and 3-$\sigma $ deviations from the best fit respectively. The vertical lines, with associated error bars, are the surface density for the annular region calculated from the best-fit X-ray $\beta $-model. The horizontal lines, with associated error bars, are the mean lensing redshift calculated from the HDF-S photometric redshift catalog of Fontana et al. (1999) using the same magnitude and color cuts as in the observed data.
Open with DEXTER

The standard model used to fit the X-ray data of the clusters is the $\beta $-model, for which the mass enclosed in a sphere of radius r is

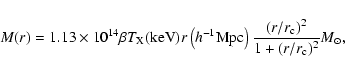\begin{displaymath}M(r) = 1.13\times 10^{14} \beta T_{\rm X}({\rm keV}) r\left(h... ...}\right) {(r/r_{\rm c})^2\over 1+(r/r_{\rm c})^2} {M}_\odot , \end{displaymath} (8)

where $T_{\rm X}$ is the X-ray temperature, $\beta $ and the core radius $r_{\rm c} $ are defined by the gas density $\rho (r) \propto [1+(r/r_c)^2]^{-3\beta +1/2}$, and the cluster is assumed to be isothermal and in hydrostatic equilibrium. For comparison with weak lensing, the mass density must be integrated along the line of sight to get the surface mass density
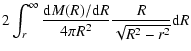                             $\displaystyle \Sigma (r)$ = $\displaystyle 2 \int _{r}^{\infty } {{\rm d}M(R)/{\rm d}R\over 4 \pi R^2} {R \over \sqrt{R^2 - r^2}} {\rm d}R$  
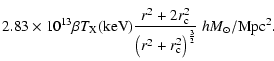  = $\displaystyle 2.83\times 10^{13} \beta T_{\rm X}({\rm keV}) {r^2 + 2r_{\rm c}^2 \over \left(r^2 + r_{\rm c}^2\right)^{3\over 2}} ~h {M}_\odot /{\rm Mpc}^2.$ (9)

This can then be integrated over a disk to give the mean surface density

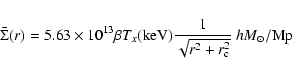\begin{displaymath}\bar{\Sigma }(r) = 5.63\times 10^{13} \beta T_x({\rm keV}) {1\over \sqrt{r^2+r_{\rm c}^2}} ~h {M}_\odot /{\rm Mpc}^2. \end{displaymath} (10)

Shown in Fig. 2 are the results when the ROSAT mass models are compared to the weak lensing $\zeta _{\rm c}$ statistic at a radius of 350  h-1kpc from the cluster center. The 350  h-1 kpc radius was arbitrarily chosen for the comparison as it is the largest radius for which the clusters have a good signal-to-noise on $\zeta _{\rm c}$ but a low enough expected value of $\kappa$ to have the systematic error in assuming that the measured value reduced shear g is actually the shear $\gamma$ be insignificant when compared to the random error on $\zeta _{\rm c}$. Further, 350  h-1kpc is also roughly the maximum radius for which all of the clusters have measured ROSAT X-ray luminosities, and thus not requiring the X-ray mass model to be extrapolated outside of the region containing measured data.

In the above comparison, all of the background galaxies were de-magnified before applying magnitude cuts to the catalog by the amount $m_{\rm demag} = m_{\rm orig} - 2.5 \log~ ((1-\kappa)^2 - \gamma ^2)$ by assuming that $\kappa (r)= \gamma (r)= g(r)$, and using the best fit $\gamma ^{-1}$ model to the measured reduced shear over a $350 ~h^{-1}~{\rm kpc} < r < r_{{\rm max}}$ range to calculate $\gamma (r)$. This is a first order correction to the magnification of the observed background galaxy population, and thus should make the observed population be on average the same as those observed in blank fields. However, because the lensing strength, and thus the magnification, is a function of the redshift of the galaxies, the average magnification which we corrected for will be slightly too low for high redshift galaxies and too high for low redshift galaxies. Thus, higher redshift galaxies will still be slightly magnified and lower redshift galaxies will be slightly de-magnified. This will result in a slight overestimation of $\bar{z}_{\rm bg}$ by this method, but from simulations we have determined this systematic error is an order of magnitude below the random errors in the measurement. In future, larger data-sets, this error could be minimized by binning the data by colors into groups with similar redshifts.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H4502F3.ps} \end{figure} Figure 3: Shown above are the best fit values for $\Sigma _{{\rm crit}}^{-1}$from comparing the X-ray $\beta $-models with the weak lensing shear profiles as a function of cluster redshift. The horizontal bars intersecting the error bars indicate how much of the error bar is due to the errors in the weak lensing mass measurement, with the remainder due to the uncertainties in the X-ray mass measurement. The four solid curves are the values of $\Sigma _{{\rm crit}}^{-1}$ for background galaxies at redshifts of 1, 1.5, 2, and 3. The dashed curve, with error bars, shows the value of $\Sigma _{{\rm crit}}^{-1}$ from the HDF-S photo-z galaxy catalog.
Open with DEXTER

As can be seen in Fig. 2, if the $\beta $-model of the X-ray clusters is extrapolated to determine the mean $\kappa$ in the annular region subtracted in $\zeta _{\rm c}$, the allowable value for $\bar{z}_{\rm bg}$ is in good agreement with that calculated from photometric redshifts of galaxies with the same magnitude and color range in the HDF-S (Fontana et al. 1999). If one is going to extrapolate the X-ray model over the region containing the measured reduced shear, however, one will obtain both a better signal-to-noise and avoid the systematic error of assuming g is $\gamma$by fitting the reduced shear profile with the $\beta $-model surface mass profile. In Fig. 3 are the best fit values of $\bar{z}_{\rm bg}$ when fitting the shear and mass models over a $300 ~h^{-1} {\rm kpc} < r < r_{\rm max}$range. The 300  h-1 kpc inner radius was chosen to avoid the large changes to the background galaxy redshift distribution which occurs due to the larger magnifications and displacements of the background galaxies near the cluster core.

For these fits, the $\beta $-model was converted from $\Sigma $to $\kappa$ by the fit value $\Sigma _{{\rm crit}}^{-1}$, and used to calculate the reduced shear profile $g(r) = \gamma (r)/(1 - \kappa (r)) = (\bar{\kappa}(r) - \kappa (r))/(1 - \kappa (r))$. The model's  $\kappa (r)$ and  $\gamma (r)$ profiles were then used to calculate and correct for the average magnification for each background galaxy as a function of distance from the cluster center. The magnitude corrected catalog then had the magnitude and color cuts applied to select the catalog used to measure the reduced shear. The measured reduced shear was then compared with the model using a $\chi ^2$ statistic, which was minimized to find the best fit $\Sigma _{{\rm crit}}^{-1}$. The resulting $\Sigma _{{\rm crit}}^{-1}$ measurements can then be converted to a $\bar{z}_{\rm bg}$ for each cluster. For a broad background galaxy redshift distribution, the resulting $\bar{z}_{\rm bg}$ is a function of the lensing cluster redshift due to the change in the $\Sigma _{\rm crit}^{-1}(z_{\rm bg}, z_{\rm cl})$ with cluster redshift. The results are in good agreement with the photometric redshift distribution of faint galaxies from the HDF-S.

It should be noted that the mean lensing background galaxy redshift is a function of magnitude, color, size, and surface brightness cuts placed on the background galaxy catalog. Because the images for the five clusters used in this comparison are similar in exposure times and seeing, the weak lensing results all use the same background galaxy redshift distribution. In general, however, this will not be the case and the mean lensing redshifts as a function of cluster redshift shown in Fig. 3 will not be the mean lensing redshifts of the observations. For each observation, the mean lensing redshift would need to be computed from a redshift catalog by applying the same cuts as are used to select the background galaxies.

4 Changes in shear strength with magnitude

As was discussed in Sect. 2, for a high-redshift lens, the strength of the shear acting on a background galaxy greatly depends on the angular distance of the background galaxy. As the ellipticity induced in the galaxy by the weak lensing shear is smaller than the typical intrinsic ellipticity of the galaxy, one cannot use this to determine angular distances of individual galaxies. One can, however, use this to measure the relative distances of two galaxy samples provided each sample has enough galaxies to reduce the mean intrinsic ellipticity of the sample well below the expected shear level. Ideally one would choose the samples in some manner, such as by using photometric redshifts, which would allow the galaxies inside each sample to be at a similar distance. It is, however, still possible to measure a mean angular distance ratio for two sets of galaxies, each of which has a broad redshift distribution.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H4502F4.ps} \end{figure} Figure 4: Shown above are values for the mean shear for the background galaxies, divided into four magnitude bins (23-24, 24-25, 25-25.7, and 25.7-26.3), relative to the mean shear of the brightest magnitude bin. Only galaxies located further than 350  h-1 kpc from the cluster centers were used to compute the mean shear. The mean shear of the three $z\sim 0.55{-}0.6$ clusters are given by the open circles and the mean shear of the three $z\sim 0.8$ clusters are given by the open squares. The filled circles and squares are the expected shear levels based on the photometric redshifts of the HDF-S galaxies in the same magnitude bins for clusters at z=0.55 and z=0.8 respectively.
Open with DEXTER

In the weak lensing limit, where $g \approx \gamma $, the shear acting upon a galaxy is a function of the lens mass, the galaxy position, the lens and galaxy redshifts, and the cosmological model. If the galaxy samples being compared have the same spatial distribution about a common lens, then the ratio of the mean shears is a function only of the redshift of the lens, the redshift distributions of the samples, and the cosmological model. If the magnification of the background galaxies is corrected for, the galaxy samples around different lenses of similar redshift can be coadded to improve the signal-to-noise of the mean shear ratio.

In Fig. 4 we show the relative strength of the mean shear signal for the three $z\sim 0.8$ clusters and the three $z\sim 0.55$ clusters in four magnitude bins. For both sets of clusters, the strength of the shear signal increases with increasing magnitude, with significances, calculated from Student's t-distribution, of 96.4%, 72.4%, and 96.0% for the $z\sim 0.5$ clusters, $z\sim 0.8$ clusters, and both sets combined respectively. This is consistent with the mean redshift of the background galaxies increasing with magnitude. Also shown in Fig. 4 are the shears which would be measured from the Fontana HDF-S photometric redshifts when using the same magnitude bins.

Due to $\Sigma _{{\rm crit}}^{-1}$ increasing more rapidly for higher redshift lenses, one should, in theory, be able to use multiple lenses at different redshifts to obtain estimates for the redshift distribution of the background galaxies. This can be seen in Fig. 4 in which the difference in the lensing strength predicted by the HDF-S photometric redshift catalogs for the $z\sim 0.8$ and $z\sim 0.55$ lenses continues to increase with increasing magnitude of the background galaxies. This difference, however, is too small to measure with this data set. We estimate that we would need a data set ten times as large (60 clusters) with the same quality of data in order to successfully apply any of the techniques (e.g. Bartelmann & Narayan 1995) to measure the background galaxy redshift distribution.

5 Discussion and conclusions

We have shown that a comparison of weak lensing shear profiles and X-ray $\beta $-models result in best-fit values of $\Sigma _{{\rm crit}}^{-1}$in good agreement with the photometric redshift distribution (Fontana et al. 1999) of the faint galaxies in the HDF-S. This is true for both a model-independent derivation of the weak lensing mass at a given radius and for directly fitting the weak lensing mass with the X-ray $\beta $-model. For both comparison methods, assuming the mean lensing redshift of the HDF-S would result in the weak lensing mass measurements being higher than the X-ray models for both of the $z\sim 0.5$ clusters, while the weak lensing masses would be less than the X-ray mass model for all three of the $z\sim 0.8$clusters. For both sets of clusters, the difference is only of marginal significance. It should be noted, however, that the $\beta $-model fit for RXJ 1716.4+6708 does not provide a good fit to the ROSAT data (Gioia et al. 1999), and that the MS 1054.4-0321 model does not include an extended structure to the west of the cluster core (Neumann & Arnaud 2000) which is included in the weak lensing measurements.

One source of systematic error in the weak lensing mass estimates can be the dilution of the shear signal from blue cluster dwarf galaxies. The background galaxy catalogs were selected from all detected galaxies with 23<R<26.3 and R-I<0.9. The color selection removed the red-sequence of cluster ellipticals from the galaxy catalogs, but would have left some fraction of the bluer cluster galaxies. Cluster galaxies at $z\sim 0.8$are redder in R-I than those at $z\sim 0.5$. As a result, applying the same color cut to both sets of clusters would remove a greater fraction of cluster spirals from the $z\sim 0.8$ background galaxy catalogs than from the $z\sim 0.5$ catalogs. From number counts of dwarf galaxies in nearby clusters (e.g. Trentham 1998), we estimate that the weak lensing shear signal, and thus the derived masses, could be under-predicted by 10-20% for the $z\sim 0.5$clusters. This estimate, however, depends greatly on a lack of evolution in the number counts of dwarf galaxies compared to the cluster L* population.

We also compared the ratio of the shear signals as a function of magnitude, and demonstrate that the measured shear does tend to increase with increasing magnitude. The amount of the increase is again in good agreement with the photometric redshifts of the HDF-S. This result is also in agreement withthat of Hoekstra et al. (2000), who compared the relative lensing strength of galaxies in an HST mosaic of MS 1054.4-0321. The level of noise in our comparison, however, is too great to attempt to obtain a meaningful mean lensing redshift as a function of magnitude for the background galaxies.

Acknowledgements
We thank Gillian Wilson, Lev Koffman, Len Cowie, Dave Sanders, John Learned, and Peter Schneider for their help and advice. We also wish to thank Megan Donahue, Isabella Gioia, and J. Patrick Henry for sharing their X-ray data with us. This work was supported by NSF Grants AST-9529274 and AST-9500515, Nasa Grant NAG5-2594, ASI-CNR, and the Deutsche Forschungsgemeinschaft under the project SCHN 342/3-1.

References


Copyright ESO 2003