Chalmers University of Technology/Göteborg University, Department of Astronomy & Astrophysics, 412 96 Gothenburg, Sweden
Received 17 February 2003 / Accepted 23 July 2003
Abstract
We study the evolution of non-linear circularly polarised Alfvén waves by
solving numerically the time-dependent equations of magnetohydrodynamics (MHD)
in one dimension.
We examine the behaviour of the waves and find that different physical
mechanisms are relevant in different ranges of ![]() .
In a low
.
In a low ![]() plasma the wave may undergo a parametric decay. This is because
the wave excites a density enhancement that travels slower than the wave
itself and thus interacts with the wave.
When
plasma the wave may undergo a parametric decay. This is because
the wave excites a density enhancement that travels slower than the wave
itself and thus interacts with the wave.
When
![]() the density enhancement does not interact with the wave and no
decay takes place, instead the Alfvén wave is reflected against the density
enhancement.
The reflection zone propagates with the speed
the density enhancement does not interact with the wave and no
decay takes place, instead the Alfvén wave is reflected against the density
enhancement.
The reflection zone propagates with the speed
![]() .
Because of that the magnetic flux is conserved which results in an amplification
of the oscillating magnetic field by a factor
.
Because of that the magnetic flux is conserved which results in an amplification
of the oscillating magnetic field by a factor
![]() .
We find that
n depends on
.
We find that
n depends on ![]() ,
and that in particular it is
,
and that in particular it is ![]() 1
for values of
1
for values of
![]() and
and ![]() 1 for
1 for
![]() .
We discuss the relevance of these mechanisms to the acceleration of the
solar wind, and the triggering of MHD turbulence in the polar wind region.
In particular these simulations can explain the presence
of inward propagating Alfvén waves in the solar corona.
.
We discuss the relevance of these mechanisms to the acceleration of the
solar wind, and the triggering of MHD turbulence in the polar wind region.
In particular these simulations can explain the presence
of inward propagating Alfvén waves in the solar corona.
Key words: MHD - waves - solar wind - stars: mass-loss
The expanding coronal model proposed by Parker (1958) predicted the existence of the solar wind. Observations by space probes showed later that there are two forms of solar wind: the slow solar wind (up to 400 km s-1) which fits the Parker model, and the fast solar wind (up to 800 km s-1) which emanates from the coronal holes, regions in the solar corona with open magnetic field lines and low density.
Large amplitude, low frequency, Alfvén waves have been observed in the solar corona for over 30 years (e.g. Belcher & Davis 1971). During the last decade Ulysses has provided plasma and magnetic field measurements that have allowed extensive investigations of the behaviour of Alfvénic turbulence in the high-latitude solar wind. The data shows a strong correlation between the fluctuations in velocity and magnetic fields (Smith et al. 1995), and revealed the presence of both inward and outward directed Alfvén waves (e.g Bavassano et al. 2000). While the outward going waves are expected to be generated at the coronal base, the source of the inward going waves in the solar wind is not yet understood.
Alfvén waves play a crucial role in several models for the acceleration of the fast solar wind (e.g. Leer et al. 1982). An attractive feature of the Alfvén waves is that they can propagate over vast distances since they are incompressible to lowest order, and therefore do not dissipate easily. However, dissipative damping is required at some point to avoid too high wind velocities (e.g. Holzer et al. 1983).
In two dimensions phase mixing
due to a transverse gradient in the phase velocity (e.g. Heyvaerts &
Priest 1983) can lead to a strong damping of the wave.
This mechanism is not available in one dimension though, and one has then
rather to consider the nonlinear coupling of the Alfvén wave with other
modes (e.g. Wentzel 1973).
A close examination of the properties of Alfvén waves shows that a
linearly polarised Alfvén wave is compressible to second order though,
because the magnetic pressure,
![]() ,
is modulated on half
the wave length of the Alfvén wave itself
(Alfvén & Fälthammar 1963).
This opens up the possibility that a high-amplitude Alfvén wave can
steepen, which was demonstrated analytically by Cohen & Kulsrud (1974).
As the wave steepens, it forms current sheets at the nodes of the
fluctuating magnetic field.
This effect has been studied in numerical simulations by Boynton
& Torkelsson (1996) and Ofman & Davila (1997).
,
is modulated on half
the wave length of the Alfvén wave itself
(Alfvén & Fälthammar 1963).
This opens up the possibility that a high-amplitude Alfvén wave can
steepen, which was demonstrated analytically by Cohen & Kulsrud (1974).
As the wave steepens, it forms current sheets at the nodes of the
fluctuating magnetic field.
This effect has been studied in numerical simulations by Boynton
& Torkelsson (1996) and Ofman & Davila (1997).
In a circularly polarised Alfvén wave, on the other hand, the magnetic pressure is constant along the wave, which is the physical reason why it is an exact solution of the nonlinear MHD equations. However, the wave can still decay via a parametric instability (e.g. Sagdeev & Galeev 1969), which is usually less important than the wave steepening for a linearly polarised Alfvén wave. In this instability a forward propagating Alfvén wave in the presence of a density fluctuation generates a forward propagating acoustic wave and a backward propagating Alfvén wave.
Parametric decay has many applications in plasma physics and astrophysics. In coronal physics it has been proposed to be a possible mechanism to trigger MHD turbulence in regions with relatively smooth density profiles like the polar wind region and to account for the small compressible fluctuations in the solar wind (Goldstein 1978). It is also a candidate for generating the inward propagating Alfvén waves in the solar wind (e.g. Tu & Marsch 1989)
The parametric decay of circularly polarised Alfvén waves has been studied both analytically (e.g. Cohen 1975; Derby 1978; Goldstein 1978; Jayanti & Hollweg 1993) and numerically by several groups (e.g. Del Zanna et al. 2001; Malara et al. 2000; Pruneti & Velli 1997; Ghosh & Goldstein 1994; Ghosh et al. 1994; Umeki & Terasawa 1992). Except for the work by Pruneti & Velli (1997) these studies have been restricted to Alfvén waves in homogeneous media. Most of these numerical simulations have studied how Alfvén waves of different frequencies interact and generate turbulence, and determine the properties of fully developed turbulence. For these purposes it is appropriate to use a model with periodic boundary conditions and introduce Alfvén waves that extend over the entire grid through the initial state (Malara et al. 2000; Del Zanna et al. 2001).
On the contrary we will study how a fresh Alfvén wave falls prey to the parametric instability, which gradually converts it into a backward propagating Alfvén wave and an acoustic wave. To do this we drive the Alfvén wave on one of the boundaries of our model. Since there is no Alfvén wave in the interior initially we are able to study how processes at the propagating wave front eventually lead to the breakdown of the entire Alfvén wave further upstream, a phenomenon that cannot be found using periodic boundary conditions. Our approach is similar to that of Boynton & Torkelsson (1996), who studied linearly polarised Alfvén waves. Since the processes that we study occur gradually it is important to use a grid that extends over many wave lengths to capture them, which limits us to using a one-dimensional model. The need for a very extended grid becomes clear if one compares the works by Torkelsson & Boynton (1998) and Ofman & Davila (1997). Torkelsson & Boynton found a much stronger damping in their one-dimensional model than Ofman & Davila did in their two-dimensional model, but most of the damping occurred beyond the outer boundary of the Ofman & Davila model.
A highly simplified numerical model such as the one that we present in this paper cannot provide a realistic representation of the physics of Alfvén waves in the solar wind, however it can still be useful since it allows us to study a limited number of physical processes in detail. The understanding that we gain from this can then serve as a guide in interpreting some aspects of more complex numerical simulations, such as the ones carried out by Tsiklauri et al. (2002) and Tsiklauri & Nakariakov (2002) and Laveder et al. (2002a,b).
The plan of the paper is the following: In Sect. 2 we describe the basic MHD equations and review the properties of the parametric decay. Our models and results are presented in Sect. 3. We discuss how the results relate to the dynamics of Alfvén waves in the solar wind in Sect. 4 and we summarise our conclusions in Sect. 5.
The equations of ideal isothermal MHD in a homogeneous medium can be
written as
| (4) |
where ![]() is the density,
is the density, ![]() the velocity, p the
pressure,
the velocity, p the
pressure, ![]() the magnetic field, and
the magnetic field, and
![]() the current density.
Equations (1) and (2) express the conservation of mass and momentum, respectively,
and Eq. (3) is the induction equation.
The constraint
the current density.
Equations (1) and (2) express the conservation of mass and momentum, respectively,
and Eq. (3) is the induction equation.
The constraint
![]() is fulfilled by
Eq. (3) if it is imposed as an initial condition.
For fully ionised hydrogen we can write the equation of state as
is fulfilled by
Eq. (3) if it is imposed as an initial condition.
For fully ionised hydrogen we can write the equation of state as
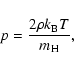 |
(5) |
where ![]() is Boltzmann's constant, T the temperature and
is Boltzmann's constant, T the temperature and
![]() the mass of the hydrogen atom.
the mass of the hydrogen atom.
In a homogeneous medium with a density ![]() and a background magnetic field
and a background magnetic field
![]() a circularly polarised forward propagating
Alfvén wave is described by the transverse magnetic field
a circularly polarised forward propagating
Alfvén wave is described by the transverse magnetic field
| (6) |
and the velocity
while for a backward propagating Alfvén wave the velocity is given by
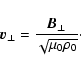 |
(8) |
In both cases the Alfvén wave obeys the dispersion relation
| (9) |
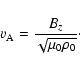 |
(10) |
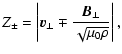 |
(11) |
| (12) |
In the one-dimensional problem that we study, there is only one additional
wave mode, an acoustic wave obeying the dispersion relation
| (13) |
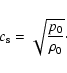 |
(14) |
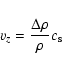 |
(15) |
In the presence of a density fluctuation a circularly polarised Alfvén wave decays into forward propagating density and magnetic waves in addition to a backward propagating magnetic wave. These waves are not necessarily normal modes of the plasma.
Galeev & Oraevskii (1963) and Sagdeev & Galeev (1969) showed that an
Alfvén wave with a frequency
![]() and a wave number
k0 can decay into a backward propagating Alfvén wave with a
frequency
and a wave number
k0 can decay into a backward propagating Alfvén wave with a
frequency ![]() and a wave number k- and a forward propagating
acoustic wave with a frequency
and a wave number k- and a forward propagating
acoustic wave with a frequency ![]() and a wave number k that
fulfill the resonance conditions
and a wave number k that
fulfill the resonance conditions
| (16) |
| k0=k-k- | (17) |
Goldstein (1978) and Derby (1978) derived the dispersion relation for low
frequency waves neglecting dispersive effects
We use the numerical code of Boynton & Torkelsson (1996) to simulate circularly polarised Alfvén waves. This code is based on the ETBFCT algorithm (Boris 1976), a form of flux-corrected transport (Boris & Book 1973). The scheme is fairly inefficient compared to modern methods; it needs about 30 to 40 grid points per wave length of the Alfvén wave, while there are schemes that require only a third of this. However the memory and time requirements for a one-dimensional simulation are sufficiently small that this is acceptable.
The waves are driven on the lower boundary of a one-dimensional box and propagate through a homogeneous medium. In all the runs the grid is sufficiently extended that the wave does not hit the upper boundary during the course of the simulation. The lower boundary condition is formulated in such a way that it only allows an outward propagating Alfvén wave. This can be a problem since backward propagating Alfvén waves are generated in the simulations. These are mostly of low amplitude though, and it is only very late in the simulations that high-amplitude Alfvén waves reach the lower boundary, and the physical processes that we are interested in occur far from the boundary then.
We study waves of different amplitudes, ![]() ,
at different values of
,
at different values of
![]() ,
the ratio of gas pressure to magnetic pressure (Table 1).
The magnetic field is strong in runs 1a-c, that is
,
the ratio of gas pressure to magnetic pressure (Table 1).
The magnetic field is strong in runs 1a-c, that is
![]() ,
intermediate in runs 2a-c and 3a-c, that is
,
intermediate in runs 2a-c and 3a-c, that is
![]() and
weak in runs 4a-c,
that is
and
weak in runs 4a-c,
that is
![]() .
.
Table 1:
Simulations of Alfvén waves in a
homogeneous medium.
The wave is characterised by the two quantities ![]() ,
the amplitude of the imposed Alfvén wave in terms of the vertical
magnetic field, and
,
the amplitude of the imposed Alfvén wave in terms of the vertical
magnetic field, and
![]() the plasma beta.
For the different Runs we further specify the length of the time step
the plasma beta.
For the different Runs we further specify the length of the time step
![]() in terms of the period of the wave, P,
the length of the computational domain, L in terms of the wave length,
in terms of the period of the wave, P,
the length of the computational domain, L in terms of the wave length,
![]() ,
and the number of grid points, N.
,
and the number of grid points, N.
As an example we look at run 1a (
![]() )
with a strong magnetic field and a
low-amplitude Alfvén wave (
)
with a strong magnetic field and a
low-amplitude Alfvén wave (
![]() ).
The propagating wave is shown in Fig. 1b.
The Alfvén wave excites a density enhancement (Fig. 1a), whose
right edge coincides with the front of the Alfvén wave, while the left
edge propagates with the lower speed
).
The propagating wave is shown in Fig. 1b.
The Alfvén wave excites a density enhancement (Fig. 1a), whose
right edge coincides with the front of the Alfvén wave, while the left
edge propagates with the lower speed ![]() .
This density enhancement is a second order effect, and its amplitude is
consequently proportional to the square of the amplitude of the Alfvén
wave.
One should note here that for a linearly polarised wave the corresponding
enhancement shows a strong sinusoidal modulation
(Boynton & Torkelsson 1996).
.
This density enhancement is a second order effect, and its amplitude is
consequently proportional to the square of the amplitude of the Alfvén
wave.
One should note here that for a linearly polarised wave the corresponding
enhancement shows a strong sinusoidal modulation
(Boynton & Torkelsson 1996).
The density discontinuity at the front of the Alfvén wave excites a
secondary compressional wave which becomes more pronounced for the higher
amplitude
run 1b (
![]() ). This wave can be seen as a weak modulation of the
density enhancement
(Figs. 1a and 2a), and also of the magnetic pressure
). This wave can be seen as a weak modulation of the
density enhancement
(Figs. 1a and 2a), and also of the magnetic pressure
![]() .
The density peaks coincide with the peaks of the
magnetic pressure making them a third order analogue of the fluctuations
found by Boynton & Torkelsson (1996, Fig. 2a).
.
The density peaks coincide with the peaks of the
magnetic pressure making them a third order analogue of the fluctuations
found by Boynton & Torkelsson (1996, Fig. 2a).
The density fluctuations serve as the necessary seeds
of the parametric instability, but due to the low amplitude of the
fluctuations the instability grows slowly.
The evolution of the backward-propagating Alfvén wave that is generated by
the instability can be followed in Figs. 2b, d, f and h.
It grows in amplitude away from the wave front,
which
enhances the growth rate of the parametric instability upstream.
Eventually, the instability is so strong that it becomes an efficient source of
a forward-propagating sound wave (Figs. 2a, c, e and g).
We get a region at
![]() in Figs. 2g and h, in which the waves
are strongly interacting. In this region there is a strong damping of the
forward-propagating Alfvén wave, and the acoustic wave is amplified until
it becomes so nonlinear that it steepens into shocks.
On the other hand since the Alfvén speed is larger than the sound speed,
the head of the Alfvén wave manages to stay ahead of the
density fluctuations and therefore remains essentially unaffected by the
parametric decay.
in Figs. 2g and h, in which the waves
are strongly interacting. In this region there is a strong damping of the
forward-propagating Alfvén wave, and the acoustic wave is amplified until
it becomes so nonlinear that it steepens into shocks.
On the other hand since the Alfvén speed is larger than the sound speed,
the head of the Alfvén wave manages to stay ahead of the
density fluctuations and therefore remains essentially unaffected by the
parametric decay.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip,bb=41 623 483 784]{H4318F1....
...m}
\includegraphics[width=8.5cm,clip,bb=41 374 483 559]{H4318F1.ps}
\end{figure}](/articles/aa/full/2003/39/aah4318/Timg78.gif) |
Figure 1:
Low amplitude magnetohydrodynamic waves propagating through a homogeneous
medium of low |
| Open with DEXTER | |
In agreement with the theoretical prediction the sound wave has a wave number
![]() .
Figures 2d and 2f show that there is a phase shift of
.
Figures 2d and 2f show that there is a phase shift of
![]() between the backward- and the forward-propagating Alfvén waves as we expect
if the backward-propagating wave is generated through the parametric
instability.
between the backward- and the forward-propagating Alfvén waves as we expect
if the backward-propagating wave is generated through the parametric
instability.
We look first at the low amplitude wave 2a.
The Alfvén wave is reflected against a density enhancement
at the front of the Alfvén wave (Fig. 3a and 3c).
The density enhancement acts like a
wall that is pushed to the right by the wave.
Figure 3c shows that the reflected wave, represented by z-, has
a phase shift
of ![]() radians relative to the mother wave, which is characteristic of
reflection at a fixed end.
To the left of the density enhancement (Fig. 3a) we see rapid
fluctuations in the
density (cf. the low
radians relative to the mother wave, which is characteristic of
reflection at a fixed end.
To the left of the density enhancement (Fig. 3a) we see rapid
fluctuations in the
density (cf. the low ![]() models).
models).
![\begin{figure}
\par\includegraphics[width=18cm,clip,bb=56 671 552 744]{H4318F2.p...
...mm}
\includegraphics[width=18cm,clip,bb=56 366 552 449]{H4318F2.ps}
\end{figure}](/articles/aa/full/2003/39/aah4318/Timg81.gif) |
Figure 2:
Magnetohydrodynamic waves propagating through a homogeneous
medium of low |
| Open with DEXTER | |
The right edge of the density enhancement travels at a speed
![]() as expected from an acoustic wave, while
the left edge of the density enhancement, that is the front of the Alfvén
wave, travels at
as expected from an acoustic wave, while
the left edge of the density enhancement, that is the front of the Alfvén
wave, travels at
![]() .
As a consequence of this, the measured wave length of the Alfvén wave is
.
As a consequence of this, the measured wave length of the Alfvén wave is
![]() ,
where
,
where
![]() .
We can see also that the wave does not show the ordinary
relation between vx and Bx that we expect for an Alfvén wave
(Fig. 3b).
While the transverse velocity component maintain the relation
.
We can see also that the wave does not show the ordinary
relation between vx and Bx that we expect for an Alfvén wave
(Fig. 3b).
While the transverse velocity component maintain the relation
![]() we find for the fluctuating magnetic field
we find for the fluctuating magnetic field
![]() .
This can be easily understood. During
half a period the injected flux of the x-component of the magnetic field is
.
This can be easily understood. During
half a period the injected flux of the x-component of the magnetic field is
![]() ,
but because the wave propagates at the speed
,
but because the wave propagates at the speed
![]() ,
this magnetic flux is compressed into a distance
,
this magnetic flux is compressed into a distance
![]() ,
which leads to that the magnetic field is amplified by the factor n.
,
which leads to that the magnetic field is amplified by the factor n.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip,bb=68 845 494 1016]{H4318F3...
...m}
\includegraphics[width=8.8cm,clip,bb=68 372 494 562]{H4318F3.ps}
\end{figure}](/articles/aa/full/2003/39/aah4318/Timg91.gif) |
Figure 3:
Magnetohydrodynamic waves propagating through a homogeneous
medium of
|
| Open with DEXTER | |
The dynamics of the reflection zone is more easily studied in a wave
with a higher amplitude, because the extent of the reflection zone
increases with the amplitude of the wave.
We show the reflection zone of model 2b at two different times in Fig. 4.
The density changes smoothly along a positive
slope between the positions A and B.
The slope becomes less steep with time since it is spreading out over a
longer distance.
To the left of A the phase speed
![]() ,
which is the speed at which the wave front is propagating, but between
A and B the phase speed increases to
,
which is the speed at which the wave front is propagating, but between
A and B the phase speed increases to ![]() .
The reason why the wave in run 2b runs slightly faster than the wave in run 2a
is that it is gaining the speed vz
of the medium in which it is propagating; a similar effect was seen in Fig. 13
of Torkelsson & Boynton (1998).
.
The reason why the wave in run 2b runs slightly faster than the wave in run 2a
is that it is gaining the speed vz
of the medium in which it is propagating; a similar effect was seen in Fig. 13
of Torkelsson & Boynton (1998).
There is a gradual damping of the Alfvén wave to the left of A (Fig. 5). This decay is accompanied by a gradual increase of the density. These changes are negligible in the low amplitude runs 2a and 3a.
The higher ![]() models 3a and 3b share the characteristics of models 2a and
2b (with n= 5), but the damping becomes more pronounced.
Because of the increase in the factor n, the wave in model 3b is slower than the
wave in run 2b (Fig. 6).
As shown in Fig. 5b, run 2b has lost
models 3a and 3b share the characteristics of models 2a and
2b (with n= 5), but the damping becomes more pronounced.
Because of the increase in the factor n, the wave in model 3b is slower than the
wave in run 2b (Fig. 6).
As shown in Fig. 5b, run 2b has lost ![]() 13.3% of its Poynting
flux between z = 0 and point A at t = 133 P.
At the same time run 3b has lost
13.3% of its Poynting
flux between z = 0 and point A at t = 133 P.
At the same time run 3b has lost ![]() 26.5% of its Poynting flux.
The stronger damping is associated with a significant modulation of the Alfvén wave
on long length scales (Fig. 6).
26.5% of its Poynting flux.
The stronger damping is associated with a significant modulation of the Alfvén wave
on long length scales (Fig. 6).
At a low magnetic pressure (runs 4a-c) the behaviour of the wave is almost independent of
its amplitude.
As an example we take the high amplitude model 4c with ![]() .
The speed of the front of the Alfvén wave is
.
The speed of the front of the Alfvén wave is ![]()
![]() in models 4a and 4b and
in models 4a and 4b and ![]()
![]() in model 4c.
The higher wave speed in run 4c is the result of that the Alfvén wave has
generated an outflow with a speed
in model 4c.
The higher wave speed in run 4c is the result of that the Alfvén wave has
generated an outflow with a speed ![]()
![]() .
Analogously to models 2 and 3, the amplitude of the magnetic field has
changed with a factor
.
Analogously to models 2 and 3, the amplitude of the magnetic field has
changed with a factor
![]() to compensate for the increase in
the speed of the wave front (Fig. 8b).
The change from sub-Alfvénic waves in runs 2 and 3 to super-Alfvénic waves
in runs 4 is accompanied by a change in the character of the reflection.
Figure 7 shows that there is no phase delay between the two Elsässer
variables
to compensate for the increase in
the speed of the wave front (Fig. 8b).
The change from sub-Alfvénic waves in runs 2 and 3 to super-Alfvénic waves
in runs 4 is accompanied by a change in the character of the reflection.
Figure 7 shows that there is no phase delay between the two Elsässer
variables ![]() ,
which is a characteristic of the reflection of a wave at a free end.
,
which is a characteristic of the reflection of a wave at a free end.
Figure 8 shows the behavior of the wave close to the reflection zone. As in models 2 and 3, the slope in density becomes less steep with time (compare Figs. 7a and 8a). The behaviour of the waves within this zone, in terms of the amplitude and the phase speed is similar to that described in Sect. 3.2 for models 2 and 3 (with n = 1.43). The difference is that the damping of the Alfvén wave outside the reflection zone is too small to be measured.
In constructing models of Alfvén wave driven stellar winds, it is
important to understand the mechanism by which the Alfvén waves are
damped. A linearly polarised Alfvén wave of high amplitude can
steepen and form current sheets even in a homogeneous medium, which
leads to a quick damping of the wave.
While circularly polarised Alfvén waves cannot steepen in this way,
they can be subject to a parametric decay into a backward propagating magnetic
wave and a forward propagating density wave.
Our simulations show
that the compression of the background medium that takes place at
the wave front of an Alfvén wave in a low ![]() plasma is sufficient
to trigger this instability. At
plasma is sufficient
to trigger this instability. At
![]() this is not sufficient to
trigger the parametric decay, but instead we find that the Alfvén wave
is reflected at the wave front, whose speed deviates from the Alfvén
speed.
this is not sufficient to
trigger the parametric decay, but instead we find that the Alfvén wave
is reflected at the wave front, whose speed deviates from the Alfvén
speed.
One can find a large range of ![]() s in the solar corona and solar wind.
Typically
s in the solar corona and solar wind.
Typically
![]() in the lower solar corona, and
in the lower solar corona, and
![]() in
the solar wind (Gary 2001). This means that different processes
may affect Alfvén waves in different parts of the solar corona/wind.
The parametric decay should be at work in the lower solar corona, and
in the presence of sufficiently large fluctuations it may also be at
work in the solar wind as indicated by the numerical simulations of
Del Zanna et al. (2001). Therefore either the parametric decay
or reflection at the wave front may be the source of the inward propagating
Alfvén waves that have been detected in the solar corona (e.g.
Bavassano et al. 2000).
in
the solar wind (Gary 2001). This means that different processes
may affect Alfvén waves in different parts of the solar corona/wind.
The parametric decay should be at work in the lower solar corona, and
in the presence of sufficiently large fluctuations it may also be at
work in the solar wind as indicated by the numerical simulations of
Del Zanna et al. (2001). Therefore either the parametric decay
or reflection at the wave front may be the source of the inward propagating
Alfvén waves that have been detected in the solar corona (e.g.
Bavassano et al. 2000).
An interesting property of the parametric decay is that it is relatively
weak at the wave front, but the backward propagating
Alfvén wave that is generated serves as a seed for the instability
further upstream, where the growth rate therefore becomes larger.
The area close to
the wave front is therefore not significantly affected by the parametric
decay, though the decay becomes strong some distance behind the wave front.
This gives rise to a self-limitation of the length of an Alfvén wave
packet, and it also suggest that, at least in a low-![]() plasma,
the Alfvén wave is the least turbulent right behind the wave front.
In a high-
plasma,
the Alfvén wave is the least turbulent right behind the wave front.
In a high-![]() plasma on the other hand one may expect to see a gradual
change in density right behind the wave front, and further upstream only
oscillations around a constant density.
plasma on the other hand one may expect to see a gradual
change in density right behind the wave front, and further upstream only
oscillations around a constant density.
In this paper we have presented numerical simulations of Alfvén waves in homogeneous media with different magnetic field strengths. In a strongly magnetised plasma the Alfvén wave decays parametrically to a backward propagating Alfvén wave and a forward propagating acoustic wave unless the amplitude of the Alfvén wave is very low. However by its very nature the parametric decay is fairly inefficient at the wave front, even when it is the cause of a strong damping upstream.
For
![]() or higher
we find a different pattern.
The wave front is propagating at the speed
or higher
we find a different pattern.
The wave front is propagating at the speed
![]() and the
magnetic field fluctuations are amplified by a factor n. n > 1
for
and the
magnetic field fluctuations are amplified by a factor n. n > 1
for
![]() but
n < 1 for
but
n < 1 for
![]() .
At the wave front the Alfvén wave is reflected by an extended region with
a positive density gradient.
The spatial extent of this region increases with time.
Inside this region the phase speed of the Alfvén wave is
increasing from
.
At the wave front the Alfvén wave is reflected by an extended region with
a positive density gradient.
The spatial extent of this region increases with time.
Inside this region the phase speed of the Alfvén wave is
increasing from
![]() to
to ![]() .
When n > 1 the reflected Alfvén wave is phase-shifted by
.
When n > 1 the reflected Alfvén wave is phase-shifted by ![]() ,
while
it does not suffer any phase-shift for n < 1. There is also a
significant gradual damping,
,
while
it does not suffer any phase-shift for n < 1. There is also a
significant gradual damping, ![]() 10-20% of the Alfvén wave when n > 1.
10-20% of the Alfvén wave when n > 1.
The results presented in this paper are derived from a highly simplified model, which allows us to isolate a few physical effects and study them in detail. This study can guide us in future investigations of the dynamics of Alfvén waves in more realistic configurations. In forthcoming papers we will discuss the effects of stratification and an expanding magnetic field.
![\begin{figure}
\par\includegraphics[width=17.4cm,clip,bb=63 507 496 609]{H4318F4...
...}
\includegraphics[width=17.4cm,clip,bb=63 368 496 472]{H4318F4.ps}
\end{figure}](/articles/aa/full/2003/39/aah4318/Timg102.gif) |
Figure 4:
Magnetohydrodynamic waves propagating through a homogeneous
medium of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip,bb=69 622 488 784]{H4318F5....
...m}
\includegraphics[width=8.8cm,clip,bb=69 374 488 560]{H4318F5.ps}
\end{figure}](/articles/aa/full/2003/39/aah4318/Timg104.gif) |
Figure 5:
Magnetohydrodynamic waves with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip,bb=69 622 488 784]{H4318F6....
...}
\includegraphics[width=8.8cm,clip,bb=69 374 488 560]{H4318F6.ps}
\end{figure}](/articles/aa/full/2003/39/aah4318/Timg105.gif) |
Figure 6:
Magnetohydrodynamic waves with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip,bb=59 622 480 784]{H4318F7....
...m}
\includegraphics[width=8.8cm,clip,bb=59 374 480 559]{H4318F7.ps}
\end{figure}](/articles/aa/full/2003/39/aah4318/Timg106.gif) |
Figure 7:
Magnetohydrodynamic waves with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip,bb=61 630 490 778]{H4318F8....
...m}
\includegraphics[width=8.6cm,clip,bb=61 376 490 553]{H4318F8.ps}
\end{figure}](/articles/aa/full/2003/39/aah4318/Timg107.gif) |
Figure 8:
Magnetohydrodynamic waves with
|
| Open with DEXTER | |
Acknowledgements
This research was sponsored by the Swedish Research Council. RT wants to thank the solar MHD group at St. Andrews for hospitality during a part of this work. UT and RT thank UKAFF, University of Leicester for hospitality during the completion of this paper. The visitor's programme at UKAFF is sponsored by the EU Fifth Framework Programme.