A&A 409, 1169-1173 (2003)
DOI: 10.1051/0004-6361:20031170
Automated Shack-Hartmann seeing measurements at the South Pole
T. Travouillon1 - M. C. B. Ashley 1 - M. G. Burton
1 - J. W. V. Storey 1 - P. Conroy 2 - G. Hovey 2 - M. Jarnyk 2 - R. Sutherland 2 - R. F. Loewenstein 3
1 - School of Physics, University of New South Wales, Sydney,
NSW, 2052, Australia
2 -
Mount Stromlo Observatory, Australian National University, ACT, 2611, Australia
3 -
University of Chicago, Yerkes Observatory, 373 W.
Geneva Street, Williams Bay, WI 53191, USA
Received 2 June 2003 / Accepted 30 July 2003
Abstract
The statistics and dynamics of the atmospheric seeing at the South Pole have been studied over a period of 101 days in
winter. These measurements have been made with the first fully
autonomous differential image motion monitor, the A-DIMM. The analysis shows
an average seeing of
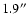 with a standard
deviation of
with a standard
deviation of
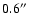 .
The extensive set of data has allowed the study of the seeing time variations,
showing that the seeing varies by a factor of two within a characteristic time of 2 hours.
.
The extensive set of data has allowed the study of the seeing time variations,
showing that the seeing varies by a factor of two within a characteristic time of 2 hours.
Key words: site testing - turbulence
As part of a site testing campaign in Antarctica, the Joint
Australian Centre for Astrophysical Research in Antarctica
(JACARA) has deployed a seeing monitor at the South Pole station.
While the median seeing of the site has already been determined
using CN2 profiles (Marks et al. 1996; Marks et al. 1999;
Travouillon et al. 2003), a direct, quantitative measurement of the
seeing has only been carried out for a limited period of time in
1996 using a DIMM (Bally et al. 1996; Loewenstein et al. 1998).
It was found that, although the South Pole is currently the
world's best ground-based observation site in terms of infrared
sky background, it has poor average seeing of about
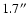 in the visible. On the other hand, the
vertical distribution of the atmospheric turbulence at the site is
very advantageous. The entire turbulence is located within a low
altitude boundary layer about 300 m high and the jet stream is
totally absent. For this reason, the South Pole is predicted to
have a larger isoplanatic angle and coherence time than temperate
sites (Marks et al. 1999; Marks 2002;
Travouillon et al. 2003).
in the visible. On the other hand, the
vertical distribution of the atmospheric turbulence at the site is
very advantageous. The entire turbulence is located within a low
altitude boundary layer about 300 m high and the jet stream is
totally absent. For this reason, the South Pole is predicted to
have a larger isoplanatic angle and coherence time than temperate
sites (Marks et al. 1999; Marks 2002;
Travouillon et al. 2003).
In order to extend our knowledge of the statistical behaviour of
the seeing conditions at the South Pole, the A-DIMM (Automated
Differential Image Motion Monitor) was specially engineered to
work totally autonomously in the cold Antarctic conditions,
measuring the seeing in a semi-continuous manner throughout the
whole Antarctic winter of 2001. The A-DIMM incorporates a
Shack-Hartmann wavefront sensor which uses a microlens array to
split the light entering the telescope and form a series of images
spanning the whole aperture. This technique is very commonly used
in adaptive optics to assess the wavefront abberation. For our
site testing purposes, the A-DIMM acts as an improved DIMM, using
an array of 24 sub-apertures instead of the standard double
aperture, thereby obtaining multiple simultaneous measurements of
the seeing.
In this paper, we present the characteristics of the A-DIMM and
its mount (G-Mount). We also present the results of its first year
of seeing measurements at the South Pole.
The A-DIMM, like all classical DIMMs relies on the method of
differential image motion between two or more sub-apertures of the
instrument to calculate the seeing parameter r0. The theory
of these instruments is described in details in
Roddier (1981).
Like all of the other site testing experiments deployed with the
AASTO (Automated Astrophysical Site Testing Observatory)
Storey et al. (1996), the A-DIMM was designed and built with three
essential requirements. The telescope must be able to endure
temperatures as low as -80 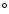 C without losing its optical
properties. It must run in a completely autonomous mode so as to
minimise maintenance and allow for remote operation via satellite.
It must also require only a very small amount of electrical power.
C without losing its optical
properties. It must run in a completely autonomous mode so as to
minimise maintenance and allow for remote operation via satellite.
It must also require only a very small amount of electrical power.
The A-DIMM (Dopita et al. 1996) was built around the optics of a 35 cm diameter Celestron C14. The tube of the telescope was
replaced by an Invar structure in order to better match the
coefficient of expansion of the Pyrex mirrors. This allowed the
A-DIMM to retain its focus between the commissioning in Australia
at
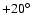 C and the installation at the South Pole at
C and the installation at the South Pole at
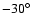 C. Any step at the edge of the window has been
removed to discourage ice build up. The telescope can regularly
park itself into heated cups to sublime any ice that could have
formed on the window.
C. Any step at the edge of the window has been
removed to discourage ice build up. The telescope can regularly
park itself into heated cups to sublime any ice that could have
formed on the window.
The automated Cassegrain instrument is capable of centering a star
by reflecting the light with a pierced mirror onto a finder CCD camera. The information on the star position is used to offset the
telescope in order to let the light pass through the pierced hole
of the mirror onto the Shack-Hartmann optics. This technique is
used to automatically centre the chosen star taken from a
pre-selected catalogue. The catalogue consists of 48 stars with
visual magnitude brighter than 3 and evenly distributed across the
sky. The script used to acquire the data analysed in this paper
runs for 10 hours. It starts observing the first star on the
catalogue and will do so for 30 min unless the star cannot be
found (because of clouds, for example). In either case, it will
then move on to the second star in the script and will continue
this operation until the script time is up. This allows us to
maximise the observation time in case of scattered cloud obscuring
parts of the sky without help of a human intervention.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{gmount_03.eps}\end{figure}](/articles/aa/full/2003/39/aa4040/Timg8.gif) |
Figure 1:
A-DIMM (right) installed at the South Pole on the
G-mount. The instrument on the left if the AFOS. |
| Open with DEXTER |
Once the star is detected and centered, the light is collimated to
form a pupil on the surface of a microlens array. Each square lens
(0.188 mm on a side) forms a separate image of the target star on
the CCD detector with a scale of 1.09(H) 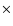 1.26(V) arc sec/pixel,
corresponding to an effective 64 mm square at the entrance aperture
of the telescope. This size is chosen to be smaller than the
typical value of the expected Fried parameter
(Travouillon et al. 2003; Marks et al. 1999) in the spectral
range of the telescope. The A-DIMM freezes the seeing with
exposure times of 10 ms. This number was chosen to be as large as
possible yet within the time range where the atmosphere retains
its statistical properties (
t<r0/vw), using typical wind
speed
1.26(V) arc sec/pixel,
corresponding to an effective 64 mm square at the entrance aperture
of the telescope. This size is chosen to be smaller than the
typical value of the expected Fried parameter
(Travouillon et al. 2003; Marks et al. 1999) in the spectral
range of the telescope. The A-DIMM freezes the seeing with
exposure times of 10 ms. This number was chosen to be as large as
possible yet within the time range where the atmosphere retains
its statistical properties (
t<r0/vw), using typical wind
speed
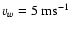 and r0=5 cm.
and r0=5 cm.
With this technique, the A-DIMM obtains 24 images from the corresponding sub-apertures,
making a total of 215 separate baselines satisfying the condition
(d > 2D). Sub-pixel centroiding is then used on each individual
image in order to determine their respective distances. The
accuracy of this method will be discussed in the next section.
Once the information on the coordinates and amplitude of each
image is compressed and stored, the A-DIMM discards the image and
repeats the observation at a rate of one image every five seconds.
While the frequency of the measurements is low compared to other
DIMMs, the large number of baselines improves our statistics.
The A-DIMM was installed at the South Pole station in the summer
1999. The telescope is driven by the G-Mount, an Alt/Az mount
supporting two telescopes. The G-mount can be programmed to
schedule the observation of the two telescopes installed. In 2000,
the A-DIMM was installed aside the AFOS (Antarctic Fibre Optic
Spectrometer, Boccas et al. 1998), but technical problems with the
AFOS allowed 100% of the observation time to be spent with the
A-DIMM during the year 2001. The overall assembly is showed in
Fig. 2.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{gmount.eps}\end{figure}](/articles/aa/full/2003/39/aa4040/Timg11.gif) |
Figure 2:
Cross section through the G-mount assembly with the
A-DIMM and AFOS telescopes. |
| Open with DEXTER |
The G-mount was installed on top on a 7.5 m high hexapod tower
which, in theory, retains its parallelism with the ground under
any wind conditions.
The data are partially processed by the A-DIMM itself in order to
reduce the bandwidth needed to send the data outside the
Antarctic. The DIMM's software calculates the centre of mass of
each of the 24 sub-aperture images that forms within a 9 pixel
square. The centroid coordinates and fluxes are recorded and
compressed before the image is discarded. Every 5 s such an
image is taken and the resulting information (using 322 bytes of
disk space) is appended to the daily file.
The differential image motion is calculated by measuring the
variance of the distance between two sub-aperture images. As seen
in Sect. 2, each baseline gives 2 estimates of the seeing. Every
5 seconds, the 215 baselines therefore measure 430 separate
distances. The variance is then calculated over 25 successive
measurements. The error analysis and the statistical treatment of
the data are now reviewed in detail.
The differential nature of DIMM's operating mode means that the
measurements are unaffected by vibrations of the telescope and
tracking errors. This is a major advantage as it eliminates most
sources of errors. However, as described in Sarazin et al. (1990) and
Tokovinin (2002), subtle effects must be taken into account to
remove potential bias in the measurement of the seeing.
The first source of bias is the accuracy of the centroiding. Under
a zero turbulence condition, the centroid position will vary due
to photon noise and algorithm error. This instrumental noise will
appear as a variance
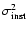 which will be assumed to
be systematic and isotropic. The instrumental variance must be
subtracted out from the total measured variance in order to obtain
the turbulence generated variance:
which will be assumed to
be systematic and isotropic. The instrumental variance must be
subtracted out from the total measured variance in order to obtain
the turbulence generated variance:
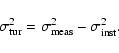 |
(1) |
The instrumental noise was evaluated from a series of short
observations of the binary star system alpha centauri. Since the
seeing has been taken out by the short exposure, the change of
distance between the two stars within a sub-aperture can only be
due to the instrumental noise. The distance between the two stars
within each sub-aperture was calculated using the same algorithm
used for the centroiding. The variance of this distance was then
computed and averaged using all 24 apertures. Under these
conditions, we found that:
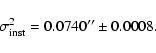 |
(2) |
This value is expected to remain the same for all stars observed,
as they have been chosen to be bright enough to have a negligible
photon noise level. In poor seeing conditions, the development of
speckles and scintillation can increase the centroiding noise.
This effect will however be small compared to the resulting
variance in the seeing between all the baselines.
In a case of multiple baseline measurements, the statistical error
is derived from the standard deviation that results from the
calculation of the seeing at each individual independent baseline.
In good seeing conditions, the centroiding of the single speckle
will be done accurately. When the seeing is poor
(>
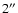 )
the star breaks up in multiple speckles
and each baseline measures a different centroid. Each seeing measurement will therefore carry a variable error, dependent in
a complicated way on the seeing value instead of a constant
percentage error for the single baseline DIMMs
(Sarazin et al. 1990).
)
the star breaks up in multiple speckles
and each baseline measures a different centroid. Each seeing measurement will therefore carry a variable error, dependent in
a complicated way on the seeing value instead of a constant
percentage error for the single baseline DIMMs
(Sarazin et al. 1990).
The error found with the A-DIMM at the South Pole is on average
17%, a value larger than the typical single aperture DIMM (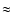 10%). This can be explained by the larger seeing values
measured at the South Pole station, as will be shown in the next
section.
10%). This can be explained by the larger seeing values
measured at the South Pole station, as will be shown in the next
section.
Table 1:
South Pole seeing as measured by the A-DIMM in 2001 at
a wavelength of 500 nm. It is compared to other seeing measurements
done at the South Pole. All values are in arcseconds.
The data presented in this paper represent an extensive coverage
of the seeing conditions at the South Pole Station. Spanning the
major part of the winter night, between the 28 May and the 6 September 2001, 588 individual measurements have been made. A statistical summary of the results is presented in
Table 1 and is compared to other measurements of the
seeing at the site.
The A-DIMM measurements confirm and extend the known seeing
characteristics of the site. Although the turbulence is known to
be concentrated in a thin boundary layer, the resulting ground
level seeing is of poor quality. The seeing drops below
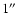 for only 10% of the time. It is noted that the A-DIMM shows a higher average seeing than the H-DIMM or the
microthermals. This can be explained by the autonomous nature of
its operation. The H-DIMM and microthermal data were taken
manually and therefore do not include the more extreme conditions
where no same person would go outside and physically observe. In
such conditions (strong wind, hazy sky) the A-DIMM continues to
take data although they are likely representative of bad seeing.
Figure 3 shows the seeing distribution.
for only 10% of the time. It is noted that the A-DIMM shows a higher average seeing than the H-DIMM or the
microthermals. This can be explained by the autonomous nature of
its operation. The H-DIMM and microthermal data were taken
manually and therefore do not include the more extreme conditions
where no same person would go outside and physically observe. In
such conditions (strong wind, hazy sky) the A-DIMM continues to
take data although they are likely representative of bad seeing.
Figure 3 shows the seeing distribution.
The statistical distribution of the A-DIMM results is in excellent
agreement with the H-DIMM (Loewenstein et al. 1998) seeing
probability. The only noticeable difference between the two data
sets comes from the worst seeing measured. The A-DIMM worst seeing
is
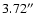 while the H-DIMM recorded seeing as poor
as
while the H-DIMM recorded seeing as poor
as
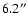 .
We believe that this difference comes
from the lower sampling speed of the A-DIMM. Extremely high seeing
values last for a very short period of time and can therefore be
missed by the A-DIMM.
.
We believe that this difference comes
from the lower sampling speed of the A-DIMM. Extremely high seeing
values last for a very short period of time and can therefore be
missed by the A-DIMM.
Looking at the long-term fluctuations of the seeing
(Fig. 4), no conclusion can be made about a seasonal
dependence of the seeing. The month of July is the most stable, as
was also noticed the year before (2000) by Travouillon at al. The
daily average seeing varies between
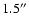 and
and
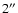 during this period while in June and August
there are variations of up to
during this period while in June and August
there are variations of up to
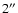 over a few days.
over a few days.
The short term temporal behaviour, has not been studied at the
South Pole before. In fact, although such data are commonly
recorded at observatories, temporal behaviour has only been, to
our knowledge, the subject of two other papers. Racine 1996
and Vernin et al. (1998) studied this characteristic at Mauna Kea and
at the observatory of the Roque de los Muchachos respectively. The
scientific motivation behind this information is the management of
of the observatory schedules. Many observatories now offer a queue
scheduling which prioritorises certain science projects for
windows of particularly good seeing. The duration of these windows
and the level of variation are therefore other figures of merit
that can be associated with a site.
To allow direct comparison, we have followed the technique
developed by Racine (1996). We introduce the temporal
structure function which measures the fractional change of the
seeing over a time period 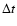 :
:
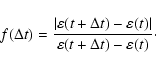 |
(3) |
This expression is related to the seeing ratio over an interval
time 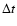 by:
by:
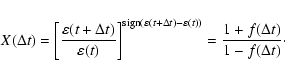 |
(4) |
Provided that the seeing distribution is log-normal
(Vernin et al. 1998), this expression should saturate at
 within a characteristic time
within a characteristic time 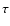 and at a growth
rate
and at a growth
rate 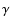 .
The temporal structure function can be represented
by the relation:
.
The temporal structure function can be represented
by the relation:
![\begin{displaymath}%
<f(\Delta t)>\;=\;<f(\infty)>\cdot\;[1-\exp(-\Delta t/\tau)\gamma].
\end{displaymath}](/articles/aa/full/2003/39/aa4040/img29.gif) |
(5) |
We have chosen to estimate the average temporal structure function
using the data from a 5 day period where the seeing was available
continuously for 4 hours at a time at intervals of 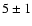 min. Each string was analysed in a manner similar
to Racine (1996) and then averaged. The data were finally
fitted to Eq. (5) with
min. Each string was analysed in a manner similar
to Racine (1996) and then averaged. The data were finally
fitted to Eq. (5) with 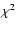 minimisation. The
fitting (see Fig. 5) yields:
minimisation. The
fitting (see Fig. 5) yields:
These results show that the seeing dispersion saturates between
one and three hours to a seeing ratio
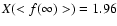 .
Racine (1996) observed a ratio of 1.56 in a characteristic
time of 17 minutes at Mauna Kea. The South Pole seeing therefore
varies more slowly but has larger amplitudes. In fact the
dispersion time at the South Pole is comparable to that measured
by Vernin et al. 1998 using a different mathematical approach at
Roque de los Muchachos (1.2 hours), although the average seeing at
that site is lower (
.
Racine (1996) observed a ratio of 1.56 in a characteristic
time of 17 minutes at Mauna Kea. The South Pole seeing therefore
varies more slowly but has larger amplitudes. In fact the
dispersion time at the South Pole is comparable to that measured
by Vernin et al. 1998 using a different mathematical approach at
Roque de los Muchachos (1.2 hours), although the average seeing at
that site is lower (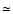
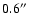 ).
).
Figure 5 shows a large scatter due to the small
amount of data averaged. This scatter is also present in the data
of Racine (1996) and Vernin et al. (1998). A component of this
scatter may be quasi-periodic and previous authors have suggested
that it may arise from gravity-driven atmospheric waves, as their
period matches the period of seeing dispersion. As described
previously, the South Pole seeing is produced by turbulence in a
boundary layer 300 m thick. Gravity waves therefore cannot explain
the variations at the South Pole. Instead, we believe that the
sharp boundary layer causes shear instability. This statement is
supported by Travouillon et al. (2003) who found that the boundary
layer turbulence was strongly correlated with vertical wind
speeds. The periodicity of the seeing might therefore follow the
frequency of the instability waves created at the boundary between
the two air masses near the ground. To investigate this
supposition further, high spatial and time resolution profiles of
the temperature in the low atmosphere would be required.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{tempstructure.EPS}\end{figure}](/articles/aa/full/2003/39/aa4040/Timg34.gif) |
Figure 5:
Average seeing dispersion as a function of time. The
line follows Eq. (5), minimising 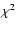 . . |
| Open with DEXTER |
In its first year of measurements, the A-DIMM has successfully
operated in an autonomous mode for a whole winter. This
demonstrates that optical astronomical instrumentation can be
engineered to function successfully in the extreme conditions of
Antarctica without the need for constant human intervention. In
2002 the telescope continued to measure the seeing in order to
obtain further statistics about the site.
So far, the results have confirmed the poor quality of the ground
level seeing. Large improvements can be expected from elevated
telescopes or adaptive optics (Lawrence 2003).
Acknowledgements
This research was supported by grants from the Australian Research Council (ARC) and the Australian Antarctic Division. Logistic
and infrastructure support were supplied by CARA and the NSF. We
also would like thank Jean Vernin for helpful
discussions. We particularly thank the CARA winterover
scientist, Charlie Kaminski, for his outstanding support.
-
Bally, J., Theil, D., Billawala, Y., et al. 1996, Publ. Astron. Soc, Aus., 13, 22-7
In the text
-
Beckmann, P. 1967, Probability in Communication Engineering
(New York: Harcourt, Brace, & Word)
-
Boccas, M., Ashley, M. C. B., Phillips, A., Schinckel, A., & Storey, J. W. V. 1998, PASP, 110, 306
In the text
NASA ADS
-
Dopita, M. A., Wood, P. R., & Hovey, G. R. 1996, PASP, 13, 39
In the text
-
Fried, D. L. 1965, J. Opt. Soc. Am., 55, 1427
NASA ADS
-
Fried, D. L. 1975, Radio Science, 10-1, 71
NASA ADS
-
Lawrence, J. S., Ashley, M. C. B., Burton, M. G., et al. 2002, PASA, 19 no. 3, 328-336
NASA ADS
-
Lawrence, J. S. J. 2003, Opt. Soc. Am., submitted
In the text
-
Loewenstein, R. F., Bero, C., Lloyd, J., et al. 1998, ASP Conf. Ser., 141, 296
In the text
-
Marks, R. D., Vernin, J., Azouit, M., et al. 1996, A&A, 118, 385
In the text
-
Marks, R. D., Vernin, J., Azouit, M., Manigault, J. F., & Clevelin, C. 1999, A&AS, 134, 161
In the text
NASA ADS
-
Marks, R. D. 2002, A&A, 385, 328
In the text
NASA ADS
-
Phillips, A., Burton, M. G., Ashley, M. C. B., et al. 1999, ApJ, 527, 1009
NASA ADS
-
Racine, R. 1996, PASP, 108, 372
In the text
NASA ADS
-
Roddier, F. 1981, in Progress in Optics, ed. E. Wolff, 19, 283
In the text
-
Sarazin, M., & Roddier, F. 1990, A&A, 227, 294
In the text
NASA ADS
-
Storey, J. W. V., Ashley, M. C. B., & Burton, M. G. 1996, PASA, 13, 35
In the text
NASA ADS
-
Tatarski, V. I. 1971, The effect of Turbulent Atmosphere on wave propagation, I.P.S.T, Jerusalem
-
Tokovinin, A. 2002, PASP, 114, 1156
In the text
NASA ADS
-
Travouillon, T., Ashley, M. C. B., Burton, M. G., & Storey, J. W. V. 2003, A&A, 400, 1163
In the text
NASA ADS
-
Vernin, J., & Mu
 oz-Tu
oz-Tu
 n,
C. 1995, PASP, 107, 265
NASA ADS
n,
C. 1995, PASP, 107, 265
NASA ADS
-
Vernin, J., & Mu
 oz-Tu
oz-Tu
 n, C. 1998, New Astron. Rev., 42, 451
In the text
NASA ADS
n, C. 1998, New Astron. Rev., 42, 451
In the text
NASA ADS
Copyright ESO 2003
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{gmount_03.eps}\end{figure}](/articles/aa/full/2003/39/aa4040/Timg8.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{gmount.eps}\end{figure}](/articles/aa/full/2003/39/aa4040/Timg11.gif)
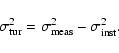
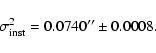
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{adimmstats.EPS}\end{figure}](/articles/aa/full/2003/39/aa4040/Timg18.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{dailyaverage.EPS}\end{figure}](/articles/aa/full/2003/39/aa4040/Timg22.gif)
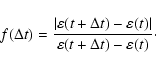
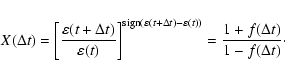
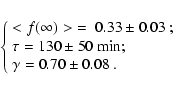
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{tempstructure.EPS}\end{figure}](/articles/aa/full/2003/39/aa4040/Timg34.gif)