S. Ivarsson1 - J. Andersen 2,3 - B. Nordström 1,2 - X. Dai 4 - S. Johansson 1 - H. Lundberg 4 - H. Nilsson 1 - V. Hill 5 - M. Lundqvist 1 - J. F. Wyart 6
1 - Atomic Astrophysics, Lund Observatory, Lund University, PO Box 43,
22100 Lund, Sweden
2 - Astronomical Observatory, Niels Bohr Institute for Astronomy, Physics &
Geophysics, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
3 - Nordic Optical Telescope Scientific Association, La Palma, Canary Islands,
Spain
4 - Atomic Physics, Department of Physics, Lund Institute of Technology, PO
Box 118, 22100 Lund, Sweden
5 - GEPI, Observatoire de Paris-Meudon (UMR 8111),
DASGAL, 2 pl. Jules Janssen, 92195 Meudon
Cedex, France
6 - Laboratoire Aimé Cotton, Centre National de la Recherche Scientifique,
Orsay, France
Received 28 May 2003 / Accepted 25 July 2003
Abstract
The radioactive decay of 238U and 232Th has recently been
used to determine ages for some of the oldest stars in the Universe. This has
highlighted the need for accurate observational constraints on production models
for the heaviest r-process elements which might serve as stable references,
notably osmium and iridium. In order to provide a firmer basis for the observed
abundances, we have performed laser-induced fluorescence measurements and Fourier
Transform Spectroscopy to determine new radiative lifetimes and branching
fractions for selected levels in Os I and Ir I. From these data, we determine new
absolute oscillator strengths and improved wavelengths for 18 Os I and 4 Ir I
lines.
A reanalysis of VLT spectra of CS 31082-001 and new results for other stars with Os and Ir
detections show that (i): the lines in the UV and ![]() 4260 Å yield
reliable Os abundances, while those at
4260 Å yield
reliable Os abundances, while those at
![]() 4135, 4420 Å are
heavily affected by blending; (ii): the Os and Ir abundances are identical
in all the stars; (iii): the heavy-element abundances in very metal-poor
stars conform closely to the scaled solar r-process pattern throughout the
range 56
4135, 4420 Å are
heavily affected by blending; (ii): the Os and Ir abundances are identical
in all the stars; (iii): the heavy-element abundances in very metal-poor
stars conform closely to the scaled solar r-process pattern throughout the
range 56 ![]() Z
Z ![]() 77; and (iv): neither Os or Ir nor any lighter
species are suitable as reference elements for the radioactive decay of Th and U.
77; and (iv): neither Os or Ir nor any lighter
species are suitable as reference elements for the radioactive decay of Th and U.
Key words: atomic data - nuclear reactions, nucleosynthesis, abundances - stars: abundances - stars: individual: CS 31082-001
Very metal-poor halo stars with greatly enhanced abundances of the heaviest
neutron-capture elements have recently been identified (Sneden et al. 1996; Hill et al. 2002).
These stars are of particular interest for two reasons: (i) their heavy
elements were produced by the r-process in a very small number (![]() 1) of
supernovae or similar violent progenitor events in the first generation of stars
in the Galaxy (and in the Universe); and (ii) the abundances of the r-process
elements can be accurately determined, due to the negligible interference from
lines of iron-peak elements. Interest in these stars was greatly heightened by
the recent discovery of uranium in the very metal-poor star CS 31082-001 (Cayrel et al. 2001),
which opened the way to a new, accurate and fundamental method to determine the
age of such ancient stars by radioactive dating.
1) of
supernovae or similar violent progenitor events in the first generation of stars
in the Galaxy (and in the Universe); and (ii) the abundances of the r-process
elements can be accurately determined, due to the negligible interference from
lines of iron-peak elements. Interest in these stars was greatly heightened by
the recent discovery of uranium in the very metal-poor star CS 31082-001 (Cayrel et al. 2001),
which opened the way to a new, accurate and fundamental method to determine the
age of such ancient stars by radioactive dating.
Testing theoretical models for the explosive nucleosynthesis of the heaviest elements, especially as regards their application to radioactive cosmochronology, places strong demands on the atomic parameters used to convert measured stellar line strengths into accurate absolute abundances. Os and Ir are of special interest in this context: These are among the heaviest stable elements that can be observed in metal-poor stars in the optical region and thus potentially more reliable reference elements for the decay of the radioactive species 238U and 232Th than Eu. 232Th/151Eu was used in conventional Th/Eu chronometry, but its initial production ratio is now known to be affected by large uncertainties (Schatz et al. 2002; Wanajo et al. 2002). However, Os and Ir also serve to define the limit in atomic mass below which the r-process elements appear to be produced in constant proportions; above this limit, at least such actinides as Th and U have a component of different origin (Hill et al. 2002; Johnson & Bolte 2002).
Accurate abundances of Os and Ir are therefore of great significance, both in radioactive cosmochronology and as constraints on the structure, variety, and nucleosynthetic yields of supernovae from the first stellar generation. This motivated us to undertake a new determination of oscillator strengths for the astrophysically most important lines of Os I and Ir I. We also redetermine the Os and Ir abundances in CS 31082-001 from an expanded set of lines, reaching significant new conclusions on the production of these elements in the first stars.
Experimental oscillator strengths for neutral osmium (Os I) were first reported by Corliss & Bozman (1962). Later, Kwiatkowski et al. (1984) measured lifetimes for six energy levels, which they used to rescale and adjust some of the f-values of Corliss & Bozman. For neutral iridium (Ir I), experimental oscillator strengths for 27 lines were determined by Gough et al. (1983). They combined radiative lifetimes, measured by a laser-excitation fluorescence technique, with experimental branching fractions obtained from spectra of a Ne-Ir hollow-cathode lamp recorded with an intensity-calibrated monochromator.
In this paper we present radiative lifetimes of four levels of Os I and one level of Ir I, measured at the Lund Laser Centre (LLC) by means of the laser-induced fluorescence (LIF) technique. We also report branching fractions, determined with the Lund UV Fourier Transform Spectrometer (FTS), for transitions from six Os I levels and two Ir I levels. Combining all these new data and one previously measured lifetime for each of Os I and Ir I (Kwiatkowski et al. 1984; Gough et al. 1983), we derive new oscillator strengths for 18 Os I and 4 Ir I lines in the wavelength region 2900-5100 Å. For all the transitions measured we also present improved centre-of-gravity wavelengths.
Osmium has seven stable isotopes with the mass numbers and relative terrestrial
abundances A=184 (0.02%), 186 (1.6%), 187 (1.6%), 188 (13.3%), 189 (16.1%),
190 (26.4%) and 192 (41.0%) (Kröger et al. 2002). The even isotopes, which account
for more than 80% of all osmium, have no hyperfine structure (hfs).
Nevertheless, a weak blue-shifted hfs component is seen for some of the strongest
transitions, resolved from the main spectral feature (see e.g. ![]() 4260 in
Fig. 1). The red-shifted component, resolved in Fig. 1, is due to the isotope shift of the isotopes A=188 and A=189. The
A=184, 186 and 187 isotopes have too low abundances to be observed.
4260 in
Fig. 1). The red-shifted component, resolved in Fig. 1, is due to the isotope shift of the isotopes A=188 and A=189. The
A=184, 186 and 187 isotopes have too low abundances to be observed.
The main spectral feature in Fig. 1 is asymmetric due to the unresolved blend of the two most abundant isotopes, A= 190 and 192, and is thus affected by isotope shift. The extensive study by Kröger et al. (2002) used laser induced fluorescence spectroscopy to resolve and measure the hyperfine structure and isotope shifts of numerous levels and lines in Os I.
The ground state and the lowest levels of Os I belong to the even-parity configurations 5d66s2 and 5d76s (Van Kleef & Klinkenberg 1961). The lowest configurations of odd parity, 5d66s6p and 5d56s26p, appear around 3 eV. The transition arrays between these two sets of levels represent the strongest lines in the Os I spectrum, and they appear in the wavelength region 2500 to 4500 Å.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{osi_fig1.ps}
\end{figure}](/articles/aa/full/2003/39/aa4030/Timg8.gif) |
Figure 1:
Observed line structure for the
5d66s2 5D4-5d66s(6D)6p z
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{iri_fig1.ps}
\end{figure}](/articles/aa/full/2003/39/aa4030/Timg9.gif) |
Figure 2:
Unresolved structure of the
5d76s2 a4F9/2-5d76s(5F)6p z
|
| Open with DEXTER | |
Iridium has two stable isotopes, A=191 and 193, with relative terrestrial abundances of 37.3% and 62.7%. The asymmetric features in the FTS spectrum are unresolved blends of hyperfine structure and/or isotope shift components, as shown by the example in Fig. 2. A detailed analysis of the hyperfine structure and isotopic shift in Ir I has been published by Sawatzky & Winkler (1989), who studied these effects by means of optical interference spectroscopy.
The observed lines in Ir I arise from transitions from the low even configurations 5d76s2 and 5d86s to the odd-parity configuration 5d76s6p (Van Kleef 1957).
Table 1: Experimental radiative lifetimes of four levels in Os I.
Table 2: Experimental radiative lifetimes of two levels in Ir I.
We have remeasured the radiative lifetimes of four levels in Os I and one level in Ir I, using the laser-induced-fluorescence (LIF) technique. A plasma cone of osmium ions and atoms was created from an osmium pellet by an ablation laser. Atoms in the expanding cone of ions were selectively photo-excited to the level under investigation by light from a pulsed tuneable dye laser, working on a red dye and pumped by a Nd:YAG laser. The dye laser light was shifted to the desired wavelengths in the near UV and deep blue using a frequency-doubling crystal and Raman shifting in a hydrogen cell. The fluorescence light due to the decay of the excited levels was then measured with a fast detection system. For levels with short lifetimes, the temporal shape of the laser pulse was also recorded, and the lifetime values were evaluated by fitting a convolution of the recorded pulse and an exponential to the fluorescence signal. The experimental set-up is described in detail by Li et al. (2000).
The general advantage of a laser produced plasma as a source of free ions and atoms is the high particle density, fairly high population in metastable levels, and the presence of high ionization stages. A major drawback is the high speed of the created particles, for neutral osmium in the range 103-104 m s-1. This sets an upper limit to the lifetimes that can be measured, because of flight-out-of-view effects. Possible systematic errors due to these effects were checked by changing the position of the slit of the detecting monochromator. Another test was to make lifetime recordings for different delays between the ablation laser pulse and the excitation laser pulse, thus isolating ions travelling with different velocities.
Based on these tests, we decided that our data for the 5d66s(6D)6p z
![]() level of Os I (lifetime
level of Os I (lifetime ![]() 800 ns) and the 5d76s(5F)6p
z
800 ns) and the 5d76s(5F)6p
z
![]() level of Ir I (lifetime 580 ns) were not sufficiently accurate to
merit publication, and we have retained the values found by Kwiatkowski et al. (1984)
and Gough et al. (1983), respectively. Kwiatkowski et al. (1984) used an oven to produce
a vapour of free Os I atoms, which should lead to smaller flight-out-of-view
effects than our laser ablation technique and hence to somewhat more reliable
results for lifetimes in the microsecond range. A similar case is the upper level
of the line at 4420 Å, which was not measured by Kwiatkowski et al. (1984) and for
which no recent lifetime measurement is thus available.
level of Ir I (lifetime 580 ns) were not sufficiently accurate to
merit publication, and we have retained the values found by Kwiatkowski et al. (1984)
and Gough et al. (1983), respectively. Kwiatkowski et al. (1984) used an oven to produce
a vapour of free Os I atoms, which should lead to smaller flight-out-of-view
effects than our laser ablation technique and hence to somewhat more reliable
results for lifetimes in the microsecond range. A similar case is the upper level
of the line at 4420 Å, which was not measured by Kwiatkowski et al. (1984) and for
which no recent lifetime measurement is thus available.
Residual experimental uncertainties are divided equally between random scatter between different recordings and such possible systematic effects. There is, indeed, a direct trade-off between these two types of error: the photon shot noise in the individual recordings may be reduced by increasing the power of the ablation laser pulse or reducing the delay between the ablation and exciting laser pulses. Both of these remedies result in a denser plasma and higher light intensity at the moment of excitation, hence in an increased photon flux. The penalty for this gain is an increased component of collisional de-excitation, immediately visible as a systematic reduction of the measured lifetime.
Our final experimental results are given in Tables 1 and 2 and compared with the earlier laboratory data. In most cases the agreement is very good. For further comparison, the lifetimes computed theoretically in Sect. 5 are also given.
Spectra of osmium and iridium were recorded with a Chelsea Instruments FT500 UV Fourier Transform Spectrometer (FTS) in the wavelength region 2500 to 7000 Å. For osmium, a commercial hollow cathode lamp was used as the light source due to the toxic nature of osmium oxide. This sealed lamp is manufactured by ISTC, USA, and contains neon as the carrier gas. The recommended maximum operating current is 20 mA, far below the values used for our home-made hollow cathode lamps, one of which was used for iridium. The iridium light source was a water-cooled hollow-cathode lamp where the cathode consists of a 50 mm long iron cylinder with a diameter of 10 mm. A piece of iridium foil was folded and inserted into the iron cylinder. Pure neon or argon or a mixture of the two were used as carrier gases for iridium, with a discharge current between 200 and 700 mA.
The observable quantity from which branching fractions are derived is the line intensity (in photons Å-1 s-1). In order to obtain accurate relative intensities for lines in different wavelength regions, the recorded spectra must be corrected for the instrumental response. This was done in two different ways for different spectral regions. In the region 2500 to 5300 Å we used Ar II lines with known branching ratios (BR) (Whaling et al. 1993), produced in an Fe-Ar hollow cathode lamp run at a pressure of 0.7 torr Ar and a current of 0.3 A. In the wavelength region 4100 to 7000 Å we used a tungsten ribbon lamp with calibrated spectral energy distribution. The uncertainty in the calibration derived from known Ar II branching ratios is estimated to be 10%. The uncertainty of the tungsten lamp calibration data is 3%, and the recorded spectrum from the lamp is reproducible within 5%.
The intensity of strong transitions involving the ground state could be affected by self absorption in the laboratory light source. In order to check for any systematic errors from this effect, we investigated the intensity ratio of pairs of lines of different strength from the same upper level as a function of the discharge current through the lamp. This method is discussed in more detail by Sikström et al. (2002). None of the measured Os I or Ir I lines showed any effect of self absorption.
Finally, in order to determine the branching fractions (BFs) for a given upper level, the relative intensities for all possible downward transitions from that level must be known. These intensities were estimated by means of theoretical atomic structure calculations (see Sect. 5). The final BFs for all measured lines are given in Tables 3 and 4.
Table 3: New Os I lifetimes, wavelengths, branching fractions, and transition probabilities.
Table 4: New Ir I lifetimes, wavelengths, branching fractions, and transition probabilities.
The previous extensive analyses of Os I (Van Kleef 1957) and Ir I (Van Kleef & Klinkenberg 1961)
were based on arc spectra in the wavelength region 2350 to 4850 Å. The
resulting wavelengths have uncertainties of about 50 mÅ. Our FTS spectra of
the hollow cathode lamp from 2500 to 7000 Å (14 300-40 000 cm-1) are
recorded at a spectral resolution of about 0.05 cm-1
(
![]() and
and
![]() 8 mÅ at 4000 Å).
The linear wavenumber scale was calibrated using Fe II lines with very accurately
measured wavelengths.
8 mÅ at 4000 Å).
The linear wavenumber scale was calibrated using Fe II lines with very accurately
measured wavelengths.
Table 5: Finding list of new experimental log(gf)-values for the Os I and Ir I transitions in Tables 3 and 4.
Most of the Os I and Ir I lines are unresolved blends due to isotope shift and hyperfine structure (see Figs. 1 and 2), and we have determined improved centre-of-gravity wavelengths for all transitions studied in this work. The air wavelengths in Tables 3 and 4 were obtained from wavenumbers using the Edlén formula (Edlén 1966). The uncertainty in the wavenumbers is estimated to vary from 0.003 cm-1 to 0.01 cm-1, depending on the S/N ratio of the observation of each individual line. The wavelength uncertainty for the strong lines around 3000 Å in Table 5 is thus smaller than 1 mÅ, whereas the uncertainty for the weak lines around 5000 Å is about 2-3 mÅ.
The branching fractions (BFs) for individual transitions from a given upper level can be computed from the observed spectral line intensities if the relative intensities for all transitions from that level are known. However, some of these transitions may be too weak to be detected, and some may appear outside the observed spectral region. Therefore, we have performed atomic structure calculations, using the Cowan code (Cowan 1981), allowing us to estimate the total branching fraction of the missing lines (i.e. the residual).
For osmium we included the odd parity configurations 5d66s6p, 5d56s26p and 5d76p and the low even group 5d66s2, 5d76s, and 5d8. Whereas the low even levels have been studied before (Gluck et al. 1964; Kröger et al. 2002), we are not aware of any earlier theoretical analysis of the odd parity levels. In advance of a revised description of Os I, it is noted that some odd parity levels have not been confirmed in the fitting process using the Cowan code (Cowan 1981). For example no J=7 level is expected below 43 000 cm-1, which leads to rejection of the 40 036 cm-1 value. In return, the 5d6(3H)6s6p 5H7 level was found at 43 263.61 cm-1 from the lines at 3518.722, 5250.463 and 5934.049 Å.
For iridium the corresponding odd parity configurations 5d76s6p, 5d66s26p, 5d86p and even parity configurations 5d76s2, 5d86s and 5d9 were included. The calculations reproduce the observed BRs to satisfactory accuracy, presented in Tables 3 and 4, and should thus give a reasonable estimate of the sum of the omitted branches, identified as residual in Tables 3 and 4, provided their sum is small compared to the relative intensities of the measured lines (Sikström et al. 2002), as is clearly the case here.
A straight application of the RCG/RCE codes (Cowan 1981) provides estimated log(gf) values for the transitions included in the calculations. They show systematic deviations from the experimental values, but differing for the different types of transition. Inasmuch as the validity of the fine structure study is confirmed by the good agreement between the theoretical and experimental Landé factors, the present work suggests that a proper scaling might be applied to the dipole transition integrals derived from the HFR method as it is done from the electrostatic and spin-orbital radial integrals in the parameter fitting process.
By combining the radiative lifetime (![]() )
and the BF one can derive the
transition probability (A-values) for lines from a particular upper level (i)
through the relation:
)
and the BF one can derive the
transition probability (A-values) for lines from a particular upper level (i)
through the relation:
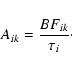 |
(1) |
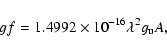 |
(2) |
Uncertainties for the A-values are quoted in Tables 3 and 4. The method by which the uncertainties are determined is described by Sikström et al. (2002). For the lifetime measurements the uncertainties are of the order of 7-8%, and the uncertainties in the BFs based on the intensity measurements range from 1% for strong lines to 10% for weak lines. The small residuals introduce very small errors in the final BFs, even though there is a discrepancy between calculated and theoretical lifetimes in Tables 1 and 2. However, there is no need to rescale the theoretical lifetimes in the calculations of the BFs for the missing lines.
For comparison with our new results, the older experimental values of log(gf) by Kurucz (1993) are given in the last column of Table 5.
![\begin{figure}
\par {\includegraphics[width=8cm,clip]{osirdiff.ps} }\end{figure}](/articles/aa/full/2003/39/aa4030/Timg36.gif) |
Figure 3: The differences between old and new experimental log(gf) values, plotted as a function of log(gf) for the Os I lines in Table 5. Error bars indicate the uncertainties of our new values. |
| Open with DEXTER | |
We have compared our new experimental log(gf) values with the
earlier data by Kurucz (1993), which are those used
to derive abundances of Os I and Ir I in the very metal-poor,
r-process enriched halo giants. Figure 3
shows the result of this comparison for Os I. As seen, there is good
agreement between the experimental results for the three strongest
lines (
![]() ). However,
already for the four lines with log(gf) near -1.5 (including those
used for stellar abundance determinations in the optical region) is
there substantial disagreement (
). However,
already for the four lines with log(gf) near -1.5 (including those
used for stellar abundance determinations in the optical region) is
there substantial disagreement (
![]() ), and for the weaker lines both the offset and the dispersion
increase even further. The sense of these deviations is such as to
suggest the presence of systematic calibration errors in the spectra
used to derive the earlier branching fractions. Similar comments
apply to the comparison with the theoretical results, except that the
scatter is even larger.
), and for the weaker lines both the offset and the dispersion
increase even further. The sense of these deviations is such as to
suggest the presence of systematic calibration errors in the spectra
used to derive the earlier branching fractions. Similar comments
apply to the comparison with the theoretical results, except that the
scatter is even larger.
For Ir I the new and previous experimental data are in excellent agreement
(
![]() ). The log(gf) values for the Ir
I lines of greatest astrophysical importance thus appear to be well-established
despite the relatively large scatter of the theoretical computations.
). The log(gf) values for the Ir
I lines of greatest astrophysical importance thus appear to be well-established
despite the relatively large scatter of the theoretical computations.
In r-process enriched, very metal-poor stars, the heavy neutron capture
elements with ![]() follow the solar r-process abundance pattern, scaled
according to the overall neutron-capture element content of the star
(Truran et al. 2002). In particular, the third r-process peak elements Os and Ir
also generally conform to the same solar r-process abundance pattern as the
elements with
follow the solar r-process abundance pattern, scaled
according to the overall neutron-capture element content of the star
(Truran et al. 2002). In particular, the third r-process peak elements Os and Ir
also generally conform to the same solar r-process abundance pattern as the
elements with
![]() (Truran et al. 2002). However, the results of
Hill et al. (2002) for CS 31082-001 suggested that the Os abundance might somewhat exceed the
scaled solar r-process value in this star. Given that the actinides (
(Truran et al. 2002). However, the results of
Hill et al. (2002) for CS 31082-001 suggested that the Os abundance might somewhat exceed the
scaled solar r-process value in this star. Given that the actinides (![]() )
are significantly overabundant in CS 31082-001 with respect to the lower-mass r-process
elements (by a factor
)
are significantly overabundant in CS 31082-001 with respect to the lower-mass r-process
elements (by a factor ![]() 2.5, or 0.4 dex), the question arises whether Os is
also overabundant in a similar manner. If so, the overabundance of the actinides
might extend to lower-mass nuclides, and Os would potentially be a useful stable
reference element with which to measure the radioactive decay of U and Th.
2.5, or 0.4 dex), the question arises whether Os is
also overabundant in a similar manner. If so, the overabundance of the actinides
might extend to lower-mass nuclides, and Os would potentially be a useful stable
reference element with which to measure the radioactive decay of U and Th.
Our log(gf) remeasurements confirm and consolidate the conclusion that Ir
conforms closely to the solar r-process abundance pattern as scaled to match
the elements with 56
![]() 68. For Os I, however, the small number of
lines used in previous abundance determinations and their relatively poor
consistency justify a re-evaluation of the few stellar Os detections
in the literature in the light of our new log(gf) values.
68. For Os I, however, the small number of
lines used in previous abundance determinations and their relatively poor
consistency justify a re-evaluation of the few stellar Os detections
in the literature in the light of our new log(gf) values.
So far, Os has been detected in five metal-poor stars: HD 115444 and HD 126238
(Sneden et al. 1998), CS 22892-052 (Sneden et al. 2003), BD+17![]() 3248
(Cowan et al. 2002) and CS 31082-001 (Hill et al. 2002). In the first two stars, the determination
is based on two UV lines only (
3248
(Cowan et al. 2002) and CS 31082-001 (Hill et al. 2002). In the first two stars, the determination
is based on two UV lines only (
![]() 2838 and 3058 Å) observed with
HST, one of which is included in the present study (3058 Å). Our log(gf)
revisions have negligible effect (0.021 dex) on the abundance of Os in these two
stars. The Os abundances of CS 22892-052 and BD+17
2838 and 3058 Å) observed with
HST, one of which is included in the present study (3058 Å). Our log(gf)
revisions have negligible effect (0.021 dex) on the abundance of Os in these two
stars. The Os abundances of CS 22892-052 and BD+17![]() 3248 are based on a
mix of UV (HST spectra) and near-UV (Keck and VLT spectra), for a total of 4
lines in the former and 5 in the latter star, of which 3 lines are also included
in the present study. Our log(gf) corrections also cause negligible revision of
the Os abundance in these two stars (+0.013 and 0.003 respectively).
3248 are based on a
mix of UV (HST spectra) and near-UV (Keck and VLT spectra), for a total of 4
lines in the former and 5 in the latter star, of which 3 lines are also included
in the present study. Our log(gf) corrections also cause negligible revision of
the Os abundance in these two stars (+0.013 and 0.003 respectively).
The Os abundance in CS 31082-001 is, however, so far based on only 3 lines in the visible
region (
![]() 4135, 4261, and 4420 Å), for which the log(gf)
values have been revised significantly (-0.03 dex and -0.07 for the first two
lines, respectively). Given the double interest of CS 31082-001 as one of the few very
metal-poor stars in which Os and Ir have been measured, and the only one in which
uranium has also been
detected along with numerous lines of Th, we decided to
re-examine the abundances of Os and Ir in this star, based on a larger set of
newly-detected lines.
4135, 4261, and 4420 Å), for which the log(gf)
values have been revised significantly (-0.03 dex and -0.07 for the first two
lines, respectively). Given the double interest of CS 31082-001 as one of the few very
metal-poor stars in which Os and Ir have been measured, and the only one in which
uranium has also been
detected along with numerous lines of Th, we decided to
re-examine the abundances of Os and Ir in this star, based on a larger set of
newly-detected lines.
Since the paper by Hill et al. (2002), new VLT spectra of CS 31082-001 have been obtained including
the region 3000-3100 Å at the same resolution (R=77 000) as the spectra
described in Hill et al. (2002) - a tribute to the efficiency of the VLT+UVES. The
co-added spectrum of CS 31082-001 was searched again for Os I and Ir I lines in the whole
wavelength range now available. No new iridium features were positively
detected, but 6 new Os I lines were identified in addition to the three listed by
Hill et al. (2002). Among the new total of 9 Os I lines, 6 have new oscillator
strengths from this paper, and we have rederived the Os abundance in CS 31082-001 from all
9 lines, using these new data. The results from the individual lines are given in
Table 6, and examples of the fits to the observed spectrum are
given in Fig. 4. The model atmosphere, spectral synthesis code,
and stellar parameters (
![]() ,
,
![]() ,
and overall metallicity) were those
adopted by Hill et al. (2002).
,
and overall metallicity) were those
adopted by Hill et al. (2002).
Table 6: Os and Ir abundances in CS 31082-001 .
Table 6 reveals a remarkable result: most features (7 out of 9)
agree on a mean Os abundance of
![]() dex, to within
dex, to within ![]() dex (1
dex (1![]() ). In contrast, two of the lines in the 4000 Å region -
i.e. two of the three Os I lines most easily observable until the near-UV
spectral region became accessible - stand out from the mean. As noted already by
Hill et al. (2002), the 4420.468 Å line is a close blend of Os I and Sm II, and
the high Os abundance derived from this feature can be reconciled with the mean
of the other lines by assuming a Sm abundance 0.15 dex higher than the average
from other lines (or by lowering log(gf) for the Sm line by 0.15 dex). Such a
Sm abundance would be only
). In contrast, two of the lines in the 4000 Å region -
i.e. two of the three Os I lines most easily observable until the near-UV
spectral region became accessible - stand out from the mean. As noted already by
Hill et al. (2002), the 4420.468 Å line is a close blend of Os I and Sm II, and
the high Os abundance derived from this feature can be reconciled with the mean
of the other lines by assuming a Sm abundance 0.15 dex higher than the average
from other lines (or by lowering log(gf) for the Sm line by 0.15 dex). Such a
Sm abundance would be only ![]() away from the mean, so we conclude that the
discrepancy for the 4420.468 Å Os line is not significant.
away from the mean, so we conclude that the
discrepancy for the 4420.468 Å Os line is not significant.
![\begin{figure}
\par {\includegraphics[angle=0,height=7cm,clip]{OsL_3057.ps}\hspa...
...*{2mm}
\includegraphics[angle=0,height=7cm,clip]{OsL_4134.ps} }
\end{figure}](/articles/aa/full/2003/39/aa4030/Timg53.gif) |
Figure 4: The Os I lines at 3058, 3301 and 4135 Å in CS 31082-001. Dots: observed spectrum; full lines: synthetic spectra computed for the abundances indicated in the figure. |
| Open with DEXTER | |
The 4135.775 Å feature appears to be very clean (see Fig. 4), but nevertheless gives a significantly higher Os abundance than all the other lines (by 0.3 dex). We have searched for possible blends which might explain this, but found nothing significant: No molecular lines are expected at this wavelength, and the only atomic lines in the immediate vicinity - Fe I 4135.755 Å and Cr I 4135.829 Å - should be far too weak to influence the Os feature (even if we artifically increase their log(gf) by +0.5 dex). We therefore suggest that an unidentified line is superimposed on this Os I feature, making abundance determinations from it unreliable.
The final osmium abundance for CS 31082-001 is found to be
![]() (1
(1 ![]() ,
n = 8), excluding the 4135.781 Å line from the mean and
weighting each line by its inverse variance (: in Table 6
denotes uncertain determinations, because the features in question are faint or
blended). The Ir I abundance is
,
n = 8), excluding the 4135.781 Å line from the mean and
weighting each line by its inverse variance (: in Table 6
denotes uncertain determinations, because the features in question are faint or
blended). The Ir I abundance is
![]() (1
(1
![]() = 2), essentially identical to the value by Hill et al. (2002) and now
also to that of Os.
= 2), essentially identical to the value by Hill et al. (2002) and now
also to that of Os.
The revised Os abundance of CS 31082-001 not only agrees with that of Ir in this star, but
results in agreement between the observed heavy-element abundances and the scaled
solar r-process in the whole mass range
![]() (see Fig.
5). Moreover, this now holds in all five very metal-poor stars with
measured Os and Ir abundances. From a theoretical point of view it was a puzzle
that Os appeared to deviate from the solar r-process pattern, because the quite
different neutron-capture scenarios described by Schatz et al. (2002) and
Wanajo et al. (2002) show little if any differences in the production of Os and Ir.
Accordingly, the apparent overabundance of Os was hard to understand when not
accompanied by a similar effect for Ir. On the other hand, the same models show
that under certain conditions the actinides can be overproduced relative to
even such nearby elements as Os and Ir (see Wanajo et al. 2002).
(see Fig.
5). Moreover, this now holds in all five very metal-poor stars with
measured Os and Ir abundances. From a theoretical point of view it was a puzzle
that Os appeared to deviate from the solar r-process pattern, because the quite
different neutron-capture scenarios described by Schatz et al. (2002) and
Wanajo et al. (2002) show little if any differences in the production of Os and Ir.
Accordingly, the apparent overabundance of Os was hard to understand when not
accompanied by a similar effect for Ir. On the other hand, the same models show
that under certain conditions the actinides can be overproduced relative to
even such nearby elements as Os and Ir (see Wanajo et al. 2002).
| |
Figure 5:
Abundance residuals of the heavy elements in five metal-poor stars
(see text) from the solar-system r-process pattern (Arlandini et al. 1999).
The normalisation was computed as the mean difference between the
solar-system r-process and the stellar abundances for each star in the
range
|
| Open with DEXTER | |
Within the limitations of the small sample (only 5 stars so far), these results
would appear to establish that (i): reliable Os abundances can be
determined from the UV lines and
![]() Å, but not from
Å, but not from
![]() Å until their blending problems have been resolved; (ii): the abundances of Os and Ir are identical in all observed stars; (iii): the observed heavy-element abundances in very metal-poor stars agree
precisely with the scaled solar r-process pattern in the entire mass range
Å until their blending problems have been resolved; (ii): the abundances of Os and Ir are identical in all observed stars; (iii): the observed heavy-element abundances in very metal-poor stars agree
precisely with the scaled solar r-process pattern in the entire mass range
![]() ;
and (iv): neither Os or Ir nor any lighter elements can
be used as stable references from which to measure the radioactive decay of Th
and U in such stars.
;
and (iv): neither Os or Ir nor any lighter elements can
be used as stable references from which to measure the radioactive decay of Th
and U in such stars.
Accordingly, reliable abundances for elements between Ir and Th (notably Pt, Bi,
and Pb) in CS 31082-001 and similar stars are needed to further constrain the models of
r-process nucleosynthesis. The exact atomic mass at which overproduction may
set in for the heaviest r-process elements, including at least the actinides,
is of special interest. Equally important are the daughter elements Pb and Bi of
the decay of Th and U, as constraints on the original amounts of the parent
nuclides as well as any amounts of Pb and Bi that might have been produced by
other means. We note in this context that Pb appears to be below even the small
solar r-process fraction in both CS 22892-052 and CS 31082-001 (Hill et al. 2002; Sneden et al. 2003).
This requires high-quality spectra in the ultraviolet region beyond the
atmospheric cutoff, which we are currently obtaining with the Hubble Space
Telescope. In addition to the Pt, Bi, and Pb abundances, these spectra will
allow an independent check of the Os I abundance from the three strong deep-UV
lines with well-determined ![]() values (see Table 5).
values (see Table 5).
Acknowledgements
We gratefully acknowledge the excellent conditions at the Lund Laser Centre and the support by its Director, Prof. Sune Svanberg, for this research, which also received financial support from the European Community under the Programme "Improving Human Potential - Access to Research Infrastructures'' (Contract No. HPRI-CT-1999-00041). Additional support was received from grants by the Swedish Research Council (to S.J. and B.N.) and the Nordic Academy for Advanced Study (NorFA; to B.N). The ESO-VLT observations of CS 31082-001 were made in the framework of the Large Programme "First Stars'' (165.N-0276(A); P.I. R. Cayrel).