1 - Department of Physical Sciences, P O Box 64, 00014 University of Helsinki, Finland
2 - Tuorla Observatory
3 - Institut für Theoretische Physik IV, Ruhr-Universität Bochum, 44780 Bochum, Germany
R. Vainio 1 - J. J. P. Virtanen 2 - R. Schlickeiser3
1 - Department of Physical Sciences, P O Box 64, 00014
University of Helsinki, Finland
2 - Tuorla Observatory![]() , University of Turku,
21500 Piikkiö, Finland
, University of Turku,
21500 Piikkiö, Finland
3 - Institut für Theoretische Physik IV,
Ruhr-Universität Bochum, 44780 Bochum, Germany
Received 2 July 2003 / Accepted 28 July 2003
Abstract
Alfvén-wave transmission through super-Alfvénic parallel
relativistic shock waves is studied. We calculate the wave
transmission coefficients for given shock properties. We show (i) that
the Alfvén waves downstream the shock wave are propagating
predominantly anti-parallel to the flow direction for low-Mach-number
shocks, as in the case of non-relativistic shocks; and (ii) that for
high-Mach-number ultra-relativistic shocks the forward and backward
downstream waves are in equipartition. For low Alfvénic Mach numbers,
the scattering center compression ratio of the shock, thus, becomes
large and the spectral index of accelerated test particles approaches
the limit
![]() at shock waves approaching the critical value
of the quasi-Newtonian Alfvénic Mach number (i.e., the ratio of
upstream fluid and Alfvén proper speeds), which depends on the shock
properties, and equals the square root of the compression ratio at the
test-wave limit. Although the inclusion of the wave electromagnetic
and velocity fields to the shock jump conditions is likely to decrease
the scattering-center compression ratio for shocks with critical Mach
numbers, values significantly above the gas compression ratio can be
expected for such shocks. Particle acceleration in weak relativistic
shocks propagating in magnetized astrophysical jets may, therefore, be
substantially more efficient than predicted by models neglecting
turbulent electric fields.
at shock waves approaching the critical value
of the quasi-Newtonian Alfvénic Mach number (i.e., the ratio of
upstream fluid and Alfvén proper speeds), which depends on the shock
properties, and equals the square root of the compression ratio at the
test-wave limit. Although the inclusion of the wave electromagnetic
and velocity fields to the shock jump conditions is likely to decrease
the scattering-center compression ratio for shocks with critical Mach
numbers, values significantly above the gas compression ratio can be
expected for such shocks. Particle acceleration in weak relativistic
shocks propagating in magnetized astrophysical jets may, therefore, be
substantially more efficient than predicted by models neglecting
turbulent electric fields.
Key words: acceleration of particles - ISM: cosmic rays - galaxies: jets - relativity - shock waves - waves
Explosive astrophysical events, such as supernova remnants, gamma-ray
bursts (GRBs) and jets of active galactic nuclei (AGNi), are of
immense importance for high-energy astrophysics, both as intense
non-thermal radiation emitters as well as probable source sites for
accelerating cosmic ray particles. The leading collapsar (Woosley
1993; Paczynski 1998) and supranova (Vietri &
Stella 1998) models for gamma-ray bursts involve relativistic
outflows (Piran 1999) that emanate from a compact source,
where due to strong stellar envelope magnetic fields and/or explosions
in a pre-existing pulsar wind bubble (Kennel & Coroniti
1984) anisotropic relativistic outflow velocities result with
initial Lorentz factors
![]() .
AGN jets can be
regarded as channeled collimated relativistic outflow components
(
.
AGN jets can be
regarded as channeled collimated relativistic outflow components
(
![]() )
propagating in the dynamic jet medium which
might be identical to the ambient interstellar medium (e.g., Dermer
& Schlickeiser 1992; Urry & Padovani 1995). In
both source classes it is of interest to unravel the basic physical
processes that convert the huge kinetic outflow energy into observable
non-thermal radiation.
)
propagating in the dynamic jet medium which
might be identical to the ambient interstellar medium (e.g., Dermer
& Schlickeiser 1992; Urry & Padovani 1995). In
both source classes it is of interest to unravel the basic physical
processes that convert the huge kinetic outflow energy into observable
non-thermal radiation.
Because the signal speeds (speed of sound and Alfvén speed) of the surrounding interstellar and intergalactic plasmas are typically smaller than the relativistic jet speeds, the formation of magnetized relativistic shock waves is a direct consequence of these violent explosive events. According to current understanding, energetic charged particles are efficiently accelerated at shocks by the first-order Fermi mechanism with power law distribution functions in particle rigidity, and subsequently give rise to the observed non-thermal radiation. By simple equipartition arguments, it is anticipated that a considerable fraction of the outflow energy is transformed into these power law distributions of energetic particles. Time-dependent modeling of the non-thermal synchrotron, synchrotron-self-Compton and external Compton cooling of energetic pairs in the evolving outflow source region are then performed to explain multi-wavelength spectra and light curves in the optically thin case. Analogous calculations in an optically thick environment very often start from energetic hadrons that via cascades involving inelastic hadron-hadron-interactions and/or photomeson interactions provide copious amounts of secondary pairs.
Simple leptonic cooling models are remarkably successful in explaining the observed multi-wavelength spectra of AGN jets (see Dermer & Schlickeiser 2002 and references therein) and GRB afterglows (e.g., Dermer et al. 2000). The observed rapid variability in the TeV light curves from Mrk 501 and Mrk 421 (Gaidos et al. 1996; Quinn et al. 1999; Aharonian et al. 1999,2001) is attributed in these models to a variable injection rate into the acceleration process (e.g., Mastichiadis & Kirk 1997; Kirk & Mastichiadis 1999), probably resulting from the shock wave propagating through a highly structured, non-uniform medium.
Acceleration of particles in non-relativistic shock waves is governed
by the first-order Fermi mechanism: particles get accelerated by
converging magnetic scattering centers at the shock. At
non-relativistic shocks, the theory is referred to as diffusive shock
acceleration (Axford et al. 1977; Krymsky 1977; Bell 1978; Blandford & Ostriker 1978). In the simplest
version of the theory, the predicted power-law spectral index of the
energy spectrum of the accelerated particles is given solely by the
compression ratio of the shock, r, as
![]() .
The
same mechanism relying on converging scattering centers at the shock
is also operative at relativistic shock waves (Peacock 1981),
although no analytical expression between the compression ratio and
the spectral index of the accelerated particles can be found in this
case (Kirk & Schneider 1987). The spectral index of the
accelerated particles is, however, mainly determined by the
compression ratio even for relativistic shocks although, unlike for
non-relativistic shocks, details of particle scattering have also an
effect on the spectral index (Kirk & Duffy1999; Kirk et
al. 2000).
.
The
same mechanism relying on converging scattering centers at the shock
is also operative at relativistic shock waves (Peacock 1981),
although no analytical expression between the compression ratio and
the spectral index of the accelerated particles can be found in this
case (Kirk & Schneider 1987). The spectral index of the
accelerated particles is, however, mainly determined by the
compression ratio even for relativistic shocks although, unlike for
non-relativistic shocks, details of particle scattering have also an
effect on the spectral index (Kirk & Duffy1999; Kirk et
al. 2000).
As noted already by Bell (1978), however, the compression ratio felt by the accelerated particles is not necessarily equal to the gas compression ratio. This is because the turbulent magnetic field responsible for the accelerated-particle scattering is generally not static in the local plasma frame. If the turbulent fields consist of low-frequency plasma waves, it is possible to transform their time dependence away by considering particle scattering in the frame co-moving with the waves. Thus, the spectral index of the particles is determined by the scattering-center compression ratio, i.e., the ratio of average shock-frame speeds of the scattering centers upstream and downstream of the shock. Acceleration of relativistic particle populations at parallel non-relativistic shocks taking account of the finite wave speeds relative to the plasma was discussed by Vainio & Schlickeiser (1998,1999,2001). They noted that it is possible to determine the average wave speeds by calculating the downstream wave amplitudes from the assumed properties of the upstream waves by using the shock jump conditions (McKenzie & Westphal 1969). Vainio & Schlickeiser (1998) noted (i) that the effect of finite wave speeds relative to the local rest frame to particle acceleration is very important in fast-mode shocks with low Alfvénic Mach numbers and (ii) that test-particle acceleration in such shocks is extremely efficient because the transmission of waves through the (super-Alfvénic) shock yields values of the scattering-center compression ratio much above the gas compression ratio.
So far, studies attempting to calculate the spectral index of accelerated particles at relativistic shocks have completely overlooked the possible role of finite wave speeds in these shocks despite the fact that both theoretical and observational estimates of the magnetic fields and densities in relativistic jets often predict relativistic values of the Alfvén speed (Appl & Camenzind 1988). In this paper, we take the first attempt to calculate the scattering-center compression ratio of a relativistic shock generalizing our previous results of Alfvén wave transmission and test particle acceleration (Vainio & Schlickeiser 1998) to the relativistic regime. In this first study, we will restrict the discussion to parallel shock waves. We will also adopt a test-wave approach and neglect the effects of wave electromagnetic and velocity fields to the gas compression ratio of the shock. Self-consistent modeling would have to take these into account at the lowest Alfvénic Mach numbers (Vainio & Schlickeiser 1999). We will also neglect the effects of possible pressure anisotropies in the upstream region (Vainio & Schlickeiser 2001), and the possible effects of the particles themselves to the downstream wave fields (Vainio 2001). These effects will, however, be qualitatively discussed in Sect. 4. A brief outline of the used notation is given as an Appendix.
In this section we will calculate the transmission coefficients of Alfvén waves in relativistic shocks, i.e., the amplitudes of the forward and backward propagating Alfvén waves downstream of the shock from assumed amplitudes of the waves in the upstream region. The approach is based on the assumption that wave lengths are much larger than the shock thickness, which allows one to consider the relativistic MHD jump conditions in their usual form despite the fact that the wave fields are actually slowly temporally variable and inhomogeneous on large scales.
We consider Alfvén waves ahead and behind a super-Alfvénic shock
front. Appl & Camenzind (1988) noted that the magnetic
fields upstream and downstream of the shock are co-planar. By using
the relativistic jump conditions, they calculated the ratio of
shock-frame tangential magnetic fields upstream (subscript 1) and
downstream (subscript 2) as (Eqs. (24) and (25) of Appl & Camenzind
1988)
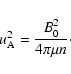 |
(2) |
Since we are considering parallel shock waves (i.e., with the
ordered magnetic field along the shock normal), the tangential
fields are composed of the fluctuating wave fields. We denote the
wave-frame magnetic field amplitudes by
![]() ,
where the subscripts + and - refer to waves propagating parallel
or anti-parallel to the flow. The phase speeds of the waves in the
shock frame are
,
where the subscripts + and - refer to waves propagating parallel
or anti-parallel to the flow. The phase speeds of the waves in the
shock frame are
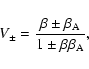 |
(3) |
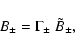 |
(4) |
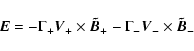 |
(6) |
| (7) |
| (8) | |||
| (9) |
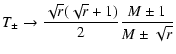 |
(12) | ||
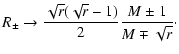 |
(13) |
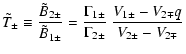 |
(14) | ||
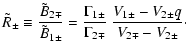 |
(15) |
Assuming the Alfvén waves to have so small amplitudes that they do not
affect the shock dynamics we can considerably simplify the analysis.
In this case, the jump conditions that determine the shock dynamics
reduce to those of a hydrodynamical shock. Thus, the energy equation
is
| (16) |
| (17) |
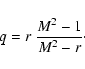 |
(18) |
In addition to the wave amplitudes, we need equations for the
wave numbers, as well. As argued by Vainio & Schlickeiser
(1998), waves conserve their shock-frame frequencies when
crossing the shock front. Thus,
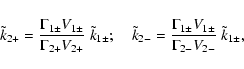 |
(19) |
Let us, next, calculate the transmission coefficients at constant
wave number ![]() for power-law spectra of upstream and
downstream waves, i.e.,
for power-law spectra of upstream and
downstream waves, i.e.,
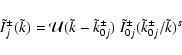 |
(20) |
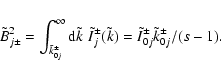 |
(21) |
We consider shock waves propagating parallel to the mean magnetic
field, and neglect the dynamical effects of the wave magnetic field.
We restrict the discussion to strong shocks, i.e., those with
negligible upstream pressure. In this case, the gas compression ratio
r is a solution of (Appl & Camenzind 1988)
We solve the compression ratio iteratively using the following scheme:
(i) fix the value of the polytropic index to
![]() ,
if
,
if
![]() ,
and to
,
and to
![]() ,
if
,
if
![]() ;
(ii) solve the compression ratio
r numerically from Eq. (24) noting that the physical root
is in the range
;
(ii) solve the compression ratio
r numerically from Eq. (24) noting that the physical root
is in the range
![]() ;
(iii) calculate a new value for
;
(iii) calculate a new value for
![]() by using
by using
![]() and Eqs. (25) and
(26); (iv) repeat the steps (ii)-(iii) until
and Eqs. (25) and
(26); (iv) repeat the steps (ii)-(iii) until
![]() differs from the value obtained in the previous round by less than
a predefined convergence criterion. The gas compression ratio and the
downstream polytropic index as a function of the proper speed of the
shock are given in Fig. 1.
differs from the value obtained in the previous round by less than
a predefined convergence criterion. The gas compression ratio and the
downstream polytropic index as a function of the proper speed of the
shock are given in Fig. 1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0038_f1}
\end{figure}](/articles/aa/full/2003/39/aa0038/Timg84.gif) |
Figure 1:
The gas compression ratio r (solid curve) and the polytropic index
|
| Open with DEXTER | |
Let us first study the wave transmission coefficients as a function of
Mach number by fixing the value of the shock speed to a
non-relativistic value and varying the Alfvén speed. We have computed
the wave transmission coefficients as a function Alfvénic Mach number
for a non-relativistic (
![]() )
parallel shock propagating
in a cold plasma with a polytropic index of
)
parallel shock propagating
in a cold plasma with a polytropic index of
![]() and a compression ratio of r=4 (Fig. 2). Note that as long as
the shock speed is non-relativistic, the same transmission
coefficients as a function of Mach number apply, but the axis for the
Alfvén speed, of course, applies only for the chosen value of
and a compression ratio of r=4 (Fig. 2). Note that as long as
the shock speed is non-relativistic, the same transmission
coefficients as a function of Mach number apply, but the axis for the
Alfvén speed, of course, applies only for the chosen value of ![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0038_f2}
\end{figure}](/articles/aa/full/2003/39/aa0038/Timg85.gif) |
Figure 2:
Alfvén-wave transmission coefficients in a parallel
non-relativistic shock (
|
| Open with DEXTER | |
At low Mach numbers,
![]() ,
the waves propagate predominantly
backward relative to the flow direction, no matter what the state of
the upstream wave field is. The physical reason for this is that a
finite value of an electric field component for the backward waves,
required to satisfy the jump conditions, requires very large values of
the magnetic field amplitude, if
,
the waves propagate predominantly
backward relative to the flow direction, no matter what the state of
the upstream wave field is. The physical reason for this is that a
finite value of an electric field component for the backward waves,
required to satisfy the jump conditions, requires very large values of
the magnetic field amplitude, if
![]() ,
i.e.,
,
i.e.,
![]() .
The infinite values of the transmission coefficients occur because of
the assumption of the negligible wave pressure and Poynting flux.
When these are taken into account, the compression ratio of the shock
becomes smaller staying below r<M2 (Vainio & Schlickeiser
1999) and, thus, the infinite values of T- and R+are avoided. At high Mach numbers, the transmission coefficients
approach the values
.
The infinite values of the transmission coefficients occur because of
the assumption of the negligible wave pressure and Poynting flux.
When these are taken into account, the compression ratio of the shock
becomes smaller staying below r<M2 (Vainio & Schlickeiser
1999) and, thus, the infinite values of T- and R+are avoided. At high Mach numbers, the transmission coefficients
approach the values
![]() and
and
![]() .
.
Let us, next, study the wave transmission coefficients as a function
of Mach number by fixing the value of the Alfvén speed and varying the
shock speed. We study the cases of upstream proper Alfvén speed
ranging from
![]() to 10 c (Figs. 3-7).
The cases with non-relativistic Alfvén speeds (
to 10 c (Figs. 3-7).
The cases with non-relativistic Alfvén speeds (
![]() )
differ very little from the above results for
non-relativistic shocks up to proper shock speeds of about
)
differ very little from the above results for
non-relativistic shocks up to proper shock speeds of about
![]() ,
but at larger shock speeds relativistic effects lowering the
compression ratio of the shock become important. On the other hand,
all transmission coefficients are very similar in the cases
,
but at larger shock speeds relativistic effects lowering the
compression ratio of the shock become important. On the other hand,
all transmission coefficients are very similar in the cases
![]() and 10.0 c indicating that, once the
Alfvén speed becomes relativistic, the only relevant parameter in the
wave transmission problem is the Mach number, like in the
non-relativistic case. Note, however, that (since
and 10.0 c indicating that, once the
Alfvén speed becomes relativistic, the only relevant parameter in the
wave transmission problem is the Mach number, like in the
non-relativistic case. Note, however, that (since ![]() and
and
![]() )
at the limits of
)
at the limits of
![]() the
asymptotic values of all the transmission coefficients are
the
asymptotic values of all the transmission coefficients are
![]() and, thus, different from the values at
non-relativistic shocks. Therefore, in relativistic high-Mach-number
shocks the wave fields in the downstream region are close to
equipartition, no matter what the propagation direction of the
upstream waves might be. At low Mach numbers, the results are
qualitatively similar to non-relativistic shocks (Vainio &
Schlickeiser 1998): the downstream wave field is
predominantly backward, regardless of the upstream wave propagation
direction. The region of backward-wave dominance, however, extends to
slightly larger Mach numbers than in non-relativistic shocks.
and, thus, different from the values at
non-relativistic shocks. Therefore, in relativistic high-Mach-number
shocks the wave fields in the downstream region are close to
equipartition, no matter what the propagation direction of the
upstream waves might be. At low Mach numbers, the results are
qualitatively similar to non-relativistic shocks (Vainio &
Schlickeiser 1998): the downstream wave field is
predominantly backward, regardless of the upstream wave propagation
direction. The region of backward-wave dominance, however, extends to
slightly larger Mach numbers than in non-relativistic shocks.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0038_f3}
\end{figure}](/articles/aa/full/2003/39/aa0038/Timg100.gif) |
Figure 3:
Alfvén-wave transmission coefficients, as measured in the
shock frame, in a parallel shock propagating into a medium with
proper Alfvén speed
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0038_f4}
\end{figure}](/articles/aa/full/2003/39/aa0038/Timg102.gif) |
Figure 4:
Alfvén-wave transmission coefficients, as measured in the
shock frame, in a parallel shock propagating into a medium with
proper Alfvén speed
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0038_f5}
\end{figure}](/articles/aa/full/2003/39/aa0038/Timg104.gif) |
Figure 5:
Alfvén-wave transmission coefficients, as measured in the
shock frame, in a parallel shock propagating into a medium with
proper Alfvén speed
|
| Open with DEXTER | |
Particle acceleration at relativistic shocks is basically due to the
same first (and second) order Fermi mechanism as in non-relativistic
shocks. The analysis of particle acceleration in relativistic shocks
is, however, more complicated than in non-relativistic shocks because
the particle distribution is anisotropic. Thus, numerical methods are
needed to solve for the spectral index of the accelerated particles in
these conditions. Two main classes of numerical methods have been
employed so far: (i) Monte Carlo simulations (Ellison et al. 1990; Bednarz & Ostrowski 1996,1998) and (ii)
solutions based on eigenfunction expansions (Kirk & Schneider
1987; Kirk et al. 2000). The numerical methods
reveal that the spectral index of the accelerated particles is no
longer independent of the underlying scattering process: large-angle
scattering and pitch-angle diffusion lead to different results
concerning this parameter. If pitch-angle diffusion is employed, large
upstream Lorentz factors (producing ![]() )
seem to yield spectral
indices close to the value of
)
seem to yield spectral
indices close to the value of
![]() (in far downstream energy
spectrum,
(in far downstream energy
spectrum,
![]() )
(Bednarz & Ostrowski
1998; Kirk et al. 2000). All of the studies so far
are, however, based on the assumption of frozen-in scattering centers,
i.e., they assume that particles scatter elastically in the local rest
frame of the plasma. With non-negligible Alfvén speeds, this can no
longer be assumed, but one instead has to consider scatterings that
are elastic in the frame of the scattering wave (where the
wave-magnetic field is static).
)
(Bednarz & Ostrowski
1998; Kirk et al. 2000). All of the studies so far
are, however, based on the assumption of frozen-in scattering centers,
i.e., they assume that particles scatter elastically in the local rest
frame of the plasma. With non-negligible Alfvén speeds, this can no
longer be assumed, but one instead has to consider scatterings that
are elastic in the frame of the scattering wave (where the
wave-magnetic field is static).
We consider an upstream plasma with wave spectra
![]() ,
i.e., a situation where
the turbulently evolving forward and backward waves have attained
equal power-law intensities in the ambient plasma. Thus, upstream of
the shock wave the normalized cross helicity,
,
i.e., a situation where
the turbulently evolving forward and backward waves have attained
equal power-law intensities in the ambient plasma. Thus, upstream of
the shock wave the normalized cross helicity,
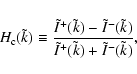 |
(27) |
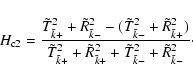 |
(28) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0038_f6}
\end{figure}](/articles/aa/full/2003/39/aa0038/Timg114.gif) |
Figure 6:
Alfvén-wave transmission coefficients, as measured in the
shock frame, in a parallel shock propagating into a medium with
proper Alfvén speed
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0038_f7}
\end{figure}](/articles/aa/full/2003/39/aa0038/Timg116.gif) |
Figure 7:
Alfvén-wave transmission coefficients, as measured in the
shock frame, in a parallel shock propagating into a medium with
proper Alfvén speed
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0038_f8}
\end{figure}](/articles/aa/full/2003/39/aa0038/Timg117.gif) |
Figure 8:
Cross helicity of the Alfvén waves at constant wave number
downstream a parallel shock wave for
u1=0.1 c (solid curve,
|
| Open with DEXTER | |
Because the downstream Alfvén speed is at most mildly relativistic, we
take the average plasma-frame speed of the downstream scattering
centers to be
![]() .
This gives the
shock-frame scattering center speed in the downstream region as
.
This gives the
shock-frame scattering center speed in the downstream region as
![]() .
We can now use
this value to compute the scattering-center compression ratio of the
shock (for
.
We can now use
this value to compute the scattering-center compression ratio of the
shock (for
![]() )
as
)
as
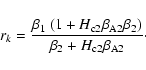 |
(29) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0038_f9}
\end{figure}](/articles/aa/full/2003/39/aa0038/Timg122.gif) |
Figure 9:
Scattering center compression ratio, rk, of a parallel
shock wave for
u1=0.1 c (solid curve,
|
| Open with DEXTER | |
Two important results can be immediately deduced from the behavior of
downstream cross helicity and scattering-center compression ratio at
low Mach numbers, i.e., just above the critical one: firstly,
accelerated particles feel a very large scattering-center compression
ratio at the shock. At the limit of rk increasing toward
infinity, particle escape from the shock to far downstream becomes
increasingly more difficult, and the spectral index approaches the
value of
![]() ,
as long as the momentum gain of the particle
per each crossing cycle of the shock is a fixed (i.e., momentum
independent) fraction of particle momentum. This is the case for
ultra-relativistic particles regardless of the shock speed. Secondly,
for such low-Mach-number relativistic shocks we can also neglect
stochastic acceleration, since the downstream waves are propagating in
one direction, only.
,
as long as the momentum gain of the particle
per each crossing cycle of the shock is a fixed (i.e., momentum
independent) fraction of particle momentum. This is the case for
ultra-relativistic particles regardless of the shock speed. Secondly,
for such low-Mach-number relativistic shocks we can also neglect
stochastic acceleration, since the downstream waves are propagating in
one direction, only.
To illustrate the effect of the Alfvén-wave transmission to particle
acceleration more quantitatively, we have used Monte Carlo simulations
to compute the spectrum of accelerated particles. Our code is a direct
generalization to the relativistic regime of the code we have used for
studying diffusive shock acceleration at non-relativistic shocks
(Vainio et al. 2000). A detailed description of the code will
be given elsewhere (Virtanen & Vainio, in preparation). For
simplicity, we employ small-angle scatterings in pitch angle relative
to the mean field (i.e., shock normal),
![]() ,
with an
isotropic pitch-angle diffusion coefficient
,
with an
isotropic pitch-angle diffusion coefficient
![]() .
The validity of this simplification may be questionable in the
downstream region, where a form like
.
The validity of this simplification may be questionable in the
downstream region, where a form like
![]() with
with
![]() might
better describe the scattering conditions in magnetized shocks (Kirk
et al. 2000), but the effect of the functional form of
might
better describe the scattering conditions in magnetized shocks (Kirk
et al. 2000), but the effect of the functional form of
![]() to the accelerated particle spectrum is typically
smaller than that of the compression ratio. We employ a single,
position dependent scattering center speed that has a value of
to the accelerated particle spectrum is typically
smaller than that of the compression ratio. We employ a single,
position dependent scattering center speed that has a value of
![]() upstream and
upstream and
![]() downstream of the shock
wave. Thus, the effect of stochastic acceleration (which we estimated
to be small) is not considered in this study. The value of the
scattering-center compression ratio was varied from rk=r to
downstream of the shock
wave. Thus, the effect of stochastic acceleration (which we estimated
to be small) is not considered in this study. The value of the
scattering-center compression ratio was varied from rk=r to ![]() (see Fig. 9 for the corresponding Mach numbers) and
three values of the proper shock speed,
(see Fig. 9 for the corresponding Mach numbers) and
three values of the proper shock speed,
![]() and 10.0 c, were considered. Statistical errors of the fitted
spectral indices are of the order of 0.065 or less in all cases. As
shown in Fig. 10, the simulated points are close to each
other in all cases, by chance, when the scattering-center compression
ratios are scaled by the gas compression ratio. As expected, the
non-relativistic diffusive shock acceleration theory does not describe
the spectral index correctly, if the shock is relativistic. The
values, however, seem to converge toward
and 10.0 c, were considered. Statistical errors of the fitted
spectral indices are of the order of 0.065 or less in all cases. As
shown in Fig. 10, the simulated points are close to each
other in all cases, by chance, when the scattering-center compression
ratios are scaled by the gas compression ratio. As expected, the
non-relativistic diffusive shock acceleration theory does not describe
the spectral index correctly, if the shock is relativistic. The
values, however, seem to converge toward
![]() as
as
![]() ,
as expected, regardless of the value of u1.
,
as expected, regardless of the value of u1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0038_f10}
\end{figure}](/articles/aa/full/2003/39/aa0038/Timg132.gif) |
Figure 10:
Spectral index of particles accelerated in a relativistic
parallel shock as a function of the scattering-center compression
ratio rk for
u1=0.1 c (triangles,
|
| Open with DEXTER | |
We have considered Alfvén-wave transmission and test-particle
acceleration in parallel relativistic shock waves propagating to a
cold plasma. Test-wave approximation has been used, i.e., the
electromagnetic and velocity fields of the waves have not been taken
into account when determining the gas compression ratio of the
shock. Under these admittedly restricting assumptions, it has been
shown that the Alfvén waves downstream of a barely super-Alfvénic
shock wave are predominantly propagating backward relative to the
direction of the flow. This has been shown to strongly affect the
scattering-center compression ratio, rk, of low-Mach-number
shocks, increasing this parameter well above the gas compression
ratio, r, of the shock. Thus, the computed power-law energy spectrum
of particles accelerated in such shock wave is significantly harder
than predicted by theories relying on particle scattering off
frozen-in magnetic fluctuations. At the test-wave limit, the
scattering-center compression ratio becomes infinite and the spectral
index of the accelerated particles approaches
![]() as the
quasi-Newtonian Alfvénic Mach number of the shock,
as the
quasi-Newtonian Alfvénic Mach number of the shock,
![]() ,
approaches the critical Mach number
,
approaches the critical Mach number
![]() from above.
from above.
Let us discuss the limitations of our assumptions to the validity of
our results. Since we are interested in relativistic shock waves, the
most severe limitation comes from our assumption of parallel shock
geometry. This is because as the upstream Lorentz factor increases to
values
![]() ,
the transverse magnetic fields in the shock
frame become amplified, and it is increasingly less probable that the
orientation of the shock is such that the ordered transverse fields
can be neglected. This should be taken into account in any attempt to
apply our results to shocks with
,
the transverse magnetic fields in the shock
frame become amplified, and it is increasingly less probable that the
orientation of the shock is such that the ordered transverse fields
can be neglected. This should be taken into account in any attempt to
apply our results to shocks with
![]() .
Significant
obliqueness of the shock would lower the value of Alfvén-wave speed
relative to the shock normal, but at the same time it would lower the
gas compression ratio of a low-Mach-number shock wave (Appl &
Camenzind 1988). The two effects work in opposite directions
in the ratio rk/r. Thus, it is not easy to deduce the net effect
of the obliqueness to the scattering-center compression ratio; we
expect it to get smaller with increasing obliquity, but a quantitative
estimate of its effect would require a calculation beyond the scope of
the present study.
.
Significant
obliqueness of the shock would lower the value of Alfvén-wave speed
relative to the shock normal, but at the same time it would lower the
gas compression ratio of a low-Mach-number shock wave (Appl &
Camenzind 1988). The two effects work in opposite directions
in the ratio rk/r. Thus, it is not easy to deduce the net effect
of the obliqueness to the scattering-center compression ratio; we
expect it to get smaller with increasing obliquity, but a quantitative
estimate of its effect would require a calculation beyond the scope of
the present study.
Another crucial assumption we made was the validity of test-wave
approximation. This was the origin of the (unphysical) singularities
of the transmission coefficients T- and R+ at
![]() that lead to the extremely high values of rk. The
singularity is removed by taking proper account of the transverse wave
fields when computing the shock's gas compression ratio. This keeps
the value of r in the physical range for fast-mode shocks,
r<M2, as was demonstrated for non-relativistic shocks by Vainio
& Schlickeiser (1999). These authors also showed that
although the singularities are avoided, the gas compression ratio at
shocks with
that lead to the extremely high values of rk. The
singularity is removed by taking proper account of the transverse wave
fields when computing the shock's gas compression ratio. This keeps
the value of r in the physical range for fast-mode shocks,
r<M2, as was demonstrated for non-relativistic shocks by Vainio
& Schlickeiser (1999). These authors also showed that
although the singularities are avoided, the gas compression ratio at
shocks with
![]() is only slightly below M2 and,
therefore, R+, T- and rk are still very large and the
accelerated particle spectrum significantly harder than the one
obtained by using the much smaller r as the value of rk. Since
the values of the transmission coefficients calculated for the
relativistic shocks do not differ too much from the values in
non-relativistic shocks at low Mach numbers (see
Figs. 2-7),
we expect this result to carry over to relativistic shocks as well.
is only slightly below M2 and,
therefore, R+, T- and rk are still very large and the
accelerated particle spectrum significantly harder than the one
obtained by using the much smaller r as the value of rk. Since
the values of the transmission coefficients calculated for the
relativistic shocks do not differ too much from the values in
non-relativistic shocks at low Mach numbers (see
Figs. 2-7),
we expect this result to carry over to relativistic shocks as well.
We have also neglected the back-reaction of the accelerated particles to the scattering Alfvén waves in our study. For a relativistic shock this is a valid assumption in the upstream region, because no extended foreshock region with backward streaming accelerated particles is expected if u1 is close to the speed of light (Kirk et al. 2000). However, as was demonstrated by Vainio (2001) using numerical simulations, the wave fields downstream the shock wave may become modified by the forward-streaming accelerated particles there. This softens the spectrum somewhat from the hardest test-particle spectra, because the particle streaming away from the shock is likely to damp the backward mode more heavily than the forward one. According to Vainio (2001), the downstream forward wave is actually amplified in non-relativistic shocks, but this might not be the case in relativistic shocks, if the Alfvén speed in the downstream region is a sizable fraction of the particle speed, as in the low-Mach-number shocks considered in this paper.
As demonstrated by Vainio & Schlickeiser (2001), pressure anisotropies upstream the shock wave can be important for Alfvén wave transmission in non-relativistic shock waves. In relativistic shocks, however, such effects require relativistic thermal speeds in the upstream region, and thus they might not be so important because of the presumably rapid cooling of such plasmas.
As demonstrated above, magneto-static (i.e., frozen-in) turbulence
description is still a valid approximation for particle scattering if
the Mach number of the shock wave is large. Thus, it is not surprising
that ultra-relativistic shocks yielding
![]() at the
magneto-static limit seem to be in good agreement with spectral
indices of gamma-ray burst afterglows (Bednarz & Ostrowski
1998). Not all relativistic shocks are, however, strong
shocks. Like in non-relativistic plasmas such as the solar corona,
freely propagating (i.e., not driven by pistons) shock waves in highly
magnetized plasmas are more likely rather weak with Mach numbers of
the order of a few or less. Thus, when applying the theory of
relativistic shock acceleration to the astrophysical observations,
simplifying assumptions such as the magneto-static limit should be
used only after due justification.
at the
magneto-static limit seem to be in good agreement with spectral
indices of gamma-ray burst afterglows (Bednarz & Ostrowski
1998). Not all relativistic shocks are, however, strong
shocks. Like in non-relativistic plasmas such as the solar corona,
freely propagating (i.e., not driven by pistons) shock waves in highly
magnetized plasmas are more likely rather weak with Mach numbers of
the order of a few or less. Thus, when applying the theory of
relativistic shock acceleration to the astrophysical observations,
simplifying assumptions such as the magneto-static limit should be
used only after due justification.
In view of our results and the above discussion, we conclude (i) that
Alfvén-wave transmission in parallel non-relativistic shocks leads to
downstream wave fields that are propagating backward relative to the
flow direction if the quasi-Newtonian Alfvénic Mach number of the
shock is close to
![]() ;
(ii) that the finite wave speeds
relative to the plasma rest frame need to be taken into account when
modeling particle acceleration in low-Mach-number relativistic shock
waves; (iii) that when these effects are taken into account,
(accelerated-particle) spectral indices as flat as
;
(ii) that the finite wave speeds
relative to the plasma rest frame need to be taken into account when
modeling particle acceleration in low-Mach-number relativistic shock
waves; (iii) that when these effects are taken into account,
(accelerated-particle) spectral indices as flat as
![]() can
be accounted for. Self-consistent treatment of Alfvén-wave
transmission, as well as modeling of wave transmission in oblique
shocks would be important and natural paths for future work on this
subject.
can
be accounted for. Self-consistent treatment of Alfvén-wave
transmission, as well as modeling of wave transmission in oblique
shocks would be important and natural paths for future work on this
subject.
We use the symbols ![]() ,
,
![]() ,
and
,
and
![]() for bulk
speeds, bulk Lorentz factors, and bulk proper speeds of the plasma
flow relative to the shock, and n, P, and
for bulk
speeds, bulk Lorentz factors, and bulk proper speeds of the plasma
flow relative to the shock, and n, P, and ![]() as rest-frame
density, pressure and energy density of the plasma. Both the specific
enthalpy of the gas and the pitch-angle cosine of an accelerated
particle are denoted by
as rest-frame
density, pressure and energy density of the plasma. Both the specific
enthalpy of the gas and the pitch-angle cosine of an accelerated
particle are denoted by ![]() ;
the local meaning of the symbol should
be fully clear from the context. The Alfvén speed, its Lorentz
factor, and the corresponding proper speed, as measured in the local
rest frame, are denoted by
;
the local meaning of the symbol should
be fully clear from the context. The Alfvén speed, its Lorentz
factor, and the corresponding proper speed, as measured in the local
rest frame, are denoted by
![]() ,
,
![]() ,
and
,
and
![]() .
As usual, quantities measured upstream [downstream] the
shock wave are denoted with subscripts 1 [2].
.
As usual, quantities measured upstream [downstream] the
shock wave are denoted with subscripts 1 [2].
![]() ,
,
![]() ,
,
![]() and
and ![]() denote the
quasi-Newtonian Alfvénic Mach-number of the shock, the gas compression
ratio, and the polytropic index and the dimensionless temperature of
the downstream gas, respectively. All speeds are measured in units of
c.
denote the
quasi-Newtonian Alfvénic Mach-number of the shock, the gas compression
ratio, and the polytropic index and the dimensionless temperature of
the downstream gas, respectively. All speeds are measured in units of
c.
The symbols V and ![]() denote speeds and corresponding Lorentz
factors related to Alfvén waves as measured in the shock frame:
denote speeds and corresponding Lorentz
factors related to Alfvén waves as measured in the shock frame:
![]() and
and
![]() are the shock-frame phase speeds and Lorentz
factors of the Alfvén waves propagating parallel (+) and
anti-parallel (-) to the flow, and Vk denotes the
scattering-center speed, i.e., an averaged wave speed relative to the
shock as felt by the accelerated particles. Wave magnetic fields are
denoted by
are the shock-frame phase speeds and Lorentz
factors of the Alfvén waves propagating parallel (+) and
anti-parallel (-) to the flow, and Vk denotes the
scattering-center speed, i.e., an averaged wave speed relative to the
shock as felt by the accelerated particles. Wave magnetic fields are
denoted by ![]() ,
wave number by k, wave spectra by
,
wave number by k, wave spectra by
![]() ,
and the normalized cross helicity of the waves by
,
and the normalized cross helicity of the waves by
![]() .
Wave-transmission and reflection coefficients are given by
.
Wave-transmission and reflection coefficients are given by
![]() and
and ![]() ,
respectively, when measured for the (wave-number
integrated) wave amplitudes (see Eqs. (10) and (11));
when measured at constant (wave-frame) wave-number (see Eqs. (22) and (23)), they are further subscripted by
k. A tilde over all these quantities (e.g.,
,
respectively, when measured for the (wave-number
integrated) wave amplitudes (see Eqs. (10) and (11));
when measured at constant (wave-frame) wave-number (see Eqs. (22) and (23)), they are further subscripted by
k. A tilde over all these quantities (e.g.,
![]() )
indicates
that values measured in the appropriate wave frame are considered;
symbols without tilde are measured in the shock
frame.
rk=Vk1/Vk2, s, and
)
indicates
that values measured in the appropriate wave frame are considered;
symbols without tilde are measured in the shock
frame.
rk=Vk1/Vk2, s, and ![]() denote the
scattering-center compression ratio of the shock, and the wave and the
accelerated-particle spectral indices, respectively.
denote the
scattering-center compression ratio of the shock, and the wave and the
accelerated-particle spectral indices, respectively.
Acknowledgements
This study is a part of the project "Collective Processes in Astrophysical Plasmas: Waves, Heating and Accelerated Particles'' co-funded by the Academy of Finland and Deutscher Akademischer Austauschdienst (DAAD). J. J. P. V. thanks the Finnish Cultural Foundation for financial support. R. S. acknowledges partial support by the Deutsche Forschungsgemeinschaft through Sonderforschungsbereich 591 and by the Bundesministerium für Bildung und Forschung (BMBF) through Verbundforschungsprogramm 05 CH1PCA 6.