We study a new nonlinear excitation mechanism of kinetic Alfvén waves (KAWs) and whistler waves (Ws) by electron beam-driven Langmuir waves (Ls). The generation conditions for the parametric decay instability L
A&A 409, 331-345 (2003)
DOI: 10.1051/0004-6361:20031104
Yu. Voitenko1,2 - M. Goossens1 - O. Sirenko1 - A. C.-L. Chian3,4
1 - Centre for Plasma Astrophysics, K.U. Leuven, Celestijnenlaan 200B, 3001
Heverlee, Belgium
2 -
Main Astronomical Observatory, National Academy of Sciences
of Ukraine, 27 Akademika Zabolotnoho St., 03680 Kyiv, Ukraine
3 -
National
Institute for Space Research - INPE, PO Box 515, 12201-970 Sao Jose dos Campos-SP,
Brazil
4 -
World Institute for Space Research - WISER, University of Adelaide, SA
5005, Australia
Received 15 May 2003 / Accepted 16 July 2003
Abstract
We study a new nonlinear excitation mechanism of kinetic
Alfvén waves (KAWs) and whistler waves (Ws) by electron
beam-driven Langmuir waves (Ls). The generation conditions for the
parametric decay instability L
![]() W + KAW are
determined and the growth rate is calculated. We show that the
resonant pairs of KAWs and whistler waves are nonlinearly coupled
to the pump Langmuir waves and their amplitudes undergo
exponential growth from the thermal level. The perpendicular
dispersion of KAWs strongly increases the coupling due to the
nonlinear current parallel to the ambient magnetic field. Our
study suggests that the nonlinear coupling of Langmuir wave energy
into KAWs and whistlers can provide an efficient sink for weakly
dispersive Langmuir waves excited by fast electron beams in the
solar corona when the electron plasma frequency is lower than the
electron gyrofrequency. This condition can be satisfied in the
low-density magnetic filaments that are rooted in the depleted
patches at the coronal base and extend to the high corona. At the
same time, the Langmuir-driven KAWs and whistlers give rise to
scattering and/or thin structures of radio emission penetrating
through, or generated in these regions. Since the decay into
sunward propagating KAWs is strongest, the nonlinearly driven KAWs
can be easily distinguished from the waves generated at the
coronal base and propagating away from the Sun. Our results may be
used in the analysis of solar radio data and for remote probing of
the coronal plasma, magnetic fields, and waves.
W + KAW are
determined and the growth rate is calculated. We show that the
resonant pairs of KAWs and whistler waves are nonlinearly coupled
to the pump Langmuir waves and their amplitudes undergo
exponential growth from the thermal level. The perpendicular
dispersion of KAWs strongly increases the coupling due to the
nonlinear current parallel to the ambient magnetic field. Our
study suggests that the nonlinear coupling of Langmuir wave energy
into KAWs and whistlers can provide an efficient sink for weakly
dispersive Langmuir waves excited by fast electron beams in the
solar corona when the electron plasma frequency is lower than the
electron gyrofrequency. This condition can be satisfied in the
low-density magnetic filaments that are rooted in the depleted
patches at the coronal base and extend to the high corona. At the
same time, the Langmuir-driven KAWs and whistlers give rise to
scattering and/or thin structures of radio emission penetrating
through, or generated in these regions. Since the decay into
sunward propagating KAWs is strongest, the nonlinearly driven KAWs
can be easily distinguished from the waves generated at the
coronal base and propagating away from the Sun. Our results may be
used in the analysis of solar radio data and for remote probing of
the coronal plasma, magnetic fields, and waves.
Key words: Sun: corona - waves - instabilities
Nonlinear wave-wave interactions significantly modify the transformation and transport of energy in space plasmas. A wave mode that is excited in an unstable plasma region can be nonlinearly converted into wave modes which posses quite different propagation and dissipation properties. These secondary modes are able to deliver energy and information over long distances and deposit the energy in ways that may be totally different from what is expected for the original wave. Langmuir waves (Ls) are an important example of this type of behavior. They are excited in the solar corona and solar wind by fast electron beams and, in turn, nonlinearly excite radio waves that freely propagate through interplanetary space and are observed on the Earth. This scenario has been first proposed by Ginzburg & Zhelezniakov (1958), and related processes have extensively studied since then (Cairns & Robinson 1998, and references therein).
The nonlinear stabilization of the beam-driven Langmuir instability (Papadopoulos et al. 1974; Grognard 1982; Cairns & Robinson 1998), and/or reabsorption of Langmuir waves by beam (Zaitsev et al. 1972; Mel'nik et al. 1999) can preserve the beam propagation and the Langmuir turbulence can survive over long distances in the solar corona and solar wind. The time-of-flight effects are also important and, together with beam/plasma nonuniformities, can produce stochastically an unstable electron bump-on-tail at any distance from the Sun. On the base of this last consideration, Robinson (1992) introduced a stochastic growth model for Langmuir waves.
The efficiency of these processes depends on the local plasma
parameters, and the various possibilities have to be carefully
examined when the nonlinear dynamics of Langmuir waves can be
determined by alternative processes. So, in their study of the
nonlinear dynamics of Langmuir waves, excited by electron beams in
the solar corona and solar wind, Cairns &
Robinson (1998) argue in favor of the electrostatic decay L
![]() S + L
S + L
![]() (in its random phase
version) rather than the modulational instability, which was first
discussed in this context by Papadopoulos et al. (1974), and wave
collapse. The nonlinear plasma emission mechanisms involving
ion-sound waves (S) are commonly accepted for explaining type III
radio emission. The original beam-driven Langmuir waves
nonlinearly decay into secondary Langmuir waves plus ion-acoustic waves (L
(in its random phase
version) rather than the modulational instability, which was first
discussed in this context by Papadopoulos et al. (1974), and wave
collapse. The nonlinear plasma emission mechanisms involving
ion-sound waves (S) are commonly accepted for explaining type III
radio emission. The original beam-driven Langmuir waves
nonlinearly decay into secondary Langmuir waves plus ion-acoustic waves (L
![]() L
L
![]() + S), and/or into (fundamental
harmonic) radio waves plus ion-acoustic waves (L
+ S), and/or into (fundamental
harmonic) radio waves plus ion-acoustic waves (L
![]() T1 + S), and/or or scatter off thermal ions. In turn, the
nonlinear coupling of two
Langmuir waves produces the second harmonic radio emission (L + L
T1 + S), and/or or scatter off thermal ions. In turn, the
nonlinear coupling of two
Langmuir waves produces the second harmonic radio emission (L + L
![]()
![]() T2). The coupling of ion-acoustic
waves with Langmuir waves (S + L
T2). The coupling of ion-acoustic
waves with Langmuir waves (S + L
![]() T1) provides yet another
channel for the fundamental radio emission, but the former, L
T1) provides yet another
channel for the fundamental radio emission, but the former, L
![]() T1 + S, seems to be more favorable (e.g.,
Thejappa & MacDowall 1998; Bárta & Karlický 2000).
T1 + S, seems to be more favorable (e.g.,
Thejappa & MacDowall 1998; Bárta & Karlický 2000).
Close temporal correlation between high-frequency Langmuir waves and low-frequency electromagnetic whistler waves has been observed recently within magnetic holes of the solar wind. In order to account for these observations, a theory has been formulated of the nonlinear coupling of Langmuir waves and whistler waves (Chian & Abalde 1999; Luo et al. 1999). It is suggested that the nonlinear interaction of Langmuir waves with whistler waves may lead to the formation of modulated Langmuir wave packets as well as the generation of circularly polarized radio waves at the plasma frequency in the solar wind.
On the other hand, two high-frequency waves with similar frequencies can nonlinearly couple via three-wave resonant interaction with a low-frequency electromagnetic wave. Several nonlinear mode-mode coupling processes, involving high-frequency electrostatic waves and low-frequency Alfvén waves, have been discussed in the past. The nonlinear generation of nonthermal electromagnetic radiation near the electron plasma frequency by Langmuir waves in space and astrophysical plasmas has been studied by Chian et al. (1994, 1997, 2000, 2002) and Lopes & Chian (1996). It was shown that large-amplitude Langmuir waves may explain the excitation of whistler-mode emission in the Earth's and Jupiter's auroral acceleration regions where the electron plasma frequency is smaller than the electron cyclotron frequency. The nonlinear coupling of Langmuir waves with Alfvén waves or whistlers can produce bursty radio emission from flares on the Sun and stars (Chian et al. 1997). All these papers restricted their analysis to interacting waves that propagate along the magnetic field.
The Alfvén waves with high perpendicular wavenumbers are known as kinetic Alfvén waves (KAWs). Linear and nonlinear properties of KAW attract increasing interest because of the strong wave-wave and wave-particle interactions that they cause (Voitenko 1998; Hollweg 1999). Nonlinear parametric processes involving oblique upper-hybrid and oblique (kinetic) Alfvén waves have been investigated by Yukhimuk et al. (1998, 1999). The nonlinear wave-wave couplings are shown to occur due to the electrostatic properties of the oblique Alfvén wave, which greatly increase the efficiency of the coupling processes. In particular, it has been shown that an upper-hybrid wave can parametrically decay into an another upper-hybrid wave and a kinetic Alfvén wave (Yukhimuk et al. 1998). Nonlinear excitation mechanism of high-frequency x- and o-mode waves by upper hybrid waves has been proposed by Yukhimuk et al. (1999). The parametric decay channels for an upper hybrid wave decaying into high-frequency x- and o-mode waves and a KAW taking part have been calculated with a special attention towards their possible role in the generation of radio emission from space plasmas. The same oblique Alfvén wave mode, KAW, can interact also with other high-frequency waves, namely - whistlers. A three-wave decay process in which two whistlers and a KAW has been considered by Chen (1977) and Taranenko & Chmyrev (1988). Here the parametric decay involves pump and daughter whistler waves and a daughter KAW. Again, the nonlinear coupling here is possible due to kinetic effects in KAWs.
Obviously, Alfvén waves with short perpendicular wavelengths are important in space plasma, and the extension of the nonlinear analysis of the wave processes including KAWs should reveal more about the fundamental physics involved (Hollweg 1999; Voitenko & Goossens 2000). In present paper we deal with a new nonlinear process in which kinetic Alfvén waves participate: the parametric excitation of KAWs and whistler waves by Langmuir waves. Besides theoretical interest, we study this process in view of its potential importance for the interpretation of the radio observations of complex wave events in the solar corona where Langmuir waves are supposed to be excited by electron beams.
The coherent wave description that we use here is directly applicable to the situation when narrow-band Lanmuir waves are excited by an electron beam. Otherwise, when the bandwidth of Langmuir waves exceeds the calculated nonlinear growth rate, a random-phase analysis should be applied (Cairns & Robinson 1998; Luo et al. 1999). The coupling coefficients that we calculated from the dynamic equation still determine the efficiency of the random-phase decay, but with the growth rate reduced by the wave dephasing. The extension of the coherent analysis of the present paper to the random-phase analysis is thus straightforward but somehaw involved, and is postponed to a separate study. In the Discussion section we provide some numerical estimations of the applicability of the parametric decay approach in corona.
The plasma emission theory based on the Langmuir wave instability
has been mainly developed for plasmas with a relatively high
density and/or weak magnetic field where the local
electron-cyclotron frequency is smaller than the local plasma
frequency,
![]() .
This condition is
satisfied in the solar wind, and is believed to be satisfied in
the solar corona also. However, low values of coronal
.
This condition is
satisfied in the solar wind, and is believed to be satisfied in
the solar corona also. However, low values of coronal ![]() (gas/magnetic pressure ratio) allow strong variations of plasma
density across the background magnetic field even if the magnetic
field varies slowly. Therefore, the magnetic filaments (or
threads, or flux tubes), which are rooted in underdense
(underheated) patches of the coronal base, should be underdense in
the low-
(gas/magnetic pressure ratio) allow strong variations of plasma
density across the background magnetic field even if the magnetic
field varies slowly. Therefore, the magnetic filaments (or
threads, or flux tubes), which are rooted in underdense
(underheated) patches of the coronal base, should be underdense in
the low-![]() coronal plasma as well, and the condition
coronal plasma as well, and the condition
![]() can be satisfied. The electron beam-driven
Langmuir instability is still strong in this situation (e.g.,
Vlahos & Rowland 1984), but the nonlinear processes involved can
be quite different. In particular, our present study suggests that
the Alfvén-whistler turbulence may provide an efficient energy
sink for Langmuir waves in a diluted solar plasma where the
electron-cyclotron frequency is larger than the plasma frequency,
can be satisfied. The electron beam-driven
Langmuir instability is still strong in this situation (e.g.,
Vlahos & Rowland 1984), but the nonlinear processes involved can
be quite different. In particular, our present study suggests that
the Alfvén-whistler turbulence may provide an efficient energy
sink for Langmuir waves in a diluted solar plasma where the
electron-cyclotron frequency is larger than the plasma frequency,
![]() .
.
We consider an oblique Langmuir wave with
![\begin{displaymath}\vec{E}_{\rm L}=(E_{{\rm L}x}\vec{e}_{x}+E_{{\rm L}z}\vec{e}_...
...\rm L}t-k_{{\rm L}x}x-k_{{\rm L}z}z\right) \right]
+{\rm c.c};
\end{displaymath}](/articles/aa/full/2003/37/aah3700/img15.gif)
An important parameter is the electron cyclotron/electron plasma
frequency ratio
![]() .
In the solar wind
.
In the solar wind
![]() ,
as is measured in situ by
satellites, and it is widely believed that at least
,
as is measured in situ by
satellites, and it is widely believed that at least
![]() in the coronal type III bursts. Here we note
that the coronal heating process is highly non-uniform, which
causes large cross-field density variations of the plasma
evaporated from the chromosphere. As the strong magnetic field
(MF) confines the plasma across MF lines in a low-
in the coronal type III bursts. Here we note
that the coronal heating process is highly non-uniform, which
causes large cross-field density variations of the plasma
evaporated from the chromosphere. As the strong magnetic field
(MF) confines the plasma across MF lines in a low-![]() coronal plasma, the hydrostatic equilibrium along MF lines gives
rise to a very nonuniform plasma density across MF in the high
corona also. Namely, the particle density decreases faster with
height where the temperature is lower, i.e., where the plasma is
underheated. In this situation, significant variations of the
plasma density can appear across the MF (i.e., in the horizontal
direction). The force balance in that direction involves both the
gas pressure and the magnetic pressure forces. Since the magnetic
field lines are frozen in the plasma,
the perpendicular imbalance of gas pressure produces the (small in low-
coronal plasma, the hydrostatic equilibrium along MF lines gives
rise to a very nonuniform plasma density across MF in the high
corona also. Namely, the particle density decreases faster with
height where the temperature is lower, i.e., where the plasma is
underheated. In this situation, significant variations of the
plasma density can appear across the MF (i.e., in the horizontal
direction). The force balance in that direction involves both the
gas pressure and the magnetic pressure forces. Since the magnetic
field lines are frozen in the plasma,
the perpendicular imbalance of gas pressure produces the (small in low-![]() plasma) variations of the magnetic pressure that keep the
total pressure constant in the horizontal direction. The
cross-field non-uniformities are observed in the form of
filamentary ray-like structures, extending radially from the
coronal base in the corona (Woo 1996). The perpendicular length
scales of density filaments are as small as 1 km at the coronal
base, and about 10 km at 2-5 solar radii. Hence we adopt the
opposite inequality,
plasma) variations of the magnetic pressure that keep the
total pressure constant in the horizontal direction. The
cross-field non-uniformities are observed in the form of
filamentary ray-like structures, extending radially from the
coronal base in the corona (Woo 1996). The perpendicular length
scales of density filaments are as small as 1 km at the coronal
base, and about 10 km at 2-5 solar radii. Hence we adopt the
opposite inequality,
![]() ,
for low-density
magnetic filaments magnetically connected with the cool patches at
the coronal base.
,
for low-density
magnetic filaments magnetically connected with the cool patches at
the coronal base.
We are interested in the temporal evolution of a trial whistler
wave with frequency
![]() and wave vector
and wave vector
![]() and a kinetic Alfvén wave
(KAW) with frequency
and a kinetic Alfvén wave
(KAW) with frequency
![]() and wave vector
and wave vector
![]() with
with
![]() .
The
whistler wave and the kinetic Alfvén wave are coupled via a
pump Langmuir wave
with frequency
.
The
whistler wave and the kinetic Alfvén wave are coupled via a
pump Langmuir wave
with frequency
![]() and wave vector
and wave vector
![]() .
For a strong three-wave coupling, the
following resonant conditions should be satisfied:
.
For a strong three-wave coupling, the
following resonant conditions should be satisfied:
The KAWs are low-frequency waves,
![]() (
(
![]() is the proton cyclotron frequency), and the
Langmuir waves are high-frequency waves, with frequencies of the
order of electron plasma frequency,
is the proton cyclotron frequency), and the
Langmuir waves are high-frequency waves, with frequencies of the
order of electron plasma frequency,
![]() .
Hence, the resonant condition (1)
can be satisfied if
.
Hence, the resonant condition (1)
can be satisfied if
![]() .
Having in
mind that the whistler frequency
.
Having in
mind that the whistler frequency
![]() ,
we see that the resonant condition can be easily satisfied only when
,
we see that the resonant condition can be easily satisfied only when
![]() ,
as we choose in our plasma model (see
Sect. 4.1 for more quantitative discussion of resonant
conditions).
,
as we choose in our plasma model (see
Sect. 4.1 for more quantitative discussion of resonant
conditions).
The wave electromagnetic fields obey Maxwell's equations
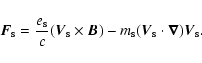
| (8) |
The plasma/magnetic pressure ratio ![]() plays an important
role for
KAWs. Indeed, the electron and/or proton temperature effects prevail when
plays an important
role for
KAWs. Indeed, the electron and/or proton temperature effects prevail when
![]() ,
while the parallel electron inertia effects
are more
important for
,
while the parallel electron inertia effects
are more
important for
![]() .
Although the condition
.
Although the condition
![]() holds for most of the solar corona, there
are regions of diluted cold plasma and/or strong magnetic field,
e.g., above magnetic spots, where
holds for most of the solar corona, there
are regions of diluted cold plasma and/or strong magnetic field,
e.g., above magnetic spots, where
![]() .
Therefore,
we take into account both the temperature effects, and the
parallel electron inertia effects for KAWs.
.
Therefore,
we take into account both the temperature effects, and the
parallel electron inertia effects for KAWs.
Since KAWs are low-frequency waves, the plasma approximation
(quasi-neutrality condition) holds:
We calculate the expressions for the electron and proton number
densities related to the KAW,
![]() and
and
![]() ,
from the equations
of motion (6) and the continuity Eqs. (7). Thus we
find
,
from the equations
of motion (6) and the continuity Eqs. (7). Thus we
find
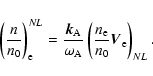
When we take into account that the electric current along the
magnetic field for a plasma with
![]() is determined
mostly by electrons, we obtain from the parallel component of
Ampere law (3) that
is determined
mostly by electrons, we obtain from the parallel component of
Ampere law (3) that
The nonlinear second-order dispersion relation is found from
Eqs. (9)-(12):
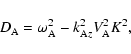
The nonlinear part ![]() is given by
is given by
For high-frequency whistlers we can neglect the proton dynamics.
With this
assumption the Maxwell equations for parallel-propagating whistler wave,
![]() ,
give
,
give
From the equation of motion (6) we obtain the electron
velocity components due to whistler:
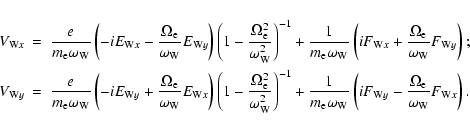
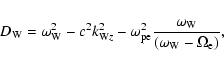
In order to calculate the nonlinear coupling coefficients we need explicit expressions for the linear responses due to all wave modes, i.e. linear expressions for the electron velocity components, electron density perturbations and magnetic field perturbations.
In the Langmuir wave,
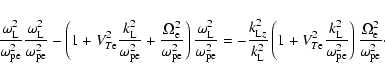
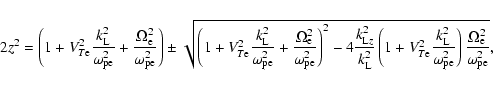
When the first term dominate under the square root in (24)
(e.g., for quasi-parallel waves
![]() ),
),
![\begin{eqnarray*}z^{2}=\frac{1}{2}\left( 1+Y^{2}+b^{2}\right) \pm
\frac{1}{2}\le...
...}\right) b^{2}\left\vert
1+Y^{2}-b^{2}\right\vert ^{-1}\right] .
\end{eqnarray*}](/articles/aa/full/2003/37/aah3700/img110.gif)
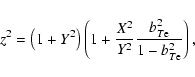
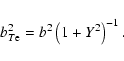
For weak wave dispersion,
![]() ,
we have
,
we have
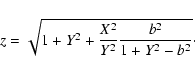
In the whistler wave we have
![]() ,
and
,
and
In the kinetic Alfvén wave
Having found the expressions for the linear plasma response we are
now in a position to calculate the second-order nonlinear source
part
![]() in the equations
for whistlers. The calculation
is straightforward but somehow involved. Inserting the linear expressions (
19)-(22) for the pump Langmuir wave into (18),
and (30)-(35) for the trial KAW, and keeping dominant
terms, we find the expression for
in the equations
for whistlers. The calculation
is straightforward but somehow involved. Inserting the linear expressions (
19)-(22) for the pump Langmuir wave into (18),
and (30)-(35) for the trial KAW, and keeping dominant
terms, we find the expression for
![]() :
:
Similarly, we find the nonlinear source term for KAWs
![]() ,
where
,
where
In this section we investigate the decay of an oblique Langmuir wave into pairs composed of resonant whistlers and KAWs. The proximity of the whistler and Langmuir wave frequencies imposes additional restrictions on this process, therefore we start with an analysis of the resonant conditions.
The resonant conditions impose restrictions on the parameters of
the interacting waves. We use the frequency matching condition,
![]() ,
and insert (23) into
(29) to get the matching equation relating the parameters of
the interacting waves:
,
and insert (23) into
(29) to get the matching equation relating the parameters of
the interacting waves:
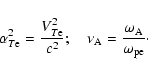
One should note that the variation of the KAW frequency in the range
![]() at fixed b produces small deviations
of the resonant value of X around the value determined mainly by
Z and by plasma parameters, b and
at fixed b produces small deviations
of the resonant value of X around the value determined mainly by
Z and by plasma parameters, b and
![]() .
In other
words, the matching equation indicates that the decay is possible
if the initial Langmuir waves adjust their perpendicular
wavenumber X, and/or parallel wavenumber Z, to the value(s)
given by the solution of matching Eq. (39). However,
the analytical solution (40) is invalid in the range
Z<0.01. The resonant diagram, valid for all Z, is shown in
Fig. 1.
.
In other
words, the matching equation indicates that the decay is possible
if the initial Langmuir waves adjust their perpendicular
wavenumber X, and/or parallel wavenumber Z, to the value(s)
given by the solution of matching Eq. (39). However,
the analytical solution (40) is invalid in the range
Z<0.01. The resonant diagram, valid for all Z, is shown in
Fig. 1.
The resonant perpendicular wavenumber
![]() ,
given by (
39), determines the resonant propagation angle for the
Langmuir decay,
,
given by (
39), determines the resonant propagation angle for the
Langmuir decay,
![]() .
If the value of b is
sufficiently close to 1 (e.g., b=1.02), the Langmuir waves
which develop resonant values of X can decay over a wide range
of Z. However, for larger values of b, the allowed range of
Z, Z<Z1, shrinks towards low Langmuir wavenumbers with an
upper boundary
.
If the value of b is
sufficiently close to 1 (e.g., b=1.02), the Langmuir waves
which develop resonant values of X can decay over a wide range
of Z. However, for larger values of b, the allowed range of
Z, Z<Z1, shrinks towards low Langmuir wavenumbers with an
upper boundary
There is another, well separated range of larger resonant Z required for the decay, Z>Z2, with
![\begin{figure}
\par\includegraphics[width=17cm,clip]{fig1.eps}\end{figure}](/articles/aa/full/2003/37/aah3700/Timg158.gif) |
Figure 1:
Resonance diagram of the decay instability: resonant
perpendicular wavenumber
|
| Open with DEXTER | |
The parallel wavenumbers of the Langmuir waves that are directly
excited by slow beams can be in the range Z>Z1 where decay
is impossible. In this case there is still a possibility that the
waves propagating in the higher-density region will reduce their
wavenumbers to
![]() ,
and eventually meet the resonant
condition for decay into KAWs and whistlers. Or some other
nonlinear process(es) redistribute Langmuir spectrum towards
smaller Z satisfying
,
and eventually meet the resonant
condition for decay into KAWs and whistlers. Or some other
nonlinear process(es) redistribute Langmuir spectrum towards
smaller Z satisfying
![]() .
.
From (13) and (17), we obtain the nonlinear
dispersion relation for the parametric decay instability of
Langmuir wave:
Using here (36) for
![]() and (38) for
and (38) for
![]() , we get an explicit expression for the nonlinear growth rate:
, we get an explicit expression for the nonlinear growth rate:
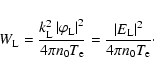
For both forward and backward propagating KAWs,
![]() ,
the
decay rate strongly depends on the perpendicular KAW wavenumber
X. It vanishes when X tends to 0 but becomes large when Xis increased. A strong instability can develop for sufficiently
high values of X.
,
the
decay rate strongly depends on the perpendicular KAW wavenumber
X. It vanishes when X tends to 0 but becomes large when Xis increased. A strong instability can develop for sufficiently
high values of X.
The nonlinear growth rate may be written in non-dimensional form,
useful for analysis:
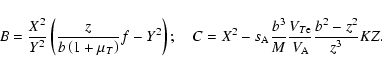
Electron beams exist in many space and astrophysical plasmas and
are identified by remote radio observations and in situ by several
satellites; A few examples are the beams related to solar bursts,
Earth's foreshocks and Earth's magnetosphere. Langmuir waves are
commonly believed to be excited in the solar corona and solar wind
by fast electron beams with a relative number density
![]() ,
that are accelerated in coronal
magnetic reconnection events to a velocity
,
that are accelerated in coronal
magnetic reconnection events to a velocity
![]() .
In turn, the beam-driven Langmuir waves produce
type III solar radio bursts (Goldman 1983; Melrose 1984). The
in-situ satellite observations in the solar wind strongly support
the picture that the Langmuir waves are indeed excited by electron
beams and eventually lead to solar type III bursts (Dulk et al.
1998; Ergun et al. 1998; Thejappa & MacDowall 1998, and
references therein). Other types of waves can be excited by
two-dimensional (in velocity space) electron beams, like oblique
whistlers, ion-cyclotron and lower-hybrid waves (Zhang et al.
1993; Wong & Smith 1994; Ergun et al. 1998). In this context we
note that the bump-on-tail instabilities of the above mentioned
modes are far weaker than the Langmuir instability for fast
diluted electron beams under coronal/solar wind conditions. As
suggested theoretically and observationally, they can only play a
complimentary role while the Langmuir instability extracts the
main part of the beam energy. Consequently, the observed Langmuir
waves are much more intense.
.
In turn, the beam-driven Langmuir waves produce
type III solar radio bursts (Goldman 1983; Melrose 1984). The
in-situ satellite observations in the solar wind strongly support
the picture that the Langmuir waves are indeed excited by electron
beams and eventually lead to solar type III bursts (Dulk et al.
1998; Ergun et al. 1998; Thejappa & MacDowall 1998, and
references therein). Other types of waves can be excited by
two-dimensional (in velocity space) electron beams, like oblique
whistlers, ion-cyclotron and lower-hybrid waves (Zhang et al.
1993; Wong & Smith 1994; Ergun et al. 1998). In this context we
note that the bump-on-tail instabilities of the above mentioned
modes are far weaker than the Langmuir instability for fast
diluted electron beams under coronal/solar wind conditions. As
suggested theoretically and observationally, they can only play a
complimentary role while the Langmuir instability extracts the
main part of the beam energy. Consequently, the observed Langmuir
waves are much more intense.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{fig2.eps}
\end{figure}](/articles/aa/full/2003/37/aah3700/Timg178.gif) |
Figure 2:
Nonlinear growth rate of the decay L
|
| Open with DEXTER | |
In this paper we focus on the high coronal levels, where the
plasma is diluted along the magnetic filaments connected to the
cool patches at the coronal base. For example, in the region where
the magnetic field B0=3.5 G, number density
n0=106 cm-3, and temperature
![]() K, we have the following values for the key
parameters of the background plasma:
K, we have the following values for the key
parameters of the background plasma:
![]() rad s<tex2htmlcommentmark>
-1,
rad s<tex2htmlcommentmark>
-1,
![]() rad s-1 (that is
rad s-1 (that is
![]() ),
),
![]() cm/s,
cm/s,
![]() cm/s (that is
cm/s (that is
![]() ,
,
![]() ,
,
![]() cm).
cm).
Typical velocities of electron beams in the solar corona can be
deduced from radio observations and from in-situ observations in
the solar wind. They lie in the range
![]() .
The initial parallel propagating Langmuir waves
that are excited by these beams have parallel wavenumbers
.
The initial parallel propagating Langmuir waves
that are excited by these beams have parallel wavenumbers
![]() for the electron
thermal velocity in corona
for the electron
thermal velocity in corona
![]() cm/s
(
cm/s
(
![]() K). When interplanetary data
are extrapolated into the
corona (see Cairns & Robinson 1998) we infer the Langmuir wave energy
K). When interplanetary data
are extrapolated into the
corona (see Cairns & Robinson 1998) we infer the Langmuir wave energy
![]() .
.
For any given ![]() ,
the beam-driven Langmuir waves can be in
3-wave resonance with whistlers and KAWs in the regions where the
perpendicular
wavenumber attains values determined by the resonant condition (39
). The initial beam-driven Langmuir waves can excite resonant
whistlers and KAWs in the coronal regions where the condition
,
the beam-driven Langmuir waves can be in
3-wave resonance with whistlers and KAWs in the regions where the
perpendicular
wavenumber attains values determined by the resonant condition (39
). The initial beam-driven Langmuir waves can excite resonant
whistlers and KAWs in the coronal regions where the condition
![]() is fulfilled. The parameter bcan be close to 1,
is fulfilled. The parameter bcan be close to 1, ![]() ,
or b can deviate from 1significantly. The condition b>1 may be satisfied in underdense
magnetic filaments at high coronal levels, or in strongly
magnetized plasmas in the low corona, where the magnetic field is
concentrated in magnetic flux tubes.
,
or b can deviate from 1significantly. The condition b>1 may be satisfied in underdense
magnetic filaments at high coronal levels, or in strongly
magnetized plasmas in the low corona, where the magnetic field is
concentrated in magnetic flux tubes.
Let us consider the decay instability L
![]() W +
KAW of weakly dispersive Langmuir waves, Z<Z1, which are
excited by fast electron beams,
W +
KAW of weakly dispersive Langmuir waves, Z<Z1, which are
excited by fast electron beams,
![]() .
These waves
undergo resonant decay in
the regions where X attains a value given by resonance condition (40
). As it follows from (45), the coupling of Langmuir wave
energy into KAWs and parallel whistlers becomes strong for large
perpendicular Langmuir/KAW wavenumbers (
.
These waves
undergo resonant decay in
the regions where X attains a value given by resonance condition (40
). As it follows from (45), the coupling of Langmuir wave
energy into KAWs and parallel whistlers becomes strong for large
perpendicular Langmuir/KAW wavenumbers (
![]() ). The
frequencies of the excited KAWs are determined by the parallel
wavenumber
). The
frequencies of the excited KAWs are determined by the parallel
wavenumber
![]() of the driving Langmuir wave and
are given by the frequency matching conditions. Note, however,
that the dependence of the nonlinear increment on the KAW
frequency is weak, so we set f=0.5. The particular value of the
KAWs' frequency is determined from the resonant condition
(39) with given Z and X.
of the driving Langmuir wave and
are given by the frequency matching conditions. Note, however,
that the dependence of the nonlinear increment on the KAW
frequency is weak, so we set f=0.5. The particular value of the
KAWs' frequency is determined from the resonant condition
(39) with given Z and X.
The nonlinear growth rate for plasma and Langmuir wave parameters
expected
in the solar corona is shown in Fig. 2 for antiparallel propagating KAWs (
![]() ). The decay into parallel-propagating KAWs is much weaker for
). The decay into parallel-propagating KAWs is much weaker for
![]() ,
and it is still weaker (but of the same
order) for
,
and it is still weaker (but of the same
order) for
![]() .
.
For all values of b=1.04, 1.1 and 1.4, the decay becomes
strong for
the corresponding resonant perpendicular wavenumbers
![]() (i.e.,
(i.e.,
![]() ). Therefore, the decay
condition
is
). Therefore, the decay
condition
is
![]() ,
and all Langmuir waves that develop these resonant
perpendicular wavenumbers, nonlinearly excite resonant whistlers
and KAWs.
,
and all Langmuir waves that develop these resonant
perpendicular wavenumbers, nonlinearly excite resonant whistlers
and KAWs.
Langmuir waves can easily develop large perpendicular wavenumbers
due to phase mixing in a plasma that is inhomogeneous in the
perpendicular (x) direction. When we take
Lx=106 m for
the inhomogeneity length-scale (Woo 1996), and use the
evolutionary (Hamilton) equation for
![]() in the form
in the form
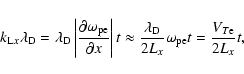
The LAW decay is sensitive to the Langmuir parallel wavenumbers,
and its
growth rate attains a maximum
![]() at
at
![]() .
The wavenumbers
of the Langmuir waves excited by fast electron beams are initially
about four times bigger,
.
The wavenumbers
of the Langmuir waves excited by fast electron beams are initially
about four times bigger,
![]() .
For these
wavenumbers the growth rate is
.
For these
wavenumbers the growth rate is
![]() if
if
![]() is
sufficiently close to unity,
is
sufficiently close to unity,
![]() ,
and the growth rate is highly reduced for larger values of
,
and the growth rate is highly reduced for larger values of
![]() (see Fig. 2). Thus, the Langmuir waves directly
driven by the beams decay strongest in the regions where
(see Fig. 2). Thus, the Langmuir waves directly
driven by the beams decay strongest in the regions where
![]() .
.
However, even in regions where
![]() deviates significantly from 1, the Langmuir waves decay fast when
they reduce parallel wavenumbers to
deviates significantly from 1, the Langmuir waves decay fast when
they reduce parallel wavenumbers to
![]() .
A most probable mechanism reducing parallel Langmuir
wavenumber in the solar corona is the density variation along
magnetic field lines. So, a local density increase of only
.
A most probable mechanism reducing parallel Langmuir
wavenumber in the solar corona is the density variation along
magnetic field lines. So, a local density increase of only
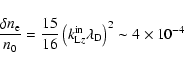
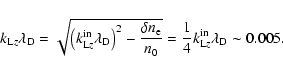
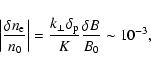
Langmuir waves excited by slow beams have also to reduce their
![]() in order to attain the allowed range of parallel
wavenumbers specified by (41), or even the range of strong
decay instability
in order to attain the allowed range of parallel
wavenumbers specified by (41), or even the range of strong
decay instability
![]() .
Again, this
may be done by parallel inhomogeneity: Langmuir waves propagating
along B0 in the direction of increasing number density will
decrease their parallel wavenumber. There are also other nonlinear
interactions, that tend to reduce the parallel wavenumber of
Langmuir waves. In one of these ways all the conditions for the
instability can be satisfied even if the Langmuir waves are
initially excited with relatively high Z (i.e., by slow beams).
.
Again, this
may be done by parallel inhomogeneity: Langmuir waves propagating
along B0 in the direction of increasing number density will
decrease their parallel wavenumber. There are also other nonlinear
interactions, that tend to reduce the parallel wavenumber of
Langmuir waves. In one of these ways all the conditions for the
instability can be satisfied even if the Langmuir waves are
initially excited with relatively high Z (i.e., by slow beams).
In the solar wind values of
![]() smaller
than 1 are measured in situ, and it is generally accepted that
smaller
than 1 are measured in situ, and it is generally accepted that
![]() in the coronal type III bursts. But
the coronal heating process is highly non-uniform, which causes
large cross-field density variations of the plasma evaporated from
chromosphere. As the strong magnetic field (MF) confines the
plasma across MF lines, the hydrostatic equilibrium tends to set
in along MF lines, which gives rise to a nonuniform plasma density
across MF in the high corona. The resulting high plasma pressure
variations across MF are easily balanced in a low-
in the coronal type III bursts. But
the coronal heating process is highly non-uniform, which causes
large cross-field density variations of the plasma evaporated from
chromosphere. As the strong magnetic field (MF) confines the
plasma across MF lines, the hydrostatic equilibrium tends to set
in along MF lines, which gives rise to a nonuniform plasma density
across MF in the high corona. The resulting high plasma pressure
variations across MF are easily balanced in a low-![]() coronal plasma by small variations of the magnetic pressure. These
nonuniformities are observed in the form of filamentary ray-like
structures of about 1 km width, extending
radially from the coronal base in the corona (Woo 1996). The condition
coronal plasma by small variations of the magnetic pressure. These
nonuniformities are observed in the form of filamentary ray-like
structures of about 1 km width, extending
radially from the coronal base in the corona (Woo 1996). The condition
![]() can be satisfied along the
low-density magnetic filaments rooted in the underheated parts of
the coronal base.
can be satisfied along the
low-density magnetic filaments rooted in the underheated parts of
the coronal base.
An alternative model to the conventional plasma-emission has been
proposed recently by Wu et al. (2002) for coronal type III radio
bursts. They suggested that x- and o-mode electromagnetic waves
are directly excited near the electron cyclotron frequency by the
electron-cyclotron maser instability (this process is similar to
the generation of AKR - auroral kilometric radiation in the
Earth's magnetosphere). An essential ingredient of this model is
the presence of underdense magnetic fibers with
![]() ,
attributed by Wu et al. to the strong
magnetic fields/low-density plasma at the coronal base. Another
critical assumption is an intense pitch-angle scattering of beam
electrons, possibly due to Alfvén waves. The resulting
electron beam distributions can be unstable with respect to
Cherenkov (bump-on-tail) and electron-cyclotron instabilities
simultaneously. But the parallel electrostatic (i.e.,
Langmuir-type) instability is still dominant in most cases, as
long as the bump-on-tail is present (see, e.g., Zhang et al.
1993). Vlahos & Rowland (1984) studied electron beams under
similar conditions and pointed out mechanisms that suppress the
pitch-angle scattering, in which case the bump-on-tail Langmuir
wave instability is by far dominant.
,
attributed by Wu et al. to the strong
magnetic fields/low-density plasma at the coronal base. Another
critical assumption is an intense pitch-angle scattering of beam
electrons, possibly due to Alfvén waves. The resulting
electron beam distributions can be unstable with respect to
Cherenkov (bump-on-tail) and electron-cyclotron instabilities
simultaneously. But the parallel electrostatic (i.e.,
Langmuir-type) instability is still dominant in most cases, as
long as the bump-on-tail is present (see, e.g., Zhang et al.
1993). Vlahos & Rowland (1984) studied electron beams under
similar conditions and pointed out mechanisms that suppress the
pitch-angle scattering, in which case the bump-on-tail Langmuir
wave instability is by far dominant.
The (random phase) "electrostatic'' decay
![]() into a secondary Langmuir wave and an ion-acoustic wave (or quasi-mode at
into a secondary Langmuir wave and an ion-acoustic wave (or quasi-mode at
![]() )
has been suggested as an efficient nonlinear
process for beam-driven Langmuir waves (Cairns & Robinson 1998;
Cairns 2000). However, the conclusion about the dominant role of
the ion-acoustic mode is not final untill the role of other wave
modes is investigated sufficiently. In particular, the kinetic
Alfvén mode can participate in Langmuir
decay, giving rise to a low-frequency electromagnetic decay
)
has been suggested as an efficient nonlinear
process for beam-driven Langmuir waves (Cairns & Robinson 1998;
Cairns 2000). However, the conclusion about the dominant role of
the ion-acoustic mode is not final untill the role of other wave
modes is investigated sufficiently. In particular, the kinetic
Alfvén mode can participate in Langmuir
decay, giving rise to a low-frequency electromagnetic decay
![]() and/or modulational
instability (Voitenko et al., in preparation).
and/or modulational
instability (Voitenko et al., in preparation).
In the present paper we have dealt with another new nonlinear process in which kinetic Alfvén waves participate: the parametric excitation of KAWs and whistler waves by Langmuir waves. The interest in this process is stimulated by the radio observations of complex wave events in the solar corona where Langmuir waves are supposed to be excited by electron beams. Our study suggests that the Alfvén-whistler turbulence may provide an efficient energy sink for Langmuir waves in a diluted solar plasma where the local electron-cyclotron frequency is higher than the local plasma frequency.
Let us compare the growth rates of the competing parametric decays
![]() and
and
![]() ,
keeping in mind that the condition
,
keeping in mind that the condition
![]() is
required for the decay into whistlers. The process
is
required for the decay into whistlers. The process
![]() is well studied for
is well studied for
![]() ,
typical in the solar wind (see, e.g., Cairns
& Robinson 1998, and references therein). However, there are
much fewer studies of the electrostatic decay in a
low-density/strong magnetic field regime
,
typical in the solar wind (see, e.g., Cairns
& Robinson 1998, and references therein). However, there are
much fewer studies of the electrostatic decay in a
low-density/strong magnetic field regime
![]() ,
which is sometimes called supercritical (Newman et al.
1994a). In comparison to the subcritical (
,
which is sometimes called supercritical (Newman et al.
1994a). In comparison to the subcritical (
![]() )
regime, there are two modifications: the perpendicular
dispersion of Langmuir waves can change its sign (see Eq.
(23)), and the electrostatic decay is primarily into oblique
Langmuir and ion-acoustic waves (Newman et al. 1994a,b; Akimoto
1995).
)
regime, there are two modifications: the perpendicular
dispersion of Langmuir waves can change its sign (see Eq.
(23)), and the electrostatic decay is primarily into oblique
Langmuir and ion-acoustic waves (Newman et al. 1994a,b; Akimoto
1995).
As a strong temperature anisotropy
![]() has been
assumed in these studies, direct comparison of our LAW growth rate
with the growth rate of the oblique electrostatic decay (L-oL)
calculated by Newman et al. and by Akimoto is impossible. If we
formally compare the LAW growth rate
has been
assumed in these studies, direct comparison of our LAW growth rate
with the growth rate of the oblique electrostatic decay (L-oL)
calculated by Newman et al. and by Akimoto is impossible. If we
formally compare the LAW growth rate
![]() (valid
for
(valid
for
![]() ,
,
![]() )
with the L-oL growth rate
given by Akimoto (1995)
)
with the L-oL growth rate
given by Akimoto (1995)
![]() (valid for
(valid for
![]() ,
where the ion sound damping
,
where the ion sound damping
![]() ),
we obtain
),
we obtain
![]()
![]() ,
i.e.,
,
i.e.,
![]() and
and
![]() are of the same order for
are of the same order for
![]() .
For higher Langmuir wavenumbers,
.
For higher Langmuir wavenumbers,
![]() ,
,
![]() .
However, the ion-acoustic wave is heavily damped
for coronal temperatures where
.
However, the ion-acoustic wave is heavily damped
for coronal temperatures where
![]() ,
and the growth
rate of the
electrostatic decay can fall below
,
and the growth
rate of the
electrostatic decay can fall below
![]() .
In our opinion, the process
.
In our opinion, the process
![]() competes
with the electrostatic decay in isothermal plasmas,
competes
with the electrostatic decay in isothermal plasmas,
![]() ,
where the efficiency of the electrostatic decay is
reduced by the strong damping of ion-acoustic mode. These
estimations indicate that an additional study is
required to determine what process is stronger for particular values of
,
where the efficiency of the electrostatic decay is
reduced by the strong damping of ion-acoustic mode. These
estimations indicate that an additional study is
required to determine what process is stronger for particular values of
![]() and Z.
and Z.
The monochromatic parametric description that we used is justified
when the nonlinear growth rate exceeds the bandwidth of the
decaying waves. This
approach has been extensively used for the narrow-band Langmuir waves (see B
árta & Karlický 2000, and references therein). The
bandwidth of the Langmuir waves excited by electron beam is
proportional to the beam velocity spread. Let us consider a simple
case when the Langmuir bandwidth is determined by the parallel
wave dispersion (23) with (X=0). The energy of excited
Langmuir waves is concentrated slightly above the wavenumber
determined from the resonant condition,
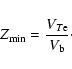
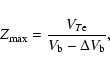
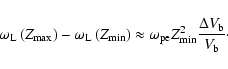
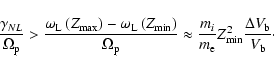
Otherwise, when the nonlinear growth rate is less than the bandwidth of the decaying waves, the random phase version of decay should be considered (Cairns & Robinson 1998). We plan to do this in our future studies. Obviously, the decay growth rate in this case is reduced by the decoherence of waves.
The bandwidth of secondary waves depends on how broad maximum has the growth rate as a function of wavenumbers of these secondary waves. Even in the case of monochromatic pump, a broadband spectrum of secondary waves can be excited if the growth rate is relatively flat. Of course, this spectrum still consists of wave pairs, each being in the three-wave parametric resonance with the pump wave.
As for the question how to distinguish between the modes of
interest (i.e., KAWs and whistlers) excited by Langmuir waves, and
the modes driven directly by beams. It is important for the
identification of dominant processes and remote diagnostics. To
this end we note that the fast 0.3c electron beam cannot
generate KAWs directly via bump-on-tail instability. Indeed, the
KAW dispersion (14) restricts the wave phase velocity to the
range
![]()
![]()
![]() ,
and since both
,
and since both ![]() and
and
![]() are much smaller than the
beam velocity (
are much smaller than the
beam velocity (
![]() ), the KAWs are off-resonant with
the beam, and, consequently, cannot extract energy from it. Even
if the Alfvén waves driven by an alternative source are
present (see, e.g., Verheest 1990), we believe that the formulae
we provide here are sufficient to distinguish the Langmuir-driven
KAWs. In particular, cross-field KAW wavelengths, determined from
the resonant conditions, in turn determine the scales and
velocities of the electron density perturbations (30)
associated with KAWs. In terms of KAW magnetic field perturbations
), the KAWs are off-resonant with
the beam, and, consequently, cannot extract energy from it. Even
if the Alfvén waves driven by an alternative source are
present (see, e.g., Verheest 1990), we believe that the formulae
we provide here are sufficient to distinguish the Langmuir-driven
KAWs. In particular, cross-field KAW wavelengths, determined from
the resonant conditions, in turn determine the scales and
velocities of the electron density perturbations (30)
associated with KAWs. In terms of KAW magnetic field perturbations
![]() ,
the relative density perturbations are
,
the relative density perturbations are
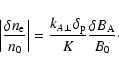
As the LAW decay exhibits a strong dependence on the pump Langmuir wavenumbers, and the electrostatic decay is relatively insensitive, the interplay between these two nonlinear processes can be complicated. For example, the beam-driven parallel Langmuir waves could first undergo electrostatic decay processes redistributing their energy towards resonance perpendicular wavenumbers, and then LAW decays come into play and eventually supplies a sink for Langmuir turbulence.
The nonlinear process that we have discussed here may play a role
also in the auroral zone of the Earth's magnetosphere, where LAW
events are registered in-situ by satellites. Spacecrafts
frequently measure intense bursts of LAW events in conjunction
with field-aligned electrons in the auroral zones (Chian et al.
1994). It is interesting to note that despite of significant
perpendicular inhomogeneities, the observed Langmuir waves'
propagation is confined to within
![]() of the geomagnetic
field in the auroral zone (Newman et al. 1994a,b). This means
that oblique wave propagation is suppressed, which can be
accounted for by the dispersion and damping of oblique Langmuir
waves (Newman 1994a). At the same time, this effect may be due to
the process that we study here: a strong decay of Langmuir waves
into whistlers and KAWs when the Langmuir waves develop resonant
perpendicular wavenumbers. For example, for
of the geomagnetic
field in the auroral zone (Newman et al. 1994a,b). This means
that oblique wave propagation is suppressed, which can be
accounted for by the dispersion and damping of oblique Langmuir
waves (Newman 1994a). At the same time, this effect may be due to
the process that we study here: a strong decay of Langmuir waves
into whistlers and KAWs when the Langmuir waves develop resonant
perpendicular wavenumbers. For example, for
![]() and
and
![]() ,
the nonlinear
Langmuir decay
into KAWs and whistlers occurs at the propagation angle
,
the nonlinear
Langmuir decay
into KAWs and whistlers occurs at the propagation angle
![]() (
(
![]() )
about
)
about
![]() .
.
As far as the dynamics of electron beams is concerned, the
situation in auroral zones is complicated by the high beam density
![]() .
This introduces dispersive effects,
and strong pitch-angle scattering of downward electrons
accelerated by electric field. The resulting electron beam
distributions become unstable with respect to electron-cyclotron
instability and generate AKR emission, but the Cherenkov
(bump-on-tail) Langmuir instability is dominant in most cases when
the bump-on-tail is present (Zhang et al. 1993).
.
This introduces dispersive effects,
and strong pitch-angle scattering of downward electrons
accelerated by electric field. The resulting electron beam
distributions become unstable with respect to electron-cyclotron
instability and generate AKR emission, but the Cherenkov
(bump-on-tail) Langmuir instability is dominant in most cases when
the bump-on-tail is present (Zhang et al. 1993).
We have investigated a new nonlinear process that is caused by
kinetic
properties of oblique (kinetic) Alfvén waves: parametric decay L
![]() W + KAW. This is plausible for the backward
propagating KAWs. The nonlinear growth rate strongly increases
with growing perpendicular wavenumber, or
W + KAW. This is plausible for the backward
propagating KAWs. The nonlinear growth rate strongly increases
with growing perpendicular wavenumber, or
![]() - dispersion
variable of the KAW.
Weakly dispersive Langmuir waves, excited by fast electron beams with
- dispersion
variable of the KAW.
Weakly dispersive Langmuir waves, excited by fast electron beams with
![]() ,
decay fastest.
,
decay fastest.
We have applied our results to the beam-driven Langmuir waves in
the solar corona and found a very short characteristic time scale
for the instability to develop,
![]() s for the parameters of coronal Langmuir waves deduced
from observations. As the nonlinear coupling of Langmuir energy
into whistlers and KAWs is possible if
s for the parameters of coronal Langmuir waves deduced
from observations. As the nonlinear coupling of Langmuir energy
into whistlers and KAWs is possible if
![]() ,
the formation of the LAW turbulence is expected in the
regions of solar corona where the magnetic field is strong and/or
the plasma is dilute. The condition
,
the formation of the LAW turbulence is expected in the
regions of solar corona where the magnetic field is strong and/or
the plasma is dilute. The condition
![]() can be satisfied in the thin (
can be satisfied in the thin (![]() 10 km) underdense filaments
guided by the magnetic field lines which are connected to the
low-temperature patches at the coronal base.
10 km) underdense filaments
guided by the magnetic field lines which are connected to the
low-temperature patches at the coronal base.
The growth rate of LAW decay critically depends on the parameter
![]() in the range
in the range
![]() :
it is large for
:
it is large for
![]() ,
but
quickly decreases with increasing
,
but
quickly decreases with increasing
![]() .
So,
the general tendency is that the faster electron beams in
.
So,
the general tendency is that the faster electron beams in
![]() regions are most efficient for
producing of LAW events. The decay instability can develop if
regions are most efficient for
producing of LAW events. The decay instability can develop if
![]() ,
where
,
where
![]() is the
resonant perpendicular wavenumber that depends on the particular
parallel wavenumber of the Langmuir wave (Eq. (40)). Since
for typical coronal parameters the resonant perpendicular
wavenumber is less than the parallel wavenumber,
is the
resonant perpendicular wavenumber that depends on the particular
parallel wavenumber of the Langmuir wave (Eq. (40)). Since
for typical coronal parameters the resonant perpendicular
wavenumber is less than the parallel wavenumber,
![]() ,
the propagation of the non-decaying
Langmuir waves is restricted to the cone
,
the propagation of the non-decaying
Langmuir waves is restricted to the cone
![]() ,
i.e., to the quasi-parallel propagation.
,
i.e., to the quasi-parallel propagation.
The situation can be different when local density variations along
magnetic field lines are present. These may be produced by, e.g.,
phase-mixed Alfvén waves, launched from the coronal base. In
this case the Langmuir waves, propagating against the density
gradient, can reduce their parallel wavenumbers to the range
![]() ,
where the decay instability is
very strong and less sensitive to
,
where the decay instability is
very strong and less sensitive to
![]() .
.
The presence of KAWs in the underdense filaments results in
fluctuations of the plasma density and velocity at length-scales
10-100 m across the magnetic field and 1-10 km along the
magnetic field. As the instability is
much stronger for antiparallel (i.e., sunward) propagating KAWs (
![]() ), the density perturbations produced by Langmuir-driven KAWs
should move sunward. Such fluctuations, moving with the Alfvén
velocity along the filaments towards the Sun, should give rise to
the scattering and/or thin structures of the coronal radio
emission. In addition, the traces of these scattering filaments
from the distant corona down to the active regions have to
pinpoint the places where the plasma is dilute and the electron
beams are accelerated.
), the density perturbations produced by Langmuir-driven KAWs
should move sunward. Such fluctuations, moving with the Alfvén
velocity along the filaments towards the Sun, should give rise to
the scattering and/or thin structures of the coronal radio
emission. In addition, the traces of these scattering filaments
from the distant corona down to the active regions have to
pinpoint the places where the plasma is dilute and the electron
beams are accelerated.
All these features can be used for diagnostic purposes, and analysis of radio data can provide observational pros and cons of the actual importance of LAW events excited by electron beams in the solar corona.
Acknowledgements
This publication results from the collaborative research in the framework of WISER - World Institute for Space Environment Research (www.cea.inpe.br/wiser). Yu. Voitenko acknowledges the financial support by the FWO Vlaanderen (grants G.0335.98 and G.0178.3), and by the Onderzoeksfonds of the K.U. Leuven (project OT/02/57). O. Sirenko acknowledges the financial support by the K.U. Leuven (grant DB.OO.18) and by the FWO Vlaanderen (grant G.0178.3). A. C.-L. Chian acknowledges the award of an 1A Senior Research Fellowship by CNPq. The authors would like to thank the referee for his valuable comments and suggestions that helped us to improve our paper.