A&A 409, 9-19 (2003)
DOI: 10.1051/0004-6361:20031060
A. Marcowith1 - J. Malzac 2,3
1 - C.E.S.R., 9 Av. du Colonnel Roche, 31028 Toulouse Cedex 4, France
2 -
Institute of Astronomy, Madingley Road, Cambridge, CB3 0HA, UK
3 -
Osservatorio di Brera, via Brera, 28, 20121 Milano, Italy
Received 14 April 2003 / Accepted 30 June 2003
Abstract
The present work investigates the calculation of absorption and emission cyclotron
line profiles in the non-relativistic and trans-relativistic regimes. We provide fits
for the ten first harmonics with synthetic functions down to 10-4 of the maximum flux with
an accuracy of 20% at worst. The lines at a given particle energy are calculated from the
integration of the Schott formula over the photon and the particle solid angles relative
to the magnetic field direction. The method can easily be extended to a larger number
of harmonics. We also derive spectral fits of thermal emission line plasmas at non-relativistic
and trans-relativistic temperatures extending previous parameterisations.
Key words: line: profiles - magnetic fields - radiation mechanisms: non-thermal, thermal
The cyclotron-synchrotron effect is one of the most important processes in astrophysics and has been invoked in solar, neutron star physics and in galactic or extra-galactic jets. At non relativistic and ultra relativistic limits, the particle emissivity is provided by well known analytical formulae.
The main contribution to the cyclotron radiation comes from low harmonics. In most astrophysical objects, this radiation is either self-absorbed or absorbed by the environment. It can even be suppressed by plasma effects such as in the Razin-Tsytovich effect. However, as stressed by different authors (Ghisellini & Svensson 1991, hereafter GS91; Mason 1992; Gliozzi et al. 1996) the cyclotron cross-section in the non- and mildly relativistic regimes is several orders of magnitude above the Thompson cross section. The cyclotron mechanism appears then as a very efficient thermalisation process in hot plasmas surrounding compact objects. At higher energies, the synchrotron photons are a supplementary source for the Comptonisation process in accretion discs coronæ, see e.g. Di Matteo et al. (1997), Ghisellini et al. (1998), hereafter GHS98, Wardzinski & Zdziarski (2000), hereafter WZ00 and Wardzinski & Zdziarski (2001).
A detailed numerical investigation of the thermalisation process in the presence of cyclo-synchrotron photons has scarcely been discussed (see however GHS98) but is of great importance for the spectral and temporal modeling of the complex spectral energy distribution produced in compact objects. Low temperature plasmas that may be found in gamma-ray bursts (in the comoving frame) and in accretion discs may produce cyclotron lines combined with synchrotron signatures. Such line features can be produced in neutron star magnetospheres probing the magnetic field.
The present work aims to propose useful fitting formulae for the first ten harmonics dominating
the emissivity for particle velocities (or normalised momentum) between
![]() (see Fig. 2 in Mahadevan et al. 1996 hereafter MNY96). We consider the case of
an isotropic electron distribution in a tangled magnetic field. The method can be extended to an arbitrary number of
harmonics. At higher energies, however, the synchrotron formulae are worth being used. The derived functions
can then be easily inserted into radiative transfer codes.
(see Fig. 2 in Mahadevan et al. 1996 hereafter MNY96). We consider the case of
an isotropic electron distribution in a tangled magnetic field. The method can be extended to an arbitrary number of
harmonics. At higher energies, however, the synchrotron formulae are worth being used. The derived functions
can then be easily inserted into radiative transfer codes.
The article is organised as follows: Sect. 2 recalls the derivation of cyclo-synchrotron emissivity. Section 3 deals with the procedures used to compute the emission and the absorption coefficient: an integration over a small frequency interval around the cyclotron resonant frequency and a direct integration over the angle between the photon and the magnetic field. These procedures are tested in Sect. 4. Section 5 provides the fitting functions in the non-thermal case, at a given particle energy. Section 6 provides the fitting functions for the emission coefficients produced in a thermal plasma.
The cyclo-synchrotron spectrum produced by one particle of mass m, charge e and velocity
![]() embedded in a uniform magnetic field B can be derived
from classical electrodynamics (see for example Bekefi 1966, chapter 6).
The emitted power spectrum, the so-called Schott formula is expressed as a sum of harmonics
peaking at a frequency
embedded in a uniform magnetic field B can be derived
from classical electrodynamics (see for example Bekefi 1966, chapter 6).
The emitted power spectrum, the so-called Schott formula is expressed as a sum of harmonics
peaking at a frequency
![]() (
(![]() ), where
), where
![]() is the Lorentz factor
of the particle. The cyclotron frequency is
is the Lorentz factor
of the particle. The cyclotron frequency is
![]() ,
where the magnetic field B is expressed
in Gauss units.
,
where the magnetic field B is expressed
in Gauss units.
The cyclotron resonance is defined by
The angles are defined relative to the dominant magnetic field direction:
![]() is the particle pitch-angle and
is the particle pitch-angle and ![]() is the
photon angle.
is the
photon angle.
Integrating Eq. (1) over the photon angle and the frequency, averaging the pitch-angle leads to
the total power emitted by one particle
At the non-relativistic limit, only the first harmonics contribute significantly to the emissivity. For the particular pitch-angle
![]() ,
and after
integration over all observer angles, the power emitted
in a given harmonic n is (Bekefi 1966)
,
and after
integration over all observer angles, the power emitted
in a given harmonic n is (Bekefi 1966)
In the relativistic limit (
![]() )
the emissivity is dominated by the harmonics
of order
)
the emissivity is dominated by the harmonics
of order
![]() .
The spectrum tends towards a continuum as the frequency interval between two harmonics
is
.
The spectrum tends towards a continuum as the frequency interval between two harmonics
is
![]() .
The synchrotron power radiated by one particle per unit frequency interval is given by
(we still assume
.
The synchrotron power radiated by one particle per unit frequency interval is given by
(we still assume
![]() )
)
The first procedure consists in integrating the expression (1)
over ![]() in a narrow frequency range
in a narrow frequency range
![]() ,
with
,
with
![]() ,
,
![]() being a positive real variable.
being a positive real variable.
Equation (1) becomes
We note that for
![]() ,
,
![]() becomes undefinite and
Eq. (8) breaks down. In this case, all the power is
radiated at the resonant frequencies, i.e.
becomes undefinite and
Eq. (8) breaks down. In this case, all the power is
radiated at the resonant frequencies, i.e.
![]() except at
frequencies
except at
frequencies
![]() and at those frequencies the power per unit frequency is actually infinite.
The total power emitted in harmonic n at pitch angle
and at those frequencies the power per unit frequency is actually infinite.
The total power emitted in harmonic n at pitch angle
![]() may be estimated by integrating Eq. (1) over frequencies around the resonance (leading to a result
similar to Eq. (6)) and then numerically over the
observer angles
may be estimated by integrating Eq. (1) over frequencies around the resonance (leading to a result
similar to Eq. (6)) and then numerically over the
observer angles ![]() .
.
Both methods fail to account for the unavoidable resonance at
frequencies
![]() that is due to the contribution from pitch
angle
that is due to the contribution from pitch
angle
![]() .
In the frequency integration method, the Dirac function is
artificially broadened over the integration bin of width
.
In the frequency integration method, the Dirac function is
artificially broadened over the integration bin of width ![]() .
This leads to an overestimate the line emissivity around the resonances,
but the resulting frequency integrated power is conserved.
In the direct integration scheme we neglected the resonant contribution
at frequencies
.
This leads to an overestimate the line emissivity around the resonances,
but the resulting frequency integrated power is conserved.
In the direct integration scheme we neglected the resonant contribution
at frequencies
![]() .
Although this procedure gives more accurate line profiles,
the frequency integrated power is slightly underestimated.
The two independent methods are compared for different particle energy regimes in Fig. 1.
They appear to be in agreement within
.
Although this procedure gives more accurate line profiles,
the frequency integrated power is slightly underestimated.
The two independent methods are compared for different particle energy regimes in Fig. 1.
They appear to be in agreement within ![]() 10% at low energies and
10% at low energies and ![]() 20% at high
particle energies. The errors (the relative difference between the
two emissivities) have been calculated down to 10-2 the line maximum. The calculated flux
obtained from the second method appears to be lower around the peak of emission at least for the first
few harmonics and at low particle energies. The discrepancy is always of the order of 10%, less
than the accuracy we aim to reach using the fitting functions. For this reason, we will only
consider the first (frequency integration) method for the tests detailed in Sect. 3.
For both methods, the numerical integration of the power spectrum over frequencies gives the total power (Eq. (3))
within a few percent.
20% at high
particle energies. The errors (the relative difference between the
two emissivities) have been calculated down to 10-2 the line maximum. The calculated flux
obtained from the second method appears to be lower around the peak of emission at least for the first
few harmonics and at low particle energies. The discrepancy is always of the order of 10%, less
than the accuracy we aim to reach using the fitting functions. For this reason, we will only
consider the first (frequency integration) method for the tests detailed in Sect. 3.
For both methods, the numerical integration of the power spectrum over frequencies gives the total power (Eq. (3))
within a few percent.
![\begin{figure}
\par\includegraphics[width=13.5cm]{3853.f1}\end{figure}](/articles/aa/full/2003/37/aa3853/Timg77.gif) |
Figure 1:
Relative differences between the two formulae (6) and (8) deriving the power emitted
by one particle. The energy is scaled to the line peak energy. The harmonics 1 and 5 are shown at three particle energies
|
| Open with DEXTER | |
The best agreements (between the two methods) were obtained using
an ![]() coefficient (associated with the frequency integration method) in the range 10-3 to a
few times 10-2. These values ensure a stable numerical integration. MNY96 have developed a similar but
different method, approximating the Dirac peak using a smooth function over a frequency interval
coefficient (associated with the frequency integration method) in the range 10-3 to a
few times 10-2. These values ensure a stable numerical integration. MNY96 have developed a similar but
different method, approximating the Dirac peak using a smooth function over a frequency interval
![]() .
They reach a good numerical stability with
.
They reach a good numerical stability with
![]() .
In the following, we use the first
method to find the fitting functions at a given particle energy (see Sect. 5), the second method has the advantage
of avoiding one integration and will be used in the thermal plasma case (see Sect. 6).
.
In the following, we use the first
method to find the fitting functions at a given particle energy (see Sect. 5), the second method has the advantage
of avoiding one integration and will be used in the thermal plasma case (see Sect. 6).
If the photon energy is much smaller than the electron kinetic energy (
![]() ,
the angle integrated cross section can be expressed by the angle
averaged emissivity
,
the angle integrated cross section can be expressed by the angle
averaged emissivity
![]() in a differential form as
in a differential form as
The absorption cross section at a given frequency for a given harmonic (
![]() ,
,
![]() and
and ![]() are fixed) is calculated using Eq. (6). While integrating over the solid angles,
we first test if the harmonic n0 is in the range of the permitted harmonics evaluated at
a given pair of angles
are fixed) is calculated using Eq. (6). While integrating over the solid angles,
we first test if the harmonic n0 is in the range of the permitted harmonics evaluated at
a given pair of angles
![]() .
The harmonic number interval is defined from Eq. (2)
by
.
The harmonic number interval is defined from Eq. (2)
by
| n1 | = | (10) | |
| n2 | = |
We first tried to recover the known cyclotron limit, the total power radiated by one particle, at a given harmonic and compared it with expression (4). The second test compares the numerical cyclotron absorption coefficient at a given harmonic with the non-relativistic coefficient provided by GS91. For the thermal plasma case, we recover the cyclotron absorption coefficients given by Chanmugam et al. (1989) (hereafter C89) and the Kirchoff law.
In the cyclotron limit (
![]() ), we integrate the first harmonics over the resonant
frequency range with a particle pitch-angle
), we integrate the first harmonics over the resonant
frequency range with a particle pitch-angle
![]() and compare our results with Eq. (4).
We plot the relative differences for different
and compare our results with Eq. (4).
We plot the relative differences for different ![]() for the first ten harmonics in Fig. 2. As can be seen,
the agreement is quite good, even if the errors increase with the harmonic number, however they
are limited to few percent.
for the first ten harmonics in Fig. 2. As can be seen,
the agreement is quite good, even if the errors increase with the harmonic number, however they
are limited to few percent.
![\begin{figure}
\par\includegraphics[width=\columnwidth]{3853.f2}\end{figure}](/articles/aa/full/2003/37/aa3853/Timg93.gif) |
Figure 2:
Relative differences between Eq. (6), the power emitted by one particle integrated over the solid angle
and Eq. (4), the power radiated by one particle in the non-relativistic regime. Both emissivities have been calculated
at a pitch-angle
|
| Open with DEXTER | |
Concerning the absorption cross section we compared our results with the analytical
expressions given by GS91. We point out that their formulae have to be corrected by a factor ![]() in
order to verify Eq. (9). Then, at low energy and at frequencies
in
order to verify Eq. (9). Then, at low energy and at frequencies ![]()
![]() ,
we did obtained
a good agreement and a cross section of the order of
,
we did obtained
a good agreement and a cross section of the order of
![]() .
In the trans-relativistic regime, we also found a good agreement at frequencies
.
In the trans-relativistic regime, we also found a good agreement at frequencies
![]() (see Fig. 8, lower panel).
(see Fig. 8, lower panel).
We plot our results in Fig. 3 for three temperatures at three different ![]() values and at different frequencies covering the first 20 harmonics. The agreement with
C89 is good (see their Tables 6A, 6C and 6E), the numerical thermal coefficient falls close to the extraordinary
mode values.
values and at different frequencies covering the first 20 harmonics. The agreement with
C89 is good (see their Tables 6A, 6C and 6E), the numerical thermal coefficient falls close to the extraordinary
mode values.
![\begin{figure}
\par\includegraphics[width=\columnwidth]{3853.f3_1}\vspace*{3mm} ...
...2}\vspace*{3mm}
\includegraphics[width=\columnwidth]{3853.f3_3}\par\end{figure}](/articles/aa/full/2003/37/aa3853/Timg102.gif) |
Figure 3:
Thermal absorption coefficients (in cm-1) at
T = 5, 15, 25 keV. The photon angles
are
|
| Open with DEXTER | |
Using the same calculation procedure, we check that both thermal emission and absorption coefficients
fulfill the Kirchoff law,
![]() .
We plot, in Fig. 4,
the relative differences between
.
We plot, in Fig. 4,
the relative differences between
![]() obtained from numerical integration with
obtained from numerical integration with
![]() versus the frequency for non-relativistic temperatures. The agreement is again good
except for
versus the frequency for non-relativistic temperatures. The agreement is again good
except for ![]() keV at
keV at
![]() where the flux is weak and the uncertainties obtained with the
numerical integration method increase.
where the flux is weak and the uncertainties obtained with the
numerical integration method increase.
![\begin{figure}
\par\includegraphics[width=7.5cm]{3853.f4}\end{figure}](/articles/aa/full/2003/37/aa3853/Timg106.gif) |
Figure 4:
Relative differences between the ratio of the calculated emission and absorption coefficients
|
| Open with DEXTER | |
We now describe the fitting function for the mono-energetic case in the non- and trans-relativistic regimes.
Whenever it was possible we used simple (essentially polynomial) functions
defined by the smallest number of parameters. Accounting for the evolution of
the line profile with the particle energy, we split our parameters into two classes: the parameters below
the energy of the line peak, the parameters above the energy of the line peak. The line normalisation with
![]() and n is also parametrised.
and n is also parametrised.
The generic form for the fitting functions is
| x | = | (13) | |
| x | = | (14) |
This value was chosen to ensure good flux estimates at frequencies between two lines maxima where in the trans-relativistic regime, two subsequent harmonics may both contribute significantly to the emissivity.
The parameters are
![]() for the line normalisation,
for the line normalisation,
![]() ,
,
![]() and
and
![]() for the line profile.
for the line profile.
Once a line is fitted, the n and ![]() dependencies of the four
primary parameters
N1, K1, I1, I2 have to be determined using other fitting functions.
The whole fitting procedure is twofold, e.g.
we first derive the previous coefficients in a grid (
dependencies of the four
primary parameters
N1, K1, I1, I2 have to be determined using other fitting functions.
The whole fitting procedure is twofold, e.g.
we first derive the previous coefficients in a grid (![]() )
using Eq. (12). We
called this the primary fitting procedure.
We then provide new fitting functions for both
)
using Eq. (12). We
called this the primary fitting procedure.
We then provide new fitting functions for both ![]() and n dependencies of the four previous
parameters, this is the secondary fitting procedure.
and n dependencies of the four previous
parameters, this is the secondary fitting procedure.
Obviously, the general fitting function (12) is not unique, other forms may be much more accurate for the primary fitting procedure but they usually require more parameters and lead to a complex second step. The solutions obtained are polynomials of degrees lower than 4, they are accurate enough to be used in a wide range of problems dealing with cyclotron radiation.
We consider two energy regimes: the cyclotron-gyro-magnetic (non-relativistic) regime defined
by
![]() and in the trans-relativistic regime defined by
and in the trans-relativistic regime defined by ![]() and
and
![]() .
Beyond this, the usual relativistic formulae apply. This choice was motivated by the
different behavior of the primary parameters in the two regimes (see next).
.
Beyond this, the usual relativistic formulae apply. This choice was motivated by the
different behavior of the primary parameters in the two regimes (see next).
For both emission and absorption lines, the second exponent, at a given harmonic,
I2(n) has been fixed at
![]() (the lowest energy considered here) and has an imposed evolution
in the non relativistic regime (up to
(the lowest energy considered here) and has an imposed evolution
in the non relativistic regime (up to
![]() ). Above, in the trans relativistic regime, we re-initialise
I2(n) to its value at
). Above, in the trans relativistic regime, we re-initialise
I2(n) to its value at
![]() and impose an other evolution with
and impose an other evolution with ![]() .
This procedure limits the
fluctuations in the other two primary parameters I1 and K1. We also had to consider the evolution
of the first harmonic individually for both emission and absorption coefficients, and the evolution of the second
harmonic also individually for the absorption coefficient.
.
This procedure limits the
fluctuations in the other two primary parameters I1 and K1. We also had to consider the evolution
of the first harmonic individually for both emission and absorption coefficients, and the evolution of the second
harmonic also individually for the absorption coefficient.
The number of parameters being high (6 parameters for the shape and one for the normalisation),
the results are unfortunately too complex to be presented in tabular forms. We have therefore decided to provide
fortran routines calculating the power spectrum for frequencies
![]() .
This procedure has been adopted for the thermal case too (see next section). All the programs are
accessible via ftp anonymous at ftp.cesr.fr/pub/synchrotron (in cyclosynchro.tar.gz). We simply
present here results in a graphical form.
.
This procedure has been adopted for the thermal case too (see next section). All the programs are
accessible via ftp anonymous at ftp.cesr.fr/pub/synchrotron (in cyclosynchro.tar.gz). We simply
present here results in a graphical form.
The units are
![]() and
and
![]() for the absorption and emission coefficients
respectively.
for the absorption and emission coefficients
respectively.
In most of the cases, the harmonics are fitted down to 10-4 the peak line flux with errors never exceeding 20%
(ratio larger than 1.25 or lower than 0.8). Exceptions may be found in Figs. 5 and 6 for frequencies
![]() at harmonic number
at harmonic number ![]() where the profile is very sharp. The flux is overestimated
here but for a restrained frequency range. However, even in these cases errors are around 20% and the higher harmonics
do not strongly contribute to the overall flux. The errors increase at the
edges of a given harmonic in the non-relativistic regime and at frequencies
where the profile is very sharp. The flux is overestimated
here but for a restrained frequency range. However, even in these cases errors are around 20% and the higher harmonics
do not strongly contribute to the overall flux. The errors increase at the
edges of a given harmonic in the non-relativistic regime and at frequencies ![]() of the order
of the order
![]() or
or
![]() in the trans-relativistic regime due to the low accuracy. The noise appearing at the edge of the frequency domain
(1-10
in the trans-relativistic regime due to the low accuracy. The noise appearing at the edge of the frequency domain
(1-10
![]() )
is due to the numerical integration method. As the flux decreases, the method would have
required a frequency dependent (increasing)
)
is due to the numerical integration method. As the flux decreases, the method would have
required a frequency dependent (increasing) ![]() in Eq. (6) to keep a smooth line profile. As
the flux at these energies are far beyond 10-4 the peak line flux, we disregarded the problem. However the
emission (or absorption) beyond
in Eq. (6) to keep a smooth line profile. As
the flux at these energies are far beyond 10-4 the peak line flux, we disregarded the problem. However the
emission (or absorption) beyond
![]() is not well reproduced since at these energies harmonics of higher order
contribute and the synchrotron formula is worth to be used. Finally note that the flux in the absorption of the first
harmonic in the trans-relativistic case is under-estimated by a factor two under
is not well reproduced since at these energies harmonics of higher order
contribute and the synchrotron formula is worth to be used. Finally note that the flux in the absorption of the first
harmonic in the trans-relativistic case is under-estimated by a factor two under
![]() for fluxes lower
than 10-2 the peak flux.
for fluxes lower
than 10-2 the peak flux.
Also presented are the non-relativistic and the relativistic limits derived by GHS98 and GS91 respectively. In Fig. 8
one can see a good agreement at frequencies
![]() between the numerical and the analytical calculations, for both
emission and absorption coefficients.
between the numerical and the analytical calculations, for both
emission and absorption coefficients.
![\begin{figure}
\par\includegraphics[width=\columnwidth,clip]{3853.f5_1}\par\includegraphics[width=\columnwidth,clip]{3853.f5_2}\end{figure}](/articles/aa/full/2003/37/aa3853/Timg137.gif) |
Figure 5:
Results for non-thermal lines at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=\columnwidth,clip]{3853.f6_1}
\includegraphics[width=\columnwidth,clip]{3853.f6_2}\end{figure}](/articles/aa/full/2003/37/aa3853/Timg138.gif) |
Figure 6:
Same as in Fig. 5 but for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=\columnwidth,clip]{3853.f7_1}
\includegraphics[width=\columnwidth,clip]{3853.f7_2}\end{figure}](/articles/aa/full/2003/37/aa3853/Timg139.gif) |
Figure 7:
Same as in Fig. 6 but for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=\columnwidth,clip]{3853.f8_1}\par\includegraphics[width=\columnwidth,clip]{3853.f8_2}\end{figure}](/articles/aa/full/2003/37/aa3853/Timg140.gif) |
Figure 8:
Same as in Fig. 6 but for
|
| Open with DEXTER | |
We computed the line spectra for the ten first harmonics at 200
different temperatures forming a logarithmic grid in the range of
![]() -1. We make available electronically a table of
emissivities in the 10 first harmonics as a function of photon frequency and a
fortran routine reading this table and interpolating between the precomputed emissivities.
The absorption coefficients can then be derived from the Kirchoff law.
-1. We make available electronically a table of
emissivities in the 10 first harmonics as a function of photon frequency and a
fortran routine reading this table and interpolating between the precomputed emissivities.
The absorption coefficients can then be derived from the Kirchoff law.
We found that the emission due to an individual harmonic can be conveniently approximated as follows:
Let
![]() be the photon frequency of the peak of harmonic n (see previous paragraph).
We define the frequencies
be the photon frequency of the peak of harmonic n (see previous paragraph).
We define the frequencies ![]() and
and ![]() so that:
so that:
| |
= | 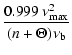 |
(15) |
| = | (16) |
We introduce the following notations:
| (17) |
| x1 | = | (18) | |
| x2 | = | (19) |
![\begin{displaymath}F(n,\Theta,\nu)=N_{1}\left(\frac{\nu}{\nu_{1}}\right)^{p_{1}}...
...2\Theta} \left(\frac{1}{x}-\frac{1}{x_{1}}+x-x1\right)\right].
\end{displaymath}](/articles/aa/full/2003/37/aa3853/img156.gif) |
(20) |
![\begin{displaymath}F(n,\Theta,\nu)=N_{\max}\exp\left[a\ln(\nu/\nu_{\max})^{2}+b\ln(\nu/\nu_{\max})^{3}\right]
\end{displaymath}](/articles/aa/full/2003/37/aa3853/img158.gif) |
(21) |
| a | = | (22) | |
| b | = | (23) |
![\begin{displaymath}F(n,\Theta,\nu)=N_{\max}\exp\left[c\ln(\nu/\nu_{\max})^{2}+d\ln(\nu/\nu_{\max})^{3}\right]
\end{displaymath}](/articles/aa/full/2003/37/aa3853/img162.gif) |
(24) |
| c | = | (25) | |
| d | = | (26) |
For
![]() :
:
![\begin{displaymath}F(n,\Theta,\nu)=N_{2}\left(\frac{\nu}{\nu_{2}}\right)^{-p_{6}...
...Theta}\left(\frac{1}{x}-\frac{1}{x_{2}}+x-x_{2}\right)\right].
\end{displaymath}](/articles/aa/full/2003/37/aa3853/img166.gif) |
(27) |
![\begin{figure}
\par\includegraphics[width=\columnwidth,clip]{3853.f9_1}\par\incl...
...]{3853.f9_2}\par\includegraphics[width=\columnwidth,clip]{3853.f9_3}\end{figure}](/articles/aa/full/2003/37/aa3853/Timg167.gif) |
Figure 9:
From top to bottom: Thermal synchrotron emission coefficients for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=\columnwidth,clip]{3853.f10_1}\par\inc...
...3853.f10_2}\par\includegraphics[width=\columnwidth,clip]{3853.f10_3}\end{figure}](/articles/aa/full/2003/37/aa3853/Timg168.gif) |
Figure 10:
Thermal synchrotron emission coefficient for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=\columnwidth,clip]{3853.f11_1}\par\inc...
...3853.f11_2}\par\includegraphics[width=\columnwidth,clip]{3853.f11_3}\end{figure}](/articles/aa/full/2003/37/aa3853/Timg169.gif) |
Figure 11:
Thermal synchrotron emission coefficient for
|
| Open with DEXTER | |
In this work, we presented two independent methods to compute the cyclo-synchrotron emission and absorption coefficients in a tangled magnetic field in the non- and trans relativistic regime. These calculations were done both for mono-energetic and thermal electrons. Only the first ten harmonics dominating the flux in theses regimes have been considered, but the procedure can easily be extended to a larger number of harmonics. We found synthetic fitting functions that reproduce our numerical results with a good accuracy (with a relative error at worst 20%). They complement the previously existing approximations valid only at higher photon and electron energies. Although these fitting functions are probably too complicated to be used in analytic calculations, they may prove very useful for numerical purposes. For instance, they could be used in high energy radiation transfer codes including both photon and particle dynamics (e.g. Coppi 1992; Stern et al. 1995). The fitting functions are made available electronically in the form of tables and fortran routines that can be easily implemented in such codes.
Acknowledgements
J.M. acknowledges financial support from the MURST (grant COFIN98-02-15-41), the European Commission (contract number ERBFMRX-CT98-0195, TMR network "Accretion onto black holes, compact stars and protostars"), and PPARC. The authors thank N.A. Webb for a careful reading of the manuscript.