A&A 409, 275-286 (2003)
DOI: 10.1051/0004-6361:20031086
C. Neiner1,2,3 - A.-M. Hubert1 - Y. Frémat1 - M. Floquet1 - S. Jankov4,5 - O. Preuss6 - H. F. Henrichs2 - J. Zorec7
1 - GEPI/UMR 8111 du CNRS, Observatoire de Paris-Meudon, France
2 - Sterrenkundig Instituut "Anton Pannekoek'', Universiteit van Amsterdam, The Netherlands
3 - RSSD, ESTEC / ESA, Keplerlaan 1, 2201 AZ Noordwijk ZH, The Netherlands
4 - Département d'Astrophysique de l'Université de Nice-Sophia Antipolis, UMR 6525 du CNRS, France
5 - Astronomical Observatory Beograd, MNTRS 1940, Volgina 7, 11050 Beograd, Serbia
6 - Max Plank Institut für Aeronomie, Lindau, Germany
7 - Institut d'Astrophysique de Paris (IAP), France
Received 21 March 2003 / Accepted 7 July 2003
Abstract
![]() Ori is a B2IIIe star for which rotational modulation and
non-radial pulsations (NRP) have been recently investigated from two independent
observational campaigns in 1998 and 1999. Putting the data of these 2 campaigns
together, and adding data obtained in 2001, we search for multiperiodicity in
the line profile variations and evidence for outbursts. From new spectropolarimetric data
obtained at the Télescope Bernard Lyot (TBL, Pic du Midi, France) in 2001
we also measure the Stokes V parameter in the polarised
light. We find evidence for the presence of a weak magnetic field in
Ori is a B2IIIe star for which rotational modulation and
non-radial pulsations (NRP) have been recently investigated from two independent
observational campaigns in 1998 and 1999. Putting the data of these 2 campaigns
together, and adding data obtained in 2001, we search for multiperiodicity in
the line profile variations and evidence for outbursts. From new spectropolarimetric data
obtained at the Télescope Bernard Lyot (TBL, Pic du Midi, France) in 2001
we also measure the Stokes V parameter in the polarised
light. We find evidence for the presence of a weak magnetic field in
![]() Ori sinusoidally varying with a period of 1.29 d. The
equivalent widths (EW) of the wind sensitive UV resonance lines also show a
variation with the same period, which we identify as the rotational period of the
star. We propose an oblique rotator model and derive
Ori sinusoidally varying with a period of 1.29 d. The
equivalent widths (EW) of the wind sensitive UV resonance lines also show a
variation with the same period, which we identify as the rotational period of the
star. We propose an oblique rotator model and derive
![]() G to
explain the observations. Moreover, we carry out an abundance analysis
and find the star to be N-enriched, a property which is shared with other
magnetic stars. We propose
G to
explain the observations. Moreover, we carry out an abundance analysis
and find the star to be N-enriched, a property which is shared with other
magnetic stars. We propose ![]() Ori as the first known
classical Be star hosting a magnetic field.
Ori as the first known
classical Be star hosting a magnetic field.
Key words: stars: magnetic fields - stars: oscillations - stars: winds, outflows - stars: individual:
![]() Ori
Ori
![]() Ori is a well-known rapidly rotating classical Be star
with spectral type B2IIIe. This type of star exhibits strongly variable winds
evidenced by rapidly variable UV resonance lines of highly ionised species, as
well as spectral and photometric variations on timescales from hours to decades.
The phases of emission in the optical and IR lines of hydrogen and several other
species are called the Be phenomenon and most likely reflect changes in the
structure of the circumstellar disk due to episodic ejections of mass. The
flattened envelope is thought to be related to the usually high rotational
velocities of Be stars. However, rotation by itself cannot explain the formation of
the disk. Non-radial pulsations and magnetic fields have been proposed as possible
additional mechanisms to explain the Be phenomenon (e.g. Osaki 1986; Underhill 1987).
Ori is a well-known rapidly rotating classical Be star
with spectral type B2IIIe. This type of star exhibits strongly variable winds
evidenced by rapidly variable UV resonance lines of highly ionised species, as
well as spectral and photometric variations on timescales from hours to decades.
The phases of emission in the optical and IR lines of hydrogen and several other
species are called the Be phenomenon and most likely reflect changes in the
structure of the circumstellar disk due to episodic ejections of mass. The
flattened envelope is thought to be related to the usually high rotational
velocities of Be stars. However, rotation by itself cannot explain the formation of
the disk. Non-radial pulsations and magnetic fields have been proposed as possible
additional mechanisms to explain the Be phenomenon (e.g. Osaki 1986; Underhill 1987).
Recently the role of rotational modulation and NRPs was investigated to explain short-term periodic variations detected in the Be star ![]() Ori, thanks to two international multisite campaigns
carried out independently at the end of 1998 (Neiner et al. 2002, hereafter N02)
and at the end of 1999 (Balona et al. 2001, hereafter B01).
Ori, thanks to two international multisite campaigns
carried out independently at the end of 1998 (Neiner et al. 2002, hereafter N02)
and at the end of 1999 (Balona et al. 2001, hereafter B01).
B01 associated the period of about P=0.97 d (f=1.03 c d-1) detected in the light and line-profile variations to the rotational period and argued that the periodic variation is due to clouds co-rotating with the star.
From their analysis of data provided by the MuSiCoS (MUltiSIte COntinuous
Spectroscopy) 1998 campaign, N02 concluded that both NRPs and rotational
modulation of orbiting clouds are needed to explain the multiperiodicity
detected in ![]() Ori. The star and the inner layers of the
circumstellar matter were found to pulsate non-radially with the period
P1=0.97 d (
f1=1.03 c d-1) associated with a NRP mode
with l=2 or 3 and |m| = 2.
Another period
P2 = 2.17 d (
f2 = 0.46 c d-1) was also detected and
attributed to material temporarily orbiting around the star then diluting in
the circumstellar environment.
The occurrence of an emission line outburst was deduced from the behavior of
spectral parameters. Analogy with outbursts detected in
Ori. The star and the inner layers of the
circumstellar matter were found to pulsate non-radially with the period
P1=0.97 d (
f1=1.03 c d-1) associated with a NRP mode
with l=2 or 3 and |m| = 2.
Another period
P2 = 2.17 d (
f2 = 0.46 c d-1) was also detected and
attributed to material temporarily orbiting around the star then diluting in
the circumstellar environment.
The occurrence of an emission line outburst was deduced from the behavior of
spectral parameters. Analogy with outbursts detected in ![]() Cen
by Rivinius et al. (1998a) was found.
At least one other period of about
P3 = 1.22 d (
f3 = 0.82 c d-1) with a weak signal power was seen in the stronger He I lines, compatible with the one detected in UV data of February 1996
(Peters 1996) and close to the rotational period that N02 derived
from their analysis of fundamental stellar parameters.
Cen
by Rivinius et al. (1998a) was found.
At least one other period of about
P3 = 1.22 d (
f3 = 0.82 c d-1) with a weak signal power was seen in the stronger He I lines, compatible with the one detected in UV data of February 1996
(Peters 1996) and close to the rotational period that N02 derived
from their analysis of fundamental stellar parameters.
The present paper reports on a global analysis of data collected during both multisite spectroscopic campaigns mentioned above. The ones obtained in 1999 were kindly put at our disposal by C. Aerts and L. A. Balona. New data acquired at the end of 2001 at TBL (Pic du Midi, France) were added.
The aim of this study is to:
(i) search for multiperiodicity in all data put together and collected over
a 4-year span, in particular to search for
frequencies close to the powerful frequency
f1 = 1.03 c d-1 detected
separately by B01 and N02, to investigate a possible beating
effect of NRPs, similar to the one reported by Rivinius et al. (1998b) in the case
of ![]() Cen;
Cen;
(ii) search for evidence for a possible outburst in 1999 and 2001 data;
(iii) study the behavior of spectral quantities expected to vary with the proposed
rotational frequency around
f3 = 0.82 c d-1;
(iv) obtain measurements of the Zeeman signature in the Stokes V parameter from the
spectropolarimetric data obtained in 2001 at TBL, to determine whether the star
hosts a magnetic field.
In Sect. 2 we present the observations. The spectral variations are studied in
Sect. 3, in the frame of non-radial pulsations and rotational modulation.
Section 4 focuses on the variations in the emission components of emission lines.
We reconsider the ![]() value of the star in Sect. 5 and determine
its stellar parameters and
the chemical abundances. In Sect. 6 we re-analyse the
IUE data of
value of the star in Sect. 5 and determine
its stellar parameters and
the chemical abundances. In Sect. 6 we re-analyse the
IUE data of ![]() Ori to derive the rotation period. In Sect. 7 we report on the possible discovery of a magnetic field in
Ori to derive the rotation period. In Sect. 7 we report on the possible discovery of a magnetic field in ![]() Ori and propose an oblique magnetic rotator model. The results are
discussed and conclusions are summarised in Sect. 8.
Ori and propose an oblique magnetic rotator model. The results are
discussed and conclusions are summarised in Sect. 8.
Spectra were obtained during the MuSiCoS campaign from November 23 to December 15 in 1998. This campaign used 8 telescopes around the world simultaneously to
obtain continuous spectroscopy. 249 spectra of ![]() Ori were
collected over the 22 night run, well distributed in time thanks to
the multisite observations. The data are described in detail in N02.
Ori were
collected over the 22 night run, well distributed in time thanks to
the multisite observations. The data are described in detail in N02.
Spectra were also obtained from November 17 to December 7 in 1999. The data are described in B01. In the present study we only use the 296 spectra obtained at SAAO with the GIRAFFE spectrograph and the 303 spectra obtained at ESO La Silla with the Coralie spectrograph, as they are of better quality.
Table 1:
Journal of TBL observations of ![]() Ori obtained
in December 2001.
Column 1 indicates the number of the polarimetric sets. Columns 2 and 3 show the
day and time of the beginning of observations. Column 4 indicates how many
polarimetric sets or individual subexposures were obtained.
Ori obtained
in December 2001.
Column 1 indicates the number of the polarimetric sets. Columns 2 and 3 show the
day and time of the beginning of observations. Column 4 indicates how many
polarimetric sets or individual subexposures were obtained.
Finally, spectropolarimetric data were obtained at TBL (Pic du Midi, France) from December 19 to 24 in 2001 with the spectropolarimeter Musicos (see next subsection). The star was observed during 8.5 hours per night. The individual subexposures of Stokes V measurements, i.e. 152 spectra, were used for spectroscopic study.
The three sets of spectra were obtained close to a minimum of emission in the long-term Be period observed by the French association of amateurs AUDE early 2000 (Buil 2001).
The Musicos échelle spectropolarimeter, with a resolving power R=35 000, is mounted at the Cassegrain focus of the 2 m Télescope Bernard Lyot (TBL) at Pic du Midi in France. Stellar light is collected in a 2'' entrance aperture in the spectral range 4500-6600 Å. Linear/circular sheet polarisers can be inserted in the beam. One half-wave and one quarter-wave retarder can also be inserted and rotated to achieve a linear or circular analysis of the stellar light.
To detect stellar magnetic fields, one analyses the circular polarisation
of the light. The observing strategy is to set the quarter-wave plate and
take 4 subexposures: one at azimuth -45![]() ,
two at azimuth 45
,
two at azimuth 45![]() ,
and one more at azimuth -45
,
and one more at azimuth -45![]() .
This gives a complete Stokes V measurement.
36 Stokes V measurements were obtained in December 2001 (see Table 1).
.
This gives a complete Stokes V measurement.
36 Stokes V measurements were obtained in December 2001 (see Table 1).
A dedicated software package, ESpRIT (Donati et al. 1997), is available at TBL
to reduce and analyse the data.
We implemented an improved version of ESpRIT, using two series of flat-fields
taken in the two positions of the quarter-wave plate, which optimizes the
extraction of the échelle orders. Fringes were removed using a fringe
template extracted from the Stokes V spectrum of a non-magnetic star
(![]() Peg) obtained during the first night of the run
and reduced in the same way as
Peg) obtained during the first night of the run
and reduced in the same way as ![]() Ori.
Ori.
Table 2:
Journal of IUE observations of ![]() Ori obtained in
February 1996. Column 1 indicates the number of the spectrum in the IUE archives.
Column 2 gives the exposure time. The Heliocentric Julian Date (HJD) minus 2 450 000 at mid-exposure is given in Col. 3.
Ori obtained in
February 1996. Column 1 indicates the number of the spectrum in the IUE archives.
Column 2 gives the exposure time. The Heliocentric Julian Date (HJD) minus 2 450 000 at mid-exposure is given in Col. 3.
After applying the Least-Squares Deconvolution (LSD), a cross-correlation
technique developed by Donati et al. (1997), one can detect a stellar magnetic field
through the Zeeman signatures generated in the shape and polarisation state of
spectral line profiles.
The LSD method combines the very small circularly polarised signatures, properly
weighted, of all available line profiles in the spectrum to increase the signal
to noise ratio.
For ![]() Ori, only 80 spectral lines, without emission, could be
used to provide a mean Stokes V profile.
These photospheric lines correspond to ions of He I,
C II, C III, N II, O II, Ne I,
Al III, Si II, Si III, S II,
Fe III, with line depths from 0.02 to 0.46 and Landé factors from 0.67 to 2.01. The line depths and Landé factors are
extracted from Kurucz models provided in the ESpRIT package
(see Donati et al. 1997). The method assumes
that the intrinsic broadening is similar for all lines.
Ori, only 80 spectral lines, without emission, could be
used to provide a mean Stokes V profile.
These photospheric lines correspond to ions of He I,
C II, C III, N II, O II, Ne I,
Al III, Si II, Si III, S II,
Fe III, with line depths from 0.02 to 0.46 and Landé factors from 0.67 to 2.01. The line depths and Landé factors are
extracted from Kurucz models provided in the ESpRIT package
(see Donati et al. 1997). The method assumes
that the intrinsic broadening is similar for all lines.
Many high-dispersion ultraviolet spectra (
![]() )
of
)
of ![]() Ori were obtained with the Short Wavelength Prime (SWP) camera
onboard the IUE satellite during more than 15 years. Table 2 presents
the journal of the 77 spectra of
Ori were obtained with the Short Wavelength Prime (SWP) camera
onboard the IUE satellite during more than 15 years. Table 2 presents
the journal of the 77 spectra of ![]() Ori obtained during a campaign with nearly continous
coverage over three days in February 1996 (Peters 1996), which were retrieved
from the INES database (http://ines.laeff.esa.es/). The other available spectra
are much less homogeneously distributed over the years and not taken during a
Balmer emission phase. The structure of their UV wind profiles appears to be
different and therefore only the February 1996 data were considered in this work.
Image SWP 56716 has unusual noise characteristics
and was ignored. Thus, we used the remaining 76 spectra to ensure the
highest homogeneity. The spectra were mapped on a uniform wavelength grid of 0.1 Å, which effectively degraded the resolving power to 12 000-15 000. The signal-to-noise ratio of the spectra is at best about 24.
Ori obtained during a campaign with nearly continous
coverage over three days in February 1996 (Peters 1996), which were retrieved
from the INES database (http://ines.laeff.esa.es/). The other available spectra
are much less homogeneously distributed over the years and not taken during a
Balmer emission phase. The structure of their UV wind profiles appears to be
different and therefore only the February 1996 data were considered in this work.
Image SWP 56716 has unusual noise characteristics
and was ignored. Thus, we used the remaining 76 spectra to ensure the
highest homogeneity. The spectra were mapped on a uniform wavelength grid of 0.1 Å, which effectively degraded the resolving power to 12 000-15 000. The signal-to-noise ratio of the spectra is at best about 24.
Table 3: Frequencies detected in the three sets of data for each studied line. The He I 6678 and Mg II 4481 lines are outside the wavelength range of the Musicos spectrograph, and therefore not studied in 2001.
We re-analysed the line profile variations (lpv) of the main lines for each campaign from 1998, 1999 and 2001 individually and for the three campaigns put together. Results are shown in Table 3 which gives the main detected frequencies for each line.
First the three sets of data are analysed separately with the same methods as in N02: the Restricted Local Cleanest (RLC) and Least Square (LS) methods. In each set the first frequency f1 = 1.03 c d-1 is always detected, with generally its first harmonic 2.06 c d-1. A second frequency 1.07 c d-1, close to the first one, is often detected. Nevertheless the phase velocity associated to this frequency is inaccurate due to the weakness of the power of the signal and to the lack of homogeneity of spectra obtained with various instrumentation during the three runs. The frequency around 0.8 c d-1 is sometimes present in periodograms of each of the three campaigns but it always has a very weak signal power. It is associated with the rotation period of the star proposed in N02. Marginal frequencies are also detected at 0.51 (in 1999 and 2001), 0.56 (in 1998), 0.93 (2-day alias of 1.07 c d-1, in 2001) and 1.17 c d-1 (2-day alias of the rotation frequency, in 1999).
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3757f1.eps}}
\end{figure}](/articles/aa/full/2003/37/aa3757/Timg20.gif) |
Figure 1: Example of power spectrum obtained for the He I 5876 line with the three datasets. |
| Open with DEXTER | |
The analysis of the three sets of data put together shows similar results. For this investigation only one spectrum out of four was used for the SAAO and ESO data obtained in 1999, in order to avoid giving a higher weight to this campaign. An example of the power spectrum obtained for the He I line 5876 is shown in Fig. 1. Note that the frequency resolution corresponds to the one from individual observing runs, rather than to the resolution expected from the complete data set (1998-2001), because the deconvolution algorithm cannot get rid of complex aliasing problem due to the large gaps between successive observing runs.
We obtained a coherent phase distribution only for the signal associated with the
frequency 1.03 c d-1. The data used in this study were taken with various
instrumentation and a rather moderate signal to noise ratio (![]() 150). The
search for other frequencies with low power close to the frequency at 1.03 c d-1 is thus difficult. We conclude that there is one main
frequency of non-radial pulsations at 1.03 c d-1. If other pulsation frequencies exist,
high quality homogeneous data such as satellite data will be necessary to confirm
them.
150). The
search for other frequencies with low power close to the frequency at 1.03 c d-1 is thus difficult. We conclude that there is one main
frequency of non-radial pulsations at 1.03 c d-1. If other pulsation frequencies exist,
high quality homogeneous data such as satellite data will be necessary to confirm
them.
The minimum intensity variation (i.e. the variation of the central depth) is investigated for lines with the best signal to noise ratio in 1999 and 2001. We do not search in the data taken in 1998, as the number of observations per line for each site is too low to expect to detect such variations.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3757f2.eps}}
\end{figure}](/articles/aa/full/2003/37/aa3757/Timg22.gif) |
Figure 2:
Variations of the minimum intensity of the He I 4921 line
observed in 1999 and the H |
| Open with DEXTER | |
In Fig. 2 variations of the minimum intensity of the He I 4921 line
observed in 1999 at ESO (Coralie data) and of the H![]() line observed in 2001
with the best S/N ratio, are folded in phase with f = 0.765 c d-1. Because the
frequency is not precise enough, the phases of 1999 and 2001 are not correlated.
However, it seems for both years that the minimum intensity varies with this
period
line observed in 2001
with the best S/N ratio, are folded in phase with f = 0.765 c d-1. Because the
frequency is not precise enough, the phases of 1999 and 2001 are not correlated.
However, it seems for both years that the minimum intensity varies with this
period ![]() d associated with the rotation, showing a
double-wave, i.e. two maxima and minima in one period.
d associated with the rotation, showing a
double-wave, i.e. two maxima and minima in one period.
At the time of MuSiCoS 1998 observations, emission was still present in the wings
of some lines during the campaign (e.g. H![]() ,
H
,
H![]() ,
He I 5876, 6678 and 7065, Si II 6347, C II 6578 and 6583). The
H
,
He I 5876, 6678 and 7065, Si II 6347, C II 6578 and 6583). The
H![]() line had a double-peaked emission (
line had a double-peaked emission (![]() )
profile with
)
profile with
![]() .
At the end of 1999 the emission was fainter,
.
At the end of 1999 the emission was fainter,
![]() for H
for H![]() ;
emission was still present in the
red helium lines but very weak in the He I 5876 line and sometimes
absent in the He I 6678 line. The Si II 6347 and C II 6578 and 6583 lines were purely photospheric.
In 2001 the emission was again increasing with
;
emission was still present in the
red helium lines but very weak in the He I 5876 line and sometimes
absent in the He I 6678 line. The Si II 6347 and C II 6578 and 6583 lines were purely photospheric.
In 2001 the emission was again increasing with
![]() at H
at H![]() .
.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3757f3.eps}}
\end{figure}](/articles/aa/full/2003/37/aa3757/Timg28.gif) |
Figure 3: Variations of the intensity of the V and R components of the He I 5876 line during the three observing runs. The data obtained in 2001 (in HJD minus 2 452 200) are plotted on the same time scale as the data obtained in 1998 (in HJD minus 2 451 100) and 1999 (in HJD minus 2 451 000) to make the comparison easier. |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3757f4.eps}}
\end{figure}](/articles/aa/full/2003/37/aa3757/Timg29.gif) |
Figure 4:
Variations of the intensity of the V plus R components of the
He I 5876, H |
| Open with DEXTER | |
The peak separation between the V and R components of the red He I lines
was found to be increasing during the MuSiCoS 1998 campaign (see N02). Associated
with an increase of the V+R quantity, this indicates the occurrence of an
outburst. No similar trend could be derived from data obtained in 1999. In 2001 we
find again a very weak tendency of an increase of the peak separation in H![]() ,
associated with an increase of V+R quantity (this latter was also seen in He I 5876), which suggests that the beginning of an outburst was probably
observed at that time.
The peak separation of the H
,
associated with an increase of V+R quantity (this latter was also seen in He I 5876), which suggests that the beginning of an outburst was probably
observed at that time.
The peak separation of the H![]() line observed in 2001
also varies as a single wave in phase with the frequency 0.765 c.d-1 associated with the rotation period (Fig. 5).
line observed in 2001
also varies as a single wave in phase with the frequency 0.765 c.d-1 associated with the rotation period (Fig. 5).
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3757f5.eps}}
\end{figure}](/articles/aa/full/2003/37/aa3757/Timg30.gif) |
Figure 5:
Variations of the separation between the V and R peaks in the
H |
| Open with DEXTER | |
The V/R ratio in the He I 5876 and 6678 lines were modulated by the frequency 1.03 c d-1 in 1998 but also by the frequency 0.46 c d-1 mainly in the first part of the run. This latter frequency was attributed by N02 to a cloud temporarily rotating around the star.
In 1999, the emission was fainter in the red He I lines. Therefore the V, R and V/R variations were more difficult to analyse. Sometimes the emission completely disappeared in the V or R component of the He I 6678 line (as in the ESO spectrum at HJD 2 451 508.7). Moreover the location of the V emission component of the He I 6678 line in the ESO spectra at the beginning of an échelle order made the determination of the continuum in this region uncertain. The V/R ratio of the He I 5876 line was weakly modulated with the frequency 1.11 c d-1 and dominated by the frequency 1.53 c d-1 (or twice 0.765 c d-1), mainly between HJD 2 451 509 and 2 451 514; the V/R ratio of the He I 6678 line was also dominated by the 1.53 or twice 0.765 c d-1 frequency (Fig. 6, upper and middle panels). This latter frequency can be related to the rotational frequency as determined in N02, which suggests the presence of two corotating regions around the star such as the clouds proposed by B01 to explain lpvs.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3757f6.eps}}
\end{figure}](/articles/aa/full/2003/37/aa3757/Timg31.gif) |
Figure 6: Variations of the intensity of the V/R components of the He I 6678 line observed in 1999 and of the He I 5876 line during the observations taken in 1999 and 2001. The plots are folded in phase with f = 0.765 c d-1 and with HJD 0 = 2 451 499 and 2 452 262.6 respectively. |
| Open with DEXTER | |
In 2001 the V/R ratio of He I 5876 was slightly increasing in amplitude over the 5-day run. It seemed again to be modulated by the frequency 0.765 c d-1 or its double, related to the rotation period (Fig. 6, lower panel).
The V/R ratio in H![]() and H
and H![]() show clear variations with the rotation
period or its half. It slowly decreases from phase 0.1 to 0.6, then
suddenly
increases, slowly decreases again from phase 0.6 to 1.1 and then suddenly
increases again (Fig. 7). This behavior can be associated
with two corotating regions
passing in front of the visible hemisphere of the star from the blue to the red
edge, one after the other.
show clear variations with the rotation
period or its half. It slowly decreases from phase 0.1 to 0.6, then
suddenly
increases, slowly decreases again from phase 0.6 to 1.1 and then suddenly
increases again (Fig. 7). This behavior can be associated
with two corotating regions
passing in front of the visible hemisphere of the star from the blue to the red
edge, one after the other.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3757f7.eps}}
\end{figure}](/articles/aa/full/2003/37/aa3757/Timg32.gif) |
Figure 7:
Variations of the intensity of the V/R components of the H |
| Open with DEXTER | |
The frequency 1.03 c d-1 never dominated the modulation of the V/R ratio of red He I lines. The frequency 0.765 c d-1 is present at times during several consecutive days, which suggests that it is related with the motion of corotating regions such as clouds. Unfortunately the sample obtained in 2001 was too short for a detailed study and, in 1999, data were obtained at best during 12 hours per day, which is insufficient to follow the rotation of such clouds and induces strong aliases in periodograms.
Table 4:
Determined values of ![]() (km s-1)
for the C II 4267, Mg II 4481 and Si III lines obtained in
1999 using the Fourier transform analysis, compared to the values given
by B01 for the same data and by N02 for the data obtained in 1998.
(km s-1)
for the C II 4267, Mg II 4481 and Si III lines obtained in
1999 using the Fourier transform analysis, compared to the values given
by B01 for the same data and by N02 for the data obtained in 1998.
In N02, ![]() was determined for He I and metal lines with two methods.
For all the lines, with both methods, the same value
was determined for He I and metal lines with two methods.
For all the lines, with both methods, the same value
![]() km s-1was found. In contrast, B01 found a similar value for the He I lines
from spectral modeling but a higher value for the metal lines.
km s-1was found. In contrast, B01 found a similar value for the He I lines
from spectral modeling but a higher value for the metal lines.
We investigate here the ![]() value of the data used in B01 with the Fourier
analysis method used in N02. Details of this method can be found in N02. Results
are shown in Table 4. We obtained a value of
value of the data used in B01 with the Fourier
analysis method used in N02. Details of this method can be found in N02. Results
are shown in Table 4. We obtained a value of ![]() similar to
what was found before for He I lines obtained in 1998 by N02.
similar to
what was found before for He I lines obtained in 1998 by N02.
![\begin{figure}
\par\resizebox{18cm}{!}{\includegraphics[clip]{3757f8.ps}}
\end{figure}](/articles/aa/full/2003/37/aa3757/Timg34.gif) |
Figure 8: Theoretical spectra (dots) compared to observations (solid line) from the Coralie spectrograph in the fitted spectral regions. |
| Open with DEXTER | |
We determine the fundamental parameters of ![]() Ori by fitting
spectral line profiles obtained by averaging the Coralie spectra (B01).
Ori by fitting
spectral line profiles obtained by averaging the Coralie spectra (B01).
As ![]() Ori is a Be star, the rotation is expected to
affect its spectrum. In their recent paper,
Chauville et al. (2001) showed that most of the Be stars rotate at the
same angular velocity ratio
Ori is a Be star, the rotation is expected to
affect its spectrum. In their recent paper,
Chauville et al. (2001) showed that most of the Be stars rotate at the
same angular velocity ratio
![]() (
(
![]() ,
where
,
where
![]() is the critical angular velocity). At this level of rotation
rates, the stars are generally supposed to flatten and to show non uniform
temperature and density distributions at their surface. In practice, it means
that a Be star may appear cooler and more evolved than it really is when one
does not take into account these gravitational darkening
effects.
is the critical angular velocity). At this level of rotation
rates, the stars are generally supposed to flatten and to show non uniform
temperature and density distributions at their surface. In practice, it means
that a Be star may appear cooler and more evolved than it really is when one
does not take into account these gravitational darkening
effects.
To study the photospheric spectra of ![]() Ori, we therefore use
the FASTROT computer code (Frémat et al. 2002; Frémat & Zorec 2003) based on an
approach very similar to the one described by Collins et al.
(1991, and references therein). This code assumes a gravitational darkening law
defined by the von Zeipel theorem and provides rotationally
deformed line profiles.
Ori, we therefore use
the FASTROT computer code (Frémat et al. 2002; Frémat & Zorec 2003) based on an
approach very similar to the one described by Collins et al.
(1991, and references therein). This code assumes a gravitational darkening law
defined by the von Zeipel theorem and provides rotationally
deformed line profiles.
NLTE plane-parallel atmosphere models represent the local temperature and density distributions at about 10 000 selected points on the stellar surface. These models are obtained with the TLUSTY198 and SYNSPEC45 computer codes (Hubeny & Lanz 1995). Microturbulence is assumed equal to 2 km s-1, which is the average value proposed by Andrievsky et al. (1999) for NLTE computations of B-type stars.
Except for neutral oxygen which is treated with the MODION IDL package, the atomic models we use are those proposed by Hubeny & Lanz on TLUSTY's web site: H: 16 levels, He I: 24 levels, He II: 20 levels, C I: 8 levels, C II: 34 levels + 5 superlevels, C III: 12 levels, N I: 13 levels, N II: 35 levels + 14 superlevels, N III: 11 levels, O I: 14 levels + 8 superlevels, O II: 36 levels + 14 superlevels, O III: 9 levels, Si I: 6 levels, Si II: 36 levels + 4 superlevels, Si III: 12 levels.
The oscillator strengths adopted to study the carbon, nitrogen, oxygen and silicon transitions are from the NIST database and are added to the Kurucz line lists provided with SYNSPEC. Stark widths of the Si II and Si III spectral lines are derived from the results of González et al. (2000), Dimitrijevic et al. (2002) and Lanz et al. (1988).
Fundamental parameters of ![]() Ori are determined by
fitting the
observed He I 4388 and 4471 transitions together with
the wings of H
Ori are determined by
fitting the
observed He I 4388 and 4471 transitions together with
the wings of H![]() .
We use a least-squares method
combined to a minimization procedure based on the MINUIT package developed at CERN. The code gives the possibility to adjust four parameters: the effective
temperature
.
We use a least-squares method
combined to a minimization procedure based on the MINUIT package developed at CERN. The code gives the possibility to adjust four parameters: the effective
temperature
![]() and the gravity
and the gravity
![]() of the non
rotating counterpart of the star, its angular velocity
of the non
rotating counterpart of the star, its angular velocity ![]() ,
and its projected rotation velocity
,
and its projected rotation velocity ![]() .
At each iteration, the stellar masses and radii are deduced by numerical
interpolation on
.
At each iteration, the stellar masses and radii are deduced by numerical
interpolation on
![]() and
and
![]() in the evolutionary tracks
computed by Schaller et al. (1992), assuming a solar metallicity.
The critical angular velocity and the
inclination angle i of the star are then derived.
in the evolutionary tracks
computed by Schaller et al. (1992), assuming a solar metallicity.
The critical angular velocity and the
inclination angle i of the star are then derived.
The error bars on the fundamental parameters are
estimated by assuming different sets of initial values during the fitting
procedure. For example, the angular
velocity ![]() is set at different values
between its extreme limits 0.57 (for which
is set at different values
between its extreme limits 0.57 (for which
![]() )
and 0.99 (after
which the star breaks). All the
fits converge to
)
and 0.99 (after
which the star breaks). All the
fits converge to
![]() ,
which is very similar to the
average value found by Chauville et al. (2001).
In the same way, the error bars on the effective temperature,
superficial gravity and projected rotation velocity correspond to the
largest deviation observed in all the fits.
,
which is very similar to the
average value found by Chauville et al. (2001).
In the same way, the error bars on the effective temperature,
superficial gravity and projected rotation velocity correspond to the
largest deviation observed in all the fits.
The fit of the hydrogen and helium lines provides a good
agreement with the values derived from
the study of the TD1 UV fluxes, i.e.
![]() K.
TD1 observations are corrected for interstellar
reddening assuming a colour excess
E(B-V) = 0.13 estimated by
Fabregat & Reglero (1990) and using the extinction laws given by
Cardelli et al. (1989) and O'Donnell (1994).
A good agreement is also found with the
computation of the Si II 4131 and Si III 4553 spectral lines, i.e.
K.
TD1 observations are corrected for interstellar
reddening assuming a colour excess
E(B-V) = 0.13 estimated by
Fabregat & Reglero (1990) and using the extinction laws given by
Cardelli et al. (1989) and O'Donnell (1994).
A good agreement is also found with the
computation of the Si II 4131 and Si III 4553 spectral lines, i.e.
![]() K and
K and
![]() .
Those test fits assume the inclination angle and the
projected rotational velocity fixed at the values given in Table 5.
.
Those test fits assume the inclination angle and the
projected rotational velocity fixed at the values given in Table 5.
The fitting procedure is then
applied assuming several values of the helium abundance. The best
agreement between observations and models is obtained for a
solar value of the He/H ratio with an
accuracy equivalent to the adopted helium abundance step:
![]() .
.
The same approach is used to estimate the CNO chemical composition of ![]() Ori (Fig. 8). In Table 6, the logarithmic
abundances are given relatively to the solar values compiled by Grevesse & Sauval (1998).
Species other than carbon, nitrogen or oxygen were taken at their
solar values.
C, N, O are usually found to be underabundant in B stars, compared to the
solar values (Gies & Lambert 1992; Gummersbach et al. 1998). This is not found in
Ori (Fig. 8). In Table 6, the logarithmic
abundances are given relatively to the solar values compiled by Grevesse & Sauval (1998).
Species other than carbon, nitrogen or oxygen were taken at their
solar values.
C, N, O are usually found to be underabundant in B stars, compared to the
solar values (Gies & Lambert 1992; Gummersbach et al. 1998). This is not found in ![]() Ori,
for which C and O have the same abundances as in the Sun and N is found to be
enriched.
Ori,
for which C and O have the same abundances as in the Sun and N is found to be
enriched.
Table 5:
Stellar parameters of ![]() Ori
obtained by fitting hydrogen and helium lines.
Ori
obtained by fitting hydrogen and helium lines.
Table 6:
Chemical composition of ![]() Ori compared to the mean chemical
composition of B stars, as derived by Gies & Lambert (1992) and of local B stars, as derived by Gummersbach et al. (1998).
The logarithmic
abundances
Ori compared to the mean chemical
composition of B stars, as derived by Gies & Lambert (1992) and of local B stars, as derived by Gummersbach et al. (1998).
The logarithmic
abundances ![]() (
(
![]() )
are given relatively to the
solar values compiled by Grevesse & Sauval (1998).
)
are given relatively to the
solar values compiled by Grevesse & Sauval (1998).
It is well known that the wind-sensitive doublet resonance lines of C IV 1550 and Si IV 1400 are variable in this star (e.g. Sonneborn et al. 1988). From a 3-day IUE campaign, Peters (1996) found that the C IV doublet varies with a period of about 1.21 d.
The top panels of Fig. 9 show an overplot of the IUE C IV and Si IV profiles, respectively, along with their variability signatures
in the bottom panels. The variability occurs mainly in the strength of the
line over a given range in velocity space, extending from -1000 to +600 km s-1 for the whole doublet. The expected variability is obtained using
a noise model for such IUE spectra as derived by Henrichs et al. (1994) with parameters
A = 24.1 and
![]() .
.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3757f9a.eps}}\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3757f9b.eps}}
\end{figure}](/articles/aa/full/2003/37/aa3757/Timg56.gif) |
Figure 9: Top panels: variation in the wind profiles of the UV C IV and Si IV lines; the fluxes are normalised to the mean spectrum. Bottom panels: variability signature, measuring the ratio of the observed variance (due to variability) to the expected variance (due to noise). |
| Open with DEXTER | |
We measure the equivalent width (EW) of the C IV and Si IV lines between -600 and -100 km s-1
with the continuum chosen at
![]() erg cm-2 s-1 Å-1 and
erg cm-2 s-1 Å-1 and
![]() erg cm-2 s-1 Å-1 respectively
and compute a least-squares fit of a sinusoid.
Weights are assigned relative to the error bars of each datapoint.
The result of the fit of the function
erg cm-2 s-1 Å-1 respectively
and compute a least-squares fit of a sinusoid.
Weights are assigned relative to the error bars of each datapoint.
The result of the fit of the function
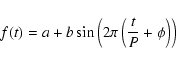 |
(1) |
The period is identified with the rotation period of the star. The equivalent width of the C IV line as a function of rotational phase is plotted in Fig. 10, with the best fit overplotted. The equivalent width of the Si IV line is also shown.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3757f10.eps}}
\end{figure}](/articles/aa/full/2003/37/aa3757/Timg66.gif) |
Figure 10: Equivalent width variations (in Å) of the UV C IV and Si IV lines, folded in phase with the rotational period P = 1.286 d. The best fit is overplotted. |
| Open with DEXTER | |
Due to the small amount of available lines and to the high rotation velocity of
the star, the magnetic measurements have large error bars.
Table 7 (available at CDS) shows the longitudinal magnetic field value B, its error bar ![]() ,
the null polarisation N, which gives an indication of the pollution
by non-stellar effects and should be zero for a perfect measurement, and its
error
,
the null polarisation N, which gives an indication of the pollution
by non-stellar effects and should be zero for a perfect measurement, and its
error ![]() .
.
The exposure time for each subexposure was 15 min, i.e. about 1/100 of the
pulsation period, to avoid smearing of the magnetic signal because of the
pulsations.
Although no strong signature appears in the individual Stokes V profiles, the
measured value of the longitudinal component of the magnetic field is found to
vary in phase with the UV period.
A sinusoidal fit through the magnetic data gives an amplitude
of the longitudinal component of
![]() G around the average
value of
G around the average
value of
![]() G, and a period of
G, and a period of
![]() d,
with
d,
with
![]() .
This fit is shown as a
solid line in Fig. 11. The period is, within the error bar,
identical to the UV period derived in Sect. 6. We consider this
coherent variation of the magnetic measurements in phase as an
evidence for the presence of a weak longitudinal magnetic field in
.
This fit is shown as a
solid line in Fig. 11. The period is, within the error bar,
identical to the UV period derived in Sect. 6. We consider this
coherent variation of the magnetic measurements in phase as an
evidence for the presence of a weak longitudinal magnetic field in ![]() Ori.
From the derived phase we determine that the maximum field occurs at
Ori.
From the derived phase we determine that the maximum field occurs at
![]() .
.
In the frame of the oblique magnetic rotator model (see Shore 1987) this period of variation corresponds to the rotation period of the star. The obtained period, corresponding to a frequency of f = 0.775 c d-1, is consistent with the value f = 0.73 c d-1 obtained in N02, f = 0.77 c d-1 obtained from the V/R analysis (Sect. 3.4.3) and f = 0.78 c d-1 obtained from the UV stellar wind analysis (Sect. 6). Due to the uncertainties we could not uniquely relate the UV phase with the magnetic phase.
We have found a weak varying longitudinal field in ![]() Ori,
consistent with an oblique magnetic dipole with a rotational period of 1.29 d.
Ori,
consistent with an oblique magnetic dipole with a rotational period of 1.29 d.
For a dipolar field, the ratio of the magnetic extremes
![]() is related to the inclination angle i and
the angle
is related to the inclination angle i and
the angle ![]() between the magnetic and the rotation axis via
(see Shore 1987)
between the magnetic and the rotation axis via
(see Shore 1987)
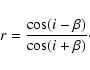 |
(2) |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3757f11.eps}}
\end{figure}](/articles/aa/full/2003/37/aa3757/Timg78.gif) |
Figure 11: Variations of the longitudinal component of the magnetic field, folded in phase with the period P = 1.29 d. |
| Open with DEXTER | |
With these values,
![]()
![]() ,
which is close to 90
,
which is close to 90![]() and therefore one of the two magnetic poles is situated just at the edge of
the visible hemisphere.
and therefore one of the two magnetic poles is situated just at the edge of
the visible hemisphere.
With this configuration it is expected that the variation in the UV lines sensitive to the wind shows only one maximum per period (Shore & Brown 1990), as indeed seen in Sect. 6 (Fig. 10).
With the known angles i and ![]() ,
mean longitudinal field B0 and
amplitude of variations of the longitudinal component
,
mean longitudinal field B0 and
amplitude of variations of the longitudinal component ![]() ,
the strength
of the magnetic field at the poles, i.e. the maximum field, can be determined
by using a centered oblique dipolar model. The model we used is described in
Neiner et al. (2003b). We used a limb darkening coefficient k = 0.4 as
established by Claret (2000) for this kind of star. We obtained
,
the strength
of the magnetic field at the poles, i.e. the maximum field, can be determined
by using a centered oblique dipolar model. The model we used is described in
Neiner et al. (2003b). We used a limb darkening coefficient k = 0.4 as
established by Claret (2000) for this kind of star. We obtained
![]() G. A greyscale plot of
the magnetic field in the visible hemisphere is shown in Fig. 12.
G. A greyscale plot of
the magnetic field in the visible hemisphere is shown in Fig. 12.
![\begin{figure}
\par\resizebox{18cm}{!}{\includegraphics[clip]{3757f12.ps}}
\end{figure}](/articles/aa/full/2003/37/aa3757/Timg82.gif) |
Figure 12:
Greyscale representation of the relative contribution of the magnetic
dipole to the integrated longitudinal magnetic field on the visible
hemisphere of |
| Open with DEXTER | |
We confirm that the frequency f1 = 1.03 c d-1, already detected by N02 in the 1998 data and B01 in the 1999 data, is also found in the data obtained in 2001. We associate this frequency with a non-radial pulsation mode (see N02).
A second frequency at about f = 0.77 c d-1 is detected and associated with the rotation period (see Sect. 8.4).
Finally several other weak frequencies are detected in the full dataset (1998+1999+2001), but the power is too low for the phase to be accurate, so we do not consider them further.
An outburst occured in ![]() Ori during the MuSiCoS campaign in
1998. It is associated with a cloud of material orbiting around the
star with a frequency of 0.46 c d-1, which disappeared after a few
revolutions around the star (see N02).
Ori during the MuSiCoS campaign in
1998. It is associated with a cloud of material orbiting around the
star with a frequency of 0.46 c d-1, which disappeared after a few
revolutions around the star (see N02).
We searched for an outburst in the data collected in 1999 and 2001. No indication of an outburst appeared in 1999 and we consider that ![]() Ori was in a quiet phase at that time. These observations
were indeed obtained very close to the minimum of emission intensity observed in
Ori was in a quiet phase at that time. These observations
were indeed obtained very close to the minimum of emission intensity observed in
![]() Ori by Buil (2001) at the beginning of 2000. In the data
obtained in 2001, we see possible indications for the beginning of an outburst
in the V+R and V/R variations, but the suggested outburst itself probably
occured after the observing run.
Ori by Buil (2001) at the beginning of 2000. In the data
obtained in 2001, we see possible indications for the beginning of an outburst
in the V+R and V/R variations, but the suggested outburst itself probably
occured after the observing run.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{3757f13a.ps}}\resizebox{8.8cm}{!}{\includegraphics[clip]{3757f13b.ps}}
\end{figure}](/articles/aa/full/2003/37/aa3757/Timg83.gif) |
Figure 13:
Sketch of |
| Open with DEXTER | |
Despite of the large error bars of the magnetic measurements, we have found
evidence for the presence of a magnetic field in the classical Be star ![]() Ori.
Ori.
The longitudinal magnetic field varies periodically. The period derived from the magnetic measurements, P = 1.29 d, corresponds to the rotational period of the star. The EW of the UV resonance lines also varies periodically. The derived period P = 1.29 d is again the rotational period.
The fact that the EW of the UV lines and the longitudinal magnetic field vary
with the rotational period is coherent with a magnetic oblique rotator model.
The correspondence in phase between the maximum of emission in the UV lines
and the maximum magnetic field value cannot be established due to the low
accuracy in the determination of the rotation period. However, our model of a
magnetic rotating dipole, applied with the parameters of ![]() Ori,
shows that only one of the magnetic pole (the positive pole) passes
through the visible hemisphere
whereas the other magnetic (negative) pole is always hidden. The same conclusion is
reached from the UV measurements which show only one maximum in the EW instead
of the two maxima usually observed for a magnetic star for which the two magnetic
poles are visible (e.g.
Ori,
shows that only one of the magnetic pole (the positive pole) passes
through the visible hemisphere
whereas the other magnetic (negative) pole is always hidden. The same conclusion is
reached from the UV measurements which show only one maximum in the EW instead
of the two maxima usually observed for a magnetic star for which the two magnetic
poles are visible (e.g. ![]() Cas, Neiner et al. 2003a).
The magnetic results and the UV results are therefore fully compatible.
Cas, Neiner et al. 2003a).
The magnetic results and the UV results are therefore fully compatible.
From our oblique dipole model we derive that the polar magnetic field is
![]() G. This value is higher than the
lower limit of about 300 G
obtained by Cassinelli et al. (2002) needed to form a magnetically torqued disk in a rapidly
rotating B2 star with its magnetic axis aligned with its rotation axis.
G. This value is higher than the
lower limit of about 300 G
obtained by Cassinelli et al. (2002) needed to form a magnetically torqued disk in a rapidly
rotating B2 star with its magnetic axis aligned with its rotation axis.
Moreover, the star is found to be N-enriched. This is also the case of ![]() Cep, the only magnetic (low velocity) Be star known up to
now (Henrichs et al. 2000), and of
Cep, the only magnetic (low velocity) Be star known up to
now (Henrichs et al. 2000), and of ![]() Cas, the only magnetic SPB star
known up to now (Neiner et al. 2003a).
Chemical peculiarities are often found in magnetic stars, because the magnetic
field inhibits mixing motions in the outer layers of the star.
Cas, the only magnetic SPB star
known up to now (Neiner et al. 2003a).
Chemical peculiarities are often found in magnetic stars, because the magnetic
field inhibits mixing motions in the outer layers of the star.
A frequency of about f = 0.77 c d-1 is detected, mainly in the
V/R ratio of red He I lines (Fig. 6), but also in other
observables such as the
peak separation of lines with an emission component (Fig. 5)
and the minimum line
intensities (Fig. 2). This frequency is associated with the rotation period of the star (P = 1.29 d).
It is detected with a strong power in the 1999 data and with a lower
power in 1998 and 2001.
Nevertheless, the V/R ratio of the H![]() and H
and H![]() lines observed in
2001 show a clear variation with this frequency (Fig. 7).
lines observed in
2001 show a clear variation with this frequency (Fig. 7).
From the search for periodicities in the lpv, we find that the V/R ratio of lines with an emission component varies with the rotation period and shows two maxima during one period (Fig. 6). This suggests the presence of two opposite regions of enhanced density corotating with the star. Note that this short-term variations in the V/R ratio is not related to the long-term V/R variations usually associated with one armed oscillations of Be stars disks.
A recent study by Preuss et al. (2003) analyses the
regions of equilibrium around a rotating star hosting a magnetic dipole field.
They obtain that the regions of stability depend on the angle ![]() between the rotation axis and the magnetic axis. When
between the rotation axis and the magnetic axis. When ![]() is small
(
is small
(
![]() ), the region of equilibrium is the magnetic
equator. When
), the region of equilibrium is the magnetic
equator. When ![]() increases (
increases (
![]() ),
equilibrium is reached in the magnetic equator but also in two regions above
the magnetic poles. The size of these polar regions increases with
),
equilibrium is reached in the magnetic equator but also in two regions above
the magnetic poles. The size of these polar regions increases with ![]() .
Finally at
.
Finally at
![]() ,
the regions of stability are the magnetic
equator (except a part which contains the rotation axis) and two cones above
the magnetic poles.
,
the regions of stability are the magnetic
equator (except a part which contains the rotation axis) and two cones above
the magnetic poles.
In our dipole model of ![]() Ori,
Ori,
![]() .
According to Preuss et al. (2003) this means that the material ejected from the star,
if it is magnetically confined, can end up in a disk in the magnetic
equator and/or in two clouds above the magnetic poles. From the
geometrical configuration of
.
According to Preuss et al. (2003) this means that the material ejected from the star,
if it is magnetically confined, can end up in a disk in the magnetic
equator and/or in two clouds above the magnetic poles. From the
geometrical configuration of ![]() Ori, only the positive
magnetic pole is clearly seen, the negative one just appears at the edge of the
visible hemisphere. Therefore if the calculation of Preuss et al.
applies to
Ori, only the positive
magnetic pole is clearly seen, the negative one just appears at the edge of the
visible hemisphere. Therefore if the calculation of Preuss et al.
applies to ![]() Ori and the material is in clouds above the poles
we would observe only one maximum
in the V/R variations at the phase of maximum field. However, we
observe two equal maxima in the V/R variations with a phase difference of 0.5.
This means that, for
Ori and the material is in clouds above the poles
we would observe only one maximum
in the V/R variations at the phase of maximum field. However, we
observe two equal maxima in the V/R variations with a phase difference of 0.5.
This means that, for ![]() Ori, the observed clouds are not
situated above the magnetic poles.
Ori, the observed clouds are not
situated above the magnetic poles.
Let us consider the global picture of a Be star hosting a magnetic dipole.
This sketch is shown in Fig. 13 for ![]() Ori. The usual
H
Ori. The usual
H![]() disk is assumed to be situated in the rotational equatorial plane.
The magnetic dipole is oblique, thus its magnetic equator lies in a different
plane than the rotational equator. These two planes intersect in two regions,
opposite to each other, hereafter refered as the Equators Intersection Regions (EIR). If the magnetic field is weak, magnetic confinement can only occur close to the
star and thus the EIR are close to the stellar surface. Note that the EIR
corotate with the rotation period. In Fig. 12, the EIR are situated
at the intersections of the thick white and black lines.
disk is assumed to be situated in the rotational equatorial plane.
The magnetic dipole is oblique, thus its magnetic equator lies in a different
plane than the rotational equator. These two planes intersect in two regions,
opposite to each other, hereafter refered as the Equators Intersection Regions (EIR). If the magnetic field is weak, magnetic confinement can only occur close to the
star and thus the EIR are close to the stellar surface. Note that the EIR
corotate with the rotation period. In Fig. 12, the EIR are situated
at the intersections of the thick white and black lines.
The wind material, flowing from the magnetic poles along the field lines, is
led to the magnetic equator. As the star rotates, the magnetic equator plane
corotates and is dragged through the rotational equator. If the magnetic field
is strong enough compared to the rotation velocity, the material is strongly
confined in the magnetic equator and the disk is formed there. This is the
case for the star ![]() Cep (Donati et al. 2001; Henrichs et al. 2000),
which hosts a weak magnetic field (about 300 G)
and is a very slow rotator (v = 28 km s-1).
On the contrary, if the rotation velocity of the star is high enough compared
to the strength of the magnetic field (e.g. for classical Be stars),
the material tends to go into the
rotational equator and forms a disk there. Two cases can be considered: either
the wind material, following the field lines, first meets the rotational equator
and stays there, conserving its angular momentum instead of
following the field lines further to the magnetic equator, or it first meets
the magnetic equator and then flows to the rotational equator via the EIR. In
both cases, the material ends up in the rotational equator plane.
Cep (Donati et al. 2001; Henrichs et al. 2000),
which hosts a weak magnetic field (about 300 G)
and is a very slow rotator (v = 28 km s-1).
On the contrary, if the rotation velocity of the star is high enough compared
to the strength of the magnetic field (e.g. for classical Be stars),
the material tends to go into the
rotational equator and forms a disk there. Two cases can be considered: either
the wind material, following the field lines, first meets the rotational equator
and stays there, conserving its angular momentum instead of
following the field lines further to the magnetic equator, or it first meets
the magnetic equator and then flows to the rotational equator via the EIR. In
both cases, the material ends up in the rotational equator plane.
As all the involved forces
contribute to put material in the EIR, it is probable that they are
denser than the rest of the disk where the magnetic and rotation forces diverge,
i.e. there are clouds at the EIR positions.
We then expect to see emission from the intersection regions and a V/R variation similar to the one observed in the H![]() and H
and H![]() lines of
lines of ![]() Ori in 2001 (Fig. 7), i.e. two slow decreases of the V/R ratio, each
of them followed by a sudden increase at the phase of maximum and minimum field.
This corresponds to the phases 0 and 0.5 in Fig. 12, when
the two clouds (intersections of the thick white and black lines) are on the
side of the star.
The variation in the peak separation of H
Ori in 2001 (Fig. 7), i.e. two slow decreases of the V/R ratio, each
of them followed by a sudden increase at the phase of maximum and minimum field.
This corresponds to the phases 0 and 0.5 in Fig. 12, when
the two clouds (intersections of the thick white and black lines) are on the
side of the star.
The variation in the peak separation of H![]() in 2001 (Fig. 5) may then be
explained as a projection effect of the magnetic equator, and thus of the
clouds, on the stellar visible hemisphere as the star rotates. The magnetic
equator and clouds are seen face on and from the side at the phases 0 and 0.5 respectively.
in 2001 (Fig. 5) may then be
explained as a projection effect of the magnetic equator, and thus of the
clouds, on the stellar visible hemisphere as the star rotates. The magnetic
equator and clouds are seen face on and from the side at the phases 0 and 0.5 respectively.
However, the contrast in density, between the clouds and the disk,
is probably stronger at epochs when the
whole disk density is lower, i.e. close to the minimum emission phase of the
star. At epochs where the disk is filled up by strong ejections of material,
the EIR clouds are probably hard to detect. That would explain why
the rotation frequency and the clouds are better detected in the
observations obtained in 1999 and 2001
than in the data of 1998 for example and why it has not been detected in earlier
observations when ![]() Ori was in a phase of stronger emission.
Ori was in a phase of stronger emission.
In Bp stars, such as the He-strong star ![]() Ori E,
patches of specific chemical abundances have been observed on the stellar
surface, in particular patches of enhanced helium abundance at
the wind base, due to chemical fractionation, i.e. decoupling of the helium
from the metals in the stellar wind (Groote & Hunger 1997). This has not been observed
in
Ori E,
patches of specific chemical abundances have been observed on the stellar
surface, in particular patches of enhanced helium abundance at
the wind base, due to chemical fractionation, i.e. decoupling of the helium
from the metals in the stellar wind (Groote & Hunger 1997). This has not been observed
in ![]() Ori, which is not a Bp star.
Ori, which is not a Bp star.
However, the magnetic star ![]() Ori E also shows clouds of
material attached to the photosphere, at the intersection regions of the
rotational and magnetic equatorial planes (Short & Bolton 1994).
As this star does not host a disk, the clouds are detected more easily.
We propose that the equatorial clouds of
Ori E also shows clouds of
material attached to the photosphere, at the intersection regions of the
rotational and magnetic equatorial planes (Short & Bolton 1994).
As this star does not host a disk, the clouds are detected more easily.
We propose that the equatorial clouds of ![]() Ori E and
Ori E and ![]() Ori build up in the same way.
Ori build up in the same way.
Acknowledgements
We are grateful to C. Aerts and L. Balona for providing the data they obtained in 1999. We thank the referee, T. Rivinius, for constructive discussions. Y.F. is supported by a Marie Curie Individual Fellowship of the European Community programme FP5 under contract number HPMF-CT-2000-00497. This research has made use of the Simbad database maintained at CDS, Strasbourg, France.