A&A 409, 387-394 (2003)
DOI: 10.1051/0004-6361:20031111
M. Roche1,2 - C. Bracco1 - C. Aime1 - H. Lantéri1 - Y. Mellier3,4
1 - UMR 6525 Astrophysique, Université de Nice Sophia Antipolis, Parc Valrose, 06108 Nice Cedex 2, France
2 -
Institut Fresnel, UMR 6133, École Nationale Supérieure de Physique de Marseille, Domaine Universitaire de Saint Jérôme, 13397 Marseille Cedex 20, France
3 -
Institut Astrophysique de Paris, UMR 7095, 98bis boulevard Arago, 75014 Paris, France
4 -
Observatoire de Paris, LERMA, UMR 8112, 61 avenue de l'Observatoire, 75014 Paris, France
Received 4 February 2003/ Accepted 17 June 2003
Abstract
We develop a self-consistent automatic procedure to
restore information from astronomical observations. It relies on
both a new deconvolution algorithm called LBCA (Lower Bound Constraint Algorithm) and
the use of the Wiener filter. In order to explore its
scientific potential for strong and weak gravitational lensing,
we process a CFHT image of the galaxy cluster Abell 370 which
exhibits spectacular strong gravitational lensing effects. A high
quality restoration is here of particular interest to map the dark
matter within the cluster. We show that the LBCA is especially
efficient to reduce
ringing effects introduced by classical deconvolution
algorithms in images with a high background. The method allows us to
make a blind detection of the radial arc and to recover morphological
properties similar to those observed from HST data. We also show that the Wiener
filter
is suitable to stop the iterative process before noise amplification,
using only the unrestored data.
Key words: galaxies: clusters: individual: cluster Abell 370 - cosmology: gravitational lensing - cosmology: dark matter - methods: data analysis - techniques: image processing
Improving image quality from ground based telescopes is therefore an important technical goal that may have a significant scientific impact when surveys are pushed to the limits. In principle, image deconvolution can both improve the image quality and enhance the flux emitted by low surface brightness galaxies. Unfortunately, because deconvolution is a slow process and often produces unwanted artifacts, like ringing, it cannot be easily used on wide field ground based images. Furthermore, in the case of very large data sets from panoramic cameras, objective convergence criteria must be defined and applied automatically to images. These technical limitations turn out to be challenging if one envisions a massive image deconvolution of surveys.
Although it is not yet applicable to large ground based data sets, we explore new image deconvolution techniques that could be used in the future. More precisely, we compare the performances of the Richardson-Lucy (RL) algorithm with a modified version called the Lower Bound Constraint Algorithm (LBCA) that has been developed in Lantéri et al. (2001). This algorithm, as well as the RL algorithm, shows noise amplification when the iteration number increases too much. A procedure to control automatically the iteration has then been implemented and validated on real data. It uses a HST image as a reference to stop the deconvolution process when a given distance between the HST image and the restored image is minimum. We choose to minimize a Euclidean distance criterion. This minimization technique also enables us to check the quality of the restoration.
Although the comparison with HST data turns out to be a successful way to test the method, it is unpractical for most images. Operating cosmological surveys will provide a huge amount of data that must be automatically processed, without any reference images. So, we generalized our empirical convergence criterion using the HST images to develop a systematic procedure to stop the deconvolution algorithm. This technique is based on the Wiener filtering and relies on the information contained in the data only.
In this first paper, we applied the deconvolution on CFHT images of the famous giant arc in Abell 370 and compare the result to HST data. Both the CFHT and the HST images are described in Sect. 2. We determine the Point Spread Function (PSF) in the CFHT image in Sect. 3 and apply the deconvolution techniques in Sect. 4. We show that the LBCA must be preferred to the standard RL algorithm. In Sect. 5, we use the technique based on the Wiener filter to stop the LBCA iterations without the need of any reference image. We show that the quality of the restored image then obtained with this independent procedure is satisfactory. We sum up our conclusions in Sect. 6.
Abell 370 is the most distant cluster of galaxies in the Abell catalogue, at a
redshift z = 0.374 (Sarazin et al. 1982). The cluster structure is dominated by
two giant elliptical galaxies, identified as ![]() and
and ![]() from the notations in Soucail et al. (1987b)
from the notations in Soucail et al. (1987b)![]() . The image of Abell 370 exhibits a giant arc extending
over 60 arcsec wide discovered by Soucail et al. (1987a)
and Lynds & Petrosian (1986). This arc has been identified as an extremely distorted image
of a background galaxy at z=0.724 (Soucail et al. 1988), thus bringing
the evidence of a cosmological gravitational lensing effect. The arc is split
into five distinct regions
. The image of Abell 370 exhibits a giant arc extending
over 60 arcsec wide discovered by Soucail et al. (1987a)
and Lynds & Petrosian (1986). This arc has been identified as an extremely distorted image
of a background galaxy at z=0.724 (Soucail et al. 1988), thus bringing
the evidence of a cosmological gravitational lensing effect. The arc is split
into five distinct regions ![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and ![]() (see Fig. 6. in the present paper) and
shows an intensity breaking between the galaxies
(see Fig. 6. in the present paper) and
shows an intensity breaking between the galaxies ![]() and
and ![]() .
The galaxies
.
The galaxies ![]() (
(
![]() ),
), ![]() (
(
![]() )
and
)
and ![]() (
(
![]() )
are superimposed to the arc. On the
contrary, the object
)
are superimposed to the arc. On the
contrary, the object ![]() belongs to it.
The detection of a weak radial arclet in a HST/WFPC1 image (noted R) has been
reported in Smail et al. (1996). Its existence was confirmed in Bézecourt et al. (1999) who argued its redshift should be about 1.3. The detection
of arclets, as well as the determination of sub-structures in the giant arc,
are important to constrain the mass profile of Abell 370 as well as to
scale its absolute mass.
belongs to it.
The detection of a weak radial arclet in a HST/WFPC1 image (noted R) has been
reported in Smail et al. (1996). Its existence was confirmed in Bézecourt et al. (1999) who argued its redshift should be about 1.3. The detection
of arclets, as well as the determination of sub-structures in the giant arc,
are important to constrain the mass profile of Abell 370 as well as to
scale its absolute mass.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{3568_fig1.eps}
\end{figure}](/articles/aa/full/2003/37/aa3568/Timg19.gif) |
Figure 1:
a) Extraction of a sub-image (
|
| Open with DEXTER | |
The direct comparison
between CFHT and HST images requires a linear transformation of
the HST image since both orientation and spatial sampling are
different. Let (x',y') and (x,y) be the spatial
coordinates of a star photocenter in the HST and CFHT images
respectively. The linear transformation between (x',y') and (x,y) may be written as:
The transformation (1) may be interpreted as a
combination of a 110![]() rotation followed by a 2.07 pixels
dilatation from the center of the galaxy
rotation followed by a 2.07 pixels
dilatation from the center of the galaxy ![]() 35 and a translation.
35 and a translation.
Ground-based observations suffer degradations due to the
transmission of light by the atmosphere and the optics. The images
obtained are then blurred by the system
atmosphere-instrumentation. The field of the CFHT image extends
over a few arcminutes and corresponds to a long exposure time. In
these conditions we can make the assumption that the degradation
due to the atmosphere is space invariant in the image plane. Such
an assumption is also safe for the instrumental distortions. The
relation between the noiseless image
![]() and the object
and the object ![]() is then a convolution one:
is then a convolution one:
The discretization of Eq. (2) leads to the
matrix relation:
| (3) |
The restoration technique we propose in this paper are then based on the deconvolution of the noisy image y by an estimated PSF in order to reconstruct the object xin the best conditions.
The first step consists in estimating the PSF from the stars (unresolved objects) in the full CFHT image.
We first identify the stars by using SExtractor (Bertin & Arnouts 1996). This software extracts
the objects in the field and gives characteristic parameters such
as the centro![]() d position, the Full Width at Half Maximum
(FWHM) in the light distribution and the magnitude of the object.
An object is defined as a number of connected pixels (fixed by
the user) above a given threshold (1.5
d position, the Full Width at Half Maximum
(FWHM) in the light distribution and the magnitude of the object.
An object is defined as a number of connected pixels (fixed by
the user) above a given threshold (1.5 ![]() in our study,
where
in our study,
where ![]() corresponds to the standard deviation of the image
background assuming a Gaussian distribution). The star
identification is then achieved by representing on a diagram the
magnitude of each object versus the FWHM. The stars gather in a
region with a FWHM approximatively constant (between 0.6'' and 0.68'')
independently of the magnitude. A refined selection is carried out
by only preserving the stars whose magnitude is greater than a
lower bound to avoid saturated stars images and smaller than a
higher one to avoid galaxy contamination. Each star image is
extracted over a
corresponds to the standard deviation of the image
background assuming a Gaussian distribution). The star
identification is then achieved by representing on a diagram the
magnitude of each object versus the FWHM. The stars gather in a
region with a FWHM approximatively constant (between 0.6'' and 0.68'')
independently of the magnitude. A refined selection is carried out
by only preserving the stars whose magnitude is greater than a
lower bound to avoid saturated stars images and smaller than a
higher one to avoid galaxy contamination. Each star image is
extracted over a
![]() pixels frame. After dropping
images exhibiting neighbors we are left with a sample of 23 individual stars images.
pixels frame. After dropping
images exhibiting neighbors we are left with a sample of 23 individual stars images.
The second step
consists in adding the 23 stars to synthesize the PSF. The
summation of these objects imposes the perfect superposition of
the photo-center of each star up to a fraction of pixel. This could
not be done directly as the light centro![]() d is not
located on an full pixel. We have to estimate the vector shift
between each star fi(x,y) where (x,y) are the spatial
coordinates and a reference one f*(x,y) chosen arbitrarily.
This is achieved by determining the argument of the inter-spectrum
between each couple of images. We first compute the Fourier
Transform (FT) for each star image noted
d is not
located on an full pixel. We have to estimate the vector shift
between each star fi(x,y) where (x,y) are the spatial
coordinates and a reference one f*(x,y) chosen arbitrarily.
This is achieved by determining the argument of the inter-spectrum
between each couple of images. We first compute the Fourier
Transform (FT) for each star image noted
![]() and
and
![]() for the reference, where (u,v) are the
spatial frequencies. Let us denote
for the reference, where (u,v) are the
spatial frequencies. Let us denote ![]() and
and ![]() the
unknown shifts between fi(x,y) and f*(x,y) along the x and
y axes respectively. The argument
the
unknown shifts between fi(x,y) and f*(x,y) along the x and
y axes respectively. The argument
![]() of the
inter-spectrum between
of the
inter-spectrum between
![]() and
and
![]() is:
is:
| (4) |
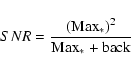 |
(5) |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{3568_fig2.eps}
\end{figure}](/articles/aa/full/2003/37/aa3568/Timg41.gif) |
Figure 2:
Normalized PSF of the A370 image.
a) Contours Plot. The contours represent successively 100, 80, 60, 40, 20, 10, 5, 3.5, 2.5, 1.5, 0.8,
0.5, 0.2, 0.1 |
| Open with DEXTER | |
We first deconvolve the A370 image with the classical Richardson-Lucy algorithm (Lucy 1974; Richardson 1972) and the PSF previously estimated:
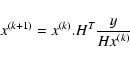 |
(6) |
To stop the iterations of the algorithm we define an error
criterion between the image reconstructed at
iteration k (denoted x(k)) and a reference image. In this
section we use the HST image (denoted
![]() )
as the reference.
We then minimize a criterion Rk based upon a relative Euclidean
distance between x(k) and
)
as the reference.
We then minimize a criterion Rk based upon a relative Euclidean
distance between x(k) and
![]() :
:
The objects in the field are rather different (giant arc, galaxies, stars...) and would not require exactly the same iteration number to be reconstructed at the best. The criterion Rk must then be computed preferably over the area to be preferentially restored. We focus here on the region of the giant gravitational arc and thus minimize Rk(see Fig. 3) within the rectangular box indicated in Fig. 1. The best reconstructed image obtained at iteration k=50 is represented in Fig. 4. Its background shows a granular structure typically of the size of the PSF. An early ringing effect (Cao et al. 1999; Lucy 1994a; Lagendijk & Biemond 1991) appears around the brightest point-like objects. It is both caused by the important background in the CFHT image and the discontinuities in the FT due to bright point-like objects (White 1993). These phenomena prevent any accurate measurement on the restored image and render necessary the use of a modified version of the algorithm to remove the oscillations. It is achieved by taking into account the background in the image and by introducing it as a lower bound constraint in the deconvolution algorithm itself. Hence, the reconstruction is not allowed to take values less than the background.
| |
Figure 3:
Relative error curve Rk between the CFHT reconstructed image and the HST one as a function of the iteration number for RL.
The images used are those of the Fig. 1, the PSF is the one of Fig. 2 and the mask used correspond to the rectangular box (
|
| Open with DEXTER | |
 |
Figure 4:
Abell 370 reconstructed image by RL at the 50th iteration.
The image used is the one of Fig. 1a, the PSF is the one of Fig. 2 and the mask used correspond to the rectangular box (
|
| Open with DEXTER | |
The LBCA is developed from a method
proposed in Lantéri et al. (2001) and studied in detail in
Roche (2001) and Lantéri et al. (2002). The method is based on the
minimization of a convex function under lower bound constraint
(denoted m). It consists in writing that at the optimum, the
Kuhn-Tucker conditions (Kuhn & Tucker 1951) are fulfilled. We then
write the algorithm under a modified gradient form using the
successive substitution method (Hildebrand 1974). After simple algebra, this leads in the
non-relaxed case to the following multiplicative expression of the
LBCA:
The lower bound m can be constant or variable over the image. The algorithm implementation is just as simple in both cases. The difficulty consists in obtaining an accurate background map specially in the region of bright structures. This estimation is out of the scope of this paper. We have then chosen to take for m a constant value overall the image estimated as the mean background in the global normalized CFHT image.
We still stop the LBCA by minimizing the Rk criterion (7). We evaluate Rk within the rectangular box of Fig. 1 as in the previous section. The corresponding Rk curve is represented in Fig. 5. The best restoration for this region of the giant arc is obtained for the iteration 269 (Fig. 6). We see from Fig. 5 that a range of about 50 iterations around this value would yield reconstructions of similar quality.
| |
Figure 5:
Relative error curve Rk between the CFHT reconstructed image and the HST one as a function of the iteration number for LBCA.
The images used are those of the Fig. 1, the PSF is the one of Fig. 2 and the mask used correspond to the rectangular box (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{3568_fig6.eps}
\end{figure}](/articles/aa/full/2003/37/aa3568/Timg51.gif) |
Figure 6: Best reconstructed image with LBCA using the HST reference image at the iteration 269. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{3568_fig7.eps}
\end{figure}](/articles/aa/full/2003/37/aa3568/Timg52.gif) |
Figure 7: Zoom on the radial arc R. HST image a), raw CFHT image b) and deconvolved CFHT image c). |
| Open with DEXTER | |
The reconstructed image with the LBCA shows an important reduction of both granularity and ringing effects.
We use a criterion derived from Rk to measure the amelioration brought by the deconvolution.
We compute a quantity D defined by:
This study shows a great amelioration carried out by the simple introduction of the lower bound constraint.
The deconvolution allows
in particular to restore severals structures in the giant arc (![]() b,
b,
![]() c,
c, ![]() g,
g, ![]() 37,
37, ![]() 62), and the breaking between
62), and the breaking between ![]() 37 and
37 and ![]() 62.
Moreover, the reconstructed image evidences a radial
gravitational arc (circle in Figs. 6 and 7c). This arc is clearly visible in the HST image (Fig. 7a) but does not appear in the raw CFHT data (Fig. 7b).
62.
Moreover, the reconstructed image evidences a radial
gravitational arc (circle in Figs. 6 and 7c). This arc is clearly visible in the HST image (Fig. 7a) but does not appear in the raw CFHT data (Fig. 7b).
Ringing residuals, while attenuated, are still present around high intensity objects. These drawbacks are due to an incorrect estimation of the background in these regions. The reconstruction can be improved by estimating a variable background.
We emphasize that the LBCA process takes the same computation time as the RL algorithm.
We have used in the previous section a HST image to stop the iterations of the deconvolution. Usually, such a reference image is not available. Further, the objective is precisely to restore information from the sole ground-based observations without any external help. So it is necessary to develop a self-consistent method relying on the ground-based data only.
The technique we used is the one proposed by Lantéri et al. (1999). It makes use of a comparison of the modulus of the Fourier transform of the deconvolved image at the iteration k with the modulus of the Fourier transform given by a Wiener filtering.
For clarity, let us briefly recall some well-known results on Wiener filtering. The Wiener filter W(u,v) is a zero-phase filter that prevents the amplification of the noise if a raw inverse filter technique is used. Denoting r the angular coordinates and u and v the 2D spatial frequencies,
![]() and
and
![]() the FT of the observation y(r) and the PSF h(r), the inverse Wiener filtered image transform
the FT of the observation y(r) and the PSF h(r), the inverse Wiener filtered image transform
![]() may be written as (Brault & White 1971):
may be written as (Brault & White 1971):
![\begin{displaymath}E_w(k)= \frac{ \parallel { \rm Abs}[\widehat{x}^{(k)} (u,v)]-...
...lel }{ \parallel {\rm Abs}[\widehat{x}_w(u,v)]
\parallel}\cdot
\end{displaymath}](/articles/aa/full/2003/37/aa3568/img63.gif) |
(13) |
| |
Figure 8:
Relative error curve Ew(k) between the modulus of the FT of the reconstructed image at
iteration k (Abs
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{3568_fig9.eps}
\end{figure}](/articles/aa/full/2003/37/aa3568/Timg66.gif) |
Figure 9: Best reconstructed image with LBCA using a criterion based on the Wiener filter at the 129th iteration. |
| Open with DEXTER | |
Both Abs
![]() and Abs
and Abs
![]() are normalized inside this mask for comparison. The
distance Ew(k) is represented as a function of the iteration number kin Fig. 8.
The best reconstruction is obtained for the iteration k = 129(Fig. 9).
The amelioration brought by the deconvolution
estimated from the D criterion (9) reaches 48%. It is close to the 53% amelioration obtained in Sect. 4.2 using the HST reference. It
shows that independently of a reference HST image, a rather
satisfying approximate solution may be found by using a stopping
criterion based on the data themselves. This procedure can be
fully and easily automated.
are normalized inside this mask for comparison. The
distance Ew(k) is represented as a function of the iteration number kin Fig. 8.
The best reconstruction is obtained for the iteration k = 129(Fig. 9).
The amelioration brought by the deconvolution
estimated from the D criterion (9) reaches 48%. It is close to the 53% amelioration obtained in Sect. 4.2 using the HST reference. It
shows that independently of a reference HST image, a rather
satisfying approximate solution may be found by using a stopping
criterion based on the data themselves. This procedure can be
fully and easily automated.
We have used a modified version of the RL algorithm, called LBCA, to deconvolve a CFHT image of Abell 370. The LBCA introduces a lower-bound constraint which
prevents the reconstructed image to take values below this bound. It allows
to reduce considerably the ringing effect that appears around bright objects
when classical algorithm are used (in particular RL). In the present paper,
the lower bound is taken equal to an estimation of the mean sky background
over the whole CFHT
![]() image.
image.
We have used at first an HST image of A370 as a reference to stop the iteration of the algorithm and to evaluate the amelioration brought by the deconvolution. An Euclidean distance criterion is then minimized between the reconstructed image at a given iteration and the HST reference to yield the best reconstruction. The LBCA reconstruction of A370 is twice as close to the HST image than the raw CFHT data, while no amelioration is brought by using the RL algorithm. Remarkably, our iterative process has permitted us to detect blindly the radial arc seen earlier in a HST image of A370 and to recover its morphological properties. This is an encouraging demonstration of its efficiency, and an interesting example of a practical application. It also emphasizes the interest of the LBCA to restore images with a high background.
In a more general case where no HST image is available, the convergence and stopping rules of the algorithm must rely on the information contained in the data themselves. We have thus developed a technique using the Wiener filter. It proceeds from an estimation of the noise in the CFHT image and the evaluation of the Power spectrum of the PSF. This method is based on the minimization of an Euclidean distance between the FT modulus of the LBCA reconstruction and the reconstructed image by the inverse Wiener filter. The best reconstructed image is close to the former one obtained with the HST as a reference.
The present study gives two important results. First, it allows us to improve the quality of an image with a high background, using a new algorithm as simple and as fast as the RL one: the LBCA. Finally, the overall data processing involving the LBCA together with the Wiener filtering may be fully automated. Hence, it could be fruitfully used for the processing of huge numbers of ground-based observations and particularly in the perspective of current or forthcoming wide field surveys.
We show in this appendix the similarities between the algorithm used in the present paper and the algorithm previously proposed by Snyder et al. (1993) and by Nunez & Llacer (1993), to take into account the effect of the background.
In our algorithm written in the form (8):
![\begin{displaymath}
x_{i}^{(k+1)} = m_{i} + (x^{(k)}_{i} - m_{i}) \left[H^T
\frac{y}{(Hx^{(k)})} \right]_{i}
\end{displaymath}](/articles/aa/full/2003/37/aa3568/img49.gif) |
(A.1) |
| (A.2) |
![\begin{displaymath}u_{i}^{(k+1)} = u^{(k)}_{i} \left[H^{\rm T}
\frac{y}{(H(u^{(k)}+m)} \right]_{i}\cdot
\end{displaymath}](/articles/aa/full/2003/37/aa3568/img69.gif) |
(A.3) |
Except for these small conceptual differences, both algorithms are similar and lead to the same results, however another important point must be underlined. Because of the convolution, the mean H(u+m) can also be written Hu + m (so the background m appears in the data space). However it does not mean that we can subtract the background m from the data y to obtain modified data y'=y-m; indeed if y is Poisson with mean Hu + m , then y' is not Poisson of mean Hu (y' might also be negative). Then, whatever the form of the algorithm, the estimated background is used in the algorithm (Hanisch 1993), but the data y must be left unchanged.