A&A 408, 1165-1177 (2003)
DOI: 10.1051/0004-6361:20031022

Latitudinal structure and north-south asymmetry of the solar wind from Lyman-$\alpha$ remote sensing by SWAN

M. Bzowski¹ - T. Mäkinen² - E. Kyrölä² - T. Summanen² - E. Quémerais³

1 - Space Research Centre PAS, Bartycka 18A, 00-716 Warsaw, Poland
2 - Finnish Meteorological Institute, Vuorikatu 15A, 00101 Helsinki, Finland
3 - Service d'Aéronomie du CNRS, BP 3, 91371 Verrières-le-Buisson, France

Received 25 February 2003 / Accepted 27 June 2003

Abstract
Based on SWAN/SOHO observations carried out during 1996-2002, we analyze latitudinal profiles of the heliospheric backscatter Lyman-$\alpha$ radiation. We use these results to investigate the ionization field of neutral hydrogen in the inner heliosphere and the latitudinal distribution of the solar wind mass flux. The the depth and latitudinal range of the equatorial depression in the Lyman-$\alpha$ backscatter glow (the so-called "groove'') are correlated with the corresponding parameters of the ionization field. We show that the groove is entirely due to latitudinal anisotropy of the solar wind, since, as we are able to demonstrate, the photoionization rate remains spherically symmetric throughout the solar cycle. During the last solar minimum the groove was well developed and stable. During the ascending phase of solar activity, it expanded in latitude (first south, then north), and disappeared altogether during the solar maximum. Shortly after the maximum it reappeared, but its structure was more complex than during the ascending phase. The groove feature is correlated with the equatorial band occupied by the slow solar wind, while the polar maxima of the Lyman-$\alpha$ intensity correspond to the fast solar wind from the polar holes. The groove observations (supported by appropriate modeling) show that during the last solar minimum the mass flux of the fast solar wind from the north and south polar holes were different from each other: a true north-south asymmetry between the polar regions was detected. During the solar minimum, the area occupied by the slow solar wind was quite stable and offset slightly to the south with respect to the solar equator: it extended to about 30$^\circ$N and 35$^\circ$S from the beginning of observations in May 1996 till 1998. Then it expanded by about $10\hbox{$^\circ$ }$ north and south, and subsequently migrated towards southern latitudes, so that it engulfed the south pole in May/June 2000. The north region of the fast wind survived longer and disappeared as late as November/December 2001. To check for the persistence of the north-south asymmetry, we analyze as a proxy the net sunspot area in the north and south hemispheres of the Sun during the 12 past solar cycles. Small north-south asymmetries are found to be commonplace during the past cycles, but the polarity of the asymmetries changes, leaving no statistically significant remnant asymmetry. This suggests that the solar dynamo is solely responsible for the asymmetry, with no remnant magnetic field from the protosolar nebula.

Key words: interplanetary medium - solar wind - Sun: UV radiation - Sun: magnetic fields - ultraviolet: solar system - Sun: corona

1 Introduction

Observations of the extraterrestrial Lyman-$\alpha$ sky background have been performed for more than 30 years now (see Holzer 1977 for review of the early effort). It was realized already at the beginning of the nineteen seventies that the glow was due to the resonant scattering of solar Lyman-$\alpha$ photons off a neutral hydrogen gas streaming past and being partly ionized by the Sun (Blum & Fahr 1970b). Had the solar ionization field been spherically symmetric, the expected Lyman-$\alpha$backscatter glow (observed from the center of the Solar System) should have cylindrical symmetry about the flow axis (Blum & Fahr 1970a). However, already early observations revealed that this was not always the case. It was hypothesized that the non-cylindrical distribution of the Lyman-$\alpha$ heliospheric glow was due to a departure of the solar wind from spherical symmetry (Lallement et al. 1985b; Kumar & Broadfoot 1978,1979; Witt et al. 1979,1981). It was further proposed that the latitudinal structure of the solar wind was connected with the heliospheric current sheet (Bertaux et al. 1996a).

Solar wind protons ionize neutral hydrogen atoms by resonant charge exchange. The ionization rate is proportional to the proton mass flux and to the reaction cross section. The latter one depends on the relative speed of colliding particles (see discussion by Bzowski 2001b). Hence, if the flux of the solar wind is higher at the solar equator than at the poles, then the ionization rate in the equatorial region is enhanced and a depression in the distribution of interplanetary hydrogen can be expected (Summanen 1996; Joselyn & Holzer 1975; Summanen et al. 1993; Lallement et al. 1995; Bertaux et al. 1996a). Such a depression, referred to as the heliospheric groove, was indeed observed in some observations of the heliospheric backscatter Lyman-$\alpha$ glow, but it was absent in some others (Ajello et al. 1993; Pryor et al. 1992; Ajello 1990; Lallement & Stewart 1990; Ajello et al. 1987; Lallement et al. 1985b; Pryor et al. 1996,1998; Bertaux et al. 1996b; Lallement et al. 1995). Based on these scarce observations it was hypothesized that the groove appears during solar minimum and disappears during maximum. To observe the anisotropies of the heliospheric glow on a more regular and systematic basis, the SWAN experiment was proposed in 1987 (Bertaux et al. 1995) and launched aboard the SOHO spacecraft in 1995. It has been successfully operated for more than 7 years now, bringing heliospheric backscatter glow data covering the time since the solar minimum in 1996 (Bertaux et al. 1999; Summanen 1996; Kyrölä et al. 1998; Summanen et al. 2001,2002; Summanen 2000; Bertaux et al. 1996b,1997b,a; Summanen et al. 1997).

From the earlier studies it was inferred that the enhancement of the ionization rate should be roughly symmetric about the solar equator (Lallement et al. 1985a; Summanen et al. 1993; Lallement et al. 1986; Lallement & Stewart 1990). Such an explanation of the observations was supported by in situ observations of the solar wind by Ulysses on its solar polar orbit during solar minimum conditions (Marsden & Smith 1997; Smith & Marsden 1995; Phillips et al. 1995b,a). During the first fast latitude scan in 1994/95, a clear bimodal structure of the solar wind was demonstrated, with a rarefied but fast wind in the polar regions and a dense but slow and gusty wind from an equatorial belt. It was soon confirmed that coronal holes are the origin of the fast and rarefied solar wind and hence the large polar holes produce the regions of reduced ionization rate, observed at high heliographic latitudes. During the second fast latitude scan, performed close to the solar maximum, no such clear separation was observed and the spacecraft was immersed in the slow and gusty wind throughout its entire scan from one pole to the other (McComas et al. 2002,2000b,a). Consequences of such structure of the solar wind for the rate of charge exchange between solar wind protons and neutral hydrogen atoms of interstellar origin were discussed by McComas et al. (1999) and Bzowski (2001b,a).

Ulysses measurements showed that the polar solar wind observed at the southern pole differed slightly but distinctly from the polar wind in the northern hemisphere (McComas et al. 2003). First evidence of such asymmetry was pointed out by Bertaux et al. (1996a) based on Lyman-$\alpha$ observations from Prognoz. Point-like measurements performed in situ are not able to tell if this difference was due to some north-south asymmetry in the solar wind, or an effect of macroscopic evolution of the solar wind during solar cycle. On the other hand, remote sensing of the solar wind by analysis of the heliospheric glow distribution has the capability to yield the macroscopic structure of solar wind and its evolution in time, but with a much lower resolution in heliolatitude and averaged over heliolongitude. The two methods are thus complementary.

In this paper we will study quantitatively the structure of solar wind during the solar minimum based on observations of the heliospheric Lyman-$\alpha$ glow, performed by SWAN and presented in Sect. 2, and on model calculations presented in Paper I (Bzowski 2003, this issue). In Sect. 3, we will discuss the evolution of solar wind from the solar cycle minimum to maximum. We will dwell, among others, on the north-south asymmetries of the solar wind. We will show qualitatively the rapid restructuring of the solar wind during transition from the solar minimum to maximum and the slower recovery of the bimodal structure at the transition from the maximum to minimum. In Sect. 4, we will show validation modeling based on the parameters of the ionization field, derived in Sect. 3. In Sect. 5, we will compare our findings with the Ulysses in-situ solar wind data and photoionization results from ground-based proxies. Section 6 presents a discussion of issues potentially affecting our results, and Sect. 7 contains some remarks on the possible origin of the north-south asymmetry of the solar wind and potential methods of tracking them in historical solar and geomagnetic data.

The results of this research bring a better understanding of the evolution of latitudinal structure of the solar wind during solar cycle and make it possible to take into account the actual hydrogen ionization field in studies of other phenomena in the heliosphere, like structure of the heliospheric interface, 3D spatial distribution of hydrogen pick-up ions, and 3D spatial distribution of $\sim$1 keV H neutrals, to name just a few.

2 Observations of heliospheric backscatter groove

The data were collected by SWAN during 13 observing campaigns, scheduled for the SOHO passages through the upwind and downwind projections of the hydrogen flow axis on the ecliptic plane. The ecliptic coordinates of the upwind direction were adopted from Quémerais et al. (1999): longitude $254\hbox{$^\circ$ }$ and latitude $8\hbox{$^\circ$ }$. The observations cover the time interval from May/June of 1996 till May/June of 2002. The intensity of the heliospheric glow was sampled with a $1\hbox{$^\circ$ }$ step in the planes perpendicular to the inflow direction. These planes are inclined at an angle equal to about $8\hbox{$^\circ$ }$ to the ecliptic and, by coincidence, to the solar equator as well. Hence they come close to but not precisely through the projections of the solar poles on sky. Since the observations were $360\hbox{$^\circ$ }$ scans of the sky, each heliolatitude was observed twice in each scan, but the locations of the lines of sight corresponding to a given heliolatitude were in different spots on sky - to the left and to the right from the upwind direction, when one selects the solar equator as the "level plane''.

The data were processed in the standard way used for all SWAN observations (Bertaux et al. 1997a): flat-fielding and cross-calibration between the two SWAN sensors were applied. To eliminate the "searchlight effect'' (Bertaux et al. 2000), the observations from a week before, a week after, and the day of the axis passage were compared. Since "searchlights'', which are regions of sky illuminated by active regions on the solar surface, rotate with the 26-day rotation of the Sun, it is reasonable to hope that during at least one of the three scans in each campaign at least one of the lines of sight observed at a given heliolatitude is free from the "searchlight'' enhancements. Consequently, for each of the campaigns always the lowest value from the three scans available for each line of sight was selected. An illustration of the scale of the searchlight effect is presented in Fig. 1. For the observing geometry used in this research, it was 25 to 50 counts during the solar minimum and $\sim$50-100 counts during the solar maximum, that is about 5 to 10% of the observed intensity.

The next step in the data processing was filtering out the contamination by stars (the "spikes'' seen in the plot) and smoothing by boxcar averaging with the window of $22.5\hbox{$^\circ$ }$. In Fig. 2, we present the resulting profiles of the groove. The panels in the left-hand column correspond to the observations performed during the summer passages through the inflow axis at the upwind side of the Sun and those in the right-hand column to the winter passages at the downwind side of the Sun. The thin lines are the raw composite profiles (with "searchlights'' eliminated but stellar contamination still present), and the thick lines are the observations with the stars removed and the boxcar averaging performed.

After this processing, the profiles to the left and to the right of the upwind-downwind direction should be identical. The observations showed that this was usually the case within reasonable limits and we wanted to take advantage of this fact to further reduce inhomogeneities in the data, but in some cases it was not possible. All profiles have data gaps caused by eliminating stellar contamination. The gaps usually occur in fixed regions in the scans and in most cases one can be confident that the results returned by the averaging are close to reality. In some cases, however, this was not true, particularly for the observations from upwind in 2001 and in 2002 in the area close to 75$^\circ$N and 75$^\circ$S. In these cases, the profile taken to the final analysis was the minimum of the left-hand and right-hand part of the scan. In the remaining cases, the left-hand and right-hand limbs of the scans were averaged.

Inspection of the left-hand and right-hand columns in Fig. 2 reveals that the intensities observed from the upwind side of the Sun are systematically higher than those observed from the downwind side. This is due to the fact that the gas density in the scan plane at the upwind side of the Sun is higher than in the scan plane at the downwind side.

In order to facilitate further analysis, the profiles of absolute intensity were scaled by dividing by the minimum value for a given scan and shifting the result so that the minimum value was assigned 0. The scaling procedure strips the data from long time-scale variations of the illuminating solar Lyman-$\alpha$ flux averaged over latitude (i.e., from the variations that result in variations of the radiation pressure $\mu$). The scaled profiles were then subjected to analysis in which the north and south depths and the north and south ranges of the groove were determined (see Paper I for definitions). The scaled profiles are presented in Fig. 3 (thick lines).

Figure 1: Raw observations from the downwind position in 1997, performed a week before (red/light gray), a week after (blue/black) and the day of the passage of SOHO through the projection of interstellar hydrogen inflow axis on the ecliptic plane (green/dark gray), are presented in the left-hand panel. The intensity is measured in SWAN counts; the data were flat-fielded and brought to common calibration between the two SWAN sensors but the stars and Milky Way contamination were not removed. The horizontal axis is the scan angle in the plane perpendicular to the upwind axis; $0\hbox {$^\circ $ }$ scan angle corresponds to the south solar pole. The right-hand panel shows the differences between the first and second scan (red/light gray), and the third and second scan (green/dark gray) to illustrate the typical magnitude of the searchlight effect during solar minimum (it is about 50 counts).

Open with DEXTER

Figure 2: Intensities observed as functions of the heliographic latitude. The dates and SOHO positions of observations are indicated in the headers of the panels. The thin lines are actual composite profiles taken for analysis, with searchlights eliminated. The solid lines are the same data with stars eliminated and boxcar smoothing performed. The data corresponding to full 360$^\circ$ scans are shown, hence the profiles observed in the left-hand and right-hand hemispheres with respect to the upwind direction can be seen.

Open with DEXTER

	Figure 2: continued.
Open with DEXTER

	Figure 2: continued.
Open with DEXTER

The striking feature of the profiles observed is a well-defined groove, reported already by Bertaux et al. (1996b) and Kyrölä et al. (1998) and seen from the beginning of observations in the middle of 1996 till the end of 1998, that is during the minimum of solar activity. The groove seemed stable and its minimum was located near the heliographic equator. In the Summer of 1999, the groove moved rapidly to the south and became much less pronounced throughout the year 2000, during the maximum of solar activity. While some structure could still be observed during that epoch, one would not be far from truth describing the groove as practically gone. During that epoch of high solar activity the intensity profile was changing its appearance quite rapidly: it featured a significant south-north gradient in summer 2001, only to show two minima in winter 2001, which deepened in summer 2002. A hint of a second minimum could be observed already in summer 2001.

In the following analysis we will use the macroscopic parametrs of the groove defined in Paper I (in particular, see Fig. 3 in this paper). These are the north and south ranges, the latitude of minimum, the north and south depths of the profile, and its resulting north-south asymmetry. The evolution of north and south range of the groove and the heliographic latitude of its minimum during the observations period are shown in Fig. 4, and the north and south depth and the north-south asymmetry in Fig. 5.

The scatter in the groove depth, especially pronounced for the northern line in Fig. 5, is mainly due to the fact that the groove profiles close to the poles were heavily contaminated by stars. The other factor is the geometry of observations: they were performed in the planes offset by 1 AU to the upwind and downwind side from the solar crosswind plane, and in consequence the imprints from solar ionization are more pronounced in the downwind plane than in the upwind plane.

3 Latitudinal structure of the ionization field

Following Bertaux et al. (1999,1996b,a), Kyrölä et al. (1998), Summanen et al. (2002,1997,2001), we interpret the existence of the groove as due to an enhancement of the hydrogen ionization rate at equatorial latitudes ("the ionization bulge''). Based on Ulysses observations (Smith & Marsden 1995; Marsden & Smith 1997; McComas et al. 1999; Phillips et al. 1995a), the ionization bulge is related to the slow solar wind, while the area of low ionization rate beyond the bulge is related to polar coronal holes, from which the fast solar wind is emitted.

In the following part of the analysis, we will employ the recommendations provided in the Conclusions section of Paper I to derive the range and height of the ionization bulge.

First we observe that between the summer of 1996 and summer of 1998, the minima of the observed profiles occurred just a little bit to the south of the solar equator. This suggests that the ionization bulge should be close to symmetric with respect to the equator and this enables us to use the theory from Paper I (Figs. 6, 7, 8, and 15) to calculate both the north and south ranges of the bulge and its north and south depths (for formal definitions, cf. Paper I). Then, from the limited analysis of the bulge profiles shifted away from its equatorial position, presented in Paper I, we infer that it is also safe to calculate the north and south ranges and the latitude of the center of the ionization bulge from the observations until winter 2000. We show them in Fig. 6 and in Table 2 here. Indeed, the calculated ranges of the ionization bulge are almost equal to each other till the end of 1998, featuring only a small shift to the south. Fully credible calculations of the heights of the bulge, however, are possible only to the end of 1998. The results for further dates are much less trustworthy because the groove profiles do not fulfill the criteria specified in Paper I; we show them in Fig. 7 with broken lines.

It is evident that during the solar minimum there existed a north-south asymmetry in the height of the ionization bulge. Both the north and the south heights were on more or less constant albeit different levels, with some fluctuations seen mainly in the northern hemisphere. Near the maximum of activity, the height of the ionization bulge was reduced to almost zero.

In 2000, the bulge was replaced with rapidly varying, multi-featured profiles of the ionization rate, as we can qualitatively infer. This coincides with disappearance of polar holes; instead, small coronal holes were observed distributed over the whole solar surface (Bilenko 2002). It seems, however, that in 2001 a north coronal hole opened again and some traces of the southern hole appeared as well. The effective profile of the ionization rate had a range extending somewhere to northern mid-latitudes, and its height was much lower than the height of the bulge observed during solar minimum (see a similar albeit deeper profile in Fig. 10b in Paper I). At the end of 2001 and in the beginning of 2002, an interesting double-minimum structure developed. Furthermore, the north-south asymmetry seems to have reversed - perhaps already at the end of 2001, and almost certainly in the summer of 2001. Without further observations we cannot tell, however, if this is a persistent trend or a transient fluctuation. Based on the modelling experience we would say that the profile of the ionization rate during the summer of 2002 had two relatively narrow maxima, occurring in the northern and southern mid-latitudes, and that the heights of these maxima were not equal in size. Some other interpretation, however, can by no means be excluded.

For the observed range of the groove about 30-40 $\hbox{$^\circ$ }$ and depth of 1.25-1.35 during the solar minimum, one would expect its north-south asymmetry about 1.05 (Fig. 5 in Paper I). The observed asymmetry is, however, twice larger. Since the maximum of the bulge is quite close to the solar equator (see the middle line in Fig. 6), which suggests that the range of the bulge should be almost symmetric with respect to the equator, we conclude that the enhanced north-south asymmetry of the bulge height is due to some asymmetry between the north and south base of the bulge. It means that the ionization rates at the solar poles inferred from these observations are slightly different.

A summary of the groove parameters is presented in Table 1, and of the parameters of the ionization bulge in Table 2.

	Figure 3: Relative groove profiles, averaged left-right (with exceptions, see text), with the minima and ranges indicated by the horizontal lines. The thin profiles at the first eight panels are the model test profiles, calculated for the ionization bulge parameters inferred from these observations and discussed later in the paper.
Open with DEXTER

	Figure 3: continued.
Open with DEXTER

4 Comparison of observed profiles with model

As a consistency check of the results, we performed a comparison of the observed groove profiles with model profiles calculated for the bulge parameters inferred from observations. We performed such analysis for the profiles observed from 1996.4 till 1999.9, that is for the time when the groove was well formed and relatively stable. While the model profiles used in the analysis in Paper I were calculated assuming a fixed value of the solar radiation pressure, in the present calculations we used the time-dependent radiation pressure model by Bzowski (2001b), based on a recent model of the solar Lyman-$\alpha$ output by Tobiska et al. (1997). The resulting test profiles are shown in thin lines in Fig. 3. In order to determine the ranges and depths of the test profiles, we subjected them to the same analysis as the observed ones. The results are shown in Figs. 4 and 5 (pale lines). One can see that the agreement is remarkably good, especially in the range of the groove. The depths of the observed and test profiles are also in good agreement, but generally the test model gives a little smaller depths than inferred from observations. A probable cause is the stellar contamination not fully removed from the observed profiles, as one can see in Fig. 3. Another conclusion is that probably the actual profiles of the ionization bulge are not so steep as those used in the modeling. The model bulge profiles were adopted following Ulysses point measurements which suggested that the transition from the fast to slow and then back from slow to fast wind occurred quite abruptly. But the rotationally-averaged boundary of the area on the Sun occupied by the slow solar wind need not be and most probably is not parallel to the solar equator, although locally the transition may be almost step-like. Rotational averaging of the bulge with the borders longitudinally "jagged'' yields profiles with slopes inclined at some angle to the level, and not with almost vertical edges, as we adopted. More detailed analysis of the profiles is beyond the scope of ths paper, since it requires a much more sophisticated modelling. But evidence that our hypothesis is justified is given by Bilenko (2002), who studied the distribution of coronal holes versus heliographic latitude during the past solar cycle-there exist distinct maxima of coronal holes densities at midlatitudies during the solar minimum and transition phases.

5 Comparison with Ulysses

The most natural validation of our results is a comparison with the Ulysses solar wind data. Profiles of the charge exchange rate from the first Ulysses Fast Latitude Scan were presented by McComas et al. (1999) and Bzowski (2001b). The Ulysses results were collected about one year earlier than the earliest observation by SWAN, but the depths and widths of the groove observed by SWAN during solar minimum are stable enough to justify an assumption that the height of the charge exchange profile had not changed significantly until 1999.

When interpreting the data from the Ulysses Fast Latitude Scan, Bzowski (2001b) adopted a fit where the levels of the charge exchange rate at the solar poles were equal to each other. When looking more closely at the data, however, one notices that the flat portions of the profiles are not perfectly symmetric, which can be seen in Fig. 8.

We fitted a straight line to the two subsets of the charge exchange data from the first Ulysses Fast Latitude Scan (the two portions of the solid line in Fig. 8). The data selection was performed on the basis that the subsets used must correspond solely to the fast solar wind and that abrupt disturbances, as corotating interaction regions, are absent. The broken line in Fig. 8 corresponds to the latitude band excluded from the fit. Using the fitted formula, we calculated the charge exchange rates at the northernmost and southernmost latitudes reached by Ulysses. They were equal to $2.65\times10^{-7}$ s^-1 (southern) and $2.37\times10^{-7}$ s^-1 (northern). The mean rate at the solar equator was taken from the fit presented by Bzowski (2001b) and it was equal to $4.58\times10^{-7}$ s^-1. Hence the south and north heights of the charge exchange bulge were equal to $q_{\rm S}=1.73$ and $q_{\rm N}=1.94$, respectively. These values are higher than the values derived from the depths of the Lyman-$\alpha$ groove (cf. Fig. 7).

We postulate that the reason for this discrepancy is photoionization. We follow the hypothesis that it is spherically symmetric (that is, its value is equal to some $\beta_{\rm ph}$ both at the poles and at the equator), and we calculate its value separately for each north and south depth of the Lyman-$\alpha$ groove, observed from 1996.43 till 1998.93. We do so by solving the following equations for $\beta_{\rm ph}$ (separately for each year and for north and south):

$$q_{\rm N} = \frac{\beta_{\rm Eqtr} + \beta_{\rm ph}} {\beta_{\rm N}+ \beta_{\rm ph}}$$ (1)

$$q_{\rm S} = \frac{\beta_{\rm Eqtr} + \beta_{\rm ph}} {\beta_{\rm S}+ \beta_{\rm ph}}$$ (2)

where $\beta_{\rm N}$ and $\beta_{\rm S}$ are the charge exchange rates at the north and south poles, derived from the above-mentioned Ulysses measurements, and $\beta_{\rm Eqtr}$ is the rate relevant for the equator. The results are presented in Fig. 9, where they are compared with the photoionization rate derived from the 10.7 cm proxy (Bzowski 2001a), corresponding to the relevant time interval.

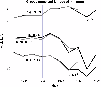	Figure 4: The north and south range of the groove of the heliospheric glow and the latitude of the minimum of the groove profile (saturated lines). Also shown are these parameters inferred from the test calculations discussed further in the paper (pale lines).
Open with DEXTER

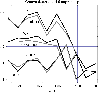	Figure 5: Groove depths north and south from observations and their ratio (saturaterd), compared with these quantities from the test modeling discussed later in the paper (pale).
Open with DEXTER

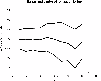	Figure 6: The range of the ionization bulge and the latitude of its center based on the groove parameters from observations and the model calculations discussed in Paper I.
Open with DEXTER

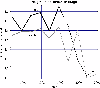	Figure 7: The north and south heights of the ionization bulge, based on the groove parameters from observations and the model calculations discussed in Paper I. The broken lines correspond to the time interval when the observed groove shape was too complex for a proper interpretation using our models (see text) but the range of the bulge could still be calculated, as shown in Fig. 6.
Open with DEXTER

Table 1: Summary of groove parameters from observations.

Table 2: Summary of ionization bulge parameters from observations.

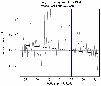	Figure 8: Hydrogen charge exchange rate inferred from the Ulysses first Fast Latitude Scan (1994-1995), see Bzowski (2001b). The solid line is fitted to the two subsets of the data marked with the solid portions of the line. The figure shows a distinct though not dramatic asymmetry in the solar wind between the north and south pole.
Open with DEXTER

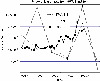Figure 9: Hydrogen photoionization rate inferred from SWAN and Ulysses observations and from modelling presented in Paper I, compared with the photoionization rate inferred from the 10.7 cm proxy. Shown are time series calculated separately from the northern and southern portions of the groove profile under assumption that the photoionization rate is spherically symmetric (blue and green/gray lines) and the rate from the 10.7 cm proxy (red/black line).

Open with DEXTER

The mean value of the photoionization rate derived from the 10.7 cm proxy is equal to $7.3\times10^{-7}$ s^-1, while the mean values from the north portion of the groove is equal to $7.6\times10^{-7}$ s^-1and from the south portion to $6.6\times10^{-7}$ s^-1. The mean value from all relevant groove measurements is thus $7.1\times10^{-7}$ s^-1.

The agreement between the values derived from the two totally independent methods is quite good, especially in the case of observations of the southern part of the groove profile. But it is not perfect and therefore we tested another hypothesis: that the photoionization rate is not spherically symmetric, but that a planar symmetry about the equator exists. The testing was carried out by solving a system of equations for $\beta_{\rm ph}$, $\beta_{\rm ph,E}$ for each groove profile observed:

 

$$q_{\rm N} \frac{\beta_{\rm Eqtr} + \beta_{\rm ph, E}} {\beta_{\rm N}+ \beta_{\rm ph}}$$ = (3)

$$q_{\rm S} \frac{\beta_{\rm Eqtr} + \beta_{\rm ph, E}} {\beta_{\rm S}+ \beta_{\rm ph}}$$ =

where $\beta_{\rm ph,E}$ corresponds to the photoionization rate at the solar equator and $\beta_{\rm ph}$ to the photoionization rate at the poles. The results, however, turned out to be discouraging: either unacceptably high (exceeding significantly the charge exchange rate), or unphysical (less than 0). Thus we feel justified to conclude that by combining the Ulysses and SWAN observations we were able to measure independently the hydrogen photoionization rate in the heliosphere during the solar minimum, and that during that interval the monthly-averaged field of photoionization rate was spherically symmetric. Further, we can thus conclude that the north-south asymmetry of the ionization rate at the solar poles, related to the solar wind flux observed by Ulysses, is not a temporal effect, but a permanent feature during the minimum activity phase of this particular solar cycle.

6 Discussion

In the modelling part of the problem one must keep in mind that the geometry of the model calculations of the backscatter glow intensity differs from the geometry of observations. Modelling was performed precisely in the crosswind plane with the Sun in the center and the model antisolar lines of sight were anchored at 1 AU from the Sun. The observations were carried out in the planes parallel to the former one, but offset 1 AU upwind and downwind, and with the lines of sight originating almost exactly at the upwind-downwind axis. We believe, however, that the differences are not essential and do not affect significantly our conclusions. In our results we see that the numerical values of parameters derived from the summer and winter observations oscillate around some mean value, a behavior that can be expected given the geometrical differences between the observations and modelling. The amplitude of the oscillations determines the accuracy of the conclusions we draw (though this does not apply to the large scatter in the north depth of the bulge-a major source of scatter is the residual stellar contamination in the data).

When modelling the shape of the profile of the ionization rate, we intentionally used functions with few free parameters. This approach turned out to be successful when interpreting the solar minimum observations of the groove, when the geometry of the solar wind was relatively simple. For the transition and maximum activity phase, a more sophisticated modelling is needed. It should involve theoretical response function of the Lyman-$\alpha$ glow to delta-like ionization profiles ("the hydrogen response function'') and deconvolution of the solar wind ionization input from the Lyman-$\alpha$ backscatter radiation response. That kind of analysis will hopefully be a subject of future studies.

We interpret the Lyman-$\alpha$ backscatter groove as entirely due to latitudinal anisotropy of the solar wind. We must emphasise, however, that it is not possible to distinguish between effects of the ionization by charge exchange and by EUV radiation based solely on observations of the Lyman-$\alpha$ backscatter glow (Bertaux et al. 1996a). The picture of evolution of the latitudinal structure of solar wind resulting from our analysis is in qualitative agreement with the results from Ulysses (McComas et al. 2000a) and from radio scintillation observations (Kojima et al. 2001).

The Lyman-$\alpha$ backscatter radiation is sensitive to immediate variations of the solar illumination (the searchlight effect), but otherwise it shows latency to large-scale variations of the ionization rate and radiation pressure. Neutral hydrogen needs about 3-6 months to adjust to changed conditions in the solar neighborhood (Rucinski & Bzowski 1995a; Bzowski et al. 2002; Rucinski & Bzowski 1995b). The temporal effects were excluded from the analysis altogether. Since, however, we are dealing with the planes where all points have the same angular distance from the upwind direction, we are doing relative measurements, and the temporal effects are related to streaming of the gas past the Sun, we believe that the only temporal effect that could go into play would be a shift by about half a year in the response of the heliospheric glow to the forcing of hydrogen gas by solar ionization, as discussed recently by Bzowski et al. (2002). Thus, the inferred ionization bulge parameters probably should be "pushed back'' in time by not more than a half of the year. The self-consistency of our approach is emphasized by the agreement of the test profiles with the observed ones. The theory used to derive the ionization bulge parameters from the backscatter groove profiles was developed based on calculations performed for a fixed value of the radiation pressure. The test profiles, however, were calculated with the use of radiation pressure values based on experimental values (Bzowski 2001a; Tobiska et al. 1997).

The Sun is rotating and hence the effective spatial distribution of the charge exchange ionization rate has rotational symmetry about the solar spin axis. Features distributed longitudinally at the solar surface get averaged in latitudinal bands. Thus, even though the solar wind is bimodal (fast and slow), the effective charge exchange ionization rate "perceived'' by neutral hydrogen has a continuous spectrum between the minimum and maximum values, which correspond, respectively, to the pure fast and slow wind. The effective charge exchange rate at a given latitude is thus proportional to the percentage of the solar surface occupied by the fast wind at this latitude band.

The remote sensing method of observations of solar wind by Lyman-$\alpha$ has the drawback of relatively low spatial resolution. Furthermore, at present we are not able to interpret quantitatively the rapid restructuring of the backscatter radiation glow profile, observed during the transition from low to high solar activity. The method has, however, the big virtue of being able to yield a global view of the solar wind in the north and south hemisphere simultaneously and on a regular basis, which is impossible in the case of point measurements carried out from a apacecraft on an orbit with the period of a few years, as Ulysses. Point measurements by Ulysses are, however, indispensable to provide absolute values of the charge exchange ionization rate at specific moments of time and solar latitudes and, together with the photoionization rates derived from proxies or actual measurements, to determine the absolute values of the solar wind flux throughout the solar cycle. Thus, the two methods are complementary.

7 Origin of the north-south asymmetry: Solar dynamo or the relict magnetic field?

The solar wind and its asymmetries are intimately related to solar magnetism. An unanswered question is whether the north-south asymmetry is entirely due to the action of solar dynamo, or a result of a relict magnetic field, frozen in from the protosolar nebula. Such relict field should probably be toroidal with some weak poloidal component, and invariable on the time scale of any solar observations available (Dicke 1979). An evidence of the presence of the remnant field would be a systematic excess of N/S field asymmetry over its solar cycle variations, persistent for the whole observations period. In contrast, if the north-south asymmetries are solely due to the solar dynamo action, then the level and sign of asymmetry should change from one solar cycle to another. The importance of such a relict field would be, among others, in extra pressure terms that should go into the hydrostatic equilibrium equations that determine the internal structure of the Sun, which would yield a need to change the standard solar model.

Evidence on the north-south asymmetry in the solar wind throughout the solar cycle has already been presented in the past based on observations from Earth-bound spacecraft. Bolton (1990); Paularena et al. (1995); and Szabó et al. (1996) discussed yearly variabilities in solar wind parameters. Szabó et al. (1996) pointed out that the annual variation in solar wind speed is strongest near solar minima. Zieger & Mursula (1998) found that the phase of annual variation in solar wind speed reverses from one solar minimum to another (depending on cycle's polarity), and that the higher speed values are observed either in March or in September, when Earth is at its highest southern and northern heliographic latitude. Mursula & Zieger (2001) and Mursula et al. (2002) postulated that such a behavior of the solar wind speed observed from Earth is a result of a north-south asymmetry in the solar wind, and in particular of a systematic displacement of the streamer belt. Further on, they discovered a close correlation between yearly averages of solar wind speed observed from Earth and geomagnetic activity (Mursula & Zieger 2001). If the correlation of the yearly variations with the solar cycle-related north-south asymmetry of the solar wind is confirmed on one hand, and if the correlation of the observed solar wind speed with the geomagnetic activity index is confirmed on the other hand, then the historical record of the geomagnetic index Ak(Hel) (Nevanlinna & Kataja 1993) can be used as a tool get some insight into the behavior of the north-south asymmetry of the solar wind in the past. In particular, one could hope to find if there is a correlation between yearly averages of the solar wind speed and the yearly averages of the total sunspot area separately in the north and south hemispheres of the Sun.

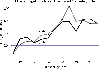	Figure 10: Total sunspot area in the northern and southern hemispheres of the Sun in the units of millionth of solar disk area, averaged over full sunspot cycles, shown as function of the sunspot cycle number.
Open with DEXTER

The only data available for a dozen of solar cycles is the total sunspot area in the north and south hemispheres (Hathaway 2003, http://science.msfc.nasa.gov/ssl/pad/solar/greenwch.htm). Sunspots are directly related to solar magnetism and solar magnetism governs the source of the solar wind. Hence sunspots are most probably a good tracer of the processes that affect the latitudinal distribution of solar wind. To get an insight into possible north-south asymmetries, we averaged the total sunspot area in the north and south hemispheres and plotted them in Fig. 10 as function of the sunspot number. The most striking feature is the increase of the net area of sunspots during the past 11 cycles, which corresponds well with the findings by Lockwood (2001) that the net flux of the solar open field systematically increases over past centuries. Apart from this it is clear that the north-south asymmetry is a typical feature of almost each solar cycle. We do not see, however, any significant residual differences between the north and south hemispheres, which suggests that the asymmetry is related to solar dynamo. While the technique of sunspot area observations was evolving over the past decades, which may have introduced systematic trends in the net sunspot area, we do not expect this could have introduced any systematic difference between the north and south hemisphere sunspot areas.

Acknowledgements

M.Bzowski gratefully acknowledges in-depth discussion on SWAN data with Dr. Rosine Lallement and an illuminating discussion on solar magnetism with Professor Wojciech Dziembowski. This research was supported by the Polish State Committee for Scientific Research Grant 2P03C 005 19 and the Scientists Exchange Cooperation Programme between the Finnish Academy and Polish Academy of Sciences.

References

 
• Ajello, J. M. 1990, J. Geophys. Res., 95, 14855 In the text  
• Ajello, J. M., Pryor, W. R., Barth, C. A., Hord, C. W., & Simmons, K. E. 1993, Adv. Space Res., 13(6) 37 In the text NASA ADS  
• Ajello, J. M., Stewart, A. I., Thomas, G. E., & Graps, A. 1987, ApJ, 317, 964 In the text NASA ADS  
• Bertaux, J.-L., Kyrölä, E., Quémerais, E., et al. 1999, Space Sci. Rev., 87, 129 In the text NASA ADS  
• Bertaux, J. L., Kyrölä, E., Quémerais, E., et al. 1995, Sol. Phys., 162, 403 In the text NASA ADS  
• Bertaux, J. L., Lallement, R., & Quémerais, E. 1996a, Space Sci. Rev., 78, 317 In the text NASA ADS  
• Bertaux, J. L., Quémerais, E., & Lallement, R. 1996b, Geophys. Res. Lett., 23, 3675 In the text NASA ADS  
• Bertaux, J. L., Quémerais, E., Lallement, R., et al. 1997a, Sol. Phys., 175, 737 In the text NASA ADS  
• Bertaux, J. L., Quémerais, E., Lallement, R., et al. 1997b, in Proceedings of the Fifth SOHO Workshop, The Corona and Solar Wind near Minimum Activity, ESA SP-404, 29-36 In the text  
• Bertaux, J.-L., Quémerais, E., Lallement, R., et al. 2000, Geophys. Res. Lett., 27, 1331 In the text NASA ADS  
• Bilenko, I. A. 2002, A&A, 396, 657 In the text NASA ADS  
• Blum, P., & Fahr, H. J. 1970a, A&A, 4, 280 In the text NASA ADS  
• Blum, P. & Fahr, H. J. 1970b, Space Res., 12, 1569 In the text  
• Bolton, S. 1990, Geophys. Res. Lett., 17, 37 In the text NASA ADS  
• Bzowski, M. 2001a, Space Sci. Rev., 97, 379 In the text NASA ADS  
• Bzowski, M. 2001b, in The Outer Heliosphere: The Next Frontiers, ed. K. Scherer, H. Fichtner, H. J. Fahr, & E. Marsch, COSPAR Colloquia Seri., 11 (Elsevier, Pergamon), 69-72 In the text  
• Bzowski, M., Summanen, T., Rucinski, D., & Kyrölä, E. 2002, J. Geophys. Res., 107, 10.1029/2001JA00141 In the text  
• Dicke, R. H. 1979, ApJ, 228, 898 In the text NASA ADS  
• Holzer, T. E. 1977, Rev. Geophys., 15, 467 In the text  
• Joselyn, J. A., & Holzer, T. E. 1975, J. Geophys. Res., 80, 903 In the text NASA ADS  
• Kojima, M., Fujiki, K., Ohmi, T., et al. 2001, J. Geophys. Res., 106, 15677 In the text  
• Kumar, S., & Broadfoot, A. L. 1978, A&A, 69, L5 In the text NASA ADS  
• Kumar, S., & Broadfoot, A. L. 1979, ApJ, 228, 302 In the text NASA ADS  
• Kyrölä, E., Summanen, T., Mäkinen, T., et al. 1998, J. Geophys. Res., 103, 14523 In the text  
• Lallement, R., Bertaux, J. L., & Dalaudier, F. 1985a, A&A, 150, 21 In the text NASA ADS  
• Lallement, R., Bertaux, J. L., & Kurt, V. G. 1985b, J. Geophys. Res., 90, 1413 In the text NASA ADS  
• Lallement, R., Holzer, T. E., & Munro, R. H. 1986, J. Geophys. Res., 91, 6751 In the text NASA ADS  
• Lallement, R., Kyrölä, E., & Summanen, T. 1995, Space Sci. Rev., 72, 456 In the text  
• Lallement, R., & Stewart, A. I. 1990, A&A, 227, 600 In the text NASA ADS  
• Lockwood, M. 2001, J. Geophys. Res., 106, 16021 In the text  
• Marsden, R. G., & Smith, E. J. 1997, Adv. Space Res., 19(6), 825 In the text NASA ADS  
• McComas, D. J., Barraclough, B. L., Funsten, H. O., et al. 2000a, J. Geophys. Res., 105, 10419 In the text  
• McComas, D. J., Elliot, H. A., Schwadron, N. A., et al. 2003, Geophys. Res. Lett., 30, 10.1029/2003GL017136 In the text  
• McComas, D. J., Elliot, H. A., & von Steiger, R. 2002, Geophys. Res. Lett., 29, 10.1029/2001GL013940 In the text  
• McComas, D. J., Funstein, H. O., Gosling, J. T., & Pryor, W. R. 1999, Geophys. Res. Lett., 26, 2701 In the text NASA ADS  
• McComas, D. J., Gosling, J. T., & Skoug, R. M. 2000b, Geophys. Res. Lett., 27, 2437 In the text NASA ADS  
• Mursula, K., Hiltula, T., & Zieger, B. 2002, Geophys. Res. Lett., 29, 10.02/2002GL015318 In the text  
• Mursula, K., & Zieger, B. 2001, Geophys. Res. Lett., 28, 95 In the text NASA ADS  
• Nevanlinna, H., & Kataja, E. 1993, Geophys. Res. Lett., 20, 2703 In the text NASA ADS  
• Paularena, K. I., Szabo, A., & Richardson, J. D. 1995, Geophys. Res. Lett., 22, 3001 In the text NASA ADS  
• Phillips, J. L., Bame, S. J., Barnes, A., et al. 1995a, Geophys. Res. Lett., 22, 3301 In the text NASA ADS  
• Phillips, J. L., Bame, S. J., Feldman, W. C., et al. 1995b, Adv. Space Res., 16(9), 85 In the text NASA ADS  
• Pryor, W. R., Ajello, J. M., Barth, C. A., et al. 1992, ApJ, 394, 363 In the text NASA ADS  
• Pryor, W. R., Ajello, J. M., Barth, C. A., et al. 1996, Geophys. Res. Lett., 23, 1893 In the text NASA ADS  
• Pryor, W. R., Lasica, S. J., Stewart, A. I. F., et al. 1998, J. Geophys. Res., 103, 26833 In the text  
• Quémerais, E., Bertaux, J.-L., Lallement, R., et al. 1999, J. Geophys. Res., 104, 12585 In the text  
• Rucinski, D., & Bzowski, M. 1995a, A&A, 296, 248 In the text NASA ADS  
• Rucinski, D., & Bzowski, M. 1995b, Adv. Space Res., 16, 121 In the text NASA ADS  
• Smith, E. J., & Marsden, R. 1995, Geophys. Res. Lett., 22, 3297 In the text NASA ADS  
• Summanen, T. 1996, A&A, 314, 663 In the text NASA ADS  
• Summanen, T. 2000, Ap&SS, 274, 143 In the text NASA ADS  
• Summanen, T., Lallement, R., Bertaux, J. L., & Kyrölä, E. 1993, J. Geophys. Res., 98, 13215 In the text  
• Summanen, T., Lallement, R., & Quémerais, E. 1997, J. Geophys. Res., 102, 7051 In the text NASA ADS  
• Summanen, T., Mäkinen, J. T. T., Kyrölä, E., & Schmidt, W. 2001, in The Outer Heliosphere: The Next Frontier, ed. K. Scherer, H. Fichtner, H. J. Fahr, & E. Marsch, COSPAR Colloquia Ser., 11 (Elsevier Pergamon), 133-136 In the text  
• Summanen, T., Mäkinen, J. T. T., Pulkkinen, T. I., et al. 2002, Adv. Space Res., 29, No. 3, 457 In the text  
• Szabó, A., Lepping, R. P., King, J. H., Paularena, K. I., & Richardson, J. D. 1996, in Solar Wind Eight, ed. D. Winterhalter, J. Gosling, S. Habbal, W. Kurth, & M. Neugebauer, (Woodbury, New York: American Institute of Physics), AIP Conf. Proc., 382, 399-401 In the text  
• Tobiska, W. K., Pryor, W. R., & Ajello, J. M. 1997, Geophys. Res. Lett., 24, 1123 In the text NASA ADS  
• Witt, N., Ajello, J. M., & Blum, P. W. 1979, A&A, 73, 133 In the text  
• Witt, N., Ajello, J. M., & Blum, P. W. 1981, A&A, 95, 80 In the text NASA ADS  
• Zieger, B., & Mursula, K. 1998, Geophys. Res. Lett., 25, 841 In the text NASA ADS