A&A 408, 1015-1028 (2003)
DOI: 10.1051/0004-6361:20031045

Probing the rotation curve of the outer accretion disk in FU Orionis objects with long-wavelength spectroscopy

G. Lodato 1 - G. Bertin 2


1 - Institute of Astronomy, University of Cambridge, Madingley Road, CB3 0HA, Cambridge, UK
2 - Università degli Studi di Milano, Dipartimento di Fisica, via Celoria 16, 20133 Milano, Italy

Received 6 March 2003 / Accepted 4 July 2003

Abstract
Studies of the Spectral Energy Distribution of Young Stellar Objects suggest that the outer disk of FU Orionis objects might be self-gravitating. In this paper we propose a method to test directly whether, in these objects, significant deviations from Keplerian rotation occur. In a first approach, we have used a simplified model of the disk vertical structure that allows us to quickly bring out effects related to the disk self-gravity. We find that the often studied optical and near-infrared line profiles are produced too close to the central object to provide significant evidence for non-Keplerian rotation. Based on parameters relevant for the case of FU Ori, we show that high-resolution long-wavelength spectroscopy, of the far-infrared H2 pure rotational lines (sometimes observed in "passive'' protostellar disks) and sub-mm CO lines, should be well suited to probe the rotation curve in the outer disk, thus measuring to what extent it is affected by the disk self-gravity. The results of the present exploratory paper should be extended soon to a more realistic treatment of the disk vertical structure.

Key words: accretion, accretion disks - gravitation - stars: pre-main sequence

1 Introduction

Very young (Class 0 or Class I) protostellar sources are thought to be characterized by a fairly high mass accretion rate (Calvet et al. 2000), but they appear to be still deeply embedded in their protostellar envelopes, so that their disk remains hidden to direct observations. On the other hand, in the more evolved T Tauri stars the mass accretion rate is generally considered to be modest, so that their disks are heated by the combined contribution of viscous dissipation and irradiation from the central star, making it more difficult to extract detailed information about the accretion process. In this context, FU Orionis objects (Hartmann & Kenyon 1996) are a rather small but remarkable class of pre-main sequence stars, because they are ideal "laboratories'' to test the process of disk accretion during the early stages of star formation. In fact, the disk of FU Orionis objects, differently from that of Class I objects, can be studied directly from its optical emission, and, differently from that of T Tauri stars, is likely to be the site of "active" accretion.

The distinctive feature of FU Orionis objects is that they undergo a violent outburst phase. During the outburst, they can increase their luminosity by more than 4 mag in a period of a few years, and then slowly return to a quiescent state on a much longer timescale. It is commonly believed that such outbursts are the result of a significant increase of the mass accretion rate in the disk which usually surrounds Young Stellar Objects. Many possible mechanisms to trigger the outburst phase have been discussed in the literature, among which are a tidal interaction with a companion star (Bonnell & Bastien 1992), the onset of a thermal instability in a partially ionized disk, when the outer disk is already accreting at a sufficiently high rate (Bell et al. 1995), or the onset of thermal instability induced by the presence of a satellite within the disk (Clarke & Syer 1996). The high accretion rate makes the emission of these systems dominated by the accretion luminosity, with only a minor contribution from the central star.

The modeling of the Spectral Energy Distribution (SED) of FU Orionis objects provides an estimate of the product $M_{\star}\dot{M}$ (as discussed below in Sect. 2.1) which turns out to be of the order of $10^{-4}~M_{\odot}^2$/yr. For a stellar mass $M_{\star}\approx M_{\odot}$, this would correspond to an accretion rate as high as $\approx $ $10^{-4}~M_{\odot}/\mbox{yr}$. "Standard'' models based on the presence of a Keplerian accretion disk lead to a satisfactory fit of the available photometric data only for wavelengths shorter than $10~\mu\mbox{m}$; the luminosity at longer wavelengths is usually much larger than expected. A flaring disk model, in which the outer disk is illuminated by the inner disk, could in principle explain the far-infrared excess, but the required amount of flaring turns out to be often too large (Kenyon & Hartmann 1991); therefore, the long-wavelength part of the SED is generally attributed to an infalling envelope, which is heated by the accretion disk luminosity.

Recently we have shown the viability of the picture (Lodato & Bertin 2001; hereafter LB) in which the long wavelength SED of FU Orionis objects is considered to be the signature of the effects of the disk self-gravity. There are already many clues that point to the importance of the disk self-gravity in thiscontext. Among these, we may recall that: (i) Submillimeter observations (Sandell & Weintraub 2001) show that the disk masses in these systems are much higher than those of T Tauri stars (indicating that they are probably younger than their low-luminosity counterparts); (ii) the modeling of the outburst in terms of a thermal instability event (Bell & Lin 1994) requires a very low value for the viscosity parameter $\alpha$, which in turn leads to a high surface density; indeed, detailed vertical structure calculations (Bell et al. 1997) show that at low values of the viscosity the disk is marginally stable against axisymmetric gravitational disturbances already at a distance significantly smaller than 1 AU from the central star. In fact, it has been suggested that FU Orionis outbursts could be triggered by a mechanism that is based on the role of the disk self-gravity (Armitage et al. 2001).

In the model proposed by LB the far infrared excess is produced by two separate contributions: (i) the higher rotation curve of the disk, in the case where the disk is sufficiently massive, enhances the viscous dissipation rate; (ii) the extra heating required to keep the outer disk marginally stable with respect to gravitational instabilities makes the surface temperature higher at large radii.

The second contribution is probably related also to non-local energy transport processes that should become important when global gravitational instabilities are present. The importance of global effects in self-gravitating disks has been brought out by means of numerical simulations (Rice et al. 2003), but further work is desired to clarify the issue of non-local transport in massive disks (Lodato & Rice, in preparation). Thus, for such second contribution, much of the discussion focuses on theoretical aspects (Balbus & Papaloizou 1999).

The importance of the first contribution can be checked by means of direct observations. In this paper we address the issue of detecting non-Keplerian rotation in protostellar disks. In passing, we note that the non-Keplerian rotation observed in some AGN accretion disks can be successfully explained by the model on which this paper is based (Lodato & Bertin 2003). Here we propose a possible measurement of the rotation of the outer disk in FU Orionis objects based on the analysis of mid-infrared and sub-millimetric spectroscopy. While sub-millimetric emission from FU Orionis objects is generally considered to come from the disk (Weintraub et al. 1991), alternative scenarios are available for the interpretation of the far-infrared emission. In fact, as we have already mentioned, Kenyon & Hartmann (1991) attribute the far infrared emission to the envelope. Here, following LB, we will assume that the far infrared emission comes from the disk.

A useful diagnostics to probe the kinematical properties of FU Orionis disks is provided by the shape of the observed line profiles. One merit of this kind of diagnostics resides in the fact that the surface temperature of the disk decreases with radius, and that the wavelength characterizing the emission from a certain annulus of the disk changes accordingly. Therefore, the study of the profiles of different lines allows us to probe the disk kinematics at different radial distances from the central accreting protostar. In particular, the observed optical and near-infrared line profiles are usually double-peaked (Kenyon et al. 1988, hereafter KHH), as expected from a rotating disk; in addition, the peak separation decreases with increasing wavelength, as expected for a disk with a decreasing temperature profile (Popham et al. 1996, hereafter PKHN). We can thus anticipate that from the peak separation at very long wavelengths in the far infrared and in the sub-mm, probing the outer disk, we should be able to tell whether the rotation is significantly different from Keplerian, hence testing the predictions of a model in which the disk self-gravity affects the shape of the rotation curve.

This kind of observations will require high spectral resolution (in order to detect small velocity differences) and high spatial resolution (in order to disentangle different kinematical components). In fact, many protostellar disks are known to possess strong molecular outflows. Therefore, a possible source of confusion in the shape of the line profiles may come from the kinematics of the outflows, that could result in asymmetries in the shape of the line profile. In this respect, the high spatial resolution that can be achieved with interferometric techniques (Guilloteau & Dutrey 1998), and, in the near future, with ALMA will eventually lead to clear-cut tests on the role of disk self-gravity in the rotation curve of protostellar disks.

The paper is organized as follows: in Sect. 2 we describe our method to test the rotation properties of the outer accretion disk; in Sect. 3 we describe the basic properties of the adopted accretion disk model based on parameters relevant for FU Ori; in Sect. 4 we describe our expectations for optical and NIR line profiles; in Sect. 5 we consider the case of mid-infrared pure rotational H2 line profiles; in Sect. 6 we describe the expected shape of sub-mm CO line emission; in Sect. 7 we draw our conclusions.

   
2 Measuring deviations from Keplerian rotation in spatially unresolved protostellar disks

The method presented in this section is an extension of the method described by KHH. Our main assumption is that the SED of FU Orionis objects is produced by an optically thick accretion disk up to wavelengths of the order of $100~\mu\mbox{m}$, consistent with studies of the millimetric continuum in these systems (Weintraub et al. 1991). The basic procedure can then be summarized as follows:

1.
The surface temperature profile $T_{\rm s}(r)$ is obtained from a parametric fit to the SED; note that in this paper we are not interested in explaining the physical origin of this profile, which we addressed in a previous article (LB). Given a value of the inclination angle i, this fit leads to a determination of the inner and outer radii of the disk, $r_{\rm in}$ and $r_{\rm out}$, and of the product $\dot{M} M_{\star}$, where $\dot{M}$ is the mass accretion rate and $M_{\star}$is the mass of the central object.

2.
The profiles of the optical-NIR lines (such as some CO absorption bands, seen in FU Orionis objects), which are produced mostly in the inner disk, are used to determine the rotational velocity in the inner Keplerian disk. For a given value of the inclination i, fitting the observed line shapes yields a measurement of $M_{\star}/r_{\rm in}$. As a result of the first two steps, we obtain separate estimates of $M_{\star}$ and $\dot{M}$. So far, the procedure is very close to that of KHH.

3.
In significantly massive disks, the line profiles at longer wavelengths should be broader than expected from a Keplerian extrapolation of the rotation curve measured in the previous step. Fitting the observed mid-infrared and sub-millimeter line profiles with the self-gravitating disk model described in Bertin & Lodato (1999, hereafter BL) will then provide a value for the lengthscale $r_{\rm s}$ that marks the transition to the non-Keplerian rotation regime (see Sect. 2.2 below). This fit will test directly the importance of the disk self-gravity, independently of the arguments that can be made in order to explain the infrared excess in the SED. Furthermore, since $r_{\rm s}$ depends on $M_{\star}$, $\dot{M}$, and on the viscosity parameter $\alpha$ (see Eq. (6) below), this fit will also lead to a measurement of the viscosity parameter $\alpha$.

   
2.1 Determining the radial temperature profile

We start by introducing the dimensionless radial coordinate $x=r/r_{\rm in}$ and the temperature scale T0 from the Keplerian model temperature profile:

 \begin{displaymath} \sigma_BT_{\rm s}^4(r)=\frac{3}{8\pi}\frac{GM_{\star}\dot{M}... ...left(\frac{r_{\rm in}}{r} \right)^3=\frac{\sigma_BT_0^4}{x^3}, \end{displaymath} (1)

where $\sigma_B$ is the Stefan-Boltzmann constant. This simple temperature profile is able to reproduce the correct spectral index of the SED at wavelengths smaller than 10  $\mu\mbox{m}$ and thus is adequate at small radii.

In the following, we would like to test the self-gravitating disk hypothesis by studying directly the rotation properties of the disk, independently of a discussion of the detailed physical processes that justify the observed SED. Therefore we consider a parametric description of the temperature profile, in line with many other investigations of YSO disks (e.g., see Beckwith & Sargent 1993; Osterloh & Beckwith 1995, who studied the sub-mm continuum of YSOs, or Thi et al. 2001, who studied emission lines). For the purpose, we thus consider a simple combination of two power laws, one describing the inner disk (and with temperature therefore proportional to r-3/4), and the other describing the outer disk, allowing for deviations from the r-3/4 dependence:

 \begin{displaymath} T_{\rm s}^4(r)=T_0^4\theta^4(x), \end{displaymath} (2)

where

\begin{displaymath}\theta^4(x)=\frac{1}{x^{3}}\left[1+\left(\frac{x}{x_t}\right)^{\beta}\right], \end{displaymath} (3)

$x_t=r_t/r_{\rm in}$ being a dimensionless radius, beyond which the temperature profile departs from the "standard'' profile, and $\beta$an appropriate power-law index.

Under the assumption that the disk emission is optically thick, the SED can be constructed by integrating in radius the blackbody spectrum. By analogy with what described in LB, we then introduce a reference frequency $\nu_0=kT_0/h$ and rescale the frequency to $\hat{\nu}=\nu/\nu_0$. For a given disk inclination i, the SED is thus given by:

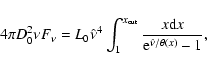\begin{displaymath}4\pi D_0^2\nu F_{\nu}=L_0\hat{\nu}^4\int_{1}^{x_{\rm out}}\frac{x\mbox{d}x} {\mbox{e}^{\hat{\nu}/\theta(x)}-1}, \end{displaymath} (4)

where

 \begin{displaymath} L_0=\frac{120}{\pi^3}r_{\rm in}^2\sigma_BT_0^4\cos i, \end{displaymath} (5)

D0 is the distance to the YSO, and $x_{\rm out}=r_{\rm out}/r_{\rm in}$.

A fit to the SED of observed objects will therefore determine the fit parameters $x_{\rm out}$, T0, L0, $\beta$, and xt. The combined knowledge of L0 and T0 (assuming the inclination angle of the disk to be known) allows us to obtain $r_{\rm in}$ and the product $M_{\star}\dot{M}$ (see Eqs. (1) and (5)).

   
2.2 The rotation curve in the presence of a self-gravitating disk

We now consider the contribution of the disk self-gravity to the rotation curve. Based on the results of BL, we introduce a typical lengthscale $r_{\rm s}$, the radius beyond which deviations from Keplerian rotation become significant, and a typical velocity scale V0, defined as follows:

 \begin{displaymath} r_{\rm s}=2GM_{\star}\left(\frac{\bar{Q}}{4}\right)^2\left(\frac{G\dot{M}} {2\alpha}\right)^{-2/3}, \end{displaymath} (6)


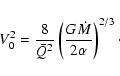\begin{displaymath}V_{0}^2=\frac{8}{\bar{Q}^2}\left(\frac{G\dot{M}}{2\alpha}\right)^{2/3}\cdot \end{displaymath} (7)

Here $\bar{Q}$ is a parameter that, for simplicity, will be set to unity (see BL). The quantity $\alpha$ is the parameter that defines the Shakura & Sunyaev (1973) viscosity prescription. The rotation curve of self-regulated, self-gravitating accretion disks is given by:

 \begin{displaymath} V^2=\frac{GM_{\star}}{r}+V_{0}^2+V_{0}^2\hat{\phi}^2(r/r_{\r... ...1}{x}+\frac{1}{x_{\rm s}}(1+\hat{\phi}^2(x/x_{\rm s}))\right], \end{displaymath} (8)

where $V_{\star}^2=GM_{\star}/r_{\rm in}$, $x_{\rm s}=r_{\rm s}/r_{\rm in}$ and $\hat{\phi}^2$ is defined in Eq. (4) of BL.

In the following, we will sometimes use the short, simplified expression "self-gravitating rotation curve" (as opposed to Keplerian rotation curve) when we will refer to the rotation curve derived from Eq. (8) for a model that includes the effects of the disk self-gravity.

   
2.3 The shape of the line profiles

In the present analysis we focus on the line shape. Therefore, we will consider only the relative contribution of the different annuli of the disk to the line intensity.

We will express the line profiles as a function of the velocity shift $\Delta v$, corresponding to the frequency shift $\Delta\nu$ from the line center $\nu_l$, so that $\Delta v/c=\Delta\nu/\nu_l$. The Doppler line profile $\phi(\Delta v,r)$ at a given radius of a disk rotating with velocity V(r) is given by:

   \begin{displaymath} \phi(\Delta v,r)=\left\{ \begin{array}{ll} \displaystyle\fra... ... los}^2(r)$ }\\ 0 & \textrm{otherwise} \par\end{array}\right. \end{displaymath}

where $V_{\rm los}(r)=V(r)\sin i$ is the maximum line-of-sight rotational velocity. Obviously, this expression takes into account only the effects related to the disk ordered motions; intrinsic effects associated with the microscopic physics of line emission and with the thermal motions inside the disk are not included.

We convolve this line profile with a Gaussian profile $\mbox{e}^{-(\Delta v/v_{\rm b})^2}$, either to simulate the effects of a finite instrumental spectral resolution R, so that $v_{\rm b}/c=1/R$, or to describe turbulent or thermal motions of the emitting species. The global line profile will be given by integrating the convolved line profile $\tilde{\phi}(\Delta v, r)$ over radius, weighted by an appropriate weight function $l(r,\nu_l)$ which expresses the relative contribution of the different annuli of the disk to the line emission:

 \begin{displaymath} F(\Delta v)=\int_{r_{\rm in}}^{r_{\rm out}} l(r,\nu_l)\tilde{\phi}(\Delta v, r) 2\pi r\mbox{d}r. \end{displaymath} (9)

The function $l(r,\nu_l)$ is specified once the details of the emission or of the absorption are known. At wavelengths where the continuum emission is optically thin, we expect to find emission lines; on the other hand, where the continuum is optically thick, emission lines are produced only if a temperature inversion in the upper layers of the disk is present, due, for example, to the effect of irradiation from the central object (Calvet et al. 1991b). If we consider FU Orionis objects, since the accretion rate is high and irradiation is not expected to be efficient, we thus expect to have absorption lines at optical and infrared wavelengths (Calvet et al. 1991a). Near infrared CO absorption bands from the disk are indeed a typical feature in FU Orionis objects (KHH). However, irradiation from the inner disk may give rise to a hot atmosphere above the disk, where emission lines can be produced. Therefore, in some cases (for example, for the optically thin FIR H2 molecular lines, see Sect. 5) we have considered both cases of absorption and emission.

In this simplified analysis we will consider for emission lines the two limiting cases of optically thick (which can be appropriate for sub-millimetric CO rotational lines) and optically thin emission (best suited for FIR pure rotational H2 emission lines, see below), so as to keep the radiative transport as simple as possible.

1.
Optically thick emission lines. In this case the brightness temperature of the emission line coincides with the physical temperature $T_{\rm s}(r)$ (see Beckwith & Sargent 1993) so that we can assume that the different annuli of the disk emit proportionally to their contribution to blackbody emission at the wavelength of the line center:

 \begin{displaymath} l(r,\nu_l)\propto\frac{1}{\mbox{e}^{h\nu_l/kT_{\rm s}(r)}-1}\cdot \end{displaymath} (10)

The expected line profile can thus be obtained directly, based on the results of modeling of the SED, as described in Sect. 2.1.

2.
Optically thin emission lines. In this case the relative contribution of the different annuli requires one additional piece of information, about the surface density radial profile $\sigma(r)$. Apart from numerical factors that do not depend on the radial coordinate or on the temperature, we can express $l(r,\nu_l)$ as:

 \begin{displaymath} l(r,\nu_l)\propto\sigma(r)\frac{\mbox{e}^{-E_{\rm up}/kT_{\rm s}(r)}}{Q(T_{\rm s}(r))}, \end{displaymath} (11)

where $E_{\rm up}$ is the energy of the upper level of the transition, and $Q(T_{\rm s}(r))$ is the partition function of the line emitting species (for example the H2 molecule; see also Thi et al. 2001). For simplicity, in this formula we have made the assumption that the line emitting species is at the same temperature as the matter responsible for the continuum emission (i.e. mostly the dust in the upper layers of the disk). However, it should be noted that this assumption would lead to very weak emission lines, difficult to observe. This has been partially confirmed by FIR observations of pure rotational H2emission lines in quiescent YSOs (Richter et al. 2002), that indeed reveal that these emission lines, if present at all, have a very weak line strength.

A more detailed discussion of the radiative transfer would require a complete accretion disk model. In the present simplified investigation, in order to proceed further from Eq. (11), we may consider a surface density profile of the form $\sigma \sim r^{-\gamma}$. The power law index $\gamma$ can be derived from spatially resolved observations of disks at mm wavelengths, where the disk emission is optically thin (Guilloteau & Dutrey 1998), and it turns out to be often close to unity (Testi et al. 2003; Piétu et al. 2003) (even for evolved objects, such as TW Hya; see Wilner et al. 2000). Therefore, the case $\gamma =1$ will be our reference case (see also the discussion is Sect. 5.4 below). (Interestingly, the self-gravitating disk solution of BL indeed predicts $\gamma =1$, but, as we did when we introduced the properties of the SED, in this paper we do not wish to address the problem of interpreting the observed profile.)

3.
Absorption lines. In this case we follow PKHN and make the simplifying assumption that the equivalent width of the line does not change with $T_{\rm s}$, so that $l(r,\nu_l)$ is proportional to the blackbody emission and will be therefore described by Eq. (10), as for optically thick emission lines. As PKHN note, this approach may not be valid above some threshold temperature (dependent on the absorption line), where the relevant molecules producing absorption disappear. We have therefore set the equivalent width to zero above this temperature (see also Sects. 4 and 5 below).

Other models of the absorption lines in FU Orionis include the use of stellar template photospheres with different temperatures, simulating the disk radial temperature profile (the disk is divided into rings, and with each ring a stellar template spectrum is associated, characterized by effective temperature equal to the disk surface temperature at that radius; KHH), or of the detailed solution of the radiative transfer in the disk atmosphere (Calvet et al. 1991a). However, such refined calculations show only minor differences with respect to estimates based on the simplest assumptions, at least for optical and near-infrared lines. More caution should be taken when applying the simple constant equivalent width assumption to longer wavelength lines (such as the H2 lines that we are going to consider in Sect. 5). In this first analysis we have decided to follow the simplified approach, being aware that for the final comparison with observations more realistic assumptions about the radiative transfer in the disk should be considered.

2.4 Other factors expected to affect the shape of the line profiles

Before concluding this section, a cautionary remark is in order. The main objective of the present paper is to show quantitatively what kind of spectroscopic observations could carry significant evidence for the presence of non-Keplerian motions in protostellar disks. In view of this goal, we have decided to consider a simplified description of the vertical structure and of the radiative transfer in the disk. Obviously, for the subsequent goal of interpreting the observations of some specific objects, many other effects concerning the dynamics, the physics and the chemistry of protostellar disks should be considered carefully. These include the possible interplay between rotation and infall in determining the shape of the line profile (Hogerheijde 2001; Belloche et al. 2002), the effect of molecular depletion (see Markwick et al. 2002 and comment at the end of Sect. 6), and the effect of other sources of gravitational field in disturbing the rotation curve. This final issue can be particularly important in the case of FU Orionis objects, for which the tidal interaction with a close "companion'' has been sometimes suggested (Bonnell & Bastien 1992) as a possible way to trigger the outburst. However, event statistics (Hartmann & Kenyon 1996) suggest that FU Orionis might be a repetitive phenomenon, with a recurrence period of $\approx $ 104-105yrs. The "companion'' should therefore lie in a very eccentric orbit, so that it should cause only a minor disturbance to the shape of the line profiles after the outburst has been triggered.

   
3 Basic parameters for a model suggested by the SED of FU Ori

In this section we apply the initial step of the procedure outlined above to the SED of FU Ori, the prototypical FU Orionis object. LB have already modeled the SED of this object in terms of a self-gravitating accretion disk, obtaining a satisfactory fit to the available data up to $100~\mu\mbox{m}$. Therefore, this object is a good candidate for testing its rotation characteristics and possible deviations from Keplerian rotation. In Table 1 we report the basic physical parameters for FU Ori obtained from the modeling of its SED in previous analyses (i.e. KHH, PKHN, and LB) and from the parametric modeling described in Sect. 2.1 and thus adopted in this work (see below).

Table 1: Accretion disk parameters for FU Ori, for the disk models of KHH, PKHN, LB, and this work. Values marked with an asterisk are assumed.

The different models cannot be easily compared to each other, because of the different parameters assumed (distance, extinction and inclination angle) and of the different modeling considered for the emission in the disk boundary layer. In particular, the main characteristics of the models are:

-
KHH assume that the net angular momentum flux in the disk is not vanishing and is given by the requirement of zero torque at the inner disk radius. The boundary layer is assumed to be at a constant temperature, corresponding to the maximum disk temperature.
-
PKHN assume that the net angular momentum flux in the disk is vanishing and include the boundary layer emission, treating it as a low-radiative-efficiency flow.
-
LB (and this work) assume that the net angular momentum flux in the disk is vanishing, but do not include the boundary layer emission.
The differences in the choice of the visual extinction AV (in magnitudes) and of the distance D0 only induce slight changes in the estimate of the product $M_{\star}\dot{M}$, when similar values for the inclination are assumed. On the other hand, the different treatment of the inner disk emission leads to a different estimate of the inner disk radius in the three models, so that $r_{\rm in}^{{\rm KHH}}\lesssim r_{\rm in}^{{\rm PKHN}}<r_{\rm in}^ {{\rm LB}}$. We interpret the relatively large value of the inner radius estimated by LB and in this work as a consequence of the fact that, with respect to PKHN, we did not include the contribution of the radiatively inefficient boundary layer, so that our inner disk radius is to be considered closer to the transition from the thin disk solution to the hot boundary layer, rather than to the actual stellar radius. Another important difference between KHH and PKHN concerns the central mass estimate: the boundary layer in the PKHN model rotates slower than Keplerian, due to the effect of the increased pressure gradient in the boundary layer. Thus, to obtain the same rotational velocity in the inner disk (to match the optical line profiles; see below) a larger central mass is required.

We will follow the work of PKHN as much as possible. Therefore, we start by assuming the extinction coefficient, distance and inclination angle provided in their analysis. In particular, the inclination angle assumed below is such that $\cos{i}=0.5$, slightly smaller than the value $\cos{i}=0.65$ derived by LB.


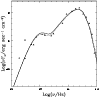  \begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{3691fig1.eps}}\end{figure} Figure 1: Spectral Energy Distribution of FU Ori. The triangles show the data (from Kenyon & Hartmann 1991), while the curves show the best fit model obtained in this work (solid line) and by LB (dotted line).
Open with DEXTER


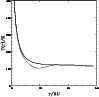  \begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{3691fig2.eps}}\end{figure} Figure 2: Surface temperature profile of FU Ori obtained in this work from a parametric model of the SED (solid line), compared to that obtained by LB (dotted line).
Open with DEXTER

With the parametric model described in Sect. 2.1 we have fitted the available photometric data (from Kenyon & Hartmann 1991), corrected by means of a standard dereddening function (Cardelli et al. 1989). The derived values for the product $M_{\star}\dot{M}$ and $r_{\rm in}$ are shown in Table 1. Figure 1 shows the observed SED of FU Ori together with our best fit (solid line) and the best fit obtained by LB with a self-gravitating disk model (dotted line). The best fit values for xt and $\beta$ (see Sect. 2.1) are: $x_t\approx 261$ (which corresponds to $r_t\approx 13$ AU) and $\beta=3$. In view of the goals of this paper, of the inhomogeneity of the SED data, and especially of the detailed discussion provided in KHH, PKHN, and LB, we will not comment here on the issue of setting uncertainties in the value of the derived parameters recorded in Table 1. We only note that the relative poor quality of the SED data might result is some ambiguities in the values of the estimated parameters, as already noted by Thamm et al. (1994).

Note that $\beta=3$ implies that the surface temperature profile is flat in the outer disk. In Fig. 2 the temperature profile of our best fit parametric model (solid line) is displayed together with the best fit model profile obtained by LB (dotted line).

   
4 Optical-NIR line profiles


  \begin{figure} \includegraphics[width=11cm]{3691fig3.eps}\end{figure} Figure 3: Optical (6170 Å) and near-IR (2.2  $\mu\mbox{m}$) predicted line profiles for FU Orionis, in the Keplerian (solid line) and self-gravitating (dotted line) model, with $r_{\rm s}\approx 18$ AU. The curves practically overlap and no differences between the two descriptions are noted.
Open with DEXTER

The contribution of the disk mass to the rotation curve depends on the size of the transition radius $r_{\rm s}$ (see Eq. (6)) in relation to the region of the disk actually probed by the available spectroscopy. In this section we will show that, in the case of a model suggested by the study of the SED of FU Ori, $r_{\rm s}$ is large enough so that the disk self-gravity has little or no influence on the optical-NIR line profiles, which are mostly produced in the inner disk. In practice, from the peak separation of the observed line profiles at these relatively short wavelengths, one can measure the ratio $M_{\star}/r_{\rm in}$, thus preparing the ground for a firm expectation of effects related to deviations from Keplerian rotation in spectroscopic studies at larger wavelengths (see following section). This section thus addresses step 2 of the procedure outlined in Sect. 2.

Here we follow PKHN and assume their value for the central mass, $M_{\star}=0.7~M_{\odot}$ (PKHN found significantly larger values of $M_{\star}$, with respect to KHH who did not include a detailed model of the inner boundary layer). Assuming $\alpha=0.034$ (the best fit value obtained by LB), we would obtain $r_{\rm s}\approx 350~r_{\rm in}\approx 18$ AU. Actually, as a result of the different estimates of $M_{\star}$ and $\dot{M}$ considered here with respect to LB, this value for $r_{\rm s}$ is smaller than that obtained by LB, leading to a higher and possibly unrealistic total disk mass ($\approx $2 $M_{\star}$). We have thus also considered the case in which $\alpha=0.1$, leading to $r_{\rm s}\approx 700~ r_{\rm in}\approx 36$ AU, better in line with the best model of LB.

We refer to the same (absorption) lines as in PKHN and KHH, i.e. metal lines at 6170 Å (at a resolution R=24 000) and CO lines at $2.2~\mu\mbox{m}$ (at a resolution R=20 000; the spectral resolutions are taken to be the same as in PKHN). The threshold temperatures above which the equivalent width of the line is taken to be vanishing are 8000 K for the optical lines, and 5000 K for the near-infrared lines. In Fig. 3 we plot, for $r_{\rm s}\approx 18$ AU, both the profile resulting from strictly Keplerian rotation (solid line) and the one resulting from the self-gravitating model (dotted line). The two different profiles are clearly indistinguishable. Note that the quantity usually referred to is not the actual absorption line profile, but the peak of the cross-correlation function of many absorption lines in the same wavelength range. This quantity is preferred from an observational point of view because it gives a way to obtain higher signal-to-noise ratios; physically, it represents the average shape of the line profile in a small wavelength range.

A similar plot for the case in which $r_{\rm s}\approx 36$ AU would again show, as expected, no significant differences in the shape of the line profiles between the strictly Keplerian model and the self-gravitating disk model.

   
5 Probing the outer disk rotation with H2 line profiles

In order to probe properties of the outer disk, so as to have a chance for detecting significant deviations from Keplerian rotation, one should consider line profiles at longer wavelengths (see Fig. 2).

Molecular hydrogen pure rotational emission lines have been observed with the Infrared Space Observatory (ISO) in many protostellar systems (Thi et al. 2001; van Dishoeck et al. 1997). However, due to the low angular resolution of ISO, it is not clear whether the H2 emission can be actually associated with the disk. Indeed, these ISO observations were not confirmed at higher spatial resolution (Richter et al. 2002). The weakness of H2 emission lines could indicate that spatial and temperature separations between the gas and the dust in the disk are small. Molecular hydrogen is a homonuclear molecule, so that the rotational emission lines result from the electric quadrupole. Therefore, they have a very low Einstein A coefficient, which makes them optically thin up to high column densities (of the order of $10^{23}~\mbox{cm}^{-2}$). We will therefore assume that these lines are optically thin, although we should be aware that, if the self-gravitating disk hypothesis is correct, then the surface density of the disk is going to be high as well, so that the optically thin assumption should eventually be re-examined. The basic line parameters of the H2 rotational lines are summarized in Table 2.

Table 2: Pure rotational H2 line parameters: central wavelength, energy of the upper level (in Kelvin), Einstein A-coefficient. From Thi et al. (2001).


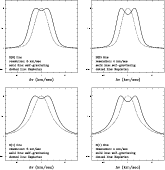  \begin{figure} \mbox{\epsfig{figure=3691fig4a.eps,height=7.15cm,width=6.8cm}\hsp... ...ce*{7mm} \epsfig{figure=3691fig4d.eps,height=7.15cm,width=6.8cm} } \end{figure} Figure 4: Molecular hydrogen absorption line profiles for disk models with self-gravitating (with $r_{\rm s}\approx 18$ AU, solid line) and Keplerian (dotted line) rotation curve. The upper panel shows the S(0) line at $28~\mu\mbox{m}$, with a resolution of 5 km s-1 ( left) and 4 km s-1 ( right); the lower panel shows the S(1) line at $17~\mu\mbox{m}$, with a resolution of 5 km s-1 ( left) and 4 km s-1( right).
Open with DEXTER


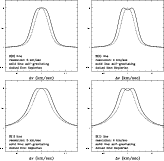  \begin{figure} {\epsfig{figure=3691fig5a.eps,height=7cm,width=6.8cm}\hspace*{7mm... ...space*{7mm} \epsfig{figure=3691fig5d.eps,height=7cm,width=6.8cm} } \end{figure} Figure 5: Same as Fig. 4, but with $r_{\rm s}\approx 36$ AU.
Open with DEXTER

A complete analysis would require the discussion of the full disk model, with an assumed vertical temperature profile, and the solution of the radiative transfer equation in the vertical direction, taking into account both viscous dissipation and external irradiation as heating sources (Calvet et al. 1991a). Here, for simplicity, we will only consider the two extreme cases of absorption lines (appropriate for the case in which viscous dissipation dominates) and of emission lines (that may be produced as an effect of irradiation of the outer disk by the inner disk), under the hypothesis that the line emitting gas is at the same temperature as the continuum emitting dust, i.e. that the gas temperature is given by $T_{\rm s}$ as derived from the modeling of the SED. The line profile will be obtained following the procedure described in Sect. 2.3.

5.1 Absorption lines

Figure 4 shows, for $r_{\rm s}\approx 18$ AU, the predicted line profiles for the Keplerian and non-Keplerian rotation curves, for the S(0) and S(1) absorption lines (here plotted "upside-down'' to allow an immediate comparison with the optical and NIR peaks), at different spectral resolutions. We have used the same input parameters as for the optical and near-infrared line profiles. The shape of the absorption line profiles is not strongly affected by the choice of the threshold temperature above which the equivalent width is taken to vanish. Lowering the threshold from 10 000 K to 1000 K only leads to a slight effect on the wings of the lines. This is because the inner regions of the disk give only a small contribution to the line profile, due to the small area they cover.

In Fig. 5 we show the same line profiles, but for the larger value of $r_{\rm s}$, i.e. $r_{\rm s}\approx 36$ AU. From these two figures, it is clear that, in order to detect the small changes in the rotation curve associated with the effects of the disk self-gravity, we should reach very high spectral resolution (see Sect. 5.3 for a discussion of the feasibility of such observations). Another interesting point is that the S(0) and S(1) line profiles, at the resolution of 5 and 4 km s-1, can be single peaked in the strictly Keplerian case and double peaked in the self-gravitating case. This would clearly distinguish between the two different pictures, if an adequate signal-to-noise ratio could be achieved. As expected, when a larger value of $r_{\rm s}$ is assumed, the effects of the disk self-gravity are less prominent.


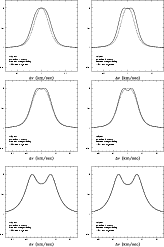  \begin{figure} {\epsfig{figure=3691fig6a.eps,height=7cm,width=6.8cm}\hspace*{7mm... ...space*{7mm} \epsfig{figure=3691fig6f.eps,height=7cm,width=6.8cm} } \end{figure} Figure 6: Molecular hydrogen emission line profiles in the self-gravitating (solid line) case and in the strictly Keplerian (dotted line) case, for the conservative model with $r_{\rm s}\approx 36$ AU. The upper panel shows the S(0) line at $28~\mu\mbox{m}$, with a resolution of 5 km s-1 ( left) and 4 km s-1 ( right); the middle panel shows the S(1) line at $17~\mu\mbox{m}$, with a resolution of 5 km s-1 ( left) and 4 km s-1 ( right); the lower panel shows the S(2) line at $12~\mu\mbox{m}$, with a resolution of 3 km s-1 ( left) and 2 km s-1 ( right).
Open with DEXTER

5.2 Emission lines

Figure 6 shows the predicted emission line profiles for the Keplerian and self-gravitating rotation curves, for the S(0), S(1) and S(2) lines at different spectral resolutions for the conservative case in which $r_{\rm s}\approx 36$ AU.

The general features of the shape of the lines are similar to the case of absorption: the lines are broader in the self-gravitating case than the corresponding lines in Keplerian disks, and they are often double-peaked, also in cases where the Keplerian lines are single-peaked. In the model where the transition radius $r_{\rm s}$ is smaller (not shown here), the effects of self-gravity are more prominent, as expected.

The shape of the S(2) line profile is practically not influenced by the modification of the rotation curve (i.e. it is mostly produced in a region where Keplerian rotation dominates). Based on the analysis of this and of the previous section, we conclude that the best lines to probe deviations from Keplerian rotation would be S(0) and S(1), because they would display some difference between the two competing models, with peak separation large enough to be detected with reasonable spectral resolution.

   
5.3 Feasibility

The above results obtained here show how deviations from Keplerian rotation can be detected with the analysis of the shape of the molecular hydrogen line profiles in the mid-infrared, provided that we can achieve high spectral resolution and a high signal-to-noise ratio. The Texas Echelon Cross Echelle Spectrograph (TEXES) operates in the wavelength range from 5.5 to 28.5  $\mu\mbox{m}$ and can reach a resolution as high as 2-3 km s-1 at the shortest wavelengths and of $\approx $5 km s-1 at $17~\mu\mbox{m}$. It has been mounted on the NASA's 3 m Infrared Telescope Facility, to confirm the existence of molecular hydrogen rotational lines apparently observed with ISO in low-mass, non-outbursting objects, such as some T Tauri and Herbig Ae stars (Richter et al. 2002). In addition, EXES, the companion instrument of TEXES, is expected to be placed on SOFIA (Stratospheric Observatory for Infrared Astronomy). Here we have demonstrated that, in principle, these two instruments have sufficient spectral resolution to measure this effect in FU Orionis disks.


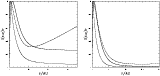  \begin{figure} {\epsfig{figure=3691fig7a.eps,height=6.5cm,width=6.7cm}\hspace*{5mm} \epsfig{figure=3691fig7b.eps,height=6.5cm,width=6.7cm} } \end{figure} Figure 7: Local emissivity as a function of radius for the S(0) (left) and S(1) (right) line profiles. Thick solid line: optically thin, $\gamma =1$; thin line: optically thin, $\gamma =1.5$; dashed line: optically thick.
Open with DEXTER

If we consider instead the capabilities of ISO, the maximum spectral resolution achievable is 10 km s-1. The predicted S(0) line profiles in FU Ori with the lower resolution of 10 km s-1 is no longer double-peaked. In the self-gravitating case there is only a slight broadening of the line profile with respect to the Keplerian case. We thus consider it unlikely that the signature of non-Keplerian rotation can be found in ISO observations.

Actually, the most serious problem with these mid-infrared line observations is to achieve a sufficiently high signal-to-noise ratio. For the case of emission lines, if the line emitting gas and the continuum emitting matter are approximately at the same temperature, we expect only weak emission lines to be present (as confirmed by Richter et al. 2002). For the case of absorption, the small absorption coefficient of the pure rotational H2transitions also leads to weak absorption lines.

   
5.4 Robustness of the H2 emission lines results

The optical thickness of the relevant lines depends on the surface density profile, which cannot be directly inferred from the modeling of the SED alone. Observations of protostellar disks, consistent with our self-gravitating disk model (BL), suggest a disk density profile of the form $\sigma\propto r^{-\gamma}$, with $\gamma\approx1$; in the previous sections, we have indeed set the surface density power law index to be $\gamma =1$.

The H2 rotational emission line are optically thin up to relatively high densities, due to their low Einstein's A-coefficient. FU Orionis objects are likely to be younger, and denser, than T Tauri and protoplanetary disks, so that for them we may even have to consider the possibility that the H2 emission is optically thick. In this section we discuss the robustness of the results presented in the previous section, with respect to the uncertainties on the optical thickness of the disk and on its surface density profile.

In Fig. 7, the local emissivity of every annulus of the disk, for the S(0) and S(1) lines, is plotted as a function of radius for three different cases, i.e.: (i) optically thin emission, $\gamma =1$, (ii) optically thin emission, $\gamma =1.5$, and (iii) optically thick emission. When the steepness of the surface density profile is increased, the peak of the emission for a certain line occurs at relatively smaller radii, as a result of the increased surface density. On the other hand, optically thick emission tends to contribute more than optically thin emission at larger radii, because in our models the temperature profile in the outer disk is approximately constant, while the optically thin emissivity rapidly decreases, being proportional to the surface density profile.


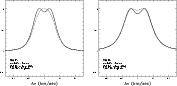  \begin{figure} {\epsfig{figure=3691fig8a.eps,height=7.5cm,width=7.3cm}\hspace*{8mm} \epsfig{figure=3691fig8b.eps,height=7.5cm,width=7.3cm} } \end{figure} Figure 8: S(1) line profile in the optically thin case, with $\gamma =1$( left) and $\gamma =1.5$ ( right).
Open with DEXTER

In Fig. 8 we show how the S(1) line profile changes when a different slope of the disk density is assumed. A steeper density profile (here we consider $\gamma =1.5$) results in a larger peak separation. This is due to the fact that a steeper surface density profile lets the inner parts of the disk, which rotate faster, contribute more prominently, with respect to the case of a less steep profile. This identifies a potential problem in the observational test that we are proposing here (for the case of optically thin line profiles). In fact, the increased contribution of the inner disk to the line emission when a steeper surface density profile is assumed may be such that the S(1) line is produced mostly at radii where the rotation curve is Keplerian. The resulting modifications to the line profiles due to the disk self-gravity would therefore become only barely visible in this case.

In practice, there is a sort of degeneracy in the appearance of optically thin line profiles with respect to the assumed model: a broader line profile can be traced either to the effects of the disk self-gravity, which enhances the rotation at large radii, or to the steepness of the disk density profile, which makes it possible for a certain emission line to originate from smaller radii, where the rotation velocity is larger.

   
6 Sub-mm CO line profiles

The discussion of the previous section shows that some H2 emission lines can be a useful tool to probe the rotation of the outer disk, although confusion may arise in the interpretation of optically thin lines because, under certain circumstances, deviations from the typical $\sigma \sim 1/r$ disk density profile can mimick those associated with deviations from Keplerian rotation.


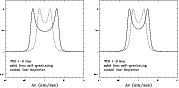  \begin{figure} {\epsfig{figure=3691fig9a.eps,height=7.65cm,width=7.45cm}\hspace*{7mm} \epsfig{figure=3691fig9b.eps,height=7.65cm,width=7.45cm} } \end{figure} Figure 9: 12CO 1-0 line profile at 110 GHz. Solid line: for a model applicable to FU Ori with a non-Keplerian rotation curve associated with a self-gravitating accretion disk; dotted line: for a strictly Keplerian model of FU Ori. The results are shown for $r_{\rm s}\approx 18$ AU ( left) and $r_{\rm s}\approx 36$ AU ( right).
Open with DEXTER

To derive more convincing conclusions about the rotation of the outer disk, it would thus be important to consider long-wavelength lines that are optically thick, so that the additional assumptions concerning the surface density profile are not needed. In this respect, some sub-mm CO lines are very interesting, because they are expected to be optically thick (Thi et al. 2001; Beckwith & Sargent 1993) and can be studied with very high spectral resolution. These global CO line profiles, observed in T Tauri and protoplanetary disks by a number of authors, usually show the typical double-peaked profile (Thi et al. 2001; Dutrey et al. 1997).

Interestingly, millimetric CO line emission has also been observed in V1331 Cyg (McMuldroch et al. 1993), an "FU Orionis object between outbursts'', which shares many features with FU Orionis objects, but has a smaller luminosity. The estimated disk mass in V1331 Cyg is $\approx $0.5 $M_{\odot}$, a further clue to the fact that FU Orionis disk mass may be fairly high.

As an example, we consider the 12CO 1-0 at 110 GHz, which is commonly observed in protostellar disks. We assume that the main limiting factor for the spectral resolution is given by turbulent or thermal broadening and we take the factor $v_{\rm b}$ in the Gaussian with which the line profile is convolved (see Sect. 2.3) to be 1 km s-1. The resulting line profiles, for the two different choices of $r_{\rm s}$, are shown in Fig. 9. The effect of self-gravity is clear in both cases.

In any case, as noted in the Introduction, care should be taken (especially for younger objects, such as FU Ori) in order to properly identify the various kinematical components (such as winds and outflows) that might contribute to the shape of the line profile. Another source of uncertainty related to CO lines is that of molecular depletion, resulting from the freezing out of molecular species onto dust grains. Many studies (see, for example, Markwick et al. 2002) have shown that, in the outer and colder disk, the column density of many species can be reduced significantly. However, these studies refer mostly to parameters appropriate for T Tauri disks, while we expect that FU Orionis disks, which are characterized by a much higher temperature, will be less subject to depletion.

   
7 Conclusions

The study of the line profiles produced in Young Stellar Objects has traditionally played a very important role in determining the physical conditions of circumstellar matter. In particular, it has been used to confirm the accretion disk origin of the luminosity of FU Orionis objects (KHH) and to test the Keplerian rotation in many T Tauri stars (Guilloteau & Dutrey 1994). In addition, spectroscopic observations may be able to probe the vertical structure of the disk (see, for example, Cheng et al. 1988 for the disks in dwarf novae).

Spatially resolved sub-mm interferometric observations of T Tauri stars have already provided interesting information about the outer disk kinematics (Guilloteau & Dutrey 1998; Simon et al. 2001). Such radio observations can reach an angular resolution of $\approx $1 $\hbox{$^{\prime\prime}$ }$. However, for objects such as FU Ori, which lies at a distance of $\approx $500 pc, the angular size of the disk (which should extend out to 50-60 AU, judging from the modeling of the SED) is likely to be as small as $\approx $0.1 $\hbox{$^{\prime\prime}$ }$.

In this paper we have exploited the wavelength dependence of the radial position of the peak of the line emissivity of the disk, to obtain additional information on the kinematical properties of the outer disk in FU Orionis objects, based on the shape of global line profiles. Our main purpose has been to define a clear cut test about the importance of the disk self-gravity in determining the rotation curve of the accretion disk in the early stages of star formation.

The method presented in this paper is based on the complementary information that can be obtained from the analysis of the optical and near-infrared line profiles (which probe the inner rotation curve, and hence set the value of the mass of the central object) and the analysis of high spectral resolution line profiles at long-wavelengths (which probe the rotation curve in the outer disk). This is a generalization of the method discussed by Kenyon et al. (1988) and Popham et al. (1996).

The high spectral resolution that can be obtained with the ground based and already operating TEXES instrument, and with its air-borne companion instrument EXES that will be on board of the SOFIA observatory (Richter et al. 2002), may indeed give us the way to distinguish between Keplerian and non-Keplerian rotation based on the analysis of pure rotational H2 lines. This in an important test about the viability of the self-gravitating disk model in FU Orionis objects, independent of the results of the SED modeling by Lodato & Bertin (2001). In addition, once we accept the self-gravitating disk model, this test will give us an alternative, independent way to measure the viscosity parameter $\alpha$, thus providing insights into the physical mechanisms that operate in protostellar disks.

As far as the shape of optically thin line profiles is concerned, we have also considered the robustness of our conclusions with respect to changes in the surface density profile of the disk. We have found that changes in the surface density profile could in principle mimick the effects obtained by changing the rotation curve of the disk. In the present study we have adopted a very simplified model for the vertical structure of the disk. More realistic models of the radiative transfer in the vertical direction would be needed to address this issue further.

An additional difficulty with the use of the proposed diagnostics for mid-infrared lines is related to the fact that an emission line at wavelengths where the dust disk is optically thick (such as the lines in the infrared wavelength range) would be produced only if there is a spatial or temperature separation between the warm gas and the dust. In this respect, the recent non-detection of H2 rotational lines from a small sample (two Herbig Ae stars and one T Tauri star) of pre-main-sequence stars by Richter et al. (2002) suggests that gas and dust are not spatially separated, as would result in some flaring disk model (Chiang & Goldreich 1997). This may indeed be the case for the highly accreting FU Orionis objects that we consider here.

Finally we have come to the conclusion that optically thick, sub-millimetric line profiles, such as those of some CO lines, often observed in protostellar disks, are basically free from the difficulties noted for the mid-infrared lines and thus represent the best tool to probe the physical conditions of the outer parts of the massive accretion disks in FU Orionis objects.

Acknowledgements
G.L. wishes to acknowledge the support of the Scuola Normale Superiore in Pisa, where most of this work has been carried out. This work has been partially supported by MIUR of Italy.

References


Copyright ESO 2003