A&A 408, 1179-1196 (2003)
DOI: 10.1051/0004-6361:20031039
G. B. Valsecchi1 - A. Milani2 - G. F. Gronchi3 - S. R. Chesley4
1 - Istituto di Astrofisica Spaziale e Fisica Cosmica,
via Fosso del Cavaliere 100, 00133 Roma, Italy
2 - Dipartimento di Matematica, Università di Pisa, via
Buonarroti 2, 56127 Pisa, Italy
3 - Dipartimento di Matematica, Università di Pisa, via
Buonarroti 2, 56127 Pisa, Italy
4 - Jet Propulsion Laboratory, 4800 Oak Grove Drive, CA-91109
Pasadena, USA
Received 19 October 2001 / Accepted 22 May 2003
Abstract
We extend Öpik's theory of close encounters of a small body
(either an asteroid or a comet) by explicitly
introducing the nodal distance and a time coordinate. Assuming that
the heliocentric motion between consecutive close encounters is
Keplerian, or given by an explicit propagator, we can compute
the initial conditions
for an encounter as functions of the outcomes of a previous one; in
this way it is possible to obtain a completely analytical theory of
resonant returns. It is found that the initial conditions of a
close encounter that lead to a resonant return must lie close to
easily computable circles on the b-plane of the first encounter.
By further assuming that the nodal distance varies uniformly with
time, due to secular perturbations, and considering the derivatives
of the coordinates on the b-plane of the second encounter with
respect to those on the b-plane of the first encounter, we compute
in the latter the location, shape and size of collision keyholes.
Key words: minor planets, asteroids - Solar system: general
The problem dealt with in this paper has deep roots in the history of astronomy. Since the end of the 18th century the study of the motion of a newly discovered small solar system body, comet D/Lexell, made it clear that comets can pass very close to the Earth, and that the gravitational perturbations at close planetary encounters can modify their orbits significantly (Lexell 1778).
Le Verrier (1844, 1848, 1857) re-analyzed the
observational record available for this comet with the purpose of
studying its motion, and found that it was not possible to determine a
unique set of orbital elements at a given epoch: a region in elements
space of non negligible size was compatible with the observations. Le
Verrier found that the six elements could be expressed as functions of
a single free parameter, which he called ![]() ,
whose value could vary
between
,
whose value could vary
between ![]() 1.5. He found also that the difference between his own
nominal orbital solution and the one given earlier by Clausen was
within the allowed range of
1.5. He found also that the difference between his own
nominal orbital solution and the one given earlier by Clausen was
within the allowed range of ![]() and, in fact, for his subsequent
studies on the motion of the comet adopted Clausen's orbit. Moreover,
Le Verrier determined the range of possible orbits for comet D/Lexell
both before the 1767 encounter with Jupiter (lowering the perihelion
distance q and making the comet observable from Earth) and after the
1779 encounter (removing the comet from visibility). This second
encounter may have been very deep and as a consequence the comet might
even have been ejected from the solar system on a hyperbolic orbit.
and, in fact, for his subsequent
studies on the motion of the comet adopted Clausen's orbit. Moreover,
Le Verrier determined the range of possible orbits for comet D/Lexell
both before the 1767 encounter with Jupiter (lowering the perihelion
distance q and making the comet observable from Earth) and after the
1779 encounter (removing the comet from visibility). This second
encounter may have been very deep and as a consequence the comet might
even have been ejected from the solar system on a hyperbolic orbit.
The papers by Le Verrier on this subject are remarkable, the more so
since they pre-date a very recent line of research (Milani
1999; Milani et al. 2000a), for which even the stated
purposes are
similar. Much of the current work aims at making the recovery of
poorly observed near-Earth asteroids feasible, and Le Verrier
concluded his first paper on the subject stating that if, in the
future, a comet would be discovered whose observations were
accountable for by using his elements for comet D/Lexell, with ![]() within the prescribed range, then the new comet would just be a new
apparition of D/Lexell.
within the prescribed range, then the new comet would just be a new
apparition of D/Lexell.
For more than a century the work by Le Verrier was forgotten and the
astronomers interested in recovering lost asteroids and comets used a
much simpler approach. They assumed that five orbital elements
were well known and only the orbital phase, that is the mean anomaly,
was subject to uncertainty. Thus the Line Of Variations (LOV),
consisting, in this simple approximation, of a segment along the mean
anomaly axis in the orbital elements space, replaced the curved line
parametrized by Le Verrier's ![]() .
This approximation is actually not
bad when the asteroid/comet has been lost by decades, because the
uncertainty along the orbit increases with time as a consequence of
the uncertainty in mean motion.
.
This approximation is actually not
bad when the asteroid/comet has been lost by decades, because the
uncertainty along the orbit increases with time as a consequence of
the uncertainty in mean motion.
Starting from Milani (1999) a precise way to compute the LOV has been developed and adapted to modern computational techniques, and it is now a standard procedure to compute a large number of multiple solutions for the orbital elements, sampling the LOV, which is, in general, curved. The motivation for this work, apart from the recovery problem, was the need to detect possible Earth impact solutions, the so called Virtual Impactors, in the near future (Milani & Valsecchi 1999; Milani et al. 1999). The assessment of the impact risk from an asteroid observed only during a single apparition cannot be accomplished by the study of one "nominal'' orbit (the solution of the least squares fit to the observations). The nominal orbit, and its neighborhood (which can be studied by linearization techniques), can provide only information on the impacts with probabilities of the order of 1/1000, and given the catastrophic nature of such an impact it is desirable to detect Virtual Impactors with much lower probability. The method currently being used (Milani et al. 2000b,c) scans hundreds of thousands of possible future close approaches, obtained by propagating all multiple solutions into the future, and applies quasi-linear techniques of target plane analysis to the most suspicious looking ones. However, it is clear that a qualitative, geometric understanding of the way these huge lists of close approaches are organized is a requirement to ensure the reliability of these automatic scans, for which human intervention must be exceptional.
The way to gain such an understanding is to go back to a simpler mathematical setting. 50 years ago Öpik began developing a theory of planetary encounters (Öpik 1951, 1976) based on a piecewise 2-body approach. That is, the small body (asteroid, comet, meteoroid) is considered to be in a heliocentric ellipse until the time of the encounter with some planet, then the dynamics is switched to a planetocentric 2-body orbit, which is (in this approximation) always hyperbolic. Then the standard formulas of 2-body scattering are applied to obtain the initial conditions of a new post-encounter heliocentric orbit. Öpik's theory was successfully used to study the statistical properties of the orbital changes resulting from close approaches, and to some extent it is still in use (Valsecchi & Manara 1997; Valsecchi et al. 1997). The main limitation is that Öpik developed the theory only for the case in which the two orbits, of the small body and of the target planet, are actually touching, that is the Minimum Orbital Intersection Distance (MOID) is zero.
Moreover, the basic theory does not consider that the subsequent encounters of the small body with the same planet (or even with another one) are not independent of the occurrence of the previous ones. The idea, now called resonant return, was implicitly contained in the work of Lexell and Le Verrier on Lexell's comet, was in fact used in spacecraft navigation since the 70s, but was first applied to asteroid close approaches only recently (Marsden 1999; Milani et al. 1999). In fact, recent work by our group has shown that the main organizing principle of the huge lists of close approaches obtained by propagating multiple solutions is that of the resonant return (also, to a lesser extent, non-resonant returns play a role).
With this background, it is possible to state the purpose of this paper in a simple way. We extend Öpik's theory of close encounters to near misses, which can occur also for a finite value of the MOID. Having developed this mathematical tool, we use it to describe how each encounter changes the condition for the next encounter, thus spawning a complicated (in principle, fractal) structure of resonant returns. This we achieve with an analytical theory, whose formulas, although long, can be implemented in a software tool allowing us to explore the geometrical structure of the following encounters in the target plane defining the circumstances of the first encounter.
Note that the analytical formulas we provide are not a replacement for the accurate numerical integrations. However, numerical integrations handle one orbit at a time, and we need to have a global view of everything that could happen as a consequence of a given encounter. Each subsequent return that could lead to an impact defines a keyhole on the target plane of the first encounter, such that an orbit through it would indeed collide with the planet. We give an explicit, semi-analytic description of the keyholes for all possible resonant returns. This allows us to draw the LOV footprint on the target plane, and its intersections with the resonant (and non-resonant) return keyholes provide information on all the subsequent encounters that are possible for an asteroid given the available observations. In the present paper the notation is sometimes different, and the geometrical derivations somewhat simplified, with respect to those contained in Valsecchi (2001), where an earlier, less complete version of this theory is presented.
The paper is organized as follows: in Sect. 2 we describe the classical theory of encounters first introduced by Öpik, and in Sect. 3 we extend it to finite nodal distances, introducing also a time coordinate, which we use in Sect. 4 to compute the initial conditions of a second encounter as functions of those of the first. This mapping between the target planes of the first and of the second encounter, together with its derivatives, allows us to compute the keyholes. In Sect. 5 we give some examples of practical application of the theory, in particular to the well known cases of the asteroids 1997 XF11 and 1999 AN10. Since the details of the analytical development may obscure the discussion of the main ideas, we have collected most of them in the appendix.
Öpik's theory of close encounters (Öpik 1976) consists of modeling the motion of a small body approaching a planet as a planetocentric two-body scattering. The relative velocity of the small body with respect to the planet defines the direction and speed of the incoming asymptote of the planetocentric hyperbolic orbit. This direction and speed are simple functions of the semimajor axis, eccentricity and inclination (a, e, i) of the heliocentric orbit of the small body, in the approximation neglecting terms of the order of the miss distance. The effect of the encounter is then computed as an instantaneous deflection of the velocity vector in the direction of the outgoing asymptote of the planetocentric hyperbolic orbit, ignoring the perturbation due to the Sun and the time it actually takes for the small body to travel along the curved path that "joins'' the two asymptotes. Interestingly, the errors involved in such an approach are smaller for closer approaches, and Öpik's theory is exact only in the limit of the minimum approach distance going to zero.
Let us consider a small body encountering a planet that moves on a
circular orbit around the Sun. To simplify the formulae, we use a
system of units such that the distance of the planet from the Sun
is 1, and the period of the planet is ![]() .
We also assume that
both the mass of the Sun and the gravitational constant are equal
to 1. We disregard the mass of the planet in the heliocentric
orbit of both the planet and the small body, thus the heliocentric
velocity of the planet is also 1.
.
We also assume that
both the mass of the Sun and the gravitational constant are equal
to 1. We disregard the mass of the planet in the heliocentric
orbit of both the planet and the small body, thus the heliocentric
velocity of the planet is also 1.
We use a planetocentric reference frame (X, Y, Z) such
that the Y-axis coincides with the direction of motion of the
planet, and the Sun is on the negative X-axis. In this system, the
components of the unperturbed planetocentric velocity vector ![]() of the small body are (Carusi et al. 1990)
of the small body are (Carusi et al. 1990)
![\begin{displaymath}\left[\begin{array}{c} U_x \\ U_y \\ U_z \end{array}\right]
=...
...e^2)}\cos{i}-1 \\ \pm\sqrt{a(1-e^2)}\sin{i} \end{array}\right]
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img14.gif)
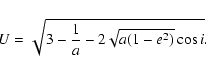
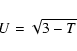
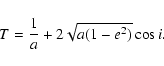
![\begin{displaymath}\left[\begin{array}{c} U_x \\ U_y \\ U_z \end{array}\right]
=...
...\phi \\ U\cos\theta \\
U\sin\theta\cos\phi \end{array}\right]
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img20.gif)
![\begin{displaymath}\left[\begin{array}{c} \cos\theta \\ \tan\phi \end{array}\right]
=\left[\begin{array}{c} U_y/U \\ U_x/U_z \end{array}\right].
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img21.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2023f1.eps}
\end{figure}](/articles/aa/full/2003/36/aa2023/Timg22.gif) |
Figure 1:
Basic geometric setup of Öpik's theory. The planet is
at the origin, moving in the direction of Y, with the Sun at
unit distance on the negative X-axis. |
| Open with DEXTER | |
We define the b-plane as the plane orthogonal to ![]() containing
the center of the planet.
The vector
containing
the center of the planet.
The vector ![]() extends from the planet to the intersection of the incoming asymptote
with the b-plane;
extends from the planet to the intersection of the incoming asymptote
with the b-plane;
![]() is the impact parameter.
is the impact parameter.
We use a planetocentric coordinate system
![]() such that
such that
![]() are coordinates on the b-plane and the
are coordinates on the b-plane and the
![]() -axis is directed along
-axis is directed along ![]() .
The
.
The ![]() -axis is
in the direction opposite to the projection on the b-plane of
the heliocentric velocity of the planet. The
-axis is
in the direction opposite to the projection on the b-plane of
the heliocentric velocity of the planet. The ![]() -axis completes
the right-handed reference frame, and is perpendicular to the
heliocentric velocity of the planet.
-axis completes
the right-handed reference frame, and is perpendicular to the
heliocentric velocity of the planet.
In this way, as will also be seen in more detail later, the shortest
segment joining the orbit of the planet and that of the small body,
corresponding to the MOID, turns out to be directed along the
![]() -axis; this is because this axis is perpendicular, by definition,
to both the Y-axis (the direction of motion of the planet), and
-axis; this is because this axis is perpendicular, by definition,
to both the Y-axis (the direction of motion of the planet), and ![]() ,
the planetocentric velocity of the small body. The
,
the planetocentric velocity of the small body. The
![]() -axis, then, can be seen as a "time coordinate'', that is, a
shift in the time of arrival of the small body at the b-plane will
mean a change only in its
-axis, then, can be seen as a "time coordinate'', that is, a
shift in the time of arrival of the small body at the b-plane will
mean a change only in its ![]() coordinate, and not in
coordinate, and not in ![]() .
In
other words, this coordinate system nicely decouples the two factors
governing the possibility of a very close encounter, i.e. distance
between orbits and encounter timing, mapping them into, respectively,
the
.
In
other words, this coordinate system nicely decouples the two factors
governing the possibility of a very close encounter, i.e. distance
between orbits and encounter timing, mapping them into, respectively,
the ![]() and the
and the ![]() -axis.
-axis.
Following Carusi et al. (1990), we define the angle ![]() by
by
![\begin{displaymath}\left[\begin{array}{c} b\sin{\psi} \\ b\cos{\psi} \end{array}\right]=
\left[\begin{array}{c} \xi \\ \zeta \end{array}\right].
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img29.gif)
![\begin{displaymath}\left[\begin{array}{c} X \\ Y \\ Z \end{array}\right]
={\bf\h...
...left[\begin{array}{c} \xi \\ \eta \\ \zeta \end{array}\right].
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img33.gif)
As a consequence of the encounter with the planet, ![]() is
rotated into
is
rotated into ![]() ,
aligned with the outgoing asymptote, without
changing the length: U=U'. The deflection angle
,
aligned with the outgoing asymptote, without
changing the length: U=U'. The deflection angle ![]() between the two
vectors is a function of U, the mass of the planet m, and the
impact parameter b according to
between the two
vectors is a function of U, the mass of the planet m, and the
impact parameter b according to
The angles ![]() and
and ![]() ,
defining the direction of the
post-encounter velocity vector
,
defining the direction of the
post-encounter velocity vector ![]() ,
can be obtained in terms of
,
can be obtained in terms of ![]() ,
,
![]() ,
,
![]() ,
,
![]() by (Carusi et al. 1990)
by (Carusi et al. 1990)
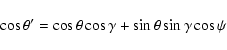
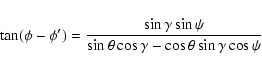
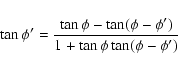
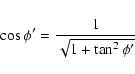
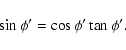
The geometry of the rotation of ![]() is illustrated in
Figs. 2 and 3; note that c, that is also
an invariant of the problem, due to the conservation of U, has a simple geometric meaning.
is illustrated in
Figs. 2 and 3; note that c, that is also
an invariant of the problem, due to the conservation of U, has a simple geometric meaning.
| |
Figure 2:
The deflection of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2023f3.eps}\end{figure}](/articles/aa/full/2003/36/aa2023/Timg52.gif) |
Figure 3:
Same as Fig. 1, but with also the
post-encounter velocity |
| Open with DEXTER | |
Öpik's theory of close encounters works as long as the region of space in which the encounter takes place is "small,'' so that the interaction can be thought of as taking place in a point. This assumption breaks down as the Tisserand parameter approaches 3, i.e., when the encounters take place at low planetocentric velocity, and therefore the assumption of a point-like interaction does not hold any more. The theory is inapplicable for a Tisserand parameter exceeding 3.
In principle, this theory could be extended to the case of an elliptic
orbit of the planet, preserving most of the formulae, provided the
angles ![]() and
and ![]() are defined with respect to the velocity of
the planet at the time of the encounter, which would generally not be
orthogonal to the Sun-planet direction.
are defined with respect to the velocity of
the planet at the time of the encounter, which would generally not be
orthogonal to the Sun-planet direction.
In its original formulation, Öpik's theory of close encounters does
not use a complete set of state variables. In a complete formulation,
the six orbital elements of the small body have to be transformed into a
set also containing six coordinates. The six coordinates used in the
extension of Öpik's theory presented in this paper are: U, ![]() ,
,
![]() ,
,
![]() ,
,
![]() and the time t0 of the crossing
of the ecliptic plane by the small body.
and the time t0 of the crossing
of the ecliptic plane by the small body.
In Appendix A.1 we provide formulae to compute the transformation from the orbital elements to this encounter-related coordinate set. In this way the theory can be used to compute actual cases of close encounters with non-zero miss distances, and its results can be compared with those coming from accurate numerical modeling of the motion. However, the formulas we are providing are linearized in the actual miss distance, and therefore cannot be used for very shallow encounters.
In the (X, Y, Z) frame, the motion along the incoming asymptote is
The simple formulae of uniform rectilinear motion allow one to decompose the search for the minimum encounter distance into two steps. First, we look for the minimum not constrained by encounter time, to find the MOID. Second, taking into account the time, we find the actual minimum encounter distance for a generic initial condition.
The Minimum Orbital Intersection Distance (MOID) is the minimum distance between the orbit of the small body and that of the planet. In the case of encounters for which Öpik's theory is applicable (Greenberg et al. 1988) there is the possibility of two local minima of the distance between the orbits, one close to each node, and we call each of these minima a local MOID.
We can derive an expression for the local MOID assuming that
the small body travels on the incoming asymptote. From the first Eq. (4), eliminating t-t0, we obtain
![\begin{displaymath}\left[\begin{array}{c} X \\ Z \end{array}\right]
=\left[\begi...
...U_x/U_y)~(Y-Y_0)+X_0 \\ (U_z/U_y)~(Y-Y_0)
\end{array}\right];
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img54.gif)
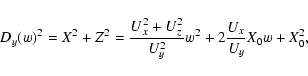
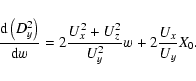
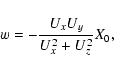
![\begin{displaymath}\min{D_y^2}=X_0^2\left[1-\frac{U_x^2}{U_x^2+U_z^2}\right]=X_0^2\cos^2\phi.
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img58.gif)
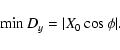
Thus a small body having an encounter at its local MOID crosses the
b-plane on the ![]() -axis, with
-axis, with
![]() and the MOID is
just
and the MOID is
just ![]() .
.
In general, the close approach does not take place at the minimum
possible distance, i.e. at the MOID. To compute the actual
minimum distance as a function of the initial conditions we have to
consider that in the (X, Y, Z)-frame, and in the rectilinear motion
approximation, the node of the orbit of the small body moves backwards
along the Y-axis with speed -1. Thus, if at t=t0 the node is
at
(X0,Y0,0), we can compute the motion of the small body from the
second Eq. (4). The distance from the planet is
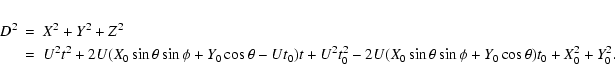
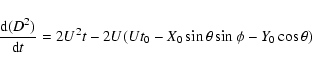
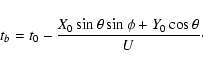
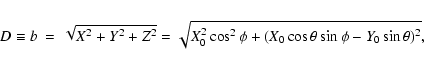
![\begin{displaymath}\left[\begin{array}{c} \xi \\ \zeta \end{array}\right]
=\left...
...hi \\
X_0\cos\theta\sin\phi-Y_0\sin\theta \end{array}\right].
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img68.gif)
Let the planetocentric angular momentum of the small body be
![]() .
At the time tb corresponding to
the minimum unperturbed distance b, we instantaneously rotate the
velocity vector, which is parallel to the incoming asymptote, about
.
At the time tb corresponding to
the minimum unperturbed distance b, we instantaneously rotate the
velocity vector, which is parallel to the incoming asymptote, about ![]() ,
so as to make it parallel to the other asymptote
,
so as to make it parallel to the other asymptote
![\begin{displaymath}\vec{U'}\equiv\left[\begin{array}{c}
U\sin\theta'\sin\phi' \...
...i'
\end{array}\right]={\bf\hat{R}}_{\vec{h}}(\gamma)\vec{U}.
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img73.gif)
![\begin{displaymath}\vec{b'}\equiv\left[\begin{array}{c} \xi' \\ 0 \\ \zeta'
\end{array}\right]={\bf\hat{R}}_{\vec{h}}(\gamma)\vec{b}.
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img75.gif)
![\begin{displaymath}\left[\begin{array}{c} X'(t_b) \\ Y'(t_b) \\ Z'(t_b) \end{arr...
...left[\begin{array}{c} \xi \\ \eta \\ \zeta \end{array}\right].
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img76.gif)
![\begin{displaymath}\left[\begin{array}{c} X'(t_b) \\ Y'(t_b) \\ Z'(t_b) \end{arr...
...
U'_y(t_b-t'_0)+Y'(t'_0) \\ U'_z(t_b-t'_0) \end{array}\right];
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img77.gif)
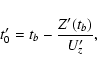
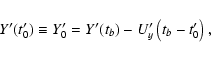
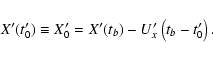
We can apply the appropriate rotations by ![]() and
and ![]() to the
post-encounter coordinates X'(tb), Y'(tb), Z'(tb), to obtain
the coordinates in the post-encounter b-plane as functions of the
pre-encounter
to the
post-encounter coordinates X'(tb), Y'(tb), Z'(tb), to obtain
the coordinates in the post-encounter b-plane as functions of the
pre-encounter ![]() and
and ![]() ,
as in Eq. (1); it
can be checked that
,
as in Eq. (1); it
can be checked that ![]() ,
as is clear from the geometry of the
rotation
,
as is clear from the geometry of the
rotation
![]() .
The complete formulas are
given in Appendix A.2.
.
The complete formulas are
given in Appendix A.2.
Let us discuss here the explicit expression for the new local MOID, i.e.
for the ![]() coordinate in the post-encounter b-plane
coordinate in the post-encounter b-plane
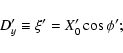
![\begin{displaymath}\xi'=\frac{\left(b^2+c^2\right)\xi\sin\theta}
{\sqrt{\left[\l...
...2\right)\sin\theta-2c\zeta\cos\theta\right]^2+4c^2\xi^2}}\cdot
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img89.gif)
Öpik's theory is not applicable for the exactly tangent and coplanar
orbits, and its validity becomes questionable for very low values of
![]() (Greenberg et al. 1988). This is unfortunate
since a small, but non negligible, number of asteroids undergoing
encounters with the Earth has
(Greenberg et al. 1988). This is unfortunate
since a small, but non negligible, number of asteroids undergoing
encounters with the Earth has
![]() .
In these cases
the interaction may become extremely complex, possibly including
temporary satellite captures, as shown by numerical
integrations (Carusi et al. 1981): an analytical theory able to
handle these cases would be much more complex than the one presented in
this paper.
.
In these cases
the interaction may become extremely complex, possibly including
temporary satellite captures, as shown by numerical
integrations (Carusi et al. 1981): an analytical theory able to
handle these cases would be much more complex than the one presented in
this paper.
The orbital period of the planet is ![]() ,
and that of the small body
after the encounter is
,
and that of the small body
after the encounter is
![]() .
If the two periods are
commensurable, that is
a'3/2=k/h with h and k integers, then
after h periods of the asteroid k periods of the planet have
elapsed, and both the planet and the small body will be back again in
the same position of the previous encounter. Such a subsequent encounter
is called a resonant return.
.
If the two periods are
commensurable, that is
a'3/2=k/h with h and k integers, then
after h periods of the asteroid k periods of the planet have
elapsed, and both the planet and the small body will be back again in
the same position of the previous encounter. Such a subsequent encounter
is called a resonant return.
Also if the ratio of the period is not exactly k/h, but is close, a subsequent encounter can take place, but the planet will be earlier or later for the encounter than it was at the previous one. The new encounter conditions can be computed as follows.
We are now going to compute the post-encounter propagation by
using Keplerian heliocentric motion, in order to be able to derive
simple analytical expressions. This approximation turns out to be
sufficiently accurate to discuss the timing, that is the ![]() coordinate, of the next encounter, but not to determine the MOID, that
is the
coordinate, of the next encounter, but not to determine the MOID, that
is the ![]() coordinate. This is further discussed in Sect. 4.4.
coordinate. This is further discussed in Sect. 4.4.
If the small body follows, after the first encounter, a Keplerian
orbit, it will be again at the same node at time
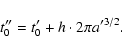
![\begin{displaymath}\delta Y_0 = -\left[{\rm mod}\left(t''_0-t'_0+\pi,2\pi\right)-\pi\right].
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img98.gif)
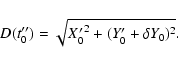
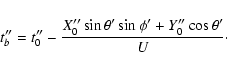
![\begin{displaymath}\left[\begin{array}{c} \xi'' \\ \zeta'' \end{array}\right]
=\...
...X''_0\cos\theta'\sin\phi'-Y''_0\sin\theta' \end{array}\right].
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img105.gif)
In order to exploit the simple geometry in the b-plane of the solutions of this problem, we discuss it in the framework of classical Öpik's theory disregarding the corrections due to the fact that the heliocentric distance of the small body at close encounter is not 1 (see Appendix A.1).
A given resonance corresponds to certain specific values of a', i.e.
of ![]() ,
that we denote with a'0 and
,
that we denote with a'0 and ![]() .
In fact, if
we constrain the post encounter orbit in such a way that the ratio of
the periods is k/h, then
.
In fact, if
we constrain the post encounter orbit in such a way that the ratio of
the periods is k/h, then
![\begin{displaymath}a'_0 = \sqrt[3]{\frac{k^2}{h^2}} \end{displaymath}](/articles/aa/full/2003/36/aa2023/img107.gif)
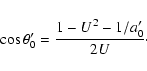
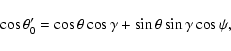
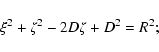
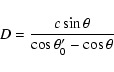
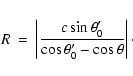
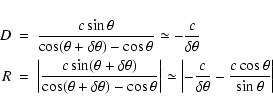
In general, the circle intersects the ![]() -axis at the values
-axis at the values
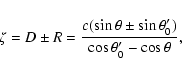
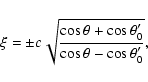
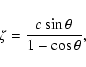
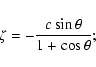
To take now into account at first order the non zero
planetocentric distance of the small body, we compute from ![]() and
and ![]() the pre-encounter heliocentric distance
the pre-encounter heliocentric distance
![]() :
:
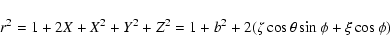
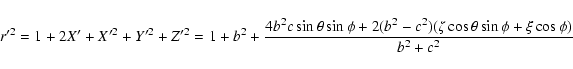
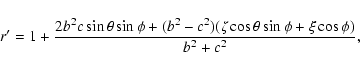
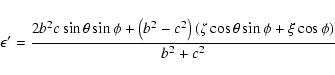
![\begin{displaymath}\epsilon'-\epsilon = \frac{2c[b^2\sin\theta\sin\phi
-c\left(\zeta\cos\theta\sin\phi+\xi\cos\phi\right)]}{b^2+c^2}\cdot
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img142.gif)
Given a, e, i, ![]() ,
we have for
,
we have for
![]() and
and
![]() ,
the values of U and
,
the values of U and
![]() computed for finite
computed for finite ![]() (see Appendix A.1):
(see Appendix A.1):
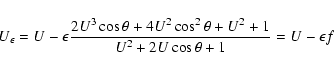
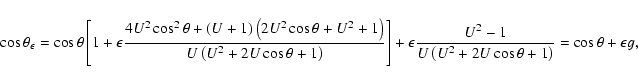
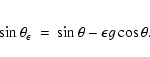
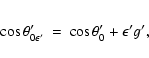
By replacing in Eq. (7) ![]() with
with
![]() and
and ![]() with
with
![]()
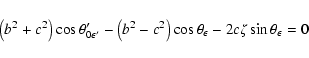
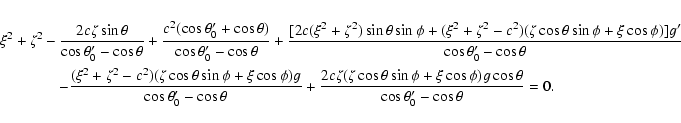
An important advantage of an analytical, albeit approximate, theory of planetary close encounters is that it gives us a key to understand how a given region on the b-plane of an encounter is mapped on the b-plane of the next encounter.
To this end, let us examine the derivatives of the coordinates ![]() ,
,
![]() on the pre-encounter b-plane of the second
encounter. They are functions of the pre-encounter coordinates
on the pre-encounter b-plane of the second
encounter. They are functions of the pre-encounter coordinates ![]() ,
,
![]() on the b-plane of the first encounter (see
Appendix A.4).
on the b-plane of the first encounter (see
Appendix A.4).
In particular, let us consider the case in which the encounters are
not too close, that is encounters for which
![]() .
This is not
too much of a limiting choice: e.g., let us consider the well-known
encounters with the Earth of 1997 XF11 in 2028 and of
1999 AN10 in 2027. For 1997 XF11,
.
This is not
too much of a limiting choice: e.g., let us consider the well-known
encounters with the Earth of 1997 XF11 in 2028 and of
1999 AN10 in 2027. For 1997 XF11,
![]() ,
and the local MOID is 0.000 19 AU, so that
in the worst case
,
and the local MOID is 0.000 19 AU, so that
in the worst case
![]() ,
,
![]() ,
while for
1999 AN10,
,
while for
1999 AN10,
![]() ,
and the local MOID is
0.000 25 AU, so that in the worst case
,
and the local MOID is
0.000 25 AU, so that in the worst case
![]() ,
,
![]() .
Thus, for both encounters the approximation
neglecting c2/b2 is justified, and we can use the approximate
expressions given in Appendix A.5. Also neglecting the
terms in
.
Thus, for both encounters the approximation
neglecting c2/b2 is justified, and we can use the approximate
expressions given in Appendix A.5. Also neglecting the
terms in
![]() is justified because of the small value
of c for the terrestrial planets, with the exception of unusually
slow encounters.
is justified because of the small value
of c for the terrestrial planets, with the exception of unusually
slow encounters.
The Jacobian matrix
![]() is computed in two steps, as described in the appendix. The first one
corresponds to the change from
is computed in two steps, as described in the appendix. The first one
corresponds to the change from ![]() to
to
![]() ,
that is
to the first encounter. The second one corresponds to the change from
,
that is
to the first encounter. The second one corresponds to the change from
![]() to
to
![]() ,
the Keplerian
propagation between the encounters; in this step we need to take into
account the dependence of
,
the Keplerian
propagation between the encounters; in this step we need to take into
account the dependence of ![]() ,
the time delay at the second
encounter, on
,
the time delay at the second
encounter, on ![]() ,
that is, on a'. On the contrary, the Keplerian
propagation does not affect the MOID, that is
,
that is, on a'. On the contrary, the Keplerian
propagation does not affect the MOID, that is
![]() .
Hence the
partial derivatives take the form
.
Hence the
partial derivatives take the form
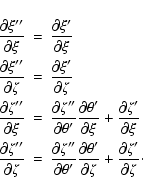
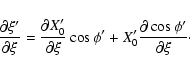
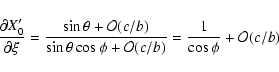
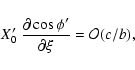
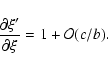
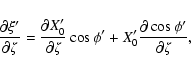
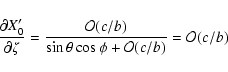
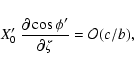
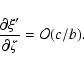
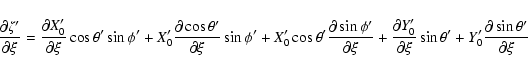
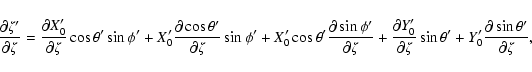
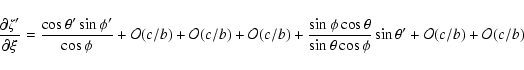
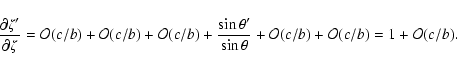
The partial derivatives of ![]() are
(disregarding terms in
are
(disregarding terms in ![]() )
)
The divergence of nearby orbits, having different a', is linear in time. However, sequences of encounters result in multiplicative accumulation of the divergence from each encounter, and thus lead to exponential divergence and chaos, with the maximum Lyapounov exponent proportional to encounter frequency.
As the expressions for
![]() and
and
![]() show,
the increase of the separation of initially
nearby particles on the b-plane of the next encounter
contains the factor
show,
the increase of the separation of initially
nearby particles on the b-plane of the next encounter
contains the factor
![]() ,
defined in
Eqs. (10) and (11), given by (disregarding terms in
,
defined in
Eqs. (10) and (11), given by (disregarding terms in ![]() ):
):
![\begin{displaymath}s(U',\theta')=
\frac{2\pi a'^{5/2}\left[U'\cos^2\theta'+\cos\...
...right]}
{\left(1-U'^2-2U'\cos\theta'\right)^{5/2}\sin\theta'};
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img198.gif)
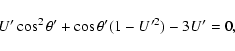
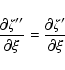
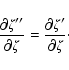
The term keyhole was introduced by Chodas (1999) to denote the small regions of the b-plane of a specific close encounter such that, if the asteroid passes through one of them, it will hit the planet at a subsequent return. That is, a keyhole is simply one of the possible pre-images of the Earth's cross section on the b-plane. The term keyhole may also be used to indicate a region on the b-plane leading not necessarily to collision, but to a very deep encounter. Thus, a keyhole is linked to a specific value of the post-encounter semimajor axis a', i.e., to the value allowing the occurrence of the next encounter at the given date.
We have seen in this section how to solve for a given
value of a', and have discussed the structure of the b-plane
circles corresponding to a given a'. However, the algorithm we use
includes a Keplerian propagation between encounters, thus
only concerns the timing of the next encounter, i.e., the value of
the ![]() -coordinate, but leaves unchanged the MOID of the next
encounter, i.e., the
-coordinate, but leaves unchanged the MOID of the next
encounter, i.e., the ![]() -coordinate.
-coordinate.
In fact, the MOID is bound to vary between encounters for two main
reasons: on a long time scale, secular perturbations (Gronchi &
Milani 2001) make it slowly evolve through the so-called Kozai
cycle, or ![]() -cycle, while on a shorter time scale significant
quasi-periodic variations are caused by planetary perturbations and,
for planets with massive satellites, by the displacement of the planet
with respect to the center of mass of the planet-satellite system.
Figure 4 shows the situation for asteroid 1997 XF11from a precise numerical integration. Large short-period variations
superimposed on the secular trend are evident, and these make an
analytical modeling of the variation of the MOID problematic.
-cycle, while on a shorter time scale significant
quasi-periodic variations are caused by planetary perturbations and,
for planets with massive satellites, by the displacement of the planet
with respect to the center of mass of the planet-satellite system.
Figure 4 shows the situation for asteroid 1997 XF11from a precise numerical integration. Large short-period variations
superimposed on the secular trend are evident, and these make an
analytical modeling of the variation of the MOID problematic.
For the purpose of obtaining the size and shape of an impact
keyhole we can, however, just model the secular variation of the
MOID as a linear term affecting ![]()
![\begin{figure}
\par\includegraphics[width=12cm,clip]{ms2023f4.eps}
\end{figure}](/articles/aa/full/2003/36/aa2023/Timg207.gif) |
Figure 4: Time variation of the nodal distance and of the MOID with respect to the Earth for 1997 XF11. |
| Open with DEXTER | |
The actual keyhole computation proceeds as follows. We want to
compute the pre-image of the point of coordinates ![]() ,
,
![]() ,
lying on the b-plane of the next encounter, that takes place h revolutions of the small body after the current encounter,
on the b-plane of the latter. We start by computing the images of two points with coordinates
,
lying on the b-plane of the next encounter, that takes place h revolutions of the small body after the current encounter,
on the b-plane of the latter. We start by computing the images of two points with coordinates ![]() ,
,
![]() and
and ![]() ,
,
![]() ,
say
,
say ![]() ,
,
![]() and
and ![]() ,
,
![]() ;
furthermore, we choose
;
furthermore, we choose ![]() and
and ![]() such that
such that
![]() .
Note that
.
Note that ![]() is in general slightly different from
is in general slightly different from ![]() ,
but by a very small amount, since in the approximation (13)
,
but by a very small amount, since in the approximation (13)
![]() is a slowly varying function of
is a slowly varying function of ![]() .
We then check whether
.
We then check whether
![]() ;
if not, we choose another pair of values for
;
if not, we choose another pair of values for
![]() and
and ![]() ,
until the condition is verified. In practice,
the segment parallel to the
,
until the condition is verified. In practice,
the segment parallel to the ![]() -axis needs to straddle one of the
resonant return circles. At this point, we find the pre-image of a
point with
-axis needs to straddle one of the
resonant return circles. At this point, we find the pre-image of a
point with ![]() ,
by using, for instance, regula falsi
iterations; let us call the coordinates of this point
,
by using, for instance, regula falsi
iterations; let us call the coordinates of this point
![]() ,
and the coordinates of its image
,
and the coordinates of its image
![]() .
If
.
If
![]() ,
where
,
where ![]() is the radius of the Earth
is the radius of the Earth ![]() augmented by the gravitational focusing
augmented by the gravitational focusing
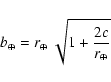
The basis of the above procedure is that, while the "horizontal''
distance on the b-plane (i.e., along ![]() )
remains essentially
unchanged between the two encounters, the "vertical'' one, along
)
remains essentially
unchanged between the two encounters, the "vertical'' one, along ![]() ,
is stretched by a large factor that, as seen in the
preceding subsection, comes almost entirely from the propagation
between the encounters. Therefore, the "pre-image'' of the Earth
on the b-plane of the encounter preceding the collision must
resemble a thickened arclet closely following the shape of the circle
corresponding to the suitable orbital period; the smallness of
the impact keyholes is mainly due to the non-area-preserving
nature of the propagation between encounters, i.e. to the large
values that can be reached by
,
is stretched by a large factor that, as seen in the
preceding subsection, comes almost entirely from the propagation
between the encounters. Therefore, the "pre-image'' of the Earth
on the b-plane of the encounter preceding the collision must
resemble a thickened arclet closely following the shape of the circle
corresponding to the suitable orbital period; the smallness of
the impact keyholes is mainly due to the non-area-preserving
nature of the propagation between encounters, i.e. to the large
values that can be reached by
![]() and
and
![]() .
.
To test the theory described in the previous Sections, we apply it to the two already mentioned cases of the encounters with the Earth of 1997 XF11 in 2028 and of 1999 AN10 in 2027; let us start from the latter.
The encounters of a rather large number of "virtual''
1999 AN10's (fictitious asteroids with orbits compatible
with the observational record available in March 1999) were
analyzed by Milani et al. (1999), using a realistic
gravitational model; around the date of closest approach (7 August 2027), the virtual asteroids have spread into a very thin
and long wire extending over a good fraction of an AU. Actually,
all the virtual 1999 AN10's at that time occupy a very small
region of
![]() space, but the small
differences in a have accumulated into a substantial spreading
in the mean anomaly, similar to what happens in the along-track
dispersion of meteoroids in streams.
space, but the small
differences in a have accumulated into a substantial spreading
in the mean anomaly, similar to what happens in the along-track
dispersion of meteoroids in streams.
We model the wire as a very large number of particles all sharing
the same values of a, e, i - such that U=0.884,
![]() ,
,
![]() - the same MOID of
0.000246 AU, so that
- the same MOID of
0.000246 AU, so that
![]() ,
and differing only in
the time of closest approach; this means that the wire, in the
b-plane, is just a segment parallel to the
,
and differing only in
the time of closest approach; this means that the wire, in the
b-plane, is just a segment parallel to the ![]() -axis that
extends to
-axis that
extends to
![]() .
.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{ms2023f5.eps}
\end{figure}](/articles/aa/full/2003/36/aa2023/Timg236.gif) |
Figure 5:
The outcomes, computed with the extended Öpik theory, of
the August 2027 encounter with the Earth of asteroid 1999AN10.
Left: final states in the a-e plane (a circle marks the
pre-encounter orbit); right: final states in the plane |
| Open with DEXTER | |
Figure 5 shows the post-encounter parameters of the
virtual asteroids; its left panel shows the situation in the a-eplane, and has to be compared with Fig. 2 of Milani et al. (2000c), while the right panel shows the plane ![]() (difference in time from closest approach) vs. P (post-encounter
orbital period), and has to be compared with Fig. 1 of Milani et al. (1999); in this panel we have also traced the same
inclined lines of the corresponding figure of Milani et al. (1999). These lines show the
conditions to encounter the Earth at
(difference in time from closest approach) vs. P (post-encounter
orbital period), and has to be compared with Fig. 1 of Milani et al. (1999); in this panel we have also traced the same
inclined lines of the corresponding figure of Milani et al. (1999). These lines show the
conditions to encounter the Earth at
![]() in, from right to
left, 2040, 2038, 2036, 2034, 2039 and 2032/2037 (the two leftmost
lines, crossing on the
in, from right to
left, 2040, 2038, 2036, 2034, 2039 and 2032/2037 (the two leftmost
lines, crossing on the
![]() axis). The encounters
correspond to resonant returns due to, respectively, the 7/13, 6/11,
5/9, 4/7, 7/12 and 3/5 mean motion resonances; the 3/5 resonance
appears twice, with the two curves on the left crossing each other,
corresponding to returns in 2037 (the less inclined one) and 2032.
axis). The encounters
correspond to resonant returns due to, respectively, the 7/13, 6/11,
5/9, 4/7, 7/12 and 3/5 mean motion resonances; the 3/5 resonance
appears twice, with the two curves on the left crossing each other,
corresponding to returns in 2037 (the less inclined one) and 2032.
The comparison of the two panels of the figure with the corresponding figures of Milani et al. (1999, 2000c) shows that the basic phenomenology of the behaviour of the virtual asteroids wire is well reproduced. Careful inspection of the figures reveals that some details are different. According to Fig. 5, some virtual asteroids can reach the 3/5 resonance, but this possibility was excluded by the computations of Milani et al. This is due, of course, to the inherent approximations taken in the analytic theory, which complements, but cannot fully replace the much more realistic and detailed numerical computations.
Figure 6 refers again to the August 2027 encounter of 1999AN10. In it, the dotted lines show the circles corresponding to the mean motion resonances 7/13, 10/17, and 11/19, leading to returns in 2040, 2044, and 2046, respectively. Close to each circle, the full lines show the keyholes leading to encounters within 4 Earth radii at each resonant return.
The reason why there are two keyholes for each resonant circle is
that, to have an encounter within a very small distance, say
![]() ,
at a specified date, two conditions must be met, since
both
,
at a specified date, two conditions must be met, since
both ![]() and
and ![]() ,
the b-plane coordinates at the next
encounter, must be small. The vicinity to the resonant circle takes
care of
,
the b-plane coordinates at the next
encounter, must be small. The vicinity to the resonant circle takes
care of ![]() ,
and Eq. (13) gives the condition on
,
and Eq. (13) gives the condition on ![]() at the previous encounter in order to have
at the previous encounter in order to have ![]() small; the latter
condition forces the keyholes not to be symmetric with respect to the
small; the latter
condition forces the keyholes not to be symmetric with respect to the
![]() -axis. Then, the keyholes are near the intersections of a
strip, of width approximately equal to
-axis. Then, the keyholes are near the intersections of a
strip, of width approximately equal to
![]() ,
parallel to the
,
parallel to the
![]() -axis, with the given resonant circle; in most cases there are
either two intersections or none.
-axis, with the given resonant circle; in most cases there are
either two intersections or none.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{ms2023f6.eps}
\end{figure}](/articles/aa/full/2003/36/aa2023/Timg238.gif) |
Figure 6:
The dotted lines show the circles, in the b-plane of the
August 2027 encounter with the Earth of 1999 AN10, corresponding
to the mean motion resonances 7/13 (upper circle), 10/17 (smaller of
the two lower circles), 11/19; these resonances lead to returns in
2040, 2044, 2046. The units for the b-plane coordinates |
| Open with DEXTER | |
The vertical segment in Fig. 6 represents the
wire of virtual asteroids at the encounter. As it can be easily
seen, the ranges in ![]() spanned by the keyholes leading to
encounters within 4 Earth radii in 2040, 2044 and 2046 are so
large that these encounters could take place even if the MOID at
the epoch of the 2027 encounter differed by several Earth radii
from that of the real 1999 AN10; this is not true only in the
case of the 2040 encounter, corresponding to the smallest circle
of Fig. 6, since in that case an increase of the MOID
of about 1 Earth radius is already sufficient to prevent the
intersection of the wire with the resonant circle.
spanned by the keyholes leading to
encounters within 4 Earth radii in 2040, 2044 and 2046 are so
large that these encounters could take place even if the MOID at
the epoch of the 2027 encounter differed by several Earth radii
from that of the real 1999 AN10; this is not true only in the
case of the 2040 encounter, corresponding to the smallest circle
of Fig. 6, since in that case an increase of the MOID
of about 1 Earth radius is already sufficient to prevent the
intersection of the wire with the resonant circle.
Let us now see how the extension of Öpik's theory described in this
paper allows us to trace the contours of collision keyholes. To this
purpose, let us examine the October 2028 encounter of 1997 XF11;
for this asteroid, U=0.459,
![]() and
and
![]() .
The pre-images of the Earth for a collision at a resonant return in 2040, are shown in Fig. 7; there are again two keyholes,
whose shape has been computed disregarding in
.
The pre-images of the Earth for a collision at a resonant return in 2040, are shown in Fig. 7; there are again two keyholes,
whose shape has been computed disregarding in
![]() and
and
![]() the smaller terms of first order in
the smaller terms of first order in ![]() ,
,
![]() (see
Appendix A.4).
(see
Appendix A.4).
![\begin{figure}
\par\includegraphics[width=12cm,clip]{ms2023f7.eps}
\end{figure}](/articles/aa/full/2003/36/aa2023/Timg241.gif) |
Figure 7: Keyholes, in the b-plane of the October 2028 encounter with the Earth of 1997 XF11, for collision at the resonant return in 2040; units for the coordinates are Earth radii. Upper left: keyhole nearer to the Earth, with the latter shown to scale for comparison (the gravitational focusing is here about 30%); upper right: keyhole farther from the Earth; lower left and lower right: enlargements of, respectively, the near and far keyholes shown in the corresponding upper panels. The resonant circle corresponding to the exact resonance is drawn with dots. |
| Open with DEXTER | |
Both keyholes span, in ![]() ,
roughly the diameter of the Earth
augmented by the gravitational focusing; it is in
,
roughly the diameter of the Earth
augmented by the gravitational focusing; it is in ![]() that a great
compression is noticeable. This compression, so to speak, is
necessary to compensate for the divergence between nearby trajectories
due to the Keplerian propagation (see Sect. 4.3). The
divergence is by a factor between 2 200 and 2 600 for the keyhole
nearer to the Earth, and by a factor of about 120 for the other
one, whose total area is thus much larger. As already remarked, the
result of the large compression in
that a great
compression is noticeable. This compression, so to speak, is
necessary to compensate for the divergence between nearby trajectories
due to the Keplerian propagation (see Sect. 4.3). The
divergence is by a factor between 2 200 and 2 600 for the keyhole
nearer to the Earth, and by a factor of about 120 for the other
one, whose total area is thus much larger. As already remarked, the
result of the large compression in ![]() is that the shape of a
collision keyhole closely follows the resonant circle to which it is
associated, thus looking like an arclet whose thickness is determined
by the derivative
is that the shape of a
collision keyhole closely follows the resonant circle to which it is
associated, thus looking like an arclet whose thickness is determined
by the derivative
![]() .
.
In Fig. 7 it is easily visible that the keyhole farthest
from the Earth is somewhat displaced from the resonant circle. This is
because the exact resonance corresponds to the circle and the return
does not take place at the resonance, but at a slightly different
value of a to compensate for the non zero value of ![]() at the
first encounter.
at the
first encounter.
Note also that this figure has been traced ignoring the correction due
to heliocentric distance of the encounter not being exactly 1 (i.e.,
due to
![]() ); however, we have checked that the terms of
the first order in
); however, we have checked that the terms of
the first order in ![]() would displace the position of the
resonant return with respect to the circle of Eq. (8) by
about 1% of the distance to the Earth.
would displace the position of the
resonant return with respect to the circle of Eq. (8) by
about 1% of the distance to the Earth.
Finally, a numerical integration, done with the software described in
Milani et al. (1999, 2000c), shows that nearby
trajectories actually diverge by a factor 134 between 2028 and 2040:
as we have just seen, the extended Öpik gives for the corresponding
derivative (
![]() )
a value of about 120;
this agreement, to within about 10%, is quite satisfactory, given the
approximations involved.
)
a value of about 120;
this agreement, to within about 10%, is quite satisfactory, given the
approximations involved.
When the MOID (i.e. ![]() )
of the orbit of a small body encountering
a planet is nearly equal the to radius R of the circle corresponding
to a given return, there are interesting consequences if also the value
of
)
of the orbit of a small body encountering
a planet is nearly equal the to radius R of the circle corresponding
to a given return, there are interesting consequences if also the value
of ![]() is close to the coordinate D of the center of the circle.
When this is the case, we must distinguish between two possibilities,
is close to the coordinate D of the center of the circle.
When this is the case, we must distinguish between two possibilities,
![]() ,
and
,
and ![]() ;
to discuss them, we will again make use of
the same type of "wire'' approximation used to discuss the previous
examples.
;
to discuss them, we will again make use of
the same type of "wire'' approximation used to discuss the previous
examples.
In the first case, ![]() ,
we have that the portion of the
wire for which
,
we have that the portion of the
wire for which
![]() is close to the resonance that
leads to the return of interest, but remains always on the same side
of the resonance itself; as a consequence, in the b-plane of
the next encounter the wire cannot straddle the
is close to the resonance that
leads to the return of interest, but remains always on the same side
of the resonance itself; as a consequence, in the b-plane of
the next encounter the wire cannot straddle the ![]() -axis, but
has to bend and leave the vicinity of the planet from the same
side from which it has approached it. This is the case of
interrupted returns discussed by Milani et al. (2000cFig. 7).
-axis, but
has to bend and leave the vicinity of the planet from the same
side from which it has approached it. This is the case of
interrupted returns discussed by Milani et al. (2000cFig. 7).
In the second case, when ![]() ,
we have interesting
consequences for the portion of the wire for which
,
we have interesting
consequences for the portion of the wire for which
![]() .
In this case, we can have a keyhole rather
different from those discussed previously, and Fig. 8
illustrates an example obtained by suitably modifying the initial
conditions leading to the two collision keyholes of 1997 XF11
discussed previously.
.
In this case, we can have a keyhole rather
different from those discussed previously, and Fig. 8
illustrates an example obtained by suitably modifying the initial
conditions leading to the two collision keyholes of 1997 XF11
discussed previously.
![\begin{figure}
\par\includegraphics[width=12cm]{ms2023f8.eps}
\end{figure}](/articles/aa/full/2003/36/aa2023/Timg246.gif) |
Figure 8: Keyhole, in the b-plane of the October 2028 encounter with the Earth of 1997 XF11, for collision at the resonant return in 2040; units for the coordinates are Earth radii. The initial conditions have been modified with respect to Fig. 7 in order to force the two keyholes of that figure to coalesce into one. Left: overall view; right: enlargement. |
| Open with DEXTER | |
On one hand, there is just one keyhole, as the wire is not
crossing the circle, but nearly tangent to it; on the other
hand, in this keyhole the divergence of orbits along ![]() is
much smaller than in the other cases.
is
much smaller than in the other cases.
To understand this, let us consider Eq. (11), giving
![]() ;
in it, the term
;
in it, the term
![]() passes through zero at
the tangency of the resonant circle, implying that also the
largest term in
passes through zero at
the tangency of the resonant circle, implying that also the
largest term in
![]() passes through
zero, while the remaining term,
passes through
zero, while the remaining term,
![]() ,
is
close to 1; this means that, somewhere in the vicinity, the entire
derivative
,
is
close to 1; this means that, somewhere in the vicinity, the entire
derivative
![]() is null, or very small,
with the consequence that the keyhole can extend substantially in
is null, or very small,
with the consequence that the keyhole can extend substantially in ![]() .
This is clearly visible in Fig. 8, where
the keyhole spans almost 40 Earth radii in
.
This is clearly visible in Fig. 8, where
the keyhole spans almost 40 Earth radii in ![]() ,
and is in
contrast with "normal'' keyholes, like those of
Fig. 7 that, along
,
and is in
contrast with "normal'' keyholes, like those of
Fig. 7 that, along ![]() ,
are thinner than the
b-plane image of the Earth by a large factor (of the order of
,
are thinner than the
b-plane image of the Earth by a large factor (of the order of
![]() that, as we have seen, in those
cases is rather large).
that, as we have seen, in those
cases is rather large).
Concerning ![]() ,
the situation is essentially governed by the
value of
,
the situation is essentially governed by the
value of
![]() that, as is easily
visible from Eq. (10), can be rather large, so that very
small changes in
that, as is easily
visible from Eq. (10), can be rather large, so that very
small changes in ![]() produce large changes
produce large changes ![]() ,
i.e. in the
timing of the next encounter, leading to the very small thickness
visible in Fig. 8.
,
i.e. in the
timing of the next encounter, leading to the very small thickness
visible in Fig. 8.
In these nearly tangent cases, especially if the condition given by Eq. (12) is fulfilled, we may have large keyholes, which represent a new, unsuspected phenomenon. The assessment of their importance for collisions in the solar system goes beyond the scope of the present paper, and is the topic of continuing research.
Acknowledgements
The authors are grateful to A. Carusi and P. Chodas for useful discussions on the subject of this paper, and are particularly indebted to the referee A. Morbidelli, whose constructive criticism led to a significant improvement of the paper. The work described here was completed at the Istituto di Astrofisica Spaziale e Fisica Cosmica of CNR and at the University of Pisa, under a contract with the Italian Space Agency (ASI), and at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration.
The pre-encounter state vector has components (U, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
t0). To compute these components from
the heliocentric elements (a, e, i,
,
t0). To compute these components from
the heliocentric elements (a, e, i, ![]() ,
,
![]() ,
f)
we have to consider where the encounter of interest takes
place.
,
f)
we have to consider where the encounter of interest takes
place.
Let us call
![]() the longitude of the planet at time t0;
then, if at that time
the longitude of the planet at time t0;
then, if at that time ![]() ,
the encounter takes place at the
ascending node, in the post-perihelion branch of the orbit if
,
the encounter takes place at the
ascending node, in the post-perihelion branch of the orbit if
![]() ,
and in the pre-perihelion branch otherwise. If at
time t0 we have
,
and in the pre-perihelion branch otherwise. If at
time t0 we have
![]() ,
the encounter takes place at the
descending node, in the post-perihelion branch of the orbit if
,
the encounter takes place at the
descending node, in the post-perihelion branch of the orbit if
![]() ,
and in the pre-perihelion branch otherwise.
,
and in the pre-perihelion branch otherwise.
Thus, taking (6) into account, and neglecting terms of second
order in the miss distance at the node, that is
![]() ,
at the ascending node we have
,
at the ascending node we have
![\begin{displaymath}\xi = \cos\phi\left[\frac{a(1-e^2)}{1+e\cos\omega}-1\right] \end{displaymath}](/articles/aa/full/2003/36/aa2023/img256.gif)
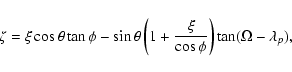
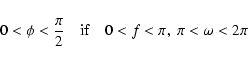
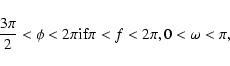
![\begin{displaymath}\xi = \cos\phi\left[\frac{a(1-e^2)}{1-e\cos\omega}-1\right] \end{displaymath}](/articles/aa/full/2003/36/aa2023/img260.gif)
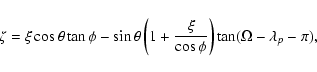
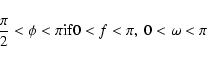
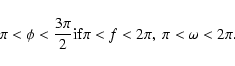
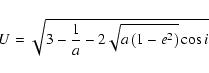
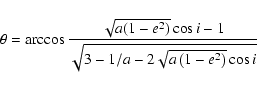
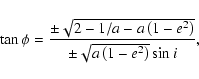
Since
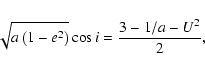
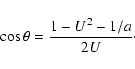
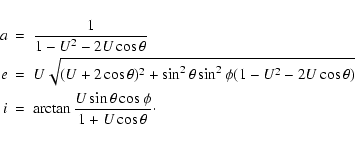
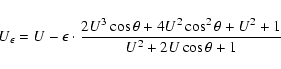
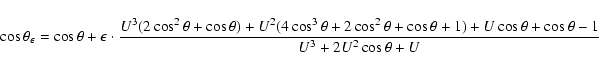
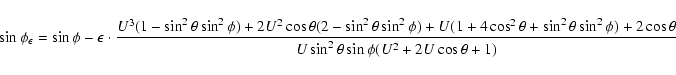
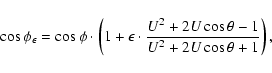
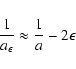
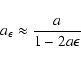
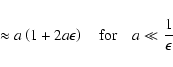
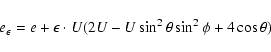
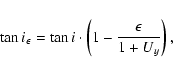
The close encounter can be seen as an operator ![]() that maps the
pre-encounter state vector
that maps the
pre-encounter state vector ![]() ,
with components
,
with components
![]() ,
into the post-encounter one
,
into the post-encounter one ![]() ,
with
components
,
with
components
![]()
![\begin{displaymath}\theta' = \arccos\frac{\left(b^2-c^2\right)\cos\theta+2c\zeta...
...ht)\sin\theta-2c\zeta\cos\theta\right]^2
+4c^2\xi^2}}{b^2+c^2} \end{displaymath}](/articles/aa/full/2003/36/aa2023/img291.gif)
![\begin{displaymath}\phi' = \arccos\frac{\left[\left(b^2-c^2\right)\sin\theta-2c\...
...^2-c^2\right)\sin\theta-2c\zeta\cos\theta\right]^2+4c^2\xi^2}} \end{displaymath}](/articles/aa/full/2003/36/aa2023/img292.gif)
![\begin{displaymath}\xi' = \frac{\left(b^2+c^2\right)\xi\sin\theta}
{\sqrt{\left[...
...^2-c^2\right)\sin\theta-2c\zeta\cos\theta\right]^2+4c^2\xi^2}} \end{displaymath}](/articles/aa/full/2003/36/aa2023/img293.gif)
![\begin{displaymath}\zeta' = \frac{\left(b^2-c^2\right)\zeta\sin\theta-2b^2c\cos\...
...^2-c^2\right)\sin\theta-2c\zeta\cos\theta\right]^2+4c^2\xi^2}} \end{displaymath}](/articles/aa/full/2003/36/aa2023/img294.gif)
![\begin{displaymath}t'_0 = t_0+\frac{2c\left[\xi\sin\phi(2\zeta\cos\theta-\xi\tan...
...
-2c\zeta\cos\theta\right]\cos\phi+2c\xi\sin\phi\right\}}\cdot
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img295.gif)
A purely Keplerian propagation can be seen as an operator
![]() that maps the post-encounter state vector
that maps the post-encounter state vector ![]() in
the pre-next-encounter one
in
the pre-next-encounter one ![]() ,
with components (U'',
,
with components (U'',
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
t''0)
,
t''0)
![\begin{displaymath}\zeta'' = \zeta'
-\left({\rm mod}\left[h\cdot2\pi a'^{3/2}+\pi,2\pi\right]-\pi\right)\sin\theta' \end{displaymath}](/articles/aa/full/2003/36/aa2023/img304.gif)
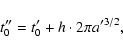
Classical Öpik's theory, which assumes that the position of the
small body coincides with that of the planet, gives
![\begin{displaymath}a' = \frac{b^2+c^2}{\left(b^2+c^2\right)\left(1-U^2\right)
-2...
...[\left(b^2-c^2\right)\cos\theta+2c\zeta\sin\theta\right]}\cdot
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img306.gif)
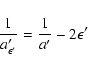
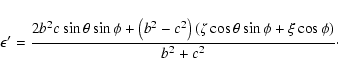
To write the derivatives, let us consider the total evolution
from before the first encounter to before the second as the
composition of the first encounter and of the Keplerian
heliocentric propagation, as seen in the previous subsections
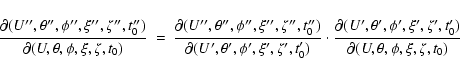
For encounters computed with the extended Öpik theory,
![\begin{displaymath}\frac{\partial(U',\theta',\phi',\xi',\zeta',t'_0)}
{\partial(...
...&
\frac{\partial t'_0}{\partial\zeta} & 1
\end{array}\right],
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img311.gif)
![\begin{displaymath}\frac{\partial(U'',\theta'',\phi'',\xi'',\zeta'',t''_0)}
{\pa...
...
\frac{\partial t''_0}{\partial\zeta'} & 1
\end{array}\right],
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img312.gif)
![\begin{displaymath}\frac{\partial\left(U'',\theta'',\phi'',\xi'',\zeta'',t''_0\r...
...
\frac{\partial t''_0}{\partial\zeta} & 1
\end{array}\right].
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img313.gif)
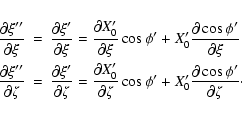
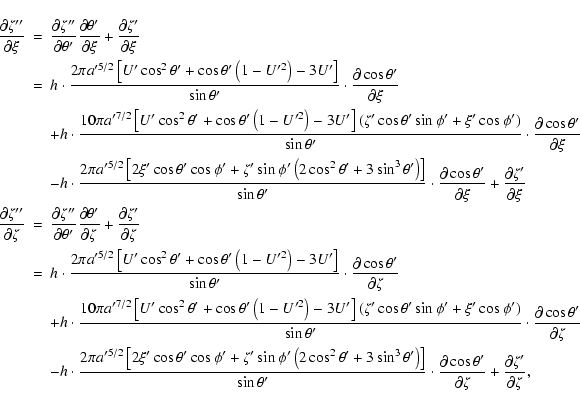
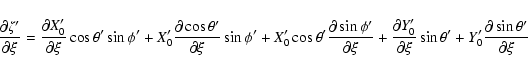
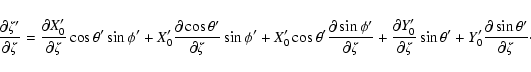
The individual derivatives entering the above expressions are
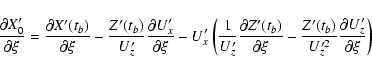
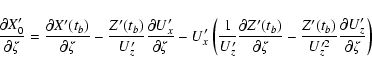
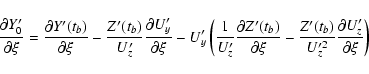
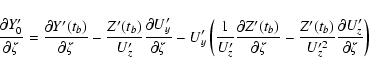
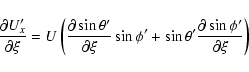
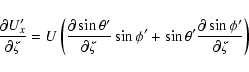
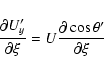
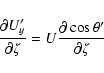
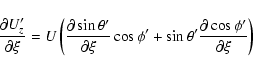
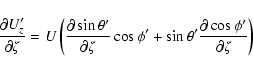
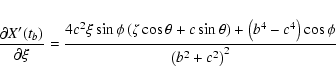
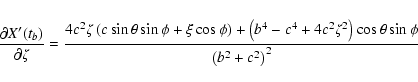
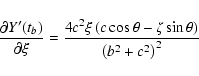
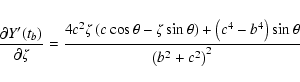

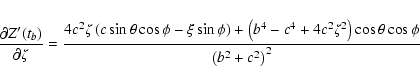
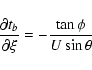
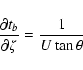
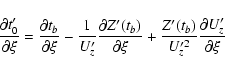
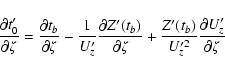
![\begin{displaymath}\frac{\partial a'}{\partial\xi} =
\frac{8Uc\xi\left(c\cos\th...
...t(b^2-c^2\right)\cos\theta+2c\zeta\sin\theta\right]\right\}^2} \end{displaymath}](/articles/aa/full/2003/36/aa2023/img338.gif)
![\begin{displaymath}\frac{\partial a'}{\partial\zeta} =
\frac{8Uc\zeta(c\cos\the...
...t(b^2-c^2\right)\cos\theta+2c\zeta\sin\theta\right]\right\}^2} \end{displaymath}](/articles/aa/full/2003/36/aa2023/img339.gif)
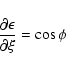
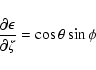
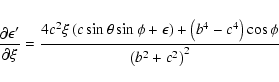
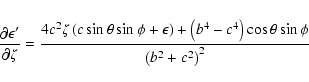
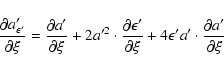
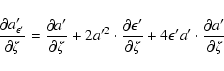
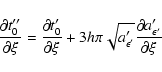
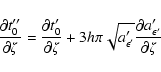
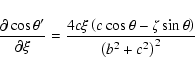
![\begin{displaymath}\frac{\partial\cos\theta'}{\partial\zeta} =
\frac{2c\left[\l...
...\theta-\zeta\sin\theta\right)\right]}
{\left(b^2+c^2\right)^2} \end{displaymath}](/articles/aa/full/2003/36/aa2023/img349.gif)
![\begin{displaymath}\frac{\partial\sin\theta'}{\partial\xi} =
-\frac{\left(b^2-c...
...ht]^2+4c^2\xi^2}}
\cdot\frac{\partial\cos\theta'}{\partial\xi} \end{displaymath}](/articles/aa/full/2003/36/aa2023/img350.gif)
![\begin{displaymath}\frac{\partial\sin\theta'}{\partial\zeta} =
-\frac{\left(b^2...
...]^2+4c^2\xi^2}}
\cdot\frac{\partial\cos\theta'}{\partial\zeta} \end{displaymath}](/articles/aa/full/2003/36/aa2023/img351.gif)
![\begin{eqnarray*}\frac{\partial\cos\phi'}{\partial\xi} & =&
\frac{2\left(\xi\si...
...ight)\sin\theta-2c\zeta\cos\theta\right]^2+4c^2\xi^2\right\}^3}} \end{eqnarray*}](/articles/aa/full/2003/36/aa2023/img352.gif)
![\begin{eqnarray*}\frac{\partial\cos\phi'}{\partial\zeta} & = &
\frac{2\cos\phi\...
...ight)\sin\theta-2c\zeta\cos\theta\right]^2+4c^2\xi^2\right\}^3}} \end{eqnarray*}](/articles/aa/full/2003/36/aa2023/img353.gif)
![\begin{eqnarray*}\frac{\partial\sin\phi'}{\partial\xi} & = &
\frac{2\left(\xi\s...
...ight)\sin\theta-2c\zeta\cos\theta\right]^2+4c^2\xi^2\right\}^3}} \end{eqnarray*}](/articles/aa/full/2003/36/aa2023/img354.gif)
![\begin{eqnarray*}\frac{\partial\sin\phi'}{\partial\zeta} &= &
\frac{2\sin\phi\l...
...\sin\theta-2c\zeta\cos\theta\right]^2+4c^2\xi^2\right\}^3}}\cdot
\end{eqnarray*}](/articles/aa/full/2003/36/aa2023/img355.gif)
When dealing with encounters of NEAs with the terrestrial
planets, we have that in many cases of interest c=m/U2 is very
small. This happens because for these planets
![]() ,
and typical values of U are around 0.5.
On the other hand, for an Earth-encountering asteroid with
,
and typical values of U are around 0.5.
On the other hand, for an Earth-encountering asteroid with
![]() ,
a rather typical value, the minimum value of b
that avoids collision is
,
a rather typical value, the minimum value of b
that avoids collision is
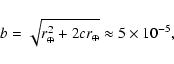
If we can assume
![]() ,
most expressions of this paper can be
approximated by much simpler formulas neglecting
,
most expressions of this paper can be
approximated by much simpler formulas neglecting
![]() terms. We have collected these approximate formulas below.
terms. We have collected these approximate formulas below.
The post-encounter state vector:
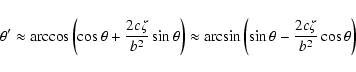
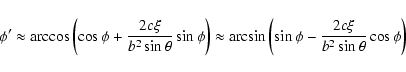
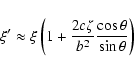
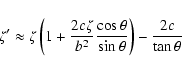
![\begin{displaymath}t'_0 \approx t_0
+\frac{2c\left[\xi\sin\phi\left(2\zeta\cos\t...
...^2\theta+\zeta^2\right)\right]}{Ub^2\sin^2\theta\cos\phi}\cdot
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img364.gif)
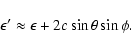
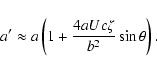
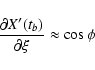
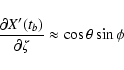
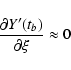
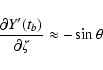
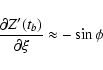
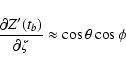
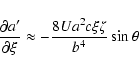
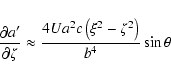
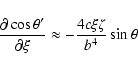
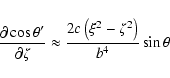
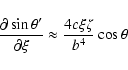
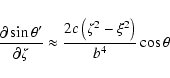
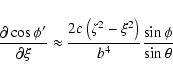
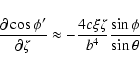
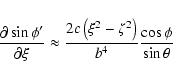

![\begin{displaymath}\frac{\partial X'_0}{\partial\xi} \approx
\frac{1}{\cos\phi}...
...ta\cos\phi-2\xi\zeta\sin\phi\right]}
{b^4\sin\theta\cos^2\phi} \end{displaymath}](/articles/aa/full/2003/36/aa2023/img384.gif)
![\begin{displaymath}\frac{\partial X'_0}{\partial\zeta} \approx
\frac{2c\xi\left...
...ta\cos\phi+2\xi\zeta\sin\phi\right]}
{b^4\sin\theta\cos^2\phi} \end{displaymath}](/articles/aa/full/2003/36/aa2023/img385.gif)
![\begin{displaymath}\frac{\partial Y'_0}{\partial\xi} \approx
\frac{\cos\theta\s...
...\sin^2\phi\right)\cos\theta\right]}{b^4\sin^2\theta\cos^2\phi} \end{displaymath}](/articles/aa/full/2003/36/aa2023/img386.gif)
![\begin{displaymath}\frac{\partial Y'_0}{\partial\zeta} \approx
-\frac{1}{\sin\t...
...2\phi\right)\cos\theta\right]}{b^4\sin^2\theta\cos^2\phi}\cdot
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img387.gif)
Encounters of interplanetary objects with the giant planets are
characterized by values of c larger than in the cases seen before,
because of the large masses of these planets. As an example, the 1779 encounter of D/Lexell with Jupiter was characterized by
![]() ;
considering that b could have been as low as
0.0003 (Le Verrier 1857), we have that for the closest
approach
;
considering that b could have been as low as
0.0003 (Le Verrier 1857), we have that for the closest
approach
![]() ,
a case in which the following simplified
expressions hold.
,
a case in which the following simplified
expressions hold.
Post-encounter state vector:
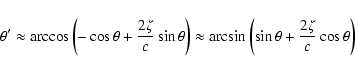
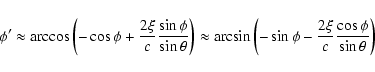
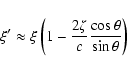
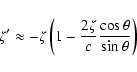
![\begin{displaymath}t'_0 \approx t_0
-\frac{2\left[\xi(2\zeta\cos\theta-\xi\tan\p...
...^2\theta+\zeta^2)\cos\phi\right]}{Uc\sin^2\theta\cos\phi}\cdot
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img394.gif)
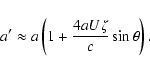
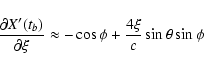
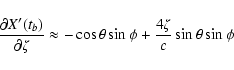
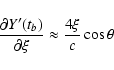
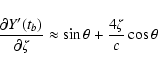
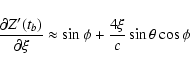
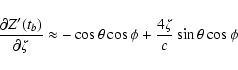
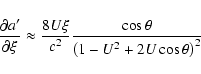
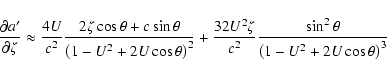
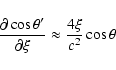
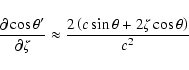
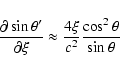
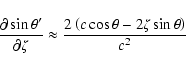
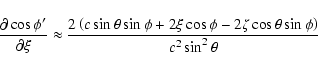
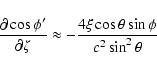
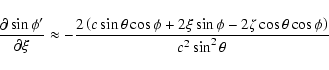
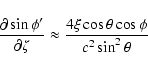
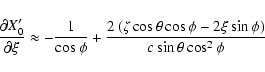
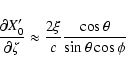
![\begin{displaymath}\frac{\partial Y'_0}{\partial\xi} \approx
-\frac{\cos\theta\...
...phi\right)\cos\theta\sin^2\phi\right]}{c\sin^2\theta\cos^2\phi}\end{displaymath}](/articles/aa/full/2003/36/aa2023/img416.gif)
![\begin{displaymath}\frac{\partial Y'_0}{\partial\zeta} \approx
\frac{1}{\sin\th...
...a\cos\phi\right)\sin\phi\right]}{c\sin^2\theta\cos^2\phi}\cdot
\end{displaymath}](/articles/aa/full/2003/36/aa2023/img417.gif)