A&A 408, 707-713 (2003)
DOI: 10.1051/0004-6361:20030966
The effects of inclination, gravity darkening and differential
rotation on absorption profiles of fast rotators
A. Reiners
Hamburger Sternwarte, Universität Hamburg,
Gojenbergsweg 112, 21029 Hamburg, Germany
Received 6 May 2003 / Accepted 20 June 2003
Abstract
Mechanisms influencing absorption line profiles of fast
rotating stars can be sorted into two groups; (i) intrinsic
variations sensitive to temperature and pressure, and (ii) global
effects common to all spectral lines. I present a detailed study on
the latter effects focusing on gravity darkening and inclination for
various rotational velocities and spectral types. It is shown that
the line shapes of rapidly and rigidly rotating stars mainly depend
on the equatorial velocity  ,
not on the projected
rotational velocity
,
not on the projected
rotational velocity  which determines the lines' widths.
The influence of gravity darkening and spectral type on the line
profiles is shown. The results demonstrate the possibility of
determining the inclination angle i of single fast rotators, and
they show that constraints on gravity darkening can be drawn for
stellar samples. While significant line profile deformation occurs
in stars rotating as fast as
which determines the lines' widths.
The influence of gravity darkening and spectral type on the line
profiles is shown. The results demonstrate the possibility of
determining the inclination angle i of single fast rotators, and
they show that constraints on gravity darkening can be drawn for
stellar samples. While significant line profile deformation occurs
in stars rotating as fast as
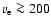 km s-1, for
slower rotators profile distortions are marginal. In these cases
spectral signatures induced by, e.g., differential rotation are not
affected by gravity darkening and the methods applicable to slow
rotators can be applied to these faster rotators, too.
km s-1, for
slower rotators profile distortions are marginal. In these cases
spectral signatures induced by, e.g., differential rotation are not
affected by gravity darkening and the methods applicable to slow
rotators can be applied to these faster rotators, too.
Key words: line: profiles - stars: rotation
1 Introduction
The information contained in line profiles of rotating stars has been
studied since the recognition of spectral Doppler broadening itself.
The multitude of different mechanisms influencing line profiles
presents a confusing picture for the possibility of determining them.
Approximations exist for rotational line broadening, (linear) limb
darkening, differential rotation, turbulence, rotational flattening
and gravity darkening, etc. While distinguishing these interacting
mechanisms is a delicate issue, in the case of slow rotators
(
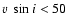 km s-1) rotational flattening and gravity
darkening can be neglected. Utilizing the Fourier transform technique
Gray (1973,1976) also showed that turbulent velocities to some
extent can be distinguished from rotation.
km s-1) rotational flattening and gravity
darkening can be neglected. Utilizing the Fourier transform technique
Gray (1973,1976) also showed that turbulent velocities to some
extent can be distinguished from rotation.
In fast rotators the situation becomes more complex, since centrifugal
forces distort the spherical shape of the stellar surface and the line
profiles depend on the inclination the star is observed under. Beyond
the additional degree of freedom this would not be a major problem if
temperature (and pressure) were not connected to gravity. With
different regions on the stellar surface having significantly
different temperatures and gas pressures, line profiles no longer can
be approximated by convolution between a single intrinsic line profile
and the rotational broadening function. For this reason, the effects
of fast rotation on line profiles often were studied for specific
absorption lines (e.g., Hardorp & Strittmatter 1968; Stoeckley 1968);
Collins & Truax (1995) come to the conclusion that the detection of
secondary effects like limb darkening and differential rotation is
improbable in line profiles of fast rotators.
Under what circumstances the approximation of various broadening
mechanisms by convolutions breaks down, only depends on the
sensitivity of the spectral line on temperature and gas pressure.
Spectral quality in terms of signal-to-noise as well as in wavelength
coverage has improved and makes possible analyses of weak absorption
features. Observers are not restricted to the extremely temperature
and pressure sensitive lines of the lightest elements H and He. Fast
rotation is the rule in stars of spectral types as late as F5, and in
the spectra of fast rotating A- and F-stars a large number of heavy
ion lines exist where the approximation of rotational broadening by a
convolution becomes valid again. Especially the deconvolution of an
"overall'' broadening function inherent in all lines by using the
methods of Least Squares Deconvolution (LSD, e.g., Cameron 2000)
can provide reliable broadening profiles independent of line specific
intrinsic mechanisms.
In this paper the effects of fast rotation are examined in detail
focusing on geometric distortions and gravity darkening on stars
observed under different inclination angles. These effects underly all
spectral lines independent of their intrinsic shape and temperature or
pressure dependencies. The modelled spectra assume no intrinsic
temperature or pressure dependence; whether this can be applied to
specific spectral lines or groups of lines has to be checked
individually.
In Reiners & Schmitt (2002a) the possibility of detecting differential
rotation in line profiles was demonstrated. This paper also answers
the question of whether the technique used there is applicable to fast
rotators, too. It shows what can be learned about gravity darkening and
inclination angle from the shape of stellar absorption line profiles.
2.1 Line-independent broadening
Absorption line profiles observed in fast rotating stars are affected
by three mechanisms inherent in all lines: (a) the projected geometry
of the star, (b) the flux distribution due to temperature variations
(known as gravity darkening) on the rotating stellar surface, and (c)
the rotation law. These three line-independent mechanisms will be
discussed in the following.
Case (a) is well understood, fast rotation diminishes the
gravitational potential at the equator and alters the star's
sphericity. As a consequence, lines of constant projected rotational
velocities no longer lie on chords but are bent (cp.,
e.g., Collins & Truax 1995). Although an analytical description of the
surface velocity distribution is not then available, calculation by
integrating over the stellar surface is unproblematic.
(b) Since the presence of gravity darkening was initially described by
von Zeipel (1924), many publications were written on the correct gravity
dependence of surface temperature. In general, gravity darkening is
described in terms of a parameter  used in the equation
used in the equation
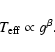 |
(1) |
The "classical'' value of
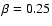 found by von Zeipel (1924) is
valid only for conservative rotation laws in stars without convective
envelopes. A value of
found by von Zeipel (1924) is
valid only for conservative rotation laws in stars without convective
envelopes. A value of
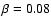 is derived for stars with
convective envelopes (Lucy 1967). Tuominen (1972) approximates a
value of
is derived for stars with
convective envelopes (Lucy 1967). Tuominen (1972) approximates a
value of
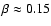 for differentially rotating stars, and
for magnetic stars without convection zones, Smith (1975) reports a
slightly different value of
for differentially rotating stars, and
for magnetic stars without convection zones, Smith (1975) reports a
slightly different value of
 .
The most comprehensive
calculations were carried out by Claret (1998), who provides tables
of stellar parameters including
.
The most comprehensive
calculations were carried out by Claret (1998), who provides tables
of stellar parameters including  for a series of stars at
various evolutionary stages. The calculations are in general agreement
with the cited works; stars of spectral types later than
for a series of stars at
various evolutionary stages. The calculations are in general agreement
with the cited works; stars of spectral types later than  A2
harboring convective envelopes have a value of
A2
harboring convective envelopes have a value of
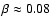 ,
for earlier-type stars,
,
for earlier-type stars,
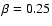 seems a good choice. These
calculations are also consistent with measurements of
seems a good choice. These
calculations are also consistent with measurements of  in
eclipsing binaries carried out by Rafert & Twigg (1980), although a large
scatter appears in the data (cp. Fig. 7 in Claret 1998).
in
eclipsing binaries carried out by Rafert & Twigg (1980), although a large
scatter appears in the data (cp. Fig. 7 in Claret 1998).
(c) Stellar rotation laws are poorly known. Our picture comes from
observations of the Sun, where the angular velocity can be
approximated as
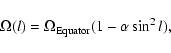 |
(2) |
with l being the latitude and
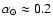 ,
i.e.,
the Equator rotating 20% faster than the Pole as derived from Sun
spots. Differential rotation in stars other than the Sun was claimed
for ten relatively slowly rotating F-type stars with values of
,
i.e.,
the Equator rotating 20% faster than the Pole as derived from Sun
spots. Differential rotation in stars other than the Sun was claimed
for ten relatively slowly rotating F-type stars with values of
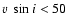 km s-1 in Reiners & Schmitt (2003) adopting
Eq. (2) as the rotation law in analogy to the solar
case. Assuming reasonable values of inclination angles i, the small
projected rotational velocities of the stars in that sample give no
reason to expect effects due to distortions of the gravitational
potential, and differential rotation is thought to be the cause of the
determined profile signatures. It is an open question, to what extent
differential rotation can be detected in faster rotators, where
deformation and gravity darkening become important.
km s-1 in Reiners & Schmitt (2003) adopting
Eq. (2) as the rotation law in analogy to the solar
case. Assuming reasonable values of inclination angles i, the small
projected rotational velocities of the stars in that sample give no
reason to expect effects due to distortions of the gravitational
potential, and differential rotation is thought to be the cause of the
determined profile signatures. It is an open question, to what extent
differential rotation can be detected in faster rotators, where
deformation and gravity darkening become important.
Stellar line profiles are subject to a number of different mechanisms
affecting their shape. Besides the mentioned effects of gravity
darkening and rotation law, limb darkening, additional (turbulent)
velocity fields and stellar surface structure like spots can
significantly contribute to the line profiles' shape. Utilizing the
Fourier transform turns out to be of great advantage in disentangling
the different effects. When approximating line broadening by
convolutions, their interaction can be studied most easily using
Fourier transforms, since the computationally complicated convolutions
become multiplications in Fourier domain (cf., e.g., Gray 1976).
Reiners & Schmitt (2002a) utilized the zeros of the Fourier transformed line
profiles to search for the subtle effects of differential rotation.
They showed that the ratio of the first two zeros q1 and q2 is a
direct indicator for solar-like - i.e., Equator faster than Pole -
differential rotation (
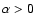 in Eq. (2)). The
value of the ratio
q2/q1 is extremely sensitive to the
profile's shape, and is unaffected by the "standard'' turbulent
velocity fields like micro- and macroturbulence even for rotational
velocities as low as 10 km s-1. Using a linear limb darkening
law with a parameter
in Eq. (2)). The
value of the ratio
q2/q1 is extremely sensitive to the
profile's shape, and is unaffected by the "standard'' turbulent
velocity fields like micro- and macroturbulence even for rotational
velocities as low as 10 km s-1. Using a linear limb darkening
law with a parameter 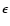 ,
in a rigidly rotating star the value
of
q2/q1 can be approximated as
,
in a rigidly rotating star the value
of
q2/q1 can be approximated as
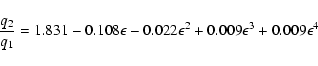 |
(3) |
(Dravins et al. 1990). Thus for a rigid rotator the value of
q2/q1is always between 1.72 and 1.83 regardless of the limb darkening coefficient.
Differential rotation significantly diminishes this ratio
(cf Reiners & Schmitt 2002a), while polar spots lead to an increase
(Reiners & Schmitt 2002b).
Since the ratio
q2/q1 turns out to be an easily accessible
parameter characteristic for the line's shape, I continue to use it
for studying the influence of gravity darkening in rapidly rotating
stars. For a more detailed discussion of the correlations between
differential rotation 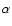 ,
the inclination angle i and
q2/q1 see Reiners & Schmitt (2002a,2003).
,
the inclination angle i and
q2/q1 see Reiners & Schmitt (2002a,2003).
The approach of this paper is to study the effects of fast rotation
universal for all absorption lines. Line specific dependencies on gas
pressure, ionization stages, etc. are not taken into account. This
approach is especially suited for studies incorporating different
lines of similar (preferably heavy) ions, e.g., with LSD methods. For
heavy ions pressure broadening is not expected to play a major role
compared to the dominant rotational broadening. For light elements
like H and He, this is not true and great care has to be take when
applying the methods to them. Although the Lorentzian profiles induced
by pressure broadening should not add additional zeros to the line
profile Fourier transforms (cp. Heinzel 1978), errors from
approximating line broadening effects by convolutions may become
significant in these cases.
The calculations were done using a modified version of the package
developed and described by Townsend (1997). Surface integration is
carried out over 25 500 visible surface elements scaling the flux
with temperature according to a Planck law. A Gaussian profile was
used as the input function, since the large rotational velocities make
the shape of the input function unimportant. For all cases the same
input function was used regardless of gravity and temperature. To
measure the zeros in Fourier transformed line profiles the accuracy
must be higher for the faster rotators; 32 768 points were used in
the transform algorithm for values of
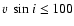 km s-1, 65 536 points for values of
km s-1, 65 536 points for values of  between
100 and 200 km s-1, and 131 072 points for
between
100 and 200 km s-1, and 131 072 points for
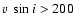 km s-1. Thus the sampling error in
q2/q1 does not
exceed a value of 0.01 for all calculations.
km s-1. Thus the sampling error in
q2/q1 does not
exceed a value of 0.01 for all calculations.
Broadening profiles are calculated and the values of
q2/q1determined for four stellar models with polar effective temperature
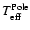 and mass given in columns two and three in
Table 1. A grid is computed in three values of
and mass given in columns two and three in
Table 1. A grid is computed in three values of
 (0.0, 0.08 and 0.25), five values of inclination angle i(10
(0.0, 0.08 and 0.25), five values of inclination angle i(10 ,
30
,
30 ,
50
,
50 ,
70
,
70 and
90
and
90 ), and values of
), and values of  between 50 and
300 km s-1 in steps of 25 km s-1 with the equatorial
velocity
between 50 and
300 km s-1 in steps of 25 km s-1 with the equatorial
velocity
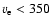 km s-1. Altogether more than 450
models are computed. The dependence of the ratio
q2/q1 on
different parameter choices is analyzed and studied in the following.
km s-1. Altogether more than 450
models are computed. The dependence of the ratio
q2/q1 on
different parameter choices is analyzed and studied in the following.
Table 1:
Parameters of the calculated models,
a and b are parameters used in Eq. (4) with values of
gravity darkening  according to Claret (1998). Note that
for all models profiles with
according to Claret (1998). Note that
for all models profiles with
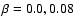 and 0.25 were analyzed.
and 0.25 were analyzed.
![\begin{figure}
\par\resizebox{8.8cm}{!} {\includegraphics[angle=-90,clip]{3947.f1}}
\end{figure}](/articles/aa/full/2003/35/aa3947/Timg32.gif) |
Figure 1:
Derived values of
q2/q1 for a
rigidly rotating F0-type star with
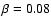 .
Different
symbols indicate inclination angles as indicated in the figure.
The value of
q2/q1 is determined by .
Different
symbols indicate inclination angles as indicated in the figure.
The value of
q2/q1 is determined by  independent of the values of i and
independent of the values of i and  .
The slope is
well approximated by the second order polynomial shown as a solid
line. .
The slope is
well approximated by the second order polynomial shown as a solid
line. |
| Open with DEXTER |
To show the dependence of
q2/q1 on  ,
in
Fig. 1
q2/q1 is plotted vs.
,
in
Fig. 1
q2/q1 is plotted vs.  for the F0 model with a gravity darkening parameter of
for the F0 model with a gravity darkening parameter of
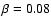 .
The region in
q2/q1 typical for a spherical surface and a
linear limb darkening law with
.
The region in
q2/q1 typical for a spherical surface and a
linear limb darkening law with
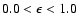 is indicated
with dotted lines (cp. Eq. (3)). Values for stars
seen under various inclination angles are distinguished by different
symbols, all values are in good agreement with the marked polynomial
indicating a smooth decline of
q2/q1 for stars rotating faster
than
is indicated
with dotted lines (cp. Eq. (3)). Values for stars
seen under various inclination angles are distinguished by different
symbols, all values are in good agreement with the marked polynomial
indicating a smooth decline of
q2/q1 for stars rotating faster
than
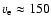 km s-1.
km s-1.
The parameter determining the value of
q2/q1 in a given
stellar model obviously is  ,
independent of the inclination
angle (and thus
,
independent of the inclination
angle (and thus  ). This means, that under the assumption
of rigid rotation, and with assumed values of
). This means, that under the assumption
of rigid rotation, and with assumed values of  ,
in fast
rotators one can in principle obtain the value of
,
in fast
rotators one can in principle obtain the value of  from the
value of
q2/q1, and thus, with the known value of
from the
value of
q2/q1, and thus, with the known value of
 ,
the inclination angle i. I will return to this point
in Sect. 4.3.
,
the inclination angle i. I will return to this point
in Sect. 4.3.
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=7.8cm,clip]{3947.f2a}\...
...ace{1cm}
\includegraphics[angle=-90,width=7.8cm,clip]{3947.f2d} }
\end{figure}](/articles/aa/full/2003/35/aa3947/Timg35.gif) |
Figure 2:
Derived values of
q2/q1 vs. equatorial
velocity  for four different stellar models (B0, A0, F0
and G0). For each model different values of the gravity
darkening parameter
for four different stellar models (B0, A0, F0
and G0). For each model different values of the gravity
darkening parameter  (0.0, 0.08 and 0.25) are indicated
using different symbols. The dependence of
q2/q1 on
(0.0, 0.08 and 0.25) are indicated
using different symbols. The dependence of
q2/q1 on
 differs for the different cases but is monotonic in
differs for the different cases but is monotonic in
 and
and  . . |
| Open with DEXTER |
In the four panels of Fig. 2 the derived values of
q2/q1 are plotted vs.  for the models of spectral
types B0, A0, F0 and G0 as specified in Table 1.
In each panel calculations for three different values of
for the models of spectral
types B0, A0, F0 and G0 as specified in Table 1.
In each panel calculations for three different values of  are
shown, the different choices of
are
shown, the different choices of  (0.0, 0.08 and 0.25) are
plotted using different symbols. The slope of
q2/q1 is well
described by a second order polynomial for all cases. The ratio
q2/q1 is diminished in rapid rotators with larger deviations
from the standard value of
q2/q1 = 1.75 the larger the value
of
(0.0, 0.08 and 0.25) are
plotted using different symbols. The slope of
q2/q1 is well
described by a second order polynomial for all cases. The ratio
q2/q1 is diminished in rapid rotators with larger deviations
from the standard value of
q2/q1 = 1.75 the larger the value
of  .
In the A0, F0 and G0 models,
q2/q1 becomes less
than 1.72 for very fast rotators depending on the value of
.
In the A0, F0 and G0 models,
q2/q1 becomes less
than 1.72 for very fast rotators depending on the value of  ,
i.e., deviations from standard line profiles are significant and in
principle observable in these stars.
,
i.e., deviations from standard line profiles are significant and in
principle observable in these stars.
The behavior of
q2/q1 with different values of the gravity
darkening parameter  can be studied in the four panels of
Fig. 2. In the B0 model no value of
q2/q1 <
1.72 appears, but the influence of
can be studied in the four panels of
Fig. 2. In the B0 model no value of
q2/q1 <
1.72 appears, but the influence of  on the ratio
q2/q1grows with later spectral type. In all cases
q2/q1 depends
monotonically on the rotational velocity
on the ratio
q2/q1grows with later spectral type. In all cases
q2/q1 depends
monotonically on the rotational velocity  with diminished
q2/q1 for larger rotational velocities. The result that the
line profiles depend more strongly on the value of
with diminished
q2/q1 for larger rotational velocities. The result that the
line profiles depend more strongly on the value of  for
stars of later spectral types, reflects the fact that the relative
temperature contrast
for
stars of later spectral types, reflects the fact that the relative
temperature contrast
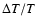 on the stellar surface is larger for
cooler stars, since
on the stellar surface is larger for
cooler stars, since 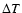 is comparable for similar values of
is comparable for similar values of
 .
Furthermore, for all models no significant variation of
q2/q1 appears for
.
Furthermore, for all models no significant variation of
q2/q1 appears for 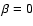 ,
i.e., without gravity darkening
the geometrical deformation does not suffice to significantly change
the shape of the line profiles.
,
i.e., without gravity darkening
the geometrical deformation does not suffice to significantly change
the shape of the line profiles.
In a larger sample of stars of similar spectral types these results
could make it feasible to determine the value of gravity darkening in
terms of the parameter  when plotting
q2/q1 vs.
when plotting
q2/q1 vs.
 .
While for many stars in such a plot the values should
fall below an upper envelope expected from the
q2/q1-
.
While for many stars in such a plot the values should
fall below an upper envelope expected from the
q2/q1- relation (the real values of
relation (the real values of  are larger than the
measured values of
are larger than the
measured values of  ), a clear threshold should mark the
upper envelope indicating the correct value of
), a clear threshold should mark the
upper envelope indicating the correct value of  .
Using a larger
sample of fast rotators of similar spectral types the ratio
q2/q1 could thus be used to determine the values of
.
Using a larger
sample of fast rotators of similar spectral types the ratio
q2/q1 could thus be used to determine the values of  from measurements of single stars.
from measurements of single stars.
4.3 Determination of i
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{3947.f3a}\hspace...
...space*{1cm}
\includegraphics[angle=-90,width=7.8cm,clip]{3947.f3d}
\end{figure}](/articles/aa/full/2003/35/aa3947/Timg40.gif) |
Figure 3:
Stars with measured values of  and
q2/q1 are seen under an inclination angle i. In the four
panels (B0, A0, F0 and G0-type stars) the approximated dependence
of i on the ratio
q2/q1 is shown for values of
and
q2/q1 are seen under an inclination angle i. In the four
panels (B0, A0, F0 and G0-type stars) the approximated dependence
of i on the ratio
q2/q1 is shown for values of
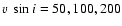 and 300 km s-1 (solid lines,
top to bottom as indicated in the upper left panel). The dashed
line marks the lowest ratio of
q2/q1 consistent with slow
rotation and extreme limb darkening, no values of
q2/q1 >
1.75 are expected.
and 300 km s-1 (solid lines,
top to bottom as indicated in the upper left panel). The dashed
line marks the lowest ratio of
q2/q1 consistent with slow
rotation and extreme limb darkening, no values of
q2/q1 >
1.75 are expected. |
| Open with DEXTER |
The ratio
q2/q1 monotonically depends on equatorial velocity
 and is independent of the inclination angle i. Assuming
a value of
and is independent of the inclination angle i. Assuming
a value of  for a fast rotator of known spectral class, the
equatorial velocity
for a fast rotator of known spectral class, the
equatorial velocity  can thus be determined from a
measurement of
q2/q1. The functions
can thus be determined from a
measurement of
q2/q1. The functions
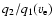 shown in Fig. 2 are approximated by the second order
polynomial
shown in Fig. 2 are approximated by the second order
polynomial
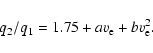 |
(4) |
The parameters a and b for the four models using the most probable
values of the parameter  according to Claret (1998) are given
in Table 1. With Eq. (4) it is
possible to derive the inclination angle i from a standard
measurement of
according to Claret (1998) are given
in Table 1. With Eq. (4) it is
possible to derive the inclination angle i from a standard
measurement of  and the value of
q2/q1.
and the value of
q2/q1.
In each panel of Fig. 3 the values of i are plotted
vs. the ratio
q2/q1 for four different values of  .
As in Fig. 2 each panel represents a stellar model
from Table 1. Functions for values of
.
As in Fig. 2 each panel represents a stellar model
from Table 1. Functions for values of
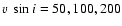 and 300 km s-1 are plotted as examples; for
calculating intermediate values of
and 300 km s-1 are plotted as examples; for
calculating intermediate values of  ,
Eq. (4) can be used with values of a and b as
given in columns five and six of Table 1. For
example, a value of
q2/q1 = 1.70 measured in a profile of an
A0-type star with
,
Eq. (4) can be used with values of a and b as
given in columns five and six of Table 1. For
example, a value of
q2/q1 = 1.70 measured in a profile of an
A0-type star with
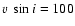 km s-1 can indicate that a
rigidly rotating star is observed under an inclination of
km s-1 can indicate that a
rigidly rotating star is observed under an inclination of
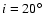 (
(
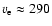 km s-1).
km s-1).
Solar-like differential rotation with the Equator faster than the Pole
diminishes the value of
q2/q1 as shown in Reiners & Schmitt (2002a); a
measurement yielding
q2/q1 < 1.72 can be due to a solar-like
rotation law with the Equator faster than the Pole. Whether very fast
rotators are subject to strong differential rotation will not be
discussed here. In Fig. 2
q2/q1 appears to be
larger than 1.72 for all stars with
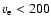 km s-1and values of gravity darkening according to Claret (1998) (cp.
Table 1). This means that a measurement of
differential rotation by determining the ratio
q2/q1 is not
affected by gravity darkening if
km s-1and values of gravity darkening according to Claret (1998) (cp.
Table 1). This means that a measurement of
differential rotation by determining the ratio
q2/q1 is not
affected by gravity darkening if
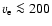 km s-1.
Interpreting gravity darkening as the reason for a measured value of
q2/q1 < 1.72, the rotational velocity (
km s-1.
Interpreting gravity darkening as the reason for a measured value of
q2/q1 < 1.72, the rotational velocity (
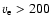 km s-1) and inclination angle of the star can be determined.
Consistency of
km s-1) and inclination angle of the star can be determined.
Consistency of  with breakup velocity can be checked. For
with breakup velocity can be checked. For
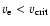 ,
differential rotation and very fast
rotation remain indistinguishable without further information. An
example is given in Sect. 6.
,
differential rotation and very fast
rotation remain indistinguishable without further information. An
example is given in Sect. 6.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{3947.f4a}\hspace...
...space*{1cm}
\includegraphics[angle=-90,width=7.8cm,clip]{3947.f4d}
\end{figure}](/articles/aa/full/2003/35/aa3947/Timg50.gif) |
Figure 4:
Values of  as measured from
the first zero of the Fourier transformed broadening profiles
plotted vs. the real values given as input to the models. The four
panels show cases of B0, A0, F0 and G0-type stars, the value of
the gravity darkening parameters
as measured from
the first zero of the Fourier transformed broadening profiles
plotted vs. the real values given as input to the models. The four
panels show cases of B0, A0, F0 and G0-type stars, the value of
the gravity darkening parameters  are chosen according to
Claret (1998). In each panel series for four different
inclination angles (
are chosen according to
Claret (1998). In each panel series for four different
inclination angles (
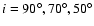 and
and
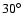 )
are differentiated, the respective values are
connected by solid lines. Dotted lines mark the identity between
real and measured values. )
are differentiated, the respective values are
connected by solid lines. Dotted lines mark the identity between
real and measured values. |
| Open with DEXTER |
To what accuracy a measurement of  is possible was
discussed in a number of publications (e.g., Collins & Truax 1995; Stoeckley 1968). It is known that measured values of
is possible was
discussed in a number of publications (e.g., Collins & Truax 1995; Stoeckley 1968). It is known that measured values of  underestimate the real values especially for very fast rotators
regardless of the data quality. To what extent a measured value is too
low, depends on the gravity darkening law and on the stellar
inclination. In the four panels of Fig. 4 the
differences between real and measured values for the B0, A0, F0 and
G0-type stars are shown using the most probable values of gravity
darkening as done above. The measured values of
underestimate the real values especially for very fast rotators
regardless of the data quality. To what extent a measured value is too
low, depends on the gravity darkening law and on the stellar
inclination. In the four panels of Fig. 4 the
differences between real and measured values for the B0, A0, F0 and
G0-type stars are shown using the most probable values of gravity
darkening as done above. The measured values of  have been
derived using the first zeros of the Fourier transform. Values for
different inclination angles are differentiated and shown with
different symbols, those derived for identical values of i are
connected by solid lines. Dashed lines mark the identity of real and
measured values. As expected, the measured values of
have been
derived using the first zeros of the Fourier transform. Values for
different inclination angles are differentiated and shown with
different symbols, those derived for identical values of i are
connected by solid lines. Dashed lines mark the identity of real and
measured values. As expected, the measured values of  may
underestimate the real ones but will never indicate too high a
projected rotational velocity. This reflects the fact that the
(equatorial) surface regions with the largest projected rotational
velocities become cooler due to gravity darkening, and thus less flux
is observed from them.
may
underestimate the real ones but will never indicate too high a
projected rotational velocity. This reflects the fact that the
(equatorial) surface regions with the largest projected rotational
velocities become cooler due to gravity darkening, and thus less flux
is observed from them.
The extent, to which a measured value of  is
systematically underestimated, depends strongly and in a well-defined
manner on the inclination angle. For constant inclination angles, the
measured value of
is
systematically underestimated, depends strongly and in a well-defined
manner on the inclination angle. For constant inclination angles, the
measured value of  is a smooth function of the real one
(cp. to Fig. 6 in Collins & Truax 1995). Underestimation of
is a smooth function of the real one
(cp. to Fig. 6 in Collins & Truax 1995). Underestimation of
 is stronger for smaller inclination angles in all models.
The deviation naturally is higher for large values of
is stronger for smaller inclination angles in all models.
The deviation naturally is higher for large values of  (and thus also of
(and thus also of  ). Thus, measured values of
). Thus, measured values of  in very rapid rotators can be corrected by determining the ratio
in very rapid rotators can be corrected by determining the ratio
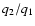 and calculating the inclination angle i as
shown in Sect. 4.3.
and calculating the inclination angle i as
shown in Sect. 4.3.
It should be noted that - in contrast to Fig. 12 in Collins & Truax (1995)
- inclination has a strong effect on the zeros of Fourier transformed
line profiles of rapid rotators; the case shown there only holds for
zero projected rotational velocity.
6 Example: Differential or fast rotation?
As an observational example the ten stars for which differential
rotation was claimed in Reiners & Schmitt (2003) are given in
Table 2 with their determined values of  and
q2/q1. According to the present calculations, these
values of
q2/q1 < 1.72 could also be interpreted as fast
rotation seen under small inclination angles i. The required values
of
and
q2/q1. According to the present calculations, these
values of
q2/q1 < 1.72 could also be interpreted as fast
rotation seen under small inclination angles i. The required values
of  and i for this interpretation are calculated and
given in columns five and six in Table 2. With one
exception all values of
and i for this interpretation are calculated and
given in columns five and six in Table 2. With one
exception all values of  are larger than break-up velocity
and thus can be excluded (it is furthermore very unlikely to find
inclination angles below 6
are larger than break-up velocity
and thus can be excluded (it is furthermore very unlikely to find
inclination angles below 6 in ten out of the 32 objects used in
that sample). Thus differential rotation remains the most probable
explanation for the peculiar shapes of these profiles.
in ten out of the 32 objects used in
that sample). Thus differential rotation remains the most probable
explanation for the peculiar shapes of these profiles.
Table 2:
Stars with measured values
q2/q1 < 1.72 from the sample of
Reiners & Schmitt (2003); differential rotation is claimed for these objects.
Interpreting the values of
q2/q1 as due to very fast rotation
seen under small inclination angles, the required values of
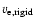 and i are given. Nine of the ten are larger than break-up
velocity.
and i are given. Nine of the ten are larger than break-up
velocity.
Line independent effects of fast stellar rotation on line profiles
were presented. Neglecting line specific variations in shape and line
depth, the effects of geometrical deformation and the role of the
gravity darkening parameter  have been outlined. Grid
calculations in gravity darkening
have been outlined. Grid
calculations in gravity darkening  ,
inclination angle i,
rotational velocity
,
inclination angle i,
rotational velocity  and spectral type with the parameter
q2/q1 classifying the profiles' shapes were carried out. The
results summarized below can be applied especially to high quality
data covering large wavelength regions where line-independent
broadening profiles may be obtained using the methods of LSD.
Applicability must be proved for each case individually, but
especially for lines of heavier ions in stars of later spectral types,
intrinsic variations of line profiles are sufficiently small and the
results of this study can directly be applied. The results can be
summarized as follows:
and spectral type with the parameter
q2/q1 classifying the profiles' shapes were carried out. The
results summarized below can be applied especially to high quality
data covering large wavelength regions where line-independent
broadening profiles may be obtained using the methods of LSD.
Applicability must be proved for each case individually, but
especially for lines of heavier ions in stars of later spectral types,
intrinsic variations of line profiles are sufficiently small and the
results of this study can directly be applied. The results can be
summarized as follows:
- 1.
- In very fast rotators (
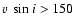 km s-1) and for
constant values of
km s-1) and for
constant values of  and similar spectral types, the value of
q2/q1 shows monotonic dependence on equatorial velocity
and similar spectral types, the value of
q2/q1 shows monotonic dependence on equatorial velocity  with
q2/q1 diminishing significantly with larger
values of
with
q2/q1 diminishing significantly with larger
values of  .
Variations with inclination i are marginal.
.
Variations with inclination i are marginal.
- 2.
- The coupling of
q2/q1 on
 depends on the
value of the gravity darkening parameter
depends on the
value of the gravity darkening parameter  and of spectral
type. Larger values of
and of spectral
type. Larger values of  lead to lower values of
q2/q1 with stronger slopes for later spectral types. Estimating the
physical values of
lead to lower values of
q2/q1 with stronger slopes for later spectral types. Estimating the
physical values of  according to Claret (1998), the
parameter
q2/q1 becomes significantly diminished in fast
rotating (
according to Claret (1998), the
parameter
q2/q1 becomes significantly diminished in fast
rotating (
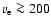 km s-1) A-, F- and G-type
stars. Independent of the inclination angle i, the equatorial
velocity
km s-1) A-, F- and G-type
stars. Independent of the inclination angle i, the equatorial
velocity  can be estimated by measuring
q2/q1,
and thus measuring
can be estimated by measuring
q2/q1,
and thus measuring  and
and
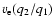 determines the inclination angle i.
determines the inclination angle i.
- 3.
- For stars with rotational velocities of
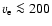 km s-1 the value of the ratio
q2/q1 does not
significantly change and is larger than 1.72 for all choices of
km s-1 the value of the ratio
q2/q1 does not
significantly change and is larger than 1.72 for all choices of
 and for all spectral types.
and for all spectral types.
- 4.
- For fixed values of
 the zeros of Fourier
transformed rotational broadening profiles do depend on inclination
angle i. A smaller value of i results in a larger difference
between the value of
the zeros of Fourier
transformed rotational broadening profiles do depend on inclination
angle i. A smaller value of i results in a larger difference
between the value of  as measured from the first zero of
the Fourier transform and its real value. Measured projected
rotational velocities are never overestimated. Deviations are as
large as 20% depending on the value of i. Using the parameter
q2/q1 this effect can be corrected for.
as measured from the first zero of
the Fourier transform and its real value. Measured projected
rotational velocities are never overestimated. Deviations are as
large as 20% depending on the value of i. Using the parameter
q2/q1 this effect can be corrected for.
As for differential rotation, it turned out that its measurement is
not affected by gravity darkening in stars rotating slower than
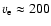 km s-1. For faster rotators, small
values of
q2/q1 can principally be due to three reasons; (i)
strong differential rotation, (ii) very fast rigid rotation (perhaps
seen under a small inclination angle), and (iii) both. The constraints
on a value of
km s-1. For faster rotators, small
values of
q2/q1 can principally be due to three reasons; (i)
strong differential rotation, (ii) very fast rigid rotation (perhaps
seen under a small inclination angle), and (iii) both. The constraints
on a value of
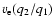 can help to clarify the
situation, e.g., if a value of
can help to clarify the
situation, e.g., if a value of  larger than breakup
velocity is needed to rule out differential rotation.
larger than breakup
velocity is needed to rule out differential rotation.
Acknowledgements
A.R. acknowledges financial support from Deutsche
Forschungsgemeinschaft DFG-SCHM 1032/10-1.
- Cameron, A. C. 2000, Lect. Note
Phys., 573, 183
In the text
- Claret, A. 1998, A&AS, 131, 395
In the text
NASA ADS
- Collins, G. W. II, &
Truax, R. J. 1995, ApJ, 439, 860
In the text
NASA ADS
- Dravins, D., Lindegren, L., &
Torkelsson, U. 1990, A&A, 237, 137
In the text
NASA ADS
- Gray, D. F. 1973, ApJ, 184, 461
In the text
NASA ADS
- Gray, D. F. 1976, The observation and
analysis of stellar photospheres (New York: Wiley)
In the text
- Hardorp, J., &
Strittmatter, P. A. 1968, ApJ, 153, 465
In the text
NASA ADS
- Heinzel, P. 1978, Bull. Astron.
Inst. Czechosl., 29, 159
In the text
NASA ADS
- Lucy, L. B. 1967, Z.
Astrophys., 65, 89
In the text
NASA ADS
- Rafert, J. B., & Twigg,
L. W. 1980, MNRAS, 193, 79
In the text
NASA ADS
- Reiners, A., & Schmitt,
J. H. M. M. 2002a, A&A, 384, 555
In the text
- Reiners, A., & Schmitt,
J. H. M. M. 2002b, A&A, 388, 1120
In the text
NASA ADS
- Reiners, A., & Schmitt,
J. H. M. M. 2003, A&A, 398, 647
In the text
NASA ADS
- Smith, R. C. 1975, MNRAS, 173, 97
In the text
NASA ADS
- Stoeckley, T. R. 1968, MNRAS,
140, 121
In the text
NASA ADS
- Townsend, R. 1997, MNRAS, 284, 839
In the text
NASA ADS
- Tuominen, I. V. 1975, Ann. Acad.
Sci. Fennicae, Ser. A, VI. Physica, 393 (3.)
In the text
- von Zeipel, H. 1924, MNRAS, 84,
655
In the text
Copyright ESO 2003
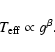
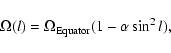
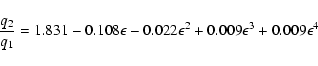
![\begin{figure}
\par\resizebox{8.8cm}{!} {\includegraphics[angle=-90,clip]{3947.f1}}
\end{figure}](/articles/aa/full/2003/35/aa3947/Timg32.gif)
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=7.8cm,clip]{3947.f2a}\...
...ace{1cm}
\includegraphics[angle=-90,width=7.8cm,clip]{3947.f2d} }
\end{figure}](/articles/aa/full/2003/35/aa3947/Timg35.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{3947.f3a}\hspace...
...space*{1cm}
\includegraphics[angle=-90,width=7.8cm,clip]{3947.f3d}
\end{figure}](/articles/aa/full/2003/35/aa3947/Timg40.gif)
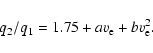
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{3947.f4a}\hspace...
...space*{1cm}
\includegraphics[angle=-90,width=7.8cm,clip]{3947.f4d}
\end{figure}](/articles/aa/full/2003/35/aa3947/Timg50.gif)