A&A 408, 553-558 (2003)
DOI: 10.1051/0004-6361:20031002

JHK'-band IOTA interferometry of the circumstellar environment of R CrB

K. Ohnaka1 - U. Beckmann1 - J.-P. Berger2,3 - M. K. Brewer4 - K.-H. Hofmann1 - M. G. Lacasse2 - V. Malanushenko5 - R. Millan-Gabet2,6 - J. D. Monnier2,7 - E. Pedretti2 - D. Schertl1 - F. P. Schloerb4 - V. I. Shenavrin8 - W. A. Traub2 - G. Weigelt1 - B. F. Yudin8


1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
2 - Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
3 - Laboratoire d'Astrophysique Observatoire de Grenoble, Domaine Universitaire, 414 rue de la Piscine, BP 53, 38041 Grenoble Cedex 9, France
4 - Department of Physics and Astronomy, University of Massachusetts, Amherst, MA 01003, USA
5 - Crimean Astrophysical Observatory, 98409 Crimea, Ukraine
6 - California Institute of Technology, 770 S. Wilson Ave. MS 100-22, Pasadena, CA 91125, USA
7 - University of Michigan, 941 Dennison Building, 500 Church Street, Ann Arbor, MI 48109-1090, USA
8 - Sternberg Astronomical Institute, Universitetskii pr. 13, 119899 Moscow, Russia

Received 28 March 2003 / Accepted 16 June 2003

Abstract
We report the first long-baseline interferometry of the circumstellar dust environment of R CrB. The observations were carried out with the Infrared Optical Telescope Array (IOTA), using our new $JH\mbox{$K^{\prime}$ }$ beam combiner which enables us to record fringes in the J, H, and $K^{\prime }$ bands simultaneously. The circumstellar dust envelope of R CrB is resolved at a baseline of 21 m along a position angle of $\sim$ $ 170^{\circ}$, and the visibilities in the J, H, and $K^{\prime }$ bands are $0.97 \pm 0.06$, $0.78 \pm 0.06$, and $0.61 \pm 0.03$, respectively. These observed visibilities, together with the $K^{\prime }$-band visibility obtained by speckle interferometry with baselines of up to 6 m, and the spectral energy distribution are compared with predictions from spherical dust shell models which consist of the central star and an optically thin dust shell. The comparison reveals that the observed J- and H-band visibilities are in agreement with those predicted by these models, and the inner radius and inner boundary temperature of the dust shell were derived to be 60-80 $R_{\star }$ and 950-1050 K, respectively. However, the predicted $K^{\prime }$-band visibilities are found to be $\sim$10% smaller than the one obtained with IOTA. Given the simplifications adopted in our models and the complex nature of the object, this can nevertheless be regarded as rough agreement. As a hypothesis to explain this small discrepancy, we propose that there might be a group of newly formed dust clouds, which may appear as a third visibility component.

Key words: techniques: interferometric - stars: circumstellar matter - stars: mass-loss - stars: individual: R CrB - stars: variable: general - infrared: stars

1 Introduction

R Coronae Borealis (R CrB) stars are characterized by irregular sudden declines in their visual light curves as deep as $\Delta V \sim 8$. They are thought to undergo ejections of dust clouds in random directions, and it is believed that the sudden deep declines observed are a result of the formation of dust clouds in the line of sight (Loreta 1934; O'Keefe 1939). However, the effective temperatures of R CrB stars are higher than $\sim$6000 K (Asplund et al. 2000), and the mechanism of dust formation in such a hostile environment is still unclear. Particularly controversial is the location of the dust formation - far from the star, at distances of $\ga$ $ 20~\mbox{$R_{\star}$ }$ (e.g. Fadeyev 1986, 1988; Feast 1996), or very close to the photosphere, at $\sim$ $ 2~\mbox{$R_{\star}$ }$ (Payne-Gaposchkin 1963). R CrB stars have hydrogen-deficient and carbon-rich atmospheres (e.g. Asplund et al. 2000), suggesting that they are post-asymptotic giant branch stars. However, their evolutionary status is little understood (see, e.g. Clayton 1996).

Ejected dust clouds are expected to be accelerated by radiation pressure. They absorb the starlight, re-emitting it in the infrared. Since R CrB stars are considered to undergo dust cloud ejections rather frequently, it is very likely that there is a group of dispersing dust clouds around the central star. No clear instantaneous correlation between the infrared and visual light curves is observed: the infrared light curves of R CrB stars do not exhibit a decline, even if the star undergoes a deep decline in the visual. Therefore, it is believed that a group of dispersing dust clouds, not one single, newly formed dust cloud, is responsible for the IR excess. Recently, Yudin et al. (2002) analyzed the infrared light curve of R CrB over 25 years and suggested that the IR excess increases with a time lag of about 4 years after the star undergoes decline events.


  \begin{figure} \par\resizebox{5cm}{!}{\rotatebox{0}{\includegraphics{3790F1.ps}}} \end{figure} Figure 1: Two consecutive interferograms of R CrB. The fringes are spectrally dispersed in the horizontal direction and are recorded simultaneously in the J, H, and $K^{\prime }$ bands, as shown in each panel. These three bands are separated by telluric absorption, which can be seen as vertical dark lanes between the J and H bands as well as between the H and $K^{\prime }$ bands.
Open with DEXTER

Our speckle interferometric observations with a spatial resolution of 75 mas have resolved the circumstellar envelope around R CrB for the first time (Ohnaka et al. 2001, hereafter Paper I). In Paper I, we show that simple, optically thin dust shell models can simultaneously reproduce the visibility and the spectral energy distribution (SED) obtained at near-maximum light in 1996 and that the inner radius of the dust shell is $\sim$80 $R_{\star }$ (19 mas) with a temperature of $\sim$900 K. Paper I also shows that the visibility and SED obtained at minimum light in 1999 are not in agreement with these models. As a possible interpretation, the presence of a newly formed dust cloud was suggested, but the spatial resolution of 75 mas was insufficient to draw a clear conclusion about the presence of additional dust clouds.

Long-baseline interferometry provides a unique opportunity to investigate the circumstellar environment of R CrB stars with higher spatial resolution. In this paper, we report the results of observations of R CrB with the Infrared Optical Telescope Array (IOTA) in the J, H, and $K^{\prime }$ bands. We compare the observed SED and visibilities with those predicted by the dust shell models which we used in Paper I and discuss possible interpretations of the observed data.

Table 1: IOTA observations for R CrB. $B_{\rm p}$: projected baseline length, PA: position angle of the projected baseline, $N_{\rm T}$: number of interferograms acquired for the target, $N_{\rm R}$: number of interferograms acquired for the reference star, T: exposure time of each frame.

   
2 IOTA observations

The interferometric observations presented in this paper were carried out with the IOTA interferometer (Traub 1998; Traub et al. 2003) on 2001 June 5 and 6. We used IOTA in the two-telescope mode: a pair of 45 cm telescopes collect starlight and collimate it into a pair of 4.5 cm beams, which are sent to the evacuated delay line tubes. The outcoming beams are filtered through dichroics, which feed the visible light onto star tracker CCDs and the infrared light into our beam combiner. This latter consists of an anamorphic lens system, a prism, and a HAWAII array detector (Weigelt et al. 2003a,b). Spectrally dispersed fringes are simultaneously recorded at all wavelengths in the range 1.0 to 2.3 $\mu $m. Figure 1 shows two examples of the interferograms obtained for R CrB.

Table 1 summarizes our observations of R CrB. R CrB was at maximum light and had a visual magnitude of approximately 6. The observations were carried out with a baseline length of 21 m along a position angle of $\sim$ $ 170^{\circ}$ on the sky.

The J-, H-, and $K^{\prime }$-band visibilities of R CrB (= modulus of the Fourier transform of the intensity distribution of the object) were derived from the spectrally dispersed J-, H-, and $K^{\prime }$-band Michelson interferograms. The data processing steps are described in the Appendix A. We derived the visibilities of R CrB to be $0.97 \pm 0.06$, $0.78 \pm 0.06$, and $0.61 \pm 0.03$ in the J (wavelength range 1.04-1.44 $\mu $m), H (1.46-1.84 $\mu $m), and $K^{\prime }$ (1.94-2.30 $\mu $m) bands, respectively. The corresponding mean spatial frequencies are 92.1 cycles/arcsec, 63.8 cycles/arcsec, and 48.8 cycles/arcsec in the J, H, and $K^{\prime }$ bands, respectively.

3 Photometry

The JHKLM photometric observations of R CrB were carried out on 2001 June 10 (only 5 days after the IOTA observations), using the 1.22 m telescope at the Crimean Laboratory of the Sternberg Astronomical Institute. UBV photometry was also carried out on the same night with the 1.25 m telescope at the Crimean Astrophysical Observatory.

The L- and M-band fluxes of R CrB vary semi-periodically on a time scale of 1260 days (Feast et al. 1997). At the time of our IOTA observations, R CrB was at maximum light in the visual as well as in the L band.

   
4 Comparison of the observed SED and visibilities with spherical dust shell models

   
4.1 Two-component model: Central star and optically thin dust shell

We first compare the observed SED and visibilities with those predicted by the two-component models adopted in Paper I. These two-component models consist of the central star and a spherical, optically thin dust shell. Generally speaking, it is difficult to examine such models and derive physical parameters of the dust shell from observed SEDs alone. However, observed visibilities can put more constraints on the models and are therefore vital for testing models as well as for deriving physical parameters. Since the details of our model are described in Paper I, we only give a summary here. In the framework of our model, the circumstellar environment around R CrB is represented by a spherical, optically thin dust shell of amorphous carbon with a single grain size of 0.01 $\mu $m, and with density proportional to r-2. The real circumstellar environment around R CrB is likely to be much more complex. However, if dust ejection occurs frequently and in random directions, such a simple, spherically symmetric shell model may be regarded as an approximation of the complicated distribution of material. An effective temperature of 6750 K and a radius of 70 $R_{\odot}$ are adopted for the central star, as described in Paper I. The temperature distribution in the shell is calculated from the thermal balance equation for an optically thin dust shell. The input parameters of our model are the temperature at the inner boundary and the optical depth of the dust shell. We use the optical depth at 0.55 $\mu $m as the reference optical depth of the dust shell. At the time of our IOTA observations, the star was at maximum light, and there were no obscuring dust clouds in the line of sight. Therefore, unlike the studies presented in Paper I, the empirical adoption of extinction due to an obscuring dust cloud in front of the star is not necessary here.

Figure 2a shows a comparison of the observed SED and those predicted by the spherical dust shell models. Three different models are calculated with three different opacities of amorphous carbon obtained by Bussoletti et al. (1987) (AC2 sample), Rouleau & Martin (1991) (AC1 sample), and Colangeli et al. (1995) (ACAR sample). The observed SED can be reproduced well with models whose inner radius is 60-80 $R_{\star }$ and inner boundary temperatures are 950-1050 K. The uncertainties of the inner temperature and inner radius are estimated to be approximately $\pm$100 K and $\pm$10 $R_{\star }$, respectively, for a given opacity data set.


  \begin{figure} \par\resizebox{8.8cm}{!}{\rotatebox{0}{\includegraphics[bb=26 417... ...{\rotatebox{0}{\includegraphics[bb=26 28 544 350,clip]{3790F2.ps}}} \end{figure} Figure 2: Comparison of the observed SED and visibilities with SEDs and visibilities predicted by two-component models consisting of the central star and an optically thin dust shell, as described in Sect. 4.1. a) The filled circles represent the photometric data obtained five days after the IOTA observations. The filled triangles represent IRAS data. The three curves represent models with different opacities for amorphous carbon. RM: Rouleau & Martin (1991), CO: Colangeli et al. (1995), BU: Bussoletti et al. (1987). $T_{\rm in}$ is the temperature at the inner boundary ( $r_{\rm in}$) of the optically thin dust shell. $\tau _{V}$ is the optical depth of a dust shell defined at 0.55 $\mu $m. b) The filled diamonds represent the J-, H-, and $K^{\prime }$-band visibilities observed with IOTA. The filled circles represent the $K^{\prime }$-band visibility obtained by speckle interferometry with the 6 m telescope at the Special Astrophysical Observatory, Russia (Paper I). For each of the RM, CO, and BU models, the predicted visibilities in the J, H, and $K^{\prime }$ bands are shown.
Open with DEXTER

In Fig. 2b, we show a comparison of the J-, H-, and $K^{\prime }$-band visibilities obtained with IOTA, together with the $K^{\prime }$-band speckle visibilities from Paper I, with those predicted from the three models. It should be noted that these predicted visibilities are calculated in the same manner as the observed visibilities are derived (see Eq. (A.3) in the Appendix A). We also note that the $K^{\prime }$-band speckle visibilities obtained at near-maximum light in 1996 and at minimum light in 1999 show no significant difference within a cut-off frequency of $\sim$13 cycles/arcsec (see Fig. 2 in Paper I), in spite of a brightness difference of 3.5 mag in the visual and of $\sim$1 mag in the L and M bands. Therefore, it would be reasonable to use these speckle visibilities for the present study to cover spatial frequencies smaller than 13 cycles/arcsec. In the discussion here, we show only the visibilities obtained at near-maximum light in 1996 for visual clarity. Figure 2b shows that the three models can reproduce the J- and H-band visibilities observed with IOTA, although the predicted visibilities are somewhat higher in the H band.

The high J-band visibility observed with IOTA suggests that the contribution of the central star is dominant in the J band and that the effect of scattering is small even in the J band, where the contribution of scattered light is expected to be the largest among the three bands. It suggests that the grain size in the dust shell may be rather small. This observational result is consistent with the result of the simple analysis of the extinction curve of an obscuring dust cloud in front of the star described in Paper I. In Paper I, we show that the extinction curve of the obscuring dust cloud in the wavelength region from the U to the I band can be approximated as $\propto$ $ \lambda^{-p}$, and p changes from $\sim$0 to $\sim$1, as the cloud disperses and becomes part of the optically thin dust shell (see Fig. 5 of Paper I). Since the extinction curve of amorphous carbon can be approximated by $\propto$ $ \lambda^{-1}$ in the small particle limit ( $2 \pi a /\lambda \ll 1$, where a is the radius of a spherical grain), the grain size is considered to be small enough to fulfill the small particle limit in the UBVRI bands when the cloud becomes part of the optically thin dust shell. We can therefore estimate the size of grains in the optically thin dust shell to be $\la$0.01 $\mu $m, which satisfies $2 \pi a /\lambda \la 0.1$ for $\lambda = 0.55$ $\mu $m. With such small grains, the contribution of scattered light is negligible, resulting in the high J-band visibility. This shows a marked contrast with the case of HD 62623, where the observed J-band visibility is lower than the H- and K-band visibilities, presumably due to a presence of large grains (Bittar et al. 2001).

For the $K^{\prime }$ band, the predicted visibilities are $\sim$10% lower than the visibility obtained with IOTA. Given the complex nature of the circumstellar environment of R CrB on the one hand and the simplifications adopted in our models on the other hand, it is difficult to draw a definitive conclusion about this discrepancy of $\sim$10%. The small discrepancy may be due to a slight deviation from spherical symmetry and/or to a presence of clumps, which are plausible for R CrB.


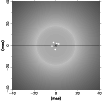  \begin{figure} \par\resizebox{8.8cm}{!}{\rotatebox{0}{\includegraphics{3790F3.ps}}}\end{figure} Figure 3: An example of the intensity distribution of a model with a group of dust clouds, which are randomly distributed at distances of between 2 $R_{\star }$ and 20 $R_{\star }$ in the plane of the sky. The intensity is represented in a logarithmic grayscale, where the brighter gray corresponds to the higher intensity. The five intensity peaks located near the central star ($\times $) correspond to newly formed dust clouds. The ring-shaped intensity distribution results from limb brightening of the inner boundary of the optically thin dust shell at 78 $R_{\star }$ (18 mas). The projected baseline used in the calculation of the visibilities is shown by the solid line.
Open with DEXTER

4.2 Cloud model: Central star, optically thin dust shell, and a group of dust clouds

Alternatively, this small discrepancy can be interpreted as an indication of the presence of an additional component, which is more compact than the optically thin dust shell with the inner radius of 60-80 $R_{\star }$. In fact, such a discrepancy between observed visibilities and predictions from two-component models had already been found in the study of the SED and visibility obtained at minimum light (Paper I). Although we tentatively assumed the presence of only one additional obscuring dust cloud in Paper I, it seems to be more realistic to postulate that there is probably a group of several newly formed dust clouds close to the central star.

In order to see if such a picture is consistent with the observed SED and visibilities, we constructed models with a group of dust clouds, in addition to the extended optically thin dust shell. We distributed a certain number of spherical dust clouds randomly in the region between $r = r_{\rm 1}$ and $r_{\rm 2}$. All clouds are assumed to emit as a blackbody of the same temperature and to have the same radius, which is adjusted so that the total flux of the clouds, the optically thin dust shell, and the central star is consistent with the observed SED. Tentatively assuming a group of five clouds, we generated 10 random distributions of hot dust clouds for a given set of ($r_{\rm 1}$, $r_{\rm 2}$). We adopted a fixed value of 2 $R_{\star }$ for $r_{\rm 1}$ and four different values of 10 $R_{\star }$, 20 $R_{\star }$, 30 $R_{\star }$, and 50 $R_{\star }$ for $r_{\rm 2}$. An example of such models is shown in Fig. 3, where a group of five intensity peaks resulting from hot dust clouds can be seen together with the large limb-brightened, optically thin dust shell.

Figure 4 shows a comparison of the observed SED and visibilities with those predicted by the models with five hot dust clouds out of the line of sight, in addition to the optically thin dust shell discussed in Sect. 4.1. The parameters of the optically thin dust shell are the same or only slightly changed, compared with those derived with the two-component models. Figure 4b shows that the $K^{\prime }$-band visibility observed with IOTA is well reproduced by the models, while the agreement of the H-band visibility is now slightly poorer than with the two-component models. It is beyond the scope of the present work to construct a more detailed model such as three-dimensional radiative transfer models including dust formation processes, and we only suggest here that the small discrepancy found in the $K^{\prime }$-band visibilities may be due to the presence of a group of newly formed hot dust clouds. The temperature and the size of the dust clouds are found to be approximately 1200 K and 2-3 $R_{\star }$, respectively. We also calculated SEDs and visibilities with a group of 10 clouds. However, as long as the radius of each cloud is properly adjusted to reproduce the observed SED, the number of dust clouds does not have a major effect on the resulting visibility functions in the relevant spatial frequency range. The parameter $r_{\rm 1}$ does not have a huge influence on the resulting visibilities, either. What matters is the global extent of the group of dust clouds, namely $r_{\rm 2}$. It turns out that $r_{\rm 2} \sim 20$ $R_{\star }$ can reproduce the observed J-, H-, and $K^{\prime }$-band visibilities fairly well. The adoption of smaller ( $r_{\rm 2} \sim 10$ $R_{\star }$) or larger ( $r_{\rm 2} \sim 30$ $R_{\star }$ and $\sim$50 $R_{\star }$) values leads to poorer matches to the observed $K^{\prime }$-band visibility.


  \begin{figure} \par\resizebox{8.8cm}{!}{\rotatebox{0}{\includegraphics[bb=27 417... ...{\rotatebox{0}{\includegraphics[bb=26 27 543 347,clip]{3790F4.ps}}} \end{figure} Figure 4: Comparison of the observed SED and visibilities with SEDs and visibilities predicted by models consisting of the central star, an optically thin dust shell, and a group of five newly formed dust clouds, as shown in Fig. 3. The dashed-dotted line in a) represents the contribution of the group of newly formed dust clouds in the RM model. See also the legend to Fig. 2.
Open with DEXTER

5 Concluding remarks

The first long-baseline interferometric observations of R CrB have been carried out at the IOTA interferometer, using our new $JH\mbox{$K^{\prime}$ }$ beam combiner, which enables us to record interferograms simultaneously in the J, H, and $K^{\prime }$ bands. The J and H visibilities and the SED obtained in the same period can be reproduced simultaneously by two-component models consisting of the central star and an optically thin dust shell with an inner radius of 60-80 $R_{\star }$ and temperatures of 950-1050 K. The $K^{\prime }$-band visibilities predicted by these models are found to be $\sim$10% lower than the observed $K^{\prime }$-band visibility. It is possible to attribute this discrepancy to the simplifications adopted in the two-component models. On the other hand, we have also shown that it may be due to the presence of a group of newly formed dust clouds close to the central star. The observed visibilities and SED can be reproduced simultaneously with such models, though not perfectly, if such a group of dust clouds extends to a radius of $\sim$20 $R_{\star }$ ($\sim$5 mas), with the temperature of each cloud $\sim$1200 K.

   
Appendix A: Data reduction procedure

The interferograms obtained with our $JH\mbox{$K^{\prime}$ }$ beam combiner are spectrally dispersed Michelson interferograms (see Fig. 1). Each pixel column of the interferograms contains a one-dimensional projection of the two-dimensional Michelson interferogram of a particular spectral channel. The spectrally dispersed Michelson interferograms cover the three near-infrared band passes J (1.04-1.44 $\mu $m), H (1.46-1.84 $\mu $m), and $K^{\prime }$ (1.94-2.30 $\mu $m). The R CrB data consist of five pairs of the object and the reference star data sets.

The derivation of the J-, H-, and $K^{\prime }$-band visibilities consists of the following image processing steps:
(1) After flat-fielding, each interferogram is processed in the following way: the power spectrum (squared modulus of the Fourier transform) of the one-dimensional Michelson interferogram of each spectral channel is calculated, and then the average over all power spectra of all spectral channels within a chosen wavelength region (e.g., J, H, or $K^{\prime }$ band) is computed. The resulting spectrally averaged power spectrum of an interferogram consists of a central peak and two symmetric off-axis peaks.
(2) Next, the detector and photon noise bias terms in each spectrally averaged power spectrum are compensated.
(3) From this bias-compensated, spectrally averaged power spectrum, the following squared raw visibility, $\mu_{\rm obj}^2$ or $\mu_{\rm ref}^2$, is derived. The squared raw visibility ( $\mu_{\rm obj}^2$ or $\mu_{\rm ref}^2$) is the ratio of the integrated off-axis fringe peak intensity in the power spectrum (= numerator of Eqs. (A.1) or (A.2)) and the central peak intensity (= normalization integral in the denominator of Eqs. (A.1) or (A.2)). The squared raw visibility $\mu_{\rm obj}^2$ of an individual interferogram of the object and the squared raw visibility  $\mu_{\rm ref}^2$ of the reference star are given by

  
$\displaystyle \mu_{\rm obj}^2 = \frac{t_{\rm obj} \int_{\lambda_1}^{\lambda_2} ... ...ac{1}{4} \int_{\lambda_1}^{\lambda_2} S_{\rm obj}^2(\lambda) ~ {\rm d}\lambda},$     (A.1)
$\displaystyle \mu_{\rm ref}^2 = \frac{t_{\rm ref} \int_{\lambda_1}^{\lambda_2} ... ...{4} \int_{\lambda_1}^{\lambda_2} S_{\rm ref}^2(\lambda) ~ {\rm d}\lambda }\cdot$     (A.2)

$V_{\rm obj}^2(\lambda, B_{\rm p,obj})$ and $V_{\rm ref}^2(\lambda, B_{\rm p,ref})$ denote the squared visibilities of the object and the reference star at the spectral channel $\lambda$ and at the projected baselines $B_{\rm p,obj}$ and $B_{\rm p,ref}$, respectively. $S_{\rm obj}(\lambda)$ is the spectral weighting function, which depends on the spectrum of the object, the atmospheric transmission at the time of the observations, the filter transmission, and the detector sensitivity. $S_{\rm ref}(\lambda)$ is the corresponding spectral weighting function for the reference star. $\lambda_1$ and $\lambda_2$ are the wavelength limits of the chosen band pass (e.g., J, H, or $K^{\prime }$ band). $t_{\rm obj}$ and $t_{\rm ref}$ are the instantaneous contrast degradation factors during the recording of an interferogram. These contrast degradation factors differ from frame to frame because of the varying overlap of the two telescope point spread functions (PSFs). Finally, the measured calibrated squared visibility $\overline{V}^2$ of the object (in the wavelength interval from $\lambda_1$ to $\lambda_2$) is given by

 \begin{displaymath}\overline{V}^2 = \frac{ <\!\!\mu_{\rm obj}^2\!\!> \overline{V... ...ambda_1}^{\lambda_2} S_{\rm obj}^2(\lambda) ~ {\rm d}\lambda}, \end{displaymath} (A.3)

where $<\!\!\mu_{\rm obj}^2\!\!>$ is the ensemble average squared raw visibility of the object (the ensemble average is calculated over all interferograms of the object), $<\!\!\mu_{\rm ref}^2\!\!>$ is the ensemble average squared raw visibility of the reference star, and $\overline{V}_{\rm ref}$ is the approximately known visibility of the reference star. Equation (A.3) is valid, since the average contrast degradation factors $<\!\!t_{\rm obj}\!\!>$ and $<\!\!t_{\rm ref}\!\!>$ are nearly identical and $\overline{V}_{\rm ref}$ is approximately given by

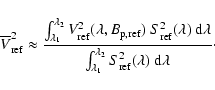\begin{displaymath}\overline{V}_{\rm ref}^2 \approx \frac{\int_{\lambda_1}^{\lam... ...a_1}^{\lambda_2} S_{\rm ref}^2(\lambda) ~ {\rm d}\lambda}\cdot \end{displaymath} (A.4)

The visibility of the reference star $\overline{V}_{\rm ref}$ at the mean spatial frequency

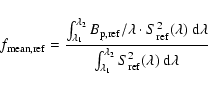\begin{displaymath}f_{\rm mean,ref} = \frac{\int_{\lambda_1}^{\lambda_2} B_{\rm... ...lambda_1}^{\lambda_2} S_{\rm ref}^2(\lambda) ~ {\rm d}\lambda} \end{displaymath} (A.5)

is derived from its uniform-disk angular diameter estimated by the method of Dyck et al. (1996). The accuracy of the calibrated visibility of the object $\overline{V}$ strongly depends on the similarity of the contrast degradation factors $<\!\!t_{\rm obj}\!\!>$ and $<\!\!t_{\rm ref}\!\!>$. This similarity was tested by reducing five different pairs of object and reference star data sets and by image motion data of the two telescope PSFs recorded during the data acquisition.

The calibrated visibility $\overline{V}$ obtained for the wavelength interval from $\lambda_1$ to $\lambda_2$ is assigned to the mean spatial frequency

 \begin{displaymath} f_{\rm mean,obj} = \frac{ \int_{\lambda_1}^{\lambda_2} B_{\... ...a_1}^{\lambda_2} S_{\rm obj}^2(\lambda) ~ {\rm d}\lambda}\cdot \end{displaymath} (A.6)

References


Copyright ESO 2003