Table 7:
The first 89 fine-structure n=2, 3 and 4 levels included in
the EIE calculation by Chen et al. 2003: comparison of calculated and
observed energies in Rydbergs for Fe XVII; "obs'' data are observed
values from NIST; the entries " SS'' ( SS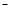 / SS
/ SS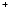 :
without/with inclusion of 2-body magnetic components) and the entries
" MCDF'' are from SUPERSTRUCTURE and GRASP calculations respectively.
:
without/with inclusion of 2-body magnetic components) and the entries
" MCDF'' are from SUPERSTRUCTURE and GRASP calculations respectively.
|
i |
SLJ |
(jj) J |
obs |
SS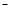 |
ss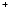 |
MCDF |
BPRM |
|
1 |
2s22p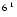 S0 S0 |
(0,0)0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
| 2 |
2s22p53s 3P
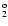 |
(3/2,1/2) 2 2 |
53.2965 |
53.3622 |
53.3666 |
53.1684 |
53.3821 |
| 3 |
3s 1P
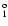 |
(3/2,1/2) 1 1 |
53.43 |
53.5044 |
53.5091 |
53.3100 |
53.5211 |
| 4 |
3s 3P
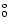 |
(1/2,1/2) 0 0 |
54.2268 |
54.2865 |
54.2865 |
54.0957 |
54.3190 |
| 5 |
3s 3P
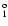 |
(1/2,1/2) 1 1 |
54.3139 |
54.3791 |
54.3697 |
54.1851 |
54.4074 |
| 6 |
3p 3S1 |
(3/2,1/2)1 |
55.5217 |
55.5686 |
55.5735 |
55.3963 |
55.6001 |
| 7 |
3p 3D2 |
(3/2,1/2)2 |
55.7787 |
55.8397 |
55.8455 |
55.6606 |
55.8654 |
| 8 |
3p 3D3 |
(3/2,3/2)3 |
55.8974 |
55.9463 |
55.9494 |
55.7791 |
55.9857 |
| 9 |
3p 1P1 |
(3/2,3/2)1 |
55.9804 |
56.0338 |
56.0404 |
55.8654 |
56.7674 |
| 10 |
3p 3P2 |
(3/2,3/2)2 |
56.1137 |
56.1597 |
56.1642 |
55.9950 |
56.2007 |
| 11 |
3p 3P0 |
(3/2,3/2)0 |
56.5155 |
56.5821 |
56.5809 |
56.4050 |
56.2221 |
| 12 |
3p 3D1 |
(1/2,1/2)1 |
56.6672 |
56.7288 |
56.7211 |
56.5495 |
56.0669 |
| 13 |
3p 3P1 |
(1/2,3/2)1 |
56.9060 |
56.9499 |
56.9420 |
56.7855 |
57.0024 |
| 14 |
3p 1D2 |
(1/2,3/2)2 |
56.9336 |
56.9817 |
56.9703 |
56.8135 |
57.0339 |
| 15 |
3p 1S0 |
(1/2,1/2)0 |
57.8894 |
58.0639 |
58.0619 |
57.9308 |
58.0358 |
| 16 |
3d 3P
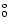 |
(3/2,3/2) 0 0 |
58.8982 |
58.9407 |
58.9578 |
58.7738 |
59.0057 |
| 17 |
3d 3P
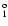 |
(3/2,3/2) 1 1 |
58.981 |
59.0188 |
59.0289 |
58.8454 |
59.0846 |
| 18 |
3d 3P
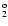 |
(3/2,5/2) 2 2 |
59.0976 |
59.1651 |
59.1659 |
58.9826 |
59.2305 |
| 19 |
3d 3F
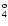 |
(3/2,5/2) 4 4 |
59.1041 |
59.1821 |
59.1799 |
58.9901 |
59.2435 |
| 20 |
3d 3F
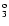 |
(3/2,3/2) 3 3 |
59.1611 |
59.2240 |
59.2347 |
59.0498 |
59.2820 |
| 21 |
3d 1D
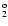 |
(3/2,3/2) 2 2 |
59.2875 |
59.3513 |
59.3630 |
59.1797 |
59.4106 |
| 22 |
3d 3D
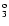 |
(3/2,5/2) 3 3 |
59.3665 |
59.4471 |
59.4466 |
59.2598 |
59.5054 |
| 23 |
3d 3D
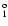 |
(3/2,5/2) 1 1 |
59.708 |
59.7865 |
59.7907 |
59.6082 |
59.8446 |
| 24 |
3d 3F
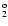 |
(1/2,3/2) 2 2 |
60.0876 |
60.1438 |
60.1431 |
59.9749 |
60.2171 |
| 25 |
3d 3D
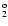 |
(1/2,5/2) 2 2 |
60.1617 |
60.2179 |
60.2045 |
60.0344 |
60.2940 |
| 26 |
3d 1F
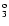 |
(1/2,5/2) 3 3 |
60.197 |
60.2627 |
60.2484 |
60.0754 |
60.3337 |
| 27 |
3d 1P
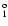 |
(1/2,3/2) 1 1 |
60.6903 |
60.8225 |
60.8212 |
60.6279 |
60.8461 |
| 28 |
2s2p63s 3S1 |
(1/2,1/2)1 |
|
63.3306 |
63.3306 |
63.2125 |
63.3658 |
| 29 |
3s 1S0 |
(1/2,1/2)0 |
|
63.7925 |
63.7925 |
63.6986 |
63.8049 |
| 30 |
3p 3P
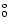 |
(1/2,1/2) 0 0 |
|
65.7338 |
65.7377 |
65.6346 |
65.7726 |
| 31 |
3p 3P
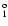 |
(1/2,1/2) 1 1 |
65.601 |
65.7687 |
65.7703 |
65.6676 |
65.8047 |
| 32 |
3p 3P
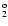 |
(1/2,3/2) 2 2 |
|
65.9299 |
65.9285 |
65.8380 |
65.9792 |
| 33 |
3p 1P
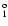 |
(1/2,3/2) 1 1 |
65.923 |
66.0723 |
66.0718 |
65.9782 |
66.1267 |
| 34 |
3d 3D1 |
(1/2,3/2)1 |
|
69.0162 |
69.0269 |
68.9221 |
69.0744 |
| 35 |
3d 3D2 |
(1/2,3/2)2 |
|
69.0351 |
69.0386 |
68.9323 |
69.0920 |
| 36 |
3d 3D3 |
(1/2,5/2)3 |
|
69.0672 |
69.0606 |
68.9518 |
69.1237 |
| 37 |
3d 1D2 |
(1/2,5/2)2 |
69.282 |
69.4358 |
69.4352 |
69.3247 |
69.4813 |
| 38 |
2s22p54s 3P
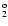 |
|
|
71.8710 |
71.8754 |
71.6517 |
|
| 39 |
2s22p54s 1P
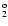 |
|
71.860 |
71.9150 |
71.9197 |
71.6983 |
|
| |
|
|
|
|
|
|
|
| 55 |
3P
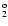 |
|
|
74.0927 |
74.1062 |
73.9033 |
|
| 56 |
2s22p54d 3F
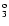 |
(3/2,3/2) 3 3 |
|
74.1082 |
74.1151 |
73.8994 |
|
| 57 |
1D
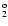 |
|
|
74.1526 |
74.1595 |
73.9456 |
|
| |
|
|
|
|
|
|
|
| 85 |
2s2p64d 1D2 |
(1/2,5/2)2 |
|
84.0504 |
84.0501 |
83.9258 |
|
| 86 |
4f 3F
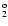 |
(1/2,5/2) 2 2 |
|
84.4770 |
84.4789 |
84.3462 |
|
| 87 |
4f 3F
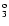 |
(1/2,5/2) 3 3 |
|
84.4793 |
84.4801 |
84.3481 |
|
| 88 |
4f 3F
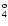 |
(1/2,7/2) 4 4 |
|
84.4853 |
84.4839 |
84.3522 |
|
| 89 |
4f 1F
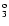 |
(1/2,7/2) 3 3 |
|
84.4957 |
84.4953 |
84.3621 |
|
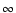 |
2s22p5 2P
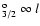 |
|
92.760 |
|
-- |
|
92.8398 |
SS calculations with statistical model scaling factors
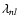 = 1.3835 1.1506 1.0837
1.0564 1.0175 1.0390 1.0511 1.0177 1.0191 1.0755
= 1.3835 1.1506 1.0837
1.0564 1.0175 1.0390 1.0511 1.0177 1.0191 1.0755
in 1s 2s 2p...4f order.
|
Source LaTeX |
All tables |
In the text