A&A 408, 621-649 (2003)
DOI: 10.1051/0004-6361:20030863
Non-spherical core collapse supernovae
I. Neutrino-driven convection,
Rayleigh-Taylor instabilities,
and the formation and propagation of metal clumps
K. Kifonidis1 -
T. Plewa1-3 -
H.-Th. Janka1 -
E. Müller1
1 - Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Straße 1,
85741 Garching, Germany
2 -
Nicolaus Copernicus Astronomical Center,
Bartycka 18, 00716 Warsaw, Poland
3 -
Center for Astrophysical Thermonuclear Flashes,
University of Chicago, 5640 S. Ellis Avenue,
Chicago, IL 60637, USA
Received 11 February 2003 / Accepted 28 May 2003
Abstract
We have performed two-dimensional simulations of core
collapse supernovae that encompass shock revival by neutrino
heating, neutrino-driven convection, explosive
nucleosynthesis, the growth of Rayleigh-Taylor
instabilities, and the propagation of newly formed metal
clumps through the exploding star. A simulation of a type II
explosion in a
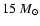 blue supergiant
progenitor is presented, that confirms our earlier type II
models and extends their validity to times as late as 5.5
hours after core bounce. We also study a type Ib-like
explosion, by simply removing the hydrogen envelope of the
progenitor model. This allows for a first comparison of
type II and type Ib evolution. We present evidence that the
hydrodynamics of core collapse supernovae beyond shock
revival differs markedly from the results of simulations
that have followed the Rayleigh-Taylor mixing starting from
ad hoc energy deposition schemes to initiate the
explosion. We find iron group elements to be synthesized in
an anisotropic, dense, low-entropy shell that expands with
velocities of
blue supergiant
progenitor is presented, that confirms our earlier type II
models and extends their validity to times as late as 5.5
hours after core bounce. We also study a type Ib-like
explosion, by simply removing the hydrogen envelope of the
progenitor model. This allows for a first comparison of
type II and type Ib evolution. We present evidence that the
hydrodynamics of core collapse supernovae beyond shock
revival differs markedly from the results of simulations
that have followed the Rayleigh-Taylor mixing starting from
ad hoc energy deposition schemes to initiate the
explosion. We find iron group elements to be synthesized in
an anisotropic, dense, low-entropy shell that expands with
velocities of  17 000 km s-1 shortly after shock
revival. The growth of Rayleigh-Taylor instabilities at the
Si/O and (C+O)/He composition interfaces of the progenitor,
seeded by the flow-structures resulting from neutrino-driven
convection, leads to a fragmentation of this shell into
metal-rich "clumps''. This fragmentation starts already
17 000 km s-1 shortly after shock
revival. The growth of Rayleigh-Taylor instabilities at the
Si/O and (C+O)/He composition interfaces of the progenitor,
seeded by the flow-structures resulting from neutrino-driven
convection, leads to a fragmentation of this shell into
metal-rich "clumps''. This fragmentation starts already
 20 s after core bounce and is complete within the
first few minutes of the explosion. During this time the
clumps are slowed down by drag, and by the positive pressure
gradient in the unstable layers. However, at
20 s after core bounce and is complete within the
first few minutes of the explosion. During this time the
clumps are slowed down by drag, and by the positive pressure
gradient in the unstable layers. However, at
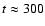 s they decouple from the flow and start to propagate
ballistically and subsonically through the He core, with the
maximum velocities of metals remaining constant at
s they decouple from the flow and start to propagate
ballistically and subsonically through the He core, with the
maximum velocities of metals remaining constant at  3500 - 5500 km s-1. This early "clump decoupling'' leads to
significantly higher
3500 - 5500 km s-1. This early "clump decoupling'' leads to
significantly higher
 velocities at t =
300 s than in one-dimensional models of the explosion,
demonstrating that multi-dimensional effects which are at
work within the first minutes, and which have been neglected
in previous studies (especially in those which dealt with
the mixing in type II supernovae), are crucial. Despite
comparably high initial maximum nickel velocities in both
our type II and our type Ib-like model, we find that there
are large differences in the final maximum nickel velocities
between both cases. In the "type Ib'' model the maximum
velocities of metals remain frozen in at
velocities at t =
300 s than in one-dimensional models of the explosion,
demonstrating that multi-dimensional effects which are at
work within the first minutes, and which have been neglected
in previous studies (especially in those which dealt with
the mixing in type II supernovae), are crucial. Despite
comparably high initial maximum nickel velocities in both
our type II and our type Ib-like model, we find that there
are large differences in the final maximum nickel velocities
between both cases. In the "type Ib'' model the maximum
velocities of metals remain frozen in at  3500 - 5500 km s-1 for
3500 - 5500 km s-1 for
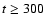 s, while in the type II model
they drop significantly for t > 1500 s. In the latter
case, the massive hydrogen envelope of the progenitor forces
the supernova shock to slow down strongly, leaving behind a
reverse shock and a dense helium shell (or "wall'') below
the He/H interface. After penetrating into this dense
material the metal-rich clumps possess supersonic speeds,
before they are slowed down by drag forces to
s, while in the type II model
they drop significantly for t > 1500 s. In the latter
case, the massive hydrogen envelope of the progenitor forces
the supernova shock to slow down strongly, leaving behind a
reverse shock and a dense helium shell (or "wall'') below
the He/H interface. After penetrating into this dense
material the metal-rich clumps possess supersonic speeds,
before they are slowed down by drag forces to  1200 km s-1 at a time of 20 000 s post-bounce. While, due
to this deceleration, the maximum velocities of iron-group
elements in SN 1987 A cannot be reproduced in case of the
considered
1200 km s-1 at a time of 20 000 s post-bounce. While, due
to this deceleration, the maximum velocities of iron-group
elements in SN 1987 A cannot be reproduced in case of the
considered
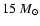 progenitor, the "type Ib''
model is in fairly good agreement with observed clump
velocities and the amount of mixing inferred for type Ib
supernovae. Thus it appears promising for calculations of
synthetic spectra and light curves. Furthermore, our
simulations indicate that for type Ib explosions the pattern
of clump formation in the ejecta is correlated with the
structure of the convective pattern prevailing during the
shock-revival phase. This might be used to deduce
observational constraints for the dynamics during this early
phase of the evolution, and the role of neutrino heating in
initiating the explosion.
progenitor, the "type Ib''
model is in fairly good agreement with observed clump
velocities and the amount of mixing inferred for type Ib
supernovae. Thus it appears promising for calculations of
synthetic spectra and light curves. Furthermore, our
simulations indicate that for type Ib explosions the pattern
of clump formation in the ejecta is correlated with the
structure of the convective pattern prevailing during the
shock-revival phase. This might be used to deduce
observational constraints for the dynamics during this early
phase of the evolution, and the role of neutrino heating in
initiating the explosion.
Key words: hydrodynamics - instabilities - nuclear reactions, nucleosynthesis abundances -
shock waves - stars: supernovae: general
The strong shock wave that has torn apart Sk
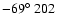 and
in consequence has given rise to Supernova SN 1987 A in the Large
Magellanic Cloud on February 23rd, 1987, has also shattered the at
that time widely shared belief that supernova explosions are
essentially spherically symmetric events. The avalanche of
observational data obtained since then from SN 1987 A has
unambiguously demonstrated that the envelope of the progenitor star
had substantially fragmented during the explosion. Fast clumps of
and
in consequence has given rise to Supernova SN 1987 A in the Large
Magellanic Cloud on February 23rd, 1987, has also shattered the at
that time widely shared belief that supernova explosions are
essentially spherically symmetric events. The avalanche of
observational data obtained since then from SN 1987 A has
unambiguously demonstrated that the envelope of the progenitor star
had substantially fragmented during the explosion. Fast clumps of
 and its decay products had formed in the innermost
regions of the ejecta and propagated out to the outer layers of the
hydrogen envelope (i.e. close to the supernova's photosphere) within
only days after core collapse (compare e.g. Mitchell et al. 2001). For
a bibliography of the observational evidence see the reviews of
Hillebrandt & Höflich (1989), Arnett et al. (1989a), McCray (1993),
Nomoto et al. (1994), Wooden (1997), Müller (1998), and the
references therein.
and its decay products had formed in the innermost
regions of the ejecta and propagated out to the outer layers of the
hydrogen envelope (i.e. close to the supernova's photosphere) within
only days after core collapse (compare e.g. Mitchell et al. 2001). For
a bibliography of the observational evidence see the reviews of
Hillebrandt & Höflich (1989), Arnett et al. (1989a), McCray (1993),
Nomoto et al. (1994), Wooden (1997), Müller (1998), and the
references therein.
Spherical symmetry is not only broken in the case of SN 1987 A. This is
apparently a generic feature, as is indicated by the spectra of a
number of core collapse SNe that have been observed for more than one
decade. Significant mixing and clumpiness of the ejecta were found for
the type II explosions SN 1995 V (Fassia et al. 1998), SN 1988 A
(Spyromilio 1991) and SN 1993 J (Spyromilio 1994; Woosley et al. 1994; Wang & Hu 1994).
In case of type Ib supernovae the indications for mixing are even
older. For instance, Filippenko & Sargent (1989) using [O I]
observations have found that the ejecta of SN 1987 F were
clumped. Even earlier, Harkness et al. (1987) in constructing synthetic
spectra encountered the first evidence. They had to overpopulate
excited states of He I by factors of  104 relative to local
thermodynamic equilibrium (LTE) conditions in order to reproduce the
characteristic strong He lines of this supernova type. It was shown
later by Lucy (1991) and Swartz et al. (1993) that the presence of the
He I lines and the implied departures from LTE can be understood in
terms of impact excitations and ionizations by nonthermal
electrons. The latter are presumed to originate from
Compton-scattering of the
104 relative to local
thermodynamic equilibrium (LTE) conditions in order to reproduce the
characteristic strong He lines of this supernova type. It was shown
later by Lucy (1991) and Swartz et al. (1993) that the presence of the
He I lines and the implied departures from LTE can be understood in
terms of impact excitations and ionizations by nonthermal
electrons. The latter are presumed to originate from
Compton-scattering of the 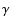 -rays from
-rays from
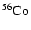 decay and
hence this hints toward significant outward mixing of
decay and
hence this hints toward significant outward mixing of
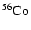 .
Artificially mixed one-dimensional explosion models of type Ib
progenitors indeed yield good fits to observed type Ib spectra and
light curves (Shigeyama et al. 1990; Woosley & Eastman 1997).
.
Artificially mixed one-dimensional explosion models of type Ib
progenitors indeed yield good fits to observed type Ib spectra and
light curves (Shigeyama et al. 1990; Woosley & Eastman 1997).
Such observations have stimulated theoretical and numerical work on
hydrodynamic instabilities, which up to now has been dichotomized into
two distinct classes. On the one hand multi-dimensional modelling of
the explosion mechanism was attempted
(Mezzacappa et al. 1998; Burrows et al. 1995; Herant et al. 1994,1992; Burrows & Fryxell 1993; Miller et al. 1993; Janka & Müller 1996),
mainly with the aim to answer the question as to which extent
convective instabilities are helpful for generating neutrino-driven
explosions. Therefore, these simulations have been constrained to the
early shock propagation phase up to about one second after core
bounce.
In contrast, hydrodynamic models of the late-time shock propagation
and the associated formation of Rayleigh-Taylor instabilities in the
expanding mantle and envelope of the exploding star
(Nagataki et al. 1998; Fryxell et al. 1991; Yamada & Sato 1990; Müller et al. 1991b; Yamada & Sato 1991; Iwamoto et al. 1997; Shigeyama et al. 1996; Müller et al. 1991a; Kane et al. 2000; Hachisu et al. 1990; Herant & Benz 1991,1992; Hachisu et al. 1991,1992; Herant & Woosley 1994; Hachisu et al. 1994; Müller et al. 1991c; Arnett et al. 1989b) have
ignored the complications of the explosion mechanism. Due to
considerable computational difficulties in resolving the relevant
spatial and temporal scales all of these latter investigations
relied on ad hoc procedures to initiate the explosion. This usually
meant that some simple form of energy deposition (by a piston or
"thermal bomb'') was used to generate a shock wave in a progenitor
model. The subsequent propagation of the blast wave was followed in a
one-dimensional simulation until the shock had reached the (C+O)/He or
the He/H interface. Then, the 1D model was mapped to a
multi-dimensional grid, and an assumed spectrum of seed perturbations
was added to the radial velocity field in order to break the spherical
symmetry of the problem and to trigger the growth of the instability.
The studies of Yamada & Sato (1991,1990), Nagataki et al. (1998,1997), and the recent 3D calculations of Hungerford et al. (2003), who investigated the effects
of metal mixing on X-ray and 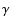 -ray spectra formation, differ
from this universally adopted approach by making use of parameterized,
aspherical shock waves.
-ray spectra formation, differ
from this universally adopted approach by making use of parameterized,
aspherical shock waves.
All Rayleigh-Taylor calculations, that have been carried out to date
for reproducing the mixing in SN 1987 A, share the same problem: With
at most 2000 km s-1 their maximum
 velocities are
significantly smaller than the observed values of
3500-4000 km s-1. Herant & Benz (1992) dubbed this problem the "nickel
discrepancy''. They also speculated that it should disappear when the
"premixing'' of the ejecta during the phase of neutrino-driven
convection is taken into account. On the other hand Nagataki et al. (1998)
do not agree with Herant & Benz. They claim that the nickel
discrepancy is resolved if the supernova shock is (mildly) aspherical.
Similar conclusions have been reached by Hungerford et al. (2003). While
Nagataki et al. as well as Hungerford et al. do not rule
out neutrino emission from the neutron star as an explanation for the
assumed asphericity of their shocks, Khokhlov et al. (1999),
Wheeler et al. (2002) and Wang et al. (2002) questioned the neutrino-driven
mechanism. Instead, they speculated on "jet-driven'' explosions,
which might originate from magneto-hydrodynamic effects in connection
with a rapidly rotating neutron star.
velocities are
significantly smaller than the observed values of
3500-4000 km s-1. Herant & Benz (1992) dubbed this problem the "nickel
discrepancy''. They also speculated that it should disappear when the
"premixing'' of the ejecta during the phase of neutrino-driven
convection is taken into account. On the other hand Nagataki et al. (1998)
do not agree with Herant & Benz. They claim that the nickel
discrepancy is resolved if the supernova shock is (mildly) aspherical.
Similar conclusions have been reached by Hungerford et al. (2003). While
Nagataki et al. as well as Hungerford et al. do not rule
out neutrino emission from the neutron star as an explanation for the
assumed asphericity of their shocks, Khokhlov et al. (1999),
Wheeler et al. (2002) and Wang et al. (2002) questioned the neutrino-driven
mechanism. Instead, they speculated on "jet-driven'' explosions,
which might originate from magneto-hydrodynamic effects in connection
with a rapidly rotating neutron star.
The above controversy demonstrates the need for models which link
observable features at very large radii to the actual energy source
and the mechanism of the explosion. Without such models,
interpretation of observational data requires caution. With the
present work, which is the first in a series of papers on
non-spherical core collapse supernova evolution, we attempt to provide
this link for the standard paradigm of neutrino-driven supernovae. We
have performed the first one and two-dimensional hydrodynamic
calculations of type II and type Ib-like explosions of blue supergiant
stars that reach from 20 ms up to 20 000 s (i.e. 5.5 hrs) after
core bounce. Thus, we follow the evolution well beyond the time of
shock eruption from the stellar photosphere. Our models include a
detailed treatment of shock revival by neutrinos, the accompanying
convection and nucleosynthesis and the growth of Rayleigh-Taylor
instabilities at the composition interfaces of the progenitor star
after shock passage. We employ high spatial resolution, which is
mandatory to follow the episodes of clump formation, mixing, and clump
propagation, by making use of adaptive mesh refinement techniques.
Preliminary results of this work, which covered the first five minutes
in the evolution of a type II supernova, were reported by
Kifonidis et al. (2000).
This paper is organized as follows: we start with an account of the
physical assumptions and numerical methods implemented in our computer
codes in Sect. 2. We then describe our stellar model
in Sect. 3. Our boundary conditions along with some
technical details of our computational strategy are discussed in
Sect. 4. This is then followed in
Sect. 5 with our description of the early evolution
up to 0.82 s after core bounce. To focus the discussion, we
restrict ourselves to one basic shock-revival model, from which we
start all subsequent calculations. To illustrate its physics as
clearly as possible, we first present the one-dimensional case in
Sect. 5.1 and then the two-dimensional results in
Sect. 5.2. In the same manner we discuss the
subsequent evolution of a type II supernova model in
Sect. 6. In Sect. 7, we
consider the problem of a type Ib explosion by simply removing the
hydrogen envelope of our progenitor. Section 8
finally contains our conclusions.
2 The codes
There is as yet no numerical code that could satisfactorily handle all
the computational difficulties encountered in the modelling of core
collapse supernovae over the time scales that we are interested in in
this paper. Fortunately, however, such a code is not mandatory for
studying the effects that are responsible for the formation and
propagation of the nickel clumps. A crucial simplification arises from
the fact that the physical character of the explosion changes
fundamentally from a neutrino-hydrodynamic to a purely hydrodynamic
problem once the shock has been revived and launched successfully by
neutrino heating. A simulation of the long-time evolution of the
ejecta can therefore be split into two parts. A neutrino-hydrodynamic
calculation that encompasses the challenges of modelling
neutrino-driven explosions but does not require an extremely high
dynamical range of the spatial resolution, since only the innermost
stellar core needs to be resolved adequately. In contrast, in the
second, hydrodynamic part, the physics of the problem simplifies to
the solution of the hydrodynamic equations because (to a good
approximation) the central neutron star influences the dynamics of the
ejecta only via its gravitational attraction and can otherwise be
disregarded. It is this part of the calculation, however, where a high
spatial resolution is essential in order to resolve the growth and
expansion of Rayleigh-Taylor instabilities.
The separation into two largely independent problems might not be
appropriate, if one is interested in an accurate determination of
quantities that are influenced by the long-time hydrodynamic evolution
of the layers near the neutron star. Among these quantities are the
yields of r-process elements and the amount of fallback, which depend
on the properties of the neutrino-driven wind as well as on the
propagation of reverse shocks through the inner ejecta. We will not
address these problems in the present work. Instead, we have developed
two different codes to solve each of the sub-tasks described above: a
modified version of the hydrodynamics code of Janka & Müller (1996) (henceforth JM96) that includes neutrino effects, and the adaptive mesh refinement (AMR) code AMRA, a FORTRAN implementation of the AMR
algorithm of Berger & Colella (1989). Here we discuss only the most important
features of these codes and give some details of our hydrodynamic
advection scheme. AMRA is described in length in Plewa & Müller (2001).
Our goal is to study the main observational consequences of
hydrodynamic instabilities in different layers of a supernova. We do
not attempt to compete with the contemporary, highly sophisticated
modelling of neutrino-driven explosions (for which an accurate
treatment of neutrino transport is indispensable). For our purpose, a
simple neutrino light-bulb algorithm, as the one of JM96, has the
advantage to save enormous amounts of computer time as compared to
detailled transport codes (see Rampp & Janka 2002, and the references
therein). Omitting the core of the neutron star and
replacing it by a boundary condition, that parameterizes its
contraction and the radiated neutrino luminosities and spectra, we
make use of the freedom to vary the neutrino properties. Thus we are
able to control the explosion time scale and the final explosion
energy in our simulations. By computing models with different values
of the parameters, we can explore the physical possibilities as a
consequence of neutrino-driven explosions. The local effects of
neutrino heating and cooling by all relevant processes are treated
reasonably well with our light-bulb scheme. However, a light-bulb
description, of course, neglects all forms of back-reactions to the
neutrino fluxes and spectra that result from neutrino absorption in
the heating layer behind the supernova shock, and from neutrino
emission associated with the accretion of matter onto the neutron
star. We have recently developed a gray, characteristics-based scheme
for the neutrino transport that accounts for spectral and luminosity
modifications due to such effects. This new treatment is currently
applied in new two and three-dimensional simulations. The calculations
in this paper, however, were still performed with the light-bulb code.
The neutrino physics is combined with an enhanced version of the PPM
hydrodynamics scheme (see below) and the equation of state (EOS) of
JM96. The baryonic component of this EOS consists of 4 nuclei
(neutrons, protons, 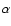 -particles and a representative nucleus of
the iron group) in nuclear statistical equilibrium (NSE). These four
species are also used to compute the energy source terms resulting
from nuclear transmutations. In addition to this small NSE
"network'', but without feedback to the EOS and the hydrodynamics, we
also evolve a 14 species nuclear reaction network to approximately
calculate the products of explosive nucleosynthesis, whose spatial
distribution we wish to follow. The latter network consists of the
13
-particles and a representative nucleus of
the iron group) in nuclear statistical equilibrium (NSE). These four
species are also used to compute the energy source terms resulting
from nuclear transmutations. In addition to this small NSE
"network'', but without feedback to the EOS and the hydrodynamics, we
also evolve a 14 species nuclear reaction network to approximately
calculate the products of explosive nucleosynthesis, whose spatial
distribution we wish to follow. The latter network consists of the
13 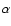 -nuclei from
-nuclei from
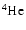 to
to
 and an additional
tracer nucleus to which we channel the flow resulting from the
reaction
and an additional
tracer nucleus to which we channel the flow resulting from the
reaction
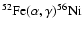 in case the electron
fraction
in case the electron
fraction 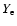 drops below 0.490 and
drops below 0.490 and
 ceases to be
the dominant nucleus synthesized in the iron group
(e.g. Thielemann et al. 1996). In this way we can "mark'' material that
freezes out from NSE at conditions of neutron excess and distinguish
it from
ceases to be
the dominant nucleus synthesized in the iron group
(e.g. Thielemann et al. 1996). In this way we can "mark'' material that
freezes out from NSE at conditions of neutron excess and distinguish
it from
 whose yield would otherwise be
overestimated. The 14 species network is solved for temperatures
between 108 K and
whose yield would otherwise be
overestimated. The 14 species network is solved for temperatures
between 108 K and
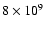 K. Above
K. Above
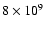 K, we
assume that nuclei have been disintegrated to
K, we
assume that nuclei have been disintegrated to 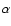 -particles. Of
course, the 14 species network is a simplification of the
nucleosynthesis processes in a supernova, since it neglects important
isotopes and production channels of the considered nuclei. Moreover,
in our current code version the heating and composition changes due to
explosive silicon, oxygen, neon, and carbon burning as described by
the 14 species network are not taken into account in the solution of
the hydrodynamics, which implies an approximation of the
thermodynamical history of the regions where nuclear burning
occurs. However, the hydrodynamic evolution should hardly be affected
in the simulations presented in this paper. This can be seen by
estimating the energy release due to nuclear transmutations. In
core-collapse supernovae three thermodynamic regimes can be
distinguished. Below
-particles. Of
course, the 14 species network is a simplification of the
nucleosynthesis processes in a supernova, since it neglects important
isotopes and production channels of the considered nuclei. Moreover,
in our current code version the heating and composition changes due to
explosive silicon, oxygen, neon, and carbon burning as described by
the 14 species network are not taken into account in the solution of
the hydrodynamics, which implies an approximation of the
thermodynamical history of the regions where nuclear burning
occurs. However, the hydrodynamic evolution should hardly be affected
in the simulations presented in this paper. This can be seen by
estimating the energy release due to nuclear transmutations. In
core-collapse supernovae three thermodynamic regimes can be
distinguished. Below
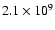 K (the minimum temperature
required for explosive Ne/C burning; Thielemann et al. 1996) nuclear burning
time scales are large compared to the hydrodynamic expansion time
scale of the layers that contain the nuclear fuel, and no appreciable
nucleosynthesis occurs. For temperatures
K (the minimum temperature
required for explosive Ne/C burning; Thielemann et al. 1996) nuclear burning
time scales are large compared to the hydrodynamic expansion time
scale of the layers that contain the nuclear fuel, and no appreciable
nucleosynthesis occurs. For temperatures
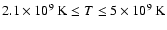 the burning time scales are
comparable to the expansion time scale, and the abundance and energy
changes need to be followed by solving a nuclear reaction
network. Above
the burning time scales are
comparable to the expansion time scale, and the abundance and energy
changes need to be followed by solving a nuclear reaction
network. Above
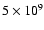 K NSE holds, i.e. the composition
adjusts immediately to temperature and density changes caused by the
hydrodynamics. In our code, energy source terms due to explosive
burning are not accounted for only in the second regime (in the NSE
regime the energy source term is obtained from the 4 species network).
For the
K NSE holds, i.e. the composition
adjusts immediately to temperature and density changes caused by the
hydrodynamics. In our code, energy source terms due to explosive
burning are not accounted for only in the second regime (in the NSE
regime the energy source term is obtained from the 4 species network).
For the
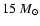 Woosley et al. (1988) progenitor that we employed
(see Sect. 3), we estimated that thermonuclear burning
in layers with temperatures
Woosley et al. (1988) progenitor that we employed
(see Sect. 3), we estimated that thermonuclear burning
in layers with temperatures
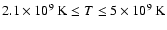 releases
releases 
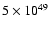 ergs. This
energy is small compared to the explosion energies of our models
(about
ergs. This
energy is small compared to the explosion energies of our models
(about
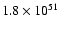 ergs), and is therefore negligible with
respect to the dynamics. This may not be true, however, in case of
other (e.g. more massive) progenitors.
ergs), and is therefore negligible with
respect to the dynamics. This may not be true, however, in case of
other (e.g. more massive) progenitors.
Gravity is taken into account in our neutrino-hydrodynamics code by
solving Poisson's equation in two spatial dimensions with the
algorithm of Müller & Steinmetz (1995). To avoid the formation of transient shock
oscillations in case general relativistic post collapse models are
used as initial data (compare JM96), we add 1D (i.e. spherical)
general relativistic corrections to the 2D Newtonian gravitational
potential as in Keil et al. (1996) (see Rampp & Janka 2002 for
details of the implementation and compare also to
van Riper 1979). These corrections are especially important in
the early phase of shock revival, since the deeper relativistic
potential well keeps the shock at significantly smaller radii than in
the Newtonian case. However, Newtonian gravity becomes an excellent
approximation at large distances from the neutron star. Therefore it
can be used once the shock has emerged from the iron core and
propagates through the oxygen shell. This is also the time when we map
our explosion models to follow the late evolution with
AMRA. In the AMR calculations Poisson's equation is solved in
one spatial dimension with an angular average of the density. The
equation of state that we employed for these simulations includes
contributions from non-relativistic, non-degenerate electrons,
photons, electron-positron pairs (the formulae for pressure and
energy density due to pairs can be derived from information given
by Witti et al. 1994) and the 14 nuclei (treated as Boltzmann gases) that
are included in the reaction network of our neutrino code. Separate
continuity equations are solved for each of these nuclei in order to
determine the mixing of the elements.
The neutrino-hydrodynamics code as well as AMRA, make use of
the HERAKLES hydrodynamics solver, an implementation of the
direct Eulerian version of the Piecewise Parabolic Method (PPM) of
Colella & Woodward (1984). HERAKLES originated from the
PROMETHEUS code of Fryxell et al. (1991). It includes the entire
functionality of PROMETHEUS, but differs from its predecessor
in the following aspects. The handling of multifluid flows of
Fryxell et al. (1991) is replaced by the Consistent Multifluid Advection scheme (CMA) of Plewa & Müller (1999). This allows for a significant reduction of
numerical diffusion of nuclear species (to the level that is
characteristic for the PPM advection scheme) without suffering from
errors in local mass conservation (see Plewa & Müller 1999). Further
improvements in reducing the numerical diffusivity of the code are
achieved by adopting the elaborate procedure for the flattening of
interpolated profiles for the (primitive) state variables that is
suggested in the Appendix of Colella & Woodward (1984). Additionally, the algorithm
for the computation of the left and right input states for the Riemann
problem is revised. The version of HERAKLES that is used as
hydrodynamic solver in our AMR calculations has been further extended
to achieve good computational performance even on small grid
patches. For this purpose a new memory interface was written, that
allows for optimal pipelining of the one-dimensional hydrodynamic
sweeps that result from dimensional splitting in multi-dimensional
calculations, while due attention is paid to optimal cache reuse. With
this memory interface the code can make efficient use of both
superscalar as well as vector computer architectures.
The most important modifications as compared to PROMETHEUS
(or other standard implementations of the PPM scheme) are, however,
the inclusion of new algorithms for the artificial viscosity and for
multi-dimensional shock detection, along with the addition of
Einfeldt's HLLE Riemann solver
(Einfeldt 1988). Following Quirk (1997,1994) we use
the Einfeldt solver for zones inside strong
grid-aligned shocks, while we retain the (less diffusive) Riemann
solver of Colella & Glaz (1985) for all remaining grid cells. The latter changes
are necessary to eliminate the odd-even decoupling instability
(Quirk 1997; Liou 2000; Quirk 1994), from which the original
Colella & Glaz solver suffers (Kifonidis et al. 2000). This numerical
failure shows up if a sufficiently strong shock is (nearly) aligned
with one of the coordinate directions of the grid, and if, in
addition, the flow is slightly perturbed. Many Riemann solvers allow
these perturbations to grow without limit along the shock surface,
thus triggering a strong rippling of the shock front and the
post-shock state. In supernova simulations, these perturbations
strongly enhance the growth of hydrodynamic instabilities, since their
amplitudes can exceed those of the intentionally introduced seed
perturbations by several orders of magnitude. In case of
neutrino-driven convection this leads to faster growth of convective
instabilities and angular wavelengths of convective bubbles which are
significantly larger than in a "clean'' calculation. This is
demonstrated in Fig. 1 where we compare entropy plots
of two simulations of neutrino-driven convection that were conducted
using spherical coordinates and the neutrino parameters given in
Sect. 5.1. The first of these
(Fig. 1a) was done with our original
PROMETHEUS version and a resolution of
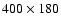 zones
and is affected by odd-even decoupling, while the second
(Fig. 1b) was obtained with the improved scheme
implemented in HERAKLES using
zones
and is affected by odd-even decoupling, while the second
(Fig. 1b) was obtained with the improved scheme
implemented in HERAKLES using
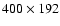 zones.
zones.
Odd-even decoupling and the associated carbuncle phenomenon
(i.e. a local occurrence of odd-even decoupling for shocks that
are only partly aligned with the
grid; LeVeque 1998; Quirk 1997,1994) have gone largely
unnoticed in the astrophysics literature and have marred almost all
multi-dimensional supernova simulations conducted to date on
cylindrical or spherical grids with hydrodynamic codes that are based
on Riemann solver type schemes (e.g. Mezzacappa et al. 1998; Hachisu et al. 1992,1994; Burrows & Fryxell 1993; Iwamoto et al. 1997; Müller et al. 1991a; Kifonidis et al. 2000; Burrows et al. 1995; Janka & Müller 1996).
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{3592f01a.ps}\hspace*{3mm}
\includegraphics[width=6.4cm,clip]{3592f01b.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg61.gif) |
Figure 1:
Entropy (in units of 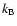 per nucleon) in Model T310
at a time of 420 ms after core bounce. The white contour
line encloses the region where the
per nucleon) in Model T310
at a time of 420 ms after core bounce. The white contour
line encloses the region where the
 mass
fraction is
mass
fraction is 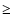 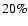 .
a) Calculation performed with the
original PROMETHEUS code showing odd-even
decoupling. Note the deformation of the shock. b)
Calculation performed with HERAKLES. .
a) Calculation performed with the
original PROMETHEUS code showing odd-even
decoupling. Note the deformation of the shock. b)
Calculation performed with HERAKLES. |
| Open with DEXTER |
3 The stellar model
As in JM96 and Kifonidis et al. (2000) the initial model adopted for our
study originated from the simulations of Bruenn (1993), who followed
core collapse and bounce of the
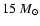 blue supergiant
progenitor of Woosley et al. (1988). We have set up our shock revival
calculations using his model WPE15 LS (180) at a time of 20 ms after
core bounce. However, Bruenn's data set extends only to layers within
the stellar He core and the original progenitor model of Woosley et al. (1988)
is no longer available. To follow the late-time propagation of the
shock in our subsequent AMR calculations we thus had to reconstruct
the outer envelope of the Woosley et al. star. For this purpose
we used a new 15
blue supergiant
progenitor of Woosley et al. (1988). We have set up our shock revival
calculations using his model WPE15 LS (180) at a time of 20 ms after
core bounce. However, Bruenn's data set extends only to layers within
the stellar He core and the original progenitor model of Woosley et al. (1988)
is no longer available. To follow the late-time propagation of the
shock in our subsequent AMR calculations we thus had to reconstruct
the outer envelope of the Woosley et al. star. For this purpose
we used a new 15
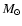 blue supergiant model
(S. E. Woosley, private communication) that was smoothly joined to
Bruenn's data by choosing a matching point at
blue supergiant model
(S. E. Woosley, private communication) that was smoothly joined to
Bruenn's data by choosing a matching point at
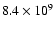 cm
(
cm
(
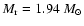 ), i.e. within the He
core. Table 1 summarizes the location of the composition
interfaces and the initial position of the
), i.e. within the He
core. Table 1 summarizes the location of the composition
interfaces and the initial position of the 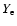 discontinuity
(that defines the boundary of the iron core according
to Woosley & Weaver 1995) of the resulting "hybrid''
discontinuity
(that defines the boundary of the iron core according
to Woosley & Weaver 1995) of the resulting "hybrid''
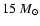 progenitor. Except for the He/H interface, the listed
radii were taken from the post-collapse data of Bruenn (1993).
progenitor. Except for the He/H interface, the listed
radii were taken from the post-collapse data of Bruenn (1993).
Since the velocity of the supernova shock and the associated growth of
Rayleigh-Taylor instabilities are very sensitive to the density
profile, we have verified in a number of one-dimensional test
calculations that the hybrid stellar model had no adverse effects on
shock propagation. In these calculations we cut out the model's iron
core and induced the explosion artificially by depositing  1051 ergs in the form of thermal energy at the inner boundary of
the silicon shell. This procedure enabled us to compare the
hydrodynamic evolution of our hybrid model with induced explosions of
newer SN 1987 A progenitor models computed by Woosley et al. (1997) (for
which no collapse calculations including neutrino transport were
available at the time we performed our simulations). No differences
pointing to numerical artifacts were found.
1051 ergs in the form of thermal energy at the inner boundary of
the silicon shell. This procedure enabled us to compare the
hydrodynamic evolution of our hybrid model with induced explosions of
newer SN 1987 A progenitor models computed by Woosley et al. (1997) (for
which no collapse calculations including neutrino transport were
available at the time we performed our simulations). No differences
pointing to numerical artifacts were found.
Table 1:
Location of chemical interfaces in our progenitor model
at 20 ms after core bounce.
4 Computational setup
To set up a shock revival simulation we adopt spherical coordinates.
We omit the innermost 0.848 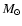 of the core of the
neutron star and replace it by the gravitational potential of a point
mass and an inner boundary which acts as a neutrino source. This
boundary is placed at a radius of
of the core of the
neutron star and replace it by the gravitational potential of a point
mass and an inner boundary which acts as a neutrino source. This
boundary is placed at a radius of
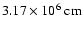 ,
which
is somewhat below the electron neutrinosphere in Bruenn's model. The
outer radial boundary is located at
,
which
is somewhat below the electron neutrinosphere in Bruenn's model. The
outer radial boundary is located at
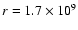 cm,
inside the C+O-core of the star. Our grid consists of 400
non-equidistant radial zones that yield a maximum resolution of
1.2 km at the neutron star and 200 km at the outer grid boundary. In
our two-dimensional models 192 angular zones are distributed uniformly
between
cm,
inside the C+O-core of the star. Our grid consists of 400
non-equidistant radial zones that yield a maximum resolution of
1.2 km at the neutron star and 200 km at the outer grid boundary. In
our two-dimensional models 192 angular zones are distributed uniformly
between
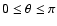 and axial symmetry is assumed around
the polar axis. Reflecting boundaries are imposed at
and axial symmetry is assumed around
the polar axis. Reflecting boundaries are imposed at
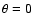 and
and
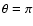 and a random initial seed perturbation is added to the
velocity field on the entire grid with a modulus of 10-3 of the
(radial) velocity of the post-collapse model. In the immediate
upstream region of the accretion shock, this corresponds to velocity
perturbations with a modulus of
and a random initial seed perturbation is added to the
velocity field on the entire grid with a modulus of 10-3 of the
(radial) velocity of the post-collapse model. In the immediate
upstream region of the accretion shock, this corresponds to velocity
perturbations with a modulus of 
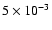 of the local
sound speed, while further outward this value decreases with the
decreasing infall velocities to
of the local
sound speed, while further outward this value decreases with the
decreasing infall velocities to  10-3.
10-3.
In order to mimic the contraction of the cooling and deleptonizing
proto-neutron star, the inner boundary is moved inward during the
computations, approximating the motion of the corresponding mass shell
in Bruenn's calculations. This is achieved by making use of the moving
grid implemented in our code (cf. JM96 for details). Free outflow is
allowed for across the outer radial boundary. With this setup, the
time-step resulting from the Courant-Friedrichs-Lewy stability
condition is typically of the order of a few 10-5 s in
one-dimensional calculations, and several 10-6 s in
two-dimensional simulations. Starting at 20 ms after core bounce the
computations are continued until 820 ms post-bounce, when the
explosion energy has saturated and all nuclear reactions have frozen
out.
By performing test calculations we have found that, in order to enable
a sufficiently detailed study of the growth of all relevant
Rayleigh-Taylor instabilities, a spatial resolution of
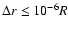 (with R being the stellar radius) is required for at
least some fraction of the time that it takes the shock to erupt from
the surface of the star. The above estimate holds for the case of a
blue supergiant like Sk
(with R being the stellar radius) is required for at
least some fraction of the time that it takes the shock to erupt from
the surface of the star. The above estimate holds for the case of a
blue supergiant like Sk
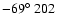 .
In case of a red
supergiant an even smaller ratio
.
In case of a red
supergiant an even smaller ratio
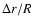 would be
necessary. Without adaptive mesh refinement and/or a moving grid such
calculations are currently unfeasible, especially in more than one
spatial dimension. While this range of spatial scales appears
formidable, for explicit codes like PPM an even more severe difficulty
is posed by the vastly differing time scales involved in the
problem. Even if the inner boundary is placed far away from the
neutron star, and the gravitational attraction of the omitted stellar
layers is taken into account by a point mass, the resulting Courant
time step is still too small to allow one to follow the evolution over
hours. The small time step is caused by fallback, which leads to high
sound speeds in the central zones because matter that falls back
toward the inner boundary is compressed and heated. The only remedies
to this problem that we have found to be practical are either a
coarsening of the grid or a shift of the inner boundary with time
towards larger radii, where smaller temperatures are
encountered. While the former is useful in 1D calculations, where the
remaining grid resolution that we achieved was still reasonable (see
below), the latter proved to be the better choice for our
two-dimensional calculations.
would be
necessary. Without adaptive mesh refinement and/or a moving grid such
calculations are currently unfeasible, especially in more than one
spatial dimension. While this range of spatial scales appears
formidable, for explicit codes like PPM an even more severe difficulty
is posed by the vastly differing time scales involved in the
problem. Even if the inner boundary is placed far away from the
neutron star, and the gravitational attraction of the omitted stellar
layers is taken into account by a point mass, the resulting Courant
time step is still too small to allow one to follow the evolution over
hours. The small time step is caused by fallback, which leads to high
sound speeds in the central zones because matter that falls back
toward the inner boundary is compressed and heated. The only remedies
to this problem that we have found to be practical are either a
coarsening of the grid or a shift of the inner boundary with time
towards larger radii, where smaller temperatures are
encountered. While the former is useful in 1D calculations, where the
remaining grid resolution that we achieved was still reasonable (see
below), the latter proved to be the better choice for our
two-dimensional calculations.
In all of our AMR simulations we have adopted spherical coordinates
and a pre-chosen AMR grid hierarchy to which we mapped the data of our
explosion models without adding any extra seed
perturbations. At radii where data from the explosion models are not
available, the structural information is taken from the progenitor
model. The inner regions of an explosion model are cut out by placing
the inner boundary of the AMR base level grid at a radius of 108 cm, which is well inside the neutrino-driven wind of the
neutron star. This baryonic mass flow is therefore neglected in the
subsequent evolution. Instead we allowed for free outflow through the
inner (as well as the outer) boundary. This is certainly a gross
simplification for the evolution of the innermost regions of the flow
during the first minute of the explosion (but becomes more realistic
later when the neutrino wind is expected to cease). By ignoring the
neutrino wind one obtains early fallback of matter through the inner
boundary. In addition, the evolution of the reverse shock, which
results from the slow-down of the main shock in the oxygen core, is
affected. This reverse shock separates the wind from the outer ejecta
at times later than  500 ms after bounce (compare
Sect. 5). Without the pressure of the wind, the
reverse shock propagates inward and is (partially) reflected at the
inner boundary because the latter is not perfectly transmitting for
numerical reasons. Although both the inward motion and reflection of
the reverse shock are expected to happen once the wind weakens (with
the reverse shock being reflected at the steep density gradient near
the neutron star "surface''), our approximations do not allow to
model these phenomena reliably in space and time. Except for resulting
in these limitations (which are not relevant for studying clump
formation and propagation), the mapping from one code to the other
worked very well and did not produce any noticeable artifacts.
500 ms after bounce (compare
Sect. 5). Without the pressure of the wind, the
reverse shock propagates inward and is (partially) reflected at the
inner boundary because the latter is not perfectly transmitting for
numerical reasons. Although both the inward motion and reflection of
the reverse shock are expected to happen once the wind weakens (with
the reverse shock being reflected at the steep density gradient near
the neutron star "surface''), our approximations do not allow to
model these phenomena reliably in space and time. Except for resulting
in these limitations (which are not relevant for studying clump
formation and propagation), the mapping from one code to the other
worked very well and did not produce any noticeable artifacts.
For our 1D AMR calculation of Sect. 6.1, we employed a
grid hierarchy with a base grid resolution of 512 zones and 7 levels
of refinement. We use two criteria to flag zones on a given level for
refinement. First, we estimate the local truncation error for the
(mass) density, momentum density, total energy density, and the
partial densities of nuclei, 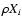 ,
using Richardson
extrapolation. Whenever the error for one of these quantities is found
to be
,
using Richardson
extrapolation. Whenever the error for one of these quantities is found
to be 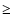 10-2 (or
10-2 (or 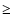 10-3 in case of the
10-3 in case of the 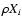 ), we
flag the corresponding zone for refinement. Independent of the
truncation error estimate, we also flag zones in which density jumps
), we
flag the corresponding zone for refinement. Independent of the
truncation error estimate, we also flag zones in which density jumps
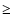 100% are encountered as compared to neighbouring zones. To
refine between different levels, we use factors of 4 in resolution
until level 5 is reached, where we switch to refinement factors of
2. With this scheme we achieve a maximum resolution equivalent to
524 288 equidistant zones. Since the outer boundary of the
computational domain is kept at the stellar radius of
100% are encountered as compared to neighbouring zones. To
refine between different levels, we use factors of 4 in resolution
until level 5 is reached, where we switch to refinement factors of
2. With this scheme we achieve a maximum resolution equivalent to
524 288 equidistant zones. Since the outer boundary of the
computational domain is kept at the stellar radius of
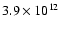 cm, this translates to an absolute resolution of
cm, this translates to an absolute resolution of
 75 km. Using this setup, we measure speed-up factors (as
compared to using a uniform grid) that are as large as 103. Still,
however, the small time step resulting from the high sound speed in
the innermost zones leads to long computing times. We therefore remove
the 7th level of the grid hierarchy after 1870 s of evolution and
thereby reduce the maximum resolution to 149 km. This zoning is kept
until t = 4770 s, when also level 6 is discarded and the rest of
the evolution followed with a maximum resolution of 298 km. It should
be noted that AMR allows one to introduce this coarsening in a rather
straightforward fashion by manually resetting the refinement flags
returned from the error estimation and zone flagging modules of the
code. The grid can even be coarsened only locally if required. Our 1D
simulation is stopped at t = 8500 s post bounce, 1700 s after
the shock has emerged from the photosphere.
75 km. Using this setup, we measure speed-up factors (as
compared to using a uniform grid) that are as large as 103. Still,
however, the small time step resulting from the high sound speed in
the innermost zones leads to long computing times. We therefore remove
the 7th level of the grid hierarchy after 1870 s of evolution and
thereby reduce the maximum resolution to 149 km. This zoning is kept
until t = 4770 s, when also level 6 is discarded and the rest of
the evolution followed with a maximum resolution of 298 km. It should
be noted that AMR allows one to introduce this coarsening in a rather
straightforward fashion by manually resetting the refinement flags
returned from the error estimation and zone flagging modules of the
code. The grid can even be coarsened only locally if required. Our 1D
simulation is stopped at t = 8500 s post bounce, 1700 s after
the shock has emerged from the photosphere.
Table 2:
Computational setup for the 2D AMR calculation T310a.
(see Sect. 6.2). The initial and final times
over which the inner and outer grid boundaries were held
fixed at
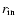 and
and
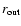 ,
are denoted by
,
are denoted by 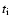 and
and 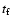 ,
respectively.
,
respectively. 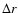 is the (absolute) resolution and
is the (absolute) resolution and
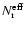 the number of equidistant radial zones
that would have been required to cover the entire star
in order to achieve a resolution of
the number of equidistant radial zones
that would have been required to cover the entire star
in order to achieve a resolution of 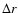 .
Exponents are given in brackets.
.
Exponents are given in brackets.
For our 2D calculations we have adopted a different approach,
combining mesh refinement with a "zooming'' algorithm for the radial
coordinate. The AMR grid is chosen such that a base-level resolution
of
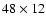 zones and four levels of refinement with refinement
factors of 4 in each dimension are employed. This results in a maximum
resolution on the finest level corresponding to 3072 equidistant zones
in radius and 768 zones in angle. Zones are flagged for refinement by
applying the same criteria as in our one-dimensional calculation for
each dimension. Adopting transmitting boundary conditions in the
radial and reflecting boundaries in the angular direction, our
computational volume is initially set up to span the domain
zones and four levels of refinement with refinement
factors of 4 in each dimension are employed. This results in a maximum
resolution on the finest level corresponding to 3072 equidistant zones
in radius and 768 zones in angle. Zones are flagged for refinement by
applying the same criteria as in our one-dimensional calculation for
each dimension. Adopting transmitting boundary conditions in the
radial and reflecting boundaries in the angular direction, our
computational volume is initially set up to span the domain
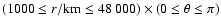 .
While
the grid boundaries in
.
While
the grid boundaries in 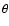 direction are kept unchanged
throughout the calculation, the zooming algorithm successively
enlarges the radial extent of the grid according to
Table 2, when the shock is approaching the outer
grid boundary,
direction are kept unchanged
throughout the calculation, the zooming algorithm successively
enlarges the radial extent of the grid according to
Table 2, when the shock is approaching the outer
grid boundary,
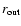 .
Whenever it is time to regrid, we also
move the inner grid boundary,
.
Whenever it is time to regrid, we also
move the inner grid boundary,
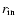 ,
away from the central
remnant. This approach allows us to concentrate the computational
effort in the post-shock and the Rayleigh-Taylor unstable regions
while avoiding overly restrictive Courant time steps due to
fallback. The times
,
away from the central
remnant. This approach allows us to concentrate the computational
effort in the post-shock and the Rayleigh-Taylor unstable regions
while avoiding overly restrictive Courant time steps due to
fallback. The times 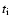 and
and 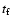 over which the radial
grid boundaries are kept fixed are given in columns one and two of
Table 2. The "zooming algorithm'' allows us to
temporally achieve a radial resolution of
over which the radial
grid boundaries are kept fixed are given in columns one and two of
Table 2. The "zooming algorithm'' allows us to
temporally achieve a radial resolution of
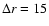 km in the
unstable layers, that is equivalent to covering the entire star with
an effective resolution of
km in the
unstable layers, that is equivalent to covering the entire star with
an effective resolution of
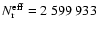 equidistant
zones. Even with this combination of mesh refinement, grid
enlargement and inner boundary movement, however, the computational
load is still significant. The two-dimensional AMR calculation that
we present in Sect. 6, and which follows the
evolution of the mixing from 820 ms to 5.5 hrs after core bounce,
requires nearly
equidistant
zones. Even with this combination of mesh refinement, grid
enlargement and inner boundary movement, however, the computational
load is still significant. The two-dimensional AMR calculation that
we present in Sect. 6, and which follows the
evolution of the mixing from 820 ms to 5.5 hrs after core bounce,
requires nearly
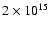 floating point operations (this
number has to be multiplied by about a factor of 5 if no adaptive mesh
is used).
floating point operations (this
number has to be multiplied by about a factor of 5 if no adaptive mesh
is used).
Finally, we note that the choice of spherical coordinates leads to
numerical artifacts along the symmetry axis of the grid. The excessive
outflows that we observe for
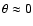 and
and
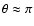 for the models in this paper are much weaker than those in
Kifonidis et al. (2000). Nevertheless, in order to avoid spurious effects,
we have excluded a cone with an opening angle of
for the models in this paper are much weaker than those in
Kifonidis et al. (2000). Nevertheless, in order to avoid spurious effects,
we have excluded a cone with an opening angle of
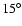 around
the polar axis for evaluating our simulations for the velocity
distributions of nucleosynthesis products and the angle-averaged
extent of the mixing of chemical elements.
around
the polar axis for evaluating our simulations for the velocity
distributions of nucleosynthesis products and the angle-averaged
extent of the mixing of chemical elements.
Table 3:
Parameters of Models O310 and T310. The (baryonic) mass of
the inner core,
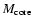 ,
that has been excluded from the
simulation, and the final neutron star mass,
,
that has been excluded from the
simulation, and the final neutron star mass,
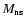 ,
are given
in solar masses. The initial and final radius of the inner core,
,
are given
in solar masses. The initial and final radius of the inner core,
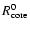 and
and
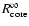 ,
respectively, are
given in km, and its initial velocity of contraction,
,
respectively, are
given in km, and its initial velocity of contraction,
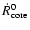 ,
in km s-1. The initial neutrino luminosities of different
flavours,
,
in km s-1. The initial neutrino luminosities of different
flavours,
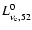 ,
,
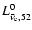 ,
and
,
and
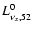 (see also the main text), are given in units of
(see also the main text), are given in units of
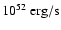 ,
and the energy loss of the inner core,
,
and the energy loss of the inner core,
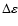 ,
in units of
,
in units of
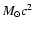 .
The explosion energy,
.
The explosion energy,
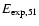 ,
and the explosion time scale,
,
and the explosion time scale,
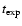 ,
are
given in
,
are
given in
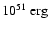 and in ms, respectively.
and in ms, respectively.
5 The first second
5.1 Evolution in one dimension
In Table 3 we summarize the basic parameters
of our one-dimensional explosion, Model O310, along with its
two-dimensional counterpart, Model T310, that will be discussed in
Sect. 5.2. As described in detail in JM96 the
models are characterized by the initial values of the electron and
heavy lepton neutrino luminosities (in units of
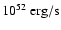 ),
),
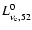 and
and
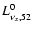 ,
and the energy loss (in units
of
,
and the energy loss (in units
of
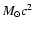 )
and lepton loss parameters of the inner iron
core,
)
and lepton loss parameters of the inner iron
core,
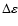 and
and
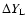 ,
respectively. The
latter parameter constrains the luminosity of electron antineutrinos
while
,
respectively. The
latter parameter constrains the luminosity of electron antineutrinos
while
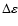 determines the characteristic time scale
for the decay of the luminosities that we assume to follow the simple
exponential law
determines the characteristic time scale
for the decay of the luminosities that we assume to follow the simple
exponential law
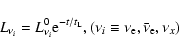 |
(1) |
where 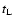 is of the order of 700 ms. The neutrino spectra are
prescribed in the same way as in JM96.
is of the order of 700 ms. The neutrino spectra are
prescribed in the same way as in JM96.
Table 3 also lists the explosion time scale,
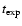 ,
measured in ms and the explosion energy at the end of
the shock-revival simulation,
,
measured in ms and the explosion energy at the end of
the shock-revival simulation,
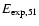 ,
in units of
,
in units of
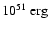 (note that the binding energy of the envelope has not
yet been subtracted from the latter). We define these quantities as
in JM96. The explosion energy is given by the sum of the
gravitational, kinetic and internal energy of all zones of the grid
where this sum of energies is positive. The explosion time scale is
defined as the time after the start of the simulation when the
explosion energy exceeds
(note that the binding energy of the envelope has not
yet been subtracted from the latter). We define these quantities as
in JM96. The explosion energy is given by the sum of the
gravitational, kinetic and internal energy of all zones of the grid
where this sum of energies is positive. The explosion time scale is
defined as the time after the start of the simulation when the
explosion energy exceeds
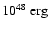 .
.
We adopt values for
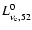 and
and
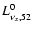 that give
rise to energetic explosions. This choice was motivated by the claim
of Herant & Benz (1992) that premixing of the
that give
rise to energetic explosions. This choice was motivated by the claim
of Herant & Benz (1992) that premixing of the
 (be it artificial
or due to neutrino-driven convection) in models with high explosion
energies of about
(be it artificial
or due to neutrino-driven convection) in models with high explosion
energies of about
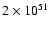 ergs leads to a resolution of the
"nickel discrepancy problem''. In their simulations of
Rayleigh-Taylor instabilities in the stellar envelope, they obtained
final maximum
ergs leads to a resolution of the
"nickel discrepancy problem''. In their simulations of
Rayleigh-Taylor instabilities in the stellar envelope, they obtained
final maximum
 velocities of up to 3000 km s-1 if they
premixed the
velocities of up to 3000 km s-1 if they
premixed the
 in their 1D initial models out to mass
coordinates of
in their 1D initial models out to mass
coordinates of
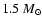 above the Fe/Si interface
(i.e. throughout 75% of the metal core of the progenitor model
of Nomoto et al. 1988).
above the Fe/Si interface
(i.e. throughout 75% of the metal core of the progenitor model
of Nomoto et al. 1988).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3592f02.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg95.gif) |
Figure 2:
Spacetime plot for the evolution of the logarithm of the
density for our one-dimensional explosion, Model O310. The
supernova shock is visible as the outermost discontinuity
that extends diagonally through the plot. Around 500 ms a
reverse shock forms in the inner ejecta that originates from
the (hardly visible) slight deceleration of the main shock in
the oxygen core. The reverse shock separates the ejecta from
the neutrino-driven wind. |
| Open with DEXTER |
With the parameters listed in Table 3, shock
revival by neutrino heating is almost instant in our simulations. The
shock shows neither long stagnation times nor phases of progression
and subsequent recession. Instead, it moves out of the iron core
without noticeable delay. To illustrate matters, we show a spacetime
plot of the evolution of the density with time for Model O310 in
Fig. 2, from which one can infer a mean shock
velocity of about 19 000 km s-1 after 0.2 s. Additionally, in
Fig. 3 we depict the evolution of the most important
hydrodynamic and thermodynamic quantities as a function of radius. The
initial post-collapse profiles are plotted with thick lines, and the
Si/O interface can be discerned by the associated entropy step at
![$\log r~ \mbox{[cm]} = 8.8$](/articles/aa/full/2003/35/aa3592/img96.gif) .
One can easily recognize the transition
of the accretion shock to an outward propagating shock with high
post-shock velocities, the rarefaction generated by the explosion and
the deleptonization and contraction of the outer layers of the
proto-neutron star in response to the contracting inner boundary.
Figure 3 also shows the neutrino-driven wind, that
is blown off the surface of the neutron star for times later than
.
One can easily recognize the transition
of the accretion shock to an outward propagating shock with high
post-shock velocities, the rarefaction generated by the explosion and
the deleptonization and contraction of the outer layers of the
proto-neutron star in response to the contracting inner boundary.
Figure 3 also shows the neutrino-driven wind, that
is blown off the surface of the neutron star for times later than
 200 ms and that has also been found in the calculations of
Burrows et al. (1995) and Janka & Müller (1996). Furthermore, a reverse shock is visible,
that forms about 500 ms after core bounce (compare
Fig. 2) when the main shock enters the oxygen core
of the star and propagates into layers with a somewhat flatter density
gradient, thereby decelerating slightly. Both shocks mark the
boundaries of a dense region that contains most of the ejecta, while
the reverse shock separates the ejecta from the neutrino-driven wind.
Shortly after the supernova shock has crossed the Fe/Si interface at
120 ms (at this time the latter has fallen in from its initial radius
of
200 ms and that has also been found in the calculations of
Burrows et al. (1995) and Janka & Müller (1996). Furthermore, a reverse shock is visible,
that forms about 500 ms after core bounce (compare
Fig. 2) when the main shock enters the oxygen core
of the star and propagates into layers with a somewhat flatter density
gradient, thereby decelerating slightly. Both shocks mark the
boundaries of a dense region that contains most of the ejecta, while
the reverse shock separates the ejecta from the neutrino-driven wind.
Shortly after the supernova shock has crossed the Fe/Si interface at
120 ms (at this time the latter has fallen in from its initial radius
of
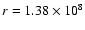 cm to
cm to
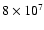 cm), a high-density
shell forms immediately behind the shock. It becomes more pronounced
after t = 500 ms when the shock has passed the Si/O interface. The
trajectory of the shell's inner boundary can be discerned in
Fig. 2 in between the supernova and reverse
shocks. This shell is one of the most interesting outcomes of our
calculations. Three important physical processes take place in this
part of the ejecta, whose mutual interaction has been neglected in
previous attempts to model supernova explosions. These processes are
cm), a high-density
shell forms immediately behind the shock. It becomes more pronounced
after t = 500 ms when the shock has passed the Si/O interface. The
trajectory of the shell's inner boundary can be discerned in
Fig. 2 in between the supernova and reverse
shocks. This shell is one of the most interesting outcomes of our
calculations. Three important physical processes take place in this
part of the ejecta, whose mutual interaction has been neglected in
previous attempts to model supernova explosions. These processes are
 -synthesis, neutrino-driven convection, and the growth
of Rayleigh-Taylor instabilities at the Si/O interface of the
progenitor's metal core. We address the physical conditions for their
occurrence in turn, focusing first on
-synthesis, neutrino-driven convection, and the growth
of Rayleigh-Taylor instabilities at the Si/O interface of the
progenitor's metal core. We address the physical conditions for their
occurrence in turn, focusing first on
 -synthesis.
-synthesis.
![\begin{figure}
\par\includegraphics[width=14.7cm,clip]{3592f03.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg99.gif) |
Figure 3:
Snapshots of the density, entropy, velocity and electron
fraction distribution in Model O310, 20 ms (heaviest line),
220 ms, 420 ms, 620 ms and 820 ms after core bounce. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=14.9cm,clip]{3592f04.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg100.gif) |
Figure 4:
Evolution of density, temperature, entropy and electron
fraction as functions of the enclosed mass for Model O310
between t = 20 ms and t = 820 ms post-bounce. The
positions of the Fe/Si and Si/O interfaces, and the 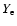 discontinuity (see text) are indicated by dotted vertical lines.
discontinuity (see text) are indicated by dotted vertical lines. |
| Open with DEXTER |
The left panels of Fig. 4 show the evolution of
the density and temperature distribution for Model O310 as a function
of the enclosed (baryonic) mass. The inner edge of the high-density
shell is stationary at a mass coordinate of
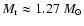 .
This mass shell marks the border between low and
high-
.
This mass shell marks the border between low and
high-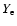 material in the expanding ejecta for times
material in the expanding ejecta for times
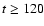 ms (right lower panel of Fig. 4),
i.e. for the epoch of
ms (right lower panel of Fig. 4),
i.e. for the epoch of
 formation. Since
formation. Since
 synthesis requires temperatures in the range of
synthesis requires temperatures in the range of 
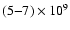 K and electron fractions
K and electron fractions
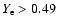 ,
we can expect that
in Model O310
,
we can expect that
in Model O310
 does not form in large amounts in regions
with mass coordinates <
does not form in large amounts in regions
with mass coordinates <
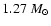 ,
where
,
where
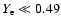 .
This is confirmed by Fig. 5, which
shows the composition 820 ms after bounce, when the post-shock
temperature has already dropped below
.
This is confirmed by Fig. 5, which
shows the composition 820 ms after bounce, when the post-shock
temperature has already dropped below
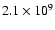 K (compare
Fig. 4) and nuclear reactions have frozen out.
Large
K (compare
Fig. 4) and nuclear reactions have frozen out.
Large
 mass fractions (
mass fractions (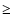 20%) are indeed only
found for
20%) are indeed only
found for
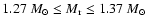 ,
i.e. they are confined to the dense shell. In total, 0.08
,
i.e. they are confined to the dense shell. In total, 0.08
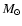 of
of
 are synthesized in Model O310. Of these,
0.04
are synthesized in Model O310. Of these,
0.04
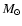 are produced by shock-induced Si-burning in
the presupernova's silicon shell (whose inner boundary was initially
located at
are produced by shock-induced Si-burning in
the presupernova's silicon shell (whose inner boundary was initially
located at
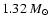 ). The remaining 0.04
). The remaining 0.04
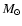 stem from the recombination of photo-disintegrated iron
core matter with high electron fraction at mass coordinates between
stem from the recombination of photo-disintegrated iron
core matter with high electron fraction at mass coordinates between
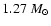 and
and
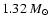 .
Between the
neutron star surface and the inner boundary of the dense shell,
i.e. for
.
Between the
neutron star surface and the inner boundary of the dense shell,
i.e. for
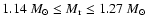 ,
,
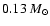 of material freezes out with
of material freezes out with
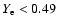 .
About 0.087
.
About 0.087
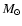 of this matter end up in the
neutronization tracer nucleus (denoted by X in
Fig. 5). The rest, which contains also a
small contribution of
of this matter end up in the
neutronization tracer nucleus (denoted by X in
Fig. 5). The rest, which contains also a
small contribution of
 ,
is mainly made up of
,
is mainly made up of
 -particles,
-particles,
 ,
,
 ,
and
,
and
 ,
i.e. the products of
,
i.e. the products of 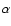 -rich freezeout in
high-entropy (low-density) material.
-rich freezeout in
high-entropy (low-density) material.
Table 4 gives an overview of the nuclear yields for our
explosion models (not including effects of eventual fallback). For a
discussion of their accuracy regarding numerical diffusion, see
Kifonidis et al. (2001), and Plewa & Müller (1999) who analyzed the effect in detail,
especially for the case of
 .
With the spatial resolution
used in the explosion models presented in this paper, the bulk of
.
With the spatial resolution
used in the explosion models presented in this paper, the bulk of
 is synthesized between about 400 ms and 700 ms after
core bounce at
is synthesized between about 400 ms and 700 ms after
core bounce at
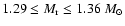 ,
in a layer
where the abundance of
,
in a layer
where the abundance of 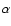 -particles decreases and
-particles decreases and
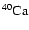 comes up (Fig. 5). However, if the spatial
resolution is increased, and thus numerical diffusion at the
comes up (Fig. 5). However, if the spatial
resolution is increased, and thus numerical diffusion at the
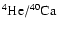 boundary is reduced, the width of the
layer of
boundary is reduced, the width of the
layer of
 production via the reaction
production via the reaction
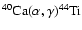 is narrowed. This decreases the
is narrowed. This decreases the
 yield by up to a factor of 3 (Kifonidis et al. 2001).
yield by up to a factor of 3 (Kifonidis et al. 2001).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3592f05.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg119.gif) |
Figure 5:
Chemical composition of Model O310 versus mass at t =
820 ms. X denotes the neutronization tracer nucleus. |
| Open with DEXTER |
Table 4:
Final total elemental yields (in
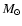 )
for
Models O310 and T310. Exponents are given in brackets.
)
for
Models O310 and T310. Exponents are given in brackets.
The yield of
 is much less sensitive to numerical
diffusion. However, it cannot be determined to much higher accuracy
than that of
is much less sensitive to numerical
diffusion. However, it cannot be determined to much higher accuracy
than that of
 because the contribution of the region
with
because the contribution of the region
with
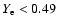 to the
to the
 production depends
sensitively on the ratio of the
production depends
sensitively on the ratio of the
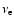 and
and
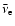 luminosities,
luminosities,
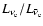 ,
and its
evolution with time. This ratio, which determines the electron
fraction in regions close to the gain radius through neutrino-matter
interactions (Janka & Müller 1996, and references therein), must be regarded
as uncertain in calculations like ours, that do not use accurate
neutrino transport. With the parameters adopted for Model O310 we
observe that
,
and its
evolution with time. This ratio, which determines the electron
fraction in regions close to the gain radius through neutrino-matter
interactions (Janka & Müller 1996, and references therein), must be regarded
as uncertain in calculations like ours, that do not use accurate
neutrino transport. With the parameters adopted for Model O310 we
observe that
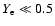 for
for
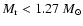 .
However, given a higher
.
However, given a higher
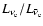 the opposite may occur, with
the opposite may occur, with 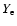 being increased in the
neutrino-heated layers to values up to and even above 0.5, as seen in
recent calculations including Boltzmann neutrino transport
(Janka et al. 2003). If this were the case, the composition would be
dominated by
being increased in the
neutrino-heated layers to values up to and even above 0.5, as seen in
recent calculations including Boltzmann neutrino transport
(Janka et al. 2003). If this were the case, the composition would be
dominated by
 also for
also for
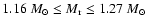 ,
while only insignificant amounts of
neutron-rich nuclei would be synthesized in these layers. Hence, the
,
while only insignificant amounts of
neutron-rich nuclei would be synthesized in these layers. Hence, the
 yield might be increased by a factor of up to about 2
compared to Model O310.
yield might be increased by a factor of up to about 2
compared to Model O310.
Just interior to the dense shell (and the
 -rich zone in
Model O310), we must expect substantial convective activity to occur,
because neutrino-matter interactions sustain a negative entropy
gradient in the neutrino-heated material throughout the entire
evolution up to 820 ms. As Fig. 4 shows, the
entropy starts to rise steeply when one moves inward from
-rich zone in
Model O310), we must expect substantial convective activity to occur,
because neutrino-matter interactions sustain a negative entropy
gradient in the neutrino-heated material throughout the entire
evolution up to 820 ms. As Fig. 4 shows, the
entropy starts to rise steeply when one moves inward from
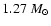 and reaches a maximum near the gain radius (and at times
later than 0.5 s at a position just downstream of the reverse
shock). This negative entropy gradient will give rise to convective
motions that, in contrast to the one-dimensional situation, will mix
high-entropy, low-
and reaches a maximum near the gain radius (and at times
later than 0.5 s at a position just downstream of the reverse
shock). This negative entropy gradient will give rise to convective
motions that, in contrast to the one-dimensional situation, will mix
high-entropy, low-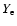 ,
matter from the deeper layers of the
iron-core with lower-entropy, high-
,
matter from the deeper layers of the
iron-core with lower-entropy, high-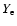 ,
material of the
outermost iron core and the silicon shell. We discuss the implications
of this in more detail in the next section.
,
material of the
outermost iron core and the silicon shell. We discuss the implications
of this in more detail in the next section.
Finally, we wish to draw attention to the outer boundary of the dense
shell. Figures 4 and 6 indicate
that after about 500 ms this boundary coincides with the star's Si/O
interface. A pronounced negative density gradient forms at this
interface which is accompanied by a positive pressure gradient
(Fig. 6). Such a configuration is Rayleigh-Taylor
unstable even in the absence of gravity (Chevalier 1976). Its
rather close spatial proximity to the convectively unstable layers at
the inner edge of the dense shell is of decisive importance for the
further evolution of the models.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3592f06.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg133.gif) |
Figure 6:
Density and pressure profiles of Model O310 at t =
820 ms. The position of the 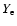 discontinuity and
of the Si/O interface are indicated by dotted vertical lines.
Note the dense shell at
discontinuity and
of the Si/O interface are indicated by dotted vertical lines.
Note the dense shell at
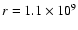 cm, and the
density and pressure gradients of opposite signs for cm, and the
density and pressure gradients of opposite signs for
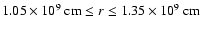 . . |
| Open with DEXTER |
5.2 Evolution in two dimensions
Repeating the calculation of the one-dimensional model O310 in two
dimensions we obtained Model T310 that develops convective activity
already 60 ms after core bounce. Fingers of buoyant, high-entropy
material with
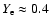 ,
and an initial angular width of
about
,
and an initial angular width of
about
 form quickly from the imposed seed
perturbations in the neutrino heated layer near the gain radius and
start to rise toward the shock into the surrounding gas of lower
entropy. While doing so they acquire a mushroom-capped shape and
display a tendency to merge into bubbles of about
form quickly from the imposed seed
perturbations in the neutrino heated layer near the gain radius and
start to rise toward the shock into the surrounding gas of lower
entropy. While doing so they acquire a mushroom-capped shape and
display a tendency to merge into bubbles of about
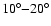 lateral width
(Fig. 1). Between the bubbles, low-entropy material
with
lateral width
(Fig. 1). Between the bubbles, low-entropy material
with
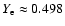 sinks inward in tube-like flows.
Compared to the one dimensional case, the convective rise of the
high-entropy gas leads to a somewhat more efficient energy transport,
and a reduced energy loss by the reemission of neutrinos from heated
matter. Therefore Model T310 exploded with an energy of
sinks inward in tube-like flows.
Compared to the one dimensional case, the convective rise of the
high-entropy gas leads to a somewhat more efficient energy transport,
and a reduced energy loss by the reemission of neutrinos from heated
matter. Therefore Model T310 exploded with an energy of
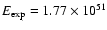 erg, which is 11% higher than in Model O310. The mean shock expansion velocity is, however, almost the same
as in Model O310.
erg, which is 11% higher than in Model O310. The mean shock expansion velocity is, however, almost the same
as in Model O310.
While the shock propagates through the Si-rich layers of the star,
 is synthesized in the high-density shell
(Sect. 5.1), which is distorted at its base by the
rising bubbles of high-entropy material. As in the one-dimensional
case, freezeout of nuclear reactions in the deleptonized bubbles leads
to high abundances of the neutronization tracer and to smaller yields
for nuclei produced by
is synthesized in the high-density shell
(Sect. 5.1), which is distorted at its base by the
rising bubbles of high-entropy material. As in the one-dimensional
case, freezeout of nuclear reactions in the deleptonized bubbles leads
to high abundances of the neutronization tracer and to smaller yields
for nuclei produced by  -rich freezeout. However, in between
the bubbles, i.e. in the down-flows mentioned above, electron
fractions are sufficiently high that
-rich freezeout. However, in between
the bubbles, i.e. in the down-flows mentioned above, electron
fractions are sufficiently high that
 is synthesized.
Hence, the inner boundary of the
is synthesized.
Hence, the inner boundary of the
 shell possesses an
aspherical shape closely tracing the inner edge of the low-entropy
(high-density) material in the convective region, while the outer
shell possesses an
aspherical shape closely tracing the inner edge of the low-entropy
(high-density) material in the convective region, while the outer
 -boundary coincides with the (spherical) shock wave as
long as the post-shock temperatures stay above
-boundary coincides with the (spherical) shock wave as
long as the post-shock temperatures stay above
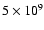 K. After complete silicon burning has ceased at
K. After complete silicon burning has ceased at
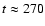 ms, an anisotropic nickel shell is left behind, while
the spherical shock continues moving outward (see
Fig. 1).
ms, an anisotropic nickel shell is left behind, while
the spherical shock continues moving outward (see
Fig. 1).
The differences in the spatial nickel distribution between Model T310
and its 1D analogue, Model O310, are relatively small, however. This
is caused by the high initial neutrino luminosities and their rapid,
exponential decline (Eq. (1)) adopted for our models. Both
assumptions favour small explosion time scales which prevents
convective bubbles to merge to large-scale structures, as in cases
where the phase of convective overturn lasts for several turn-over
times. Lowering the neutrino luminosities (and the explosion
energies), we obtain stronger convection that largely distorts the
shock wave by developing big bubbles of neutrino-heated material (see
Janka & Müller 1996; Kifonidis et al. 2000, 2001; and
Janka et al. 2001 for examples). Adopting constant core luminosities in
contrast to the exponential law of Eq. (1), we can
produce models that exhibit the vigorous boiling behaviour reported by
Burrows et al. (1995). Such cases can finally develop global anisotropies,
showing a dominance of the m=0, l=1 mode of convection (see
Janka et al. 2003; Scheck et al., in preparation). As a consequence,
convection can lead to huge deviations of the spatial distribution of
iron group nuclei from spherical symmetry, much stronger than those
visible in Fig. 1. Convection can also change the
nucleosynthetic yields of iron group nuclei, because it enhances
neutronization by cycling high-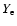 material from outer layers
through the regions near the gain radius where the gas loses lepton
number (Kifonidis et al. 2001; Janka et al. 2001). Due to our adopted
material from outer layers
through the regions near the gain radius where the gas loses lepton
number (Kifonidis et al. 2001; Janka et al. 2001). Due to our adopted
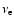 and
and
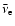 luminosities the gas cannot regain high
luminosities the gas cannot regain high 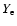 values when it moves outward again. This leads to
values when it moves outward again. This leads to
 yields that are about 6% smaller in Model T310 as compared to the 1D
case, Model O310, while the final yield of the neutronization tracer
shows the opposite behaviour and is 15% larger in Model T310 than in
Model O310. These effects are comparatively small in Model T310, again
mainly due to the short explosion time scale of this model.
yields that are about 6% smaller in Model T310 as compared to the 1D
case, Model O310, while the final yield of the neutronization tracer
shows the opposite behaviour and is 15% larger in Model T310 than in
Model O310. These effects are comparatively small in Model T310, again
mainly due to the short explosion time scale of this model.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{3592f07.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg141.gif) |
Figure 7:
Fractional mass of different elements contained within the
velocity interval
![$[v_{\rm r},v_{\rm r}+{\rm d}v_{\rm r}]$](/articles/aa/full/2003/35/aa3592/img29.gif) as a function of the
radial velocity
as a function of the
radial velocity 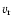 in Model T310. The resolution is
in Model T310. The resolution is
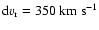 . . |
| Open with DEXTER |
The distribution of the elements in velocity space is of significant
importance for an understanding of the evolution of the supernova
beyond the first second. Since Models O310 and T310 barely differ in
this respect we discuss only the two-dimensional case. In
Fig. 7 we plot as functions of the radial
velocity 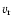 and time, the fractions of the total mass of
and time, the fractions of the total mass of
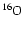 ,
,
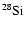 ,
,
 and
and
 that
are contained within the velocity intervals
that
are contained within the velocity intervals
![$[v_{\rm r},v_{\rm r}+{\rm d}v_{\rm r}]$](/articles/aa/full/2003/35/aa3592/img29.gif) with
with
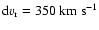 .
At t = 120 ms, when the
shock is travelling through the outermost layers of the iron core,
substantial amounts of material from the silicon and oxygen shells are
either still near hydrostatic equilibrium or falling towards the
shock. Consequently the peak and wings of the mass distributions of
the respective elements have zero and negative velocities. As the
post-shock temperature begins to drop below
.
At t = 120 ms, when the
shock is travelling through the outermost layers of the iron core,
substantial amounts of material from the silicon and oxygen shells are
either still near hydrostatic equilibrium or falling towards the
shock. Consequently the peak and wings of the mass distributions of
the respective elements have zero and negative velocities. As the
post-shock temperature begins to drop below
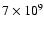 K,
reassembly of
K,
reassembly of 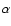 -particles to heavier nuclei starts in the
immediate post-shock region and leads to initially small abundances of
-particles to heavier nuclei starts in the
immediate post-shock region and leads to initially small abundances of
 and
and
 ,
the bulk of which has velocities
around
,
the bulk of which has velocities
around
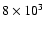 km s-1.
km s-1.
Only 100 ms later (t = 220 ms) the explosion gains momentum, and
the shock propagates through the silicon shell and encounters
substantially smaller maximum infall velocities of only
3000 km s-1. This leads to the cutoff of the high velocity wings of
silicon and oxygen at
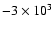 km s-1. Downstream of the
shock,
km s-1. Downstream of the
shock,
 is synthesized as the dominant nucleus in
regions of explosive silicon burning, while also
is synthesized as the dominant nucleus in
regions of explosive silicon burning, while also
 is
built up in smaller amounts. The spatial neighborhood of these two
nuclei is reflected in their velocity distributions, which both peak
around
is
built up in smaller amounts. The spatial neighborhood of these two
nuclei is reflected in their velocity distributions, which both peak
around
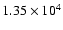 km s-1. However, in contrast to
km s-1. However, in contrast to
 ,
some
,
some
 also forms by
also forms by  -rich
freezeout in the rising convective blobs that at this stage show the
highest velocities on the grid. This causes the broad wing in the
velocity distribution of
-rich
freezeout in the rising convective blobs that at this stage show the
highest velocities on the grid. This causes the broad wing in the
velocity distribution of
 up to
up to
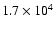 km s-1,
while maximum
km s-1,
while maximum
 velocities reach
velocities reach
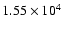 km s-1. The velocity distribution for the
neutronization tracer shows a behaviour similar to
km s-1. The velocity distribution for the
neutronization tracer shows a behaviour similar to
 .
.
At 420 ms the supernova's explosion energy is still increasing and
has led to maximum
 velocities as high as
velocities as high as
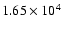 km s-1. Substantial amounts of silicon have also
been accelerated outward. A stratification of these elements in
velocity space is beginning to emerge because the positive velocity
gradient behind the shock (see Fig. 3) results in
higher velocities in the post-shock region as compared to gas in the
deeper layers of the ejecta. Meanwhile, the neutrino-driven wind has
begun to blow off material from the proto-neutron star surface with
velocities in excess of
km s-1. Substantial amounts of silicon have also
been accelerated outward. A stratification of these elements in
velocity space is beginning to emerge because the positive velocity
gradient behind the shock (see Fig. 3) results in
higher velocities in the post-shock region as compared to gas in the
deeper layers of the ejecta. Meanwhile, the neutrino-driven wind has
begun to blow off material from the proto-neutron star surface with
velocities in excess of
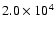 km s-1(Fig. 3). Traces of
km s-1(Fig. 3). Traces of
 in the wind, that
has a composition dominated by
in the wind, that
has a composition dominated by 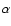 -particles and neutron-rich
nuclei, can be seen at these velocities. The distribution of
-particles and neutron-rich
nuclei, can be seen at these velocities. The distribution of
 in velocity space is somewhat uncertain. We have noted
in Sect. 5.1 that the bulk of
in velocity space is somewhat uncertain. We have noted
in Sect. 5.1 that the bulk of
 is
synthesized at the boundary of layers with high
is
synthesized at the boundary of layers with high
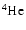 and
and
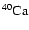 abundances. The location of this region coincides with
the maximum of the
abundances. The location of this region coincides with
the maximum of the
 abundance
(Fig. 5). Thus, the peaks of both elements
are found at comparable velocities (
abundance
(Fig. 5). Thus, the peaks of both elements
are found at comparable velocities (
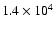 km s-1;
Fig. 7). We note again, however, that the
spatial distribution and the yield of
km s-1;
Fig. 7). We note again, however, that the
spatial distribution and the yield of
 are severely
affected by numerical diffusion (Plewa & Müller 1999). The location of the
are severely
affected by numerical diffusion (Plewa & Müller 1999). The location of the
 peak at t = 420 ms (Fig. 7)
might actually occur at much lower velocities, if numerical diffusion
(and thereby
peak at t = 420 ms (Fig. 7)
might actually occur at much lower velocities, if numerical diffusion
(and thereby
 synthesis at the
synthesis at the
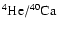 boundary) is substantially reduced. In
this case, the contribution from the slower, deeper layers of the
ejecta, just downstream of the reverse shock, might dominate. Indeed
this material causes the second, smaller
boundary) is substantially reduced. In
this case, the contribution from the slower, deeper layers of the
ejecta, just downstream of the reverse shock, might dominate. Indeed
this material causes the second, smaller
 peak near
peak near
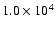 km s-1 at t = 820 ms (lower right panel of
Fig. 7).
km s-1 at t = 820 ms (lower right panel of
Fig. 7).
The velocities of the fastest regions that contain
 reach a maximum of
reach a maximum of
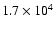 km s-1 around t = 620 ms and
decrease slightly to
km s-1 around t = 620 ms and
decrease slightly to
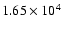 km s-1 at t = 820 ms. It is
obvious, that these
km s-1 at t = 820 ms. It is
obvious, that these
 velocities are much larger than
those observed in SN 1987 A and that some slow-down of this material
must have taken place later. In fact, we will show in
Sect. 6.2 that excessive deceleration of this material
during the subsequent evolution is the main problem for an explanation
of the observed
velocities are much larger than
those observed in SN 1987 A and that some slow-down of this material
must have taken place later. In fact, we will show in
Sect. 6.2 that excessive deceleration of this material
during the subsequent evolution is the main problem for an explanation
of the observed
 velocities in SN 1987 A.
velocities in SN 1987 A.
Summarizing our one and two-dimensional results for the evolution
within the first second, we note that a Rayleigh-Taylor unstable
density inversion can form at the Si/O interface of a blue supergiant.
The quickly expanding
 is situated just interior to this
interface and is distributed anisotropically in an inhomogeneous
layer. This results in a seed perturbation for the Rayleigh-Taylor
unstable regions. We will show in the following sections that the
magnitude of this perturbation is sufficient to induce significant
outward mixing of
is situated just interior to this
interface and is distributed anisotropically in an inhomogeneous
layer. This results in a seed perturbation for the Rayleigh-Taylor
unstable regions. We will show in the following sections that the
magnitude of this perturbation is sufficient to induce significant
outward mixing of
 .
.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{3592f08a.ps}\hspace*{4mm}
\includegraphics[width=9.9cm,clip]{3592f08b.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg155.gif) |
Figure 8:
a) Evolution of the density in our one-dimensional type II
supernova simulation Model
 (left). The
dotted lines indicate the positions of the Si/O, (C+O)/He and
He/H interfaces 0.82 s after core bounce. b) Shock velocity
as a function of shock radius in Model
(left). The
dotted lines indicate the positions of the Si/O, (C+O)/He and
He/H interfaces 0.82 s after core bounce. b) Shock velocity
as a function of shock radius in Model
 ,
and radial dependence of ,
and radial dependence of 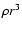 for our progenitor model
(right). Note the deceleration of the shock after it has
crossed the (C+O)/He interface at
for our progenitor model
(right). Note the deceleration of the shock after it has
crossed the (C+O)/He interface at
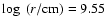 and the He/H interface at
and the He/H interface at
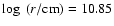 .
The
increase of the shock velocity for .
The
increase of the shock velocity for
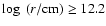 is due to the steep drop of the density in the
atmosphere of the star.
is due to the steep drop of the density in the
atmosphere of the star. |
| Open with DEXTER |
6 Beyond the first second: A type II model
6.1 One-dimensional evolution
![\begin{figure}
\par\includegraphics[width=16.3cm,clip]{3592f09.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg156.gif) |
Figure 9:
Structure of Model
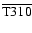 ,
a) 20 s (left), and b) 300 s
after bounce (right). Shown are (from top) the density,
pressure, velocity, sound speed, and mass fractions as
functions of radius. Note the unstable regions (shaded in
grey) near the Si/O, (C+O)/He and He/H composition
interfaces, where the density and pressure gradients have
opposite signs. At t=300 s, the density gradient at the
inner edge of the dense shell that has formed below the He/H
interface is in the process of steepening into a reverse
shock (compare also Fig. 8a). Note also the
enormous drop of the velocity in the layers that are enriched
in ,
a) 20 s (left), and b) 300 s
after bounce (right). Shown are (from top) the density,
pressure, velocity, sound speed, and mass fractions as
functions of radius. Note the unstable regions (shaded in
grey) near the Si/O, (C+O)/He and He/H composition
interfaces, where the density and pressure gradients have
opposite signs. At t=300 s, the density gradient at the
inner edge of the dense shell that has formed below the He/H
interface is in the process of steepening into a reverse
shock (compare also Fig. 8a). Note also the
enormous drop of the velocity in the layers that are enriched
in
 ,
from 6000 km s-1 at 20 s to 1300 km s-1 at 300 s. ,
from 6000 km s-1 at 20 s to 1300 km s-1 at 300 s. |
| Open with DEXTER |
Once the shock wave has been launched by neutrino heating and the
explosion energy has saturated, the further evolution of the supernova
depends strongly on the density profile of the progenitor star.
According to the analytic blast wave solutions of Sedov (1959), the
shock decelerates whenever it encounters a density profile that falls
off with a flatter slope than  r-3 (i.e. for increasing
r-3 (i.e. for increasing
 ), while for density profiles steeper than
), while for density profiles steeper than  r-3 (i.e. for decreasing
r-3 (i.e. for decreasing
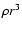 )
it accelerates. Since
models of supernova progenitors (see e.g. Woosley & Weaver 1995)
do not show a density structure that can be described by a single
power-law, an unsteady shock propagation results that in turn gives
rise to Rayleigh-Taylor unstable pressure and density gradients at the
composition interfaces of the star. In this section we follow shock
propagation beyond the first second with our AMR code in one spatial
dimension to illustrate these effects. In order to obtain the closest
possible approximation to the energetics of the two-dimensional case,
with which we will compare our results in the following section, we
start this 1D calculation from an angularly averaged version of our 2D
explosion, Model T310, (instead of the one-dimensional model O310).
We will henceforth refer to the one-dimensional results of this
section as Model
)
it accelerates. Since
models of supernova progenitors (see e.g. Woosley & Weaver 1995)
do not show a density structure that can be described by a single
power-law, an unsteady shock propagation results that in turn gives
rise to Rayleigh-Taylor unstable pressure and density gradients at the
composition interfaces of the star. In this section we follow shock
propagation beyond the first second with our AMR code in one spatial
dimension to illustrate these effects. In order to obtain the closest
possible approximation to the energetics of the two-dimensional case,
with which we will compare our results in the following section, we
start this 1D calculation from an angularly averaged version of our 2D
explosion, Model T310, (instead of the one-dimensional model O310).
We will henceforth refer to the one-dimensional results of this
section as Model
 .
.
![\begin{figure}
\par\includegraphics[width=14.8cm,clip]{3592f10.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg158.gif) |
Figure 10:
Logarithm of the total, time-integrated, linear growth
rate in the unstable layers near the Si/O and (C+O)/He
composition interfaces of Model
 at
different times. The linear growth rates increase with time
and reach amplification factors
at
different times. The linear growth rates increase with time
and reach amplification factors  1012 within the
first 300 s (i.e. five minutes) of the explosion. 1012 within the
first 300 s (i.e. five minutes) of the explosion. |
| Open with DEXTER |
Figure 8a displays the evolution of the density for
this model. The locations of the Si/O, (C+O)/He, and He/H interfaces
at the start of the calculation (i.e. 0.82 s after bounce) are also
indicated. In Fig. 8b we show the shock velocity as
a function of shock radius for times later than about one second after
core bounce, along with the radial variation of 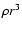 for our
progenitor model. When the shock wave crosses the (C+O)/He interface
at
for our
progenitor model. When the shock wave crosses the (C+O)/He interface
at
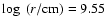 ,
1.8 s after bounce, its propagation
speed is as high as
,
1.8 s after bounce, its propagation
speed is as high as  20 000 km s-1. Thereafter, a rapid
decrease of the shock velocity can be seen, since
20 000 km s-1. Thereafter, a rapid
decrease of the shock velocity can be seen, since 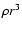 increases, i.e. the density profile in the He core falls off with a
more shallow slope than
increases, i.e. the density profile in the He core falls off with a
more shallow slope than
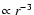 .
The deceleration lasts until
the blast wave has reached the outer layers of the He core and enters
a narrow region of decreasing
.
The deceleration lasts until
the blast wave has reached the outer layers of the He core and enters
a narrow region of decreasing 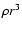 around
around
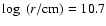 .
This region is characterized by a rapid drop of the density
just below the He/H interface (see Fig. 8a). Here
the shock temporarily accelerates to about 9000 km s-1(Fig. 8b). Once it has passed the He/H interface
around 80 s after core bounce, the evolution resembles that after the
crossing of the (C+O)/He interface. A gradual deceleration of the
shock to 4000 km s-1 occurs, until the blast wave enters the atmosphere
of the star and finally accelerates to more than 20 000 km s-1, while
propagating off the numerical grid.
.
This region is characterized by a rapid drop of the density
just below the He/H interface (see Fig. 8a). Here
the shock temporarily accelerates to about 9000 km s-1(Fig. 8b). Once it has passed the He/H interface
around 80 s after core bounce, the evolution resembles that after the
crossing of the (C+O)/He interface. A gradual deceleration of the
shock to 4000 km s-1 occurs, until the blast wave enters the atmosphere
of the star and finally accelerates to more than 20 000 km s-1, while
propagating off the numerical grid.
Every time the shock decelerates, it leaves behind a positive pressure
gradient which slows down the post-shock layers. The shocked material
thus piles up and forms a high-density post-shock shell. Note that
layers which are sufficiently far downstream of the shock may be out
of sonic contact with it, i.e. on the time scale of the supernova
expansion these layers may not be reached by sound waves originating
in the immediate post-shock region. In this case, the only way in
which information can be mediated to the deeper layers is through a
supersonic wave. Therefore their slow-down proceeds via a reverse
shock, that forms at the inner boundary of the high-density shell of
decelerated matter and starts to propagate inwards in mass. The
reverse shocks as well as the dense shells that form after the main
shock has passed the Si/O, (C+O)/He and He/H interfaces, can be
clearly seen in Fig. 8a in the density structures
for 0.82 s, 20 s and 1500 s, respectively. It is also apparent that
the density profiles for the latter two times show a striking
similarity in the region that is bounded by the forward and the
reverse shocks.
In a one-dimensional calculation, where hydrodynamic instabilities are
absent, dense shells, that have formed during earlier phases of the
evolution, are preserved provided the numerical diffusivity of the
employed hydrodynamic scheme is sufficiently small. This is
demonstrated by the left panel of Fig. 9
which shows some flow quantities 20 s after core bounce. Note that
two high-density peaks are visible between the forward and reverse
shock at that time. The inner is the one that formed at the Si/O
interface (Sect. 5.1). It contains mainly silicon
and oxygen. The outer one has formed at the (C+O)/He interface and
contains carbon and oxygen. In the layers of these shells that are
shaded in gray in Fig. 9, negative density
and positive pressure gradients exist. Thus, already at this early
time, Rayleigh-Taylor instabilities may grow in these regions
(Chevalier 1976). This is confirmed quantitatively by performing a
linear stability analysis (see e.g. Müller et al. 1991b; Iwamoto et al. 1997, and the references therein;
note that our calculations differ from these previous simulations
because we start from a model that has a consistent explosion history,
instead of having the explosion energy artificially deposited in the
stellar core).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3592f11.ps}\end{figure}](/articles/aa/full/2003/35/aa3592/Timg161.gif) |
Figure 11:
Logarithm of the total, time-integrated, linear growth
rate in the unstable layers near the Si/O, (C+O)/He and He/H
composition interfaces of Model
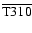 at
different times.
Comparing the amplitudes of the growth rates at the Si/O and
(C+O)/He interfaces with those given in
Fig. 10 one can see that these have
saturated after 300 s (in fact the curves for 300 s,
1600 s, and 3000 s are not visible individually because
they are identical within plotting accuracy). Note, however,
that the rate for the instability at the He/H interface is
still increasing between 300 s and 3000 s.
at
different times.
Comparing the amplitudes of the growth rates at the Si/O and
(C+O)/He interfaces with those given in
Fig. 10 one can see that these have
saturated after 300 s (in fact the curves for 300 s,
1600 s, and 3000 s are not visible individually because
they are identical within plotting accuracy). Note, however,
that the rate for the instability at the He/H interface is
still increasing between 300 s and 3000 s. |
| Open with DEXTER |
In Fig. 10 we plot for different times the total,
time-integrated growth rate
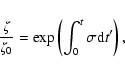 |
(2) |
i.e. the factor by which a (small) perturbation with an initial
amplitude 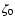 would be magnified at time t according to linear
perturbations theory. The growth rate of the instability,
would be magnified at time t according to linear
perturbations theory. The growth rate of the instability, 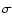 ,
is
given by
,
is
given by
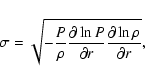 |
(3) |
(e.g. Müller et al. 1991b), where we have assumed the fluid to be
incompressible for simplicity. Within only 20 s after bounce, the
amplification factor grows to about 106 in both unstable regions,
which are separated by a narrow stable layer at
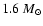 .
Both growth rates are increasing until 300 s after
bounce and saturate thereafter. The right panel of
Fig. 9 shows that at t=300 s the metal
core of the star has piled up to a high-density zone that includes the
two unstable interfaces. At this time, the shock has already passed
the He/H interface and a third unstable region has formed at the outer
edge of the dense shell that the shock has left behind at the He/H
interface. The evolution of the growth rate in this region is shown
in Fig. 11. At t=300 s it is much smaller than
the rates for the instabilities at the Si/O and (C+O)/He
interfaces. However, while the latter reach their maxima at this
epoch, the growth rate at the He/H interface still increases. It
reaches about the same level as the growth rates at the two inner
interfaces at 3000 s after core bounce.
.
Both growth rates are increasing until 300 s after
bounce and saturate thereafter. The right panel of
Fig. 9 shows that at t=300 s the metal
core of the star has piled up to a high-density zone that includes the
two unstable interfaces. At this time, the shock has already passed
the He/H interface and a third unstable region has formed at the outer
edge of the dense shell that the shock has left behind at the He/H
interface. The evolution of the growth rate in this region is shown
in Fig. 11. At t=300 s it is much smaller than
the rates for the instabilities at the Si/O and (C+O)/He
interfaces. However, while the latter reach their maxima at this
epoch, the growth rate at the He/H interface still increases. It
reaches about the same level as the growth rates at the two inner
interfaces at 3000 s after core bounce.
This behaviour is opposite to that found in the calculations of
Müller et al. (1991b), where the instability initially grows faster at the He/H
interface and only after some time is surpassed by the growth at the
(C+O)/He interface. It is very likely, that this result of
Müller et al. (1991b) is caused by the fact that they started their stability
analysis as well as their 2D calculations 300 s after core bounce.
Reliable calculations of the Rayleigh-Taylor growth, however,
require consideration of the very early moments of the
explosion. While the results of the linear stability analysis are
certainly invalid quantitatively once non-linear growth sets in, the
above conclusion is substantiated by our two-dimensional
calculations. It is also supported by results of Iwamoto et al. (1997) who
found a similar behaviour for the growth of the instability at the
(C+O)/He and He/H interfaces of their 2D models for SN 1993 J.
To our knowledge, large growth rates for Rayleigh-Taylor instabilities
at the Si/O interface of a massive star have never been reported
before. We can only speculate about the reason for the absence of this
unstable layer in previous simulations. Either it was caused by the
fact that the explosion was initiated artificially by depositing
energy in an ad hoc way, or it was caused by insufficient numerical
resolution, or by differences in the structure of the progenitor stars
that were employed in these studies. The latter is obviously the case
for the simulations of Arnett et al. (1989b), Fryxell et al. (1991) and Müller et al. (1991b) who
used a stellar model at the end of carbon burning for their
calculations. Also a combination of the effects listed above is
possible. High-resolution studies with our hydrodynamic code applied
to different progenitor models may be required to clarify this issue.
We stress this point because the two-dimensional models to be
discussed in the next section demonstrated that the instability at the Si/O interface is the most crucial one for determining the
subsequent evolution.
6.2 Two-dimensional evolution
6.2.1 Clump formation and mixing
In contrast to the one-dimensional case, in two (and three) spatial
dimensions the dense shells that form at the composition interfaces
can fragment into a set of smaller clumps that may decouple from the
flow and move ballistically through the ejecta. Such a fragmentation
actually occurs in our models due to the spatial proximity of the
Rayleigh-Taylor unstable zones near the Si/O and (C+O)/He interfaces
and the convective layers. To demonstrate these effects, we present a
two-dimensional type II supernova calculation that was started from
the shock-revival model T310. In what follows we will refer to this
simulation as Model T310a. To illustrate its hydrodynamic evolution we
show plots![[*]](/icons/foot_motif.gif) of the mass
density and the partial densities of the nuclei
of the mass
density and the partial densities of the nuclei
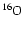 ,
,
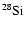 and
and
 .
.
![\begin{figure}
\par\begin{tabular}{ccc}
\includegraphics[width=5.5cm,height=11.2...
...[width=5.5cm,height=11.2cm,clip]{f12f_cmyk_600dpi.eps}\end{tabular}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg167.gif) |
Figure 12:
Logarithm of the density (top) and of the partial densities
(bottom) of
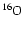 (blue),
(blue),
 (green),
and
(green),
and
 (red) in
Model T310a at selected early epochs. Data values are coded
according to the color bars given for each frame. In case of
the partial densities, colors other than red, green and blue
(resulting from the superposition of these color channels)
indicate mixing of the composition. From left to right a) t
= 4 s, b) t = 10 s, c) t = 20 s. Note the change of
the radial scale. The supernova shock is visible as the
outermost circular discontinuity in the density plots.
(red) in
Model T310a at selected early epochs. Data values are coded
according to the color bars given for each frame. In case of
the partial densities, colors other than red, green and blue
(resulting from the superposition of these color channels)
indicate mixing of the composition. From left to right a) t
= 4 s, b) t = 10 s, c) t = 20 s. Note the change of
the radial scale. The supernova shock is visible as the
outermost circular discontinuity in the density plots. |
| Open with DEXTER |
![\begin{figure}
\par\begin{tabular}{ccc}
\includegraphics[width=5.5cm,height=11.2...
...[width=5.5cm,height=11.2cm,clip]{f13f_cmyk_600dpi.eps}\end{tabular}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg168.gif) |
Figure 13:
Same as Fig. 12. a) t = 100 s
(left), b) t = 300 s (middle), c) t = 1500 s
(right). Note the change of the radial scale. |
| Open with DEXTER |
Figure 12a displays the situation 4 s after
core bounce, when the supernova shock has already crossed the (C+O)/He
interface of the star. The anisotropic structures that can be seen in
this figure are strikingly similar to those visible 420 ms after
bounce (Fig. 1b). This indicates that the low-density
(high-entropy) layers of the ejecta, that were heated by neutrinos,
expand essentially self-similarly during the first few seconds of the
explosion. However, outside of the high-entropy mushrooms, and exactly
as in the one-dimensional case, material of the Si and C+O layers of
the star piles up in two dense shells. Ten seconds after core bounce
(Fig. 12b) also the high-entropy gas is
affected, and the low-density mushrooms have been compressed to flat
structures. Only 10 s later (Fig. 12c) the
compression has become so strong that the density distribution no
longer resembles the flow-structures of the shock revival phase. A
second reverse shock has formed as a consequence of the deceleration
of the main shock in the He core (Sect. 6.1). It is
visible as the dark discontinuity at
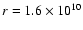 cm in
Fig. 12c. The initial mushrooms have imprinted
a strong long-wavelength perturbation both on the dense shell behind
the Si/O interface and at the (C+O)/He interface. Superposed upon this
perturbation, small-scale disturbances start to grow along the entire
Si/O interface where also about 10 cusps (not counting the features
near the symmetry axis) begin to develop that are located about
cm in
Fig. 12c. The initial mushrooms have imprinted
a strong long-wavelength perturbation both on the dense shell behind
the Si/O interface and at the (C+O)/He interface. Superposed upon this
perturbation, small-scale disturbances start to grow along the entire
Si/O interface where also about 10 cusps (not counting the features
near the symmetry axis) begin to develop that are located about
 apart. Interestingly, the positions of these cusps do
not coincide with those of the former mushrooms that are
located in the regions between the cusps. The cusps themselves
seem to be pushed by the denser material that constituted the former
down-flows between the mushrooms. It is exactly in these dense
regions, where
apart. Interestingly, the positions of these cusps do
not coincide with those of the former mushrooms that are
located in the regions between the cusps. The cusps themselves
seem to be pushed by the denser material that constituted the former
down-flows between the mushrooms. It is exactly in these dense
regions, where
 had formed during the first 250 ms of
the explosion. Although most of the
had formed during the first 250 ms of
the explosion. Although most of the
 is originally
located in a layer just interior to the unstable zone at the Si/O
interface (see Fig. 12a and compare also
Fig. 9 for the one-dimensional model), the
dense regions with their larger momentum cannot be slowed down as
strongly as their neighbouring matter so that they penetrate outward
much farther. This becomes evident in the plots for t = 100 s
(Fig. 13a). The cusps have already grown
into separate fingers that start to rise through the (C+O)/He
interface and impose a long-wavelength perturbation onto these
layers. Concurrently, the smallest scale perturbations that are
resolved on our grid have grown to small mushrooms at the Si/O
interface and start to mix
is originally
located in a layer just interior to the unstable zone at the Si/O
interface (see Fig. 12a and compare also
Fig. 9 for the one-dimensional model), the
dense regions with their larger momentum cannot be slowed down as
strongly as their neighbouring matter so that they penetrate outward
much farther. This becomes evident in the plots for t = 100 s
(Fig. 13a). The cusps have already grown
into separate fingers that start to rise through the (C+O)/He
interface and impose a long-wavelength perturbation onto these
layers. Concurrently, the smallest scale perturbations that are
resolved on our grid have grown to small mushrooms at the Si/O
interface and start to mix
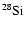 outwards while
outwards while
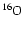 is mixed inwards in between them. The growth of Rayleigh-Taylor
fingers from the former dense Ni-"pockets'' has important
consequences for the interpretation of observational data and will be
addressed in more detail in Sect. 7.
is mixed inwards in between them. The growth of Rayleigh-Taylor
fingers from the former dense Ni-"pockets'' has important
consequences for the interpretation of observational data and will be
addressed in more detail in Sect. 7.
At t=100 s the supernova shock has already passed the He/H
interface. Furthermore, the reverse shock that had formed due to the
slow-down of the main shock in the He core starts to propagate inward
in radius. This reverse shock decelerates the innermost layers of the
ejecta until it is reflected at the inner boundary and moves outward
again, compressing the inner metal core of the star
(Figs. 13b and c). Five minutes after
bounce, the metal core itself is totally shredded by the instability.
Showing a density contrast to the ambient material of up to a factor
of 5, the fingers have grown into the typical mushroom shape, which is
caused by Kelvin-Helmholtz instabilities
(Fig. 13b). Almost the entire metal core has
thereby been carried through a substantial fraction of the He core,
while in turn helium-rich gas was mixed into the metal core in
"pockets'' between the fingers. These low-density helium tongues can
be discerned as the black regions around the blueish oxygen plumes in
the abundance plots of Fig. 13. Note that
there is a second helium-rich region closer to the center of the
models, interior to the red, green, and blue-colored zones. This
region contains material that experienced a high-entropy freezeout of
nuclear reactions, and thus shows high abundances of
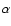 -particles and nuclei like
-particles and nuclei like
 .
In between this
.
In between this
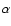 -rich layer and the regions of
-rich layer and the regions of
 dominance (the
patches of dense material colored in red and pink in the abundance
panel of Fig. 13; see also
Fig. 9 for the one-dimensional case) one
encounters neutron-rich nuclei. These nuclear species participate in
the mixing. The closer they are located to the unstable interfaces,
the stronger their spatial distribution is affected.
dominance (the
patches of dense material colored in red and pink in the abundance
panel of Fig. 13; see also
Fig. 9 for the one-dimensional case) one
encounters neutron-rich nuclei. These nuclear species participate in
the mixing. The closer they are located to the unstable interfaces,
the stronger their spatial distribution is affected.
At 1500 s after bounce, the flow in the mixing region has become
very complex because of the interaction of the instabilities at the
former Si/O and (C+O)/He interfaces and the action of Kelvin-Helmholtz
instabilities in the shear flows along the fingers
(Fig. 13c). During this phase, and depending
on the spatial resolution, our simulations show a tendency for the
edges of the fingers to fragment into smaller structures. This
fragmentation appears to be more pronounced for models with small
explosion energies. In this case, the time-scale for the fingers to
cross the He core may increase sufficiently to allow for substantial
growth of fluid-dynamic instabilities at the boundaries of the
fingers.
While the central regions of the star are turned inside out, a dense
shell can be seen 1500 s after bounce just below the border between
helium core and hydrogen envelope
(Fig. 13c). It is this prominent shell that
we also found in the one-dimensional calculation
(Sect. 6.1) as a result of the deceleration of the main
shock in the hydrogen envelope. Note that like in the one-dimensional
case, the density gradient at the inner edge of the shell steepens
into a reverse shock. In the one-dimensional calculation, the layers
of the metal core are well behind this reverse shock until t =
2600 s. Only then has the reverse shock propagated sufficiently deep
inward in mass to reach the (C+O)/He interface (see also
Kane et al. 2000 and Müller et al. 1991b). In our two-dimensional
simulation, however, the fastest mushrooms already start to penetrate
through the reverse shock at 1500 s after bounce
(Fig. 13c). This interaction of the
metal-enriched clumps with the reverse shock has not been pointed out
in any previous study of Rayleigh-Taylor instabilities in type II
supernova progenitors. It has important consequences for the velocity
distribution of the elements because it leads to a strong deceleration
of the clumps. We will address this issue in more detail below. For
the moment we only note that after penetrating through the reverse
shock and entering the high-density He-shell, the clumps move
supersonically relative to the ambient medium. As a result they are
dissipating a large fraction of their kinetic energy in bow shocks and
strong acoustic waves. The wave fronts can be seen in
Figs. 14a-c which show the interaction of
the clumps with the shell between 5000 s and 20 000 s after
bounce. Figure 14 also suggests that during
this interaction the spatial distribution of the heavy elements inside
the clumps is almost entirely homogenized. This causes the light blue
and whitish regions in the abundance plots (lower panels of
Figs. 14a-c) due to the superposition of
the single colors that were assigned to the different elements. The
interaction with the reverse shock also leads to mixing of ambient
helium into the clumps, with the helium mass fraction becoming
comparable to that of the heavy elements. Before, the clumps contained
only small amounts of helium that was admixed to them during the first
 300 s from the central zone of
300 s from the central zone of 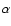 -rich freezeout by the
development of the Rayleigh-Taylor instabilities.
-rich freezeout by the
development of the Rayleigh-Taylor instabilities.
To facilitate a comparison of Model T310a with one-dimensional work,
upon which most attempts to reproduce observations of nucleosynthetic
yields and their distribution are based, we summarize the extent of
mixing as a function of the enclosed mass in
Fig. 15. The left panel shows the distribution
of the mass fractions for the original presupernova model. At a time
of 20 000 s after bounce (right panel), elements like
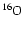 and
and
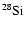 ,
that made up the original metal core have been
mixed almost homogeneously throughout the inner
,
that made up the original metal core have been
mixed almost homogeneously throughout the inner
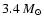 ,
along with the newly synthesized
,
along with the newly synthesized
 .
The
only nuclear species that are not mixed this far out in mass are the
neutronization tracer and, to an even lesser extent,
.
The
only nuclear species that are not mixed this far out in mass are the
neutronization tracer and, to an even lesser extent,
 .
These nuclei were synthesized in the innermost layers
of the neutrino-heated ejecta very close to the collapsed core.
.
These nuclei were synthesized in the innermost layers
of the neutrino-heated ejecta very close to the collapsed core.
Note that the mixing is confined to the former He core of the star
(i.e. the inner
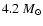 ). This can be understood from
Fig. 14: the dense He-shell, that forms just
below the He/H interface, acts like an impenetrable wall for the metal
clumps and shields the hydrogen envelope from becoming enriched with
heavy elements. This result may appear somewhat surprising because, as
we have shown by the linear stability analysis
(Sect. 6.1), the He/H interface of the Woosley et al. (1988) star
is Rayleigh-Taylor unstable. However, since we did not impose any
seed perturbations in our AMR simulations and since the supernova
shock is almost perfectly spherically symmetric when it crosses the
He/H interface, the evolution of these layers proceeds initially
one-dimensionally. This turns out to be true even in models where much
more vigorous neutrino-driven convection imposes noticeable
asphericities on the shock during its revival. Such asphericities,
however, are smoothed out during the subsequent propagation of the
shock through the helium core. The only deviations from spherical
symmetry that perturb the He/H interface in Model T310a are the waves
that are excited when the metal-enriched clumps hit the inner edge of
the dense shell below the interface at times
). This can be understood from
Fig. 14: the dense He-shell, that forms just
below the He/H interface, acts like an impenetrable wall for the metal
clumps and shields the hydrogen envelope from becoming enriched with
heavy elements. This result may appear somewhat surprising because, as
we have shown by the linear stability analysis
(Sect. 6.1), the He/H interface of the Woosley et al. (1988) star
is Rayleigh-Taylor unstable. However, since we did not impose any
seed perturbations in our AMR simulations and since the supernova
shock is almost perfectly spherically symmetric when it crosses the
He/H interface, the evolution of these layers proceeds initially
one-dimensionally. This turns out to be true even in models where much
more vigorous neutrino-driven convection imposes noticeable
asphericities on the shock during its revival. Such asphericities,
however, are smoothed out during the subsequent propagation of the
shock through the helium core. The only deviations from spherical
symmetry that perturb the He/H interface in Model T310a are the waves
that are excited when the metal-enriched clumps hit the inner edge of
the dense shell below the interface at times
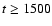 s. However, these perturbations encounter only a moderately
unstable He/H interface at these late times, in accordance with the
linear stability analysis (Fig. 11) which shows
that after
s. However, these perturbations encounter only a moderately
unstable He/H interface at these late times, in accordance with the
linear stability analysis (Fig. 11) which shows
that after
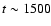 s the integrated growth rate,
s the integrated growth rate, 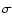 ,
increases only slightly. The mixing at the He/H interface is therefore
rather weak. The instability at this interface has apparently evolved
into the non-linear regime by
,
increases only slightly. The mixing at the He/H interface is therefore
rather weak. The instability at this interface has apparently evolved
into the non-linear regime by
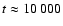 s, showing a
multitude of small and somewhat bent fingers. However, these do not
grow appreciably up to 20 000 s after bounce, when we stopped our 2D
simulation. At this time the flow near the interface expands nearly
self-similarly, i.e. the small fingers move with the same velocity as
the medium between them. Note that the perturbations of the He/H
interface that result from the accoustic waves are quite different
from those used to initiate the instability in all previous studies.
In the latter, seed perturbations of the order of 10% of the radial
velocity were imposed on the entire star about 300 s after shock
formation. With perturbations of this magnitude it is indeed possible
to obtain strong mixing at the He/H interface of our progenitor. We
have found such extended mixing in the late evolution of the
hydrodynamic model discussed in Kifonidis et al. (2000), which suffered
strongly from odd-even decoupling, and was therefore perturbed in the
radial velocity by
s, showing a
multitude of small and somewhat bent fingers. However, these do not
grow appreciably up to 20 000 s after bounce, when we stopped our 2D
simulation. At this time the flow near the interface expands nearly
self-similarly, i.e. the small fingers move with the same velocity as
the medium between them. Note that the perturbations of the He/H
interface that result from the accoustic waves are quite different
from those used to initiate the instability in all previous studies.
In the latter, seed perturbations of the order of 10% of the radial
velocity were imposed on the entire star about 300 s after shock
formation. With perturbations of this magnitude it is indeed possible
to obtain strong mixing at the He/H interface of our progenitor. We
have found such extended mixing in the late evolution of the
hydrodynamic model discussed in Kifonidis et al. (2000), which suffered
strongly from odd-even decoupling, and was therefore perturbed in the
radial velocity by  20% at t=300 s. However, even in this
model the nickel was mixed out only to a mass coordinate of
20% at t=300 s. However, even in this
model the nickel was mixed out only to a mass coordinate of
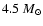 after 10 000 s.
after 10 000 s.
![\begin{figure}
\par\begin{tabular}{ccc}
\includegraphics[width=5.5cm,height=11.2...
...s[width=5.5cm,height=11.2cm,clip]{f14f_cmyk_600dpi.eps}\end{tabular}\end{figure}](/articles/aa/full/2003/35/aa3592/Timg177.gif) |
Figure 14:
Same as Fig. 12. a) t = 5000 s
(left), b)
t = 10 000 s (middle), c)
t = 20 000 s
(right). Note the change of the radial scale. The circular
orange/black boundary in the upper right panel corresponds to
the outer edge of the computational domain, which the
supernova shock has crossed long before. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{3592f15.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg178.gif) |
Figure 15:
Evolution of the extent of mixing in Model T310a. Left:
initial composition. Right: composition 20 000 s after core
bounce. The neutronization tracer is denoted with "X''.
Note that all heavy elements are confined to the helium core
(i.e. to the innermost
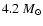 of the star)
even as late as 20 000 s after core bounce.
of the star)
even as late as 20 000 s after core bounce. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=14.8cm,clip]{3592f16.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg180.gif) |
Figure 16:
Logarithm of the fractional mass of different elements that
is contained within the velocity interval
![$[v_{\rm r},v_{\rm r}+{\rm d}v_{\rm r}]$](/articles/aa/full/2003/35/aa3592/img29.gif) as a function of the radial velocity
as a function of the radial velocity 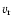 in Model
T310a at various epochs. The resolution is
in Model
T310a at various epochs. The resolution is
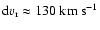 .
Note the different scales for
the radial velocity in the left and right panels. .
Note the different scales for
the radial velocity in the left and right panels. |
| Open with DEXTER |
6.2.2 Clump propagation and velocity
distribution of nucleosynthetic products
In Fig. 16 we show for times from 4 s until
20 000 s after bounce the logarithm of the fractional masses for
several nuclei that are contained within the velocity interval
![$[v_{\rm r},v_{\rm r}+{\rm d}v_{\rm r}]$](/articles/aa/full/2003/35/aa3592/img29.gif) as a function of the radial velocity.
Obviously, there occurs a bulk deceleration of the material from
velocities as large as
as a function of the radial velocity.
Obviously, there occurs a bulk deceleration of the material from
velocities as large as  14 000 km s-1 at a time of 4 s after
bounce to
14 000 km s-1 at a time of 4 s after
bounce to  5000 km s-1 after 50 s. This is caused by the
enormous deceleration that the shock and the post-shock material
experience after the shock has entered the He core. The deceleration
and the associated compression also cause the clear tendency of the
mass distributions of the elements to narrow down in velocity space
(Fig. 16).
5000 km s-1 after 50 s. This is caused by the
enormous deceleration that the shock and the post-shock material
experience after the shock has entered the He core. The deceleration
and the associated compression also cause the clear tendency of the
mass distributions of the elements to narrow down in velocity space
(Fig. 16).
Shortly before the shock crosses the (C+O)/He interface (i.e. for
times
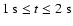 )
the abundance maxima of
different elements are well-separated in radius. Together with the
post-shock velocity gradient (Sect. 5.2) this
results in maxima of the velocity distributions of different nuclei
that are well-separated in velocity space. However, this separation
disappears within the first 50 s after bounce due to the strong
compression: being squeezed into a very dense shell, different nuclear
species are getting very close in radius and thus they reflect the
velocities that are prevailing in this shell. The first nuclei to
become affected by the compression are
)
the abundance maxima of
different elements are well-separated in radius. Together with the
post-shock velocity gradient (Sect. 5.2) this
results in maxima of the velocity distributions of different nuclei
that are well-separated in velocity space. However, this separation
disappears within the first 50 s after bounce due to the strong
compression: being squeezed into a very dense shell, different nuclear
species are getting very close in radius and thus they reflect the
velocities that are prevailing in this shell. The first nuclei to
become affected by the compression are
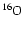 ,
,
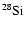 and
and
 ,
since these are located closest to the supernova
shock. A narrow peak forms in the velocity distribution of these
elements already between 4 s and 10 s after bounce
(Fig. 16). Being centered around 8500 km s-1 at t
= 10 s, the peak gradually recedes to
,
since these are located closest to the supernova
shock. A narrow peak forms in the velocity distribution of these
elements already between 4 s and 10 s after bounce
(Fig. 16). Being centered around 8500 km s-1 at t
= 10 s, the peak gradually recedes to  3500 km s-1 at
t=50 s. The maximum velocities of
3500 km s-1 at
t=50 s. The maximum velocities of
 and
and
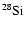 are larger than this value by about 1500 km s-1, while a small fraction
of
are larger than this value by about 1500 km s-1, while a small fraction
of
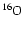 is found at somewhat larger velocities,
still. Elements that are located closer to the inner boundary of the
computational domain (i.e.
is found at somewhat larger velocities,
still. Elements that are located closer to the inner boundary of the
computational domain (i.e.
 and the neutronization
tracer) show broader distributions in velocity space during the first
and the neutronization
tracer) show broader distributions in velocity space during the first
 10 s of the explosion, until the strong compression also
affects their spatial distribution and leads to a homogenization of
all profiles in Fig. 16 around 50 s after
bounce. This homogenization is actually fortunate for a comparison of
our results to observational data, since it makes the late-time
velocity distributions of nuclei in our models fairly robust against
uncertainties that affect the nucleosynthesis in the neutrino-heated
matter. In particular, the velocity profiles of
10 s of the explosion, until the strong compression also
affects their spatial distribution and leads to a homogenization of
all profiles in Fig. 16 around 50 s after
bounce. This homogenization is actually fortunate for a comparison of
our results to observational data, since it makes the late-time
velocity distributions of nuclei in our models fairly robust against
uncertainties that affect the nucleosynthesis in the neutrino-heated
matter. In particular, the velocity profiles of
 and of
the neutronization tracer nucleus are finally rather similar. Hence,
it is not very relevant for the velocity distributions of these nuclei
that nucleosynthesis in the inner ejecta depends on unknown details of
the neutrino luminosities and spectra, which determine whether
and of
the neutronization tracer nucleus are finally rather similar. Hence,
it is not very relevant for the velocity distributions of these nuclei
that nucleosynthesis in the inner ejecta depends on unknown details of
the neutrino luminosities and spectra, which determine whether
 or mere neutron-rich nuclei are produced.
or mere neutron-rich nuclei are produced.
Up to a time of 300 s, when the Rayleigh-Taylor instabilities are
still developing, the maximum velocity of
 is steadily
decreasing, dropping to values of
is steadily
decreasing, dropping to values of  3500 km s-1. This maximum
velocity is found in the mushroom caps of the Rayleigh-Taylor fingers.
In the early stages of their existence these "clumps'' have to
propagate through a rather dense medium. In addition they "feel'' the
positive pressure gradient in the unstable layers. Hence they are
decelerated appreciably, but less than the expansion of the
surrounding matter is slowed down by this pressure gradient. Around
300 s, however, the density contrast between the clumps and their
environment has grown substantially. In addition, at this time the
sound speed is about 1400 km s-1 in the layers of the He core through
which the clumps propagate, while the "background'' flow is expanding
with
3500 km s-1. This maximum
velocity is found in the mushroom caps of the Rayleigh-Taylor fingers.
In the early stages of their existence these "clumps'' have to
propagate through a rather dense medium. In addition they "feel'' the
positive pressure gradient in the unstable layers. Hence they are
decelerated appreciably, but less than the expansion of the
surrounding matter is slowed down by this pressure gradient. Around
300 s, however, the density contrast between the clumps and their
environment has grown substantially. In addition, at this time the
sound speed is about 1400 km s-1 in the layers of the He core through
which the clumps propagate, while the "background'' flow is expanding
with  3000 km s-1. Comparing this to the clump velocity of
3500 km s-1 we find that at t = 300 s the clumps move relative to
the He core with about 500 km s-1, i.e. their motion relative to the
background is subsonic and the drag they experience is rather
small. As a result, the clumps "decouple'' from the flow and start to
move ballistically through the remaining part of the helium core, with
the maximum
3000 km s-1. Comparing this to the clump velocity of
3500 km s-1 we find that at t = 300 s the clumps move relative to
the He core with about 500 km s-1, i.e. their motion relative to the
background is subsonic and the drag they experience is rather
small. As a result, the clumps "decouple'' from the flow and start to
move ballistically through the remaining part of the helium core, with
the maximum
 velocity remaining roughly constant for
times between 300 s and 1500 s. At approximately the latter time
the clumps penetrate through the reverse shock at the inner edge of
the dense shell that has formed below the He/H interface. After
entering this shell they are strongly decelerated, and the maximum
velocities of all elements drop to
velocity remaining roughly constant for
times between 300 s and 1500 s. At approximately the latter time
the clumps penetrate through the reverse shock at the inner edge of
the dense shell that has formed below the He/H interface. After
entering this shell they are strongly decelerated, and the maximum
velocities of all elements drop to  1200 km s-1 as is visible for
a time of 20 000 s after core bounce in
Fig. 16. These values are significantly smaller
than those observed in SN 1987 A. Note that prior to the interaction
of the clumps with the shell, the nickel velocities of our models are in accordance with the velocities observed in SN 1987 A,
i.e. a good match to the observations is prevented by the formation of
the dense shell in the outer He core of our models. Several effects
cause the strong slow-down of the clumps in the shell. They can be
discussed by considering the expression for the drag force
1200 km s-1 as is visible for
a time of 20 000 s after core bounce in
Fig. 16. These values are significantly smaller
than those observed in SN 1987 A. Note that prior to the interaction
of the clumps with the shell, the nickel velocities of our models are in accordance with the velocities observed in SN 1987 A,
i.e. a good match to the observations is prevented by the formation of
the dense shell in the outer He core of our models. Several effects
cause the strong slow-down of the clumps in the shell. They can be
discussed by considering the expression for the drag force
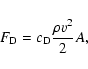 |
(4) |
where A is the cross sectional area of a clump, 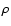 the ambient
fluid density, v the velocity of the clumps relative to the ambient
fluid, and
the ambient
fluid density, v the velocity of the clumps relative to the ambient
fluid, and 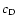 the drag coefficient. Since the clumps have to pass
through a reverse shock they enter an environment with a smaller mean expansion velocity than in the layers upstream of the
shock. Their velocity v relative to the new background is therefore
higher than it was before they crossed the shock and amounts to
the drag coefficient. Since the clumps have to pass
through a reverse shock they enter an environment with a smaller mean expansion velocity than in the layers upstream of the
shock. Their velocity v relative to the new background is therefore
higher than it was before they crossed the shock and amounts to
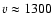 km s-1 at t = 1500 s. In addition
km s-1 at t = 1500 s. In addition 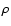 is larger
in the post-shock region. Both effects increase the drag by
increasing the ram pressure
is larger
in the post-shock region. Both effects increase the drag by
increasing the ram pressure 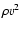 .
The sound speed in the
post-shock layers is rather small (890 km s-1) at t =
1500 s. Therefore, the clumps move supersonically through the
dense medium, with Mach numbers
.
The sound speed in the
post-shock layers is rather small (890 km s-1) at t =
1500 s. Therefore, the clumps move supersonically through the
dense medium, with Mach numbers
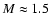 .
The drag coefficient
.
The drag coefficient 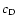 of a projectile increases steeply in the subsonic/supersonic
transition (this is the well-known "sound barrier''). The effect is
even more pronounced if the projectile's shape is roundish (as in the
case considered here) and not pointed. Together with the increase in
ram pressure, the supersonic motion leads to a large rise of
of a projectile increases steeply in the subsonic/supersonic
transition (this is the well-known "sound barrier''). The effect is
even more pronounced if the projectile's shape is roundish (as in the
case considered here) and not pointed. Together with the increase in
ram pressure, the supersonic motion leads to a large rise of 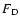 ,
and hence to significant energy dissipation.
,
and hence to significant energy dissipation.
The interaction of the clumps with the reverse shock resembles the
well-studied problem of a (planar) shock interacting with an
overdense, spherical, interstellar cloud that is in pressure
equilibrium with its surroundings (see Klein et al. 1994, and the references
therein). In this case it has been shown that the interaction
can be divided into four stages. In the first phase, the blast wave
strikes the cloud driving a shock into the cloud and a reflected shock
into the (shocked) intercloud medium. The reflected shocks resulting
from this phase correspond to the bow-shocks that we observe and which
pervade the entire dense helium shell in our simulation between
3000 s and 20 000 s after bounce
(Sect. 6.2.1). In the second stage the cloud is
compressed into a pancake-like structure. Indications of this
phenomenon can be seen in Fig. 13c. The
third stage is the reexpansion phase in which the cloud expands
laterally. This increases its cross section, A, and thus hastens
its deceleration (see Figs. 14a-c). In the
fourth and final phase the cloud is destroyed by vorticity generation
due to the development of Rayleigh-Taylor and Kelvin-Helmholtz
instabilities at its surface. We do not observe a complete
disintegration of the metal clumps according to this last phase in our
simulations. It is not clear, whether this is due to numerical
reasons, due to the fact that we might have simply stopped our
simulations too early for the instabilities to grow appreciably, or
due to differences in the physics of both problems. In our case the
density contrast between a clump and the medium upstream as well as
downstream of the reverse shock (the former quantity is a constant in
Klein et al. 1994) is time-dependent, because the overall expansion
decreases the densities. Furthermore, our reverse shock has a Mach
number 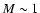 and is thus not very strong, in contrast to the
shocks studied by Klein et al. (1994), for which
and is thus not very strong, in contrast to the
shocks studied by Klein et al. (1994), for which 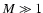 .
In addition, the
mushroom caps of our Rayleigh-Taylor fingers have typical radii
.
In addition, the
mushroom caps of our Rayleigh-Taylor fingers have typical radii
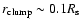 ,
with
,
with 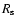 being the radius
of the reverse shock. Thus they do not satisfy the small clump
criterion (
being the radius
of the reverse shock. Thus they do not satisfy the small clump
criterion (
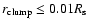 )
that Klein et al. (1994)
assumed for their study. Finally, our problem has a more complicated
geometry and equation of state. Recent experiments of
)
that Klein et al. (1994)
assumed for their study. Finally, our problem has a more complicated
geometry and equation of state. Recent experiments of 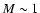 shocks in air interacting with a cylindrical column of high-density
gas (Fishbine 2002; Zoldi 2002) indicate that the gas column is
strongly ablated, developing significant vorticity at its
edges. However, it is not entirely destroyed.
shocks in air interacting with a cylindrical column of high-density
gas (Fishbine 2002; Zoldi 2002) indicate that the gas column is
strongly ablated, developing significant vorticity at its
edges. However, it is not entirely destroyed.
Klein et al. (1994) report that for the shock-cloud interaction problem,
about 120 zones per cloud radius are required to reduce numerical
viscosity in a second-order Godunov-type hydrodynamic scheme to the
point that converged results can be obtained. With  20 zones
per clump radius our resolution is much lower. Resolution studies are
required in order to decide whether our velocity distributions are
numerically converged. The same holds for answering the question
whether the clumps will get dispersed and mixed with the material of
the "helium wall'', or whether they can survive as individual
entities. Note also that in the end 3D calculations will be required
since the drag coefficient,
20 zones
per clump radius our resolution is much lower. Resolution studies are
required in order to decide whether our velocity distributions are
numerically converged. The same holds for answering the question
whether the clumps will get dispersed and mixed with the material of
the "helium wall'', or whether they can survive as individual
entities. Note also that in the end 3D calculations will be required
since the drag coefficient, 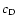 ,
and the cross section, A, in
Eq. (4) depend on clump shape, which can lead to
quantitative differences in three-dimensional as compared to our
two-dimensional simulations. The Rayleigh-Taylor fingers that one
finds in a two-dimensional calculation are comparable to genuine 3D
"mushrooms'' only along the polar axis of the 2D grid. Along the
equator one actually obtains toroidal structures because of the
assumption of axial symmetry (see Kane et al. 2000, and the references
therein). Judging from the 2D results of Klein et al. (1994) and the
3D calculations of Stone & Norman (1992) for the shock-cloud interaction
problem, we have little doubt, however, that independent of the
dimensionality of the calculation the metals must slow down
appreciably. We consider this to be a potentially serious problem for
obtaining high velocities for the metals in the H-envelopes of type II
supernova models. Efficient re-acceleration mechanisms operating at
later phases of the evolution are currently unknown.
,
and the cross section, A, in
Eq. (4) depend on clump shape, which can lead to
quantitative differences in three-dimensional as compared to our
two-dimensional simulations. The Rayleigh-Taylor fingers that one
finds in a two-dimensional calculation are comparable to genuine 3D
"mushrooms'' only along the polar axis of the 2D grid. Along the
equator one actually obtains toroidal structures because of the
assumption of axial symmetry (see Kane et al. 2000, and the references
therein). Judging from the 2D results of Klein et al. (1994) and the
3D calculations of Stone & Norman (1992) for the shock-cloud interaction
problem, we have little doubt, however, that independent of the
dimensionality of the calculation the metals must slow down
appreciably. We consider this to be a potentially serious problem for
obtaining high velocities for the metals in the H-envelopes of type II
supernova models. Efficient re-acceleration mechanisms operating at
later phases of the evolution are currently unknown.
Actually there is no physical reason to expect an acceleration of
matter (relative to the observer's frame) by the instabilities. The
pressure gradient in the Rayleigh-Taylor unstable layers of the ejecta
is positive, i.e. these layers are decelerated. In
fact it is this deceleration that leads to the formation of
Rayleigh-Taylor fingers: Since overdense parcels of gas have a larger
momentum than the neighbouring material, they cannot be slowed
down as efficiently as the surrounding matter and hence they start to
move outward relative to their ambient medium. During no time,
however, the clumps are accelerated with respect to the observer's
rest frame. The reason why we obtain high
 velocities
in the early evolution of our models is the fact that the nickel
clumps decouple from the (continuously decelerated) background flow
and subsequently move ballistically through the ejecta. By decoupling
from the background, the clumps can nearly conserve their high initial
velocity beyond the time of decoupling and thus move outward in mass
until they become comoving with the outer ejecta. It must be noted,
though, that these high initial
velocities
in the early evolution of our models is the fact that the nickel
clumps decouple from the (continuously decelerated) background flow
and subsequently move ballistically through the ejecta. By decoupling
from the background, the clumps can nearly conserve their high initial
velocity beyond the time of decoupling and thus move outward in mass
until they become comoving with the outer ejecta. It must be noted,
though, that these high initial
 velocities are only
obtained if clump formation starts sufficiently early, i.e. within the
first
velocities are only
obtained if clump formation starts sufficiently early, i.e. within the
first  10 s after bounce, when the velocity in the
10 s after bounce, when the velocity in the
 -rich layers is still high (compare
Fig. 9a). If clump formation is delayed by
a few 100 s, the
-rich layers is still high (compare
Fig. 9a). If clump formation is delayed by
a few 100 s, the
 velocities have already dropped to
values <1500 km s-1 (Fig. 9b) and it
becomes impossible to obtain high velocities by "clump decoupling''
during the subsequent evolution. This is the reason why earlier
investigations of Rayleigh-Taylor mixing in type II supernovae, which
started from one-dimensional models 300 s after bounce, obtained only
low
velocities have already dropped to
values <1500 km s-1 (Fig. 9b) and it
becomes impossible to obtain high velocities by "clump decoupling''
during the subsequent evolution. This is the reason why earlier
investigations of Rayleigh-Taylor mixing in type II supernovae, which
started from one-dimensional models 300 s after bounce, obtained only
low
 velocities. The only exception were some of the SPH
calculations of Herant & Benz (1992) which showed nickel velocities of
velocities. The only exception were some of the SPH
calculations of Herant & Benz (1992) which showed nickel velocities of  3000 km s-1. As stated by the authors, this result is a direct
consequence of an assumed premixing of
3000 km s-1. As stated by the authors, this result is a direct
consequence of an assumed premixing of
 throughout 75%
of the metal core of the 1D explosion model of a
throughout 75%
of the metal core of the 1D explosion model of a
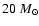 progenitor, from which they started their 2D calculations at
t=300 s. In contrast to their approach, in which this (early)
mixing was put in by hand, we have attempted to perform consistent and
continuous high-resolution 2D simulations of the entire shock
propagation through the star. Doing so, we find that even if one
succeeds to obtain high metal velocities during the first minutes of
the explosion, there is no guarantee that these velocities will remain
high throughout the later evolution. As we discussed earlier, a main
obstacle to overcome is the interaction of the metal clumps with the
reverse shock below the He/H interface, which dramatically reduces the
nickel velocities in our simulations. It is not clear to us why this
nickel deceleration is not present in the models of
Herant & Benz.
progenitor, from which they started their 2D calculations at
t=300 s. In contrast to their approach, in which this (early)
mixing was put in by hand, we have attempted to perform consistent and
continuous high-resolution 2D simulations of the entire shock
propagation through the star. Doing so, we find that even if one
succeeds to obtain high metal velocities during the first minutes of
the explosion, there is no guarantee that these velocities will remain
high throughout the later evolution. As we discussed earlier, a main
obstacle to overcome is the interaction of the metal clumps with the
reverse shock below the He/H interface, which dramatically reduces the
nickel velocities in our simulations. It is not clear to us why this
nickel deceleration is not present in the models of
Herant & Benz.
Herant & Benz (1992) reported that the energy release due to the radioactive
decay of
 and
and
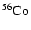 is inefficient to
significantly boost the nickel velocities over the first few
months. However, further studies of this effect, which should start
from models like ours and use more accurate hydrodynamic schemes and
higher resolution than the calculations of Herant & Benz (1992) are clearly
required. At present, we have to conclude that high final clump
velocities can only be obtained if the clumps decouple sufficiently
early from the background flow, and if the helium wall and the
associated reverse shock do not form. The latter requires that the
main shock does not decelerate in the hydrogen envelope, i.e. the
density gradient outside the He core has to be steeper than
is inefficient to
significantly boost the nickel velocities over the first few
months. However, further studies of this effect, which should start
from models like ours and use more accurate hydrodynamic schemes and
higher resolution than the calculations of Herant & Benz (1992) are clearly
required. At present, we have to conclude that high final clump
velocities can only be obtained if the clumps decouple sufficiently
early from the background flow, and if the helium wall and the
associated reverse shock do not form. The latter requires that the
main shock does not decelerate in the hydrogen envelope, i.e. the
density gradient outside the He core has to be steeper than  r-3. A situation where this might hold is the case of a type Ib
supernova explosion. The progenitors of type Ib supernovae are thought
to be stripped He cores that lack a thick hydrogen envelope. In this
case the shock directly enters the tenuous atmosphere of the star once
it leaves the dense part of the He-rich layers.
r-3. A situation where this might hold is the case of a type Ib
supernova explosion. The progenitors of type Ib supernovae are thought
to be stripped He cores that lack a thick hydrogen envelope. In this
case the shock directly enters the tenuous atmosphere of the star once
it leaves the dense part of the He-rich layers.
7 Beyond the first second: A type Ib model?
To confirm the effect of a steeper density decline upon clump
propagation we have removed the outer envelope of our progenitor model
and replaced it by power-law profiles for the density and temperature
of the form
Herein 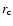 is the radius at which the original model was cut,
is the radius at which the original model was cut,
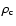 and
and 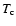 are the density and temperature at that radius, and
n=4.25 and m = 1.32 are the adopted power-law indices for the
density and temperature profiles, respectively. We have chosen
are the density and temperature at that radius, and
n=4.25 and m = 1.32 are the adopted power-law indices for the
density and temperature profiles, respectively. We have chosen
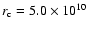 cm, i.e. we placed the cut still inside the He
core at a mass coordinate
cm, i.e. we placed the cut still inside the He
core at a mass coordinate
 ,
while the mass
of the new envelope amounted to
,
while the mass
of the new envelope amounted to
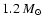 .
Note that this simple setup of a "type Ib progenitor'' lacks internal
consistency. It does not take into account that mass-loss due to winds
(or binary interaction) will gradually alter the entire structure of
the star during its evolution and that the density profile at the
onset of core collapse obtained from a consistent stellar evolutionary
calculation will therefore look different from our model. For this
reason the calculations discussed below can only demonstrate effects
in principle, and the simulations should be repeated with generic
type Ib progenitors (e.g. Woosley et al. 1995) to discuss observationally
relevant aspects in detail. In the context of the present work we
refrained from doing so but wished to start with our explosion model T310 as described in Sect. 5.2, and follow clump
propagation in our truncated progenitor with AMRA until 3000 s after bounce. At this epoch the expansion is already
self-similar, i.e. the clumps are "frozen in'' and move with the same
velocity as the ambient medium.
.
Note that this simple setup of a "type Ib progenitor'' lacks internal
consistency. It does not take into account that mass-loss due to winds
(or binary interaction) will gradually alter the entire structure of
the star during its evolution and that the density profile at the
onset of core collapse obtained from a consistent stellar evolutionary
calculation will therefore look different from our model. For this
reason the calculations discussed below can only demonstrate effects
in principle, and the simulations should be repeated with generic
type Ib progenitors (e.g. Woosley et al. 1995) to discuss observationally
relevant aspects in detail. In the context of the present work we
refrained from doing so but wished to start with our explosion model T310 as described in Sect. 5.2, and follow clump
propagation in our truncated progenitor with AMRA until 3000 s after bounce. At this epoch the expansion is already
self-similar, i.e. the clumps are "frozen in'' and move with the same
velocity as the ambient medium.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{3592f17.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg204.gif) |
Figure 17:
Same as Fig. 16 but for Model T310b
and times of 300 s, 1500 s and 3000 s after bounce. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{3592f18.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg205.gif) |
Figure 18:
Logarithm of the density in Model T310b at a time of
1500 s after bounce. |
| Open with DEXTER |
The simulation in this section, to which we will henceforth refer to
as Model T310b, was performed with a maximum resolution of
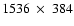 zones. Otherwise we used the same computational strategy
as for Model T310a of Sect. 6.2. Not surprisingly, the
evolution in Model T310b proceeded identically to the previous type II
supernova model, T310a, for the first 50 s, i.e. the time it took
the shock to reach the mass coordinate where we truncated the original
progenitor and where the density in the modified model now starts to
decline steeply. It is remarkable, however, that the velocity profiles
for all chemical elements show only minor differences between Model T310b (Fig. 17) and Model T310a (compare
Fig. 16) even as late as 300 s after bounce.
This also indicates that the lower resolution used in Model T310b has
only small effects on the overall dynamics. However, it suppresses
smale-scale fragmentation due to Kelvin-Helmholtz instabilities which
is visible in Fig. 13c but not in
Fig. 18. Significant differences between both cases
start to develop only for times later than 300 s. As we expected,
the formation of a reverse shock and an associated dense helium shell
is absent in the outer core of Model T310b (compare
Fig. 18 with Fig. 13c).
Instead of suffering from a deceleration in such a dense environment
the metal clumps can now expand freely into a tenuous medium, i.e. the
velocity profiles of all chemical elements do not change any more
after 300 s (Fig. 17). Maximum velocities of
3500 km s-1 are obtained for
zones. Otherwise we used the same computational strategy
as for Model T310a of Sect. 6.2. Not surprisingly, the
evolution in Model T310b proceeded identically to the previous type II
supernova model, T310a, for the first 50 s, i.e. the time it took
the shock to reach the mass coordinate where we truncated the original
progenitor and where the density in the modified model now starts to
decline steeply. It is remarkable, however, that the velocity profiles
for all chemical elements show only minor differences between Model T310b (Fig. 17) and Model T310a (compare
Fig. 16) even as late as 300 s after bounce.
This also indicates that the lower resolution used in Model T310b has
only small effects on the overall dynamics. However, it suppresses
smale-scale fragmentation due to Kelvin-Helmholtz instabilities which
is visible in Fig. 13c but not in
Fig. 18. Significant differences between both cases
start to develop only for times later than 300 s. As we expected,
the formation of a reverse shock and an associated dense helium shell
is absent in the outer core of Model T310b (compare
Fig. 18 with Fig. 13c).
Instead of suffering from a deceleration in such a dense environment
the metal clumps can now expand freely into a tenuous medium, i.e. the
velocity profiles of all chemical elements do not change any more
after 300 s (Fig. 17). Maximum velocities of
3500 km s-1 are obtained for
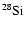 ,
,
 ,
,
 ,
and for the neutronization tracer, while
,
and for the neutronization tracer, while
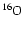 expands with velocities as high as 5500 km s-1.
expands with velocities as high as 5500 km s-1.
Figure 19 displays the extent of the mixing
(averaged over angle) for this model at a time of 3000 s. The newly
synthesized nuclei are mixed throughout the inner
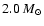 of the star. Figure 19 should be
compared to the plots of "Model 4B'' of Woosley & Eastman (1997), who computed
synthetic spectra from one-dimensional explosion models of a
of the star. Figure 19 should be
compared to the plots of "Model 4B'' of Woosley & Eastman (1997), who computed
synthetic spectra from one-dimensional explosion models of a
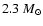 He core (originating from a
He core (originating from a
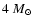 He star) and demonstrated that very good agreement with
observed spectra of SN 1984 L near maximum light could be
achieved. This was only the case, however, if they artificially mixed
He star) and demonstrated that very good agreement with
observed spectra of SN 1984 L near maximum light could be
achieved. This was only the case, however, if they artificially mixed
 into the helium rich layers assuming an exponential
decline of the
into the helium rich layers assuming an exponential
decline of the
 mass fraction,
mass fraction,
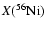 ,
with
the enclosed mass. The value of
,
with
the enclosed mass. The value of
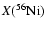 decreased below
10-3 only at a mass coordinate of
decreased below
10-3 only at a mass coordinate of 
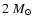 .
Different from Model 4B of Woosley & Eastman (1997) our Model T310b
(Fig. 19) shows a plateau-like distribution
with high nickel mass fractions (
.
Different from Model 4B of Woosley & Eastman (1997) our Model T310b
(Fig. 19) shows a plateau-like distribution
with high nickel mass fractions (
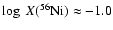 )
up to the outer edge of the nickel-enriched core. The latter
coincides with that of the Woosley & Eastman model. Whether this is
sufficient to cause an adequately large flux of ionizing
)
up to the outer edge of the nickel-enriched core. The latter
coincides with that of the Woosley & Eastman model. Whether this is
sufficient to cause an adequately large flux of ionizing
 -photons in the He envelope in case of our more massive star
(
-photons in the He envelope in case of our more massive star
(
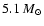 instead of
instead of
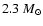 for
Woosley & Eastman's "Model 4B'') can only be decided by calculating
detailed spectra. Our purpose here is only to demonstrate that
multi-dimensional hydrodynamic models, with a consistent treatment of
the early phases of the explosion, can yield strong mixing of the
metal and He core that is a prerequisite to produce a good match
between calculated and observed spectra and light curves of type Ib
supernovae (Shigeyama et al. 1990; Hachisu et al. 1994;
Woosley & Eastman 1997). Hachisu et al. (1994) have shown that in order to obtain a
sufficient amount of mixing in multi-dimensional simulations with
artificially triggered Rayleigh-Taylor instabilities, the amplitude of
the seed perturbations must exceed 5% of the radial expansion
velocity at the time the shock crosses the unstable interfaces in the
metal core. Our models demonstrate that such a degree of perturbation
can be naturally obtained as a result of neutrino-driven convection
during the first second of the explosion.
for
Woosley & Eastman's "Model 4B'') can only be decided by calculating
detailed spectra. Our purpose here is only to demonstrate that
multi-dimensional hydrodynamic models, with a consistent treatment of
the early phases of the explosion, can yield strong mixing of the
metal and He core that is a prerequisite to produce a good match
between calculated and observed spectra and light curves of type Ib
supernovae (Shigeyama et al. 1990; Hachisu et al. 1994;
Woosley & Eastman 1997). Hachisu et al. (1994) have shown that in order to obtain a
sufficient amount of mixing in multi-dimensional simulations with
artificially triggered Rayleigh-Taylor instabilities, the amplitude of
the seed perturbations must exceed 5% of the radial expansion
velocity at the time the shock crosses the unstable interfaces in the
metal core. Our models demonstrate that such a degree of perturbation
can be naturally obtained as a result of neutrino-driven convection
during the first second of the explosion.
A most remarkable feature of Model T310b is the fact that the number
of Rayleigh-Taylor fingers at times
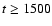 s is correlated
with (indeed it is essentially equal to) the number of down-flows that
developed in the convective layer of neutrino heating behind the shock
(compare Fig. 18 to Fig. 1b). This
correlation, although initially present, is destroyed in Model T310a,
where the interaction of the clumps with the reverse shock and the
dense helium shell results in a stronger non-linear evolution with
substantial vorticity generation and mixing. As the structure of
down-flows and neutrino-heated bubbles characterizes the mode of the
convective pattern that prevails within the shock-revival phase, it
carries important information about the mechanism that initiates the
explosion. It would be interesting if our finding is generic, and if
it also holds for cases where the pattern of neutrino-driven
convection develops much larger modes than those obtained in our
simulations. At present, however, one must be cautious not to
overinterpret our result, which is based on a single 2D model. A
confirmation of the existence of a tight correlation between the
patterns of the early post-shock convection and the final
instabilities in the mantle of the exploding star will probably
require well-resolved 3D calculations and parameter studies with
different explosion and progenitor models.
s is correlated
with (indeed it is essentially equal to) the number of down-flows that
developed in the convective layer of neutrino heating behind the shock
(compare Fig. 18 to Fig. 1b). This
correlation, although initially present, is destroyed in Model T310a,
where the interaction of the clumps with the reverse shock and the
dense helium shell results in a stronger non-linear evolution with
substantial vorticity generation and mixing. As the structure of
down-flows and neutrino-heated bubbles characterizes the mode of the
convective pattern that prevails within the shock-revival phase, it
carries important information about the mechanism that initiates the
explosion. It would be interesting if our finding is generic, and if
it also holds for cases where the pattern of neutrino-driven
convection develops much larger modes than those obtained in our
simulations. At present, however, one must be cautious not to
overinterpret our result, which is based on a single 2D model. A
confirmation of the existence of a tight correlation between the
patterns of the early post-shock convection and the final
instabilities in the mantle of the exploding star will probably
require well-resolved 3D calculations and parameter studies with
different explosion and progenitor models.
![\begin{figure}
\par\includegraphics[width=16.1cm,clip]{3592f19.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg214.gif) |
Figure 19:
Same as Fig. 15, but for Model
T310b. Left: initial composition. Right: composition
3000 s after core bounce. |
| Open with DEXTER |
8 Conclusions
We have presented a study of hydrodynamic instabilities in a type II
and a type Ib-like supernova model that has improved upon earlier
simulations by starting the explosion by means of neutrino heating
behind the stalled supernova shock and by following the hydrodynamics
of this explosion well beyond shock-breakout from the stellar
photosphere. The consistency of the hydrodynamic evolution that was
thereby achieved allows for the following conclusions.
The effects discussed above could not be seen in previous studies of
Rayleigh-Taylor instabilities in core collapse supernovae where the
explosion was started by ad hoc energy deposition (using pistons or
thermal bombs). Especially the high
 velocities, the
strong mixing triggered at the Si/O interface, and the very short
growth time-scale of the instabilities at the Si/O and (C+O)/He
interfaces (minutes as compared to hours) are in clear contrast to
what has been reported in previous studies, especially in those which
dealt with the mixing in type II supernovae. Of all earlier works,
only the type Ib studies of Hachisu et al. (1994) and the SN 1993 J
simulations of Iwamoto et al. (1997) agree qualitatively with the
evolution that we observe for the first minutes of the explosion. Both
of these studies found, as we do, that Rayleigh-Taylor instabilities
at the (C+O)/He interface of the progenitor stars grow within minutes
after core collapse. However, they did not observe the instability at
the Si/O interface. Moreover, they had to assume large seed
perturbations to induce the mixing, whereas in our case the
perturbations are a natural consequence of neutrino-driven convection.
velocities, the
strong mixing triggered at the Si/O interface, and the very short
growth time-scale of the instabilities at the Si/O and (C+O)/He
interfaces (minutes as compared to hours) are in clear contrast to
what has been reported in previous studies, especially in those which
dealt with the mixing in type II supernovae. Of all earlier works,
only the type Ib studies of Hachisu et al. (1994) and the SN 1993 J
simulations of Iwamoto et al. (1997) agree qualitatively with the
evolution that we observe for the first minutes of the explosion. Both
of these studies found, as we do, that Rayleigh-Taylor instabilities
at the (C+O)/He interface of the progenitor stars grow within minutes
after core collapse. However, they did not observe the instability at
the Si/O interface. Moreover, they had to assume large seed
perturbations to induce the mixing, whereas in our case the
perturbations are a natural consequence of neutrino-driven convection.
The crucial difference between our type II model T310a and all other
type II supernova simulations (except for the work of
Iwamoto et al. 1997) is the fact that our metal core starts to
fragment within only about 20 s after bounce, when the velocity in
the
 -rich layers is still high (see
Fig. 9a). This leads to an early decoupling
of the clumps from the background flow, enabling the clumps to
conserve the high velocity that the flow possesses at early times.
Not allowing for early clump formation and decoupling, as it has been
done in nearly all previous multi-dimensional simulations of type II
supernovae by starting the calculations hundreds of seconds after core
bounce from 1D initial models, has the effect that the velocities of
the
-rich layers is still high (see
Fig. 9a). This leads to an early decoupling
of the clumps from the background flow, enabling the clumps to
conserve the high velocity that the flow possesses at early times.
Not allowing for early clump formation and decoupling, as it has been
done in nearly all previous multi-dimensional simulations of type II
supernovae by starting the calculations hundreds of seconds after core
bounce from 1D initial models, has the effect that the velocities of
the
 -rich layers have dropped to values
-rich layers have dropped to values  1500 km s-1 at the start of the multi-dimensional calculation
(Fig. 9b). It therefore becomes impossible
to obtain high velocities by the Rayleigh-Taylor instabilities during
the subsequent evolution.
1500 km s-1 at the start of the multi-dimensional calculation
(Fig. 9b). It therefore becomes impossible
to obtain high velocities by the Rayleigh-Taylor instabilities during
the subsequent evolution.
In fact, the situation becomes even worse at later times. We find
that our Model T310a is initially successful in yielding high
 velocities: once the
velocities: once the
 clumps in this
model have decoupled from the flow, they propagate ballistically and
subsonically through the helium core. Due to their subsonic motion,
they do not dissipate much of their kinetic energy and the maximum
clumps in this
model have decoupled from the flow, they propagate ballistically and
subsonically through the helium core. Due to their subsonic motion,
they do not dissipate much of their kinetic energy and the maximum
 velocities remain high at 3500 km s-1. However, this
changes when the clumps reach the outer helium core and encounter the
reverse shock and the dense (Rayleigh-Taylor unstable) "wall'' that
are left behind by the main shock below the He/H interface. When the
clumps penetrate through the reverse shock into this wall, 1500 s
after core bounce, they are decelerated due to supersonic drag to
velocities <1500 km s-1. An interaction of the clumps with the
reverse shock is also present in data of previous type II supernova
simulations (Müller et al. 1991b,a). However, its importance for clump
propagation was not recognized because
velocities remain high at 3500 km s-1. However, this
changes when the clumps reach the outer helium core and encounter the
reverse shock and the dense (Rayleigh-Taylor unstable) "wall'' that
are left behind by the main shock below the He/H interface. When the
clumps penetrate through the reverse shock into this wall, 1500 s
after core bounce, they are decelerated due to supersonic drag to
velocities <1500 km s-1. An interaction of the clumps with the
reverse shock is also present in data of previous type II supernova
simulations (Müller et al. 1991b,a). However, its importance for clump
propagation was not recognized because
-
due to the late phase when previous multi-dimensional calculations
were started, clump formation at the (C+O)/He interface was only about
to set in at
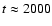 s, when the reverse shock had
propagated sufficiently far inward in mass to reach this interface,
s, when the reverse shock had
propagated sufficiently far inward in mass to reach this interface,
-
the initial clump velocities and the densities in the shell downstream
of the reverse shock were low, leading to less pronounced effects
during the interaction,
-
and the employed numerical resolution was insufficient to resolve the
non-linear waves that characterize this interaction.
A final difference between Model T310a and previous type II supernova
simulations is the fact that we do not obtain strong mixing at the
He/H interface. Unless we add artificial perturbations to these
layers, as it was done in all previous studies, the mixing remains
very weak. This might indicate that neutrino-driven convection is not
able to provide perturbations that are sufficiently strong to cause
the large-scale mixing that was observed in SN 1987 A. However, final
conclusions regarding this point are not possible before
Rayleigh-Taylor simulations have been performed which start from a
globally aspherical situation, as seen in recent calculations of
neutrino-driven explosions (Janka et al. 2003; Scheck et al., in
preparation).
Taken together, the effects revealed by our simulations demonstrate
that the evolution proceeds multi-dimensionally from the earliest
moments. Convective instabilities during the shock-revival phase
cannot be neglected. They lead to very early growth of Rayleigh-Taylor
instabilities and thus to high initial clump velocities what in turn
determines the character of the late-time hydrodynamic evolution. By
starting from 1D initial models hundreds of seconds after core bounce,
all earlier investigations of Rayleigh-Taylor mixing in type II
supernovae have therefore missed essential parts of the physics of the
problem.
Supernova 1987 A still remains an enigma, though. Given the (late)
deceleration of the clumps below the He/H interface in Model T310a, we
wonder whether the conflicting maximum
 velocities
between our models and the observations point to deficiencies of the
"standard'' blue supergiant progenitors, or to missing physics in our
shock-revival simulations. There are indications that the progenitor
of SN 1987 A might have been the result of a merger of two smaller
stars (Podsiadlowski 1992) and that therefore its structure might
not be accounted for reliably by "standard'' stellar evolutionary
calculations. Numerical studies of such mergers have recently been
performed by Ivanova et al. (2002). Although their models show density profiles
in the hydrogen envelope that look similar to the one of our
progenitor (N. Ivanova, private communication), it remains to be seen
in future simulations whether for these models the evolution differs
from what we have reported here.
velocities
between our models and the observations point to deficiencies of the
"standard'' blue supergiant progenitors, or to missing physics in our
shock-revival simulations. There are indications that the progenitor
of SN 1987 A might have been the result of a merger of two smaller
stars (Podsiadlowski 1992) and that therefore its structure might
not be accounted for reliably by "standard'' stellar evolutionary
calculations. Numerical studies of such mergers have recently been
performed by Ivanova et al. (2002). Although their models show density profiles
in the hydrogen envelope that look similar to the one of our
progenitor (N. Ivanova, private communication), it remains to be seen
in future simulations whether for these models the evolution differs
from what we have reported here.
Sources of uncertainty in our calculations that may affect the
velocities of chemical elements are the still limited numerical
resolution and especially the differences between two-dimensional
versus three-dimensional hydrodynamics. The smaller drag that clumps
experience in three dimensions (Kane et al. 2000) may lead to higher
initial clump velocities after the fragmentation of the metal core and
thus to a farther penetration of the clumps through the helium
"wall''. This might result in higher final
 velocities
than in two dimensions. An extension of our calculations to three
dimensions with a similar resolution as in the 2D case appears hardly
feasible in view of present computer resources. Further insight
might, however, be gained by laser experiments (Robey et al. 2001; Drake et al. 2002; Klein et al. 2003; Kane et al. 2001, and the
references therein), and
hydrodynamic code validation experiments as those described by
Fishbine (2002) and Zoldi (2002) before well-resolved 3D
hydrodynamic simulations will become available.
velocities
than in two dimensions. An extension of our calculations to three
dimensions with a similar resolution as in the 2D case appears hardly
feasible in view of present computer resources. Further insight
might, however, be gained by laser experiments (Robey et al. 2001; Drake et al. 2002; Klein et al. 2003; Kane et al. 2001, and the
references therein), and
hydrodynamic code validation experiments as those described by
Fishbine (2002) and Zoldi (2002) before well-resolved 3D
hydrodynamic simulations will become available.
There has been much speculation about large-scale anisotropies caused
by jets in the explosion of SN 1987 A
(Wang et al. 2002; Khokhlov et al. 1999; Wheeler et al. 2002). However, convincing and
consistent (MHD) calculations of the formation and propagation of such
jets and an associated explosion have not yet been performed. It is
unclear whether in this scenario nickel velocities can be obtained
that are in agreement with those observed in SN 1987 A. An initial
anisotropy of the explosion, that might lead to high initial nickel
velocities, would have to work against the same effects in the
envelope that we find to be important in our simulations. The
interaction with the reverse shock and the dense helium shell might
not only slow down fast metal clumps, it might also reduce an initial
anisotropy of the ejecta. Judging from the experience gained from our
calculations, we doubt that the spatial resolution in simulations of
anisotropic explosions that have been performed to date
(Nagataki et al. 1998,1997; Khokhlov et al. 1999) was sufficient to study these effects
reliably. The origin of the prolate deformation of the ejecta of SN
1987 A (Wang et al. 2002) must therefore be regarded to be unknown. In
fact, there is currently neither observational nor theoretical
evidence that unambiguously demands the assumption of a "jet-driven''
explosion. The deformation could as well be linked to an anisotropic
initiation of the explosion due to neutrino heating
(Janka et al. 2003; Plewa et al., in preparation). On the other hand
it might also be caused by stellar rotation as a result of a merger
history of the progenitor.
While clearly substantial work is required in case of SN 1987 A, our
"type Ib'' Model T310b is in reasonably good agreement with
observations of extragalactic type Ib supernovae. Due to the absence
of dense shell and reverse shock formation in the He core of this
model, the metal-rich clumps are not decelerated once they start to
propagate ballistically through the ambient gas and the final metal
velocities of
3500-5500 km s-1 are sufficiently high. In addition,
the extent of the mixing in this model is comparable to what
Woosley & Eastman (1997) had to assume in their "Model 4B'' to model the spectrum
of SN 1984 L. This result is very encouraging. It indicates that the
interaction of neutrino-driven convection with the Rayleigh-Taylor
instabilities in the stellar mantle is able to account for important
aspects of the mixing of different elements in type Ib supernovae
which are known from spectral and light curve calculations for more
than a decade.
Another interesting aspect of Model T310b is the fact that without the
strong non-linear interaction of the clumps with the reverse shock,
perturbations originating from the shock-revival phase are reflected
in the final flow structures of the Rayleigh-Taylor instabilities.
This may enable one to deduce information about the pattern of the
neutrino-driven convection from observations of the distribution of
metals in the ejecta of type Ib supernovae. The possibility to obtain
such a unique piece of evidence from ejecta properties is exciting.
However, before such conclusions can be drawn, our results need to be
ascertained by making use of a larger number of shock-revival
simulations with different properties and a greater range of (type Ib
and type Ic) progenitors. We believe that in the end very
well-resolved 3D simulations will be required to prove the existence
of such a correlation. If confirmed it might provide us with a means
to probe the physics linked to the explosion mechanism even for
extragalactic supernovae.
Finally, we emphasize that clump deceleration due to the interaction
with the reverse shock might be crucial for a correct interpretation
of observations of the different supernova types. It can cause
different final metal clump velocities even if the initiation of the
explosion proceeds similarly in different stars. The latter must
actually be expected for the neutrino-heating mechanism, because the
post bounce models of supernova cores are rather similar, regardless
of whether they originate from type II or type Ib progenitors (Rampp
et al., in preparation). On the other hand, clump deceleration depends
on the structure of the envelope of the progenitor and a sequence is
conceivable where its importance varies with the type of the
supernova, being strongest in (some fraction of?) type II events and
weaker or absent in type Ib and Ic supernovae. Unfortunately,
observational data of metal clump velocities are currently sparse and
hence they do not allow one to test this hypothesis. Photospheric
velocities, as those published recently by Hamuy (2003), are not
very helpful in this respect because they only probe the outer, faster
expanding layers of the ejecta. To enlarge the data base recourse must
be made to measurements of velocities in supernova remnants. Clumps
moving with up to  6000 km s-1 were, however, observed in Cas A
(van den Bergh 1971; Thorstensen et al. 2001), which is probably the remnant of a
type Ib explosion (Fesen & Becker 1991), and clump velocities of up to
6000 km s-1 were, however, observed in Cas A
(van den Bergh 1971; Thorstensen et al. 2001), which is probably the remnant of a
type Ib explosion (Fesen & Becker 1991), and clump velocities of up to  6000 km s-1 and
6000 km s-1 and  4000 km s-1 were measured shortly after the
explosion in the type Ib SN 1987 F (Filippenko & Sargent 1989) and
the type IIb SN 1993 J (Spyromilio 1994), respectively. All of
these objects are assumed to be connected to progenitors with small or
lacking hydrogen envelopes. On the other hand Aschenbach (2002) and
Aschenbach et al. (1995) deduce low mean expansion velocities of about 2000 km s-1for the clumps in the Vela supernova remnant (using their angular
distance to the pulsar, the age of the latter and the distance of the
remnant), that are in reasonably good agreement with our type II Model
T310a. In fact, the Vela clumps show Mach cones and appear to move at
present as slow as
4000 km s-1 were measured shortly after the
explosion in the type Ib SN 1987 F (Filippenko & Sargent 1989) and
the type IIb SN 1993 J (Spyromilio 1994), respectively. All of
these objects are assumed to be connected to progenitors with small or
lacking hydrogen envelopes. On the other hand Aschenbach (2002) and
Aschenbach et al. (1995) deduce low mean expansion velocities of about 2000 km s-1for the clumps in the Vela supernova remnant (using their angular
distance to the pulsar, the age of the latter and the distance of the
remnant), that are in reasonably good agreement with our type II Model
T310a. In fact, the Vela clumps show Mach cones and appear to move at
present as slow as  500 km s-1 (Aschenbach et al. 1995; Aschenbach 2002),
indicating that supersonic drag plays an important role even in the
supernova remnant phase.
500 km s-1 (Aschenbach et al. 1995; Aschenbach 2002),
indicating that supersonic drag plays an important role even in the
supernova remnant phase.
Acknowledgements
We thank S. E. Woosley and S. Bruenn for providing us with the
progenitor and post-bounce models, respectively, that we have used to
construct our initial data, and our referee, C. Fryer, for his
comments on the manuscript. KK and HTJ are grateful for support by the
Sonderforschungsbereich 375 on "Astroparticle Physics'' of the
Deutsche Forschungsgemeinschaft. The work of TP was supported in part
by the US Department of Energy under Grant No. B341495 to the Center
of Astrophysical Thermonuclear Flashes at the University of Chicago,
and in part by grant 2.P03D.014.19 from the Polish Committee for
Scientific Research. The simulations were performed on the CRAY J916,
NEC SX-4B and NEC SX-5/3C computers of the Rechenzentrum Garching, and
on the IBM Night Hawk II of the Max-Planck-Institut für
Astrophysik.
-
Arnett, W. D., Bahcall, J. N., Kirshner, R. P., & Woosley, S. E.
1989a, ARA&A, 27, 629
In the text
NASA ADS
-
Arnett, W. D., Fryxell, B., & Müller, E. 1989b, ApJ,
341, L63
In the text
NASA ADS
-
Aschenbach, B. 2002, in Neutron Stars, Pulsars, and Supernova Remnants,
Proc. of the 270th WE-Heraeus Seminar, ed. W. Becker, H. Lesch, &
J. Trümper (Garching: Max-Planck-Institut für extraterrestrische
Physik), 13
In the text
-
Aschenbach, B., Egger, R., & Trümper, J. 1995, Nature, 373, 587
In the text
NASA ADS
-
Berger, M. J., & Colella, P. 1989, J. Comput. Phys., 82, 64
In the text
NASA ADS
-
Bruenn, S. W. 1993, in Nuclear Physics in the Universe, ed. M. W. Guidry, &
M. R. Strayer (Bristol: IOP), 31
In the text
-
Burrows, A., & Fryxell, B. A. 1993, ApJ, 418, L33
In the text
NASA ADS
-
Burrows, A., Hayes, J., & Fryxell, B. A. 1995, ApJ, 450, 830
In the text
NASA ADS
-
Chevalier, R. A. 1976, ApJ, 207, 872
In the text
NASA ADS
-
Colella, P., & Glaz, H. M. 1985, J. Comput. Phys., 59, 264
In the text
NASA ADS
-
Colella, P., & Woodward, P. R. 1984, J. Comput. Phys., 54, 174
In the text
-
Drake, R. P., Robey, H. F., Hurricane, O. A., et al. 2002, ApJ, 564,
896
In the text
NASA ADS
-
Einfeldt, B. 1988, SIAM J. Num. Anal., 25, 294
In the text
-
Fassia, A., Meikle, W. P. S., Geballe, T. R., et al. 1998, MNRAS, 299,
150
In the text
NASA ADS
-
Fesen, R. A., & Becker, R. H. 1991, ApJ, 371, 621
In the text
NASA ADS
-
Filippenko, A. V., & Sargent, W. L. W. 1989, ApJ, 345, L43
In the text
NASA ADS
-
Fishbine, B. 2002, Los Alamos Res. Quart., 3, 6
In the text
-
Fryxell, B., Müller, E., & Arnett, W. D. 1991, ApJ, 367, 619
In the text
NASA ADS
-
Hachisu, I., Matsuda, T., Nomoto, K. I., & Shigeyama, T. 1990, ApJ,
358, L57
In the text
NASA ADS
-
Hachisu, I., Matsuda, T., Nomoto, K. I., & Shigeyama, T. 1991, ApJ, 368, L27
In the text
NASA ADS
-
Hachisu, I., Matsuda, T., Nomoto, K. I., & Shigeyama, T. 1992, ApJ, 390, 230
In the text
NASA ADS
-
Hachisu, I., Matsuda, T., Nomoto, K. I., & Shigeyama, T. 1994, A&AS, 104, 341
In the text
NASA ADS
-
Hamuy, M. 2003, ApJ, 582, 905
In the text
NASA ADS
-
Harkness, R. P., Wheeler, J. C., Margon, B., et al. 1987, ApJ, 317,
355
In the text
NASA ADS
-
Herant, M., & Benz, W. 1991, ApJ, 370, L81
In the text
NASA ADS
-
Herant, M., & Benz, W. 1992, ApJ, 387, 294
In the text
NASA ADS
-
Herant, M., Benz, W., & Colgate, S. 1992, ApJ, 395, 642
In the text
NASA ADS
-
Herant, M., Benz, W., Hix, W. R., Fryer, C. L., & Colgate, S. A. 1994, ApJ,
435, 339
In the text
NASA ADS
-
Herant, M., & Woosley, S. E. 1994, ApJ, 425, 814
In the text
NASA ADS
-
Hillebrandt, W., & Höflich, P. 1989, Rep. Prog. Phys., 52, 1421
In the text
NASA ADS
-
Hungerford, A. L., Fryer, C. L., & Warren, M. S. 2003, ApJ, submitted
In the text
-
Ivanova, N., Podsiadlowski, P., & Spruit, H. 2002, MNRAS, 334, 819
In the text
NASA ADS
-
Iwamoto, K., Young, T. R., Nakasato, N., et al. 1997, ApJ, 477, 865
In the text
NASA ADS
-
Janka, H.-T., Buras, R., Kifonidis, K., Plewa, T., & Rampp, M. 2003, in From
Twilight to Highlight: The Physics of Supernovae, ed. W. Hillebrandt, &
B. Leibundgut (Berlin: Springer)
In the text
-
Janka, H.-T., Kifonidis, K., & Rampp, M. 2001, in LNP 578: Physics
of Neutron Star Interiors, ed. D. Blaschke, N. Glendenning, & A. Sedrakian
(Berlin: Springer), 333
In the text
-
Janka, H.-T., & Müller, E. 1996, A&A, 306, 167
In the text
NASA ADS
-
Kane, J., Arnett, W. D., Remington, B. A., et al. 2000, ApJ, 528, 989
In the text
NASA ADS
-
Kane, J. O., Robey, H. F., Remington, B. A., et al. 2001, Phys. Rev. E, 63,
55 401
In the text
-
Keil, W., Janka, H.-T., & Müller, E. 1996, ApJ, 473, L111
In the text
NASA ADS
-
Khokhlov, A. M., Höflich, P. A., Oran, E. S., et al. 1999, ApJ,
524, L107
In the text
NASA ADS
-
Kifonidis, K., Plewa, T., Janka, H.-T., & Müller, E. 2000, ApJ,
531, L123
In the text
NASA ADS
-
Kifonidis, K., Plewa, T., & Müller, E. 2001, in AIP Conf. Proc.
561: Tours Symp. on Nuclear Physics IV, ed. M. Arnould, M. Lewitowicz,
Y. T. Oganessian, et al.
(Melville, New York: American Institute of Physics), 21
In the text
-
Klein, R. I., Budil, K. S., Perry, T. S., & Bach, D. R. 2003, ApJ,
583, 245
In the text
NASA ADS
-
Klein, R. I., McKee, C. F., & Colella, P. 1994, ApJ, 420, 213
In the text
NASA ADS
-
LeVeque, R. J. 1998, in Computational Methods for Astrophysical Fluid Flow, ed.
O. Steiner, & A. Gautschy (Berlin: Springer), 1
In the text
-
Liou, M.-S. 2000, J. Comput. Phys., 160, 623
In the text
NASA ADS
-
Lucy, L. 1991, ApJ, 383, 308
In the text
NASA ADS
-
McCray, R. 1993, ARA&A, 31, 175
In the text
NASA ADS
-
Mezzacappa, A., Calder, A. C., Bruenn, S. W., et al. 1998, ApJ, 495, 911
In the text
NASA ADS
-
Miller, D. S., Wilson, J. R., & Mayle, R. W. 1993, ApJ, 415, 278
In the text
NASA ADS
-
Mitchell, R. C., Baron, E., Branch, D., et al. 2001, ApJ, 556, 979
In the text
NASA ADS
-
Müller, E. 1998, in Computational Methods for Astrophysical Fluid Flow, ed.
O. Steiner, & A. Gautschy (Berlin: Springer), 371
In the text
-
Müller, E., Fryxell, B., & Arnett, W. D. 1991a, in
Supernova 1987 A and Other Supernovae, ed. J. Danziger, & K. Kjär
(Garching: European Southern Observatory), 99
In the text
-
Müller, E., Fryxell, B., & Arnett, W. D. 1991b, A&A,
251, 505
In the text
NASA ADS
-
Müller, E., Fryxell, B., & Arnett, W. D. 1991c, in Elba
Workshop on Chemical and Dynamical Evolution of Galaxies, ed. F. Federini,
J. Franco, & F. Matteucci (Pisa: ETS Editrice), 394
In the text
-
Müller, E., & Steinmetz, M. 1995, Comput. Phys. Commun., 89, 45
In the text
NASA ADS
-
Nagataki, S., Hashimoto, M.-A., Sato, K., & Yamada, S. 1997, ApJ,
486, 1026
In the text
NASA ADS
-
Nagataki, S., Shimizu, T. M., & Sato, K. 1998, ApJ, 495, 413
In the text
NASA ADS
-
Nomoto, K. I., Shigeyama, T., Kumagai, S., & Hashimoto, M.-A. 1988,
Proc. Astron. Soc. Austr., 7, 490
In the text
NASA ADS
-
Nomoto, K. I., Shigeyama, T., Kumagai, S., Yamaoka, H., & Suzuki, T.
1994, in Supernovae, Les Houches Session LIV, ed. S. A. Bludman,
R. Mochkovitch, & J. Zinn-Justin (Amsterdam: Elsevier/North-Holland)
In the text
-
Plewa, T., & Müller, E. 1999, A&A, 342, 179
In the text
NASA ADS
-
Plewa, T., & Müller, E. 2001, Comput. Phys. Commun., 138, 101
In the text
NASA ADS
-
Podsiadlowski, P. 1992, PASP, 104, 717
In the text
NASA ADS
-
Quirk, J. J. 1994, Int. J. Num. Meth. Fluids, 18, 555
In the text
-
Quirk, J. J. 1997, in Upwind and High-Resolution Schemes, ed.
M. Yousuff Hussaini, B. van Leer, & J. van Rosendale (Berlin: Springer), 550
In the text
-
Rampp, M., & Janka, H.-T. 2002, A&A, 396, 361
In the text
NASA ADS
-
Robey, H. F., Kane, J. O., Remington, B. A., et al. 2001, Phys.
Plasmas, 8, 2446
In the text
NASA ADS
-
Sedov, L. I. 1959, Similarity and dimensional methods in mechanics (London:
Infosearch)
In the text
-
Shigeyama, T., Iwamoto, K., Hachisu, I., Nomoto, K. I., & Saio, H.
1996, in Supernovae and supernova remnants, Proc. of the International
Astronomical Union Coll. 145, ed. R. McCray, & Z. Wang (Cambridge, UK:
Cambridge University Press), 129
In the text
-
Shigeyama, T., Nomoto, K. I., Tsujimoto, T., & Hashimoto, M.-A. 1990,
ApJ, 361, L23
In the text
NASA ADS
-
Spyromilio, J. 1991, MNRAS, 253, 25P
In the text
NASA ADS
-
Spyromilio, J. 1994, MNRAS, 266, L61
In the text
NASA ADS
-
Stone, J. M., & Norman, M. L. 1992, ApJ, 390, L17
In the text
NASA ADS
-
Swartz, D. A., Filippenko, A. V., Nomoto, K. I., & Wheeler, J. C.
1993, ApJ, 411, 313
In the text
NASA ADS
-
Thielemann, F.-K., Nomoto, K. I., & Hashimoto, M. 1996, ApJ, 460, 408
In the text
NASA ADS
-
Thorstensen, J. R., Fesen, R. A., & van den Bergh, S. 2001, AJ, 122,
297
In the text
NASA ADS
-
van den Bergh, S. 1971, ApJ, 165, 457
In the text
NASA ADS
-
van Riper, K. A. 1979, ApJ, 232, 558
In the text
NASA ADS
-
Wang, L., & Hu, J. 1994, Nature, 369, 380
In the text
NASA ADS
-
Wang, L., Wheeler, J. C., Höflich, P., et al. 2002, ApJ, 579, 671
In the text
NASA ADS
-
Wheeler, J. C., Meier, D. L., & Wilson, J. R. 2002, ApJ, 568, 807
In the text
NASA ADS
-
Witti, J., Janka, H.-T., & Takahashi, K. 1994, A&A, 286, 841
In the text
NASA ADS
-
Wooden, D. H. 1997, in Astrophysical Implications of the Laboratory Study of
Presolar Materials, ed. T. J. Bernatowicz, & E. Zinner (Woodbury: American
Institute of Physics), 317
In the text
-
Woosley, S. E., & Eastman, R. 1997, in Thermonuclear Supernovae, ed.
P. Ruiz-LaPuente, R. Canal, & J. Isern (Dordrecht: Kluwer), 821
In the text
-
Woosley, S. E., Eastman, R. G., Weaver, T. A., & Pinto, P. A. 1994,
ApJ, 429, 300
In the text
NASA ADS
-
Woosley, S. E., Heger, A., Weaver, T. A., & Langer, N. 1997, MPA Preprint,
1024
In the text
-
Woosley, S. E., Langer, N., & Weaver, T. A. 1995, ApJ, 448, 315
In the text
NASA ADS
-
Woosley, S. E., Pinto, P. A., & Ensman, L. 1988, ApJ, 324, 466
In the text
NASA ADS
-
Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181
In the text
NASA ADS
-
Yamada, S., & Sato, K. 1990, ApJ, 358, L9
In the text
NASA ADS
-
Yamada, S., & Sato, K. 1991, ApJ, 382, 594
In the text
NASA ADS
-
Zoldi, C. 2002, Ph.D. Thesis, State University of New York at Stony Brook
In the text
Copyright ESO 2003
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{3592f01a.ps}\hspace*{3mm}
\includegraphics[width=6.4cm,clip]{3592f01b.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg61.gif)
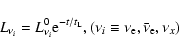
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3592f02.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg95.gif)
![\begin{figure}
\par\includegraphics[width=14.7cm,clip]{3592f03.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg99.gif)
![\begin{figure}
\par\includegraphics[width=14.9cm,clip]{3592f04.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg100.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3592f05.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg119.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3592f06.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg133.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{3592f07.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg141.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{3592f08a.ps}\hspace*{4mm}
\includegraphics[width=9.9cm,clip]{3592f08b.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg155.gif)
![\begin{figure}
\par\includegraphics[width=16.3cm,clip]{3592f09.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg156.gif)
![\begin{figure}
\par\includegraphics[width=14.8cm,clip]{3592f10.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg158.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3592f11.ps}\end{figure}](/articles/aa/full/2003/35/aa3592/Timg161.gif)
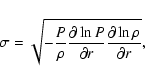
![\begin{figure}
\par\begin{tabular}{ccc}
\includegraphics[width=5.5cm,height=11.2...
...[width=5.5cm,height=11.2cm,clip]{f12f_cmyk_600dpi.eps}\end{tabular}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg167.gif)
![\begin{figure}
\par\begin{tabular}{ccc}
\includegraphics[width=5.5cm,height=11.2...
...[width=5.5cm,height=11.2cm,clip]{f13f_cmyk_600dpi.eps}\end{tabular}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg168.gif)
![\begin{figure}
\par\begin{tabular}{ccc}
\includegraphics[width=5.5cm,height=11.2...
...s[width=5.5cm,height=11.2cm,clip]{f14f_cmyk_600dpi.eps}\end{tabular}\end{figure}](/articles/aa/full/2003/35/aa3592/Timg177.gif)
![\begin{figure}
\par\includegraphics[width=16cm,clip]{3592f15.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg178.gif)
![\begin{figure}
\par\includegraphics[width=14.8cm,clip]{3592f16.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg180.gif)
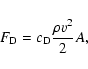
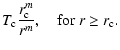
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{3592f17.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg204.gif)
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{3592f18.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg205.gif)
![\begin{figure}
\par\includegraphics[width=16.1cm,clip]{3592f19.ps}
\end{figure}](/articles/aa/full/2003/35/aa3592/Timg214.gif)