A&A 408, 409-414 (2003)
DOI: 10.1051/0004-6361:20031010
D. Richard 1-3
1 - NASA, Ames Research Center, MS 245-3, Moffett Field, California 94035, USA
2 - LUTH, Observatoire de Paris, 92190 Meudon Cedex, France
3 - GIT-SPEC, Commissariat à l'Énergie Atomique, l'Orme des Merisiers, 91190 Gif-sur-Yvette, France
Received 12 June 2002 / Accepted 17 June 2003
Abstract
In this paper we argue that differential rotation can possibly sustain hydrodynamic turbulence in the absence of a magnetic field. We explain why
the non-linearities of the hydrodynamic equations (i.e. turbulent diffusion) should not be neglected, either as a simplifying approximation or based on boundary counditions (Hawley et al. 1999). The consequences of lifting this hypothesis are studied for the flow stability and the enhanced turbulent transport.
We develop a simple general model for the energetics of turbulent fluctuations in differentially rotating flows. By taking into account the non-linearities of the equations of motions, we give constraints on the mean flow properties for the possible development of shear instability. The results from recent laboratory experiments on rotating flows show - in agreement with the model - that the pertinent parameter for stability appears to be the Rossby number Ro. The laboratory experiments seem to be compatible with Ro<-1/2 and Ro > 1 in the inviscid or high rotation rates limit. Our results, taken in the inviscid limit, are coherent with the classical linear stability analysis, in the sense that the critical perturbation equals zero on the marginal linear stability curve. We also propose a prescription for turbulent viscosity which generalize the ![]() -prescription derived in Richard & Zahn (1999).
-prescription derived in Richard & Zahn (1999).
Key words: hydrodynamics - instabilities - turbulence
Differentially rotating flows are present in a wide variety of Astrophysical systems, including stellar interiors, accretion disks, or gaseous planets. Analytical studies teach us that differentially rotating flows are unstable, according to linear stability theory, whenever their angular momentum is decreasing outward (Rayleigh 1916). These flows have been extensively studied but they do not exist in astrophysical context. Nevertheless, linear stability does not mean stability. This is because turbulence is genuinely a non-linear phenomenon. Even when the primary instability is linear in nature, the self-sustenance of fully-developed turbulence requires for the non-linearities to enter the game at least - but not only - for the saturation of amplitudes. In that sense, linear stability analysis is limited to predict, for a restricted class of flows, their instability and only the very early development of the bifurcated solution. It also means that linear analysis predicts instabilities but does not predict unconditional stability. Numerical models fail to maintain hydrodynamical turbulence in Keplerian flows (Balbus et al. 1996). Based on past laboratory experiments from the 1930's (Taylor 1936; Wendt 1933), differentially rotating flows can become unstable for Reynolds numbers of order 10 000, a figure that to our knowledge has not been reached in published numerical simulations of Keplerian flows.
Richard & Zahn (1999) have shown, using laboratory experiments published in the 1930's, that differentially rotating flows exhibit finite-amplitude instabilities in the case where both angular velocity and angular momentum are increasing outward, a class of flows relevant for stellar interiors models. Recent laboratory studies (Richard et al. 2002), showed that the class of flows experiencing shear instabilities is much wider, as demonstrated by experimental results. We aim in this paper to find some hints about the physical mechanisms involved in these instabilities.
In this section we present the basic equations for the evolution of turbulent fluctuations. We discuss the relevant approximations that can be done and their implications regarding the properties of the turbulence and the mean flow.
We consider the equation of motion for a viscous incompressible flow,
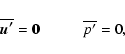 |
(3) |
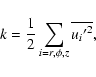 |
(10) |
In this section we will be considering the effect of neglecting the non-linear terms (i.e. turbulent diffusion) in Eqs. (7)-(9) and (11). There are several reasons why one would neglect the non-linearities of the hydrodynamic equations. The first one is to simplify the system by neglecting terms that are difficult to treat in an analytical stability analysis. Other reasons might include the belief that the physical system is such that the non-linearities actually have a negligible effect on its local or global evolution. Neglecting a priori such terms based on their local effect is rather difficult, considering that little is know on their actual amplitude which does depend closely on the intrinsic nature of the turbulence. Another option is to consider spatially averaged equations and make some hypothesis on the boundary conditions of the systems. For accretion disks, it has been argue that the average over the whole flow or part of the flow of the turbulent diffusion terms eventually vanishes. Making this hypothesis is equivalent to saying that there is no energy flux through the boundaries of the system. This is valid for an isolated system, but it seems unlikely for a disk, as it would not allow for energy transfer with its surroundings, in particular the central star. It does not seem realistic just by considering the mass flux between the two objects. It is likely that such energy transfer occurs through the boundary layer between the star and the disk. Imposing that condition also formally implies that the turbulent stress tensor vanishes on all boundaries, meaning that there is no turbulent viscosity at the edges of the disk. Furthermore, the radial velocity also has to vanish at the boundaries. We could also consider the properties of the boundaries beyond which the system cannot be considered as a continuous medium, hence cease to be described accurately by the equations of hydrodynamics. The description of the interactions between the fluid component of the disk and its outer non-continuous part is not a straightforward task. Our last argument on this matter is to point that these turbulent diffusion terms are the ones that are modeled by the anomalous turbulent viscosity. Neglecting them is equivalent to making the assumption that there is no turbulent viscosity, no enhanced transport. It is then an inevitable result that starting with such a truncated set of equations, one reaches the conclusion that there is no such transport.
Considering only the linear terms of the turbulent transport equations will give us insights - by definition - only on the linear stability of the flow.
The linearized set of equations is:
In the following sections, will focus on the case of linearly stable flows (i.e. where
![]() )
and consider the energy equations including
the turbulent diffusion.
)
and consider the energy equations including
the turbulent diffusion.
We first consider the case where dissipation due to molecular viscosity can be neglected. We define u the characteristic turbulent velocity (e.g. the root-mean-square velocity) and ![]() the length scale characteristic of the spatial variations of the velocity fluctuations, and we pose
the length scale characteristic of the spatial variations of the velocity fluctuations, and we pose
![\begin{figure}
\par\includegraphics[width=12cm,clip]{2792f1.ps}
\end{figure}](/articles/aa/full/2003/35/aa2792/Timg56.gif) |
Figure 1:
Stability diagram of Couette-Taylor flow in the (
|
|
|
|
Crn |
|
Czn | Cn |
| >0 | <0 | >0 | <0 | 0 | <0 |
| <0 | >0 | <0 | >0 | 0 | <0 |
We have seen that there always exists a sink term for one of the components of the energy fluctuations. A necessary condition for the existence of self-sustained turbulence is then that the non-linear terms overcome this negative production term (for the azimuthal component when
![]() ,
for the radial one when
,
for the radial one when
![]() ). Namely, from Eqs. (17) and (18)
). Namely, from Eqs. (17) and (18)
| |
(28) | ||
| (29) |
Following the same path as in the inviscid case, we now add the viscous constraints to Eqs. (17)-(20):
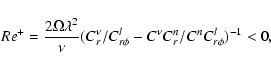 |
(39) |
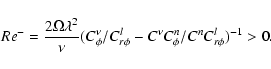 |
(40) |
|
|
|
Crn |
|
Czn | Cn | ||
| >0 | <0 | >0 | <0 | >0 | <0 | >0 | >0 |
| <0 | >0 | <0 | >0 | >0 | <0 | >0 | >0 |
Considering all of the above, we expect that there exists a critical Rossby number for each class of flows - namely flows with
![]() and flows with
and flows with
![]() .
This result can be verified by using experimental results on differentially rotating flows. This can be done by examining the value of the Rossby number at the onset of shear turbulence observed in laboratory Couette-Taylor experiment. The Couette-Taylor experiment consist of two coaxial cylinder between which the fluid is sheared, resulting in a differentially rotating azimuthal flow. Experimental results on stability (Richard et al. 2002) can actually be fitted with the values
.
This result can be verified by using experimental results on differentially rotating flows. This can be done by examining the value of the Rossby number at the onset of shear turbulence observed in laboratory Couette-Taylor experiment. The Couette-Taylor experiment consist of two coaxial cylinder between which the fluid is sheared, resulting in a differentially rotating azimuthal flow. Experimental results on stability (Richard et al. 2002) can actually be fitted with the values
![]() for
for
![]() ,
,
![]() ,
for
,
for
![]() ,
,
![]() and
and
![]() .
This is consistent with the picture of a constant critical Rossby number with a viscous correction vanishing for high rotation rates or low viscosity.
.
This is consistent with the picture of a constant critical Rossby number with a viscous correction vanishing for high rotation rates or low viscosity.
Radial turbulent transport of angular momentum is quantified by the second-order correlation product
![]() .
The time evolution for this
quantity after some rearrangement and spatial averaging over the azimuthal direction
.
The time evolution for this
quantity after some rearrangement and spatial averaging over the azimuthal direction ![]() ,
and the introduction of correlation coefficients, is given by:
,
and the introduction of correlation coefficients, is given by:
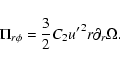 |
(42) |
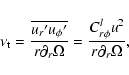 |
(43) |
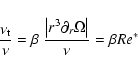 |
(45) |
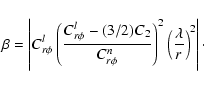 |
(46) |
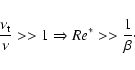 |
(47) |
In the case of a bounded flow, keeping up the assumption of isotropic turbulence, we have to assume that ![]() will be of order of a macro-scale d. The stability criteria for a viscous flow is modified as
will be of order of a macro-scale d. The stability criteria for a viscous flow is modified as ![]() is constrained to smaller values than for a free shear flow (therefore being closer to the inviscid values of
is constrained to smaller values than for a free shear flow (therefore being closer to the inviscid values of
![]() ,
according to Eqs. (37) and (38)) while for the inviscid case it remains unchanged. The radial transport will also be modified, as we have, according to Eq. (44)
,
according to Eqs. (37) and (38)) while for the inviscid case it remains unchanged. The radial transport will also be modified, as we have, according to Eq. (44)
This expression can be approximated in the case of narrow-gap Couette-Taylor experiment by taking for d the distance between the two cylinders ![]() .
.
We have shown that a simple model of turbulent fluctuations energetics can explain laboratory experiment results on differentially rotating flow.
The equations of motion show that shear instabilities can develop in rotating flows, as long as the non-linearities are taken
into account. Making reasonable assumptions about the necessary properties of the velocity correlation products, we derived formal expressions
for the control parameters for stability. Comparison with laboratory results confirms that the relevant parameter is the Rossby number. In the case of a viscous flow, the critical Rossby numbers exhibit a
![]() correction, therefore converging toward the same constant
critical Rossby numbers as in the inviscid case, for large rotation rates. The turbulent viscosity inferred is consistent with the prescription previously proposed by Richard & Zahn (1999). The critical amplitude of perturbations are also consistent with linear stability theory results in the inviscid limit. We would like to stress the importance of the pressure fluctuations in the growth and self-sustaining of this kind of turbulence. Even though the time average of the related terms vanish from the velocity fluctuation equations, they can be seen as the main engine for isotropizing the turbulence, hence disappearing
in time average when isotropy is acheived.
correction, therefore converging toward the same constant
critical Rossby numbers as in the inviscid case, for large rotation rates. The turbulent viscosity inferred is consistent with the prescription previously proposed by Richard & Zahn (1999). The critical amplitude of perturbations are also consistent with linear stability theory results in the inviscid limit. We would like to stress the importance of the pressure fluctuations in the growth and self-sustaining of this kind of turbulence. Even though the time average of the related terms vanish from the velocity fluctuation equations, they can be seen as the main engine for isotropizing the turbulence, hence disappearing
in time average when isotropy is acheived.
Complementary work is needed, in the laboratory or numerically, in order to seek whether the two particular values or the critical Rossby number matching the experimental results on the Couette-Taylor experiment are genuine to that system or are of more "universal" value.
Acknowledgements
The author would like to thank J.-P. Zahn, O. Dauchot, B. Dubrulle, F. Daviaud, S. Davis, J. Cuzzi, R. Young, A. Steinacker, F. Hersant and J.-M. Huré for stimulating discussions and support. This work was supported by the Programme National de Physique Stellaire (PNPS), the Commissariat à l'Énergie Atomique and by a Research Associateship from the National Research Council/National Academy of Sciences.
The turbulent transport equations are given here in cylindrical coordinates (![]() ). Viscous diffusion is omitted
). Viscous diffusion is omitted