A&A 408, 43-49 (2003)
DOI: 10.1051/0004-6361:20030954
A. Del Popolo
Dipartimento di Matematica, Università Statale
di Bergamo,
via dei Caniana 2, 24129 Bergamo, Italy
Feza Gürsey Institute, PO Box 6 Çengelköy, Istanbul, Turkey
Bo
![]() çi University, Physics Department,
80815 Bebek, Istanbul, Turkey
çi University, Physics Department,
80815 Bebek, Istanbul, Turkey
Received 7 May 2003 / Accepted 17 June 2003
Abstract
The constraints obtained
by several authors (Eke et al. 1998; Henry 2000)
on the estimated values of
![]() ,
n and
,
n and ![]() are revisited in the light of recent theoretical developments: 1) new theoretical mass functions; 2) a more accurate mass-temperature relation, also determined for arbitrary
are revisited in the light of recent theoretical developments: 1) new theoretical mass functions; 2) a more accurate mass-temperature relation, also determined for arbitrary
![]() and
and
![]() .
I re-derive the X-ray Temperature Function (XTF), similarly to Henry (2000) and Eke et al. (1999), re-obtaining the constraints on
.
I re-derive the X-ray Temperature Function (XTF), similarly to Henry (2000) and Eke et al. (1999), re-obtaining the constraints on
![]() ,
n,
,
n, ![]() .
The result shows that changes in the mass function and M-T relation produces an increase in
.
The result shows that changes in the mass function and M-T relation produces an increase in
![]() of
of ![]()
![]() and similar results in
and similar results in ![]() and n.
and n.
Key words: cosmology: theory - large-scale structure of Universe - galaxies: formation
Galaxy clusters represents the virialization stage of exceptionally high peaks of initial density perturbations
on comoving scales of ![]()
![]() ,
and as such they provide useful cosmological probes. The evolution
in the abundance of clusters is strongly dependent on the cosmological density parameter,
,
and as such they provide useful cosmological probes. The evolution
in the abundance of clusters is strongly dependent on the cosmological density parameter,
![]() (Evrard 1989; Oukbir & Blanchard 1992; Eke et al. 1996; Donahue et al. 1998; Borgani et al. 1999).
X-ray observations provide a very efficient method to identify distant clusters down to a given X-ray flux limit, and hence within a known survey volume for each luminosity,
(Evrard 1989; Oukbir & Blanchard 1992; Eke et al. 1996; Donahue et al. 1998; Borgani et al. 1999).
X-ray observations provide a very efficient method to identify distant clusters down to a given X-ray flux limit, and hence within a known survey volume for each luminosity, ![]() .
For this reason, most studies using clusters as cosmological probes are based on X-ray samples.
It is well known that clusters are strong X-ray emitters and so cluster evolution can be inferred from the study of X-ray properties of distant clusters. The amount of observational data concerning high-redshift cluster properties has increased in the past years. EMSS (Henry et al. 1992; Gioia & Luppino 1994), ASCA (Donahue 1996; Henry 1997) and ROSAT (Ebeling et al. 1997; Rosati et al. 1998).
In addition, galaxy velocity dispersions for a well-defined sample of high-redshift clusters (Carlberg et al. 1996) are provided by the CNOC survey. The Press & Schechter (1974) (hereafter PS) formalism has been heavily used to model the cluster population. The combination of the PS mass function and the X-ray cluster catalogs represents a unique opportunity to constraint cosmological parameters, (e.g. the mass density parameter,
.
For this reason, most studies using clusters as cosmological probes are based on X-ray samples.
It is well known that clusters are strong X-ray emitters and so cluster evolution can be inferred from the study of X-ray properties of distant clusters. The amount of observational data concerning high-redshift cluster properties has increased in the past years. EMSS (Henry et al. 1992; Gioia & Luppino 1994), ASCA (Donahue 1996; Henry 1997) and ROSAT (Ebeling et al. 1997; Rosati et al. 1998).
In addition, galaxy velocity dispersions for a well-defined sample of high-redshift clusters (Carlberg et al. 1996) are provided by the CNOC survey. The Press & Schechter (1974) (hereafter PS) formalism has been heavily used to model the cluster population. The combination of the PS mass function and the X-ray cluster catalogs represents a unique opportunity to constraint cosmological parameters, (e.g. the mass density parameter,
![]() ).
Although the analytical framework of the PS model has been greatly
refined and extended (e.g., Lacey & Cole 1993), it is well known that the PS mass function,
while qualitatively correct, disagrees with the results of
N-body simulations.
The quoted discrepancy is not surprising since the PS model, as any other analytical model,
should make several assumptions to get simple analytical predictions.
).
Although the analytical framework of the PS model has been greatly
refined and extended (e.g., Lacey & Cole 1993), it is well known that the PS mass function,
while qualitatively correct, disagrees with the results of
N-body simulations.
The quoted discrepancy is not surprising since the PS model, as any other analytical model,
should make several assumptions to get simple analytical predictions.
There are different methods to trace the evolution of the cluster number density:
a) The X-ray temperature function (XTF) has been presented for local (e.g. Henry & Arnaud 1991) and distant clusters (Eke et al. 1998; Henry 2000). The mild evolution of the XTF has been interpreted as a strong indication for a low density universe (
![]() ).
).
b) The evolution of the X-ray luminosity function (XLF).
The results for
![]() obtained span the entire range of acceptable solutions:
obtained span the entire range of acceptable solutions:
![]() (see Reichart et al. 1999).
The reasons leading to the quoted discrepancies has been studied in several papers (Eke et al. 1998; Reichart et al. 1999; Donahue & Voit 1999; Borgani et al. 2001).
(see Reichart et al. 1999).
The reasons leading to the quoted discrepancies has been studied in several papers (Eke et al. 1998; Reichart et al. 1999; Donahue & Voit 1999; Borgani et al. 2001).
Although the quoted uncertainties has been so far of minor importance with respect to the paucity of observational data, a breakthrough is needed in the quality of the theoretical framework if high-redshift clusters are to take part in the high-precision-era of observational cosmology.
These reasons lead me to re-calculate the constraints on
![]() ,
n and
,
n and ![]() ,
using the XTF.
In Sect. 2, I re-calculate the XTF, as done by Henry (2000) and Eke et al. (1998) and obtained
constraints for
,
using the XTF.
In Sect. 2, I re-calculate the XTF, as done by Henry (2000) and Eke et al. (1998) and obtained
constraints for
![]() and n and
and n and ![]() .
Section 3 is devoted to results and to conclusions.
.
Section 3 is devoted to results and to conclusions.
The mass function (MF) is a critical ingredient in putting strong constraints on
cosmological parameters (e.g.,
![]() ).
Observationally the local mass function has been derived from
measuring masses of individual clusters from galaxy velocity dispersions or
other optical properties by Bahcall & Cen (1993), Biviano et al. (1993), and
Girardi et al. (1998). However, the estimated virial masses for individual clusters
depend rather strongly on model assumptions.
As argued by Evrard et al. (1996) on the basis of hydrodynamical
N-body simulations, cluster masses may be presently more accurately
determined from a temperature measurement
and a mass-temperature relation determined from detailed observations
or numerical modeling.
Thus alternatively, as a well-defined observational quantity,
the X-ray temperature function (XTF) has been measured,
which can be converted to the MF by means of the mass-temperature relation.
).
Observationally the local mass function has been derived from
measuring masses of individual clusters from galaxy velocity dispersions or
other optical properties by Bahcall & Cen (1993), Biviano et al. (1993), and
Girardi et al. (1998). However, the estimated virial masses for individual clusters
depend rather strongly on model assumptions.
As argued by Evrard et al. (1996) on the basis of hydrodynamical
N-body simulations, cluster masses may be presently more accurately
determined from a temperature measurement
and a mass-temperature relation determined from detailed observations
or numerical modeling.
Thus alternatively, as a well-defined observational quantity,
the X-ray temperature function (XTF) has been measured,
which can be converted to the MF by means of the mass-temperature relation.
The cluster temperature function is defined as:
Comparison of the predictions of the PS theory with the SCDM and OCDM cosmologies, performed by Tozzi & Governato (1998) and Governato et al. (1999), have shown discrepancies between PS predictions and N-body simulations, increasing with increasing z.
In the following, I'll use the mass function modified as
described in Del Popolo (2000b)
and an improved form of the M-T relation in order to calculate the mass function (Del Popolo 2000a).
These are respectively given by:
| K(m1,x) | = | ||
| (4) |
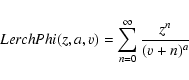 |
(5) |
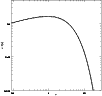 |
Figure 1: Comparison of various mass functions. The dotted line represents Sheth & Tormen (2002) prediction, the solid line that of Jenkins et al. (2001) and the dashed line that of Del Popolo (2000b). |
| Open with DEXTER | |
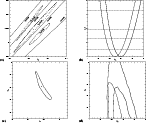 |
Figure 2:
a) The |
| Open with DEXTER | |
Similarly, it necessary to give arguments to use Eq. (3) instead of
the new mass/X-ray temperature relations obtained from simulations or
Chandra data within the last year (see, e.g., Pierpaoli et al. 2001, 2003
for a reference). As shown in Del Popolo (2002a), Eq. (3) reduces to a similar equation to that
used in Pierpaoli et al. (2001) (Eq. (13)), in the early-time, namely:
Introducing Eq. (2) into Eq. (1) and using the M-T relation, in the peculiar case that
the variance is given by:
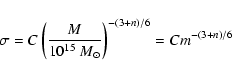 |
(7) |
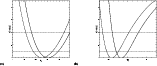 |
Figure 3:
|
| Open with DEXTER | |
I get:
![\begin{numcases}{\hspace*{-2mm}}
\frac{{\rm d}N}{{\rm d}T}=\frac{N_1(m,z)}{N_2(m...
...t_1^{\frac 23}
+\frac{K_0(m_1,x)}{M_{0}^{8/3}}
\right]}\nonumber
\end{numcases}](/articles/aa/full/2003/34/aah4510/img42.gif) |
(8) (9) |
In order to use the same notation and variance of Henry (2000), the constant C is defined as:
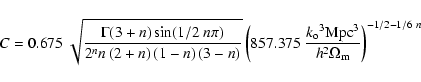 |
(10) |
![\begin{displaymath}L_1 =\prod_i^N\left[\lambda (z_i,L_i){\rm d}z{\rm d}L{\rm e}^...
...d}L}\right]\prod_j{\rm e}^{-\lambda (z_j,L_j){\rm d}z{\rm d}L}
\end{displaymath}](/articles/aa/full/2003/34/aah4510/img49.gif) |
(11) |
At this point, we can fit the data described in Sect. 2 of Henry (2000) to the theory previously described using
the quoted maximum likelihood method.
The most general description of the results requires the three parameters of the fit. I show these results
in Fig. 2, where I plotted the results for the open model.
It is straightforward to read off the value of n, which is
at the 68% confidence for the open model.
These values shows that the correction introduced by the new form of the mass function and M-T relation gives rise to higher values of
![]() (
(
![]() ,
while it is
,
while it is
![]() for Henry 2000) and
for Henry 2000) and
![]() (
(
![]() in Henry 2000).
The presentation in Fig. 2a is somewhat difficult to appreciate,
so we also give the constraints for fewer parameters. In Fig. 2b,
I plot
in Henry 2000).
The presentation in Fig. 2a is somewhat difficult to appreciate,
so we also give the constraints for fewer parameters. In Fig. 2b,
I plot ![]() (likelihood)
for the parameter
(likelihood)
for the parameter
![]() .
The solid line is obtained
from the model of this paper while the dotted line is that
calculated by Henry (2000). The dashed lines represent various
confidence levels (68%, 90%, 95%, 99%). Constraints are
relatively tight when considering this single parameter. I find
that
.
The solid line is obtained
from the model of this paper while the dotted line is that
calculated by Henry (2000). The dashed lines represent various
confidence levels (68%, 90%, 95%, 99%). Constraints are
relatively tight when considering this single parameter. I find
that
![]() at the 68% confidence
level and at
at the 68% confidence
level and at
![]() the at 95% confidence level for the open model.
the at 95% confidence level for the open model.
The constraints in Fig. 2a are plotted into a more conventional
format in Fig. 2c. Three parameters are still required, but the
constraints on n and k0 are collapsed into ![]() .
Figure 2c, plots the 68% confidence contours for the parameters
.
Figure 2c, plots the 68% confidence contours for the parameters ![]() ,
and
,
and
![]() for the open model (see also
Henry 2000, Fig. 9).
In Fig. 2d, I plot the constraints on
for the open model (see also
Henry 2000, Fig. 9).
In Fig. 2d, I plot the constraints on
![]() and
and
![]() obtained using the same 25 clusters used in Henry
(2000), for the local sample, while the high redshift sample is
constituted from all the EMSS clusters with z>0.3 and RX J0152.7-1357 (see Henry 2002). The solid lines are the 1 and 2
obtained using the same 25 clusters used in Henry
(2000), for the local sample, while the high redshift sample is
constituted from all the EMSS clusters with z>0.3 and RX J0152.7-1357 (see Henry 2002). The solid lines are the 1 and 2 ![]() contours obtained using the mass function and the M-T relation of this paper, while the dashed line is the 1
contours obtained using the mass function and the M-T relation of this paper, while the dashed line is the 1 ![]() contour obtained using the PS mass function and the M-T relation
of Pierpaoli et al. (2001).
contour obtained using the PS mass function and the M-T relation
of Pierpaoli et al. (2001).
For a CDM spectrum, the expression for the XTF is much more complicated. It can be obtained combining Eq. (2),
Eq. (1), and our M-T relation.
The mass variance
can be obtained once a spectrum, P(k), is fixed, by:
In this paper, I have revisited the constraints obtained
by several authors (Eke et al. 1998; Henry 2000)
on the estimated values of
![]() ,
n and
,
n and ![]() in the light of recent theoretical developments: new theoretical mass functions, a more accurate mass-temperature relation, also determined for arbitrary
in the light of recent theoretical developments: new theoretical mass functions, a more accurate mass-temperature relation, also determined for arbitrary
![]() and
and
![]() .
I repeated the Henry (2000) analysis but differently from the quoted paper, I changed the mass function and M-T relation, adopting again those of Del Popolo (2000a,b).
The new form of the mass function and M-T relation gives rise to higher values of
.
I repeated the Henry (2000) analysis but differently from the quoted paper, I changed the mass function and M-T relation, adopting again those of Del Popolo (2000a,b).
The new form of the mass function and M-T relation gives rise to higher values of
![]() (
(
![]() in my estimation, while it is
in my estimation, while it is
![]() for Henry 2000) and
for Henry 2000) and
![]() ,
in my estimation, while
,
in my estimation, while
![]() in Henry (2000).
I have also obtained some constraints on
in Henry (2000).
I have also obtained some constraints on
![]() and
and
![]() obtained using the same 25 clusters used in Henry (2000), for the local sample, while the high redshift sample is constituted from all the EMSS clusters with z>0.3 and RX J0152.7-1357
(see Henry 2002). The 1
obtained using the same 25 clusters used in Henry (2000), for the local sample, while the high redshift sample is constituted from all the EMSS clusters with z>0.3 and RX J0152.7-1357
(see Henry 2002). The 1 ![]() contours obtained using the mass function and the M-T relation of this paper
shows that for
contours obtained using the mass function and the M-T relation of this paper
shows that for ![]() ,
it is
,
it is
![]() in the case of Henry (2002) and
in the case of Henry (2002) and
![]() in my estimation. The figure shows the constraints to
in my estimation. The figure shows the constraints to
![]() for different values of
for different values of
![]() .
Similar results to that obtained in the previous comparison with the Henry (2000) results
are obtained changing data and method, by following Eke et al. (1998). I obtain a value of
.
Similar results to that obtained in the previous comparison with the Henry (2000) results
are obtained changing data and method, by following Eke et al. (1998). I obtain a value of
![]() ,
while in Eke et al. (1998)
,
while in Eke et al. (1998)
![]() ,
and
,
and
![]() while in Eke et al. (1998)
while in Eke et al. (1998)
![]() .
This shows again an increase in
.
This shows again an increase in
![]() ,
also in agreement with Eke et al. (1998) calculation taking account of changes in the threshold for collapse suggested by Tozzi & Governato (1998)
,
also in agreement with Eke et al. (1998) calculation taking account of changes in the threshold for collapse suggested by Tozzi & Governato (1998)![]() .
As previously told, this paper has its aim that of studying how "systematic uncertainties" can influence the values of some cosmological parameters. It is well known that in literature the values obtained for
.
As previously told, this paper has its aim that of studying how "systematic uncertainties" can influence the values of some cosmological parameters. It is well known that in literature the values obtained for
![]() span the range
span the range
![]() (Reichart et al. 1999).
(Reichart et al. 1999).
Sadat et al. (1998) and Reichart et al. (1999)
Blanchard & Bartlett (1998)
found results consistent with
![]() .
Viana & Liddle (1999) found that
.
Viana & Liddle (1999) found that
![]() with
with
![]() at the 90% confidence level and
at the 90% confidence level and
![]() still viable. Blanchard et al. (1998) found almost identical results (
still viable. Blanchard et al. (1998) found almost identical results (
![]() with
with
![]() at the 95% confidence level).
Eke et al. (1998) found
at the 95% confidence level).
Eke et al. (1998) found
![]() .
It is interesting to note (as previously mentioned) that Viana & Liddle (1999) used the same data set as Eke et al. (1998) and showed that uncertainties both in fitting local data and in the theoretical modeling could significantly change the final results: they found
.
It is interesting to note (as previously mentioned) that Viana & Liddle (1999) used the same data set as Eke et al. (1998) and showed that uncertainties both in fitting local data and in the theoretical modeling could significantly change the final results: they found
![]() as a preferred value with a critical density model acceptable at <90% c.l.
as a preferred value with a critical density model acceptable at <90% c.l.
Different results were obtained by Bahcall et al. (1997) (
![]() ), Fan et al. (1997) (
), Fan et al. (1997) (
![]() ), Bahcall & Fan (1998) (
), Bahcall & Fan (1998) (
![]() )
and several other authors.
More recent studies has been published, giving constraints on
)
and several other authors.
More recent studies has been published, giving constraints on ![]() and
and
![]() :
Pierpaoli et al. (2003) using a sample updated from HIFLUGCS they found a 68% confidence range of
:
Pierpaoli et al. (2003) using a sample updated from HIFLUGCS they found a 68% confidence range of
![]() for a standard
for a standard ![]() CDM model, while using the XLF from the REFLEX survey they obtain
CDM model, while using the XLF from the REFLEX survey they obtain
![]() for the same standard
for the same standard ![]() CDM model. Schuecker et al. (2002), using the REFLEX cluster sample
and analyzing simultaneously the large scale clustering and the mean abundance of galaxy clusters get precise constraints on the normalized cosmic matter density
CDM model. Schuecker et al. (2002), using the REFLEX cluster sample
and analyzing simultaneously the large scale clustering and the mean abundance of galaxy clusters get precise constraints on the normalized cosmic matter density
![]() (
(
![]() )
and the linear theory rms fluctuations in mass,
)
and the linear theory rms fluctuations in mass, ![]() (
(
![]() ). WMAP (Wilkinson Microwave Anisotropy Probing) precision data enabled accurate testing of cosmological models. Spergel et al. (2003) found that
). WMAP (Wilkinson Microwave Anisotropy Probing) precision data enabled accurate testing of cosmological models. Spergel et al. (2003) found that
![]() ,
,
![]() ,
where
h=0.71+0.04-0.03. The formal random errors given
in WMAP are of the 5% level while they are higher in our study. At this regard, I want to recall that the principal goal of the present study is not that of determining with high precision the values of the quoted cosmological parameters but to show how different values
,
where
h=0.71+0.04-0.03. The formal random errors given
in WMAP are of the 5% level while they are higher in our study. At this regard, I want to recall that the principal goal of the present study is not that of determining with high precision the values of the quoted cosmological parameters but to show how different values![]() ,
discrepancies in the values of cosmological parameter quoted in literature
are connected to a different mass function and M-T relation (the basic aim of the present work is to study how systematic
uncertainties in the application of the X-ray temperature function and
mass/X-ray temperature relation can influence the estimates of
important cosmological parameters).
,
discrepancies in the values of cosmological parameter quoted in literature
are connected to a different mass function and M-T relation (the basic aim of the present work is to study how systematic
uncertainties in the application of the X-ray temperature function and
mass/X-ray temperature relation can influence the estimates of
important cosmological parameters).
The reasons leading to the quoted discrepancies has been studied
in several papers (Eke et al. 1998; Reichart et al. 1999; Donahue
& Voit 1999; Borgani et al. 2001). According to Reichart (1999)
unknown systematic effects may be plaguing great part of the
quoted results.
Our analysis shows that improvements in the mass function and M-T relation increases the value of
![]() .
The effect of this increase is unable to enhance significantly the probability that
.
The effect of this increase is unable to enhance significantly the probability that
![]() in the case of
constraints like that of Fan et al. (1997) (
in the case of
constraints like that of Fan et al. (1997) (
![]() )
or Bahcall & Fan (1998) (
)
or Bahcall & Fan (1998) (
![]() ), and can give a small contribution even in the case of larger values for the value of the constraints obtained.
However, in any case it shows that even small correction in the physics of the collapse can induce noteworthy effects on the constraints obtained. Moreover, even changing the data or the way they are analyzed gives different results. As an example, changing their low-redshift sample, Donahue & Voit (1999) showed a change in
), and can give a small contribution even in the case of larger values for the value of the constraints obtained.
However, in any case it shows that even small correction in the physics of the collapse can induce noteworthy effects on the constraints obtained. Moreover, even changing the data or the way they are analyzed gives different results. As an example, changing their low-redshift sample, Donahue & Voit (1999) showed a change in
![]() from 0.45 to 0.3.
Furthermore, as observations are reaching the first epoch of cluster assembly, treating them as dynamical relaxed and virialized systems is undoubtly an oversemplification. Hierarchical clustering scenario predicts that
a fraction between 0.3 and 0.6 of the z=1 population of clusters are observed less than 1 Gyr after the last major merger event and then are likely to be in a state of non-equilibrium. Although the quoted uncertainties has been so far of minor importance with respect to the paucity of observational data, a breakthrough is needed in the quality of the theoretical framework if high-redshift clusters are to take part in the high-precision-era of observational cosmology.
from 0.45 to 0.3.
Furthermore, as observations are reaching the first epoch of cluster assembly, treating them as dynamical relaxed and virialized systems is undoubtly an oversemplification. Hierarchical clustering scenario predicts that
a fraction between 0.3 and 0.6 of the z=1 population of clusters are observed less than 1 Gyr after the last major merger event and then are likely to be in a state of non-equilibrium. Although the quoted uncertainties has been so far of minor importance with respect to the paucity of observational data, a breakthrough is needed in the quality of the theoretical framework if high-redshift clusters are to take part in the high-precision-era of observational cosmology.
Acknowledgements
I am grateful to the referee P. Schuecker and to Prof. N. Ercan for helpful and stimulating discussions during the period in which this work was performed.