A&A 408, 331-335 (2003)
DOI: 10.1051/0004-6361:20030917
V. Urpin
A. F. Ioffe Institute for Physics and Technology,
SU 194021, St. Petersburg, Russia
Isaak Newton Institute of Chili, Branch in St. Petersburg,
Russia
Received 3 February 2003 / Accepted 22 May 2003
Abstract
Young neutron stars formed in core collapse or originating
in the merger of a binary neutron star system may possess
significant differential rotation. We consider the stability
properties of such hot (non-superfluid) differentially rotating
neutron stars. Compared to ordinary stars, the criteria of
hydrodynamic instability of neutron stars can be different because
generally the thermal diffusivity and viscosity are of the same
order of magnitude and are relatively large. For example, the
well-known Goldreich-Schubert instability can manifest itself only
in rapidly rotating stars and is strongly suppressed if rotation is
slow. The rotational instabilities in neutron stars can grow on the
thermal or dynamical timescale.
Key words: MHD - stars: neutron - stars: rotation - stars: pulsars: general
It is generally believed that young neutron stars formed in
the collapse of a massive star should be rapidly rotating due to the
conservation of the angular momentum of the collapsing core.
Most likely, this rotation is non-uniform because even if the
progenitor rotates uniformly, collapse will generate a significant
amount of differential rotation. Numerical simulations of rotating
core collapse indicate that the angular velocity in a newly formed
neutron star should be appreciably non-uniform (see Mönchmeyer
& Müller 1989; Janka & Mönchmeyer 1989; Zwerger &
Müller 1997; Rampp et al. 1998). During a
convective stage that lasts ![]() 30-40 s (Miralles et al. 2000, 2002) and seems to be inevitable in protoneutron
stars, the original distribution of the angular velocity may
evolve to even a more complex one. During this stage, the angular
momentum is basically transported by convection and
neutron finger instability and can be very rapid. Perhaps,
turbulent Reynolds stresses result in the angular velocity
dependent on both the radial and polar coordinates like that of
the Sun where the departure from a uniform rotation reaches about
30%. When convection is exhausted and the neutron star becomes
transparent to neutrinos it is still rather hot and, therefore,
the matter is likely to be in a normal (non-superfluid) state in the
core. The non-superfluid neutrino transparent stage can last from
hours to thousands of years depending on the model of cooling and
superfluidity, and our consideration will concern this stage.
Note that accretion of supernova remnant material may also drive
differential rotation during this stage (Watts & Andersson 2002).
Differential rotation can also be maintained by stellar
oscillations. For instance, recent papers on r-modes argued
that the modes can drive differential rotation via non-linear
effects (Rezzolla et al. 2000; Levin & Ushomirsky 2001).
30-40 s (Miralles et al. 2000, 2002) and seems to be inevitable in protoneutron
stars, the original distribution of the angular velocity may
evolve to even a more complex one. During this stage, the angular
momentum is basically transported by convection and
neutron finger instability and can be very rapid. Perhaps,
turbulent Reynolds stresses result in the angular velocity
dependent on both the radial and polar coordinates like that of
the Sun where the departure from a uniform rotation reaches about
30%. When convection is exhausted and the neutron star becomes
transparent to neutrinos it is still rather hot and, therefore,
the matter is likely to be in a normal (non-superfluid) state in the
core. The non-superfluid neutrino transparent stage can last from
hours to thousands of years depending on the model of cooling and
superfluidity, and our consideration will concern this stage.
Note that accretion of supernova remnant material may also drive
differential rotation during this stage (Watts & Andersson 2002).
Differential rotation can also be maintained by stellar
oscillations. For instance, recent papers on r-modes argued
that the modes can drive differential rotation via non-linear
effects (Rezzolla et al. 2000; Levin & Ushomirsky 2001).
There are only a few possibilities that can be contemplated as
mechanisms of the angular momentum transport during the
neutrino-transparent non-superfluid stage: viscosity, hydrodynamic and
hydromagnetic instabilities, and large scale motions caused by
the magnetic field if the latter has been generated in the core
by convection. Viscosity seems to be not very efficient at
large scales because it can redistribute the angular momentum
only on a relatively long timescale. The characteristic timescale
of viscous dissipation,
![]() ,
can be estimated as
,
can be estimated as
![]() where L is the lengthscale of the angular velocity
and
where L is the lengthscale of the angular velocity
and ![]() is the kinematic viscosity. If the star is transparent
to neutrinos, viscosity is mainly determined by the scattering of
neutrons and has been calculated in the classical paper by Flowers
& Itoh (1976). A simple fitting formula for their numerical
results has been obtained by Cutler et al. (1990).
Using this fit and assuming that L is comparable to the neutron
star radius, we can estimate
is the kinematic viscosity. If the star is transparent
to neutrinos, viscosity is mainly determined by the scattering of
neutrons and has been calculated in the classical paper by Flowers
& Itoh (1976). A simple fitting formula for their numerical
results has been obtained by Cutler et al. (1990).
Using this fit and assuming that L is comparable to the neutron
star radius, we can estimate
![]() as
102- 103 yrs
that probably is comparable to (or longer than) the duration of
a non-superfluid stage.
as
102- 103 yrs
that probably is comparable to (or longer than) the duration of
a non-superfluid stage.
If there is a sufficiently strong magnetic field in the neutron
star then large-scale motions induced by the field can redistribute
the angular momentum by magnetic braking (Shapiro 2000).
Differential rotation twists lines of a frozen-in poloidal
magnetic field and amplifies the toroidal field. This process
generates Alfvén waves, which can transport the angular
momentum within the star and even carry out some angular momentum
from the star to the surrounding plasma. Note, however,
that the efficiency of this mechanism is very sensitive to assumptions
regarding the density of external plasma,
![]() .
For example,
a simple estimate of the magnetic braking timescale proposed by
Shapiro (2000) shows that this process is more efficient than viscous
damping only at
.
For example,
a simple estimate of the magnetic braking timescale proposed by
Shapiro (2000) shows that this process is more efficient than viscous
damping only at
![]() even if the magnetic
field is as strong as 1012 G, where
even if the magnetic
field is as strong as 1012 G, where ![]() is the density of the
neutron star. For smaller
is the density of the
neutron star. For smaller
![]() ,
Alfvén waves inside the
neutron star dissipate on a viscous timescale.
,
Alfvén waves inside the
neutron star dissipate on a viscous timescale.
The angular momentum can also be transported by turbulent motions if differential rotation is unstable. Since a spatial dependence of the angular velocity is likely to be complex, the neutron star can be subject to hydrodynamic instabilities. The stability properties of differentially rotating neutron stars and radiative zones of ordinary stars can be essentially different because the viscous and thermal timescales are generally relatively short for small-scale disturbances in neutron stars and are generally comparable. This can change qualitatively, for example, the criterion of the well-known Goldreich-Schubert instability (Goldreich & Schubert 1967) that arises on the thermal timescale.
Hydrodynamic instabilities can be of importance for neutron stars originating in the merger of a binary neutron star system as well. In their numerical simulations, Rasio & Shapiro (1999) and Shibata & Uryu (2000) found that coalescence will form a differentially rotating remnant with the core rotating faster than the envelope. Note that differentially rotating neutron stars can support significantly more rest mass than their uniformly rotating counterparts (Baumgarte et al. 2000). Hydrodynamic instabilities in the remnant will destroy differential rotation and may lead to delayed collapse and a delayed gravitational wave burst.
In this paper, we derive the stability criteria for differentially
rotating neutron stars. Our consideration assumes the neutron
stars that are relatively cold to be transparent to neutrinos but
are still sufficiently hot to be in a normal (non-superfluid)
state. This evolutionary stage begins at the age ![]() 40 s and
can last from hours to
40 s and
can last from hours to ![]() 103 years depending on the model.
The paper is organized as follows. In Sect. 2, we derive the
dispersion equation governing the rotational modes of a
differentially rotating neutron star. In Sect. 3, the conditions
of instability are obtained. The growth rate of instability is
calculated in Sect. 4. A discussion of the results is given
in Sect. 5.
103 years depending on the model.
The paper is organized as follows. In Sect. 2, we derive the
dispersion equation governing the rotational modes of a
differentially rotating neutron star. In Sect. 3, the conditions
of instability are obtained. The growth rate of instability is
calculated in Sect. 4. A discussion of the results is given
in Sect. 5.
Consider the core of a neutron star rotating with the angular
velocity
![]() ,
where (s,
,
where (s, ![]() ,
z) are
cylindrical coordinates. We consider axisymmetric short wavelength
perturbations with the space-time dependence
,
z) are
cylindrical coordinates. We consider axisymmetric short wavelength
perturbations with the space-time dependence
![]() where
where
![]() is the
wavevector,
is the
wavevector,
![]() .
Small perturbations will
be indicated by subscript 1, whilst unperturbed quantities will
have no subscript, except for indicating vector components when
necessary. In the unperturbed state, the star is in hydrostatic
equilibrium,
.
Small perturbations will
be indicated by subscript 1, whilst unperturbed quantities will
have no subscript, except for indicating vector components when
necessary. In the unperturbed state, the star is in hydrostatic
equilibrium,
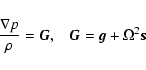 |
(1) |
We use the Boussinesq approximation since the e-folding time
of short wavelength instabilities associated with shear is typically
much longer than the period of a sound wave with the same wavelength.
Then, the linearized equations governing the behaviour of small
perturbations in the lowest order in
![]() read
read
| (2) |
| (3) |
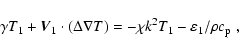 |
(4) |
The neutrino emissivity depends on details of the internal structure
but can generally be expressed in terms of ![]() and T,
and T,
![]() (see, e.g., Maxwell 1979). Then,
(see, e.g., Maxwell 1979). Then,
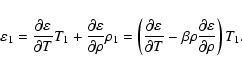 |
(5) |
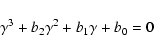 |
(6) |
| Q2 | = | 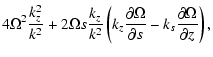 |
|
| = | ![$\displaystyle - \beta (\Delta \nabla T) \cdot \left[ \vec{G} -
\frac{\vec{k}}{k^{2}} (\vec{k} \cdot \vec{G}) \right] ,
\;\; \omega_{\nu} = \nu k^{2} ,$](/articles/aa/full/2003/34/aa3561/img34.gif) |
||
| = | 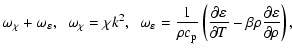 |
Equation (6) describes three low-frequency modes that can
exist in rotating non-magnetic neutron star. The sound waves are
excluded from consideration in the Boussinesq approximation.
The condition that at least one of the roots of Eq. (6) has
a positive real part (unstable mode) is equivalent to one of the
following inequalities
| (7) |
Substituting the values of b0, b1 and b2, we can
rewrite the second condition (7) as
![\begin{displaymath}(\omega_{\rm T} + \omega_{\nu}) \omega_{\rm g}^{2} + 2 \omega_{\nu}
[Q^{2} + (\omega_{\rm T} + \omega_{\nu})^{2}] < 0.
\end{displaymath}](/articles/aa/full/2003/34/aa3561/img44.gif) |
(8) |
| (9) |
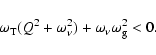 |
(10) |
| Q2 < 0, | (11) |
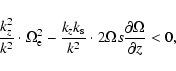 |
(12) |
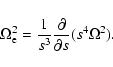 |
(13) |
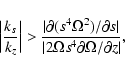 |
(14) |
Consider the criteria (8) and (10) in more detail. In neutron
stars transparent to neutrinos, we have typically
![]() .
Since
.
Since
![]() and
and
![]() increase
rapidly when the wavelength decreases, neither of the conditions (8) or (10) can be satisfied for very short wavelengths. Therefore,
we consider Eqs. (8) and (10) at
increase
rapidly when the wavelength decreases, neither of the conditions (8) or (10) can be satisfied for very short wavelengths. Therefore,
we consider Eqs. (8) and (10) at
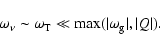 |
(15) |
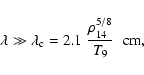 |
(16) |
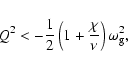 |
(17) |
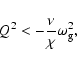 |
(18) |
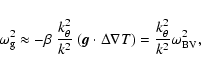 |
(19) |
The conditions (17) and (18) depend on the direction of ![]() .
To obtain the true necessary conditions of instability, we have to
minimize these expressions as functions of
.
To obtain the true necessary conditions of instability, we have to
minimize these expressions as functions of ![]() .
For both the
inequalities (17) and (18), a dependence on
.
For both the
inequalities (17) and (18), a dependence on ![]() has the same
form and can be represented as
has the same
form and can be represented as
| F(ks, kz) = A ks2 - C kz ks + D kz2 < 0, | (20) |
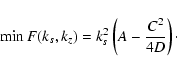 |
(21) |
| C2 > 4 A D. | (22) |
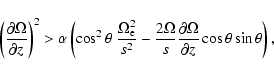 |
(23) |
Solving the inequality (23) for
![]() ,
we
obtain that Eq. (23) is fulfilled if
,
we
obtain that Eq. (23) is fulfilled if
![\begin{displaymath}\frac{\partial \Omega}{\partial z} > \frac{\alpha \Omega}{s}
...
...}^{2}}{\alpha \Omega^{2}} \right)^{1/2} -
\sin \theta \right],
\end{displaymath}](/articles/aa/full/2003/34/aa3561/img84.gif) |
(24) |
![\begin{displaymath}\frac{\partial \Omega}{\partial z} < -\frac{\alpha \Omega}{s}...
...}^{2}}{\alpha \Omega^{2}} \right)^{1/2} +
\sin \theta \right].
\end{displaymath}](/articles/aa/full/2003/34/aa3561/img85.gif) |
(25) |
In the case of a rapidly rotating star,
![]() ,
we have
,
we have
![]() and
and
![]() ,
and Eqs. (24) and (25) yield
,
and Eqs. (24) and (25) yield
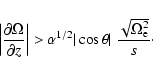 |
(26) |
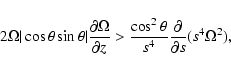 |
(27) |
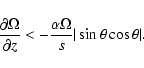 |
(28) |
Consider the growth rate of rotational instabilities.
Since the coefficients of Eq. (6) are real there exist
three real roots or one real and two complex conjugate roots.
The number of roots with a positive real part is determined
by Routh criterium (DiStefano III et al. 1994),
which states that the number of unstable modes of a cubic
Eq. (6) is given by the number of changes of sign in the
sequence
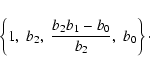 |
(29) |
The roots
![]() (i=1,2,3) of the cubic Eq. (6) can
be represented as
(i=1,2,3) of the cubic Eq. (6) can
be represented as
![]() .
The expressions
for xi are
.
The expressions
for xi are
| (30) |
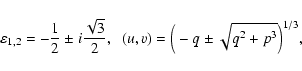 |
(31) |
| q | = | 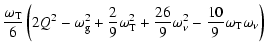 |
|
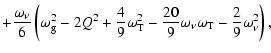 |
|||
| p | = | ![$\displaystyle \frac{1}{3}
\left[ Q^{2} + \omega_{\rm g}^{2} - \frac{1}{3}( \omega_{\rm T} -
\omega_{\nu} )^{2} \right]$](/articles/aa/full/2003/34/aa3561/img102.gif) |
Under the condition (15) (or (16)), we have from the expressions (30), (31) with the accuracy in terms ![]()
![]() ,
,
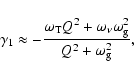 |
(32) |
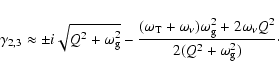 |
(33) |
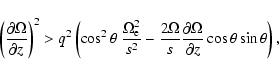 |
(34) |
Contrary to the classical Goldreich-Schubert instability that
arises on the thermal time scale, the rotational instabilities
in neutron stars can grow either on the thermal or dynamical
timescale. If
![]() then the growth
rate is
then the growth
rate is
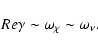 |
(35) |
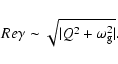 |
(36) |
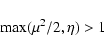 |
(37) |
We considered hydrodynamic stability of differentially rotating
neutron stars during the evolutionary stage when they are
non-superfluid and transparent to neutrinos. Differentially
rotating neutron stars can be formed either in core collapse or
in the merger of binary neutron stars. If the Rayleigh stability
criterion is fulfilled then the rotational instabilities can arise
only if the angular velocity depends on z. However, the
instabilities caused by this dependence in
neutron stars turns out to be qualitatively different from those
in ordinary stars. The classical Goldreich-Schubert instability
that likely operates in ordinary stars can arise at any
![]() .
In neutron stars, the
rotational instabilities can appear only if
.
In neutron stars, the
rotational instabilities can appear only if
![]() exceeds some threshold value. This value depends on
the angular velocity of a neutron star and can be small for
rapidly rotating stars with
exceeds some threshold value. This value depends on
the angular velocity of a neutron star and can be small for
rapidly rotating stars with
![]() or large for
slowly rotating stars with
or large for
slowly rotating stars with
![]() .
The difference
to ordinary stars is caused by a particular character of kinetic
processes in neutron stars where viscosity is large and generally
comparable to the thermal diffusivity. Unfortunately, calculations
of the Brunt-Vaisala frequency,
.
The difference
to ordinary stars is caused by a particular character of kinetic
processes in neutron stars where viscosity is large and generally
comparable to the thermal diffusivity. Unfortunately, calculations
of the Brunt-Vaisala frequency,
![]() ,
in young neutron
stars have some problems because it depends on a poorly known
equation of state. However, most likely this frequency is of
the order of
102-103 s-1. Therefore, the critical
value of the period, discriminating between the rapid unstable and
slow stable rotation in neutron stars, is approximately 0.1-0.01 s.
,
in young neutron
stars have some problems because it depends on a poorly known
equation of state. However, most likely this frequency is of
the order of
102-103 s-1. Therefore, the critical
value of the period, discriminating between the rapid unstable and
slow stable rotation in neutron stars, is approximately 0.1-0.01 s.
Contrary to the classical Goldreich-Schubert instability, the
rotational instabilities in neutron stars can arise either on the thermal
or dynamical timescale. If the condition (37) is fulfilled
then the growth time of instability is comparable to the rotation
period. Otherwise, the growth rate is determined by the thermal
effects, and the corresponding growth time is ![]()
![]() .
For perturbations with
.
For perturbations with
![]() km, the growth time is
km, the growth time is ![]() 100 days, whereas
perturbations with
100 days, whereas
perturbations with
![]() m grow on a timescale
m grow on a timescale ![]() 10 s.
10 s.
In the present paper, we have addressed the behaviour only of
axisymmetric perturbations. It is clear, however, that the obtained
results can apply to nonaxisymmetric perturbations with the azimuthal
wavelength much longer than the vertical or radial ones,
![]() .
Note that, generally,non-axisymmetric
perturbations can also undergo other instabilities (e.g., the r-mode
instability, see Andersson et al. 1999). Interaction
of the neutron star crust with turbulent motions caused by
rotational instabilities may result in small irregularities of the
measured periods of young pulsars.
.
Note that, generally,non-axisymmetric
perturbations can also undergo other instabilities (e.g., the r-mode
instability, see Andersson et al. 1999). Interaction
of the neutron star crust with turbulent motions caused by
rotational instabilities may result in small irregularities of the
measured periods of young pulsars.
Acknowledgements
This work has been supported by the Spanish Ministery of Science and Technology (grant AYA2001-3490-C02-02).