M. Schirmer1,2 - T. Erben1 - P. Schneider1 - G. Pietrzynski3,4 - W. Gieren3 - S. Carpano5 - A. Micol6 - F. Pierfederici7,6
1 - Institut für Astrophysik und Extraterrestrische Forschung (IAEF), Universität Bonn,
Auf dem Hügel 71, 53121 Bonn, Germany
2 -
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany
3 -
Universidad de Concepción, Grupo de Astronomia, Casilla 160-C, Concepción, Chile
4 -
Warsaw University Observatory, Al. Ujazdowskie 4, 00-478 Warsaw, Poland
5 -
Institut für Astronomie und Astrophysik, Universität Tübingen,
Sand 1, 72076 Tübingen, Germany
6 -
Space Telescope European Coordinating Facility, Karl-Schwarzschild-Strasse 1,
85748 Garching, Germany
7 -
National Optical Astronomy Observatory, 950 North Cherry Avenue, Tucson, USA
Received 13 May 2003 / Accepted 27 June 2003
Abstract
The Garching-Bonn Deep Survey (GaBoDS) is a virtual 12 square degree cosmic shear and
cluster lensing survey, conducted with the WFI@2.2 m MPG/ESO telescope at La Silla. It consists of
shallow, medium and deep random fields taken in R-band in subarcsecond seeing conditions at
high galactic latitude. A substantial amount of the data was taken from the ESO archive, by
means of a dedicated ASTROVIRTEL program.
In the present work we describe the main characteristics and scientific goals of GaBoDS. Our strategy for mining the ESO data archive is introduced, and we comment on the Wide Field Imager data reduction as well. In the second half of the paper we report on clusters of galaxies found in the background of NGC 300, a random archival field. We use weak gravitational lensing and the red cluster sequence method for the selection of these objects. Two of the clusters found were previously known and already confirmed by spectroscopy. Based on the available data we show that there is significant evidence for substructure in one of the clusters, and an increasing fraction of blue galaxies towards larger cluster radii. Two other mass peaks detected by our weak lensing technique coincide with red clumps of galaxies. We estimate their redshifts and masses, and check for possible X-ray counterparts in deep XMM observations.
Key words: cosmology: miscellaneous - galaxies: clusters: general - astronomical data bases: miscellaneous - gravitational lensing
The amplitude of the distortions induced into galaxy images is of the order of a few percent for lensing by large-scale structure, and up to ten percent in the case of cluster lensing, depending on the mass of the cluster under consideration. The intrinsic ellipticities of galaxy images dominate the noise of the shear signal. Thus, a weak lensing analysis requires deep data with good PSF properties in order to measure enough galaxy ellipticities with sufficient accuracy. A large field of view and independent lines of sight guarantee a representative view of the universe, beating down the effect of cosmic variance. Deep wide field surveys provide this kind of data.
The Garching-Bonn Deep Survey (hereafter: GaBoDS) is a mostly virtual survey and covers a sky area
of more than 12 square degrees with the Wide Field Imager![]() at the MPG/ESO 2.2 m telescope. Compared to other telescopes (VLT, CFHT,
CTIO, WHT, KPNO) that have been successfully used for cosmic shear surveys so far (van Waerbeke et al. 2000,2001; Maoli et al. 2001; Kaiser et al. 2000; Wittman et al. 2000; Bacon et al. 2000,2002), the 2.2 m telescope is small in size,
yet it offers an outstanding image quality. It allows for an independent confirmation of previously
obtained results, and the detection of possibly remaining systematics in the data as well as in the
measurement process.
at the MPG/ESO 2.2 m telescope. Compared to other telescopes (VLT, CFHT,
CTIO, WHT, KPNO) that have been successfully used for cosmic shear surveys so far (van Waerbeke et al. 2000,2001; Maoli et al. 2001; Kaiser et al. 2000; Wittman et al. 2000; Bacon et al. 2000,2002), the 2.2 m telescope is small in size,
yet it offers an outstanding image quality. It allows for an independent confirmation of previously
obtained results, and the detection of possibly remaining systematics in the data as well as in the
measurement process.
In this paper we use weak gravitational lensing to detect dark matter haloes by looking for coherent shear patterns in galaxy images (Schneider 1996). In this manner galaxy clusters are detected directly relying on their most fundamental property, their mass, which is independent of their dynamical state and luminosity. Since structure formation in the Universe is highly sensitive to the cosmological model, shear-selected samples of dark matter haloes will yield new insights into the process of cluster formation (see Wittman et al. 2001,2002; Erben et al. 2000; Dahle et al. 2002; Miyazaki et al. 2002; Margoniner et al. 2003, for shear-selected haloes). Based on simulations of the large-scale structure (Jain & van Waerbeke 2000) as well as on predictions from Press-Schechter models (Kruse & Schneider 2000) one expects some 10 shear-selected dark matter haloes per square degree. Therefore, the number of mass peaks in the GaBoDS data is expected to be of the order of 100. The mass of these peaks strongly depends on their redshift, as is shown in Sect. 5.
This work is organized as follows. In Sect. 2 we discuss our strategy for data mining the ESO archive. An outline of the main characteristics of the GaBoDS fields follows in Sect. 3, together with a compact overview of our WFI data reduction process in Sect. 4. Subsequently we report on the detection of galaxy clusters by means of weak lensing and the red cluster sequence method (Gladder & Yee 2000) in the NGC 300 GaBoDS field, and give a more detailed analysis for one of the clusters therein. We conclude in Sect. 6.
It is clear that "data quality'' is a very ambiguous term, highly dependent on the science which is to be drawn from the data. Given the involved and time consuming reduction of WFI data, we wanted to assess as best as possible the quality of archival data before any request or data reduction. This is straight forward for items such as the total exposure time, available filters, presence of bright objects, availability of calibration frames, and the ambient conditions during which the observation were performed (moon; clouds; seeing, according to the seeing monitor). However, not all of those can be expressed in terms of numbers; some judgement has to be done upon visual inspection of the data. Other data quality issues, such as image seeing or PSF properties can not be evaluated without more complex operations on the data itself. To address most of these points, the following demands were defined to ASTROVIRTEL and querator:
| Target | Exposure time | Image seeing |
| B08p3 | 4900 (5600) | 0
|
| B08p2 | 4900 (5600) | 0
|
| B08p1 | 4500 (5600) | 0
|
| B0800 | 7200 (8300) | 0
|
| B08m1 | 4500 (6000) | 0
|
| B08m2 | 4000 (5800) | 0
|
| B08m3 | 5400 (6000) | 0
|
| Pal3 | 5000 (6120) | 1
|
| AM1 | 7500 (7620) | 1
|
| Comparison1 | 5300 (9300) | 0
|
| C04p1 | 4000 (5600) | 0
|
| C04p3 | 4000 (5600) | 0
|
| C04m2 | 4000 (4800) | 0
|
| C04m3 | 4000 (4800) | 0
|
| NGC 300 | 15 100 ( |
1
|
| C04p2 | 4000 (5600) | 0
|
| C04m1 | 4000 (4800) | 0
|
| C04m4 | 4000 (4800) | 0
|
| C0400 | 4800 (5600) | 0
|
In this way a list of useful candidate fields was extracted from the archive, minimizing the amount
of unusable data slipping into the reduction process. Fields that were rejected at this late
step suffered from scattered light or had very bad PSF properties![]() . Checking for PSF anisotropies in an image was very time
consuming and thus not blindly performed on all data in the archive.
. Checking for PSF anisotropies in an image was very time
consuming and thus not blindly performed on all data in the archive.
Using the enhanced querator we found about 5 square degrees (20 pointings) of data in
the ESO archive which satisfied our criteria, not counting the already known fields such as the ones from the EIS Deep Public Survey. This was twice the area we expected, but it must be
noted that 15 of the pointings were done by a single observer, searching for trans-neptunian objects.
The efficiency of our archive search with querator was about 75%, i.e. three out of four candidate
fields were usable. Table 1 lists the fields found together with their image
seeing.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{H4523F01.eps}
\end{figure}](/articles/aa/full/2003/33/aah4523/Timg33.gif) |
Figure 1: Sky distribution of the GaBoDS fields. The size of the symbols depicts the covered sky area. All fields are at high galactic latitude. |
![\begin{figure}
\includegraphics[width=8.6cm,clip]{H4523F02.eps}
\end{figure}](/articles/aa/full/2003/33/aah4523/Timg34.gif) |
Figure 2: Exposure times in GaBoDS. The peak at 56 ksec represents the Chandra Deep Field South (CDF-S). |
Such quality of the data can only be achieved with a very carefully and frequently refocused telescope.
The effect of a slightly defocused telescope on the PSF is shown in the remaining three panels of Fig. 3. One can see that anisotropies become significant once the detector is out of focus.
Furthermore, the PSF rotates by 90 degrees when one passes through the focal plane. This is characteristic
for tangential and sagittal astigmatism. Still the PSF of WFI@2.2 is very homogeneous over the field of
view, even when crossing chip borders. Thus larger dither patterns can be used for the observations, and
a single smooth model can be fitted to the PSF in the stacked mosaic (see also Fig. 6
in Sect. 5).
| Sky coverage | Data source, depth of field |
|
1.75
|
ESO Imaging Survey + GOODS |
| (medium, one deep) | |
| 5.00
|
ASTROVIRTEL (mostly shallow, one deep) |
| 1.25
|
COMBO-17 survey (deep) |
| 1.25
|
ESO distant cluster survey |
| (shallow, medium) | |
| 0.25
|
NTT Deep Field, from the IR group at the |
| MPI für extraterrestrische Physik (deep) | |
| 0.25
|
Capodimonte Deep Field (deep) |
An almost fully automatic pipeline for WFI reduction was developed, based on existing software
modules wherever possible, such as EIS drizzle![]() ,
the Terapix
,
the Terapix![]() software suite, FLIPS
software suite, FLIPS![]() (J.-C. Cuillandre, not yet publicly
available), Eclipse
(J.-C. Cuillandre, not yet publicly
available), Eclipse![]() ,
Imcat
,
Imcat![]() (N. Kaiser) and LDAC
(N. Kaiser) and LDAC![]() (E. Deul, Leiden Data Analysis Center)
(catalogue format and handling). IRAF was not used in the pipeline, apart from the drizzle
coaddition, since it did not allow efficient scripting and reduction of this specific kind of data.
A number of bash shell scripts were wrapped around those tools (mostly stand-alone C programs),
allowing for an efficient, flexible and almost fully automatized end-to-end reduction of WFI
data in parallel mode. The usage of the pipeline is not restricted to the WFI@2.2, but data from
other instruments such as FORS1/2@VLT, ISAAC@VLT, SUPRIMECAM@SUBARU, MOSAIC-I@CTIO, MOSAIC-II@KPNO and
WFI@AAO has already been successfully reduced. Supported architectures are Solaris, AIX, Linux and
Dec-Alpha. The package will be released together with a detailed technical description (Erben et al.,
in preparation).
(E. Deul, Leiden Data Analysis Center)
(catalogue format and handling). IRAF was not used in the pipeline, apart from the drizzle
coaddition, since it did not allow efficient scripting and reduction of this specific kind of data.
A number of bash shell scripts were wrapped around those tools (mostly stand-alone C programs),
allowing for an efficient, flexible and almost fully automatized end-to-end reduction of WFI
data in parallel mode. The usage of the pipeline is not restricted to the WFI@2.2, but data from
other instruments such as FORS1/2@VLT, ISAAC@VLT, SUPRIMECAM@SUBARU, MOSAIC-I@CTIO, MOSAIC-II@KPNO and
WFI@AAO has already been successfully reduced. Supported architectures are Solaris, AIX, Linux and
Dec-Alpha. The package will be released together with a detailed technical description (Erben et al.,
in preparation).
Our pipeline was designed with the GaBoDS data in mind, i.e. empty fields at high galactic latitude, with a fairly large dither pattern of up to 3$.^$0, and a very large number of single exposures per pointing. Still, the usage of the GaBoDS pipeline is not resticted to empty fields only. This is shown in Sect. 5, where we present an analysis of galaxy clusters behind NGC 300.
Overscan correction, debiasing, flat fielding: apart from the astrometric, photometric and coaddition processes, all chips are processed individually, allowing for an easy parallelization of the code.
During pre-reduction, any instrumental signatures present in the data are removed. This includes
overscan correction, bias subtraction and flat fielding with skyflats![]() . For the master biases all bias frames
are median combined with outlier rejection. Flat fields are combined in the same way, but each
flat exposure is normalised to 1 before the combination. Thus the different gains in the science
images are still present after the flat fielding step. This is because we found that the chip-to-chip
gain variations can be better determined from a superflat, which is drawn from already flatfielded
exposures.
. For the master biases all bias frames
are median combined with outlier rejection. Flat fields are combined in the same way, but each
flat exposure is normalised to 1 before the combination. Thus the different gains in the science
images are still present after the flat fielding step. This is because we found that the chip-to-chip
gain variations can be better determined from a superflat, which is drawn from already flatfielded
exposures.
Creation of a superflat: residuals of around 3-4% after normal flat fielding are common for WFI@2.2 m, depending on sky brightness and the filter in use. A superflat is computed for correction of this effect, by median combining all images from a given observing run, using outlier rejection. Pixels that are affected by stars or galaxies are detected with SExtractor (Bertin & Arnouts 1996) and masked beforehand. In doing so we prevent the bright extended haloes around stars contributing to the superflat. The image constructed this way is then heavily smoothed, yielding an illumination correction image for every chip. All images are divided by their individual illumination correction. They are also normalised to the same (the highest) gain, which is accurately determined by comparing the modes of the individual superflats. Remaining residuals in the sky background are typically below 2%, and in the case of absence of bright stars, even below 1%.
Defringing:
besides the illumination correction a fringing model is calculated by subtracting the illumination
correction from the previous superflat. Hereby it is assumed![]() that the amplitudes of the observed fringes scale directly with the sky background. The
fringing model is then individually scaled for each image and subtracted. Fringing in the R-band
is of the order of a few percent for WFI@2.2. Its correction makes sense only if more than
that the amplitudes of the observed fringes scale directly with the sky background. The
fringing model is then individually scaled for each image and subtracted. Fringing in the R-band
is of the order of a few percent for WFI@2.2. Its correction makes sense only if more than ![]() 10
images were used in the calculation of the model. Otherwise the pixel-to-pixel noise in the fringing
model is larger than the fringing amplitude itself. This would introduce more noise into the individual
defringed images than what is taken out by the correction of the lower frequency fringes. Since we are
interested in measuring shapes of faint and small galaxies we want to avoid additional pixel-to-pixel
noise. However, all images in the GaBoDS survey were constructed from many more than just 10 images, thus the contribution of additional high frequency noise is small, and we profit from taking out the gentle fringing pattern. In the case of the redder I-band the fringing can be much more prominent, and is in general more difficult to remove.
10
images were used in the calculation of the model. Otherwise the pixel-to-pixel noise in the fringing
model is larger than the fringing amplitude itself. This would introduce more noise into the individual
defringed images than what is taken out by the correction of the lower frequency fringes. Since we are
interested in measuring shapes of faint and small galaxies we want to avoid additional pixel-to-pixel
noise. However, all images in the GaBoDS survey were constructed from many more than just 10 images, thus the contribution of additional high frequency noise is small, and we profit from taking out the gentle fringing pattern. In the case of the redder I-band the fringing can be much more prominent, and is in general more difficult to remove.
In the first step, high S/N objects in each image are detected by SExtractor, and a catalogue of
non-saturated stars is generated. Based on a comparison with the USNO-A2 astrometric reference catalogue,
a zero-order, single shift astrometric solution is calculated for each chip in every exposure. For a single-chip camera with a small field of view such an approach is often sufficient, but it no longer holds for multiple chip cameras with a large field of view. CCDs can be rotated with respect to each other, tilted against the focal plane, and in general cover areas at a distance from the
optical axis, where field distortions become prominent![]() . Figure 4 shows the difference between a zero order (single shift with respect to a reference
catalogue) and a full astrometric second order solution per CCD. From this figure it is obvious that
the simple shift-and-add approach will not work for the whole mosaic. The issue is further complicated
by the gaps between the CCDs and large dither patterns that are used to cover them. Thus, chips with
very different distortions overlap. In addition, due to the large field of view, the observed patch of
the sky must no longer be treated as a flat plane, but as a spherical curved surface.
. Figure 4 shows the difference between a zero order (single shift with respect to a reference
catalogue) and a full astrometric second order solution per CCD. From this figure it is obvious that
the simple shift-and-add approach will not work for the whole mosaic. The issue is further complicated
by the gaps between the CCDs and large dither patterns that are used to cover them. Thus, chips with
very different distortions overlap. In addition, due to the large field of view, the observed patch of
the sky must no longer be treated as a flat plane, but as a spherical curved surface.
In the second step we use Mario Radovich's Astrometrix![]() (Terapix) package to fit third order
polynomials to every chip in every exposure, in order to correct for the above mentioned effects and to
find a global astrometric solution. For this purpose all high S/N objects (stars and galaxies) detected
in the first step are identified with each
other, including those from the overlap regions. The latter ones are most important in establishing a
global astrometric (and photometric) solution, since the accuracy of available reference catalogues
such as the USNO-A2 (0
(Terapix) package to fit third order
polynomials to every chip in every exposure, in order to correct for the above mentioned effects and to
find a global astrometric solution. For this purpose all high S/N objects (stars and galaxies) detected
in the first step are identified with each
other, including those from the overlap regions. The latter ones are most important in establishing a
global astrometric (and photometric) solution, since the accuracy of available reference catalogues
such as the USNO-A2 (0
![]() 2 rms) is insufficient for sub-pixel registration. Thus the astrometric
solution is determined from the data itself. The USNO-A2 is used only to fix the solution with respect
to absolute sky coordinates within 0
2 rms) is insufficient for sub-pixel registration. Thus the astrometric
solution is determined from the data itself. The USNO-A2 is used only to fix the solution with respect
to absolute sky coordinates within 0
![]() 2 rms. With Astrometrix we consistently achieve
an internal astrometric accuracy of 1/20-1/10th of a pixel (0
2 rms. With Astrometrix we consistently achieve
an internal astrometric accuracy of 1/20-1/10th of a pixel (0
![]() 02-0
02-0
![]() 01), thus the
final PSF is mostly determined by the intrinsic PSFs of the single exposures (see Fig. 3).
Additional, artificial seeing and PSF anisotropies are introduced into the stacked image on a very low
level only, even for very large data sets such as the CDF-S, consisting of 150 WFI@2.2 R-band exposures.
This is a crucial requirement for our weak lensing analysis.
01), thus the
final PSF is mostly determined by the intrinsic PSFs of the single exposures (see Fig. 3).
Additional, artificial seeing and PSF anisotropies are introduced into the stacked image on a very low
level only, even for very large data sets such as the CDF-S, consisting of 150 WFI@2.2 R-band exposures.
This is a crucial requirement for our weak lensing analysis.
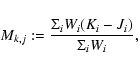 |
(1) |
![\begin{displaymath}\chi^{2}=\sum_{k,j}^{N_{{\rm over}}}\left[M_{k,j}-(ZP_{k}-ZP_{j})\right]^{2}.
\end{displaymath}](/articles/aa/full/2003/33/aah4523/img44.gif) |
(2) |
We now describe our approach to assign an individual weight map for every science image.
In a first step, a pixel is assigned its normalised skyflat value as a weight, which contains the
information about relative gains between the CCDs and pixel-to-pixel sensitivities. Contrary to
other methods, we do not detect `bad' pixels (hot or cold pixels, pixels affected by cosmics,
reflections or satellite tracks) by intercomparing all images in the stack, but on the individual
images themselves. For the detection of permanent image defects, such as hot or dead pixels and
bad columns, we use dark frames and superflat images. Affected pixels are set to zero in the
corresponding weight map. Thus every chip in the WFI mosaic has its own basic weight map after the
first step. Weight maps created in this way are the same for all exposures in a data set unless
they were flatfielded with different skyflats or taken several weeks apart.
In a second step these weight images are adjusted individually for every image. Remaining hot pixels and cosmics are easily identified with SExtractor in conjunction with Eye (Terapix), since they appear much sharper than the stellar PSF even under good seeing conditions. Bright reflections and satellite tracks, however, need to be masked by hand, the only step in the pipeline which is not yet automatized. Moving objects like asteroids go unmasked and show up as dashed lines in the stacked image. During coaddition the individual weight maps are scaled with correction factors for airmass and varying photometric conditions. Changing seeing conditions from image to image can be included on an optional basis, too. All individual weight maps are resampled and coadded in exactly the same way as the respective science images, yielding the noise properties for all pixels in the final coadded image (see Fig. 5 for an example).
For the coaddition the EIS drizzle in IRAF is used. It allows for a weighted mean coaddition, guaranteeing the best S/N in the stacked image. The resampling strategy ensures that the PSF is not artificially bloated in the stack, and that a varying pixel scale is correctly taken into account also from a photometric point of view. Alternatively, one can use swarp (E. Bertin, Terapix), which contrary to drizzle, makes use of much more advanced resampling algorithms and does not lead to correlated noise in the stacked image. However, the differences between swarp and drizzle vanish if many images are stacked, which is the case in GaBoDS.
Four factors determine the value of an output pixel in the coadded image.
We have the input pixel value Ii from the science chip and an associated value Wi in
the weight map. Ii represents the part of the input pixel that is mapped onto the
corresponding output pixel. Besides, Ii is scaled with factors fi to the consistent
photometric zeropoint and to a fixed exposure time (we chose 1 s for this purpose):
| fi=10-0.4 ZPi/ti, | (3) |
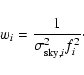 |
(4) |
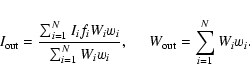 |
(5) |
Upon visual inspection in the Digitized Sky Survey (DSS) before the data retrieval request, we
recognized two concentrations of fainter galaxies north-east and south-east of NGC 300, at the edge of
the WFI@2.2 field. 21 spectra were taken for the first concentration by Cappi et al. (1998) (hereafter CHM98),
confirming a cluster at redshift 0.165. The second, less prominent concentration is known as EDCC-499
at a redshift of 0.117 (Collins et al. 1995). Hereafter we refer to these clusters as CL0056.03-37.55
(CL0053-37 in CHM98) and CL0056.02-37.90, respectively, using their epoch 2000.0 equatorial coordinates.
The WFI@2.2 data for NGC 300 was taken for the ARAUCARIA project (Pietrzynski et al. 2002a), an attempt to
fine-tune the distance ladder by comparing different distance indicators such as cepheids, blue
supergiants, tip of the red giant branch, and planetary nebulae for various nearby galaxies. Since
NGC 300 was monitored in 34 nights between July 1999 and January 2000, the creation of deep
multicolour images was feasible![]() .
.
The photometric zeropoint of the coadded V-band image was determined by matching stellar magnitudes
to the secondary standard stars established by Pietrzynski et al. (2002b) in the Johnson-Cousins system.
No calibration was available for the R-band, for which a zeropoint was determined based on the
expected V-R colour for the red sequence of CL0056.03 (z=0.165). We estimate it to be accurate
within 0
![]() 1, which is sufficient for the analysis presented here since it does not rely on
highly accurate absolute photometry.
1, which is sufficient for the analysis presented here since it does not rely on
highly accurate absolute photometry.
For the production of colour catalogues the coadded images were normalised so that their mean
background noise
![]() .
They were then coadded without further rescaling, yielding a
high signal-to-noise detection image. For this stack an adapted weight map was created combining
the individual weight images accordingly. For the creation of a colour catalogue we used the detection
image, the detection weight map and the unnormalised images from filters V and R, as an input for
SExtractor. Thus the flux for objects in different filters was measured within the same aperture,
yielding relative colour information for galaxies with good internal accuracy. A further advantage of this
approach was that the objects detected in the single catalogues for the V- and R-bands were already in
the same order and easily merged into one colour catalogue. We calculated the galaxy colours from isophotal
magnitudes (MAG_ISO), and used MAG_AUTO for the magnitudes themselves.
.
They were then coadded without further rescaling, yielding a
high signal-to-noise detection image. For this stack an adapted weight map was created combining
the individual weight images accordingly. For the creation of a colour catalogue we used the detection
image, the detection weight map and the unnormalised images from filters V and R, as an input for
SExtractor. Thus the flux for objects in different filters was measured within the same aperture,
yielding relative colour information for galaxies with good internal accuracy. A further advantage of this
approach was that the objects detected in the single catalogues for the V- and R-bands were already in
the same order and easily merged into one colour catalogue. We calculated the galaxy colours from isophotal
magnitudes (MAG_ISO), and used MAG_AUTO for the magnitudes themselves.
We use the aperture mass statistics
![]() (Schneider 1996) for the
detection of galaxy clusters.
(Schneider 1996) for the
detection of galaxy clusters.
![]() is a filtered integral of the projected mass
distribution,
is a filtered integral of the projected mass
distribution, ![]() ,
inside an aperture. Its definition reads
,
inside an aperture. Its definition reads
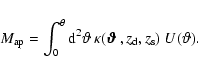 |
(6) |
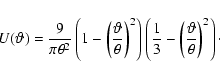 |
(7) |
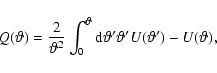 |
(8) |
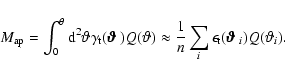 |
(9) |
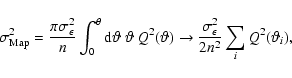 |
(10) |
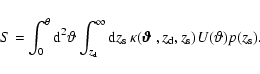 |
(11) |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{H4523F07.eps}
\end{figure}](/articles/aa/full/2003/33/aah4523/Timg75.gif) |
Figure 7:
Photometric redshift distribution for the Chandra Deep Field South,
determined from UBVRI WFI@2.2 photometry. The redshifts were estimated with hyperz (solid
line) (Bolzonella et al. 2000). Only objects that had a good redshift fit of
|
Figure 8 shows some predicted S/N ratios for massive haloes as a function of redshift. From this
plot we see that clusters with masses of
![]() are detectable up to a redshift
of
are detectable up to a redshift
of
![]() ,
and those with
,
and those with
![]() can be found up to
can be found up to
![]() for a
filter size of 3$.^$2 (4$.^$0, not shown). We are not sensitive to structures with
for a
filter size of 3$.^$2 (4$.^$0, not shown). We are not sensitive to structures with
![]()
![]() at the 3$.^$2 scale, but can detect them at the 4$.^$0 scale
up to z=0.14. For comparison, S/N ratios are also shown for the case when background galaxies are at
somewhat higher redshift (z0=0.5).
The S/N ratio for
at the 3$.^$2 scale, but can detect them at the 4$.^$0 scale
up to z=0.14. For comparison, S/N ratios are also shown for the case when background galaxies are at
somewhat higher redshift (z0=0.5).
The S/N ratio for
![]() peaks in a given data field can also be determined from the data
itself, by randomizing ellipticities while keeping galaxy positions fixed. In the following we make
use of this fact. For the weak lensing analysis the R-band image was used. To avoid any biasing of the detection algorithm, NGC 300 was masked and replaced by the mean sky background, removing most of
the flux present in the image. With SExtractor all objects with at least 6 connected pixels
peaks in a given data field can also be determined from the data
itself, by randomizing ellipticities while keeping galaxy positions fixed. In the following we make
use of this fact. For the weak lensing analysis the R-band image was used. To avoid any biasing of the detection algorithm, NGC 300 was masked and replaced by the mean sky background, removing most of
the flux present in the image. With SExtractor all objects with at least 6 connected pixels ![]()
![]() above the sky background noise were detected. This catalogue contained 44 146 objects. The
shear estimates for these objects were determined with the KSB algorithm as proposed by Kaiser et al. (1995).
An extensive description of our approach using the KSB method, including the PSF corrections, can be found in Erben et al. (2001). Figure 6 shows the measured and the corrected PSF
anisotropies for this particular field. After filtering, the background galaxy catalogue contained
12 694 objects with securely determined shapes, a detection significance
above the sky background noise were detected. This catalogue contained 44 146 objects. The
shear estimates for these objects were determined with the KSB algorithm as proposed by Kaiser et al. (1995).
An extensive description of our approach using the KSB method, including the PSF corrections, can be found in Erben et al. (2001). Figure 6 shows the measured and the corrected PSF
anisotropies for this particular field. After filtering, the background galaxy catalogue contained
12 694 objects with securely determined shapes, a detection significance ![]() (calculated by KSB) and a bright magnitude limit of R>23.0. This translates to the above mentioned number density of
(calculated by KSB) and a bright magnitude limit of R>23.0. This translates to the above mentioned number density of
![]() 20 galaxies per square arcmin.
20 galaxies per square arcmin.
Figure 9 shows the
![]() results for various filter widths. As can be seen, we recovered
CL0056.03 in all but the largest filter scale at a 3
results for various filter widths. As can be seen, we recovered
CL0056.03 in all but the largest filter scale at a 3![]() level within 50-100
level within 50-100
![]() south of the cluster centre, whereas CL0056.02 was not detected. For the latter cluster useful shear information could only be obtained from about 30% of the area which would be available if the cluster
did not lie next to the field corner in a region with bad image quality. This increased the
noise in
south of the cluster centre, whereas CL0056.02 was not detected. For the latter cluster useful shear information could only be obtained from about 30% of the area which would be available if the cluster
did not lie next to the field corner in a region with bad image quality. This increased the
noise in
![]() by a factor of
by a factor of ![]() 3. The argument of field truncation also holds for CL0056.03,
but to a much lesser extent. There the useable field was limited by the edge of the image, 2$.^$5
east of the cluster centre, and NGC 300 5$.^$5 south-west. From our previous S/N considerations we
conclude that a mass of
3. The argument of field truncation also holds for CL0056.03,
but to a much lesser extent. There the useable field was limited by the edge of the image, 2$.^$5
east of the cluster centre, and NGC 300 5$.^$5 south-west. From our previous S/N considerations we
conclude that a mass of ![]()
![]() at redshift of z=0.165 would produce a
comparably significant
at redshift of z=0.165 would produce a
comparably significant
![]() detection.
detection.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{H4523F09.eps}
\end{figure}](/articles/aa/full/2003/33/aah4523/Timg86.gif) |
Figure 9:
The
|
The
![]() statistics furthermore picks up a number of other peaks. In the upper left panel of Fig. 9, the one for the smallest filter scale, we find a
statistics furthermore picks up a number of other peaks. In the upper left panel of Fig. 9, the one for the smallest filter scale, we find a ![]() peak that drops to
peak that drops to ![]() in the upper right panel, and vanishes for larger filter scales (clump "C''). Another peak
below CL0056.03 is detected at the
in the upper right panel, and vanishes for larger filter scales (clump "C''). Another peak
below CL0056.03 is detected at the ![]() level for all but the largest filter scale (clump "A'').
Both peaks lie within 50
level for all but the largest filter scale (clump "A'').
Both peaks lie within 50
![]() and 20-70
and 20-70
![]() of two clumps of red galaxies, as is shown in the next section. There we determine their redshifts
of two clumps of red galaxies, as is shown in the next section. There we determine their redshifts
![]() and
and
![]() .
Our S/N calculations then yield masses of
.
Our S/N calculations then yield masses of
![]() and
and
![]() for these two clumps and for the filter scales
in which they are detected most significantly. See also Fig. 14 for those two
concentrations of red galaxies.
for these two clumps and for the filter scales
in which they are detected most significantly. See also Fig. 14 for those two
concentrations of red galaxies.
Besides, a stable peak is found inside the mask of NGC 300, with a detection limit of
![]() for the three smaller filter scales. Such a detection is not surprising, since
for the three smaller filter scales. Such a detection is not surprising, since
![]() is a highly non-local measure. It can pick up those parts of the shear field
from a possible cluster hidden behind NGC 300 that extend beyond NGC 300 itself. Shear fields
for massive clusters of galaxies have been traced beyond 10
is a highly non-local measure. It can pick up those parts of the shear field
from a possible cluster hidden behind NGC 300 that extend beyond NGC 300 itself. Shear fields
for massive clusters of galaxies have been traced beyond 10
![]() of cluster centres (see Clowe & Schneider 2002, for examples), thus a sufficiently massive cluster behind NGC 300 could easily be
picked up. The detection in question is at the very outer edge of the galaxy disk, but the
confusion limit of foreground stars in NGC 300 is already reached. Yet the optical thickness
of the disk is still small, so that three larger and brighter isolated galaxies can be seen
within a 2
of cluster centres (see Clowe & Schneider 2002, for examples), thus a sufficiently massive cluster behind NGC 300 could easily be
picked up. The detection in question is at the very outer edge of the galaxy disk, but the
confusion limit of foreground stars in NGC 300 is already reached. Yet the optical thickness
of the disk is still small, so that three larger and brighter isolated galaxies can be seen
within a 2
![]() wide window. Thus, if there was a massive lower redshift cluster
such as CL0056.03 at this position, it could be seen through the disk.
There is no indication for such an object at this position. More distant clusters, however, could no longer be identified as such, since their smaller and fainter images are drowned in the foreground
confusion.
wide window. Thus, if there was a massive lower redshift cluster
such as CL0056.03 at this position, it could be seen through the disk.
There is no indication for such an object at this position. More distant clusters, however, could no longer be identified as such, since their smaller and fainter images are drowned in the foreground
confusion.
| Red clump |
|
|
| A |
|
|
| B |
|
|
| C |
|
|
| D |
|
|
In a (V-R,R) colour-magnitude diagram (Fig. 11), plotted for all galaxies
in the vicinity of NGC 300, we loosely selected a red cluster sequence with
0.67<V-R<0.87,
13.0<R<21.0. The sky distribution for objects inside this window is plotted in
Fig. 13
(big red dots), whereas all other objects with R<21 and outside the window are shown as small
dots. We then calculated the rms of the projected density of all red sequence members, and overlaid
isodensity sigma-contours for their distribution. The smoothing length for the density was 3$.^$6.
We recover CL0056.03 and CL0056.02 at the ![]() and
and ![]() level in overdensity, respectively.
Thus the cluster sequence we selected in the colour-magnitude diagram is actually a merger of two
clusters of galaxies.
level in overdensity, respectively.
Thus the cluster sequence we selected in the colour-magnitude diagram is actually a merger of two
clusters of galaxies.
The remaining galaxies that lay within the red sequence window, but which did not belong
to either of the two clusters, did not clump throughout the rest of the field on a level higher than ![]() .
Furthermore, all galaxies brighter than R=20 and outside the red sequence window
showed no clumping at a level higher than
.
Furthermore, all galaxies brighter than R=20 and outside the red sequence window
showed no clumping at a level higher than ![]() .
We additionally checked the clustering properties
of all objects brighter than R=23,
by moving a rectangular aperture over all relevant galaxies in the colour-magnitude distribution.
We did not find any highly significant clumping apart from galaxies with
1.37<V-R<1.56, 19.0<R<22.5.
There we found four significant overdensities "A'' to "D'',
with "A'' and "C'' coincident with
.
We additionally checked the clustering properties
of all objects brighter than R=23,
by moving a rectangular aperture over all relevant galaxies in the colour-magnitude distribution.
We did not find any highly significant clumping apart from galaxies with
1.37<V-R<1.56, 19.0<R<22.5.
There we found four significant overdensities "A'' to "D'',
with "A'' and "C'' coincident with
![]() detections (see above). Table 3
summarises the properties and redshift estimates based on the track for elliptical galaxies in
Fig. 12.
We see that all clumps lie at similar redshifts, with some ambiguity for clump "C''. Actually, peaks "A'' and "B'' could form a connected system if spectroscopically confirmed to be at the same redshift.
More details are given in the caption of Fig. 14.
detections (see above). Table 3
summarises the properties and redshift estimates based on the track for elliptical galaxies in
Fig. 12.
We see that all clumps lie at similar redshifts, with some ambiguity for clump "C''. Actually, peaks "A'' and "B'' could form a connected system if spectroscopically confirmed to be at the same redshift.
More details are given in the caption of Fig. 14.
For CL0056.03, in the innermost bin 11 out of 19 galaxies have measured redshifts, in the second bin it is 10 out of 60 galaxies, and in the outermost bin none of the 34 galaxies have known redshifts. 10 galaxies appear to lie above the upper envelope (V-R>0.87) of the cluster sequence,7 of those are from the second distance bin, and the rest comes from the third bin. Their number is in agreement with the expected amount of interlopers. 4 of those 10 galaxies are spatially concentrated within 1$.^$2. None of the 10 has spectroscopically determined redshifts, we assume that they are in the background of CL0056.03 since they lie beyond the upper envelope of V-R<0.87 as defined by the red sequence.
A closer inspection of the colour-magnitude diagram for CL0056.03 reveals several features:
| (13) |
| (14) |
For CL0056.02 we find similar, but less significant results. The cluster sequence is broader
and not so well-defined than the one for CL0056.03. There is no clear cut-off towards redder colours.
Only galaxies inside the innermost distance bin and with R<19 form a tight sequence with
![]() .
Galaxies in the second bin have a considerably larger scatter for brighter
magnitudes, but a smaller one at the faint end as compared to CL0056.03. Objects within 385 kpc show
a clear colour evolution with a slope of
.
Galaxies in the second bin have a considerably larger scatter for brighter
magnitudes, but a smaller one at the faint end as compared to CL0056.03. Objects within 385 kpc show
a clear colour evolution with a slope of
![]() for R>18.5. Beyond 385 kpc the galaxy
population becomes significantly bluer, 83% of them lie below the red sequence. The fraction of blue
galaxies is larger than for CL0056.03 in the outer two annuli, whereas in the cluster cores
their fraction is comparable. We note that the data quality in the field around CL0056.02 is
significantly lower than for CL0056.03, increasing the photometric errors. Table 4
summarises this effect for both clusters.
for R>18.5. Beyond 385 kpc the galaxy
population becomes significantly bluer, 83% of them lie below the red sequence. The fraction of blue
galaxies is larger than for CL0056.03 in the outer two annuli, whereas in the cluster cores
their fraction is comparable. We note that the data quality in the field around CL0056.02 is
significantly lower than for CL0056.03, increasing the photometric errors. Table 4
summarises this effect for both clusters.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{H4523F12.eps}
\end{figure}](/articles/aa/full/2003/33/aah4523/Timg112.gif) |
Figure 12: Shown are predictions for the WFI@2.2 V-R colours of elliptical galaxies as a function of redshift (Bruzual & Charlot 1993; Bolzonella et al. 2000). Based on the track that includes evolutionary effects we estimate the redshifts for the shear-selected red clumps. |
![\begin{figure}
\par\includegraphics[width=17.4cm,clip]{H4523F13.eps}
\end{figure}](/articles/aa/full/2003/33/aah4523/Timg113.gif) |
Figure 13:
Galaxies inside the lower red cluster sequence of
Fig. 11 are shown as big dots. The small dots indicate galaxies brighter
than R=21 which do not fall inside the red sequence window. The overlaid contours are isodensity
contours for the red sequence members, smoothed at a 3$.^$6 scale, and starting with the
|
![\begin{figure}
\par\includegraphics[width=17.4cm,clip]{H4523F14.eps}
\end{figure}](/articles/aa/full/2003/33/aah4523/Timg115.gif) |
Figure 14:
Shown is the distribution of galaxies inside the upper red
cluster sequence of Fig. 11 (big dots). The small dots indicate galaxies
brighter than R=22.5 which do not fall inside the red sequence window. Clump "A'' is a very tight concentration of nine galaxies with R<22.3 within 25
|
| Distance from | Galaxies | Fraction of | est. No. of |
| cluster centre | with(out) z | blue galaxies | interlopers |
| CL0056.03 | |||
| 0-200 kpc | 11 (8) | 0.26 | 0.6 |
| 200-740 kpc | 10 (50) | 0.35 | 6.8 |
| 740-1080 kpc | 0 (34) | 0.57 | 6.5 |
| CL0056.02 | |||
| 0-143 kpc | 1 (6) | 0.29 | 0.6 |
| 143-430 kpc | 1 (26) | 0.59 | 4.5 |
| 430-780 kpc | 0 (23) | 0.83 | 6.2 |
| ID | RA (2000.0) | DEC (2000.0) | v |
|
z | m |
| 1 | 00:56:10.23 | -37:34:07.9 | 51570 | 282 | 0.17202 | 1 |
| 2 | 00:56:09.22 | -37:33:59.5 | 50799 | 51 | 0.16945 | 1 |
| 3 | 00:56:07.07 | -37:33:49.4 | 51628 | 138 | 0.17221 | 1 |
| 4 | 00:56:09.71 | -37:33:39.9 | 50709 | 120 | 0.16915 | 1 |
| 5 | 00:56:01.49 | -37:33:31.6 | 49315 | 111 | 0.16450 | 1 |
| 6 | 00:56:06.41 | -37:33:18.0 | 49754 | 154 | 0.16596 | cD 1 |
| 7 | 00:55:57.50 | -37:32:51.5 | 46839 | 38 | 0.15624 | 2 |
| 8 | 00:55:58.90 | -37:33:00.7 | 48490 | 50 | 0.16175 | 2 |
| 9 | 00:56:02.76 | -37:33:03.9 | 49588 | 192 | 0.16541 | 1 |
| 10 | 00:56:04.76 | -37:33:00.3 | 50394 | 117 | 0.16810 | 1 |
| 11 | 00:56:04.75 | -37:32:51.0 | 51594 | 84 | 0.17210 | 1 |
| 12 | 00:55:55.59 | -37:32:20.2 | 48514 | 145 | 0.16183 | 2 |
| 13 | 00:55:56.74 | -37:32:35.4 | 49555 | 123 | 0.16530 | 2 |
| 14 | 00:55:57.74 | -37:32:23.4 | 48256 | 101 | 0.16096 | 2 |
| 15 | 00:55:59.32 | -37:32:35.2 | 49041 | 145 | 0.16358 | 2 |
| 16 | 00:55:59.09 | -37:32:18.2 | 48888 | 117 | 0.16307 | cD 2 |
| 17 | 00:56:01.32 | -37:32:41.9 | 50168 | 187 | 0.16734 | 2 |
| 18 | 00:56:02.45 | -37:32:18.0 | 47381 | 138 | 0.15805 | 2 |
| 19 | 00:56:02.41 | -37:32:05.7 | 49097 | 113 | 0.16377 | 2 |
| 20 | 00:55:56.18 | -37:31:48.3 | 49439 | 14 | 0.16491 | 2 |
| 21 | 00:56:09.54 | -37:31:49.0 | 49863 | 107 | 0.16633 | 1 |
| Clump |
|
|
|
|
|
|
50521 | 879 |
|
|
|
48697 | 960 |
Figure 17 shows the redshifts of galaxies as a function of distance from the
geometric cluster centre, defined as the centre of the connection line between
![]() and
and
![]() .
We find different mean redshifts for the galaxies around
.
We find different mean redshifts for the galaxies around
![]() and
and
![]() ,
translating into a velocity difference of
,
translating into a velocity difference of ![]()
![]() .
The velocity dispersions of the two clumps are thus significantly smaller than the one given in
CHM98 for the whole system, as is the total dynamical mass. Details can be found in Table 6.
In order to obtain a more rigorous estimate for the significance of this discrepancy, we used Monte
Carlo simulations. Galaxy redshifts were randomly distributed 106 times while keeping galaxy
positions fixed, destroying any possible correlation between redshift and position. In only 95 out of the 106 cases do we find a higher mean redshift for the clump around
.
The velocity dispersions of the two clumps are thus significantly smaller than the one given in
CHM98 for the whole system, as is the total dynamical mass. Details can be found in Table 6.
In order to obtain a more rigorous estimate for the significance of this discrepancy, we used Monte
Carlo simulations. Galaxy redshifts were randomly distributed 106 times while keeping galaxy
positions fixed, destroying any possible correlation between redshift and position. In only 95 out of the 106 cases do we find a higher mean redshift for the clump around
![]() and a lower one for the other than in the observed data, meaning a
and a lower one for the other than in the observed data, meaning a ![]() significance.
In addition, we checked whether the two distributions with
significance.
In addition, we checked whether the two distributions with
![]() and
and
![]() can be drawn from the same parent distribution with
can be drawn from the same parent distribution with
![]() .
We created 105 random realisations of this parent Gaussian
distribution, each containing 21 velocities that were ordered. Every realisation was split into
two sub-samples, having the same number of overlapping objects in velocity space as the real data,
shown in Fig. 17. These sub-samples contained 10 and 11 mock galaxies,
and it was checked whether the difference in their mean velocities was larger than the observed
.
We created 105 random realisations of this parent Gaussian
distribution, each containing 21 velocities that were ordered. Every realisation was split into
two sub-samples, having the same number of overlapping objects in velocity space as the real data,
shown in Fig. 17. These sub-samples contained 10 and 11 mock galaxies,
and it was checked whether the difference in their mean velocities was larger than the observed
![]() .
We found that in 96.9% of all cases the observed velocity histogram
could not be drawn from a single Gaussian distribution, thus the clumps probably did not yet mix.
.
We found that in 96.9% of all cases the observed velocity histogram
could not be drawn from a single Gaussian distribution, thus the clumps probably did not yet mix.
We note that the velocity difference between
![]() and
and
![]() themselves, however,
is
themselves, however,
is
![]() and thus much lower than the difference between the sub-clumps. We conclude
that the 21 measured redshifts for CL0056.03 are probably not representative for the
and thus much lower than the difference between the sub-clumps. We conclude
that the 21 measured redshifts for CL0056.03 are probably not representative for the ![]() 113 cluster
member candidates, as identified by their colours.
113 cluster
member candidates, as identified by their colours.
In the following a simple dynamical model is used in order to check whether the system is
gravitationally bound or unbound. A linear orbit of the clumps is assumed, i.e. there is no
shear or rotation component. The system is seen under some inclination angle ![]() ,
with
,
with
![]() if the clumps were aligned along the line of sight. Based on Newtonian dynamics
the condition of a bound system can be written as
if the clumps were aligned along the line of sight. Based on Newtonian dynamics
the condition of a bound system can be written as
![]() ,
or, taking into account
the inclination angle
,
or, taking into account
the inclination angle ![]() ,
as
,
as
Our interpretation for the dynamical state of CL0056.03 is thus that the eastern clump is closer to us and the western one further away, and that the system is in a pre-collision phase with the two clumps approaching each other, since probably no mixing has yet taken place. In addition, there is some indication from the imaging data itself, arguing for this scenario: both the eastern and the western clump are embedded in large, but well separated haloes, each measuring about 340 kpc. The halo around the western clump, in particular, shows tidal features. We take this as an evidence for ongoing tidal stripping and merging processes inside the clumps, but probably no encounter has yet taken place between them. In the spectra taken by CHM98 no emission lines are found for the cluster members, thus there is no sign for nuclear activity or major star formation. The other scenario is that there was already an encounter and the two clumps are receding, which would place the western clump closer to the observer. Based on the small number of spectra the latter state can not be ruled out.
Besides the two sub-clumps there is some evidence for a more extended structure in CL0056.03.
In Fig. 13 a filament is seen, extending to about 7
![]() north
and 4
north
and 4
![]() south of the cluster centre, but not lined up with the cluster centre itself.
The angle between this linear filament and the orientation of CL0056.03 is
south of the cluster centre, but not lined up with the cluster centre itself.
The angle between this linear filament and the orientation of CL0056.03 is ![]() 40 degrees.
North of CL0056.03 at (
40 degrees.
North of CL0056.03 at (![]() :55:45.6,
:55:45.6,
![]() :24:46), however, the small cluster Abell S0102
is found at a redshift of z=0.056. A contamination of the possible filament by member galaxies
of Abell S0102 cannot be ruled out. Furthermore, 5$.^$2 from the cluster centre and in the
direction of the cluster orientation, an isolated elliptical galaxy with R=14.4 and V-R=0.745
is found, 0.05 mag bluer than the cluster sequence. Its distance to the centre of Abell S0102 is 6$.^$2. Based on the present data it cannot be concluded whether this elliptical is isolated
in space or a physical member at the fringes of one of the two clusters.
:24:46), however, the small cluster Abell S0102
is found at a redshift of z=0.056. A contamination of the possible filament by member galaxies
of Abell S0102 cannot be ruled out. Furthermore, 5$.^$2 from the cluster centre and in the
direction of the cluster orientation, an isolated elliptical galaxy with R=14.4 and V-R=0.745
is found, 0.05 mag bluer than the cluster sequence. Its distance to the centre of Abell S0102 is 6$.^$2. Based on the present data it cannot be concluded whether this elliptical is isolated
in space or a physical member at the fringes of one of the two clusters.
Making use of the high quality of the R-band exposures, we showed that one of the two clusters
(CL0056.03) can be detected by its weak gravitational shear signal. The second cluster (CL0056.02)
was not found in the weak lensing data, probably due to field truncation and insufficient image quality.
Besides, two other significant and coherent shear patterns were detected. Both of them coincide with
significant overdensities of red galaxies, for which we gave redshift and mass estimates, based on
their apparent colour and lensing strength. A third shear detection was seen behind NGC 300 itself,
but there is no further evidence from background light for a cluster of galaxies at this position.
Thus, apart from this hidden detection, all
![]() peaks equal to or higher than
peaks equal to or higher than ![]() in
filter scales
in
filter scales ![]() 3$.^$2 coincide with overdensities of red galaxies. These
3$.^$2 coincide with overdensities of red galaxies. These
![]() peaks, however, are at the limit of what can be concluded from this data set. The tidal gravitational
fields of more massive clusters of galaxies imprint shear fields in the images of background galaxies
that are easily detected on the
peaks, however, are at the limit of what can be concluded from this data set. The tidal gravitational
fields of more massive clusters of galaxies imprint shear fields in the images of background galaxies
that are easily detected on the ![]() level and beyond (Clowe & Schneider 2002).
level and beyond (Clowe & Schneider 2002).
Based on the high virial mass of CL0056.03, derived from spectroscopic data by CHM98, and the
comparatively shallow weak lensing signal, a closer analysis of this cluster was performed. A highly
significant correlation between redshift and the position of galaxies in the cluster is
found, indicating the existence of two sub-clumps, separated by
![]() in velocity
space. Based on the present data and the derived lensing mass it cannot be concluded whether the system is
gravitationally bound. By looking at the projected sky distribution of galaxies with similar properties
in a (V-R,R) colour-magnitude diagram, we find an extended filament of galaxies inclined to the cluster's
major axis. Without further spectroscopic data of galaxies in this filament its nature can not
be further clearified. We take the presented properties as evidence that CL0056.03 is a younger
cluster in formation and has not yet reached its equilibrium state.
in velocity
space. Based on the present data and the derived lensing mass it cannot be concluded whether the system is
gravitationally bound. By looking at the projected sky distribution of galaxies with similar properties
in a (V-R,R) colour-magnitude diagram, we find an extended filament of galaxies inclined to the cluster's
major axis. Without further spectroscopic data of galaxies in this filament its nature can not
be further clearified. We take the presented properties as evidence that CL0056.03 is a younger
cluster in formation and has not yet reached its equilibrium state.
CL0056.03 shows a clear and tight red sequence in the (V-R,R) colour-magnitude space, with an increasing fraction of bluer galaxies towards larger cluster radii. CL0056.02 also shows a red sequence, the results presented for this cluster, however, are more uncertain due to field truncation and inferior data quality.
Acknowledgements
The authors thank Nathalie Fourniol and Benoit Pirenne (ESO archive), for their excellent assistance of our frequent and substantial data requests. Furthermore the kind provision of FLIPS by Jean-Charles Cuillandre is greatly appreciated. MS thanks Matthias Bartelmann, Oliver Czoske, Evanthia Hatziminaoglou, Lindsay King, Joan-Marc Miralles and Stella Seitz for providing photometric redshift estimates, further discussions and many corrections. WG and GP gratefully acknowledge support for this research from the Chilean Center for Astrophysics FONDAP 15010003. SC was supported by the German Ministry for Science and Education (BMBF) under the grant number 50OX0002. The support given by ASTROVIRTEL, a Project funded by the European Commission under FP5 Contract No. HPRI-CT-1999-00081, is acknowledged. This work was furthermore supported by the BMBF through the DLR under the project 50 OR 0106, by the BMBF through DESY under the project 05AE2PDA/8, and by the Deutsche Forschungsgemeinschaft (DFG) under the project SCHN 342/3-1.