A&A 407, L73-L77 (2003)
DOI: 10.1051/0004-6361:20031088

Probing the cosmic ray population of the giant elliptical galaxy M 87 with observed TeV ${\gamma }$-rays

C. Pfrommer - T. A. Enßlin

Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str.1, Postfach 1317, 85741 Garching, Germany

Received 27 May 2003 / Accepted 15 July 2003

Abstract
We examine the cosmic ray proton (CRp) population within the giant elliptical galaxy M 87 using the TeV ${\gamma }$-ray detection of the HEGRA collaboration. In our scenario, the ${\gamma }$-rays are produced by decaying pions which result from hadronic CRp interactions with thermal gas of the interstellar medium of M 87. By comparing the ${\gamma }$-ray emission to upper limits from EGRET, we constrain the spectral index of the CRp population to $\alpha_{\rm GeV}^{\rm TeV}<2.275$ within our scenario. Both the expected radial ${\gamma }$-ray profile and the required amount of CRp support this hadronic scenario. The accompanying radio mini-halo of hadronically originating cosmic ray electrons is outshone by the synchrotron emission of the relativistic jet of M 87 by one order of magnitude. According to our predictions, the future GLAST mission should allow us to test this hadronic scenario.

Key words: ${\gamma }$-rays: theory - cosmic rays - galaxies: individual: M 87 - galaxies: cooling flows - intergalactic medium - radiation mechanisms: non-thermal

   
1 Introduction

The giant elliptical galaxy M 87 is an intensively studied object in our direct extragalactic vicinity situated at a distance of 17 Mpc (Neilsen & Tsvetanov 2000). The announcement of the TeV ${\gamma }$-ray detection of M 87 at a 4-$\sigma$ significance level by the HEGRA collaboration (Aharonian et al. 2003) using imaging atmospheric Cerenkov techniques was the first discovery of TeV ${\gamma }$-rays from a radio galaxy with a jet whose axis forms a relatively large angle with the line of sight of roughly 30$^\circ$-35$^\circ$ (Bicknell & Begelman 1996). On the basis of the limited event statistics the detected emission is inconclusive whether it originates from a point source or an extended source. Despite testing for burstlike behavior of M 87 no time variation of the TeV ${\gamma }$-ray flux has been found. This detection provides the unique possibility for probing different ${\gamma }$-ray emission scenarios and thus provides new astrophysical insight into high energy phenomena of this class of objects.

In the literature, there are three different types of model predicting ${\gamma }$-ray emission from objects like M 87: In the first scenario, the GeV/TeV ${\gamma }$-ray emission is generated by the active galactic nucleus (AGN), and possibly related to processed radiation of the relativistic outflow (Dermer et al. 1997). Particularly, inverse Compton (IC) scattering of cosmic microwave background photons off electrons within the jet which have been directly accelerated or reaccelerated as well as the Synchrotron Self Compton scenario could lead to ${\gamma }$-ray emission (Bai & Lee 2001). Secondly, dark matter annihilation or decay processes could be another conceivable source of ${\gamma }$-ray emission, such as the hypothetical neutralino annihilation (Baltz et al. 2000). Finally, hadronic cosmic ray proton (CRp) interactions with the thermal ambient gas would produce pion decay induced ${\gamma }$-rays as well as inverse Compton and synchrotron emission by secondary cosmic ray electrons (CRe) (Vestrand 1982). These processes are possible due to the long lifetimes of CRp comparable to the Hubble time (Völk et al. 1996), long enough to diffuse away from the production site and to maintain their distribution throughout the cluster volume. Because of the strong dependence of this hadronic process on particle density, the giant radio galaxy M 87, located inside the central cooling flow region of the Virgo cluster, is expected to be a major site of ${\gamma }$-ray emission (Pfrommer & Enßlin 2003).

This work uses the hadronic scenario to model the resulting ${\gamma }$-ray emission. Thus it probes the CRp population by the recent TeV ${\gamma }$-ray observations yielding either an upper limit or a detection on the CRp population, provided this scenario applies. However, this approach only constrains the CRp within the central region of intracluster medium (ICM) of the Virgo cluster which is dominated by the interstellar medium (ISM) of the radio galaxy M 87. In the following, we use the term ICM for both. It should be emphasized that this hadronic scenario predicts stationary ${\gamma }$-ray emission and will be ruled out if the emission is found to be time-variable (barring the existence of a second component). This, however, would result in even tighter constraints on the CRp population owing to the absence of inescapably accompanying ${\gamma }$-ray emission.

   
2 ${\gamma }$-ray emission from hadronic CRp interactions

The differential number density distribution of a CRp population can be described by a power-law in momentum $p_{\rm p}$,

 \begin{displaymath} f_{\rm p}(\vec{r}, p_{\rm p}) ~{\rm d}p_{\rm p}~{\rm d}V = ... ... \left(\frac{c~{\rm d}p_{\rm p}}{\mbox{GeV}}\right)~ {\rm d}V, \end{displaymath} (1)

where the normalization $\tilde{n}_{\rm CRp}(\vec{r})$ is determined by different models of spatial distribution of the CRp population (see Sect. 3).

If the CRp population within the cooling flow region had time to loose energy by means of Coulomb interactions in the plasma (Gould 1972), the low energy part of the spectrum would be modified. This can be treated approximately by imposing a lower momentum cutoff

 \begin{displaymath} p_{\rm min} = \beta_{\rm p}\gamma_{\rm p}~m_{\rm p}~c \simeq... ...rac{n_{\rm e}}{0.1~\mbox{cm}^{-3}} \right)~ \mbox{GeV} c^{-1}, \end{displaymath} (2)

where we inserted typical values for M 87. The kinetic energy density of such a CRp population is

 \begin{displaymath} \varepsilon_{\rm CRp}(\vec{r})= \frac{\tilde{n}_{\rm CRp}(\... ...p}^{1-\alpha} \left( \sqrt{1+\tilde{p}^2} - 1 \right)\right], \end{displaymath} (3)

where $\mathcal{B}_x(a,b)$ denotes the incomplete beta-function, $x = (1+\tilde{p}^2)^{-1}$, and $\tilde{p} = \frac{p_{\rm min}}{m_{\rm p}~c}$.

The CRp interact hadronically with the thermal ambient gas and produce pions, provided their momentum exceeds the kinematic threshold $p_{\rm thr} = 0.78 \mbox{ GeV }c^{-1}$ of the reaction. The neutral pions decay into ${\gamma }$-rays while the charged pions decay into secondary electrons (and neutrinos). Only the CRp population above the kinematic threshold $p_{\rm thr}$ is visible through its decay products in ${\gamma }$-rays and thus constrained by this work while its lower energy part can not in general be limited by considering hadronic interactions only.

An analytic formula describing the omnidirectional (i.e. integrated over $4~\pi$ solid angle) differential ${\gamma }$-ray source function resulting from $\pi^0$-decay is given in Pfrommer & Enßlin (2003):

 \begin{displaymath} q_\gamma(\vec{r},E_\gamma)~{\rm d}E_\gamma~{\rm d}V\simeq \s... ...^{-\delta} \right]^{-\alpha/\delta}{\rm d}E_\gamma~{\rm d}V, \end{displaymath} (4)

where $n_{\rm N}(\vec{r})$ is the target nucleon density in the ICM assuming primordial element composition. The formalism also includes the detailed physical processes at the threshold of pion production like the velocity distribution of CRp, momentum dependent inelastic CRp-p cross section, and kaon decay channels. The shape parameter $\delta$ and the effective cross section $\sigma_{\rm pp}$ depend on the spectral index of the ${\gamma }$-ray spectrum according to
  
                                       $\displaystyle \delta = 0.14 ~\alpha^{-1.6} + 0.44\qquad\mbox{and}$ (5)
    $\displaystyle \sigma_{\rm pp} = 32 \cdot \left(0.96 + {\rm e}^{4.4 ~-~ 2.4~\alpha}\right)\mbox{ mbarn}.$ (6)

Provided the CRp population has a power-law spectrum, the relation of the hadronic ${\gamma }$-ray flux $\mathcal{F}_\gamma$ in different energy bands can easily be found using the analytic formulae for the integrated ${\gamma }$-ray source density (Pfrommer & Enßlin 2003),
 
$\displaystyle \frac{\mathcal{F}_\gamma \left(E_1 < E_\gamma < E_2\right)}{ \mat... ...\right)} = \frac{A_\gamma\left(E_1, E_2\right)}{A_\gamma\left(E_3, E_4\right)},$     (7)
$\displaystyle \mbox{where~~} A_\gamma(E_i,E_j) = \left[\mathcal{B}_x\left(\frac{\alpha + 1}{2~\delta}, \frac{\alpha - 1}{2~\delta}\right)\right]_{x_i}^{x_j}$     (8)
$\displaystyle \mbox{and~~} x_{i,j} = \left[1+\left(\frac{m_{\pi^0}~c^2}{2~E_{i,j}} \right)^{2~\delta}\right]^{-1}\cdot$     (9)

Here we introduced the abbreviation [f(x)]x1x2 = f(x2) - f(x1). This relation for hadronic ${\gamma }$-ray fluxes is independent of any specific model of CRp spatial distribution as long as the same physical mechanism governs the CRp distribution in both energy bands.

Using the HEGRA ${\gamma }$-ray flux for M 87 of $\mathcal{F}_\gamma (E > 730 \mbox{ GeV}) = 9.6 \times 10^{-13}~ \gamma\mbox{ cm}^{-2} \mbox{ s}^{-1}$(Aharonian et al. 2003), and requiring the expected ${\gamma }$-ray flux above 100 MeV to be smaller than the EGRET upper limit $\mathcal{F}_\gamma (E > 100 \mbox{ MeV}) = 2.18 \times 10^{-8}~ \gamma\mbox{ cm}^{-2} \mbox{ s}^{-1}$(Reimer et al. 2003), we are able to constrain the CRp spectral index to $\alpha~<~2.275$. For this calculation, we assume a constant CRp spectral index $\alpha_{\rm GeV}^{\rm TeV}$ extending from the GeV to TeV energy regime. In the case of steeper spectra in the TeV region, the CRp spectrum needs to be bent in a convex fashion or to exhibit a low energy cutoff in order to meet the requirement imposed by EGRET.

   
3 Spatial distributions of CRp within the ICM

In the following, we introduce three models for the spatial distribution of CRp within the ICM. The origin of the CRp population is not specified in the first two models, but the CRp may be accelerated by shock waves of cluster mergers, accretion shocks, or result from supernova driven galactic winds.

The isobaric model assumes that the average kinetic CRp energy density $\varepsilon_{{\rm CRp}} (\vec{r})$ is a constant fraction of the thermal energy density $\varepsilon_{\rm th} (\vec{r})$ of the ICM

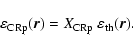\begin{displaymath}\varepsilon_{\rm CRp}(\vec{r}) = X_{\rm CRp}~ \varepsilon_{\rm th}(\vec{r}). \end{displaymath} (10)

The thermal energy density $\varepsilon_{\rm th} (\vec{r})$ is obtained from a spherically symmetric temperature profile (Pfrommer & Enßlin 2003) and a double $\beta$-model of electron densities adapted to X-ray observations of M 87 (Matsushita et al. 2002).

The adiabatic model assumes the CRp population to be originally isobaric to the thermal population but to become adiabatically compressed during the formation of the cooling flow without relaxing afterwards:

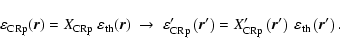\begin{displaymath}\varepsilon_{\rm CRp}(\vec{r}) = X_{\rm CRp}~\varepsilon_{\rm... ...eft(\vec{r}'\right)~\varepsilon_{\rm th}\left(\vec{r}'\right). \end{displaymath} (11)

Adiabatic compression of CRp changes the scaling parameter  $X_{\rm CRp}$ to

 \begin{displaymath} X'_{\rm CRp}(\vec{r}) = X_{\rm CRp}~\left(\frac{n'_{\rm e}(... ...rm cluster}} {T_{\rm e}'(\vec{r})} \right)^{(\alpha + 2)/3} , \end{displaymath} (12)

where $T_{\rm cluster}$ denotes the electron temperature in the outer region of Virgo. The last step assumes hydrostatic equilibrium of the gas during this transition.

Diffusion of CRp away from M 87: The relativistic plasma bubbles produced by M 87 likely contain relativistic protons, which can partly escape into the thermal ICM (Enßlin 2003). Most of the CRp that have been injected into the cluster center are either diffusively transported into the surrounding ICM or form relativistic bubbles which rise in the gravitational potential of the cluster due to buoyant forces (Churazov et al. 2001, and references therein).

Momentum dependent CRp diffusion in a turbulent magnetic field with a Kolmogorov-type spectrum on small scales would result in spectral steepening and therefore would violate the limits on the spectral index $\alpha_{\rm GeV}^{\rm TeV}$ obtained in Sect. 2 provided there is no sharp upper cutoff in the CRp spectrum. Thus we adopt for simplicity the scenario of passive advective transport of CRp in a turbulent flow with a diffusion coefficient $\kappa$ independent of momentum. The time-dependent CRp distribution function reads for short (duration $\Delta t$) point-like injection with CRp injection rate $Q(p_{\rm p})$ at time t=0

 \begin{displaymath} f_{\rm p}(r,p_{\rm p},t) = \frac{Q(p_{\rm p})~ \Delta t}{(4... ...ppa)^{3/2}}~ \exp\left(-\frac{r^2}{4~ t~ \kappa}\right)\cdot \end{displaymath} (13)

In a quasi-stationary situation, which is a valid approximation for timescales longer than the typical CRp diffusion timescale in the case of a stationary or short-term intermittent CRp source, the integrated CRp distribution function is approximately given by

 \begin{displaymath} f_{\rm p}(r,p_{\rm p}) = \int_0^t \!{\rm d}t' f_{\rm p}\lef... ...appa}~ {\rm erfc}\left(\frac{r}{\sqrt{4~ t~ \kappa}}\right), \end{displaymath} (14)

where ${\rm erfc}(x)$ denotes the complementary error function which is responsible for the spatial cutoff at the characteristic diffusion scale $R_{\rm diff} = \sqrt{6~ t~\kappa}$. While assuming a power-law shaped  $Q(p_{\rm p})$, the CRp distribution of Eq. (1) can be written within the framework set by this model as

 \begin{displaymath} f_{\rm p}(r,p_{\rm p}) = \frac{\tilde{n}_{{\rm CRp},0}~ c... ...) \left(\frac{p_{\rm p}~c}{\mbox{GeV}}\right)^{-\alpha}\cdot \end{displaymath} (15)

Following Pfrommer & Enßlin (2003), the averaged CRp luminosity of M 87 can be estimated to be
 
$\displaystyle \frac{L_{\rm CRp}}{\kappa} = \frac{4\pi~m_{\rm p}c^2~ \tilde{n}_{... ...t)^{1-\alpha}\! \mathcal{B}\left(\frac{\alpha-2}{2}, \frac{3-\alpha}{2}\right).$     (16)

Considering an energy dependent mean-free-path for diffusion would require fine-tuning of this model while simultaneously enlarging the accessible parameter space. While the resulting profiles should only be slightly affected by this change, this could possibly alter our conclusions concerning the normalization $\tilde{n}_{{\rm CRp},0}$. However, this would only add further uncertainty to $\tilde{n}_{{\rm CRp},0}$ which already depends on two unknown parameters, the lifetime of the source t and the diffusion coefficient $\kappa$.

   
4 Modeled ${\gamma }$-ray profiles

The ${\gamma }$-ray flux profiles $f_\gamma(\vec{r}_\bot, E_\gamma > E_{\rm thr})$ are obtained by integrating the ${\gamma }$-ray source function $q_\gamma(\vec{r},E_\gamma)$ of Eq. (4) above a threshold energy $E_{\rm thr}$, successively projecting and convolving the spherically symmetric profiles with the point spread function (PSF) of HEGRA, ${\rm PSF}(\vec{r}_\bot) = \exp[-\vec{r}^2_\bot/(2~ \sigma^2)] /(2~ \pi~ \sigma^2)$. Resolution studies based on observations of the Crab Nebula with HEGRA indicate a width of $\sigma = 0.08\hbox {$^\circ $ }$, assuming a differential spectral index of $\alpha = 2.7$ (Daum et al. 1997). However, for flatter power-law spectra being preferred by our hadronic ${\gamma }$-ray model (see Sect. 2), the width will be smaller owing to increasing mean ${\gamma }$-ray energy. This leads to an increase of ${\gamma }$-ray induced particles of the air shower and therefore better quality of shower reconstruction according to a smaller relative Poissonian error. For a rough estimate, we rescaled the width of the PSF using the scaling of the mean ${\gamma }$-ray energies above the instrumental threshold, yielding $\sigma = 0.05\hbox {$^\circ $ }$ with $\alpha = 2.2$.


  \begin{figure} \par\resizebox{8.4cm}{!}{ \includegraphics[clip]{Fe271_f1.eps}}\end{figure} Figure 1: a) Modeled ${\gamma }$-ray surface flux profiles $f_\gamma (r_\bot )$ as function of impact parameter $r_\bot $ in our three different models for the spatial distribution of the CRp population. They are normalized by comparing the integrated ${\gamma }$-ray flux above 730 GeV to HEGRA data of M 87 within the innermost two data points. b) Comparison of detected to integrated ${\gamma }$-ray flux $\mathcal{F}_\gamma(\theta^2)$ within the central aperture and the innermost annuli for different models of spatial CRp distribution as well as two different widths of the PSF. The thick black lines correspond to $\sigma = 0.05\hbox {$^\circ $ }$ whereas the thin grey lines are calculated for $\sigma = 0.08\hbox {$^\circ $ }$. The vertical dashed line separates the data from the noise level at a position corresponding to $r_\bot = 37.5$ kpc.
Open with DEXTER

Table 1: Consequences for the CRp scaling parameter $X_{\rm CRp}$ and $\tilde{n}_{{\rm CRp},0}$ by comparing the integrated flux above 730 GeV to HEGRA data of the radio galaxy M 87 within the innermost two data points corresponding to $\theta = 0.126\hbox {$^\circ $ }$. The spatial distribution of CRp is given by the isobaric, the adiabatic, and the diffusion model, respectively (see Sect. 3). In the first two cases the values are calculated for a CRp population with and without lower cutoff $p_{\rm min}$ while in the latter case two different lifetimes of the source have been considered. Note that the averaged CRp luminosity $L_{\rm CRp}$ scales with $\kappa_{29} = \kappa/(10^{29} \mbox{ cm}^2 \mbox{ s}^{-1})$.

The line-of-sight integration was performed out to a radius of $R_{\rm max} \simeq 3$ Mpc which corresponds to the characteristic distance where the $\beta$-model of electron densities is no longer applicable due to accretion shocks of the cluster. The resulting ${\gamma }$-ray profiles are shown in Fig. 1. The normalization of the surface fluxes depends on the assumed scaling between CRp and thermal energy density, which is fixed by comparing the integrated flux above 730 GeV to the innermost two ${\gamma }$-ray flux data points of HEGRA (Aharonian et al. 2003) corresponding to $\theta = 0.126\hbox {$^\circ $ }$ or $r_\bot = 37.5$ kpc. Although there are distinct morphological differences visible in the three spatial CRp models, the convolution with the PSF leads to very similar profiles for the expected HEGRA ${\gamma }$-ray counts within the uncertainties. To demonstrate this, we compare the integrated ${\gamma }$-ray flux $F_\gamma(E_\gamma > E_{\rm thr})$ for different annuli of equal solid angle elements centered on the source to the HEGRA data for the two different widths of the PSF discussed above (Fig. 1).

5 Consequences for the CRp population in M 87

By employing the technique described in Sect. 4, we explore the consequences for the CRp scaling parameters $X_{\rm CRp}$ and $\tilde{n}_{{\rm CRp},0}$ in the particular models of CRp spatial distributions. The resulting values, shown in Table 1, have been obtained using a PSF of width $\sigma = 0.05\hbox {$^\circ $ }$, however there are no significant changes in $X_{\rm CRp}$ for $\sigma = 0.08\hbox {$^\circ $ }$. The values of the CRp scaling parameter $X_{\rm CRp}$ inferred from M 87 are comparable to the one in our Galaxy, which is of order unity (Parker 1969). Since the HEGRA ${\gamma }$-ray measurements probe only the central region of the Virgo cluster which is dominated by the elliptical radio galaxy M 87, a composition of ISM and ICM is observed, potentially mixed by convective motion within the cooling flow (Churazov et al. 2001). Therefore we expect $X_{\rm CRp}$ to be smaller than in our Galaxy, but significantly higher than upper limits obtained in nearby cooling flow clusters, which are less than 20% (Pfrommer & Enßlin 2003).

In the case of diffusion of CRp away from M 87, we are able to constrain the averaged CRp luminosity $L_{\rm CRp}$ of the central AGN by assuming a plausible value for the diffusion coefficient $\kappa$. The inferred values are of the same order as instantaneous jet power estimates of M 87, $L_{\rm jet} \simeq 10^{43}\mbox{ erg}\mbox{ s}^{-1}$ (Bicknell & Begelman 1996). Thus, we limit a combination of diffusion efficiency of CRp into the ambient thermal medium and average jet power by this approach.

Because of the scaling behavior of $X_{\rm CRp}$ in the isobaric and adiabatic models, we quantify the influence of a lower cutoff $p_{\rm min}$ on the population of CRp due to Coulomb interactions in the plasma by taking the ratio of CRp energy densities $\varepsilon_{\rm CRp}(p_{\rm min})$ with and without lower cutoff (see Eq. (3)). Such a cutoff yields lower values of $X_{\rm CRp}$ and therefore smaller contribution to the ${\gamma }$-ray flux in the energy range of EGRET once the CRp momentum cutoff $p_{\rm min}$ exceeds the kinematic threshold $p_{\rm thr} = 0.78 \mbox{ GeV }c^{-1}$ of the hadronic interaction. Thus, cooling of the CRp population allows for steeper power-law distributions.

6 Synchrotron emission by hadronic CRe

Following the formalism described in Pfrommer & Enßlin (2003), we compute the synchrotron emission of CRe resulting from hadronic CRp interactions. Integrating the expected radio surface brightness profiles over the solid angle element corresponding to the ${\gamma }$-ray emission region and assuming magnetic fields of the form $B(r) = 10~ \mu\mbox{G}~ [n_{\rm e}(r) /n_{\rm e}(0)]^{0.5}$, we expect hadronic synchrotron fluxes $F_\nu = F_0~ [\nu/(1.4 \mbox{ GHz})]^{-\alpha/2}$, where F0 = 11 Jy and 16 Jy for $\alpha = 2.1$ and 2.2. However, this hypothetical radio mini-halo is outshone by the synchrotron emission of the relativistic jet, which shows a flux level of $F_{1.4~{\rm GHz}} = (220\pm 11)$ Jy (Kuehr et al. 1981). The hadronic radio surface profiles which are characterized by a smooth morphology fall short by roughly one order of magnitude even at impact parameters of some arcminutes compared to observed profiles of Rottmann et al. (1996).

7 Predictions for next generation Cerenkov telescopes and GLAST

There are three different scenarios predicting ${\gamma }$-ray emission from objects like M 87, namely processed radiation of the relativistic outflow, dark matter annihilation, and the hadronic scenario. The predictions of these types of model differ predominantly in morphology, existing time-variability, and spectral signatures. The radio galaxy M 87 which is well within the field of view of the next generation Cerenkov telescopes MAGIC[*], HESS[*], and VERITAS[*] should therefore serve as a unique source for testing these scenarios. While the angular resolution of these telescopes is comparable to the previously attained resolution, the flux sensitivities have strongly improved. These developments should allow for ${\gamma }$-ray spectroscopy by Cerenkov experiments in the near future, providing the opportunity of scrutinizing existing time-variation, and thus being able to constrain different ${\gamma }$-ray emission scenarios.

The LAT instrument onboard GLAST[*] will complement this research to even lower energies ranging from 20 MeV up to 300 GeV. Given a CRp population described by a single power-law spectral index $\alpha=\alpha_{\rm GeV}^{\rm TeV}$ extending from the GeV to TeV energy regime as well as a CRp scaling parameter $X_{\rm CRp}$ of Table 1, we calculated the expected integrated ${\gamma }$-ray flux above 20 MeV. In the isobaric model, the ${\gamma }$-ray flux estimates are $\mathcal{F}_\gamma(>20 \mbox{ MeV}) /(\gamma \mbox{ cm}^{-2} \mbox{ s}^{-1})= 6.0\times 10^{-8}, 1.3\times 10^{-7}$, and $2.3 \times 10^{-7}$ for $\alpha_{\rm GeV}^{\rm TeV} = 2.1,$ 2.2, and 2.27, respectively. This is well above the sensitivity limit of GLAST. The energy resolution of GLAST will even provide the possibility to disentangle the pion decay induced signature from inverse Compton emission of high-energetic electrons or positrons due to the energy resolution which is better than 10% and is sufficient to resolve the pion decay induced peak in the ${\gamma }$-ray spectrum.

8 Conclusion

Using TeV ${\gamma }$-ray detections of M 87 by the HEGRA collaboration, it is for the first time possible to constrain the CRp population of an elliptical galaxy. By comparing to EGRET upper limits on the ${\gamma }$-ray emission, we constrain the CRp spectral index $\alpha_{\rm GeV}^{\rm TeV}$, provided the ${\gamma }$-ray emission is of hadronic origin and the population is described by a single power-law ranging from the GeV to TeV energy regime.

By investigating three different models for the spatial distribution of the CRp and applying those to realistic electron density and temperature profiles obtained from X-ray observations, we calculate ${\gamma }$-ray flux profiles resulting from hadronic CRp interactions with the thermal ambient gas using an analytic formalism (Pfrommer & Enßlin 2003). After convolving with the HEGRA point spread function, we compare the integrated ${\gamma }$-ray flux $F_\gamma(E_\gamma > 730 \mbox{ GeV})$ for different annuli of equal solid angle elements centered on the source. Based on the available data we find good morphological agreement of all our models with these HEGRA Cerenkov observations.

In the isobaric and adiabatic CRp model, the consequences for the CRp scaling parameter $X_{\rm CRp}$ drawn from normalization of our ${\gamma }$-ray flux profiles to HEGRA observations yield slightly smaller values when comparing to our Galaxy with $X_{\rm CRp}\sim 1$, depending on the CRp spectral index. This is because of the sensitivity of the observations to both the ISM of M 87 and the ICM of the central cooling flow region of Virgo, where $X_{\rm CRp}\lesssim 0.2$ (Pfrommer & Enßlin 2003). Especially for $\alpha_{\rm GeV}^{\rm TeV} \simeq 2.1$ or lower momentum cutoffs of the CRp population due to Coulomb cooling processes, we obtain smaller contributions of CRp pressure to the ambient medium. By exploring our diffusion model and comparing our constraints on the CRp luminosity $L_{\rm CRp}$ to mechanical jet power estimates of M 87, we show the ability of TeV ${\gamma }$-ray observations to constrain a combination of energy fraction of CRp escaping from the radio plasma and average jet power of the AGN.

The expected radio emission by hadronically produced CRe is roughly one order of magnitude smaller compared to the synchrotron emission of the jet. Therefore it will be a challenge for future radio observations to disentangle the hadronic and jet emission components. Future Cerenkov observations should at least be able to severely constrain the parameter space of different ${\gamma }$-ray emission scenarios. Finally, by investigating the ${\gamma }$-ray flux in the energy regime of GLAST, we predict values which should allow to scrutinize this hadronic model in contrast to other scenarios providing us with the possibility of entering a new era of precision high energy cluster physics.

Acknowledgements
We wish to thank Matthias Bartelmann, Sebastian Heinz, Francesco Miniati, Björn Malte Schäfer, Olaf Reimer, and an anonymous referee for carefully reading the manuscript and their constructive remarks.

References


Copyright ESO 2003