A&A 407, L73-L77 (2003)
DOI: 10.1051/0004-6361:20031088
C. Pfrommer - T. A. Enßlin
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str.1, Postfach 1317, 85741 Garching, Germany
Received 27 May 2003 / Accepted 15 July 2003
Abstract
We examine the cosmic ray proton (CRp) population within the giant
elliptical galaxy M 87 using the TeV ![]() -ray detection of the HEGRA
collaboration. In our scenario, the
-ray detection of the HEGRA
collaboration. In our scenario, the ![]() -rays are produced by decaying
pions which result from hadronic CRp interactions with thermal gas of the
interstellar medium of M 87. By comparing the
-rays are produced by decaying
pions which result from hadronic CRp interactions with thermal gas of the
interstellar medium of M 87. By comparing the ![]() -ray emission to upper
limits from EGRET, we constrain the spectral index of the CRp population to
-ray emission to upper
limits from EGRET, we constrain the spectral index of the CRp population to
![]() within our scenario. Both the
expected radial
within our scenario. Both the
expected radial ![]() -ray profile and the required amount of CRp
support this hadronic scenario. The accompanying radio mini-halo of
hadronically originating cosmic ray electrons is outshone by the synchrotron
emission of the relativistic jet of M 87 by one order of magnitude. According
to our predictions, the future GLAST mission should allow us to test this
hadronic scenario.
-ray profile and the required amount of CRp
support this hadronic scenario. The accompanying radio mini-halo of
hadronically originating cosmic ray electrons is outshone by the synchrotron
emission of the relativistic jet of M 87 by one order of magnitude. According
to our predictions, the future GLAST mission should allow us to test this
hadronic scenario.
Key words:
![]() -rays: theory - cosmic rays -
galaxies: individual: M 87 - galaxies: cooling flows - intergalactic medium -
radiation mechanisms: non-thermal
-rays: theory - cosmic rays -
galaxies: individual: M 87 - galaxies: cooling flows - intergalactic medium -
radiation mechanisms: non-thermal
The giant elliptical galaxy M 87 is an intensively studied object in
our direct extragalactic vicinity situated at a distance of 17 Mpc
(Neilsen & Tsvetanov 2000). The announcement of the TeV ![]() -ray detection
of M 87 at a 4-
-ray detection
of M 87 at a 4-![]() significance level by the HEGRA collaboration
(Aharonian et al. 2003) using imaging atmospheric Cerenkov techniques
was the first discovery of TeV
significance level by the HEGRA collaboration
(Aharonian et al. 2003) using imaging atmospheric Cerenkov techniques
was the first discovery of TeV ![]() -rays from a radio galaxy with a jet
whose axis forms a relatively large angle with the line of sight of roughly
30
-rays from a radio galaxy with a jet
whose axis forms a relatively large angle with the line of sight of roughly
30![]() -35
-35![]() (Bicknell & Begelman 1996). On the basis of the limited
event statistics the detected emission is inconclusive whether it originates
from a point source or an extended source. Despite testing for burstlike
behavior of M 87 no time variation of the TeV
(Bicknell & Begelman 1996). On the basis of the limited
event statistics the detected emission is inconclusive whether it originates
from a point source or an extended source. Despite testing for burstlike
behavior of M 87 no time variation of the TeV ![]() -ray flux has been found.
This detection provides the unique possibility for probing different
-ray flux has been found.
This detection provides the unique possibility for probing different
![]() -ray emission scenarios and thus provides new astrophysical insight
into high energy phenomena of this class of objects.
-ray emission scenarios and thus provides new astrophysical insight
into high energy phenomena of this class of objects.
In the literature, there are three different types of model predicting
![]() -ray emission from objects like M 87: In the first scenario, the
GeV/TeV
-ray emission from objects like M 87: In the first scenario, the
GeV/TeV ![]() -ray emission is generated by the active galactic nucleus
(AGN), and possibly related to processed radiation of the relativistic outflow
(Dermer et al. 1997). Particularly, inverse Compton (IC) scattering of
cosmic microwave background photons off electrons within the jet which have
been directly accelerated or reaccelerated as well as the Synchrotron Self
Compton scenario could lead to
-ray emission is generated by the active galactic nucleus
(AGN), and possibly related to processed radiation of the relativistic outflow
(Dermer et al. 1997). Particularly, inverse Compton (IC) scattering of
cosmic microwave background photons off electrons within the jet which have
been directly accelerated or reaccelerated as well as the Synchrotron Self
Compton scenario could lead to ![]() -ray emission
(Bai & Lee 2001). Secondly, dark matter annihilation or decay
processes could be another conceivable source of
-ray emission
(Bai & Lee 2001). Secondly, dark matter annihilation or decay
processes could be another conceivable source of ![]() -ray emission, such as
the hypothetical neutralino annihilation (Baltz et al. 2000). Finally,
hadronic cosmic ray proton (CRp) interactions with the thermal ambient gas
would produce pion decay induced
-ray emission, such as
the hypothetical neutralino annihilation (Baltz et al. 2000). Finally,
hadronic cosmic ray proton (CRp) interactions with the thermal ambient gas
would produce pion decay induced ![]() -rays as well as inverse Compton and
synchrotron emission by secondary cosmic ray electrons (CRe)
(Vestrand 1982). These processes are possible due to the long
lifetimes of CRp comparable to the Hubble time (Völk et al. 1996),
long enough to diffuse away from the production site and to maintain their
distribution throughout the cluster volume. Because of the strong dependence
of this hadronic process on particle density, the giant radio galaxy M 87,
located inside the central cooling flow region of the Virgo cluster,
is expected to be a major site of
-rays as well as inverse Compton and
synchrotron emission by secondary cosmic ray electrons (CRe)
(Vestrand 1982). These processes are possible due to the long
lifetimes of CRp comparable to the Hubble time (Völk et al. 1996),
long enough to diffuse away from the production site and to maintain their
distribution throughout the cluster volume. Because of the strong dependence
of this hadronic process on particle density, the giant radio galaxy M 87,
located inside the central cooling flow region of the Virgo cluster,
is expected to be a major site of ![]() -ray emission (Pfrommer & Enßlin 2003).
-ray emission (Pfrommer & Enßlin 2003).
This work uses the hadronic scenario to model the resulting ![]() -ray
emission. Thus it probes the CRp population by the recent TeV
-ray
emission. Thus it probes the CRp population by the recent TeV ![]() -ray
observations yielding either an upper limit or a detection on the CRp
population, provided this scenario applies. However, this approach only
constrains the CRp within the central region of intracluster medium (ICM) of
the Virgo cluster which is dominated by the interstellar medium (ISM) of the
radio galaxy M 87. In the following, we use the term ICM for both. It should be
emphasized that this hadronic scenario predicts stationary
-ray
observations yielding either an upper limit or a detection on the CRp
population, provided this scenario applies. However, this approach only
constrains the CRp within the central region of intracluster medium (ICM) of
the Virgo cluster which is dominated by the interstellar medium (ISM) of the
radio galaxy M 87. In the following, we use the term ICM for both. It should be
emphasized that this hadronic scenario predicts stationary ![]() -ray
emission and will be ruled out if the emission is found to be time-variable
(barring the existence of a second component). This, however, would result in
even tighter constraints on the CRp population owing to the absence of
inescapably accompanying
-ray
emission and will be ruled out if the emission is found to be time-variable
(barring the existence of a second component). This, however, would result in
even tighter constraints on the CRp population owing to the absence of
inescapably accompanying ![]() -ray emission.
-ray emission.
The differential number density distribution of a CRp population can be
described by a power-law in momentum ![]() ,
,
If the CRp population within the cooling flow region had time to loose energy
by means of Coulomb interactions in the plasma (Gould 1972),
the low energy part of the spectrum would be modified. This can be treated
approximately by imposing a lower momentum cutoff
The CRp interact hadronically with the thermal ambient gas and produce pions,
provided their momentum exceeds the kinematic threshold
![]() of the reaction. The neutral pions decay into
of the reaction. The neutral pions decay into
![]() -rays while the charged pions decay into secondary electrons (and
neutrinos). Only the CRp population above the kinematic threshold
-rays while the charged pions decay into secondary electrons (and
neutrinos). Only the CRp population above the kinematic threshold
![]() is visible through its decay products in
is visible through its decay products in ![]() -rays and
thus constrained by this work while its lower energy part can not in general be
limited by considering hadronic interactions only.
-rays and
thus constrained by this work while its lower energy part can not in general be
limited by considering hadronic interactions only.
An analytic formula describing the omnidirectional (i.e. integrated over
![]() solid angle) differential
solid angle) differential ![]() -ray source function resulting from
-ray source function resulting from
![]() -decay is given in Pfrommer & Enßlin (2003):
-decay is given in Pfrommer & Enßlin (2003):
Using the HEGRA ![]() -ray flux for M 87 of
-ray flux for M 87 of
![]() (Aharonian et al. 2003), and requiring the expected
(Aharonian et al. 2003), and requiring the expected ![]() -ray flux above
100 MeV to be smaller than the EGRET upper limit
-ray flux above
100 MeV to be smaller than the EGRET upper limit
![]() (Reimer et al. 2003), we are able to constrain the CRp spectral index to
(Reimer et al. 2003), we are able to constrain the CRp spectral index to
![]() .
For this calculation, we assume a constant CRp spectral
index
.
For this calculation, we assume a constant CRp spectral
index
![]() extending from the GeV to TeV energy
regime. In the case of steeper spectra in the TeV region, the CRp spectrum
needs to be bent in a convex fashion or to exhibit a low energy cutoff in order
to meet the requirement imposed by EGRET.
extending from the GeV to TeV energy
regime. In the case of steeper spectra in the TeV region, the CRp spectrum
needs to be bent in a convex fashion or to exhibit a low energy cutoff in order
to meet the requirement imposed by EGRET.
The isobaric model assumes that the average kinetic CRp energy density
![]() is a constant fraction of the thermal energy density
is a constant fraction of the thermal energy density
![]() of the ICM
of the ICM
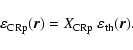 |
(10) |
The adiabatic model assumes the CRp population to be originally isobaric
to the thermal population but to become adiabatically compressed during the
formation of the cooling flow without relaxing afterwards:
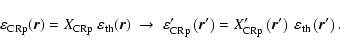 |
(11) |
Diffusion of CRp away from M 87: The relativistic plasma bubbles produced by M 87 likely contain relativistic protons, which can partly escape into the thermal ICM (Enßlin 2003). Most of the CRp that have been injected into the cluster center are either diffusively transported into the surrounding ICM or form relativistic bubbles which rise in the gravitational potential of the cluster due to buoyant forces (Churazov et al. 2001, and references therein).
Momentum dependent CRp diffusion in a turbulent magnetic field with a
Kolmogorov-type spectrum on small scales would result in spectral steepening
and therefore would violate the limits on the spectral index
![]() obtained in Sect. 2 provided
there is no sharp upper cutoff in the CRp spectrum. Thus we adopt for
simplicity the scenario of passive advective transport of CRp in a turbulent
flow with a diffusion coefficient
obtained in Sect. 2 provided
there is no sharp upper cutoff in the CRp spectrum. Thus we adopt for
simplicity the scenario of passive advective transport of CRp in a turbulent
flow with a diffusion coefficient ![]() independent of momentum. The
time-dependent CRp distribution function reads for short (duration
independent of momentum. The
time-dependent CRp distribution function reads for short (duration ![]() )
point-like injection with CRp injection rate
)
point-like injection with CRp injection rate
![]() at time t=0
at time t=0
The ![]() -ray flux profiles
-ray flux profiles
![]() are obtained by integrating the
are obtained by integrating the ![]() -ray source function
-ray source function
![]() of Eq. (4) above a threshold energy
of Eq. (4) above a threshold energy
![]() ,
successively projecting and convolving the spherically
symmetric profiles with the point spread function (PSF) of HEGRA,
,
successively projecting and convolving the spherically
symmetric profiles with the point spread function (PSF) of HEGRA,
![]() .
Resolution studies based on observations of the Crab
Nebula with HEGRA indicate a width of
.
Resolution studies based on observations of the Crab
Nebula with HEGRA indicate a width of
![]() ,
assuming a
differential spectral index of
,
assuming a
differential spectral index of
![]() (Daum et al. 1997).
However, for flatter power-law spectra being preferred by our hadronic
(Daum et al. 1997).
However, for flatter power-law spectra being preferred by our hadronic
![]() -ray model (see Sect. 2), the width will be smaller
owing to increasing mean
-ray model (see Sect. 2), the width will be smaller
owing to increasing mean ![]() -ray energy. This leads to an increase of
-ray energy. This leads to an increase of
![]() -ray induced particles of the air shower and therefore better quality
of shower reconstruction according to a smaller relative Poissonian error. For
a rough estimate, we rescaled the width of the PSF using the scaling of the
mean
-ray induced particles of the air shower and therefore better quality
of shower reconstruction according to a smaller relative Poissonian error. For
a rough estimate, we rescaled the width of the PSF using the scaling of the
mean ![]() -ray energies above the instrumental threshold, yielding
-ray energies above the instrumental threshold, yielding
![]() with
with
![]() .
.
|
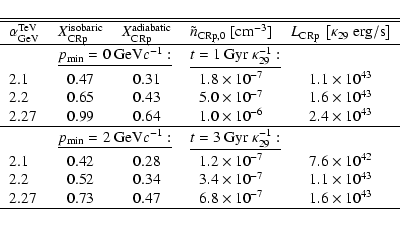
By employing the technique described in Sect. 4, we explore
the consequences for the CRp scaling parameters
![]() and
and
![]() in the
particular models of CRp spatial distributions. The resulting values, shown in
Table 1, have been obtained using a PSF of width
in the
particular models of CRp spatial distributions. The resulting values, shown in
Table 1, have been obtained using a PSF of width
![]() ,
however there are no significant changes in
,
however there are no significant changes in
![]() for
for
![]() .
The values of the CRp scaling parameter
.
The values of the CRp scaling parameter
![]() inferred from
M 87 are comparable to the one in our Galaxy, which is of order unity
(Parker 1969). Since the HEGRA
inferred from
M 87 are comparable to the one in our Galaxy, which is of order unity
(Parker 1969). Since the HEGRA ![]() -ray measurements probe
only the central region of the Virgo cluster which is dominated by the
elliptical radio galaxy M 87, a composition of ISM and ICM is observed,
potentially mixed by convective motion within the cooling flow
(Churazov et al. 2001). Therefore we expect
-ray measurements probe
only the central region of the Virgo cluster which is dominated by the
elliptical radio galaxy M 87, a composition of ISM and ICM is observed,
potentially mixed by convective motion within the cooling flow
(Churazov et al. 2001). Therefore we expect
![]() to be smaller than
in our Galaxy, but significantly higher than upper limits obtained in nearby
cooling flow clusters, which are less than 20% (Pfrommer & Enßlin 2003).
to be smaller than
in our Galaxy, but significantly higher than upper limits obtained in nearby
cooling flow clusters, which are less than 20% (Pfrommer & Enßlin 2003).
In the case of diffusion of CRp away from M 87, we are able to constrain the
averaged CRp luminosity
![]() of the central AGN by assuming a plausible
value for the diffusion coefficient
of the central AGN by assuming a plausible
value for the diffusion coefficient ![]() .
The inferred values are of the
same order as instantaneous jet power estimates of M 87,
.
The inferred values are of the
same order as instantaneous jet power estimates of M 87,
![]() (Bicknell & Begelman 1996). Thus, we limit a
combination of diffusion efficiency of CRp into the ambient thermal medium and
average jet power by this approach.
(Bicknell & Begelman 1996). Thus, we limit a
combination of diffusion efficiency of CRp into the ambient thermal medium and
average jet power by this approach.
Because of the scaling behavior of
![]() in the isobaric and adiabatic
models, we quantify the influence of a lower cutoff
in the isobaric and adiabatic
models, we quantify the influence of a lower cutoff
![]() on the
population of CRp due to Coulomb interactions in the plasma by taking the ratio
of CRp energy densities
on the
population of CRp due to Coulomb interactions in the plasma by taking the ratio
of CRp energy densities
![]() with and without lower
cutoff (see Eq. (3)). Such a cutoff yields lower values of
with and without lower
cutoff (see Eq. (3)). Such a cutoff yields lower values of
![]() and therefore smaller contribution to the
and therefore smaller contribution to the ![]() -ray flux in the
energy range of EGRET once the CRp momentum cutoff
-ray flux in the
energy range of EGRET once the CRp momentum cutoff
![]() exceeds the
kinematic threshold
exceeds the
kinematic threshold
![]() of the hadronic
interaction. Thus, cooling of the CRp population allows for steeper power-law
distributions.
of the hadronic
interaction. Thus, cooling of the CRp population allows for steeper power-law
distributions.
The LAT instrument onboard GLAST![]() will complement this research to even
lower energies ranging from 20 MeV up to 300 GeV. Given a CRp population
described by a single power-law spectral index
will complement this research to even
lower energies ranging from 20 MeV up to 300 GeV. Given a CRp population
described by a single power-law spectral index
![]() extending from the GeV to TeV energy
regime as well as a CRp scaling parameter
extending from the GeV to TeV energy
regime as well as a CRp scaling parameter
![]() of Table 1, we
calculated the expected integrated
of Table 1, we
calculated the expected integrated ![]() -ray flux above 20 MeV. In the
isobaric model, the
-ray flux above 20 MeV. In the
isobaric model, the ![]() -ray flux estimates are
-ray flux estimates are
![]() ,
and
,
and
![]() for
for
![]() 2.2, and 2.27, respectively. This is
well above the sensitivity limit of GLAST. The energy resolution of GLAST will
even provide the possibility to disentangle the pion decay induced signature
from inverse Compton emission of high-energetic electrons or positrons due to
the energy resolution which is better than 10% and is sufficient to resolve
the pion decay induced peak in the
2.2, and 2.27, respectively. This is
well above the sensitivity limit of GLAST. The energy resolution of GLAST will
even provide the possibility to disentangle the pion decay induced signature
from inverse Compton emission of high-energetic electrons or positrons due to
the energy resolution which is better than 10% and is sufficient to resolve
the pion decay induced peak in the ![]() -ray spectrum.
-ray spectrum.
By investigating three different models for the spatial distribution of the CRp
and applying those to realistic electron density and temperature profiles
obtained from X-ray observations, we calculate ![]() -ray flux profiles
resulting from hadronic CRp interactions with the thermal ambient gas using an
analytic formalism (Pfrommer & Enßlin 2003). After convolving with the HEGRA point
spread function, we compare the integrated
-ray flux profiles
resulting from hadronic CRp interactions with the thermal ambient gas using an
analytic formalism (Pfrommer & Enßlin 2003). After convolving with the HEGRA point
spread function, we compare the integrated ![]() -ray flux
-ray flux
![]() for different annuli of equal solid angle elements centered
on the source. Based on the available data we find good morphological agreement
of all our models with these HEGRA Cerenkov observations.
for different annuli of equal solid angle elements centered
on the source. Based on the available data we find good morphological agreement
of all our models with these HEGRA Cerenkov observations.
In the isobaric and adiabatic CRp model, the consequences for the CRp scaling
parameter
![]() drawn from normalization of our
drawn from normalization of our ![]() -ray flux profiles
to HEGRA observations yield slightly smaller values when comparing to our
Galaxy with
-ray flux profiles
to HEGRA observations yield slightly smaller values when comparing to our
Galaxy with
![]() ,
depending on the CRp spectral index. This is
because of the sensitivity of the observations to both the ISM of M 87 and the
ICM of the central cooling flow region of Virgo, where
,
depending on the CRp spectral index. This is
because of the sensitivity of the observations to both the ISM of M 87 and the
ICM of the central cooling flow region of Virgo, where
![]() (Pfrommer & Enßlin 2003). Especially for
(Pfrommer & Enßlin 2003). Especially for
![]() or lower momentum cutoffs of the CRp population due to Coulomb cooling
processes, we obtain smaller contributions of CRp pressure to the ambient
medium. By exploring our diffusion model and comparing our constraints on the
CRp luminosity
or lower momentum cutoffs of the CRp population due to Coulomb cooling
processes, we obtain smaller contributions of CRp pressure to the ambient
medium. By exploring our diffusion model and comparing our constraints on the
CRp luminosity
![]() to mechanical jet power estimates of M 87, we show the
ability of TeV
to mechanical jet power estimates of M 87, we show the
ability of TeV ![]() -ray observations to constrain a combination of energy
fraction of CRp escaping from the radio plasma and average jet power of the
AGN.
-ray observations to constrain a combination of energy
fraction of CRp escaping from the radio plasma and average jet power of the
AGN.
The expected radio emission by hadronically produced CRe is roughly one order
of magnitude smaller compared to the synchrotron emission of the jet.
Therefore it will be a challenge for future radio observations to disentangle
the hadronic and jet emission components. Future Cerenkov observations
should at least be able to severely constrain the parameter space of different
![]() -ray emission scenarios. Finally, by investigating the
-ray emission scenarios. Finally, by investigating the ![]() -ray
flux in the energy regime of GLAST, we predict values which should allow to
scrutinize this hadronic model in contrast to other scenarios providing us with
the possibility of entering a new era of precision high energy cluster physics.
-ray
flux in the energy regime of GLAST, we predict values which should allow to
scrutinize this hadronic model in contrast to other scenarios providing us with
the possibility of entering a new era of precision high energy cluster physics.
Acknowledgements
We wish to thank Matthias Bartelmann, Sebastian Heinz, Francesco Miniati, Björn Malte Schäfer, Olaf Reimer, and an anonymous referee for carefully reading the manuscript and their constructive remarks.