A&A 407, 779-786 (2003)
DOI: 10.1051/0004-6361:20030867
A. G. Tevzadze1 - G. D. Chagelishvili1 - J.-P. Zahn2 - R. G. Chanishvili1 - J. G. Lominadze 1
1 - Center for Plasma Astrophysics, Abastumani
Astrophysical Observatory, Kazbegi 2a, 380060 Tbilisi, Georgia
2 -
LUTH, Observatoire de Paris, 92190 Meudon, France
Received 24 March 2003 / Accepted 3 June 2003
Abstract
This is a sequel to Paper I (Chagelishvili et al. 2003),
where we presented the so-called bypass concept for the onset of
turbulence in shearing flows. According to this concept, which was
worked out during the last decade by the hydrodynamic community
for spectrally stable flows,
vortical perturbations undergo transient growth by extracting
energy from the shear (a linear process), thereby reaching an
amplitude which is sufficient to allow for non-linear interactions
which, by positive feedback, sustain turbulence. In Paper I we described this
transient growth for 2D perturbations in a Keplerian disk; we
showed that their kinematics was the same as in plane-parallel
flow, and thus that they were not modified by the presence of
the Coriolis force. In the present paper, we pursue our goal of
applying the bypass scenario to astrophysical disks: we
investigate the linear dynamics of 3D small-scale vortical
perturbations for single spatial harmonics,
in stably stratified, differentially rotating disks,
again in the framework of a nonmodal analysis. We find that these 3D
perturbations also undergo substantial transient growth,
and that they reach a peak amplitude that is comparable to that
of 2D perturbations, as long as their vertical scale remains of the
order of the azimuthal scale. When the vertical wave-number exceeds
the azimuthal one, the amplification rate is
reduced, but this may be more than compensated to by
the huge Reynolds
number and the high shear rate characterizing astrophysical
Keplerian disks. Whereas in 2D the Coriolis force had no impact
on the transient growth, in 3D this
force somewhat constricts the characteristics of the perturbation
dynamics in disk flows, and the initial transient growth is
followed by some reduction in amplitude.
These differences are quantitative, rather than of fundamental
character.
But the 3D case presents two interesting
novelties. In plane parallel flow, the perturbations do not decay
after their transient amplification, but their energy stays on
a plateau before being dissipated through viscous friction.
More importantly, especially for the astrophysicist,
in disk flow the 3D vortex mode perturbations excite
density-spiral waves, whose energy also settles on a plateau
before viscous dissipation. These local
vortex mode perturbations fit naturally into the bypass concept of
hydrodynamic shear turbulence, which was first developed for
plane-parallel flows. We submit that these perturbations
will also play an important role in the onset and in the maintenance of
turbulence in Keplerian disks.
Key words: accretion, accretion disks - hydrodynamics - instabilities - turbulence
The prevailing explanation for the accretion process that operates in astrophysical disks is that these disks are turbulent, and that the turbulence is responsible for the inflow of matter and the outward transport of angular momentum. The question that then arises is that of the instability that produces this turbulence. This is not a trivial problem, because cylindrical rotation with a Keplerian profile is linearly (spectrally) stable, since angular momentum increases outward and since there is no extremum of vorticity. A solution has been obtained by Balbus & Hawley (1991), who showed that a weak magnetic field allows for a linear instability, called magneto-rotational instability (MRI). Subsequent numerical investigations followed that instability into the nonlinear (turbulent) regime, and they demonstrated that the turbulent transport then proceeds in the right direction. Thus for most astrophysicists, the question is settled: it is the MRI that is responsible for the turbulent transport.
However, this linear instability does not preclude the existence of other instabilities, and it is impossible to predict at the present stage which one is responsible for the actual turbulence in accretion disks. Also, a significant portion of planetary disks is not ionized enough to allow for the MRI. Thus it makes sense to explore alternate routes that may lead to turbulence, and to start with the hydrodynamic case. One is encouraged in this approach by the recent detection of turbulence in a Couette-Taylor experiment (Richard 2001), under conditions similar to those of a Keplerian disk, namely when angular momentum increases and angular velocity decreases outward.
One possible route to hydrodynamic turbulence is through transient growth of small amplitude perturbations, which extract their energy from the shearing flow. In this scenario, the amplitude of some vortex mode perturbations increases algebraically by a linear mechanism until it reaches the level where the nonlinear interactions, by redistributing energy among modes and providing positive feedback, are able to sustain turbulence. This concept, termed "bypass'', has been intensively developed in recent years by the fluid dynamics community; for a bibliography of the subject, we refer the reader to Paper I (Chagelishvili et al. 2003).
In Paper I, we analyzed the dynamics of 2-dimensional
perturbations, with velocity components in the r (radial,
shearwise) and ![]() (azimuthal, streamwise) directions. We
showed that, in the shearing sheet approximation (i.e. in the
limit of large wavenumber, when curvature can be neglected), the
energy equations are identical in the plane-parallel (Cartesian)
case and in the Keplerian case, after suitable renormalization of
the pressure. The same is true for the equations describing the
temporal evolution of a spatial Fourier harmonics (SFH), meaning
that the Coriolis force does not interfer with the linear
dynamics. Singling out a vortex mode with initial wave-vector
(azimuthal, streamwise) directions. We
showed that, in the shearing sheet approximation (i.e. in the
limit of large wavenumber, when curvature can be neglected), the
energy equations are identical in the plane-parallel (Cartesian)
case and in the Keplerian case, after suitable renormalization of
the pressure. The same is true for the equations describing the
temporal evolution of a spatial Fourier harmonics (SFH), meaning
that the Coriolis force does not interfer with the linear
dynamics. Singling out a vortex mode with initial wave-vector
![]() ,
we found that its energy grows by a factor
,
we found that its energy grows by a factor
![]() ,
before decaying and being dissipated
through viscous friction.
,
before decaying and being dissipated
through viscous friction.
The present paper is a sequel to Paper I, extending its results to
3-dimensional perturbations, in a medium that is stably
stratified in the z-direction; this medium can be either an
astrophysical disk or the fluid in a laboratory experiment. When
the linear scale of the perturbation is much smaller in the radial
and azimuthal directions than in the direction perpendicular to
the disk (the vertical direction), i.e.
![]() where H is the half thickness of the disk (or the
pressure scale-height), the problem reduces to the 2D case treated
in Paper I; it was examined by Lominadze et al. (1988) and by
Fridman (1989). On the other hand, Ioannou & Kakouris (2001)
considered the global perturbations where
where H is the half thickness of the disk (or the
pressure scale-height), the problem reduces to the 2D case treated
in Paper I; it was examined by Lominadze et al. (1988) and by
Fridman (1989). On the other hand, Ioannou & Kakouris (2001)
considered the global perturbations where
![]() Here we shall focus on perturbations that are influenced by
the stratification, and that may come closer to isotropy, namely
Here we shall focus on perturbations that are influenced by
the stratification, and that may come closer to isotropy, namely
![]() .
.
A few words about the mathematical method used in our study, namely the non-modal analysis, that allowed for the significant advances achieved in this field during the last decade. After changing the variables from the laboratory to a co-moving frame, this non-modal analysis consists of describing the temporal evolution of the perturbations expanded in spatial Fourier harmonics (SFH), without performing any spectral expansion in time. This approach considerably simplifies the mathematical formalism of the problem and, completed by numerical calculations, it reveals important properties that are overlooked in the classical modal analysis.
In addition to the linear mechanism of non-exponential energy exchange between the shear flow and its perturbations, which is the basis of the bypass concept, a novel phenomenon was discovered through this non-modal approach, namely the linear mechanism of wave excitation by vortices (see Chagelishvili et al. 1997, 2000). Indeed, we shall see below that the 3D vortex mode perturbations, after transient growth, excite density-spiral waves, which then participate also in the dynamical processes in Keplerian disks.
The paper is organized as follows. The physical approximations and the mathematical formalism are introduced in Sect. 2. In Sect. 3 we present the numerical analysis of the linear dynamics of 3D vortex mode perturbations, including the excitation of density-spiral waves. We summarize and discuss the results in Sect. 4.
Consider a differentially rotating thin inviscid hydrodynamic disk
around a central object located at r=z=0. For simplicity the
equilibrium disk is assumed to be non self-gravitating, and to be
locally isothermal, with constant adiabatic sound speed. The
relations between the basic physical characteristics for this
disk, such as angular velocity of rotation ![]() ,
sound speed
,
sound speed
![]() ,
pressure and density scale height (H), local mean
values of pressure (P0) and density
,
pressure and density scale height (H), local mean
values of pressure (P0) and density ![]() ,
are well known
(cf. Ryu & Goodman 1992):
,
are well known
(cf. Ryu & Goodman 1992):
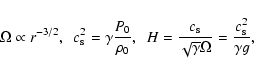 |
(1) |
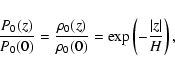 |
(2) |
As in Paper I, we shall write the dynamical equations in the local
co-moving Cartesian frame at the particular point
![]() :
:
| (3) |
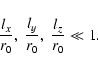 |
(4) |
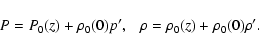 |
(5a) |
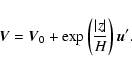 |
(5b) |
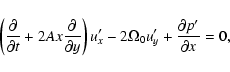 |
(6a) |
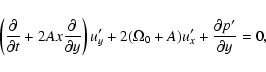 |
(6b) |
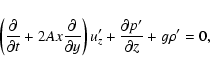 |
(6c) |
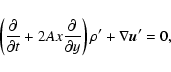 |
(6d) |
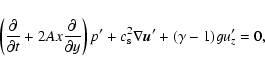 |
(6e) |
![\begin{displaymath}A \equiv {1 \over 2} \left[ r {\partial \Omega \over \partial r}
\right]_{r=r_0}
\end{displaymath}](/articles/aa/full/2003/33/aa3767/img46.gif) |
(7) |
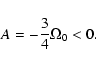 |
(8) |
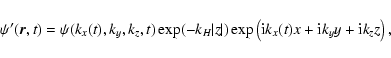 |
(9a) |
| kx(t) = kx(0) - 2A ky t, | (9b) |
Equations (6a)-(6e) and (9a,b) lead to the dynamical equations for
the SFH:
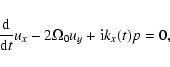 |
(10a) |
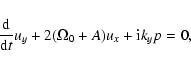 |
(10b) |
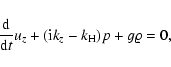 |
(10c) |
![\begin{displaymath}{{\rm d} \over {\rm d} t}\varrho + {\rm i}\left[k_x(t) u_x + {\rm i}
k_y u_y + \left(k_z + {\rm i}k_H\right)u_z\right] = 0 ,
\end{displaymath}](/articles/aa/full/2003/33/aa3767/img56.gif) |
(10d) |
![\begin{displaymath}{{\rm d} \over {\rm d} t}p + {\rm i}c_{\rm s}^2\left[k_x(t) u...
...(k_z + {\rm i} k_H\right) u_z\right] + (\gamma-1) g ~ u_z = 0.
\end{displaymath}](/articles/aa/full/2003/33/aa3767/img57.gif) |
(10e) |
![\begin{displaymath}{\cal I} = \left[ k_y u_x - k_x(t) u_y \right] - 2{\rm i}
(\O...
...rm H}) \over (\gamma-1)g}
\left( p - c_{\rm s}^2 \rho \right).
\end{displaymath}](/articles/aa/full/2003/33/aa3767/img58.gif) |
(11) |
To avoid complex coefficients (and consequently complex physical
variables) in the dynamical equations, we renormalize the perturbed
variables in the following way:
| (12a) |
| s | 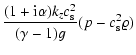 |
||
| = | (12b) |
| (12c) |
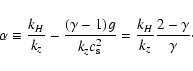 |
(12d) |
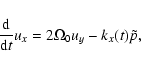 |
(13a) |
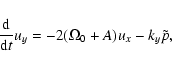 |
(13b) |
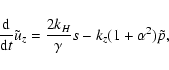 |
(13c) |
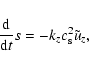 |
(13d) |
![\begin{displaymath}{{\rm d} \over {\rm d} t} {\tilde p} = c_{\rm s}^2 \left[ k_x(t) u_x +
k_y u_y + k_z {\tilde u_z} \right] .
\end{displaymath}](/articles/aa/full/2003/33/aa3767/img71.gif) |
(13e) |
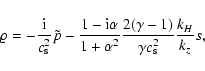 |
(14a) |
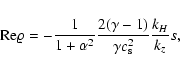 |
(14b) |
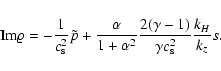 |
(14c) |
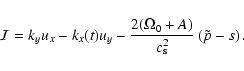 |
(15) |
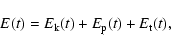 |
(16a) |
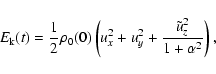 |
(16b) |
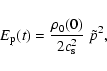 |
(16c) |
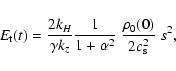 |
(16d) |
Note that the spectral density of the energy would be conserved in
the shearless limit; its variation is due to the velocity shear of
the flow:
The dispersion equation for our system may be obtained in the
shearless limit (A=0) using the full Fourier expansion of the
variables, including time (
![]() ):
):
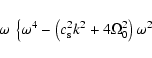
![\begin{displaymath}\left. \quad+ c_{\rm s}^2 \left[ N_{\rm B}^2 k_\perp^2 + 4 \Omega_0^2
\left(k_z^2 + k_H^2\right) \right] \right\} = 0
\end{displaymath}](/articles/aa/full/2003/33/aa3767/img90.gif) |
(18) |
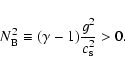 |
(19) |
![\begin{displaymath}\omega_s^2 ={ 1 \over 2} \left( c_{\rm s}^2 k^2 + 4 \Omega_0^...
...^2 k^2 + 4 \Omega_0^2\right)^2 }
\right)^{1 \over 2} \right] ,
\end{displaymath}](/articles/aa/full/2003/33/aa3767/img96.gif) |
(20) |
![\begin{displaymath}\omega_{g\Omega}^2 ={ 1 \over 2} \left( c_{\rm s}^2 k^2 + 4 \...
...^2 k^2 + 4 \Omega_0^2\right)^2 }
\right)^{1 \over 2} \right] ,
\end{displaymath}](/articles/aa/full/2003/33/aa3767/img99.gif) |
(21) |
| (22) |
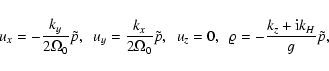
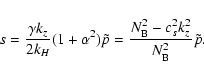 |
(23) |
In previous works, the role of this vortex mode has been often underestimated (cf. Dwarkadas & Balbus 1996; Ryu & Goodman 1992; Goodman & Balbus 2001), or it has been confused with fictitious displacements that arise in the Lagrangian formalism (see Friedman & Schutz 1978). This mode has been ignored also in the recent paper by Goodman and Balbus (2001), which retains only the wave modes.
The velocity shear has a profound effect on the perturbations,
since it permits the extraction of energy from the mean flow (see
Eq. (18)). This results in the transient growth of the vortex mode
perturbations - the subject of our study. This phenomenon has the
same nature as the amplification of vortical perturbations in
parallel flows with constant shear rate (cf. Moffatt 1967;
Criminale & Drazin 1990; Gustavsson 1991; Reddy & Henningsson
1993; Chagelishvili et al. 1994). Moreover, as was found and
described in Chagelishvili et al. (1997, 2000), in relatively
complex flows, where vortex mode coexists with wave modes (which
is the case of Keplerian flow); the velocity shear causes their
linear coupling: vortices are able to excite waves even in the
linear approximation. According to Chagelishvili et al.
(1997), the efficiency of the wave excitation mechanism is
determined by the value of the ratio of the shear parameter to the
frequency of the considered wave mode:
| (24) |
| |
= | 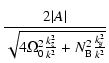 |
|
| = | 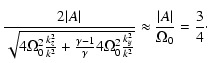 |
(25) |
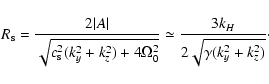 |
(26) |
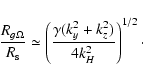 |
(27) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ms3767-f1.eps}
\end{figure}](/articles/aa/full/2003/33/aa3767/Timg116.gif) |
Figure 1:
Dynamics of the perturbation SFH in the Keplerian
disk ( left column) and plane shear flow ( right column). From
top to bottom:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{ms3767-f2.eps}
\end{figure}](/articles/aa/full/2003/33/aa3767/Timg117.gif) |
Figure 2: The same as in Fig. 1, but at kz/ky=1. Initial perturbations correspond to the pure vortex mode with equal vertical and azimuthal length-scale. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{ms3767-f3.eps}
\end{figure}](/articles/aa/full/2003/33/aa3767/Timg118.gif) |
Figure 3: The same as in Fig. 1, but at kz/ky=10. Initial perturbations correspond to the pure vortex mode with length-scale much shorter in the vertical then in the azimuthal direction. |
| Open with DEXTER | |
Equations (13), (14), together with the appropriate initial values, pose the initial value problem describing the dynamics of a perturbation SFH in the Keplerian disk. We solve this system with initial values corresponding to pure vortex mode perturbations. The numerical calculations are performed using the Matlab ODE solver, an explicit Runge-Kutta implementation with the 4(5) pair of Dormand-Prince. Potential vorticity is conserved with an accuracy of 10-7.
Since we are primarily interested in the transient growth of
vortex perturbations in AD and its comparison with the similar
process in plane shear flow, we analyze the dynamics of plane
shear flow in the same manner. For this purpose we set g=0,
kH=0, ![]() ,
,
![]() and A < 0 in Eqs. (13), (14). The evolution of vortex mode SFH, in disk flow and plane
shear flows, are presented in Figs. 1, 2 and 3 for different
ratios of the vertical and azimuthal wave-numbers kz/ky:
0.1,
1, 10; in all cases
kx(0)/ky = - 150. All calculations for
the plane case are carried out with the same kinematic shear
parameter. (When comparing the figures, note that the graphs are
not on the same scale.)
and A < 0 in Eqs. (13), (14). The evolution of vortex mode SFH, in disk flow and plane
shear flows, are presented in Figs. 1, 2 and 3 for different
ratios of the vertical and azimuthal wave-numbers kz/ky:
0.1,
1, 10; in all cases
kx(0)/ky = - 150. All calculations for
the plane case are carried out with the same kinematic shear
parameter. (When comparing the figures, note that the graphs are
not on the same scale.)
The numerical results demonstrate the effect of rotation and
vertical stratification on the transient growth in Keplerian
disks. We see that quasi-2D vortex mode perturbations (i.e. with
![]() )
are amplified by nearly the same factor as in
plane shear flow (Fig. 1). This amplification is slightly less in
the
)
are amplified by nearly the same factor as in
plane shear flow (Fig. 1). This amplification is slightly less in
the
![]() case (Fig. 2), whereas the transient growth is
strongly reduced for vortex mode perturbations with
case (Fig. 2), whereas the transient growth is
strongly reduced for vortex mode perturbations with
![]() (Fig. 3).
(Fig. 3).
But the calculations reveal also a novel linear effect which
accompanies the evolution of vortex mode perturbations in the
Keplerian disk, namely the excitation of density-spiral waves
(![]() modes, or gravito-inertial waves),
which may play an important role in the onset
and in the maintenance of turbulence in AD. For a physical
description of this excitation we refer to Chagelishvili et al.
(1997). The phenomenon is clearly visible in Figs. 1-3, in the
graphs of uz,
modes, or gravito-inertial waves),
which may play an important role in the onset
and in the maintenance of turbulence in AD. For a physical
description of this excitation we refer to Chagelishvili et al.
(1997). The phenomenon is clearly visible in Figs. 1-3, in the
graphs of uz,
![]() and E(t)/E(0). Starting
with a pure the vortex/aperiodic SFH at
kx(0)/ky<0, the
perturbation energy reaches a peak value at time
and E(t)/E(0). Starting
with a pure the vortex/aperiodic SFH at
kx(0)/ky<0, the
perturbation energy reaches a peak value at time
![]() .
After that maximum, the SFH undergoes nearly
periodic oscillations, meaning that the vortex mode excites a
density-spiral wave corresponding to the same SFH; the result is a
mixed vortex-wave SFH.
.
After that maximum, the SFH undergoes nearly
periodic oscillations, meaning that the vortex mode excites a
density-spiral wave corresponding to the same SFH; the result is a
mixed vortex-wave SFH.
While the vortex energy steadily decreases after the maximum, as
in the 2D case considered in Paper I, the wave energy remains
constant, and is responsible for the plateau in the E(t) graphs. (In that respect, the disk case bears some similarity with
the plane case, where the energy also settles on a plateau.) The
plateau energy is more then one order of magnitude lower then the
peak energy. For
kz/ky = 0.1 (Fig. 1) the normalized peak
energy is
![]() (very close to the theoretical
value
(very close to the theoretical
value
![]() derived in Paper I)
and the plateau energy is 10.9. For
kz/ky = 1 (Fig. 2) the peak energy is slightly lower:
derived in Paper I)
and the plateau energy is 10.9. For
kz/ky = 1 (Fig. 2) the peak energy is slightly lower:
![]() ,
whereas that of the plateau is much higher than in the
preceding case:
,
whereas that of the plateau is much higher than in the
preceding case:
![]() .
This indicates that the
excitation of the wave mode is much stronger when
.
This indicates that the
excitation of the wave mode is much stronger when
![]() .
.
Note that in the plane case
![]() is always positive. Since the flux of
angular momentum is determined by
is always positive. Since the flux of
angular momentum is determined by
As it appears, the action of the Coriolis force reduces the rate
of transient amplification and it somewhat changes its character
in 3D. Consider the case kz = ky (Fig. 2). One sees that, in
the plane flow, the SFH energy increases transiently, but tends
monotonically and smoothly to some
![]() when
when
![]() (
(
![]() ). In the disk case, the SFH energy
reaches its peak value
). In the disk case, the SFH energy
reaches its peak value
![]() at kx(t)=0, but after that
it decreases, and settles on a plateau with energy
at kx(t)=0, but after that
it decreases, and settles on a plateau with energy
![]() at a
time where
at a
time where
![]() .
To estimate quantitatively the
effect of rotation, we have to compare
.
To estimate quantitatively the
effect of rotation, we have to compare
![]() with
with
![]() or/and
or/and
![]() .
These quantities are determined by the values
of
kx(0)/ky and kz / ky: substantial transient growth
occurs when kz is less or of the order of ky. Let us
introduce the parameter
.
These quantities are determined by the values
of
kx(0)/ky and kz / ky: substantial transient growth
occurs when kz is less or of the order of ky. Let us
introduce the parameter
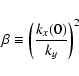 |
(30) |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{ms3767-f4.eps}
\end{figure}](/articles/aa/full/2003/33/aa3767/Timg141.gif) |
Figure 4:
Maximum normalized energy
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ms3767-f5.eps}
\end{figure}](/articles/aa/full/2003/33/aa3767/Timg143.gif) |
Figure 5:
E(t)/E(0) vs. t for the Keplerian disk and plane
cases, for kz = ky and for values of |
| Open with DEXTER | |
Let us analyze the above results in terms of the Reynolds number,
which we define as
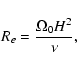 |
(31) |
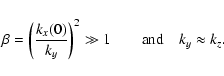 |
(33) |
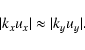 |
(34) |
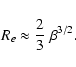 |
(35) |
In the present paper we focused our attention on the transient growth of small scale vortices in stably stratified Keplerian disk flow. For the sake of comparison, the analysis of the disk flow was performed in parallel with that of the non-rotating plane shear flow. Let us recall the main results concerning linear dynamics.
The transient amplification of vortices, together with the
phenomenon of wave excitation by these vortices, appear to be a
promising mechanism leading to the onset of turbulence in
astrophysical disks. These vortex mode perturbations fit
naturally into the recently developed concept of bypass transition
to turbulence for plane smooth shear flows. The detailed
description of the concept was presented in Paper I. Here we only
recall the four basic steps of the bypass scenario:
(i) the
linear "drift" of SFH of the vortex mode in the k-space;
(ii) the transient growth of SFH;
(iii) viscous
dissipation;
(iv) nonlinear processes that close the
feedback loop of the transition by mode mixing and angular
redistribution of SFH in the k-space.
In this scenario the nonlinear processes do not contribute to the energy growth, as they would in genuine nonlinear instability, but they serve to close the loop, providing positive feedback.
In the classical bypass concept, the main contributors to turbulence in shear flows are the vortex mode perturbations. But in Keplerian disks, according to the presented study, after transient growth, vortex mode perturbations are converted into density-spiral waves, and these long-lived waves become ingredients of the system. Hence, most likely, wave-wave nonlinear interactions will contribute significantly to step (iv). Moreover, in 3 dimensions much richer possibilities exist for such interactions than in 2 dimensions, and therefore more opportunities are offered for positive feedback.
To conclude, the linear phase of the bypass concept is now well established, and this scenario appears as a very promising route to turbulence in Keplerian disks. It remains necessary to confirm the existence of positive nonlinear feedback, which is required to sustain turbulence, and this can only be achieved through numerical simulations, performed at high Reynolds number. Thanks to the steady progress of computer performance, this goal should be reached in the not-so-distant future.
Acknowledgements
This work is supported by the International Science and Technology Center grant G-553. G.D.C. would like to acknowledge the hospitality of Observatoire de Paris (LUTH). The authors wish to thank the referee for helpful remarks.