1 - Isaac Newton Institute of Chile, Ministerio de Educacion de Chile, Casilla 8-9, Correo 9, Santiago, Chile
2 - Department of Astronomy, Sofia University and Isaac Newton Institute of Chile Bulgarian Branch, 1164 Sofia, Bulgaria

Abstract
We present new CCD photometry of the Small Magellanic Cloud star cluster Lindsay 1 in UBVI filters. It is the first photometry in U and I filters. We determine the reddening E(B-V)=0.014. Using a variety of metallicity indicators in the optical and the infrared regions we determine a cluster metallicity ${\rm [Fe/H]}_{\rm CG97}=-1.05\pm0.14$ and ${\rm [M/H]}=-0.83\pm0.14$ . We find that Lindsay 1 has an age of 9-10 Gyr.

Key words: galaxies: clusters: general - stars: Hertzsprung-Russell (HR) and C-M diagrams - galaxies: stellar content - galaxies: Magellanic Clouds - galaxies: individual: SMC - galaxies: star clusters

The investigation of the intermediate age star clusters in the Magellanic Clouds is a well-known and powerful tool to test evolutionary theories for combination of masses and metallicities not presented in our Galaxy. Lindsay 1 is one of the brightest clusters in Lindsay's second list of SMC clusters (Lindsay 1958). Several photometric investigations can be found in the literature for this cluster. Gascoigne (1966) presented the first color-magnitude diagram and concluded that there are no blue cluster stars above the plate limit and no horizontal branch stars. He did not discover any variable stars in L 1. Gascoigne (1980) provided photographic CMD to V=21. Later Gascoigne et al. (1981) made a CMD to V 22. The first modern CCD investigation was published by Olszewski et al. (1987). They investigated Lindsay 1 with the CTIO 4-m telescope and the RCA prime focus CCD system. The BV CCD photometry reached below the level of the main-sequence turnoff in the L 1 field. From the morphology structure of the cluster CMD they reported reddening, metal abundance, distance and age.

All these papers are based on BV filters only. The goal of this paper is to present a new analysis of Lindsay 1. We use UBV and I images taken with the 1.3 m Warsaw telescope, Las Campanas Observatory and JHK photometry available in the 2 MASS Second Incremental Data Release catalogue. We determine the reddening, metallicity and age of the cluster.

2 Observations and data reduction

Our analysis is based on a set of "blue" UB and "red" VI CCD frames obtained in October 1999 with the 1.3 m Warsaw telescope, Las Campanas Observatory with the $2048\times2048$ CCD camera. The array scale was $0.417\hbox{$^{\prime\prime}$ }~{\rm pixel}^{-1}$ , giving fields of view of $14\hbox{$^\prime$ }\times 14\hbox{$^\prime$ }$ . Six 600 s and three 1500 s U, nine 120 s and three 360 s B, six 60 s and three 180 s V, and six 90 s and three 120 s I frames were taken in perfect observational conditions with a seeing of about 1 arcsec and a mean airmass around 1.4. After cosmic ray rejection all the frames in each filter were summed into one final image. The stellar photometry was carried out for these summed frames using DAOPHOT/ALLSTAR (Stetson 1993). The instrumental values were then transformed to the standard system using 11 standard stars from Alcaino et al. (1990) in the field of view. We used the "least squares" method to calculate a straight line that best fits the data for these standard stars. The following set of transformation equations is obtained:

$B-V=1.021_{\pm0.016}(b-v)-0.479_{\pm0.017}\hspace{4pt} (\sigma(BV)=0.015)$

$V-I=0.976_{\pm0.013}(v-i)+0.048_{\pm0.013}\hspace{4pt} (\sigma(VI)=0.014)$

$V=0.995_{\pm0.014}v+0.033_{\pm0.023}(B-V)-3.974_{\pm0.025}$
$(\sigma(V)=0.038)$

$U=0.988_{\pm0.015}u-0.076_{\pm0.047}(B-V)-7.321_{\pm0.108}$
$(\sigma(U)=0.044)$

where u,v,b-v,v-i are the instrumental magnitudes and colors and U,V,B-V,V-I are the magnitudes and colors in the standard system. The standard error values for the coefficients are given with small digits after each coefficient. The coefficient uncertainties correspond to the linear fits. The uncertainties of the reported sigma - $\sigma$ refer to the statistical Gaussian distribution of the residuals.

Our final photometric list contains 1688 stars with formal DAOPHOT V and B-V errors less than 0.25 mag. The complete data set is given in Table 1, available in the electronic form of the Journal. The artificial star technique (Stetson & Harris 1988; Stetson 1991a,b) was used to determine the completeness limits of the data. Our photometry is complete at (U, B, V, I) = (20.8, 21.4, 21.3, 20.3) mag. The central region of the cluster is completely resolved and this is the reason why completeness tests depending on the position of the star were not carried out. The comparison with BV photometry of Olszewski et al. (1987) shows à good agreement - the mean differences in colors and magnitudes are: $(B-V)=(B-V)_{\rm O87}+0.008$ and $V = V_{\rm O87}+0.011$ , respectively. The residuals of the measurements of 102 randomly sampled stars brighter than V=22 observed in both studies are plotted in Fig. 1 as a function of the magnitudes and colors derived in the present investigation. As can be seen, no systematic trend is present in the V magnitudes, but there is a slight trend visible in the B-V colors for the redder stars.

$\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{ms3755f1.ps}}\end{figure}$	Figure 1: Comparison of the V magnitudes and B-V colors derived here with the photometry of Olszewski et al. (1987). The comparison is in the sense of this work minus Olszewski et al. (1987).
Open with DEXTER

3 Color-magnitude diagram

3.1 Overall CMD morphology

The field star contamination around Lindsay 1 is small. Nevertheless we decided to decontaminate the cluster's CMD. We used cluster limiting radius r=500 pixels $(r=210\hbox{$^{\prime\prime}$ })$ encircling the most probable cluster members. This area contains cluster stars + SMC field stars. The SMC field stars alone are selected in a circle outside the cluster with the same radius of 500 pixels. The (B-V,V) CMDs of "cluster + field" and "field" are girded and the stars in each box in the two diagrams are counted. Then an equivalent number of stars is removed from the single boxes of the "cluster + field" CMD on the basis of the number of field stars found in the "field" CMD alone (right panel in Fig. 2). This procedure was applied in the field star decontamination of all other CMDs.

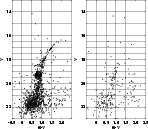$\begin{figure} \par\resizebox{13cm}{!}{\includegraphics{ms3755f2.ps}}\end{figure}$	Figure 2: The (B-V,V) color-magnitude diagram for Lindsay 1 + field stars within $210\hbox {$^{\prime \prime }$ }$ (left panel). The field CMD (right panel) is based on all stars in the area with the same radius outside the cluster.
Open with DEXTER

The (B-V, V) and (V-I, I) CMDs for Lindsay 1, decontaminated as described above, are presented in Fig. 3. L 1 has a well-populated red giant branch extending to V=16.72 and B-V=1.64. There are four brighter stars from the extended giant branch. The brightest of them reaches V=16.40 and B-V=2.11. All these stars are relatively close to the cluster center; they are located above or near the tip of the RGB in all three CMDs, and thus with a great probability they are cluster members. Another definitive features of the CMDs are RGB bump and red horizontal branch (RHB). The bump is located at $V=19.30 \pm 0.05$ and $B-V\approx0.94$ (see Sect. 3.4). The RHB is located at $V=19.35\pm 0.05$ . Its position was determined by averaging the magnitudes of all RHB stars and finding the maximum of the luminosity function in the region of the RHB (RGB stars were removed). The cluster also presents a well-populated subgiant branch (SGB). Our photometry limit is right after the main-sequence turnoff point so that the photometry is not deep enough to outline well the turnoff point. According to Olszewski et al. (1987) it is located at V=22.3 and $B-V\approx0.35$ . Blue CMDs are convenient to separate the asymptotic giant branch stars (AGB) from the RGB stars. We used the (U-V, U) diagram presented in Fig. 4. Our 22 candidates for AGB stars are shown with filled circles in Fig. 3 (panels a and b) and Fig. 4.

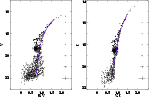$\begin{figure} \par\resizebox{13cm}{!}{\includegraphics{ms3755f3.ps}} \end{figure}$	Figure 3: The (B-V, V) and (V-I, I) CMDs for Lindsay 1. Candidate AGB stars are represented by filled circles. (B-V, V) and (V-I, I) ridgelines are also shown.
Open with DEXTER

Mean ridgelines of the main branches of Lindsay 1 were determined from the (B-V,V), (V-I, V) and (V-I, I) diagrams. All cluster stars were used. The mean ridgelines were determined following the polynomial-fitting technique by Sarajedini (1994). A first rough selection of RGB stars was performed by eye, removing the HB and AGB candidate stars. Polynomial laws in the forms B-V=F(V), V-I=F(V) and V-I=F(I) were used. The stars deviating by more than $2\sigma$ in color from the fitting relation in several iterations were rejected. The standard error of the resulting fit is 0.03. The mean ridgelines of the fainter part of the CMD (V>19mag; upper part of the RGB, and the SGB) were determined by dividing these branches into bins and computing in each bin the average color and magnitude. Table 2 presents the mean points for each branch. In Fig. 3 the CMDs in panels a and b are shown with mean ridgelines.

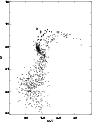$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{ms3755f4.ps}} \end{figure}$	Figure 4: The (U-V, U) CMD for Lindsay 1. Candidate AGB stars are presented with filled circles.
Open with DEXTER

3.2 Reddening

The question of the precise reddening of the cluster is always crucial. Olszewski et al. (1987) adopt E(B-V)=0.03 for L 1. This value can be assumed as an average from the estimation of Mould et al. (1984) - E(B-V)=0.04 and Burstein & Heiles (1982) maps implying a reddening between 0.00 and 0.03 towards L 1. We decided to apply a technique for the simultaneous determination of metallicity and reddening (SRM) using the (V-I,V) CMD proposed in Sarajedini (1994). The shape of the cluster RGB in our case cannot be represented in a satisfactory way by a second or a third order polynomial so we used a higher-order polynomial and applied the "numerical solution" of this method. The results are $E(V-I)=0.01\pm 0.02$ and ${\rm [Fe/H]=-1.31\pm0.16}$ . The SRM method was applied in the (B-V, V) plane, too. Following Ferraro et al. (1999) we derived an identical reddening $E(B-V)=0.014\pm0.02$ but different value for the metallicity ${\rm [Fe/H]=-0.84\pm0.13}$ . The reddening is similar within the errors to the reddening obtained in Alcaino et al. (1990) - 0.03, but differs from the value of 0.06, obtained in Mighell et al. (1998). A possible explanation is the difference in the polynomial approximations of RGB, or slight difference in the zeropoints of both photometries, or a combination of them.

3.3 Metallicity

The shape of the RGB in a GSC is sensitive to the abundance of heavy elements and insensitive to the helium and the age. The metallicity of the cluster can be determined from the slope of the RGB. A complete set of RGB parameters and metallicity indicators in the BV plane (both in the Carretta & Gratton 1997 (CG97) [Fe/H] scale and in the corresponding global [M/H] scale) are presented in Ferraro et al. (1999). The "global metallicity" [M/H] assumes an $\alpha$ -element enhancement of $[\alpha/{\rm Fe}] = 0.28$ for ${\rm [Fe/H]} < -1$ . For L 1 we used the mean ridgelines to measure the following RGB parameters: $(B-V)_{0,\rm g}$ , defined as the RGB color at the HB level; the two RGB slopes, S_2.0 and S_2.5, defined as the slope of the line connecting the intersection of the RGB and HB with the points along the RGB located, respectively, 2.0 and 2.5 mag brighter than the HB; $\Delta V_{1.1}$ , $\Delta V_{1.2}$ and $\Delta V_{1.4}$ - defined as magnitude differences between the HB and RGB at the fixed colors (B-V)₀ = 1.1, 1.2 and 1.4 mag. The corresponding metallicity values are given in Table 3. The derived metallicity, based on an average over the values of the slope of the RGB in the (B-V,V) diagram, is ${\rm [Fe/H]}_{\rm CG97}=-0.82\pm0.16$ and ${\rm [M/H]}=-0.70\pm0.16$ on the CG97 scale.

As an additional metallicity indicator we used the intrinsic (V-I)₀ color of the giant branch at an absolute I magnitude of M_I=-3.0 calibrated in Da Costa & Armandroff (1990). The adopted true distance modulus to the SMC was (m-M)₀=18.85. The derived abundance in the Zinn & West (1984) scale is ${\rm [Fe/H]}_{\rm ZW84}=-1.24\pm0.17$ .

There is a cross-identification for 94 of the RGB stars with the JHK photometry given in the 2 MASS Second Incremental Data Release Catalogue. The photometric data for these stars are given in Table 4, available in the electronic form of the Journal. This fact allowed us to investigate the RGB behavior in the JK and VK planes also and to use the calibrators of the metallicity in the infrared. The (J-K,K) and (V-K,K) CMDs for the brightest RGB stars are given in Fig. 5. Ferraro et al. (2000) presented a set of RGB parameters and metallicity indicators in the IR. We used the mean ridgelines given in Table 2 to measure the following RGB parameters: (J-K)₀^-3, (J-K)₀^-4, (J-K)₀^-5, (J-K)₀^-5.5, (V-K)₀^-3, (V-K)₀^-4, (V-K)₀^-5, (V-K)₀^-5.5, defined as intrinsic (J-K)₀ and (V-K)₀ colors of the RGB measured at different absolute K magnitudes ( M_K=-3,-4,-5,-5.5). The metallicity values derived in this way are given in Table 3. The final metallicity, based on an average over these values, is ${\rm [Fe/H]}_{\rm CG97}=-1.06\pm0.16$ and ${\rm [M/H]}=-0.88\pm0.17$ on the CG97 scale.

Recently Ivanov & Borissova (2002) presented an investigation of the behavior of the RGBs of a sample of 27 Galactic globular clusters. This research was based on data from the Two Micron All Sky Survey. They derived calibrations for the RGB slope, zero point and tip. Using their Eq. (4) we derived ${\rm [Fe/H]}_{\rm CG97}=-1.01\pm0.15$ .

The derived final metallicity, based on the weighted mean of the above defined values as listed in Table 3 (for additional details see the next paragraph), is ${\rm [Fe/H]}_{\rm CG97}=-1.05\pm0.14$ and ${\rm [M/H]}=-0.83\pm0.14$ .

3.4 Red Giant Branch

The so-called RGB bump, corresponding to a point in the evolution of RGB stars, was first predicted by theoretical models and subsequently observed in many clusters. Lindsay 1 presents a clearly-outlined RGB bump. The break of the slope of the cumulative RGB luminosity function is a common technique used to locate the RGB bump (Fusi Pecci et al. 1990). The observed differential and integrated luminosity functions for the Lindsay 1 RGB are shown in Fig. 6. As can be seen, the RGB bump of L 1 is very well defined at $V=19.30 \pm 0.05$ .

The magnitude difference between the RGB luminosity function "bump" and the HB level, $\Delta V_{\rm HB}^{\rm bump}$ is a metallicity indicator recalibrated by Ferraro et al. (1999). Using their calibration equations we calculated ${\rm [Fe/H]}_{\rm CG97}=-1.09\pm0.10$ and ${\rm [M/H]}=-0.91\pm0.10$ .

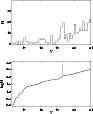$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{ms3755f6.ps}} \end{figure}$	Figure 6: The observed differential (top) and integrated (bottom) luminosity function for the Lindsay 1 RGB.
Open with DEXTER

Bono et al. (2001) defined the new parameter $R_{\rm bump}$ as the ratio between the number of stars in the bump region $V_{\rm bump}\pm 0.4$ and the number of RGB stars in the interval $V_{\rm bump}+0.5< V < V_{\rm bump}+1.5$ . In our case we calculated $R_{\rm bump}=0.58\pm 0.04$ . Comparison of the $R_{\rm bump}$ parameter with the cluster sample of Bono et al. (2001) shows its normal location with respect to the other clusters in this sample. This suggests that the L 1 bump has not been affected by the occurrence of noncanonical deep mixing that might affect the chemical composition around a H-burning shell during the early evolution of L 1 red giants.

The field star contamination around Lindsay 1 is sparse and the central region of the cluster is completely resolved. These facts allowed us to obtain reliable ratios: $R=N_{\rm HB}/N_{\rm HB}$ ; $R'=N_{\rm HB}/N_{\rm R+A}$ where $\rm R+A$ indicates RGB plus AGB stars; $R1=N_{\rm AGB}/N_{\rm RGB}$ ; and $R2=N_{\rm AGB}/N_{\rm HB}$ . We adopted the Zoccali et al. (2000) definition of $N_{\rm RGB}$ as RGB stars brighter than the zero-age HB (ZAHB, which is approximately equivalent to the lower envelope of the red HB). The ratios are: $R=1.33\pm 0.10$ , $R'=1.09\pm 0.8$ , $R1=0.21\pm 0.05$ and $R2=0.16\pm 0.04$ .

4 Age determination

Two main methods are currently used to measure relative ages: the so-called vertical method (based on the difference between TO luminosity with respect to HB level), and the horizontal method, which is based on the accurate determination of the color difference $\delta(B-V)_{\rm TO}^{\rm RGB}$ between the base of the RGB and the TO. Unfortunately our photometry is not deep enough to apply neither of these methods. Sarajedini et al. (1995) proposed an age indicator for globular clusters with predominately red HBs based on the color difference, d_(B-V), between the mean color of the red HB (clump) and the RGB at the level of the HB. We measured $d_{(B-V)}=0.172\pm0.007$ which given an age of $9\pm1$ Gyr for Lindsay 1. We used a metallicity value of ${\rm [Fe/H]}=-1.05$ , obtained in this work. The derived age value is between the ages obtained in Sarajedini et al. (1995), of 7.7 Gyr and in Olszewski et al. (1987), of 10-12 Gyr. It is important to note that the curve representing the predictions of the synthetic horizontal branch model for 9 Gyr, plotted in Fig. 4 of Sarajedini et al. (1995) is vertical and the metallicity dependence is weak.

On the basis of the RGB and HB models, Ferraro et al. (1999) derived the relation for the RGB bump location (their Eq. (3)). This location depends on the metallicity and $\log t_9$ , where t₉ is the age in Gyr. Using this equation and adopting the true distance modulus to SMC (m-M)₀=18.85 we calculated the age of about 10 Gyr.

5 Summary

In this paper, we have provided the moderately deep new UBVI CCD photometry of SMC star cluster Lindsay 1. This is also the first CCD photometry in U and I filters. The (U-V, U), (B-V, V) and (V-I, I) CMDs, decontaminated of the field stars, was constructed. Applying two different methods, we determined the reddening E(B-V)=0.014. Using a variety of metallicity indicators in the optical and the infrared regions we have found a final cluster metallicity ${\rm [Fe/H]}_{\rm CG97}=-1.05\pm0.14$ and ${\rm [M/H]}=-0.83\pm0.14$ . This value is about 0.3 dex higher than the commonly accepted ${\rm [Fe/H]}=-1.35$ . We have found that Lindsay 1 has an age of 9-10 Gyr which cannot differ from other estimations.

The SMC star cluster Lindsay 1

First UI photometric study

1 Introduction