We present results from an investigation of the clustering evolution of field galaxies between a redshift of
A&A 407, 855-868 (2003)
DOI: 10.1051/0004-6361:20030992
S. Phleps - K. Meisenheimer
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
Received 15 November 2002 / Accepted 25 June 2003
Abstract
We present results from an investigation of the clustering evolution
of field galaxies between a redshift of ![]() and the present
epoch. The current analysis relies on a sample of
and the present
epoch. The current analysis relies on a sample of ![]() 3600 galaxies from the Calar Alto Deep Imaging
Survey (CADIS). Its multicolor classification and redshift
determination is reliable up to
3600 galaxies from the Calar Alto Deep Imaging
Survey (CADIS). Its multicolor classification and redshift
determination is reliable up to
![]() .
The redshift distribution extends to
.
The redshift distribution extends to ![]() ,
with
formal errors of
,
with
formal errors of
![]() .
Thus the amplitude
of the three-dimensional correlation function can be estimated by
means of the projected correlation function
.
Thus the amplitude
of the three-dimensional correlation function can be estimated by
means of the projected correlation function
![]() .
The validity
of the deprojection was tested on the Las Campanas Redshift Survey
(LCRS), which also serves as a "local'' measurement. We developed a
new method to overcome the influence of redshift errors on
.
The validity
of the deprojection was tested on the Las Campanas Redshift Survey
(LCRS), which also serves as a "local'' measurement. We developed a
new method to overcome the influence of redshift errors on
![]() .
We parametrise the evolution of the clustering strength with redshift by
a parameter q, the values of which give directly the deviation of the evolution
from the global Hubble flow:
.
We parametrise the evolution of the clustering strength with redshift by
a parameter q, the values of which give directly the deviation of the evolution
from the global Hubble flow:
![]() .
From a subsample of bright galaxies we
find
.
From a subsample of bright galaxies we
find
![]() (for
(for
![]() ,
,
![]() ),
),
![]() (for
(for
![]() ,
,
![]() ), and
), and
![]() (for
(for
![]() ,
,
![]() ), that is a significant
growth of the clustering strength between z=1 and the present epoch.
From linear theory of dark matter clustering growth one would only expect q=-2for a flat high-density model. Moreover, we establish that the measured clustering
strength depends on galaxy type: galaxies with early type SEDs
(Hubble type: E0 to
Sbc) are more strongly clustered at redshifts
), that is a significant
growth of the clustering strength between z=1 and the present epoch.
From linear theory of dark matter clustering growth one would only expect q=-2for a flat high-density model. Moreover, we establish that the measured clustering
strength depends on galaxy type: galaxies with early type SEDs
(Hubble type: E0 to
Sbc) are more strongly clustered at redshifts ![]() than later types. The evolution of the amplitude of the two-point
correlation function for these "old'' galaxies is much slower
(
than later types. The evolution of the amplitude of the two-point
correlation function for these "old'' galaxies is much slower
(
![]() for
for
![]() ,
,
![]() ).
Since the evolution of the clustering of bright and early type galaxies
seems to converge to the same value in the local universe, we conclude
that the apparent strong evolution of clustering among all bright
galaxies is dominated by the effect that weakly clustered starburst
galaxies which are common at high redshifts
).
Since the evolution of the clustering of bright and early type galaxies
seems to converge to the same value in the local universe, we conclude
that the apparent strong evolution of clustering among all bright
galaxies is dominated by the effect that weakly clustered starburst
galaxies which are common at high redshifts
![]() have dimmed
considerably since then. Thus the true clustering of massive galaxies
is better followed by the early types. This provides both a natural
explanation for the seemingly conflicting results of previous studies and
accords with the absence of "faint blue galaxies'' in the local universe.
have dimmed
considerably since then. Thus the true clustering of massive galaxies
is better followed by the early types. This provides both a natural
explanation for the seemingly conflicting results of previous studies and
accords with the absence of "faint blue galaxies'' in the local universe.
Key words: cosmology: large scale structure of Universe - galaxies: evolution
First systematic analyses of the distribution of galaxies and clusters did not occur before galaxy catalogues with large numbers of objects were drawn up - the first analyses of the clustering properties of galaxies were based on the Shane-Wirtanen, the Zwicky catalogue, and the catalogue of Abell clusters, and the results are outlined in a number of fundamental papers by Peebles (and co-workers) (Peebles 1973,1974; Peebles & Hauser 1974; Hauser & Peebles 1973; Peebles & Groth 1975; Peebles 1975).
Only a few years later the CfA survey was completed (Davis & Peebles 1983; Davis et al. 1982), and the analysis brought a distribution to light, which was amazingly inhomogeneous - filaments, sheets, walls and large voids emerged, and it became clear that the local universe is in fact far from homogeneous.
The local universe has later been studied using the largest catalogues available today, the Las Campanas Redshift Survey (Shectman et al. 1996), the Sloan Digital Sky Survey (York et al. 2000; Stoughton et al. 2002), and the 2dFGRS (Colless et al. 2001).
It was shown by a number of authors that in the local universe Galaxies are biased
tracers of mass, i.e. older galaxies are much more strongly
clustered than young, starforming galaxies, bright galaxies are more
strongly clustered than faint galaxies
(Loveday et al. 1995; Norberg et al. 2002; Willmer et al. 1998; Zehavi et al. 2002a; Guzzo et al. 1997; Iovino et al. 1993; Davis & Geller 1976; Santiago & Strauss 1992; Hermit et al. 1996; Lahav & Saslaw 1992).
The exploration of the
processes which lead to the different clustering of
galaxies of different Hubble types can help us to understand the
interaction between the pure structure growth of the dissipationless
dark matter component and the development of the baryonic matter into
stars and galaxies. In principle, the evolution of the correlation
function can also place constraints on the cosmological parameters
which determine the geometry and dynamics of our universe.
Detailed observations of the evolution of the clustering strength of different
galaxy types have to be compared to model predictions (large N-body
simulations including starformation and feedback,
to disentangle dark matter clustering growth and the evolution of the
bias. A first attempt was made by Kauffmann et al. (1999a,b), who carried
out a semianalytic simulation of galaxy
formation and clustering in a ![]() CDM cosmology, in which they analysed the
clustering evolution of
galaxies with differing luminosity, color, morphology and
starformation rate.
CDM cosmology, in which they analysed the
clustering evolution of
galaxies with differing luminosity, color, morphology and
starformation rate.
For the investigation of structure formation and evolution,
measurements of the clustering strength extending to redshifts of
![]() are required. Until
recently, there have been only few ways to study the large
scale structure of the universe at redshifts
are required. Until
recently, there have been only few ways to study the large
scale structure of the universe at redshifts ![]() ,
see for example
Le Fèvre et al. (1996), and Carlberg et al. (2000). Not only the
shallow depths of most surveys, but also missing redshift information
or too small number statistics have limited the possibilities of
analysing the data with regard to structure formation. In general,
two different types of surveys have to be distinguished - large
angle surveys, which are limited to relatively bright apparent
magnitudes, and pencil-beam surveys with small, but very deep fields.
Furthermore, one can distinguish between surveys that contain
only a small number of galaxies, but with very accurate redshift
information (deduced from spectroscopy), and surveys that provide
huge catalogues of galaxies, but without or with rather limited
redshift information. The Calar Alto Deep Imaging Survey (CADIS), see Hippelein et al. (2003),
is a deep
pencil-beam survey, the output of which at
present is a catalogue of
,
see for example
Le Fèvre et al. (1996), and Carlberg et al. (2000). Not only the
shallow depths of most surveys, but also missing redshift information
or too small number statistics have limited the possibilities of
analysing the data with regard to structure formation. In general,
two different types of surveys have to be distinguished - large
angle surveys, which are limited to relatively bright apparent
magnitudes, and pencil-beam surveys with small, but very deep fields.
Furthermore, one can distinguish between surveys that contain
only a small number of galaxies, but with very accurate redshift
information (deduced from spectroscopy), and surveys that provide
huge catalogues of galaxies, but without or with rather limited
redshift information. The Calar Alto Deep Imaging Survey (CADIS), see Hippelein et al. (2003),
is a deep
pencil-beam survey, the output of which at
present is a catalogue of
![]() classified objects to
classified objects to
![]() .
Around 4000 of these galaxies have reasonably
well determined redshifts inferred by means of multicolour
methods (
.
Around 4000 of these galaxies have reasonably
well determined redshifts inferred by means of multicolour
methods (
![]() ). This unique data base provides the
possibility to investigate
the evolution of galaxy clustering from a redshift of
). This unique data base provides the
possibility to investigate
the evolution of galaxy clustering from a redshift of
![]() to the
present epoch.
to the
present epoch.
Usually, structure is described in terms of n-point correlation
functions, the simplest of which is the two-point correlation
function. In practice, computing the three-dimensional real-space
two-point correlation function requires very accurate
distances. Peculiar velocities as well as redshift errors distort the
redshift-space relation, and by making the distribution more
Poisson-like, increase the noise. Different methods have been
developed to overcome these problems. If no
redshifts are available at
all, it is possible to obtain information about the three dimensional
distribution of galaxies by deprojecting the two-dimensional angular
correlation function ![]() .
If peculiar velocities are not
negligible, or the data suffer from large redshift errors, one can use
the deprojection of the projected correlation function
(Davis & Peebles 1983) to deduce
the clustering strength of the three-dimensional distribution. This
method is used to derive the results of the present paper.
.
If peculiar velocities are not
negligible, or the data suffer from large redshift errors, one can use
the deprojection of the projected correlation function
(Davis & Peebles 1983) to deduce
the clustering strength of the three-dimensional distribution. This
method is used to derive the results of the present paper.
This paper is structured as follows: The Calar Alto Deep Imaging Survey and the data used for the analysis
are described in Sect. 2. An introduction into the
fundamental principles of three- and two-dimensional correlation
functions and the deprojection method used in this paper is given in
Sect. 3. In Sect. 4 we investigate the
evolution of the galaxy clustering from a redshift of ![]() to
today, in Sect. 5 the results are discussed.
to
today, in Sect. 5 the results are discussed.
The seven CADIS fields measure
![]() each and are
located at high Galactic latitudes to avoid dust absorption and
reddening. In all fields the total flux on the IRAS 100
each and are
located at high Galactic latitudes to avoid dust absorption and
reddening. In all fields the total flux on the IRAS 100 ![]() m maps
is less than 2 MJy/sr which corresponds to
EB-V <0.07. Therefore
we do not have to apply any colour corrections. As a second selection
criterion the fields should not contain any star brighter than
m maps
is less than 2 MJy/sr which corresponds to
EB-V <0.07. Therefore
we do not have to apply any colour corrections. As a second selection
criterion the fields should not contain any star brighter than
![]() in the CADIS R band. In fact the brightest star
in the four fields under consideration has an R magnitude of
in the CADIS R band. In fact the brightest star
in the four fields under consideration has an R magnitude of
![]() .
Furthermore, the fields are chosen such that there
should be at least one field with an altitude of at least
.
Furthermore, the fields are chosen such that there
should be at least one field with an altitude of at least ![]() above the horizon of Calar Alto being observable at any time
throughout the year. Among the CADIS fields three equatorial fields
allow follow-up observations with the VLT.
above the horizon of Calar Alto being observable at any time
throughout the year. Among the CADIS fields three equatorial fields
allow follow-up observations with the VLT.
All observations were performed on Calar Alto, Spain, in the optical wavelength region with the focal reducers CAFOS (Calar Alto Faint Object Spectrograph) at the 2.2 m telescope and MOSCA (Multi Object Spectrograph for Calar Alto) at the 3.5 m telescope. For the NIR observations the Omega Prime camera was used.
In each filter, a set of 5 to 15 individual exposures was taken. The images of one set were then bias subtracted, flatfielded and cosmic corrected, and then coadded to one deep sumframe. This basic data reduction steps were done with the MIDAS software package in combination with the data reduction and photometry package MPIAPHOT (developed by H.-J. Röser and K. Meisenheimer).
The measured counts are translated into physical fluxes outside the terrestrial atmosphere by using a set of "tertiary'' spectrophotometric standard stars which were established in the CADIS fields, and which are calibrated with secondary standard stars (Oke 1990; Walsh 1995) in photometric nights.
From the physical fluxes, magnitudes and colour indices (an object's brightness ratio in any two filters, usually given in units of magnitudes) can be calculated. The CADIS magnitude system is described in detail in Wolf et al. (2001c) and Fried et al. (2001).
With a typical seeing of
![]() a morphological star-galaxy
separation becomes unreliable at
a morphological star-galaxy
separation becomes unreliable at ![]() where
already many galaxies appear compact. Quasars have point-like
appearance, and thus can not be distinguished from stars by
morphology. Therefore a classification scheme was developed, which is
based solely on template spectral energy distributions (SEDs)
(Wolf et al. 2001c,b). The classification algorithm basically
compares the observed colours of each object with a colour library of
known objects. This colour library is assembled from observed spectra
by synthetic photometry performed on an accurate representation of the instrumental
characteristics used by CADIS.
where
already many galaxies appear compact. Quasars have point-like
appearance, and thus can not be distinguished from stars by
morphology. Therefore a classification scheme was developed, which is
based solely on template spectral energy distributions (SEDs)
(Wolf et al. 2001c,b). The classification algorithm basically
compares the observed colours of each object with a colour library of
known objects. This colour library is assembled from observed spectra
by synthetic photometry performed on an accurate representation of the instrumental
characteristics used by CADIS.
The spectral library for galaxies is derived
from the mean averaged spectra of Kinney et al. (1996). From
these, a grid
of 20 100 redshifted spectra was formed covering
redshifts from z=0 to z=2 in steps of
![]() and 100
different intrinsic SEDs, from old populations
to starbursts (SED=1 corresponds to an E0 galaxy, whereas SED=100is a starburst galaxy).
and 100
different intrinsic SEDs, from old populations
to starbursts (SED=1 corresponds to an E0 galaxy, whereas SED=100is a starburst galaxy).
Using the minimum variance estimator (for details see Wolf et al. 2001c), each
object is assigned a type
(star - QSO - galaxy), a redshift (if it is
not classified as star), and an SED. The formal errors in this
process depend on magnitude and type of the
object. For the faintest galaxies (I>22) they are of the order of
![]() ,
and
,
and
![]() ,
respectively.
,
respectively.
Note that we do not apply any morphological star/galaxy separation or use other criteria. The classification is purely spectrophotometric.
Details about the performance and reliability of the classification are given in Wolf et al. (2001c), and Wolf et al. (2001b).
Rest-frame luminosities can be estimated directly combining the redshift information and flux measurements in the 16 filters; we do not apply evolutionary corrections.
Four CADIS fields have been fully analysed so far (for coordinates see
Table 1). We
identified 4540 galaxies with ![]() .
Out of these, 3626 are located in
the redshift range
.
Out of these, 3626 are located in
the redshift range
![]() ,
where we have analysed their
clustering properties. The number of galaxies per field is given
in Table 1, together with the number of bright galaxies
(
,
where we have analysed their
clustering properties. The number of galaxies per field is given
in Table 1, together with the number of bright galaxies
(
![]() ).
).
Table 1:
The coordinates of the four fields investigated so far,
and the number of galaxies per field, ![]() and
and
![]() ,
also given is the number of bright galaxies (
,
also given is the number of bright galaxies (
![]() )
in this redshift and apparent magnitude range.
)
in this redshift and apparent magnitude range.
![\begin{figure}
\par\includegraphics[angle=270,width=7.6cm,clip]{ms3311figure1.ps}
\end{figure}](/articles/aa/full/2003/33/aa3311/Timg68.gif) |
Figure 1: Redshift distribution galaxies with I<23 in the four CADIS fields. The "smoothed'' redshift distribution can be described by a Gaussian. The dotted lines indicate the redshift range, in which the clustering properties of the galaxies are analysed. |
| Open with DEXTER | |
We can further divide our sample into different subsamples and investigate the clustering properties of galaxies of different SED types, or different absolute restframe B magnitudes.
Since CADIS is a pencil beam survey with a field of view of
![]() ,
it is of little use to estimate the correlation
length r0 from the measurement, because it is well outside the
measured range of distances. Instead we will deduce the amplitude
of
,
it is of little use to estimate the correlation
length r0 from the measurement, because it is well outside the
measured range of distances. Instead we will deduce the amplitude
of ![]() at a comoving separation of
r=1 h-1 Mpc.
at a comoving separation of
r=1 h-1 Mpc.
Throughout this work correlation functions are determined by using
the estimator invented
by Landy & Szalay (1993):
Random errors of ![]() can be calculated from Poisson statistics (Baugh 1996):
can be calculated from Poisson statistics (Baugh 1996):
![\begin{displaymath}\sigma_{{\rm Poisson}}=\sqrt{\frac{(1+\xi(r))}{[DD]}},
\end{displaymath}](/articles/aa/full/2003/33/aa3311/img80.gif) |
(4) |
The real space two-point correlation function can only be calculated directly, if redshift information is available with very high precision, and if peculiar velocities are negligible. This is definitely not the case for the multicolour data of CADIS. However, it is possible to derive the parameters by inverting two-dimensional distributions.
If ![]() is assumed to be a power law (Eq. (2)),
the correlation length r0 of the three-dimensional distribution can be
calculated.
is assumed to be a power law (Eq. (2)),
the correlation length r0 of the three-dimensional distribution can be
calculated.
The disadvantage of this method is that the inversion is highly dependent on the redshift selection function assumed for the survey, which is not a direct observable. Any method which makes direct use of the measured redshifts, like the projected correlation function, gives much more robust results.
For small angles
![]() .
The projected correlation function is defined as
.
The projected correlation function is defined as
![\begin{displaymath}r_{\rm p}=\left[d_{\rm A}(i)+d_{\rm A}(j)\right]\tan(\theta_{ij}/2),
\end{displaymath}](/articles/aa/full/2003/33/aa3311/img92.gif) |
(6) |
If
![]() ,
then Eq. (5) yields
,
then Eq. (5) yields
With
![]()
| (9) |
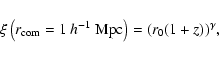 |
(11) |
The mean galaxy density is determined from the observed galaxy counts in each
field, which does not necessarily represent the the true density (Groth & Peebles 1977).
The estimator will be on average biased low with respect to the
true correlation by a constant amount
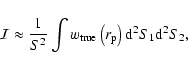 |
(14) |
![\begin{displaymath}\frac{{\rm d}\pi}{{\rm d}z}=\frac{c}{H_0}\bigg[(1+z)\left[\Om...
...\Lambda)(1+z)^2+\Omega_\Lambda\right]^{\frac{1}{2}}\bigg]^{-1}
\end{displaymath}](/articles/aa/full/2003/33/aa3311/img118.gif) |
(20) |
In order to determine
![]() we use the two-dimensional correlation
amplitude estimated according to Landy & Szalay (1993),
we use the two-dimensional correlation
amplitude estimated according to Landy & Szalay (1993),
![]() in the following:
in the following:
The choice of the integration limit ![]() in Eq. (18) or Eq. (23) is
somewhat arbitrary. To capture the bulk of the correlation signal,
the integration limits should exceed the
redshift separation corresponding to the
correlation length r0, i.e. be larger than the redshift corresponding to
the pairwise velocity dispersion, and of course they have to be larger
than the uncertainty
in the redshift determination.
in Eq. (18) or Eq. (23) is
somewhat arbitrary. To capture the bulk of the correlation signal,
the integration limits should exceed the
redshift separation corresponding to the
correlation length r0, i.e. be larger than the redshift corresponding to
the pairwise velocity dispersion, and of course they have to be larger
than the uncertainty
in the redshift determination.
These requirements set lower limits to the value of ![]() .
But
how large a
.
But
how large a ![]() should be chosen? Very large values of
should be chosen? Very large values of ![]() might more completely integrate the correlation signal, but they do
so at the cost of considerably increased noise, for two reasons:
First, the larger the separation of two galaxies along
the line of sight, the more meaningless (in terms of true distance)
the projected separation perpendicular to the line of sight
becomes. Second, in the extreme case that a pair of galaxies
is separated by physical distances
might more completely integrate the correlation signal, but they do
so at the cost of considerably increased noise, for two reasons:
First, the larger the separation of two galaxies along
the line of sight, the more meaningless (in terms of true distance)
the projected separation perpendicular to the line of sight
becomes. Second, in the extreme case that a pair of galaxies
is separated by physical distances ![]() along the line of
sight, it is most likely not correlated at all, since the correlation
function decreases very fast with distance. Nevertheless, such pairs can display a
very small projected separation and would therefore be regarded as
strongly correlated.
along the line of
sight, it is most likely not correlated at all, since the correlation
function decreases very fast with distance. Nevertheless, such pairs can display a
very small projected separation and would therefore be regarded as
strongly correlated.
In order to find the appropriate integration limits for our sample, we used the Las
Campanas Redshift Survey, in the following LCRS. The LCRS is
described in detail by Shectman et al. (1996). The survey
has a median redshift of
![]() ,
and
therefore can be regarded as "local''; the
mean error in redshift is
,
and
therefore can be regarded as "local''; the
mean error in redshift is
![]() ,
that is
,
that is
![]() km s-1.
km s-1.
We calculated the projected correlation function of
the six LCRS stripes for increasing integration limits ![]() ,
fitted the amplitudes at
,
fitted the amplitudes at
![]() (the fit was
done in the range
(the fit was
done in the range
![]() Mpc (
Mpc (
![]() )
to make
sure we fit where the signal to noise is high) and then calculated the
weighted mean of the six stripes. Also the choice of
)
to make
sure we fit where the signal to noise is high) and then calculated the
weighted mean of the six stripes. Also the choice of
![]() kpc allows the most direct comparison with the CADIS data,
where we fit the amplitude at
kpc allows the most direct comparison with the CADIS data,
where we fit the amplitude at
![]() kpc (at the mean
redshift of the survey (
kpc (at the mean
redshift of the survey (![]() )
this corresponds to a
comoving separation of
)
this corresponds to a
comoving separation of
![]() kpc).
Thus, differences in
kpc).
Thus, differences in ![]() have little influence on the comparison.
have little influence on the comparison.
As can be seen in Fig. 2, the estimated amplitude of the projected
correlation function rises very steeply with increasing
integration limits, and approaches a plateau when peculiar velocities become
unimportant and the undistorted correlation signal is sampled.
The maximum value is reached around
![]() ,
corresponding to
,
corresponding to
![]() .
Obviously the amplitude of the
projected correlation function reaches its asymptotic value
at the point where the integration limits have about the same size as
the typical velocity dispersion in clusters (
.
Obviously the amplitude of the
projected correlation function reaches its asymptotic value
at the point where the integration limits have about the same size as
the typical velocity dispersion in clusters (
![]() km s-1).
km s-1).
Adding errors in the redshift measurement basically lead to increasing noise in the correlation signal. If the clustering in redshift space is more and more washed out (the redshift distribution becomes more and more Poisson-like), the amplitude decreases, especially at small scales.
To prove this assumption and to estimate the size of the effect, we
assigned artificial errors to the measured redshifts of the galaxies
in the LCRS catalogue. The errors were randomly drawn out of a
Gaussian error distribution:
| (24) |
![\begin{displaymath}p(\Delta z)=\frac{1}{\sqrt{2
\pi}~\sigma}\exp\left[-\frac{1}{2}\left(\frac{\Delta z}{\sigma_z}\right)^2\right]\cdot
\end{displaymath}](/articles/aa/full/2003/33/aa3311/img146.gif) |
(25) |
![\begin{figure}
\par\includegraphics[angle=270,width=7.6cm,clip]{ms3311figure2.ps}
\end{figure}](/articles/aa/full/2003/33/aa3311/Timg148.gif) |
Figure 2:
The influence of redshift measurement errors on the
projected two-point correlation function.
|
| Open with DEXTER | |
Note
that the estimate for the amplitude is systematically lowered in the
presence of significant redshift errors. For
errors of
![]() ,
we find that the maximum amplitude is a factor 1.2
lower than in the case of the unchanged data.
For a differential comparison between various redshift intervals a
diminished amplitude is in any case no problem, provided one uses the LCRS in its
modified form (with artificial redshift errors simulated exaclty as
those found in the CADIS survey) as local reference.
,
we find that the maximum amplitude is a factor 1.2
lower than in the case of the unchanged data.
For a differential comparison between various redshift intervals a
diminished amplitude is in any case no problem, provided one uses the LCRS in its
modified form (with artificial redshift errors simulated exaclty as
those found in the CADIS survey) as local reference.
We calculated the projected correlation function for the CADIS data in
three different redshift bins of similar size,
![]() ,
,
![]() ,
,
![]() .
.
A random catalogue consisting of 30 000 randomly distributed "galaxies'' was generated for each CADIS field with the same properties as the real data. The surroundings of bright stars in our fields were masked out. The same mask is applied to the random catalogue.
The calculation was carried out for a
flat high-density model (
![]() ,
,
![]() ), a
hyperbolic low-density model (
), a
hyperbolic low-density model (
![]() ,
,
![]() ), and
a flat low-density model with non-zero comological constant (
), and
a flat low-density model with non-zero comological constant (
![]() ,
,
![]() ).
).
For the CADIS data the projected correlation function
![]() was
fitted over the range
was
fitted over the range
![]() Mpc (
Mpc (
![]() ), whereas the LCRS data was fitted in the range
), whereas the LCRS data was fitted in the range
![]() Mpc (
Mpc (
![]() ), see
Fig. 3. The fitted
amplitudes A at
), see
Fig. 3. The fitted
amplitudes A at
![]() kpc for CADIS and at
kpc for CADIS and at
![]() kpc for the LCRS, respectively, and the
amplitude of the three-dimensional correlation function at
kpc for the LCRS, respectively, and the
amplitude of the three-dimensional correlation function at
![]() Mpc derived from them, are listed in Table 2 (we have left
Mpc derived from them, are listed in Table 2 (we have left ![]() as a free parameter).
as a free parameter).
![\begin{figure}
\par\includegraphics[angle=270,width=7.4cm,clip]{ms3311figure3.ps...
...3mm}
\includegraphics[angle=270,width=7.4cm,clip]{ms3311figure5.ps}
\end{figure}](/articles/aa/full/2003/33/aa3311/Timg161.gif) |
Figure 3: Measured projected correlation function in three redshift bins, for the flat standard model (top), an open model (middle), and for a flat universe with a non-zero cosmological constant (below). Note that the binning in the highest redshift bin is different. Note also that the calculation was carried out in proper coordinates as measured by an observer at the particular redshift under consideration. The lines are the best fits of the data in the indicated range. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{ms3311figure6.ps}
\end{figure}](/articles/aa/full/2003/33/aa3311/Timg163.gif) |
Figure 4:
The amplitudes of the projected
correlation function at
|
| Open with DEXTER | |
The solid line is the amplitude measured from
the weighted mean, the dotted lines are the ![]() levels. The spread of the measured values around the mean is
reasonably small, and within their errors they lie within the error of
the weighted mean.
levels. The spread of the measured values around the mean is
reasonably small, and within their errors they lie within the error of
the weighted mean.
Although the projected distances at which the amplitudes are fitted are
still close to the largest separations measured, the measured amplitude
A and the slope ![]() are independent, the error
are independent, the error
![]() is negligible, and therefore the second term in
Eq. (13) is negligible. Then
is negligible, and therefore the second term in
Eq. (13) is negligible. Then
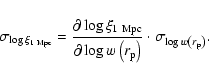 |
(26) |
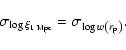 |
(27) |
Table 2:
The measured amplitude of the projected correlation function in
different redshift intervals, at
![]() kpc for CADIS and at
kpc for CADIS and at
![]() kpc for the LCRS (first lines),
respectively, the integral constraint
kpc for the LCRS (first lines),
respectively, the integral constraint ![]() and
and
![]() as calculated from the
as calculated from the ![]() -corrected amplitudes
of
-corrected amplitudes
of
![]() ,
for different world
models. Numbers in italic indicate that this values are inferred from
the LCRS.
,
for different world
models. Numbers in italic indicate that this values are inferred from
the LCRS.
![\begin{figure}
\par\includegraphics[angle=270,width=7.6cm,clip]{ms3311figure7.ps}
\end{figure}](/articles/aa/full/2003/33/aa3311/Timg176.gif) |
Figure 5:
Redshift distribution of faint (
|
| Open with DEXTER | |
Table 3:
The measured amplitude of the projected correlation function at
![]() kpc for the bright (
kpc for the bright (
![]() )
galaxies, the integral constraint
)
galaxies, the integral constraint ![]() ,
and
,
and
![]() ,
calculated from the
,
calculated from the ![]() -corrected A, for different world
models. Note that for the bright
sample the calculation for the first redshift bin was started at
z=0.25 instead of z=0.2, because there are only very few bright
galaxies at redshifts smaller than 0.3.
-corrected A, for different world
models. Note that for the bright
sample the calculation for the first redshift bin was started at
z=0.25 instead of z=0.2, because there are only very few bright
galaxies at redshifts smaller than 0.3.
The data point of the LCRS is included in the fit for q. Its error is
extremely small compared to the CADIS data, and thus it dominates the
fit. If we exclude the LCRS from the fit, we get
![]() ,
,
![]() ,
and
,
and
![]() (cosmologies in the same order as
above). The slopes are systematically steeper, although still the same
within their errors. However, the reduced
(cosmologies in the same order as
above). The slopes are systematically steeper, although still the same
within their errors. However, the reduced ![]() of the fits
including the LCRS is smaller than that without.
We regard this as a corroboration
that the connection to the local universe indeed improves the
determination of q.
of the fits
including the LCRS is smaller than that without.
We regard this as a corroboration
that the connection to the local universe indeed improves the
determination of q.
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{ms3311figure8.ps...
...mm}
\includegraphics[angle=270,width=7.5cm,clip]{ms3311figure10.ps}
\end{figure}](/articles/aa/full/2003/33/aa3311/Timg184.gif) |
Figure 6:
The evolution of the clustering strength (the amplitude of
the three-dimensional correlation function at at a
comoving separation of 1 h-1 Mpc) with
redshift. The integral constraint |
| Open with DEXTER | |
The dependency of the parameter q on the cosmology chosen for the
calculation is as follows: the estimate of
![]() as calculated from Eq. (22) is the
product of
as calculated from Eq. (22) is the
product of
![]() (as defined in Eq. (21)), and the
integral given in Eq. (23).
The physical distances
(as defined in Eq. (21)), and the
integral given in Eq. (23).
The physical distances ![]() are stretched (or compressed, respectively)
corresponding to the cosmology, that means the individual histograms
are stretched (or compressed, respectively)
corresponding to the cosmology, that means the individual histograms
![]() ,
,
![]() and
and
![]() are
shifted along the
are
shifted along the ![]() axis. However, the
estimator
axis. However, the
estimator
![]() is unaffected, because all histograms
are shifted in the same way. The integral
is unaffected, because all histograms
are shifted in the same way. The integral
![]() of
course changes with cosmology, thus the dependence of the amplitude of
the projected correlation function on cosmology is due to the
integration along the line of sight. Since we fit always at the same
physical scale (
of
course changes with cosmology, thus the dependence of the amplitude of
the projected correlation function on cosmology is due to the
integration along the line of sight. Since we fit always at the same
physical scale (
![]() kpc for CADIS), the values of
kpc for CADIS), the values of
![]() we deduce from
we deduce from
![]() show the same dependency on
cosmology. The differences in
show the same dependency on
cosmology. The differences in
![]() are increasing
with increasing redshift. At our highest redshift bin (
are increasing
with increasing redshift. At our highest redshift bin (
![]() )
we expect
)
we expect
![]() ,
hence we expect (and find) the
amplitudes of the correlation function to differ by the same
factor. The integral constraint only depends on the measured
correlation function (see Eqs. (15) to (17). It is, though estimated with large errors in
the highest redshift bin, of the order of 25% of the measured
amplitude at
316 h-1 kpc in all cosmologies, thus this additional
offset does not change the ratio of the amplitudes in different
cosmologies. If we consider the "local'' measurement not to change with
cosmology, then we expect the parameter q to change (due to the
change in
,
hence we expect (and find) the
amplitudes of the correlation function to differ by the same
factor. The integral constraint only depends on the measured
correlation function (see Eqs. (15) to (17). It is, though estimated with large errors in
the highest redshift bin, of the order of 25% of the measured
amplitude at
316 h-1 kpc in all cosmologies, thus this additional
offset does not change the ratio of the amplitudes in different
cosmologies. If we consider the "local'' measurement not to change with
cosmology, then we expect the parameter q to change (due to the
change in
![]() at the highest redshift bin) by
at the highest redshift bin) by
![]() between the matter-dominated
flat cosmology and the flat cosmology with non-zero cosmological constant. We find
between the matter-dominated
flat cosmology and the flat cosmology with non-zero cosmological constant. We find
![]() .
The slightly larger difference measured by
us is caused by the bin at
.
The slightly larger difference measured by
us is caused by the bin at
![]() (see Fig. 6).
(see Fig. 6).
Before analysing the SED type dependent evolution of galaxy clustering, we compare our results with previous attempts to study the clustering evolution with redshift. In the literature there are essentially only two investigations of the evolution of galaxy clustering, that can be compared with the present work: one analysis by Le Fèvre et al. (1996) which has been carried out in the framework of the Canada France Redshift Survey (in the following CFRS), and one by Carlberg et al. (2000), done on the CNOC sample (Canadian Network for Observational Cosmology).
Le Fèvre et al. (1996) used the projected correlation function to
investigate the spatial clustering of 591 galaxies
between
![]() ,
in five CFRS fields (for a description of
the survey see Lilly et al. (1995) and Schade et al. (1995), respectively) of
approximately the same size as our
CADIS fields. The objects are primarily located in three parallel
strips for each of the five fields, within which almost 100%
spectroscopic sampling was obtained, separated by regions where few
spectroscopic observations were carried out. The galaxies with
spectroscopic redshifts have
,
in five CFRS fields (for a description of
the survey see Lilly et al. (1995) and Schade et al. (1995), respectively) of
approximately the same size as our
CADIS fields. The objects are primarily located in three parallel
strips for each of the five fields, within which almost 100%
spectroscopic sampling was obtained, separated by regions where few
spectroscopic observations were carried out. The galaxies with
spectroscopic redshifts have
![]() .
They
computed the projected correlation function
in three redshift bins between
.
They
computed the projected correlation function
in three redshift bins between
![]() ,
,
![]() ,
and
,
and
![]() ,
with integration limits of
,
with integration limits of
![]() .
For the connection to z=0 they took values
of r0(z=0) from Loveday et al. (1995) and Hudon & Lilly (1996).
.
For the connection to z=0 they took values
of r0(z=0) from Loveday et al. (1995) and Hudon & Lilly (1996).
Figure 7 shows the amplitude of the three dimensional
correlation function at
![]() Mpc, deduced from the
projected correlation function, in comparison with our own data.
Since they did not apply corrections for the missing variance, we
calculated
Mpc, deduced from the
projected correlation function, in comparison with our own data.
Since they did not apply corrections for the missing variance, we
calculated
![]() without adding
without adding ![]() to the
measured amplitudes of
to the
measured amplitudes of
![]() .
For
direct comparison, we have to multiply our measured amplitudes of
the projected correlation function of the complete sample by
.
For
direct comparison, we have to multiply our measured amplitudes of
the projected correlation function of the complete sample by
![]() in order to allow for the large
errors of the CADIS multicolour redshifts (see Sect. 3).
in order to allow for the large
errors of the CADIS multicolour redshifts (see Sect. 3).
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{ms3311figure11.ps}
\end{figure}](/articles/aa/full/2003/33/aa3311/Timg197.gif) |
Figure 7:
The amplitudes of the three dimensional correlation
function at
|
| Open with DEXTER | |
Le Fèvre et al. (1996) claim that if
r0(z=0)=5 h-1 Mpc,
![]() .
The fit of their data
points, including a direct connection to z=0, that does not take the
different properties of the samples into account, formally yields
.
The fit of their data
points, including a direct connection to z=0, that does not take the
different properties of the samples into account, formally yields
![]() .
If the connection to z=0 is disregarded, we
find
.
If the connection to z=0 is disregarded, we
find
![]() from their data.
from their data.
This exercise shows that the value of q derived from the CFRS solely depends on
the connection to the present epoch. To deduce a reliable result, it is
indispensable to take into account that the catalogues to be compared
have to consist of
the same mix of Hubble types and luminosities, as we have seen, bright
galaxies are more strongly clustered. It is not possible to
estimate the evolution of the clustering strength by comparing a sample of
intrinsically faint galaxies at redshifts ![]() with the bright
galaxies which dominate the local measurements. The comparison between
different samples has to be carried out in a selfconsistent way.
The integral constraint, which they did not take into account, is
different in different redshift intervals (see Table 2), and thus alters the result. Also
the measured amplitude of the
projected correlation function depends on the redshift
accuracy and the appropriate choice of the integration limits.
with the bright
galaxies which dominate the local measurements. The comparison between
different samples has to be carried out in a selfconsistent way.
The integral constraint, which they did not take into account, is
different in different redshift intervals (see Table 2), and thus alters the result. Also
the measured amplitude of the
projected correlation function depends on the redshift
accuracy and the appropriate choice of the integration limits.
Thus we conclude that their measurement is consistent with ours, but they did not treat the local measurement selfconsistently.
Carlberg et al. (2000) carried out an analysis of the clustering evolution
on a sample of 2300 bright galaxies from the CNOC survey. The survey
itself is described in detail in Yee et al. (1996). The galaxies have
k-corrected and evolution-compensated R luminosities
![]() (H0=100 km s-1). The redshift
distribution extends to z=0.65. For comparison with z=0, they
selected a comparable sample from the LCRS. They also do not
apply corrections for the integral constraint, but since the survey area
of the CNOC is large (extending over
(H0=100 km s-1). The redshift
distribution extends to z=0.65. For comparison with z=0, they
selected a comparable sample from the LCRS. They also do not
apply corrections for the integral constraint, but since the survey area
of the CNOC is large (extending over
![]() in total)
in total)
![]() is expected to be negligible at the scales they investigate
(
is expected to be negligible at the scales they investigate
(
![]() Mpc).
The parameter
Mpc).
The parameter ![]() (see Groth & Peebles 1977; Efstathiou et al. 1991)
that they use for the parametrisation of the
clustering evolution can of course be related to the parameter q
(see Groth & Peebles 1977; Efstathiou et al. 1991)
that they use for the parametrisation of the
clustering evolution can of course be related to the parameter q
Their values indicate a much slower evolution of the clustering than our results. The reason for the descrepancy might be the different sample selection - the CNOC galaxies have been selected to be bright in the R band, whereas the galaxies in our sample have bright blue luminosities. As we will show in the next section, the clustering growth of blue and red galaxies evolves differently, and in fact the q values we derived for our subsample of early type galaxies are within the errors identical with the values estimated by Carlberg et al. (2000).
Le Fèvre et al. (1996) separated their sample into red and blue galaxies
(bluer and redder
than the Coleman et al. (1980) Sbc spectral energy distribution), and found that they
have comparable clustering amplitues at z>0.5. Here we show that
this is not the case, at redshifts ![]() red galaxies are
more
strongly clustered than blue ones.
red galaxies are
more
strongly clustered than blue ones.
The galaxy library used for the multicolour classification resembles regular grids in redshift and SED, thus the Hubble type can also be estimated from the observations. This enables us to investigate the evolution of the clustering of different populations of galaxies.
We devided the sample into two SED bins, with
![]() ,
including
galaxy types E to Sbc (1355 galaxies), and SED>60,
including Sds to
Starbursts (2311 galaxies), respectively. Galaxies with earlier SEDs have smaller
redshift errors, therefore we primarily concentrate on the investigation of
the evolution of the large scale structure of the galaxies in the
,
including
galaxy types E to Sbc (1355 galaxies), and SED>60,
including Sds to
Starbursts (2311 galaxies), respectively. Galaxies with earlier SEDs have smaller
redshift errors, therefore we primarily concentrate on the investigation of
the evolution of the large scale structure of the galaxies in the
![]() sample.
sample.
Figure 8 shows
![]() for the different redshift
bins, in comparison with the projected correlation function of all
galaxies, for a flat
for the different redshift
bins, in comparison with the projected correlation function of all
galaxies, for a flat
![]() model. The early type galaxies show significantly stronger clustering
than the late types. Table 4 lists the
amplitudes at
model. The early type galaxies show significantly stronger clustering
than the late types. Table 4 lists the
amplitudes at
![]() kpc, fitted between
kpc, fitted between
![]() kpc
and
kpc
and
![]() kpc, and the integral constraint
kpc, and the integral constraint ![]() .
.
![\begin{figure}
\par\includegraphics[angle=270,width=7.35cm,clip]{ms3311figure12....
...m}
\includegraphics[angle=270,width=7.35cm,clip]{ms3311figure13.ps}
\end{figure}](/articles/aa/full/2003/33/aa3311/Timg213.gif) |
Figure 8:
The projected correlation function in three different
redshift bins; upper panel: early type galaxies in comparison with all
galaxies (only the fits are shown as grey lines), lower panel: late
type galaxies in comparison with all
galaxies for
|
| Open with DEXTER | |
Table 4:
The measured amplitude of the projected correlation function at
![]() kpc and the integral constraint
kpc and the integral constraint ![]() ,
in
different redshift intervals for two SED
bins, for different world models.
,
in
different redshift intervals for two SED
bins, for different world models.
Table 5:
The amplitudes of the three-dimensional correlation
function ![]() at a comoving distance of r=1 Mpc, for red
(
at a comoving distance of r=1 Mpc, for red
(![]() )
and blue (SED>60) galaxies; the integral constraint
has been taken into account in the calculation.
)
and blue (SED>60) galaxies; the integral constraint
has been taken into account in the calculation.
The late type galaxies have large redshift errors, and they are
intrinsically only very weakly clustered. Although their
number density is high, the large errors and the low correlation signal
result in a highly
uncertain measurement of their clustering amplitudes (the measurement is shown for
the
![]() ,
,
![]() case), which would make a
reliable estimate of the clustering evolution impossible. Also the late type sample is
at high redshifts dominated by relatively bright galaxies, whereas at
lower redshifts the rather low-mass,
fainter galaxies, which are only very weakly clustered, are currently undergoing
periods of high starformation rates. A galaxy classified as extreme
late type at z=1 may have evolved
into an Sa at z=0, thus we are not dealing with a homogeneous
sample. A measurement of the clustering evolution of late type
galaxies is therefore not meaningful at this point.
case), which would make a
reliable estimate of the clustering evolution impossible. Also the late type sample is
at high redshifts dominated by relatively bright galaxies, whereas at
lower redshifts the rather low-mass,
fainter galaxies, which are only very weakly clustered, are currently undergoing
periods of high starformation rates. A galaxy classified as extreme
late type at z=1 may have evolved
into an Sa at z=0, thus we are not dealing with a homogeneous
sample. A measurement of the clustering evolution of late type
galaxies is therefore not meaningful at this point.
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{ms3311figure14.eps}
\end{figure}](/articles/aa/full/2003/33/aa3311/Timg216.gif) |
Figure 9:
The evolution of the clustering strength (at a
comoving separation of 1 h-1 Mpc) with
redshift, for early type ( |
| Open with DEXTER | |
Table 6:
The parameter q for early type (![]() )
galaxies,
for a fit done without taking the the LCRS point into account, and
for a fit including it. The evolution of the bright sample
is shown for comparison.
)
galaxies,
for a fit done without taking the the LCRS point into account, and
for a fit including it. The evolution of the bright sample
is shown for comparison.
These values of q,
![]() ,
,
![]() ,
,
![]() (see Table 6 for the corresponding
cosmological models) are within their errors identical to the values
deduced by Carlberg et al. (2000) from the red CNOC galaxies (they found
(see Table 6 for the corresponding
cosmological models) are within their errors identical to the values
deduced by Carlberg et al. (2000) from the red CNOC galaxies (they found
![]() ,
,
![]() ,
,
![]() for the
cosmologies in the same order as above, see
previous section).
for the
cosmologies in the same order as above, see
previous section).
1. Bright galaxies are more strongly clustered than faint galaxies and show
significant growth in clustering since
![]() .
.
At redshifts around
![]() the CADIS data are dominated by
rather faint galaxies, which show smaller clustering amplitudes than
brighter ones. On the other hand, the LCRS sample consists mainly of
intrinsically bright galaxies. In order to be able to compare our high
redshift data self-consistently with the local measurement from the
LCRS, we measured the amplitude of the correlation function from a
subsample of bright galaxies (
the CADIS data are dominated by
rather faint galaxies, which show smaller clustering amplitudes than
brighter ones. On the other hand, the LCRS sample consists mainly of
intrinsically bright galaxies. In order to be able to compare our high
redshift data self-consistently with the local measurement from the
LCRS, we measured the amplitude of the correlation function from a
subsample of bright galaxies (
![]() ). We find a
significant growth of the clustering strength for this bright
subsample:
). We find a
significant growth of the clustering strength for this bright
subsample:
For the
![]() cosmology we
find q = -2.2 that is
cosmology we
find q = -2.2 that is
![]() .
This might be compared with the theoretical predictions
by Kauffmann et al. (1999a). They use N-body simulations of dark matter
(DM) to derive the clustering of DM halos at 0 < z < 5 and
semi-analytic models in order to assign a galaxy of certain type and
luminosity to each DM halo. Although many properties of their mock
galaxies population are only in loose accordance with observations,
their result seems robust: the clustering strength of
bright galaxies (
.
This might be compared with the theoretical predictions
by Kauffmann et al. (1999a). They use N-body simulations of dark matter
(DM) to derive the clustering of DM halos at 0 < z < 5 and
semi-analytic models in order to assign a galaxy of certain type and
luminosity to each DM halo. Although many properties of their mock
galaxies population are only in loose accordance with observations,
their result seems robust: the clustering strength of
bright galaxies (
![]() )
on 2 Mpc scales follows
closely that of the DM halos they are imbedded out to
)
on 2 Mpc scales follows
closely that of the DM halos they are imbedded out to
![]() (bias parameter
(bias parameter
![]() ).
They find a 3.5-fold increase of
).
They find a 3.5-fold increase of
![]() between
z=1 and z=0. If one takes into account that the increase should be
higher on 1 Mpc scales and that our limit for "bright galaxies'' is 1
magnitude fainter (i.e. it includes less massive halos) it seems
that the
the clustering evolution predicted by
between
z=1 and z=0. If one takes into account that the increase should be
higher on 1 Mpc scales and that our limit for "bright galaxies'' is 1
magnitude fainter (i.e. it includes less massive halos) it seems
that the
the clustering evolution predicted by ![]() CDM models is in agreement with
our measurements.
CDM models is in agreement with
our measurements.
2. At high redshifts, early type galaxies are more strongly clustered than the bright galaxies and the clustering strength of the early type galaxies evolves much more slowly than that of the bright galaxies.
A plausible explanation for the different evolution of the clustering properties of the early type galaxies arises in the context of biased galaxy formation (Brainerd & Villumsen 1994; Bardeen et al. 1986). The first galaxies are born in a highly clustered state, because they form in the bumps and wiggles which are superimposed on the very large-scale density enhancements. The next generations of galaxies form later in the wings of the large-scale enhancements, and are therefore less and less clustered. While the universe expands, the galaxies evolve, age, and eventually merge to form larger, brighter galaxies and ellipticals, and generally add to the population of earlier type galaxies, while new galaxies form at later times in less and less clustered environments. Merging creates galaxies, "which suddenly'' add to the old population. A merger event also reduces not only the number of galaxies, but also the number of small pair separations in a sample, which reduces the probability of finding pairs of galaxies at small distances - and thus supresses the amplitude of the correlation function. Fried et al. (2001) found the density evolution of the early type and the late type galaxy population in the CADIS galaxy sample suggestive of merging.
Although the clustering strength of the underlying dark matter density field increases with redshift, the biasing decreases. The net effect is a very slowly rising clustering amplitude of the early type (old) galaxies.
Thus, the measured rate of the clustering growth depends on the mixture of galaxy types one observes at different redshifts.
3. The evolution of the clustering amplitude of early and bright
galaxies converges to the same value at ![]() .
.
The convergence of the evolution of the clustering of bright galaxies
and galaxies with SEDs earlier than Sbc towards the same local
measurement can also be understood if one takes into account that
galaxies evolve and hence the population mix one observes changes with
redshifts. The comoving number density of weakly clustered starburst
galaxies increases with increasing redshifts,
whereas the space density of the
highly clustered very early type (E-Sa) galaxies decreases by a
factor of ![]() from z=0 to z=1 (Fried et al. 2001). In our
highest redshift bins the clustering signal of the bright subsample is
presumably dominated by a weakly clustered population of galaxies,
which at that time were bright, and blue. At z=0 these weakly
clustered blue galaxies have vanished, and now the majority of the
early type galaxies (which had later, bluer SEDs at higher
redshifts), are also bright, thus at the present epoch there is
a large overlap between the bright and the early type samples. Thus we
conclude that the apparent strong growth of clustering of the bright
galaxies is dominated by the fading of the unclustered, blue
population.
from z=0 to z=1 (Fried et al. 2001). In our
highest redshift bins the clustering signal of the bright subsample is
presumably dominated by a weakly clustered population of galaxies,
which at that time were bright, and blue. At z=0 these weakly
clustered blue galaxies have vanished, and now the majority of the
early type galaxies (which had later, bluer SEDs at higher
redshifts), are also bright, thus at the present epoch there is
a large overlap between the bright and the early type samples. Thus we
conclude that the apparent strong growth of clustering of the bright
galaxies is dominated by the fading of the unclustered, blue
population.
To understand exactly how galaxy evolution influences the measurement of the growth of structure, and the evolution of the large scale structure influences the evolution of galaxies, we need detailed investigations of the evolution of both the correlation function and the luminosity function of galaxies with different SEDs.
Larger, wide angle deep surveys have only recently become
available, and one of them is the COMBO 17 survey (Classifying Objects by Medium-Band Observations in 17 filters, Wolf et al. (2001a)), in some respect
the successor of CADIS. The complete catalogue will include
![]() galaxies with
galaxies with ![]() ,
in 1
,
in 1
![]()
![]() ,
with SED and
morphological information. This amazing data base can be used for
various investigations, using the projected correlation function. The
higher statistic allows for a more detailed analysis of the evolution
of the clustering of different galaxie types and their relation to the
underlying dark matter density field.
,
with SED and
morphological information. This amazing data base can be used for
various investigations, using the projected correlation function. The
higher statistic allows for a more detailed analysis of the evolution
of the clustering of different galaxie types and their relation to the
underlying dark matter density field.
The clustering properties of
starburst galaxies at higher redshifts can be investigated using the
emission line galaxies observed by the CADIS emission-line survey
using an imaging Fabry-Perot interferometer (Hippelein et al. 2003). These galaxies, which have been detected and classified by their
emission lines, have redshifts with an accuracy of 120 km s-1 -
good enough to calculate the three-dimensional correlation function
directly. The special observing technique samples galaxies in distinct
narrow redshift bins, which allows for the investigation of the
evolution of the clustering properties of emission line galaxies
between a redshift of
![]() and
and
![]() .
.
The observations have to be compared to theoretical predictions. We plan to carry out a large cosmological simulation including starformation and feedback. The individual galaxies will be assigned an SED according to their stellar masses and starformation histories, so we can perform synthetic photometry applying our CADIS or COMBO 17 filter set to the synthetic spectra. Thus we will be able to "observe'' the mock galaxies at different redshifts, and directly compare the simulations to our observations.
Acknowledgements
We thank J. A. Peacock for many valuable and helpful discussions.
We thank all those involved in the Calar Alto Deep Imaging Survey, especially H.-J. Röser and C. Wolf, without whom carrying out the whole project would have been impossible.
We are greatly indebted to the anonymous referee who pointed out several points which had not received sufficient attention in the original manuscript. This led to a substantial improvement of the paper.
We also thank M. Alises and A. Aguirre for their help and support during many nights at Calar Alto Observatory, and for carefully carrying out observations in service mode.