A&A 407, 121-135 (2003)
DOI: 10.1051/0004-6361:20030872
F. D. Barazza 1 - B. Binggeli 1 - H. Jerjen 2
1 - Astronomisches Institut, Universität Basel, Venusstrasse 7,
4102 Binningen, Switzerland
2 -
Research School of Astronomy and Astrophysics, The Australian National
University, Mt Stromlo Observatory, Cotter Road, Weston ACT 2611, Australia
Received 29 January 2003 / Accepted 20 May 2003
Abstract
We have carried out surface photometry and an isophotal analysis for
a sample of 25 early-type dwarf (dE and dS0)
galaxies in the Virgo cluster based on CCD images
taken at the VLT with FORS1 and FORS2. For each galaxy we present B
and R-band surface brightness profiles, as well as the radial colour (B-R)
profile.
We give total apparent BR magnitudes, effective radii, effective surface
brightnesses and total colour indices. The light profiles have been fitted with
Sérsic models and the corresponding parameters are compared to the ones for
other classes of objects. In general, dEs and dS0s bridge
the gap in parameter space between the giant ellipticals and the low-luminosity
dwarf
spheroidals in the Local Group, in accordance with previous findings.
However, the observed profiles of the brightest cluster dwarfs show
significant deviations from a simple Sérsic model, indicating that there is
more inner structure than just a nucleus. This picture is reinforced by our
isophotal analysis where complex radial
dependencies
of ellipticity, position angle, and isophotal shape parameter a4
are exhibited not only by objects like IC 3328, for which the presence of
a disk component has been confirmed, but by many apparently normal dEs as well.
In addition, we find a relation between the effective surface
brightness, at a given luminosity, and the strength of the offset of the
galaxy's nucleus with respect
to the center of the isophotes. Dwarfs with large nuclear offsets also tend
to have stronger isophotal twists. However, such twists are
preferentially found in apparently round (
![]() )
galaxies
and are always accompanied by significant radial changes of the ellipticity,
which clearly
points to a projection effect. In sum, our findings suggest
the presence of substructure in most, and preferentially in the less
compact, bright early-type dwarfs.
The physical (dynamical) meaning of this has yet to be explored.
)
galaxies
and are always accompanied by significant radial changes of the ellipticity,
which clearly
points to a projection effect. In sum, our findings suggest
the presence of substructure in most, and preferentially in the less
compact, bright early-type dwarfs.
The physical (dynamical) meaning of this has yet to be explored.
Key words: galaxies: fundamental parameters - galaxies: photometry - galaxies: structure - galaxies: clusters: individual: Virgo - galaxies: dwarf - galaxies: elliptical and lenticular, cD
On the other hand, enormous progress has recently been made at the kinematic "frontline''. After almost a decade of stagnation of kinematic measurements (see Ferguson & Binggeli 1994), several groups are now reporting their (partially conflicting) results on the (non-) rotational properties of early-type dwarfs. For instance, Geha et al. (2001) used Keck II to measure rotation profiles for six Virgo dwarfs. No evidence of significant rotation was found among the target objects. A similar programme is being run at the VLT (de Rijcke et al. 2002). The earlier conjecture that dwarf ellipticals in general are not rotation-supported is definitively confirmed by these studies (also Thomas et al. 2003). However, it has also become clear that among the brightest cluster early-type dwarfs, in particular the dS0s, there are many rotation-supported systems (Simien & Prugniel 2002).
There are also photometric hints about the existence of disk galaxies among the bright cluster early-type dwarfs. Jerjen et al. (2000, 2001) discovered weak spiral structures and a bar in two Virgo dEs and subsequently Barazza et al. (2002) found spiral and bar features in three additional objects. These findings are in fact based on the same VLT images for which surface photometry is presented in the present paper. Deep, high-resolution VLT imaging, providing a sufficiently large field of view, is certainly ideally suited for the study of the photometric properties of Virgo and Fornax dEs. With the present surface photometry and isophotal analysis of 25 early-type Virgo dwarfs based on high-quality B and R VLT images we aim at a more systematic exploration of the structural complexity of dwarf ellipticals. We especially address the question whether a Sérsic model is an appropriate representation of the empirical surface brightness profiles of dEs. The isophotal analysis is used to derive ellipticity, position angle and isophotal shape profiles. In addition, we map nuclear offsets and isophotal twists of the sample dEs. Overall, our findings show that these seemingly dull stellar systems are quite complex in structure. Dwarf elliptical galaxies are neither the scaled down version of giant ellipticals nor simply the final state of a star forming dwarf irregular galaxy that has converted all its gas into stars.
The plan of this paper is as follows. In Sect. 2 we introduce the dwarf galaxy sample and provide some global photometric parameters. The data reduction and photometric calibration are described in Sect. 3. Sections 4 and 5 are dedicated to the surface photometry and the isophotal analysis. The discussion and summary is given in Sect. 6.
Within these constraints, the sample was selected so as to get a
good coverage in velocity space
(-730 kms-1
![]() kms-1) and in the
celestial distribution (
kms-1) and in the
celestial distribution (
![]() ;
;
![]() ). The core sample contained 16 bright early-type dwarfs which,
however, could be increased by 9 more dwarfs, as these happened to lie in
the field of view of the CCD. Among these are five rather faint dwarfs
(VCC 0850, VCC 0962, VCC 0998, VCC 1093, VCC 1129). The total sample considered
here is comprised therefore of 25 objects, 22 of which were imaged in B and R filters (or
). The core sample contained 16 bright early-type dwarfs which,
however, could be increased by 9 more dwarfs, as these happened to lie in
the field of view of the CCD. Among these are five rather faint dwarfs
(VCC 0850, VCC 0962, VCC 0998, VCC 1093, VCC 1129). The total sample considered
here is comprised therefore of 25 objects, 22 of which were imaged in B and R filters (or ![]() ,
which is the corresponding filter used on FORS2; in the
following we only use R) and three (IC 3303, IC 3518, UGC 7854) in R only.
,
which is the corresponding filter used on FORS2; in the
following we only use R) and three (IC 3303, IC 3518, UGC 7854) in R only.
Table 1: Basic data and model-free parameters of the early-type dwarfs considered in this study (extinction-corrected).
The images were obtained using the first two units of the Very Large
Telescope (VLT) at ESO Paranal Observatory in service mode over a period of two
semesters: at UT1+FORS1 (Antu) during an observing run on July 10-14, 1999 and
at UT2+FORS2 (Kueyen) during dark time periods in March-May 2000. The detectors
of the FORS (FOcal Reducer/Low dispersion Spectrograph) instruments are thinned
and anti-reflection-coated Tektronix (FORS1) and SiTE (FORS2) CCDs with
![]() pixels. By default, service observations were taken in
standard resolution mode, with a high gain and a pixel scale of
pixels. By default, service observations were taken in
standard resolution mode, with a high gain and a pixel scale of
![]() pixel-1 that yields a field of view of
pixel-1 that yields a field of view of
![]() .
The CCDs were read out in the four-port mode, i.e. four amplifiers read out
one quarter of the CCD each. Three exposures of 400-600 s durations with
slightly different pointings were secured in each filter for each galaxy.
More details of the observations are to be reported elsewhere (Jerjen et al., in preparation). The basic properties of the sample galaxies are listed in
Table 1. The columns are as follows:
.
The CCDs were read out in the four-port mode, i.e. four amplifiers read out
one quarter of the CCD each. Three exposures of 400-600 s durations with
slightly different pointings were secured in each filter for each galaxy.
More details of the observations are to be reported elsewhere (Jerjen et al., in preparation). The basic properties of the sample galaxies are listed in
Table 1. The columns are as follows:
Cols. (1) and (2): identifications of the galaxies; for the coordinates
see
VCC.
Col. (3): morphological type in the classification system of
Sandage & Binggeli (1984), taken from the VCC;
Col. (4): absolute B-band magnitude, based on the apparent magnitude
given in Col. 6 and a mean Virgo cluster distance of 17 Mpc;
Col. (5): heliocentric radial velocity in km s-1(from the VCC and Binggeli et al. 1993,
except for VCC 0928, where the value of Conselice
et al. 2001 is given).
The following entries are from the photometry presented below (Sect. 4).
We give their
meaning here as well. It should be noted that all values in magnitudes are
corrected for galactic extinction using the maps of Schlegel et al. (1998).
Values with a colon are uncertain.
Cols. (6) and (9): total apparent magnitude in B and R,
respectively;
Cols. (7) and (10): effective radius in arcsec
![]() in B and R, respectively;
in B and R, respectively;
Cols. (8) and (11): effective surface brightnesses in B
![]() and R
and R
![]() ,
respectively;
,
respectively;
Col. (12): total (mean) B-R colour index.
The mean absolute magnitude in B for all dwarfs is
![]() .
Taking only the 16 dwarfs originally selected into account (without the five
faint
objects mentioned above) we get
.
Taking only the 16 dwarfs originally selected into account (without the five
faint
objects mentioned above) we get
![]() ,
which is
indeed rather bright for dwarf galaxies. The mean colour of the sample is
,
which is
indeed rather bright for dwarf galaxies. The mean colour of the sample is
![]() .
This is quite blue for early-type dwarfs, but
there are three very blue outliers whose colour might be affected by other
objects: parts of VCC 0962 (
B-R = 1.04) are hidden by a bright foreground
star, VCC 0815 (
B-R = 1.05) probably has a bright background object near its
nucleus, and VCC 0850 (
B-R = 1.06) is partially overlapping with VCC 0846.
Excluding these three dwarfs we get
.
This is quite blue for early-type dwarfs, but
there are three very blue outliers whose colour might be affected by other
objects: parts of VCC 0962 (
B-R = 1.04) are hidden by a bright foreground
star, VCC 0815 (
B-R = 1.05) probably has a bright background object near its
nucleus, and VCC 0850 (
B-R = 1.06) is partially overlapping with VCC 0846.
Excluding these three dwarfs we get
![]() .
.
Table 2:
Mean systematic uncertainties in surface brightness
due to sky flattening problems and maximum radii for full elliptical
integration. A ![]() sign
indicates that the whole galaxy
is on the frame.
sign
indicates that the whole galaxy
is on the frame.
Next the frames were cleaned of disturbing foreground stars or background galaxies. The regions around the galaxies were automatically cleaned with an algorithm designed for this purpose, whereas objects on the galaxy itself were erased by hand.
For the photometric zero-pointing we used standard
stars from Landolt (1992). The
fields
with the standard stars had been imaged several times during the observing
nights.
We could therefore determine the zero point and extinction parameters for
each night separately.
The center, as well as the ellipticity and position angle of the major axis for
each galaxy were determined at the isophotal level of ![]()
![]() by means of the ellipse fitting routine FIT/ELL3. These
parameters were then used to obtain a growth curve (integrated light profile)
by integrating the galaxy light in elliptical apertures of fixed center,
ellipticity and position angle of the major axis. Some bright galaxies in
our sample could not be integrated completely in this way
because they had not been placed at
the center of the frame, but slightly off in order to have enough regions
for the background fitting. In these cases we integrated the outer parts
of the galaxy only in one quadrant (obviously the one opposite to the quadrant
containing the center)
and extrapolated the results to the whole galaxy.
In Table 2, Cols. 5 and 6 we give the equivalent (maximum)
radii for the B and R frames,
respectively, up to which a full
integration was possible. A
by means of the ellipse fitting routine FIT/ELL3. These
parameters were then used to obtain a growth curve (integrated light profile)
by integrating the galaxy light in elliptical apertures of fixed center,
ellipticity and position angle of the major axis. Some bright galaxies in
our sample could not be integrated completely in this way
because they had not been placed at
the center of the frame, but slightly off in order to have enough regions
for the background fitting. In these cases we integrated the outer parts
of the galaxy only in one quadrant (obviously the one opposite to the quadrant
containing the center)
and extrapolated the results to the whole galaxy.
In Table 2, Cols. 5 and 6 we give the equivalent (maximum)
radii for the B and R frames,
respectively, up to which a full
integration was possible. A ![]() -sign indicates that the whole galaxy
is on the frame.
In the case of VCC 1254 only one quadrant was used for the whole galaxy,
as it is located very close to the giant M 49.
-sign indicates that the whole galaxy
is on the frame.
In the case of VCC 1254 only one quadrant was used for the whole galaxy,
as it is located very close to the giant M 49.
As described above, we determined the growth curve for each galaxy by
integrating the galaxy light in elliptical apertures. The intensity at which
this curve becomes asymptotically flat yields the total apparent
magnitude. In a few cases, however, the first integration promptly led to a
reasonably flat growth curve. Usually the outer shape of the growth curve shows
a continuous increase or a maximum followed by a continuous decrease, indicating
a slight, erroneous excess or
deficiency in the sky level. The shape of the curve can therefore be
used to do a fine-tuning of the sky level by simply adding or subtracting
a constant to the whole frame. Once the growth curve is corrected
to be asymptotically flat, the effective radius can then be read off where the
growth curve reaches
half of its asymptotic value. Using the equation
| (1) |
Surface brightness profiles can be obtained by differentiating the growth curve
with respect to equivalent radius
![]() ,
where a and b are the
major-
and minor-axis, respectively. We used a resolution of
,
where a and b are the
major-
and minor-axis, respectively. We used a resolution of
![]() ,
which
corresponds to two pixel lengths. The extinction-corrected profiles
are shown in Fig. 1 (left
column on top). The upper curve is the R profile and the lower curve the
B profile. Error bars are only shown for the B profile. They can be
considered as upper limits for the profile in R. Only in the outer parts the
error bars are larger than the plot symbols. The errors have been estimated
using the remaining gradients on the frame after flat fielding
and the intensity of the subtracted
background. They therefore indicate the accuracy of the profile at the
corresponding surface brightness level and do not take into account the fact
that in some cases only one quarter of the galaxy light has been integrated.
,
which
corresponds to two pixel lengths. The extinction-corrected profiles
are shown in Fig. 1 (left
column on top). The upper curve is the R profile and the lower curve the
B profile. Error bars are only shown for the B profile. They can be
considered as upper limits for the profile in R. Only in the outer parts the
error bars are larger than the plot symbols. The errors have been estimated
using the remaining gradients on the frame after flat fielding
and the intensity of the subtracted
background. They therefore indicate the accuracy of the profile at the
corresponding surface brightness level and do not take into account the fact
that in some cases only one quarter of the galaxy light has been integrated.
In the bottom left panel of Fig. 1 we plot the B-R colour profile. For dwarf galaxies in general one would expect rather flat profiles, i.e. no strong colour gradients. In the case of dwarf ellipticals a positive gradient, i.e. a reddening towards the outer parts, could be explained by the presence of a younger population of stars in the center, where the last star formation event took place (Vader et al. 1988). Surprisingly, almost half of the galaxies in our sample (10) exhibit a negative colour gradient, getting bluer towards the outer parts. This could mean that there is a metallicity gradient in these galaxies. Indeed, for five of these objects either a disk component has been discovered or at least indications of the presence of a disk have been found (Jerjen et al. 2000; Barazza et al. 2002). A separate, more elaborate investigation of the colour properties of dwarf ellipticals is in preparation (Barazza et al. 2003).
Table 3: Parameters of the Sérsic fit and of the isophotal analysis.
The surface brightness profiles of dwarf galaxies, including dEs,
can usually be fitted quite
well by an exponential model (De Vaucouleurs 1959; Binggeli & Cameron 1991).
However, the profiles of bright early-type dwarfs are known to deviate
considerably from an exponential law (Caldwell & Bothun 1987;
Binggeli &
Cameron 1993). This deviation depends systematically on the luminosity of the
dwarfs. Bright objects show a shallow luminosity excess in the inner parts,
which cannot be caused by the presence of a nucleus. A better representation
of the profiles of early-type dwarfs is provided by a Sérsic model
(Sérsic 1968). This model, which is a simple generalization of De
Vaucouleurs' r1/4 and exponential laws, can be written as
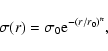 |
(2) |
| (3) |
In Fig. 2 we plot these parameters versus absolute magnitude in B. For
comparison we have added a sample of giant ellipticals and S0s from Caon et al.
(1993), the data for the dEs and dSphs of the Local Group from Jerjen et al.
(2000), and the large photographic sample of early-type dwarfs in
Virgo
(partly
coinciding with ours) from Binggeli & Jerjen (1998). The ![]() diagram
(top panel) shows a rather tight relation comprising
all different types of spheroidal objects. As already found and commented
upon by Jerjen & Binggeli (1997) and Jerjen et al. (2000),
the early-type
dwarfs
perfectly bridge the gap between the faint dSphs of the local group and the
giant ellipticals. The known dichotomy between Es and dEs in a
luminosity-central surface brightness plot (e.g. Binggeli & Cameron 1991)
vanishes in the Sérsic representation.
Note that the dichotomy between core and power-law
systems among normal Es (e.g. Faber et al. 1997) also disappears here:
the Sérsic
diagram
(top panel) shows a rather tight relation comprising
all different types of spheroidal objects. As already found and commented
upon by Jerjen & Binggeli (1997) and Jerjen et al. (2000),
the early-type
dwarfs
perfectly bridge the gap between the faint dSphs of the local group and the
giant ellipticals. The known dichotomy between Es and dEs in a
luminosity-central surface brightness plot (e.g. Binggeli & Cameron 1991)
vanishes in the Sérsic representation.
Note that the dichotomy between core and power-law
systems among normal Es (e.g. Faber et al. 1997) also disappears here:
the Sérsic ![]() values are not actual but extrapolated
central surface brightnesses from fitting the profiles outside the
central few 100 parsecs; the dichotomies mentioned are
restricted to those inner regions.
values are not actual but extrapolated
central surface brightnesses from fitting the profiles outside the
central few 100 parsecs; the dichotomies mentioned are
restricted to those inner regions.
The relations in the remaining two plots are not as striking, although in both diagrams a certain continuity between the different galaxy classes is evident, above all among the ellipticals. In contrast, the faint local group dSphs stand slightly apart.
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{ms3537f14.ps}
\end{figure}](/articles/aa/full/2003/31/aa3537/Timg68.gif) |
Figure 2:
The parameters of the best-fitting Sérsic model, central surface
brightness ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{ms3537f15.ps}
\end{figure}](/articles/aa/full/2003/31/aa3537/Timg69.gif) |
Figure 3: Effective surface brightness in R plotted versus the mean, absolute residual between profile observed and model-profile (see text for details). The error bars represent the mean error of the profile in the corresponding range. |
| Open with DEXTER | |
The best-fitting Sérsic model profiles are plotted as solid lines through the
data points in Fig. 1 (upper left panel). The general trend of the observed
profiles is matched quite well by the models. However, in some cases the
decrease of the observed profile is not as smooth as the model in the inner
parts. This is shown in the second plot of the first column in Fig. 1, where
the difference between the observed profiles and the models is plotted. Error
bars are shown for every other data point (mostly smaller than the plot
symbols). The large residuals caused by the nuclei are not very surprising,
as the very central parts (r <4
![]() )
have been excluded for the fit, but a few of the bright
objects show considerable deviations from the model in the regions just outside
of the nucleus as well. A rather strong scatter is shown by the dwarfs where a
spiral structure has been discovered (IC 0783, IC 3328). Hence, in these cases a
bad fit might be expected. But also "normal'' dEs, like VCC 0928 or NGC 4415,
show a remarkable deviation.
)
have been excluded for the fit, but a few of the bright
objects show considerable deviations from the model in the regions just outside
of the nucleus as well. A rather strong scatter is shown by the dwarfs where a
spiral structure has been discovered (IC 0783, IC 3328). Hence, in these cases a
bad fit might be expected. But also "normal'' dEs, like VCC 0928 or NGC 4415,
show a remarkable deviation.
In order to quantify the deviations and to find out whether they are related to
other properties of the galaxies, we determined the mean, absolute residual
between the observed profile and the fit (only for the R-band data):
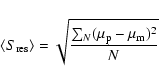 |
(4) |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{ms3537f16.ps}
\end{figure}](/articles/aa/full/2003/31/aa3537/Timg77.gif) |
Figure 4: Comparison of our total apparent magnitude in B (filled circles) and R(open circles) (upper panel) and of the central surface brightness from the Sérsic fit in B (filled circles) and R (open circles) (lower panel) to data from the literature. |
| Open with DEXTER | |
In the lower panel of Fig. 4 we compare our central surface brightnesses in B and R, derived by a Sérsic fit, to the data of Binggeli & Jerjen (1998) and
Durrell
(1997), respectively. Obviously, the two brightest objects strongly disagree.
The fact
that Binggeli and Jerjen used growth-curves for the fitting procedure cannot
account
for these differences (see their discussion of this point), nor could
a difference in the seeing play a role here, as the Sérsic law fitting
is done outside the central 3
![]() or 4
or 4
![]() .
However, since
brighter
objects usually have a steeper rise of the profile in the central parts, only
slightly
different Sérsic fits can have large deviations of the central surface
brightness. Also, the brightest objects show generally the strongest deviations
from the Sérsic law (see Sect. 4.3 above).
.
However, since
brighter
objects usually have a steeper rise of the profile in the central parts, only
slightly
different Sérsic fits can have large deviations of the central surface
brightness. Also, the brightest objects show generally the strongest deviations
from the Sérsic law (see Sect. 4.3 above).
Since the center of the ellipse searched for is a free parameter in the fitting
procedure,
we could simultaneously measure the distance, ![]() ,
between the nucleus
(or the center of the innermost isophote for not-nucleated dwarfs) and the
center
of the overall brightness distribution. This allows to determine a possible
off-center position of the nucleus or the concentricity of the successive
isophotes.
The isophotal contours of the sample galaxies are shown in Fig. 5.
,
between the nucleus
(or the center of the innermost isophote for not-nucleated dwarfs) and the
center
of the overall brightness distribution. This allows to determine a possible
off-center position of the nucleus or the concentricity of the successive
isophotes.
The isophotal contours of the sample galaxies are shown in Fig. 5.
In order to investigate whether there are correlations between the isophotal
parameters and other properties of the galaxies, we determined their mean,
global values.
The range within which the averaging was performed was again the same as for the
profile fitting: outside the central
![]() and above an isophotal level
of
and above an isophotal level
of
![]() .
Following the procedures of Ryden et al. (1999),
the parameters of the isophotes contributing to the
mean have been weighted by the fraction of intensity corresponding to that
isophote. In this way the faint outer regions, where the errors are large,
are automatically given less weight.
Hence, the intensity - or luminosity - weighted mean is:
.
Following the procedures of Ryden et al. (1999),
the parameters of the isophotes contributing to the
mean have been weighted by the fraction of intensity corresponding to that
isophote. In this way the faint outer regions, where the errors are large,
are automatically given less weight.
Hence, the intensity - or luminosity - weighted mean is:
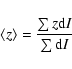 |
(5) |
We omit VCC 1254 in this analysis, since its isophotal parameters can not be
determined with the required accuracy, due to its proximity to M 49.
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{ms3537f17.ps}
\end{figure}](/articles/aa/full/2003/31/aa3537/Timg86.gif) |
Figure 5:
Isophotal contours of the R-band images. The galaxy name is given
in the
upper left corner. The surface brightness of the innermost isophote is indicated
in
the upper right corner, the interval is 0.25 mag. The images are
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{ms3537f18.ps}
\end{figure}](/articles/aa/full/2003/31/aa3537/Timg87.gif) |
Figure 5: continued. |
| Open with DEXTER | |
Giant ellipticals as well as dwarf ellipticals owe their name to the fact that
the
shape of their isophotes is nearly elliptical. The shape parameter a4 has
been
developed in order to quantify the deviations of the isophotes from an
elliptical
shape and to find correlations between these deviations and other properties of
the
galaxies. Isophotes whose a4 is negative are called boxy, since their shape
resembles a rectangle, and those with a positive a4 are called disky, because
they are more pointed, lemon-like, than the corresponding ellipse. It is
generally
believed that a galaxy with disky isophotes has a disk component; however, only
disks
seen nearly edge-on can be identified by a4 (Carter 1987; Rix &
White 1990). Moreover, there is a relation between a4 and the radio and X-ray
emission (at least for giant ellipticals), in the sense that boxy ellipticals
tend
to be the stronger sources. These correlations are shown in the study of Bender
et al. (1989), who also find that apparently more flattened
galaxies are either disky or boxy, whereas
rounder objects tend to have
![]() (see their Fig. 1). A similar trend
for
dwarf ellipticals as well is shown by Ryden et al. (1999).
Interestingly,
however, these authors find about a
dozen rather flattened galaxies which do not have boxy or disky isophotes,
i.e. strongly flattened
dwarfs
do not show a gap in the distribution of a4 between boxy and disky. We find
the
same behavior in our sample. In Fig. 6 we plot ellipticity versus a4/a*100.
The
lines are the same as in Bender et al. (1989) and bracket the distribution of
giant ellipticals. The general trend that rounder galaxies have
(see their Fig. 1). A similar trend
for
dwarf ellipticals as well is shown by Ryden et al. (1999).
Interestingly,
however, these authors find about a
dozen rather flattened galaxies which do not have boxy or disky isophotes,
i.e. strongly flattened
dwarfs
do not show a gap in the distribution of a4 between boxy and disky. We find
the
same behavior in our sample. In Fig. 6 we plot ellipticity versus a4/a*100.
The
lines are the same as in Bender et al. (1989) and bracket the distribution of
giant ellipticals. The general trend that rounder galaxies have
![]() seems
to be valid for giants as well as for dwarfs. On the other hand, we find
flattened
dwarfs
(
seems
to be valid for giants as well as for dwarfs. On the other hand, we find
flattened
dwarfs
(
![]() )
with
)
with
![]() - in contrast to the findings for giants
and
in
agreement with Ryden et al. (1999).
- in contrast to the findings for giants
and
in
agreement with Ryden et al. (1999).
However, in view of the profiles for a4 shown in Fig. 1, the significance of
its
weighted average is not so evident. Most of the profiles show large scattering
and
frequently change between the boxy and disky regime. Others have a boxy inner
part and a disky outer part (or vice versa), rendering it difficult to asses a
unique
interpretation to the whole galaxy. For instance, VCC 1093 is strongly disky
in the
central parts, but has nevertheless a negative global
![]() .
O. Lehmann (diploma thesis, Basel 2002, unpublished)
has tried to reproduce the a4 profiles of a number of individual
cases
with multi-component models. By evaluating a best set of component parameters a
satisfactory solution could indeed be found for most dwarfs. However, these
models are probably not unique, nor do they seem to be physically very
meaningful,
as Stiavelli et al. (1991) have shown that the isophotal shape of being
either boxy or disky might depend on the viewing angle.
A more promising approach would involve 3D models along the lines of Ryden
(1992).
.
O. Lehmann (diploma thesis, Basel 2002, unpublished)
has tried to reproduce the a4 profiles of a number of individual
cases
with multi-component models. By evaluating a best set of component parameters a
satisfactory solution could indeed be found for most dwarfs. However, these
models are probably not unique, nor do they seem to be physically very
meaningful,
as Stiavelli et al. (1991) have shown that the isophotal shape of being
either boxy or disky might depend on the viewing angle.
A more promising approach would involve 3D models along the lines of Ryden
(1992).
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{ms3537f19.ps}
\end{figure}](/articles/aa/full/2003/31/aa3537/Timg91.gif) |
Figure 6:
Ellipticity versus shape parameter represented as a4/a*100 for
dE, (N)s
(solid circles) and dS0, (N)s (open circles). The lines are the same like in
Fig. 1
of Bender et al. (1989) and indicate the distribution of giant ellipticals.
Shown are
also the |
| Open with DEXTER | |
Nevertheless, for some individual cases the (projected) shape parameter is quite straightforward to interpret. Consider for example the a4-profile of IC 3388 (Fig. 1): all isophotes in the radius range used are disky, hence, it is justified to classify the galaxy as a whole as disky, suggesting that it hosts a disk component. Or NGC 4431, where a hidden bar has been discovered (Barazza et al. 2002): the boxyness of the a4-profile in the central parts clearly reflects the bar and the radius, where the isophotes become disky indicates the extend of the bar.
In general, the nature of dE nuclei is still unknown; mostly they are regarded as massive compact star clusters which form separate dynamical entities, without being totally decoupled from the rest of the galaxy. They might have formed in the last burst of star formation in the evolutionary transition from dwarf irregulars to dEs (Davies & Phillipps 1988). Simulations suggest that such nuclei oscillate about the center of the galaxy (Miller & Smith 1992; Taga & Iye 1998). However, in these simulations the rotation of the main body is a crucial condition, which would not be complied by most of the dwarf ellipticals. On the other hand, Sweatman (1993) showed in his models that oscillations of central objects can also be explained by inherent motions due to statistical fluctuations, without going back to rotation.
More recently it was suggested that the nuclei could be the result
of the merging of several globular clusters which sunk to the center of the
galaxy
through dynamical friction (Lotz et al. 2001). In the same study it was also
shown that
brighter nuclei tend to be in brighter host galaxies. However, a lower globular
cluster specific frequency (SN) suggested for dE, Ns cannot be found; on the
contrary, dE, N have a higher SN than dEs (Miller et al. 1998). Oh & Lin (2000) studied
a
similar scenario including extra galactic tidal perturbations accounting for the
fact that
nucleated dEs are more concentrated to the center of the cluster than
non-nucleated dEs.
In addition, they found that the nuclei may be slightly off-center within
![]() 1 Gyr
after each globular cluster merger event. Indeed, in their study of 78 nucleated
dwarf
ellipticals and dwarf S0s, Binggeli et al. (2000) (hereafter BBJ) found that
1 Gyr
after each globular cluster merger event. Indeed, in their study of 78 nucleated
dwarf
ellipticals and dwarf S0s, Binggeli et al. (2000) (hereafter BBJ) found that
![]() 20% of the objects have off-centered nuclei. They also found a weak
correlation
between the strength of the offset and the effective surface brightness: fainter
objects
tend to have larger offsets. However, since the resolution of their data was
rather low,
the significance of this effect is not clear.
20% of the objects have off-centered nuclei. They also found a weak
correlation
between the strength of the offset and the effective surface brightness: fainter
objects
tend to have larger offsets. However, since the resolution of their data was
rather low,
the significance of this effect is not clear.
We therefore did the same analysis with our data, i.e. for each galaxy we
determined
the distances between the centers of the isophotes and the position of the
nucleus.
In case of an object without nucleus, i.e. for a dE, the innermost isophote was
taken as reference.
Due to the photon noise a small offset is always measured, even in the case of
an
exactly centered nucleus. To assess the resulting systematic and random errors
we followed BBJ and
performed Monte Carlo
simulations for the method described, using model galaxies with nuclei placed at
the
center or slighly offset. It turned out that the noise causes a minimum offset
of
![]() ,
i.e. one pixel length, and that a real offset is always
underestimated,
i.e. offsets measured larger than
,
i.e. one pixel length, and that a real offset is always
underestimated,
i.e. offsets measured larger than
![]() are real and are at the same time
lower limits of the real displacements.
(For details of the measurement and of the error estimation see BBJ.) In Fig. 7
we
plot the logarithm of the nuclear offsets obtained versus effective surface
brightness
in R. Here we distinguish between dEs and dE, N. The dashed line indicates our
lower
detection limit of
are real and are at the same time
lower limits of the real displacements.
(For details of the measurement and of the error estimation see BBJ.) In Fig. 7
we
plot the logarithm of the nuclear offsets obtained versus effective surface
brightness
in R. Here we distinguish between dEs and dE, N. The dashed line indicates our
lower
detection limit of
![]() .
The relation for the dE, Ns is evident: objects with
lower effective surface brightnesses tend to have larger nuclear offsets,
confirming the results of BBJ.
With a correlation coefficient of 0.498 for the 16 dE, Ns, the relation is
significant just at the 95% level.
This cannot be due to larger errors in determining the
position of a
nucleus of a fainter object, as these uncertainties always lead to an
underestimation
of the offsets (see above). We would therefore rather assume that, for example,
the three dE, Ns with
.
The relation for the dE, Ns is evident: objects with
lower effective surface brightnesses tend to have larger nuclear offsets,
confirming the results of BBJ.
With a correlation coefficient of 0.498 for the 16 dE, Ns, the relation is
significant just at the 95% level.
This cannot be due to larger errors in determining the
position of a
nucleus of a fainter object, as these uncertainties always lead to an
underestimation
of the offsets (see above). We would therefore rather assume that, for example,
the three dE, Ns with
![]() have larger offsets than the ones
measured.
have larger offsets than the ones
measured.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{ms3537f20.ps}
\end{figure}](/articles/aa/full/2003/31/aa3537/Timg93.gif) |
Figure 7:
The logarithm of the nuclear offset versus the effective surface
brightness
in R. The dashed line indicates our lower detection limit of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms3537f21.ps}
\end{figure}](/articles/aa/full/2003/31/aa3537/Timg94.gif) |
Figure 8: The logarithm of the nuclear offset versus the residual effective surface brightness, calculated with respect to the mean relation between effective surface brightness and absolute magnitude (in R), for dE, N galaxies only. Dashed line as in Fig. 7. |
| Open with DEXTER | |
We also plot, in Fig. 8,
the nuclear offset versus the deviation of the observed
![]() from the mean
from the mean
![]() expected for the observed luminosity.
The underlying mean relation between absolute magnitude and effective surface
brightness for the 16 dE, N galaxies, to which the residual
expected for the observed luminosity.
The underlying mean relation between absolute magnitude and effective surface
brightness for the 16 dE, N galaxies, to which the residual
![]() values refer,
is given by the equation
values refer,
is given by the equation
![]() .
The relation between
the nuclear offset and the residual surface brightness (Fig. 8) is
indeed stronger than the direct relation (Fig. 7). In particular, the two dE, Ns with
the highest nuclear offsets are not the ones of lowest surface brightness (see Fig. 7),
but they clearly have unusually low surface brightness for their luminosity
(Fig. 8). The correlation coefficient for the relation shown in Fig. 8 is 0.879,
which corresponds to a significance level above 99.9%.
.
The relation between
the nuclear offset and the residual surface brightness (Fig. 8) is
indeed stronger than the direct relation (Fig. 7). In particular, the two dE, Ns with
the highest nuclear offsets are not the ones of lowest surface brightness (see Fig. 7),
but they clearly have unusually low surface brightness for their luminosity
(Fig. 8). The correlation coefficient for the relation shown in Fig. 8 is 0.879,
which corresponds to a significance level above 99.9%.
In the context of the scenarios mentioned above, the relations found in Figs. 7 and 8
might be interpreted as follows: assuming that a central star cluster would
oscillate
around the center of the galaxy, we would expect that the oscillations are the
stronger
the shallower the potential well, i.e. the fainter the
effective surface brightness is - either in an absolute sense (Fig. 7), or
more likely in
a relative sense with respect to the mean value expected for the luminosity
(Fig. 8).
On the other hand, if the nucleus is
the result of the merging of several globular clusters, a correlation between
offset
and
![]() or
or
![]() is not a natural outcome, e.g. Oh & Lin (2000)
do not find a magnification of the effective radius after a merger event in
their models. The
case of simple oscillations is therefore more likely.
is not a natural outcome, e.g. Oh & Lin (2000)
do not find a magnification of the effective radius after a merger event in
their models. The
case of simple oscillations is therefore more likely.
Using the usual range (
![]() )
we
determined the largest isophotal twist,
)
we
determined the largest isophotal twist,
![]() ,
of the galaxies in our
sample
(Col. 10 of Table 3). In Fig. 9 we plot the twists derived versus
ellipticity.
,
of the galaxies in our
sample
(Col. 10 of Table 3). In Fig. 9 we plot the twists derived versus
ellipticity.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms3537f22.ps}
\end{figure}](/articles/aa/full/2003/31/aa3537/Timg97.gif) |
Figure 9:
Isophotal twist,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{ms3537f23.ps}
\end{figure}](/articles/aa/full/2003/31/aa3537/Timg99.gif) |
Figure 10:
Isophotal twist,
|
| Open with DEXTER | |
Besides the twist-ellipticity relation, we also found a weaker correlation
between
twist and effective surface brightness. Thus, a connection between isophotal
twist
and nuclear offset might be expected and is indeed present, at least for the
dE, Ns.
Figure 11 shows that galaxies with stronger twists have larger nuclear
offsets (correlation coefficient for the 16 dE, Ns = 0.506, giving a
statistical significance better than 95%).
As the measurement of the offsets should not be affected by projection
effects,
the origin of the relation in Fig. 11 is difficult to understand. However,
assuming that the isophotal twists are real, the connections between effective
surface brightness/radius, offset, and twist might indicate that less compact
objects also
tend to have stronger anomalies in their isophotal properties.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{ms3537f24.ps}
\end{figure}](/articles/aa/full/2003/31/aa3537/Timg100.gif) |
Figure 11:
Isophotal twist,
|
| Open with DEXTER | |
We provide surface brightness profiles in both filters and radial colour
gradients.
All profiles have been fitted by a Sérsic model and the corresponding
parameters
have been derived. Plotting these best fitting parameters together with the
ones for giant
ellipticals and local group dwarfs versus absolute magnitude (Fig. 2), we
confirm
the finding of Jerjen & Binggeli (1997) and Jerjen et al.
(2000) that the cluster dwarfs perfectly bridge the
gap between giant ellipticals and dwarf spheroidals, indicating that there is
one, continuous family of spheroidal stellar systems, provided
the central few 100 pc of these galaxies is not considered.
However, considering in detail the fits obtained, we find
several profiles with rather large deviations from the models, in particular in
the more central parts. By defining a mean,
absolute residual,
![]() ,
taking into account also the
errors
of the profiles, we find that bright galaxies,
having
,
taking into account also the
errors
of the profiles, we find that bright galaxies,
having
![]() mag, show the strongest deviations from the Sérsic
form.
We suggest that in addition to the objects
with disk structure (spiral or bar) signatures (Jerjen et al.
2000;
Barazza et al. 2002) where strong residuals might be expected, some of
the bright dwarfs may be quite complex in structure, possibly being
two-component
systems as well.
mag, show the strongest deviations from the Sérsic
form.
We suggest that in addition to the objects
with disk structure (spiral or bar) signatures (Jerjen et al.
2000;
Barazza et al. 2002) where strong residuals might be expected, some of
the bright dwarfs may be quite complex in structure, possibly being
two-component
systems as well.
As most of the sample galaxies are nucleated, we have also searched for the
presence
of off-center nuclei. Most nuclei are indeed slightly off center.
Defining ![]() as the offset of the nucleus
from the center of the overall light distribution, we have looked for
systematic relations between
nuclear offsets
and other galaxy properties. We confirm the existence of a relation between
as the offset of the nucleus
from the center of the overall light distribution, we have looked for
systematic relations between
nuclear offsets
and other galaxy properties. We confirm the existence of a relation between ![]() and
the effective surface brightness, which was first suggested by Binggeli et al. (2000): galaxies with fainter effective
surface brightnesses tend to have larger nuclear offsets.
An even stronger relation is found to hold between
and
the effective surface brightness, which was first suggested by Binggeli et al. (2000): galaxies with fainter effective
surface brightnesses tend to have larger nuclear offsets.
An even stronger relation is found to hold between ![]() and the
residual effective radius, determined with respect to the mean relation between
effective surface brightness and absolute magnitude, i.e. dwarfs with lower than
average surface brightness at a given magnitude have larger nuclear offsets.
The most plausible explanation of the phenomenon is that the nuclei
are simply oscillating about the centers in the shallow potential wells of
these galaxies,
as suggested by numerical simulations (Miller & Smith 1992; Taga & Iye 1998).
The shallower the potential well (the lower the surface brightness), the higher
the expected amplitude of the oscillations.
and the
residual effective radius, determined with respect to the mean relation between
effective surface brightness and absolute magnitude, i.e. dwarfs with lower than
average surface brightness at a given magnitude have larger nuclear offsets.
The most plausible explanation of the phenomenon is that the nuclei
are simply oscillating about the centers in the shallow potential wells of
these galaxies,
as suggested by numerical simulations (Miller & Smith 1992; Taga & Iye 1998).
The shallower the potential well (the lower the surface brightness), the higher
the expected amplitude of the oscillations.
In addition, we determined isophotal twists, i.e. the largest changes of the
position angles of the major axes within the range used for the isophotal
analysis.
We find a clear dependence of the twists measured on ellipticity in that
large
twists occur only in galaxies with
![]() .
On the other hand, most of
these
galaxies are likely intrinsically more flattened, as the distribution of
intrinsic
ellipticities has a maximum at
.
On the other hand, most of
these
galaxies are likely intrinsically more flattened, as the distribution of
intrinsic
ellipticities has a maximum at ![]() 0.3.
Assuming that the objects are intrinsically triaxial ellipsoids,
we suggest that the twists observed, always being accompanied by changing
axis ratios, are caused by projection effects.
0.3.
Assuming that the objects are intrinsically triaxial ellipsoids,
we suggest that the twists observed, always being accompanied by changing
axis ratios, are caused by projection effects.
In view of the results of the isophotal analysis we conclude that less compact dwarf galaxies generally tend to have stronger irregularities like off-centered nuclei or twisted isophotes, than more compact systems. However, with the available data we cannot decide whether these properties are caused by external perturbations or are due to the presence of substructures in these objects. Moreover, projection effects may play a crucial role in producing certain isophotal properties. Assuming that dwarf elliptical galaxies are intrinsically triaxial systems, the twists observed could be explained in terms of projection effects caused by changing axial ratios in apparently round galaxies that are intrinsically more flattened.
Acknowledgements
We thank the referee, Dr. N. Caldwell, for his constructive comments. F.D.B. and B.B. are grateful to the Swiss National Science Foundation for financial support.
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{ms3537f01.ps}
\end{figure}](/articles/aa/full/2003/31/aa3537/Timg102.gif) |
Figure 1:
Plots of the basic parameters for the photometry and the isophotal
analysis
versus equivalent radius |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{ms3537f02.ps}
\end{figure}](/articles/aa/full/2003/31/aa3537/Timg103.gif) |
Figure 1: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{ms3537f03.ps}
\end{figure}](/articles/aa/full/2003/31/aa3537/Timg104.gif) |
Figure 1: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{ms3537f04.ps}
\end{figure}](/articles/aa/full/2003/31/aa3537/Timg105.gif) |
Figure 1: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{ms3537f05.ps}\end{figure}](/articles/aa/full/2003/31/aa3537/Timg106.gif) |
Figure 1: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{ms3537f06.ps}\end{figure}](/articles/aa/full/2003/31/aa3537/Timg107.gif) |
Figure 1: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{ms3537f07.ps}\end{figure}](/articles/aa/full/2003/31/aa3537/Timg108.gif) |
Figure 1: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{ms3537f08.ps}\end{figure}](/articles/aa/full/2003/31/aa3537/Timg109.gif) |
Figure 1: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{ms3537f09.ps}\end{figure}](/articles/aa/full/2003/31/aa3537/Timg110.gif) |
Figure 1: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{ms3537f10.ps}\end{figure}](/articles/aa/full/2003/31/aa3537/Timg111.gif) |
Figure 1: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{ms3537f11.ps}\end{figure}](/articles/aa/full/2003/31/aa3537/Timg112.gif) |
Figure 1: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\par\includegraphics[width=13.6cm,clip]{ms3537f12.ps}\end{figure}](/articles/aa/full/2003/31/aa3537/Timg113.gif) |
Figure 1: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{ms3537f13.ps}\end{figure}](/articles/aa/full/2003/31/aa3537/Timg114.gif) |
Figure 1: continued. |
| Open with DEXTER | |