A&A 406, 393-401 (2003)
DOI: 10.1051/0004-6361:20030719
R. Mohayaee1 - U. Frisch1 -
S. Matarrese2 -
A. Sobolevski![]() 1,3
1,3
1 - Département Cassini, Observatoire de la Côte d'Azur,
BP 4229, 06304 Nice Cedex 4, France
2 -
Dipartimento di Fisica "Galileo Galilei'' and INFN, Sezione di
Padova,
via Marzolo 8, 35131 Padova, Italy
3 - Department of Physics, M. V. Lomonossov Moscow State
University, 119992 Moscow, Russia
Received 12 March 2003 / Accepted 12 May 2003
Abstract
A new method for
reconstruction of the
primordial density fluctuation field
is presented.
Various previous approaches to this problem rendered non-unique
solutions. Here,
it is demonstrated that the initial positions of dark matter
fluid elements, under the hypothesis
that their displacement is the gradient of a convex potential, can
be reconstructed uniquely.
In our approach, the cosmological reconstruction
problem is reformulated as an assignment problem
in optimization theory. When tested against numerical simulations,
our scheme yields excellent reconstruction on scales larger than a few
megaparsecs.
Key words: reconstruction - Lagrangian methods - convexity - optimization
The present distribution of galaxies brought to us by redshift surveys indicates that the Universe on large scales exhibits a high degree of clumpiness with coherent structures such as voids, great walls, filaments and clusters. The cosmic microwave background (CMB) explorers, however, indicate that the Universe was highly homogeneous billions of years ago. When studying these data, among the questions that are of concern in cosmology are the initial conditions of the Universe and the dynamics under which it grew into the present Universe. CMB explorers provide us with valuable knowledge into the initial conditions of the Universe, but the present distribution of the galaxies opens a second, complementary window on the early Universe.
Unravelling the properties of the early Universe from the present data is an instance of the general class of inverse problems in physics. In cosmology this problem is frequently tackled in an empirical way by taking a forward approach. In this approach, a cosmological model is proposed for the initial power spectrum of dark matter. Next, a particle representation of the initial density field is made which provides the initial data for an N-body simulation which is run using Newtonian dynamics and is stopped at the present time. Subsequently, a statistical comparison between the outcome of the simulation and the observational data can be made, assuming that a suitable bias relation exists between the distribution of galaxies and that of dark matter. If the statistical test is satisfactory then the implication is that the initial condition was viable; otherwise one changes the cosmological parameters and goes through the whole process again. This is repeated until one obtains a satisfactory statistical test, affirming a good choice for the initial condition.
However, this inverse problem does not have to be necessarily dealt with in a forward manner. Can one fit the present distribution of the galaxies exactly rather than statistically and run it back in time to make the reconstruction of the primordial density fluctuation field? The Newtonian gravity is time-reversible; therefore, had the present velocities of the galaxies been known in addition to their positions, one would have been able to integrate the equations of motions back in time and solve the reconstruction problem trivially. As a matter of fact, however, the peculiar velocities of only a few thousands of galaxies are known out of the hundreds of thousands whose redshifts have been measured. Indeed, one goal of reconstruction is to evaluate the peculiar velocities of the galaxies and in this manner put direct constraints on cosmological parameters.
Without a second boundary condition, reconstruction would thus be an infeasible task. For reconstruction so far we have only mentioned the present positions of the galaxies. The second condition is the homogeneity of the initial density field: as we go back in time, the peculiar velocities of the galaxies vanish. This corresponds to discarding the decaying mode, which is the assumption used throughout this paper (see also discussion in Sect. 2.1 of Brenier et al. 2003). Thus, contrary to the forward approach where one solves an initial-value problem, in the reconstruction approach one is dealing with a two-point boundary value problem. In the former, one starts with the initial positions and velocities of the particles and solves Newton's equations arriving at a unique final position and velocity for a given particle (with certain mathematical reservations discussed, e.g., by Buchert & Ehlers 1997; Ehlers & Buchert 1997). In the latter one does not always have uniqueness. This has been one of the shortcomings of reconstruction, which was consequently taken to be an ill-posed problem.
In this work, we report on a new method of reconstruction which guarantees uniqueness. In Sect. 2, we review the previous works on reconstruction. We describe our mathematical formulation of reconstruction problem in Sect. 3 and show that cosmological reconstruction problem, under our hypotheses, is an instance of an assignment problem in optimization theory. In Sect. 4, we describe the numerical algorithms to solve the assignment problem. In Sect. 5, we test our reconstruction method with numerical N-body simulation both in real and redshift spaces.
The history of reconstruction goes back to the work of Peebles
(Peebles 1989) on tracing the orbits of the members of the local
group. In his approach, reconstruction was solved as a variational
problem. Instead of solving the equations of motion, one searches for
the stationary points of the corresponding Euler-Lagrange action. The
action in the comoving coordinates is (Peebles 1980)
![\begin{displaymath}\delta S=
\int_0^{t_0}
{\rm d}t
\left[
{\partial {\cal L}\ove...
...artial\dot{\vec{x}}_i}\cdot{\delta\dot{\vec{x}}_i}
\right]
=0,
\end{displaymath}](/articles/aa/full/2003/29/aah4384/img28.gif) |
(2) |
The components
![]() of the orbit of the ith particle are
modelled as
of the orbit of the ith particle are
modelled as
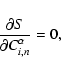 |
(6) |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{peebles.ps}\end{figure}](/articles/aa/full/2003/29/aah4384/Timg38.gif) |
Figure 1: A schematic demonstration of Peebles' reconstruction of the trajectories of the members of the local neighbourhood using a variational approach based on the minimization of the Euler-Lagrange action. In most cases there is more than one allowed trajectory due to orbit crossing (closely related to the multistreaming of the underlying dark matter fluid). The pink (darker) orbits correspond to taking the minimum of the action whereas the yellow (brighter) orbits were obtained by taking the saddle-point solution. Of particular interest is the orbit of N6822 which in the former solution is on its first approach towards us and in the second solution is in its passing orbit. A better agreement between the evaluated and observed velocities was shown to correspond to the saddle point solution. |
| Open with DEXTER | |
Although rather successful when applied to catalogues such as NBGC (Tully 1988), reconstruction with such an aim, namely establishing bounds on cosmological parameters using measured peculiar velocities, could not be applied to larger galaxy redshift surveys, containing hundreds of thousands of galaxies for the majority of which the peculiar velocities are unknown. For large datasets, it is not possible to use the velocities to choose the right orbit from the many physically possible ones. In order to resolve the problem of multiple solutions (the existence of many mathematically possible orbits) one normally had to do significant smoothing and then try the computationally costly reconstruction using Peebles variational approach (Shaya et al. 1995; Branchini et al. 2001). However, one was still not guaranteed to have chosen the right orbit (see Hjortland 1999 for a review of the action variational method).
The multiple solution can be caused by various factors. For example, the discretization in the numerical integrations (7) can produce spurious valleys in the landscape of the Euler-Lagrange action. However, even overcoming all these numerical artifacts one is still not guaranteed uniqueness. There is a genuine physical reason for the lack of uniqueness which is often referred to in cosmology as multistreaming.
Cold dark matter (CDM) is a collisionless fluid with no velocity dispersion. An important feature that arises in the course of the evolution of a self-gravitating CDM Universe is the formation of multistream regions on which the velocity field is non-unique. These regions are bounded by caustics at which the density is divergent. At a multistream point where velocity is multiple-valued, a particle can have many different mathematically viable trajectories each of which would correspond to a different stationary point of the Euler-Lagrange action which is no longer convex.
In addition to variational approach to reconstruction, there is the well-known POTENT reconstruction of the three-dimensional velocity field from its radial component (Dekel et al. 1990). The POTENT method is the non-iterative Eulerian version of the earlier iterative Lagrangian method (Bertschinger & Dekel 1989) and assumes potential flow in Eulerian space. POTENT finds the velocity potential field by integrating the radial components of the velocities along the line of sight. Being an Eulerian method, its validity does not extend much beyond the linear Eulerian regime.
In following works, using POTENT reconstructed velocity field or the density field obtained from the analysis of the redshift surveys, the gravitational potential field was also reconstructed (Nusser & Dekel 1992). The gravitational potential was then traced back in time using the so-called Zel'dovich-Bernoulli equation which combines the Zel'dovich approximation with the Euler momentum conservation equation. Later on, it was further shown (Gramann 1993) that the initial gravitational potential is more accurately recovered using the Zel'dovich-continuity equation which combines the Zel'dovich approximation with the mass continuity equation (Nusser et al. 1991). For a summarizing discussion of various inversion techniques see, e.g., Susperregi & Buchert (1997).
However, these procedures are valid only as long as the density
fluctuations are in the Eulerian linear or quasi-linear regimes
(defined by
![]() ).
They do not robustly recover the initial
density in regions of high density
where the present-day structures are highly nonlinear
(
).
They do not robustly recover the initial
density in regions of high density
where the present-day structures are highly nonlinear
(
![]() ). Therefore, they
require that the final density field be
smoothed quite heavily to remove
any severe nonlinearities, before the dynamical evolution equations
are integrated backward in time.
). Therefore, they
require that the final density field be
smoothed quite heavily to remove
any severe nonlinearities, before the dynamical evolution equations
are integrated backward in time.
Here, we describe a new method of reconstruction (Frisch et al. 2002) which not only overcomes the problem of nonuniqueness encountered in the least-action-based methods but also remains valid well beyond linear Eulerian approximations employed in many other popular reconstruction methods, few of which we have discussed.
Thus, reconstruction is a well-posed problem for as long as we avoid
multistream regions. The mathematical formulation of this problem is as
follows (Frisch et al. 2002). Unlike most of the previous works
on reconstruction where one studies the
Euler-Lagrange action, we start from a constraint equation, namely the mass
conservation,
| (8) |
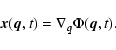 |
(10) |
| (11) |
| ; | (12) |
![\begin{displaymath}\delta I=\int_{\vec{x}} \left[2\rho(\vec{x})(\vec{x}-\vec{q})
\cdot \delta \vec{x}\right] {\rm d}^3x,
\end{displaymath}](/articles/aa/full/2003/29/aah4384/img60.gif) |
(15) |
| (16) |
Discretising the cost (14) into equal mass units yields
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{piza-marseille.ps}
\end{figure}](/articles/aa/full/2003/29/aah4384/Timg71.gif) |
Figure 2:
Solving the reconstruction problem as an assignment problem. An example of a
system of N=9 particles is sketched. The cost matrix is shown. For
example the entry C32 is the cost of getting from the Lagrangian
position |
| Open with DEXTER | |
If one were to solve the assignment problem for N particles directly, one would need to search among N! possible permutations for the one which has the minimum cost. However, advanced assignment algorithms exist which reduce the complexity of the problem from factorial to polynomial (so far at best to approximately N2.5 for our problem as verified by numerical tests, e.g., Burkard & Derigs 1980 and Bertsekas 1998). Before discussing these methods, let us briefly comment on a class of stochastic algorithms, which do not give uniqueness and hence should be avoided.
In the PIZA method of solving the assignment problem (Croft & Gaztañaga 1997),
initially a random
pairing between N Lagrangian and
N Eulerian coordinates is made. Starting from this initial random one-to-one
assignment, subsequently a pair (corresponding to two Eulerian and
two Lagrangian positions) is chosen at random.
For example, let us consider the randomly-selected pair
![]() and
and
![]() which have been assigned in the initial random
assignment to
which have been assigned in the initial random
assignment to ![]() and
and ![]() respectively. Next one swaps
their Lagrangian coordinates and assigns
respectively. Next one swaps
their Lagrangian coordinates and assigns ![]() to
to ![]() and
and ![]() to
to ![]() in this example. If
in this example. If
| (18) |
In spite of these problems associated with PIZA-type algorithms in solving the assignment problem, it has been shown (Narayanan & Croft 1999) in a point-by-point comparison of the reconstructed with the true initial density field from a N-body simulation, that PIZA performs better than other methods such as those based on Eulerian formulation of Zel'dovich approximation (discussed at the end of Sect. 2). There are various deterministic algorithms which guarantee that the optimal assignment is found. An example is an algorithm written by Hénon (Hénon 1995), demonstrated in Fig. 4. In this approach, a simple mechanical device is built which solves the assignment problem. The device acts as an analog computer: the numbers entering the problem are represented by physical quantities and the equations are replaced by physical laws.
One starts with N columns Bs (which represent the Lagrangian positions of the particles) and N rows, As (which represent the Eulerian positions of the particles). On each row there are N studs whose lengths are directly related to the distances between that row and each column. The columns are given weights of 1 and the rows act as floats and are given negative weights of -1.
The potential energy of the system shown in Fig. 4,
within an additive constant, is
Initially, all rods are maintained at a fixed position by two additional rods P and Q with the row Ai
above column Bj, so that there is no contact
between the rows and the studs. Next, the rods are released by removing the
holds P and Q and the system starts evolving: rows go down
and columns go
up and the contacts are made with the studs. Aggregates of rows and columns
are progressively formed. As new contacts are made, these aggregates are
modified and thus a complicated evolution
follows which is graphically demonstrated with a
simple example in Fig. 5. One can then show that an
equilibrium where the potential energy (19) of the system is minimum
will be reached after a finite time. It can then be shown that if the
system is in equilibrium and the column Bj is in contact with row Aithen the force fij is the optimal solution of the assignment problem. The
potential energy of the corresponding equilibrium is equivalent to the total
cost of the optimal solution.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{exactpizaseed1-exactpizaseed2-2.ps}
\end{figure}](/articles/aa/full/2003/29/aah4384/Timg77.gif) |
Figure 3: The lack of uniqueness in the results of two runs using a stochastic algorithm to solve the assignment problems. In the stochastic algorithm, based on pair-interchange, one searches for, what is frequently referred to in pure mathematics as, a monotonic map instead of a true cyclic monotone map. The red and blue points (stars and boxes respectively) are the perfectly-reconstructed Lagrangian positions using the same stochastic code with two different random seeds. The outputs of the two runs do not coincide, meaning that the reconstructed Lagrangian positions (and hence peculiar velocities) depend on the initial random assignment and on the random pair interchange. The lack of uniqueness in this case is superficial and a shortcoming of the chosen numerical method. Such difficulties do not arise when deterministic algorithms are used to solve the assignment problem. |
| Open with DEXTER | |
Thus, in our reconstruction method, the initial positions of the particles are uniquely found by solving the assignment problem. This result was based on our reconstruction hypothesis. We could test the validity of our hypothesis by direct comparison with numerical N-body simulations which is what we shall demonstrate later in this section. However, it is worth commenting briefly on the theoretical, observational and numerical justifications for our hypothesis. It is well-known that the Zel'dovich approximation (Zel'dovich 1970) works well in describing the large-scale structure of the Universe. In the Zel'dovich approximation particles move with their initial velocities on inertial trajectories in appropriately redefined coordinates. It is also known that the Zel'dovich approximation may be written as the first order of a systematic Lagrangian perturbation theory (Buchert 1992) and that in the absence of the decaying mode the irrotationality of the particle displacements (expressed in Lagrangian coordinates) remains valid even at the second-order in the Lagrangian perturbation theory (Moutarde et al. 1991; Buchert 1994; Catelan 1995). This provides the theoretical motivation for our first hypothesis.
The lack of transversally extended multistream regions is confirmed by the geometrical properties of the cosmological structures. In the presence of significant multistreaming such as the one that occurs in the Zel'dovich approximation, one could not expect the formation of long-lived structures such as filaments and great walls which is observed in numerical N-body simulations: these structures would form and would smear out and disappear rapidly. This is not backed by numerical simulations. The latter show the formation of concentrated shock-like structures described well by the Burgers model (a model of shock formation and evolution in a compressible fluid), which has been extensively used to describe the large-scale structure of the Universe (Gurbatov & Saichev 1984; Shandarin & Zel'dovich 1989). The success of Burgers model indicates that a viscosity-generating mechanism operates at small scales in collisionless systems resulting in the formation of shock-like structures rather than caustic-like structures (a related discussion may be found in Buchert & Dominguez 1998).
In spite of this evidence in support of our reconstruction
hypothesis, one needs to test it before applying it
to real galaxy catalogues.
We have tested our reconstruction against numerical N-body simulation. We ran
a ![]() CDM simulation of 1283 dark matter particles, using the
adaptive P3M code HYDRA (Couchman et al. 1995). Our cosmological
parameters are
CDM simulation of 1283 dark matter particles, using the
adaptive P3M code HYDRA (Couchman et al. 1995). Our cosmological
parameters are
![]() and a box size of
200 Mpc/h. We took two sparse samples
of 17 178 and 100 000 particles corresponding
to grids of 6 Mpc and 3 Mpc respectively, at z=0 and
placed them initially on a uniform grid.
For the 17 178 particle reconstruction,
the sparse sampling was done by first selecting a
subset of 323 particles on a regular Eulerian grid
and then selecting all the particles which remained inside a
spherical cut of radius half the size
of the simulation box.
The sparse sample of 100 000 points was made randomly.
An assignment algorithm, similar
to that of Hénon described in
Figs. 4 and 5,
is used
to find the correspondences between the Eulerian and the Lagrangian
positions. The results of our test are shown in Fig. 6.
and a box size of
200 Mpc/h. We took two sparse samples
of 17 178 and 100 000 particles corresponding
to grids of 6 Mpc and 3 Mpc respectively, at z=0 and
placed them initially on a uniform grid.
For the 17 178 particle reconstruction,
the sparse sampling was done by first selecting a
subset of 323 particles on a regular Eulerian grid
and then selecting all the particles which remained inside a
spherical cut of radius half the size
of the simulation box.
The sparse sample of 100 000 points was made randomly.
An assignment algorithm, similar
to that of Hénon described in
Figs. 4 and 5,
is used
to find the correspondences between the Eulerian and the Lagrangian
positions. The results of our test are shown in Fig. 6.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{henonmarseille-1.ps}
\end{figure}](/articles/aa/full/2003/29/aah4384/Timg79.gif) |
Figure 4: Hénon's mechanical device which solves the assignment problem. The device acts as an analog computer. The rows Ai remain parallel to the y axis, are constrained to move vertically and have positive weights. The columns Bj remain parallel to the x axis, can only move vertically and have negative weights. Vertical studs are placed on the columns, in such a way that each stud enforces a minimal distance between row Ai and column Bj. Initially all rods are kept at fixed positions by stops Pand Q. Then the rods are released by removing the stops Q and P and the system starts evolving. Rows go down and columns go up and aggregates of rows and columns are made. Thus a complex evolution takes place. The rules for the formation of aggregates is demonstrated by a simple example in the figure that follows. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{henonmarseille-2.ps}
\end{figure}](/articles/aa/full/2003/29/aah4384/Timg80.gif) |
Figure 5:
A step-by-step ((a) to (l)) progress of Hénon's algorithm on a simple
example with three initial and final positions (columns and rows) is shown.
The table on the top right shows the values of the costs (distances between
rows and columns). When executing the algorithm by hand, it is convenient
to keep track of the distances between the rows and the studs, i.e. the
quantities
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{fig2-periodic-1-10to4.ps}
\end{figure}](/articles/aa/full/2003/29/aah4384/Timg84.gif) |
Figure 6:
Test of MAK reconstruction of the Lagrangian positions,
using a |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{mak1-piza_nonmonotonic_seed1.ps}
\end{figure}](/articles/aa/full/2003/29/aah4384/Timg85.gif) |
Figure 7: A comparison of a PIZA-type, stochastic method, versus our MAK, deterministic method of solving the assignment problem is shown. The outputs of the simulation used for Fig. 6 have also been used here. In the stochastic method, almost one billion pair interchanges are made, at which point the cost-reduction cannot be reduced anymore. However, even with such a large number of interchanges, the number of exactly reconstructed points is well below that achieved by MAK. The upper sets are the scatter plots of reconstructed versus simulation Lagrangian positions for PIZA (left top set) and for MAK (right top set). The lower sets are histograms of the distances between the reconstructed Lagrangian positions and those given by the simulation. The bin sizes are taken to be slightly less than one mesh. Hence, all the points in the first (darker) bin correspond to those which have been exactly reconstructed. Using PIZA, we achieve a maximum of about 5000 out of the 17 178 points exactly-reconstructed positions whereas with MAK this number reaches almost 8000 out of 17 178 points. Note that, for the sole purpose of comparing MAK with PIZA it is not necessary to account for periodicity corrections, which would improve both performances equally. Accounting for the periodicity improves exactly-reconstructed MAK positions to almost 11 000 points out of 17 178 points used for reconstruction, as shown in the upper inset of Fig. 6. Starting with an initial random cost of about 200 million (Mpc/h)2 (5000 in our box unit which runs from zero to one), after one billion pair interchange, a minimum cost of about 1 960 000 (Mpc/h)2 (49 in our box unit) is achieved. Continuing to run the code on a 2 GHz DEC alpha workstation, consuming almost a week of CPU time, does not reduce the cost any further. With the MAK algorithm, the minimum cost is achieved, on the same machine, in a few minutes. The cost for MAK is 1 836 000 (Mpc/h)2 (45.9 in box units) which is significantly lower than the minimum cost of PIZA. Considering that the average particle displacement in one Hubble time is about 10 Mpc/h (about 1/20 of the box size) this discrepancy between MAK and PIZA costs is rather significant. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{redshift-mak-sim.ps}
\end{figure}](/articles/aa/full/2003/29/aah4384/Timg86.gif) |
Figure 8:
Reconstruction test in redshift space with the same data as that used for
real-space reconstruction tested in the
upper left histogram of Fig. 6. The velocities are smoothed
over a sphere of radius 2 Mpc/h. The
observer is taken to be at the centre of the simulation box.
The Lagrangian reconstructed points are plotted against the simulation
Lagrangian positions using the quasi-periodic projection coordinates used
for the scatter plot of Fig. 6.
The histogram corresponds to the distances between the
reconstructed and the simulation Lagrangian positions
for each Eulerian position.
The bins of the histogram
are smaller than one mesh and the first one corresponds to
exactly-reconstructed Lagrangian positions. We obtain |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{redshiftmak-realmak.ps}
\end{figure}](/articles/aa/full/2003/29/aah4384/Timg87.gif) |
Figure 9:
Comparison of redshift versus real space reconstruction allows a test of the
robustness of MAK reconstruction against systematic errors. The same data
as those used for Fig. 8 has been used to obtain the
above result. In both real and redshift space,
large number (almost |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{failed.ps}
\end{figure}](/articles/aa/full/2003/29/aah4384/Timg88.gif) |
Figure 10:
A thin slice (26 Mpc/h) of the box (of sides 200 Mpc/h) of
the
|
| Open with DEXTER | |
It is instructive to compare our results presented in Fig. 6
with those obtained by a stochastic PIZA-type algorithm.
Figure 7 demonstrates such a comparison.
We see that not only the stochastic algorithms do not guarantee uniqueness,
as demonstrated in Fig. 3,
but also the number of exactly reconstructed points by these algorithms are
much below those obtained by our deterministic algorithm.
When reconstructing from observational data, in redshift space, the galaxies
positions are displaced radially by an amount proportional to the radial
component of the peculiar velocity in the line of sight.
Thus for real catalogues, the cost minimization need be performed using redshift
space coordinates (Valentine et al. 2000).
The redshift position of a galaxy is given by
| (21) |
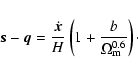 |
(23) |
We have also performed MAK reconstruction with the redshift-modified cost function which led to somewhat degraded results but at the same time provided an approximate determination of peculiar velocities (see Fig. 8). More accurate a determination of peculiar velocities can be made using second-order Lagrangian perturbation theory (Buchert & Ehlers 1993; Munshi et al. 1994). Therefore the question that one asks at this point is: where does reconstruction perform poorly? In Fig. 10 we have demonstrated this fact, by highlighting the points where reconstruction fails by more than 6 Mpc/h. A plot of the distance between the reconstructed and simulated Lagrangian positions versus the density in a sphere of about 5 Mpc/h confirms that, as expected, reconstruction becomes less accurate in the denser regions. Figure 10 highlights where exact reconstruction fails. We see that exact reconstruction is not achieved in particular in the dense regions. Achieving reconstruction at small scales remains a subject of on-going research. As long as multistreaming effects are unimportant, that is above a few megaparsecs, uniqueness of the reconstruction is guaranteed. Approximate algorithms capturing such highly nonlinear effects are now being developed.
Acknowledgements
We thank E. Branchini, T. Buchert, M. Hénon, J. A. de Freitas Pacheco and P. Thomas for discussions and comments. U.F. thanks the Indo-French Center for the Promotion of Advanced Research (IFCPAR 2404-2). A.S. is supported by a CNRS Henri Poincaré fellowship and RFBR 02-01-01062. R.M. is supported by the European Union Marie Curie Fellowship HPMF-CT-2002-01532.