The analysis of forbidden lines, such as E2 and M1, in the atomic spectra emitted by certain ions is important for the study of the plasma in astrophysical objects and fusion devices. Transition rates between
A&A 406, 741-749 (2003)
DOI: 10.1051/0004-6361:20030660
E. Charro - S. López-Ferrero - I. Martín
Departamento de Química Física, Universidad de Valladolid, 47011 Valladolid, Spain
Received 23 December 2002 / Accepted 2 April 2003
Abstract
The analysis of forbidden lines, such as E2 and M1,
in the atomic spectra emitted by certain ions is
important for the study of the plasma in
astrophysical objects and fusion devices.
Transition rates between
![]() and
and
![]() levels in
levels in
![]() ions that belong to
the aluminium sequence have
been calculated with the
Relativistic Quantum Defect Orbital (RQDO)
method. The present data
are tested by comparison with other
theoretical data available in the literature, and
the regularity of the transition intensities along
the isoelectronic sequence for both (E2 and M1) lines,
as well as their competition, are also analysed.
ions that belong to
the aluminium sequence have
been calculated with the
Relativistic Quantum Defect Orbital (RQDO)
method. The present data
are tested by comparison with other
theoretical data available in the literature, and
the regularity of the transition intensities along
the isoelectronic sequence for both (E2 and M1) lines,
as well as their competition, are also analysed.
Key words: atomic data - methods: numerical
Within the last few years, the determination of atomic
oscillator strengths and related properties for
ionized systems has been an active research
area on account of its considerable interest in
astrophysics, plasma physics, laser physics and
thermonuclear fusion research.
In astrophysics, transitions from metastable
levels of highly ionized atoms are observed
in emission in low-density media.
It is well known that line intensities and ratios
provide excellent diagnostics for temperature
and density and consequently for
elemental abundances (Feldman 1981; Herter et al. 1982). In
the laboratory,
the
![]() configurations of medium-Z
elements have attracted considerable attention
in recent years as spectroscopic diagnostics in Tokamak plasmas. This
is due to the fact that they may give rise to strong lines at much longer
wavelengths (
configurations of medium-Z
elements have attracted considerable attention
in recent years as spectroscopic diagnostics in Tokamak plasmas. This
is due to the fact that they may give rise to strong lines at much longer
wavelengths (
![]() Å) than other transitions in the same ion.
However, it is still difficult to measure accurately
oscillator strengths, particularly
for highly ionizad atoms where the available experimental
techniques have
limitations, and the reproduction in the laboratory
of the very extreme conditions
to which the constituents of the universe are
subjected is extremely difficult.
Å) than other transitions in the same ion.
However, it is still difficult to measure accurately
oscillator strengths, particularly
for highly ionizad atoms where the available experimental
techniques have
limitations, and the reproduction in the laboratory
of the very extreme conditions
to which the constituents of the universe are
subjected is extremely difficult.
Experimental transition rates for forbidden lines are scarce and, in most cases, missing when the degree of ionization is higher than 2. It is therefore necessary to rely upon theoretical values. One way to assess the quality of a given theoretical method is a comparison of the so-obtained results with some other measurable quantity which might be available (mostly the observed energies), and by comparison with the results supplied by other computers codes.
On the theoretical side, quantum-mechanical calculations have, thus, become crucial in the accomplishment of these goals. Wiese (1987) long pointed out the usefulness of procedures which account for relativistic effects, the mass production of data for complex atomic systems with increasingly refined semiempirical approaches; and the application of regularities among transition rates, such as the dependence on the nuclear charge, for the scaling of transition rates along isoelectronic sequeces or spectral series.
Many calculations have been done for the ions isoelectronic with Al, most of them corresponding to allowed transitions. In this context, we have reported oscillator strengths corresponding to dipole-allowed transitions for a group of Al-like ions ( Z = 13 - 103) in a previous paper (Lavín et al. l997), in which the Relativistic Quantum Defect Orbital (RQDO) method, was employed. For forbidden transitions, no data have been reported with this method for this sequence before the present calculations.
Certain forbbiden transitions only become possible through the fine-structure
splitting of an LS term into a series of J levels. Examples are
the M1 and E2 transitions between the
![]()
![]() and
and
![]()
![]() levels in
the aluminium sequence. In the
non-relativistic approximation, these levels are degenerate.
Calculations for the 3p
levels in
the aluminium sequence. In the
non-relativistic approximation, these levels are degenerate.
Calculations for the 3p
![]()
![]() transition, corresponding to both E2 and M1 forbidden mechanisms, have presently been
performed with the RQDO
method, for the aluminium-like elements ranging
from Sc IX (Z = 21) to Hg LXVIII (Z = 80).
It is well known that fine-structure lines are interesting from
a spectroscopic point of view, given their usefulness in spectral
analysis in astrophysics and fusion plasma research.
transition, corresponding to both E2 and M1 forbidden mechanisms, have presently been
performed with the RQDO
method, for the aluminium-like elements ranging
from Sc IX (Z = 21) to Hg LXVIII (Z = 80).
It is well known that fine-structure lines are interesting from
a spectroscopic point of view, given their usefulness in spectral
analysis in astrophysics and fusion plasma research.
The systematic trend of the A-values for E2 and M1 transitions along the isoelectronic sequence has also been analysed in this work. In previous works (e.g., Lavín et al. l997) we studied the systematic trends of E1 spectral lines. The regular behaviour of oscillator strengths along isoelectronic sequences has proven to be a useful tool for analysing a large body of f-value data. It may also be exploited to obtain additional oscillator strengths by simple interpolation techniques (Martin & Wiese 1996).
Some theoretical E2 and M1 transition rates for
aluminium-like elements
are available in the
literature. The most extensive group of data
has been published by
Huang (1986), who calculated transition
rates for the ions comprised in the
![]() range with the multiconfiguration Dirac-Fock (MCDF) technique.
range with the multiconfiguration Dirac-Fock (MCDF) technique.
In the present work, we deal with heavy ions and in high degree of ionization for which the relativistic contributions to the wavefunctions and energies of the levels involved in the transitions may not be negligible. We have consequently followed a theoretical method that gives explicit account of relativistic effects, the Relativistic Quantum Defect Orbital (RQDO) formalism, as mentioned above.
For over a decade, we have applied the RQDO method (Martín & Karwowski 1991; Karwowski & Martín 1991; Martín et al. 2000) to the calculation of atomic data in several isoelectronic sequences (see, e.g. Martín et al. 1993; Lavín et al. 1997; Charro & Martín 1998; Charro et al. 1996, 1997, 2000, 2001). The RQDO formalism, as opposed to sophisticated and costly self-consistent-field procedures, is a simple but reliable analytical method based on a model Hamiltonian. It has the great advantage that the computational effort is not increased for Z-high systems. The convenience of employing exactly solvable model potentials for calculating atomic transition rates manifests itself not only from a practical point of view but also because of the involved physical implications, when they are capable of achieving a good balance between computational effort and accuracy of results. In the present calculations, a general good accord between the RQDO transition probabilities and the comparative theoretical data is also found.
The Relativistic Quantum Defect Orbital (RQDO) method has been described in detail in previous papers (Karwowski & Martín 1991; Martín et al. 2000). Therefore, we shall only briefly summarise its most fundamental aspects.
The relativistic formulation of the Quantum Defect Orbital (QDO) formalism, as developed by Martín & Karwowski (1991) and Karwowski & Martín (1991) was based on the decoupling of the Dirac second-order equation, and in the interpretation of the resulting solutions that had been carried out by Karwowski & Kobus (1985, 1986). These authors generalised the decoupling procedure of Biedenharn (1962) in such a way that it may be applied to the case of a general atomic spherical potential. They also showed that both the large and small components of the Dirac wavefunction may be recovered without any computational effort.
The quantum defect orbitals are solutions of the Schr
![]() dinger equation
(Simons 1974; Martín & Simons 1975, 1976)
dinger equation
(Simons 1974; Martín & Simons 1975, 1976)
![\begin{displaymath}\left[- \frac{{\rm d}^2}{{\rm d}r^2}~ + \frac{\chi (\chi + 1 ...
...~ \right] {\psi_k}^{\rm QD} = 2 E^{\rm QD} {\psi_k}^{\rm QD},
\end{displaymath}](/articles/aa/full/2003/29/aa3440/img19.gif) |
(1) |
| (2) |
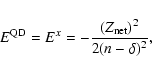 |
(3) |
Analogously to the nonrelativistic case, Eq. (1), the RQDO equation is written as
![\begin{displaymath}\left[- \frac{{\rm d}^2}{{\rm d}r^2}~ + \frac{\Lambda(\Lambda...
...~ \right] {\psi_k}^{\rm RD} = 2 e^{\rm RD} {\psi_k}^{\rm RD},
\end{displaymath}](/articles/aa/full/2003/29/aa3440/img26.gif) |
(4) |
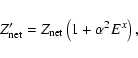 |
(5) |
| (6) |
| (7) |
The relativistic quantum defect is determined empirically.
We have
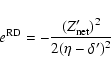 |
(8) |
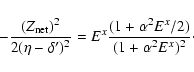 |
(9) |
| (10) |
The most important difference between the RQDO and QDO equations is the explicit dependence of the former on the total angular momentum quantum number k. As a consequence, values of the relativistic quantum defect are determined from the fine structure energies rather than from their centers of gravity. The corresponding relativistic quantum defect orbitals are different for each component of a multiplet and, if c = 0, they retain the nodal structure of the large components of the hydrogenic Dirac wave function.
The Relativistic Quantum Defect Orbital is expressed in terms of Kummer's
functions,
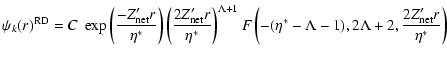 |
(11) |
![\begin{displaymath}C~ = \left(\frac {2Z'_{\rm net} }{\eta^* }\right)^{1/2} \left...
... - \Lambda )}\right]^{1/2} \frac {1}{ \Gamma (2 \Lambda + 2)}
\end{displaymath}](/articles/aa/full/2003/29/aa3440/img37.gif) |
(12) |
Since the effective Hamiltonian
in Eq. (4) includes a screening term, the relativistic
quantum defect orbitals are
approximately valid in the core region of space. Core
polarization effects are implicitly included in the calculations, as
they are accounted for in the ![]() parameter
of the model Hamiltonian. On the other hand, given the one-electron nature of the RQDO formalism, it can be expected to perform better in highly excited states, where the active electron interacts less with the core and other valence electrons, than in low-lying energy states. The relativistic
quantum defect orbitals lead to closed-form analytical expresions for
the transition integrals. This allows one to calculate transition
probabilities and oscillator strengths by simple algebra
and with high computational costs/efficiency ratio.
parameter
of the model Hamiltonian. On the other hand, given the one-electron nature of the RQDO formalism, it can be expected to perform better in highly excited states, where the active electron interacts less with the core and other valence electrons, than in low-lying energy states. The relativistic
quantum defect orbitals lead to closed-form analytical expresions for
the transition integrals. This allows one to calculate transition
probabilities and oscillator strengths by simple algebra
and with high computational costs/efficiency ratio.
The RQDO methodology supplies one-electron radial wavefunctions, characterized by the n, l and j quantum numbers (Martín & Karwowski 1991), that we employ in the transition matrix elements for the initial and final states of the active electron. These correspond to levels of a given L, S and J symmetry in many-electron atoms.
Let us consider electric multipole radiation.
The operator responsible for the interaction of
this radiation with an atomic system is
the electric multipole moment introduced
by the general expression
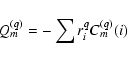 |
(13) |
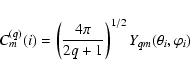 |
(14) |
In the particular case of q = 2,
the transitions take place via the electric quadrupole mechanism, E2.
In this context, the electric quadrupole line strength for a transition
between two states within the LSJ-coupling, which is the
coupling scheme followed throughout in this work, in
the notation of Condon & Shortley (1935),
is given by the equation
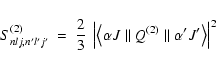 |
(15) |
| (16) |
| (17) |
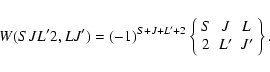 |
(18) |
| S(2)nlj,n'l'j' | = | ||
| = | |||
| (19) |
Thus, the reduced matrix element
![]() provides the relative strengths of different multiplets.
We can write this reduced matrix element as the product of a single-electron
reduced matrix element
provides the relative strengths of different multiplets.
We can write this reduced matrix element as the product of a single-electron
reduced matrix element
![]() ,
which depends on only the quantum
numbers of the jumping electron, and a factor that we
shall call the multiplet factor,
,
which depends on only the quantum
numbers of the jumping electron, and a factor that we
shall call the multiplet factor,
![]() :
:
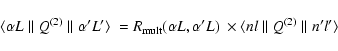 |
(20) |
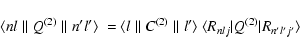 |
(21) |
![\begin{displaymath}\langle l \parallel C^{(2)} \parallel l' \rangle = [l,l']
\le...
...\begin{array}{ccc}
l & 2 & l' \\
0 & 0 & 0
\end{array}\right)
\end{displaymath}](/articles/aa/full/2003/29/aa3440/img67.gif) |
(22) |
| (23) |
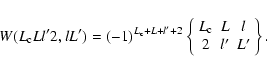 |
(24) |
| (25) |
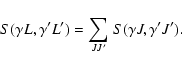 |
(26) |
| (27) |
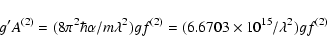 |
(28) |
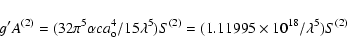 |
(29) |
Let us consider now the magnetic multipole radiation.
The operator responsible for the interacton of this radiation
with matter is
the magnetic multipole moment introduced
by the general expression
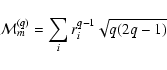
![$\displaystyle \left \{ \frac {1}{q + 1}
\left [C_m ^{(q -1)} \times l_i^1 \right ]^{q} +
\left[ C_m ^{(q -1)}(i) \times s_i^1 \right ]_m^{q} \right \}\cdot$](/articles/aa/full/2003/29/aa3440/img78.gif) |
(30) |
![\begin{displaymath}\ {\cal M}_m^{(1)} = \sum_i \frac {1}{2} \left[ l_i^1 + 2 s_i^1 \right]
\end{displaymath}](/articles/aa/full/2003/29/aa3440/img79.gif) |
(31) |
In this context, the formulae
for the probability of magnetic
dipole (M1) transitions do not contain radial integrals,
an thus, the line strength,
![]() ,
is independent
of the frequency of the transition.
,
is independent
of the frequency of the transition.
The magnetic dipole line strength for a transition
between two states within the LSJ-coupling, in
the notation of Condon & Shortley (1935),
is given by the equation
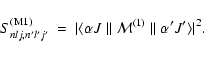 |
(32) |
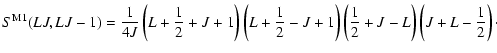 |
(33) |
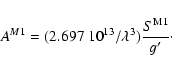 |
(34) |
Regularities in individual oscillator strengths along an isoelectronic sequence as functions of the nuclear charge have been predicted for E1 transitions from conventional perturbation theory (Cohen & Dalgarno 1966; Dalgarno & Parkinson 1967). We shall now extend this procedure to the analysis of electric quadrupole transitions.
If we denote the generalised radial transition integral
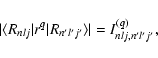 |
(35) |
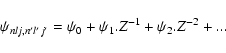 |
(36) |
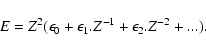 |
(37) |
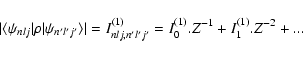 |
(38) |
The dipole line strength, or squared radial integral Eq. (38), may be written as:
| Snlj,n'l'j'(1) = S0(1).Z-2 + S1(1).Z-3+ S2(1).Z-4+ ... | (39) |
| fnlj,n'l'j'(1) = f0(1) + f1(1).Z-1+ f2(1).Z-2+ ... | (40) |
| Snlj,n'l'j'(2) = S0(2).Z-4 + S1(2).Z-5+ S2(2).Z-6+ ... | (41) |
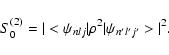 |
(42) |
| An'l'j',nlj(2) = A0(2).Z6 + A1(2).Z5 + A2(2).Z4 + A3(2).Z3+ ..., | (43) |
| fnlj,n'l'j'(2) = f0(2).Z2 + f1(2).Z + f2(2) + f3(2).Z-1+ ..., | (44) |
| fnlj,n'l'j'(2) . Z-2 = f0(2) + f1(2).Z-1+ f2(2).Z-2+ ... | (45) |
| flj,l'j'(2) = f3(2).Z-1+ f4(2).Z-2+ ... | (46) |
In the RQDO context, the quantum defects are often
extracted from energy level data.
As energy levels, we have employed those provided from
the critical compilation by Kelly (1987). These data
comprise the elements from Al I to Kr XXIV.
Given that the transitions we can
study are constrained by the availability of observed
energy levels, for the ions for which no data were found,
interpolated (e.g. Br XXIII) and extrapolated (
![]() )
energy values have been used.
In order to do this, we first fitted the experimental
energy data (belonging to ions between Z = 13 and Z= 36, with the
exception of the value for Z = 35) to a polynomic dependence
of the nuclear
charge, Z. The expression obtained for the 3p
)
energy values have been used.
In order to do this, we first fitted the experimental
energy data (belonging to ions between Z = 13 and Z= 36, with the
exception of the value for Z = 35) to a polynomic dependence
of the nuclear
charge, Z. The expression obtained for the 3p
![]() level is,
level is,
| (47) |
As we advance in the sequence, a Z-value will be reached for which the spin-orbit coupling scheme can no longer be expected be pure LSJ scheme but an intermediate one between that and jj. We have not changed, however, the formulation of either the radial functions or the angular factors employed in the calculation of oscillator strengths at any point in the sequence. We expect that the use of emppirical energy data will, at least to some extent, account for intermediate coupling, as it does, at all values of Z, for configuration interaction.
Other input data also needed in the RQDO
calculations are the ionization energies of the atomic
systems. The corresponding values from Al I to Kr XXIV
have been taken from Kelly (1987).
Analogously to the energy levels, a fitting of the experimental
data (with the exception of Br XXIII) has led to the following expression
for the ionization energy in terms of powers of Z
| I.E. = -2.07672 - 369447 Z + 17639.8 Z2 - 70.2101 Z3 | (48) |
In Table 1, the wavelengths corresponding to the
3p
![]()
![]() spectral line for a large number of Al-like ions
are collected. The data employed in the present calculations are
compared with those reported by Huang (1986). In Table 2, the
presently calculated oscillator strengths are
compared with
those reported by Huang (1986), which are,
to our knowledge, the only data existing in the literature,
as regards these transitions and atomic systems. No
experimental results have been found.
spectral line for a large number of Al-like ions
are collected. The data employed in the present calculations are
compared with those reported by Huang (1986). In Table 2, the
presently calculated oscillator strengths are
compared with
those reported by Huang (1986), which are,
to our knowledge, the only data existing in the literature,
as regards these transitions and atomic systems. No
experimental results have been found.
Table 1:
Wavelenght (![]() in
in ![]() )
for the
)
for the
![]() spectral line in the aluminium sequence.
spectral line in the aluminium sequence.
The values supplied by Huang (1986), have been calculated with the multiconfiguration Dirac-Fock (MCDF) computer code of Desclaux (1975), which includes contributions from the Breit interaction, as well as those from the Lamb shifts. Huang included all the configurations that arise from within the n = 3 complex in his calculations.
The E2 and M1 f-values collected in Table 2,
comprise the ions from Sc IX (Z = 21) up to Hg LXVIII (Z = 80).
The magnetic dipole the line strength
has been taken as 1.3333
![]() according to Eq. (33).
according to Eq. (33).
Table 2:
E2 and M1 oscillator strengths
for the
![]() spectral line.
spectral line.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{ALFIG1.eps}
\end{figure}](/articles/aa/full/2003/29/aa3440/Timg107.gif) |
Figure 1:
Systematic trends of the transition rates for the
3p
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{ALFIG2.eps}
\end{figure}](/articles/aa/full/2003/29/aa3440/Timg108.gif) |
Figure 2:
Systematic trends of the transition rates for the
3p
|
| Open with DEXTER | |
The main contribution to the intensity of the spectral line can be analysed by comparing the f-values corresponding to the M1 and E2 transitions for each ion of the sequence. The contribution of the E2 transition turns out to be negligible with respect to that of the M1 transition, the latter being several orders of magnitude larger than the former. An inspection of Table 2 reveals a rather good general agreeement between our results and those reported by Huang (1986).
Additionally, in Figs. 1 and 2, the behaviour of the E2 and M1 transition probabilities, respectively, along the isoelectronic sequence is analysed in graph form. The value of Log A has been plotted against the atomic number, Z, from Z = 21 up to Z = 80. The MCDF (Huang 1986) data have also been included. These figures serve two purposes. One is to show the agreement or deviations between our results and the MCDF calcuations. The second is to reflect the systematic trends complied with by the individual RQDO A-values along the isoelectronic sequence, which have long been considered as a qualitative proof of correctness (Wiese & Kelleher 1998) and can be used for the interpolation or extrapolation of non-calculated data.
In Fig. 3, we show only the present RQDO data in order to show the
competition between both mechanism (E2 and M1) for the same transition.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{ALFIG3.eps}
\end{figure}](/articles/aa/full/2003/29/aa3440/Timg109.gif) |
Figure 3:
Competition between the electric quadrupole (E2) and
the magnetic dipole (M1) mechanism in the
3p
|
| Open with DEXTER | |
Regularities in individual oscillator strengths along an isoelectronic sequence as functions of the nuclear charge have long been predicted from conventional perturbation theory (Cohen & Dalgarno 1966; Dalgarno & Parkinson 1967), and their usefulness in analysing the f-values has been repeatedly stressed (see, e.g., Martin & Wiese 1996 and references therein).
The oscillator strengths or transition rates for strong analogous (
![]() )
transitions of homologous
atoms are expected to be similar on account of the analogous outer
electron structure of such elements.
Thus, all alkali elements, for example, would be expected to exhibit similar f-values
for the leading lines in a Rydberg series, and it is, indeed,
well known that the principal resonance lines for the alkalis have f-values close to unity.
However, one has to consider that as the
elements within a chemical family become heavier, the outer atomic structure
becomes modified due to the presence
of unfilled electron shells. Generally, the systematic behaviour for
homologous atoms is not expected to be as closely adhered to as for the
case of a given transition along an isoelectronic
sequence, where the electron configuration
remains the same and only a scaling of
the nuclear charge occurs, but it is observed in some cases.
As an illustration, Figs. 4 and 5 display the behaviour
of the transition rate
for the
)
transitions of homologous
atoms are expected to be similar on account of the analogous outer
electron structure of such elements.
Thus, all alkali elements, for example, would be expected to exhibit similar f-values
for the leading lines in a Rydberg series, and it is, indeed,
well known that the principal resonance lines for the alkalis have f-values close to unity.
However, one has to consider that as the
elements within a chemical family become heavier, the outer atomic structure
becomes modified due to the presence
of unfilled electron shells. Generally, the systematic behaviour for
homologous atoms is not expected to be as closely adhered to as for the
case of a given transition along an isoelectronic
sequence, where the electron configuration
remains the same and only a scaling of
the nuclear charge occurs, but it is observed in some cases.
As an illustration, Figs. 4 and 5 display the behaviour
of the transition rate
for the ![]()
![]()
![]() spectral line
for two sequences, those of aluminium (n=2) and
Boron (n=3) against
spectral line
for two sequences, those of aluminium (n=2) and
Boron (n=3) against ![]() .
.
![]() is defined as the charge of the atomic core
(
is defined as the charge of the atomic core
(
![]() ), where Z is the nuclear
charge and N is the number of core electrons. In this way, following the
spectroscopic notation, for a neutral atom we have
), where Z is the nuclear
charge and N is the number of core electrons. In this way, following the
spectroscopic notation, for a neutral atom we have ![]() .
The values for the transition rates via the magnetic dipole (M1) mechanism are shown in Fig. 4, and for the transition
via the quadrupole (E2) mechanism in Fig. 5.
The RQDO A-values plotted for B-like ions have been taken
from Charro et al. (2001).
.
The values for the transition rates via the magnetic dipole (M1) mechanism are shown in Fig. 4, and for the transition
via the quadrupole (E2) mechanism in Fig. 5.
The RQDO A-values plotted for B-like ions have been taken
from Charro et al. (2001).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa3440f4.eps}
\end{figure}](/articles/aa/full/2003/29/aa3440/Timg115.gif) |
Figure 4:
Systematic trends for the fine-structure
3p
|
| Open with DEXTER | |
The RQDO procedure has once more proved to be a very useful tool for estimating transition rates and oscillator strengths. In the particular case of the Al-like ions, a general, satisfying, agreement is found between the RQDO results and those obtained with the rather more elaborate MCDF procedure which accounts for a great deal of electron correlation (Huang 1986).
Finally, the RQDO A-values for the E2 and M1 transitions follow the expected systematic trends along the isoelectronic sequence, which have long been considered as a qualitative proof of correctness and can be exploited for the interpolation or extrapolation of non-calculated data. We are confident in that the present RQDO f-values, may be potentially useful in astrophysics and fusion plasma research.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ALFIG5.eps}
\end{figure}](/articles/aa/full/2003/29/aa3440/Timg116.gif) |
Figure 5:
Systematic trends for the fine-structure
3p
|
| Open with DEXTER | |
Acknowledgements
This work has been supported by the DGI of the Ministry of Science and Technology within Project No. BQU2001-2935-CO2-O2 and the J.C.L. within Project No. VA119/02.