1 - Department of Physics and Astronomy, Arizona State University, Tempe, AZ 85287-1504, USA
2 - Space Science Department, Rutherford Appleton Lab, Chilton, Oxon OX11 0QX, UK

Abstract
We present ISO-LWS spectral line observations of the [OI] 63 and 146 $\mu$ m lines, the [CII] 158 $\mu$ m line, and the [NII] 122 $\mu$ m line at 17 positions in the HII region S125. We model this emission by a two-dimensional geometrical blister model, utilizing the parameters derived from our previous modeling of the HII, HI and FIR dust emission in this source, thereby deriving an interpretation of the region that takes account of the thermal continuum radiation and the line emission self- consistently. We show very good agreement with the observed line emission in the central region, but in order to fit the spatial profile, it is necessary to allow for a systematic increase in the gas temperature along the PDR boundary with decreasing distance from the ionizing star. This would not be predicted by PDR models, hence we suggest that the size distribution of small grains responsible for the photoelectric heating may be changing along the boundary, depending on the distance from the star. The model shows that the HII region, the PDR region, as well as H₂molecular region all make contributions to the emission observed in these fine structure lines and that accurate modeling of the PDR region needs to include the radiation coupling between the ionized region and the neutral molecular cloud. Comparison with values derived from one-dimensional, constant density slab models shows the present blister modeling giving higher G₀ values for the radiation field at the PDR boundary.

Key words: HII regions - ISM: individual objects: S125- ISM: dust, extinction - infrared: ISM

The HII region S125 (IC 5146) is an ionized region formed on the near side of a molecular cloud by the single B0.5 star $\rm BD +46^{\circ}$ 3474, and showing nearly symmetrical emission characteristic of a blister type region viewed face-on. The distance to S125 is taken as 960 pc (Crampton & Fisher 1974); a slightly larger distance is recently given by Herbig & Dahm (2002) (cf. Sect. 6). Roger & Irwin (1982, RI hereafter) presented a model to reproduce the emission profiles of both the radio continuum from the HII region and the HI 21 cm emission from the photodissociation region (PDR). Using in addition ISO LWS continuum observations from two perpendicular scans across the center of the nebula, Aannestad & Emery (2001, herafter AE) modeled the continuum emission of the region with both the RI model and an axisymmetric blister model. Assuming enhanced far-infrared (FIR) emission properties for the dust compared to typical interstellar silicate-graphite dust, the models could fairly well account for the central FIR emission. However, AE found it necessary to account for an additional FIR continuum component in a roughly symmetrical region around and at the periphery of the HII region. This component appeared to contribute up to about 50% of the observed 45-200 $\mu$ m emission, and may represent a distribution of embedded objects at an early stage of protostellar evolution.

Here we present the FIR fine structure line observations from the LWS scans and attempt to model the line emission within the constraints of the earlier blister model parameters, as determined from the continuum onservations. Since some of the emission comes from the HII region and some from the PDR and the molecular regions, the modeling is necessary in order to separate the contributions and deduce the individual properties of the regions.

In Sect. 2 we present the line observations, while Sect. 3 summarizes the model properties. Section 4 describes the treatment of the line emission, and the calculations are presented in Sect. 5. Discussion is in Sect. 6 and conclusions are presented in Sect. 7.

2 The observed far-infrared lines

The LWS scans are crosswise at 45 degrees with respect to the right ascension and declination directions and centered on the position RA(2000) = $21^{{\rm h}}53^{{\rm m}}33^{{\rm s}}, \delta (2000) = 47^{\circ}16'18''$ . Figure 1 shows the 17 scan positions on an image from the Digitized Sky Survey (Skyview Virtual Telescope). The scan positions are separated by 3' from center to center. The approximately 80^'' FWHM beam is also indicated. The ionizing star is at a position 0.68^' West and 0.29^' South of the central raster position.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{H4401F1.epsi} \end{figure}$	Figure 1: Raster scan positions for the LWS beam in a $0.5^{\circ } \times 0.5^{\circ }$ view centered on ${\rm RA} (2000) = 21^{{\rm h}}53^{{\rm m}}33^{{\rm s}}, \delta (2000) = 47^{\circ }16'18''$ . North is up and RA increases to the left.
Open with DEXTER

The lines observed are the 63 $\mu$ m (J=1-2) and 146 $\mu$ m (J=0-1) from the ³P ground term of OI, the 158 $\mu$ m ( J=3/2-1/2) line from the ²P ground term of CII, and the 122 $\mu$ m (J=2-1) line from the ³P ground term of NII. All the lines are seen in the central positions, but in the outer positions only the 63 $\mu$ m and the 158 $\mu$ m lines are observed. The ionization potential for NII is 14.5 eV, so the NII line is formed only within the ionized region. The observed line strengths are listed for each position in the scans in Table 1, together with the observed FIR continuum flux from 45 to 200 $\mu$ m. The data were recorded with the mode LWS01 and processed with the standard pipeline. The spectral scans were imported into the ISAP interactive processing package for averaging and extracting the observed line parameters. This involved a linear fit across selected portions of the spectrum on either side of the line that was then used to remove the underlying continuum. A best fit Gaussian profile was used to obtain the center wavelength and integrated flux of the line, together with some basic statistics of the fit. The errors shown in Table 1 are estimates of the uncertainties taking into account these statistical values together with estimates of systematic effects. The values entered for the line observations are the intensities S (erg cm^-2 s^-1 sr^-1) = $fF/\Omega _{B}$ , where F is the observed flux, f is the extended source correction, and $\Omega_{B}$ is the effective beamwidth. The quantities f and $\Omega_{B}$ have been taken from Table 5.10 in the ISO Handbook (Gry et al. 2002). For the 45-200 $\mu$ m continuum we have entered the values from Table 1 of AE using $\Omega_{B}=1.18\times 10^{-7}$ sr.

3 The model

Much of the theoretical treatment of infrared emission from photodissociated regions has assumed a one-dimensional slab geometry with a constant density into the cloud, but with a full treatment of the thermal and chemical structure of the gas (e.g., Tielens & Hollenbach 1985; Hollenbach et al. 1991; Kaufman et al. 1999). In addition, the external radiation field is treated as a free parameter, normalized to the general interstellar field. As a development of this, we model the S125 region as a two-dimensional structure and allow for an axisymmetric density gradient. Whilst gaining a more representative geometry, it has been necessary to adopt a more simplified thermal treatment, and to exclude any chemistry except for a detailed account of the HI/H₂ conversion. The modeled PDR structure arises directly from coupling to the ionization structure and with the actual radiation field through the HII region, as well as conforming to the continuation of the axisymmetric density gradient. The input stellar radiation field is taken from a PHOENIX model atmosphere NLTE calculation by Aufdenberg (1998, private communication) for a star of effective temperature 30 000 K and has an ionizing photon luminosity of $3.5 \times 10^{47}$ photons/s. The resulting blister model properties are summarized below, but the reader is referred to AE for the details. We emphasize that our basic model for the line data is the same as the best-fit model found by AE for the continuum observations, with no changes in the parameters so that it addresses all this data self-consistently.

3.1 Geometry

It is assumed that the HII region and the PDR are formed in the outer parts of a molecular cloud with an exponential density gradient. From the fits to the HII continuum emission and to the HI 21 cm line emission profiles, AE found a scale height of 0.65 pc, and a total density (H+He) of 60 cm^-3at the ionizing star. Also, from modeling of the dust continuum emission, AE found it necessary to require a very low dust/gas mass ratio ( $\leq$ 10^-6) in the HII region and a region of radius 0.3 pc devoid of dust and gas surrounding the star. The PDR region, however, was found to have a normal dust/gas mass ratio ( $8 \times 10^{-3}$ , but with a much enhanced population of very small (50 Å) dust grains.

Figure 2 shows the blister ionization and dissociation boundaries in an r, $\theta$ plane (ionizing star at r=0, $\theta = 0^{\circ}$ outward along the axis), together with the observed lines of sight for positions N - Q. It is assumed that we are viewing this blister face-on. The photo-dissociation HI/H₂ boundary is defined by 2N(H₂)/(N(H)+2N(H₂)) = 0.5. Also shown as dashed lines are density contours, which are vertical to the symmetry axis. We note that the density profile in the ionized gas along the symmetry axis is very similar to that given by a photoevaporative flow profile (Bertoldi & Draine 1996) with the present geometry showing a cloud of curvature radius 1.3 pc with an axial distance from the ionizing source to the ionization front of 0.78 pc. Such flow profiles have been applied to a range of structure sizes, for example, Sankrit & Hester (2000) fitting for structures in M16, giving a curvature radius of 0.065 pc and a distance to the ionization front of 0.16 pc.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{H4401F2.vps.epsi} \end{figure}$	Figure 2: Blister ionization boundaries for H⁰/H⁺, He⁰/He⁺, C⁺/C⁺⁺, and the H₂/H⁰ photo-dissociation boundary. The heavy solid line shows the "evacuated'' region around the ionizing star. Also shown are the total density contours for 100, 250, 500, and 1000 cm^-3, as well as 4 lines of sight for the positions shown in Fig. 1.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{H4401F3.epsi} \end{figure}$	Figure 3: The absorption cross section for the PDR dust and the dust in the HII region as assumed in the model. The dotted curve (DL dust) shows the absorption for a recent model that includes PAH-type dust (Weingartner & Draine 2001a; Li & Draine 2001).
Open with DEXTER

3.2 Abundances

3.3 Dust

Figure 3 shows the absorption cross section per H atom for this dust with the parameters of the PDR region, i.e. $a_{\rm {min}} = 0.058~ \mu$ m, $a_{\rm {max}} = 0.25 ~\mu$ m, and fractional abundances of Si and C of (0.5, 0.48) and (0.35, 0.27) locked up in the (large, very small) grains, respectively. The ratio R_V of selective to total visual extinction is 4.3. The lower curve is the absorption curve for the dust within the HII region, where the dust appears to be strongly depleted (cf. AE). For reference we also show the absorption for the recent carbonaceous-silicate grain model of Weingartner & Draine (2001a) for the value R_V = 4.0. In comparison we note the stronger far-UV absorption in the PDR dust due to the large number of very small grains, and the much enhanced FIR absorption due to a combination of optical properties and shape effects. The wavelength dependence at long wavelengths is approximately $\lambda ^{-1}$ , which is also assumed in many of the PDR models referred to earlier. A similar dependence is observed for the FIR emission in many sources.

3.4 Temperature structure

The far-UV radiation field G₀ at the PDR surface for the S125 HII blister (in units of $1.6 \times 10^{-3}$ erg cm^-2 s^-1) ranges from about 60 for $\theta = 70^{\circ}$ , to about 10³ for $\theta = 180^{\circ}$ . The corresponding range in the surface gas density n₀ is about 10-200 cm^-3 (at distances r of 3.0 and 0.8 pc, respectively). PDR slab models show that the surface temperature is primarily determined by the ratio G₀/n₀. In the present analysis this is found to be fairly constant with a value of 5-6 which, in the calculations of Kaufman et al. (1999) (cf. their Fig. 1), corresponds to a temperature of 500-1000 K, with the higher values applying to the lower densities. These values are higher than in earlier work (Hollenbach et al. 1991; Spaans et al. 1994), where, for our values of G₀ and n₀, typically the temperature would be 100-200 K in a surface layer of visual extinction $A_{V} \leq 1$ . The higher temperatures in the Kaufman et al. models are a consequence of PAH heating, and is therefore closely tied to the far-UV optical depth. In the earlier work on S125, AE assumed a simple dependence of the gas temperature on the average dust temperature and on the optical depth at 0.1 $\mu$ m, and took the PDR boundary temperature to be 500 K, independent of distance from the star. We assume the same temperature structure here, but will also (cf. Sect. 5) consider possible variations from this.

Figure 4 shows the PDR gas temperature as a function of the visual extinction for some of the lines of sight (cf. Fig. 2). The upper panel is for the assumption of a constant boundary temperature independent of the angle $\theta$ , and all the lines of sight fall between the two curves given for positions N and R. The lower panel shows the temperature variation for a boundary temperature that varies with the angle $\theta$ in the way indicated that better satisfies the observed spatial profile of the fine-structure lines (Sect. 5).

In Table 2 we summarize the main properties for the blister model. Note that some properties are limited by how far into the molecular cloud the calculations are carried. Also, the listed neutral masses and total luminosity does not include any contrubution from the additional FIR component required to explain the observed luminosity.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{H4401F4.epsi} \end{figure}$

Figure 4: The gas temperature in the PDR as a function of the visual extinction. Upper panel: the PDR boundary temperature is assumed to be 500 K independent of direction from the central star; all lines of sight fall between the two curves shown for positions N and R. Lower panel: the PDR boundary temperature is assumed to vary with angle as shown; such a variation gives a spatial profile for the fine- structure lines in much better agreement with the observations.

Open with DEXTER

4 The fine-structure lines

4.1 The OI lines

In the PDR region, the collision partners are electrons, H and He atoms, and H₂ molecules. For the electron collision strengths, we have fit the values given by Bell et al. (1998) for T = 50 - 3000 K by Chebyshev polynomials. The electron density in the PDR region is set equal to the C⁺ density. The H and He collision strengths are from the Péquignot (1990) expressions with corrections as in Péquignot (1996). The corresponding de-excitation rates are close to earlier values (Tielens & Hollenbach 1985), except for the $\rm {^{3}P_{1}-^{3}P_{0}}$ transition, where the new rates are an order of magnitude smaller. For the molecular excitation we use the rate coefficients for para- and ortho- H₂ calculated by Jaquet et al. (1992) for the temperature range 20-1500 K. We assume the thermal value of 1:3 for the para:ortho abundance ratio. Since the excitation rates are very similar for the two species, the actual value of this ratio is not important here. The H₂ collision rates are substantially larger than the H collision rates, except for the $\rm {^{3}P_{1}-^{3}P_{0}}$ transition, where rates are 1-2 orders of magnitude smaller for the PDR temperatures.

4.2 OIII, NIII, and NII lines

4.3 The CII line

4.4 Optical depth effects

The blister has an exponential density increase into the molecular cloud, but our calculations are stopped when either: 1) a 10 $\mu$ m dust optical depth from the central star $\geq$ 0.5, or 2) a distance is reached of 30 scale heights from the central star. For S125 this corresponds to visual extinctions $A_{V} \lesssim 5$ . The calculation encompasses the molecular cloud "surface layer'' where the observed fine-structure lines are formed. Further into the cloud, in addition to the temperature becoming too low for excitation, C⁺ and O are converted into C and/or CO, and may be additionally depleted onto the dust grains. The hydrogen nucleon column densities in these calculations are therefore limited to $N_{\rm H} \leq 10^{22}$ cm^-2. This means, however, that both the OI 63 $\mu$ m and the C⁺ 158 $\mu$ m lines become optically thick for all the observed lines of sight. Typically, when the calculations are stopped, $\tau(63~\mu \rm m) \lesssim 10$ , and $\tau(158 ~\rm\mu m) \lesssim 5$ . The [OI] 146 $\mu$ m line, however, is optically thin, even going through a region with a very slight negative optical depth for these PDR conditions.

For a given line of sight, the intensity for a line of wavelength $\lambda _{ij}$ is calculated in the semi-infinite slab approximation:

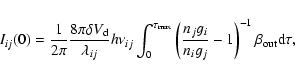
$\begin{displaymath}I_{ij}(0) = \frac{1}{2\pi }\frac{8\pi \delta V_{\rm d}}{\lamb... ...}g_{i}}{n_{i}g_{j}}-1\right)^{-1}\beta _{\rm out}{\rm d}\tau , \end{displaymath}$

To illustrate optical depth effects, Fig. 5 shows how the line ratios [OI] 63 $\mu$ m/146 $\mu$ m and [OI]63 $\mu$ m/ [CII]158 $\mu$ m vary with density and temperature for optical depths in the 63 $\mu$ m line of 0.01, 1.0 and 5.0. The optical depth $\tau _{\rm {out}}$ is the outward optical depth in a uniform, semi-infinite slab. For this purpose, only excitation by atomic hydrogen has been included. In the low density limit, the OI 63 $\mu$ m/146 $\mu$ m line ratio is independent of optical depth with a value of 17 and 45 for T = 500 K and 100 K, respectively. For the moderate densities considered here, the ratio decreases to 13 and 40, respectively, as the 63 $\mu$ m line optical depth increases from 0 to 10. Note that only in the optically thin limit (upper panel) is the [OI]63 $\mu$ m/[CII]158 $\mu$ m ratio proportional to the O/C abundance ratio (a value of 2 is assumed in these figures). We see that the optical depth strongly affects the line ratios for high density - low temperature conditions, while the effects for low density - low temperature conditions are quite small. However, even for relatively low densities as considered here, assuming optically thin conditions leads to overestimates of either temperature and/or density.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{H4401F5.epsi} \end{figure}$	Figure 5: Far-infrared line ratios as functions of temperature and hydrogen density in a semi-infinite, uniform slab for three values of the [OI] 63 $\mu$ m optical depth, considering only excitation by atomic hydrogen. The abundance ratio O/C = 2. For clarity, only the upper panel has the grid values of temperature and density indicated.
Open with DEXTER

5 Calculations

The contribution to the [OI] and [CII] line intensities from collisional excitation by H₂ is substantial in our calculations. In the central positions, it provides $\gtrsim$ 1/3 of the total intensity, while in the outer positions it contributes $\gtrsim$ 2/3 of the line intensities. Also, the contribution by the HII region is large for the central positions, varying from 10-20% for the [OI] 63 $\mu$ m, 146 $\mu$ m lines to 40% for the [CII] 158 $\mu$ m line. Figure 6 shows the line emissivities (erg cm^-3 s^-1) along the two lines of sight for positions N and P. The temperature structure is that of the lower panel in Fig. 4. Note that the positive direction is into the blister, and opposite to the abscissa in Fig. 2. The HII/PDR boundary is at 0.75 pc, -0.21 pc, and the HI/H₂ transitions is at 1.7 pc, 1.4 pc for the N, P lines of sight, respectively (cf. Fig. 2). For clarity, the values for the [CII] 158 $\mu$ m line has been decreased by 2 and 3 orders of magnitude for positions N and P, respectively. It is apparent that accounting for emission in both ionized gas and in fully molecular gas is important for understanding PDR emission in these fine-structure lines.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{H4401F6.epsi} \end{figure}$	Figure 6: Line emissivities in erg cm^-3 s^-1 for the fine structure lines along the N (upper panel) and P (lower panel) lines of sight. Positive distance is into the blister (increasing density). For clarity the CII line emissivity is decreased by 2 and 3 orders of magnitude for positions N and P, respectively.
Open with DEXTER

Figures 7-9 show the calculated line intensities for the OI and CII lines along the ISO scans A - I and J - R together with the observed values. The upper solid curve in each panel is the total line intensity, while the lower curve is for the contribution by the HII region only. The line intensities are matched very well in the center position, but points immediately around the center (M and O) are higher in intensity than calculated by up to a factor of 2.8. This seems to reflect the same result as found by AE, i.e. additional emission is present symmetrically placed around the center. However, contrary to the observed dust continuum emission, the observed line emission falls below the model emission in the other positions further away from the center.

The most direct interpretation of this is that the gas temperature at the boundary decreases with distance from the central star, rather than staying approximately constant as predicted by the theory of PDR heating and cooling (approx. constant G₀/n₀). To parameterize this in the present model, we have taken the boundary temperature to be an increasing function of the angle $\theta$ for the closed portion of the $r,~\theta$ plane. The dashed lines in Figs. 7-9 show the resulting model intensities if $T_{\rm {boundary}} = 5 \theta - 300$ K for 80 $^{\circ} \leq \theta \leq 160 ^{\circ}$ , $T_{\rm {boundary}} = 500$ K for $\theta \geq 160^{\circ}$ , $T_{\rm {boundary}} = 100$ K for $\theta \leq 80^{\circ}$ . The temperature structure in this case is shown in the lower panel of Fig. 4. Possible physical reasons for a variation of the boundary temperature are discussed in Sect. 6.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{H4401F7.epsi} \end{figure}$

Figure 7: Observed and calculated line intensities (erg cm^-2 s^-1 sr^-1) for the [OI] 63 $\mu$ m line; upper panel for the scan positions J - R; lower panel for the scan positions A - I of Fig. 1. The upper and lower solid lines show the calculated values for the full model (constant boundary temperature) and the HII region only. The dashed curves show the calculated values with an assumed variation for the neutral gas boundary temperature (cf. Sect. 5).

Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{H4401F8.epsi} \end{figure}$	Figure 8: Observed and calculated line intensities for the [OI] 146 $\mu$ m line; upper panel for the scan positions J - R; lower panel for the scan positions A - I of Fig. 1. Curves and units as in Fig. 7.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{H4401F9.epsi} \end{figure}$	Figure 9: Observed and calculated line intensities for the [CII] 158 $\mu$ m line; upper panel for the scan positions J - R; lower panel for the scan positions A - I of Fig. 1. Curves and units as in Fig. 7.
Open with DEXTER

The observed intensities of the [NII] 122 $\mu$ m line for the central positions (Table 1) are $(1{-}2)\times 10^{-5}$ erg cm^-2 s^-1 sr^-1, while our calculated values are $(2{-}5)\times 10^{-5}$ erg cm^-2 s^-1 sr^-1. As a comparison with more generalized models, we have run the one-dimensional photoionization code CLOUDY (version C94.00, Ferland 2000) for a constant density ionized shell that has the same emission measure (about 8000 cm^-6 pc) as observed and is subject to the same ionizing luminosity (9.3 $\times 10^{36}$ erg s^-1, Kurucz 30 000 K model atmosphere) as in our calculations. With an inner radius of the shell set to 0.3 pc (our evacuated region around the star), and an average constant hydrogen density of 130 cm^-3 (in our blister model the density in the HII region ranges from 85 cm^-3 at 0.3 pc to 180 cm^-3 at the HII boundary), the outer radius of the shell (0.8 pc) and the H⁺ column density ( $1.9\times 10^{20}$ cm^-2) agree well with our blister parameters along the central line of sight ( $\theta = 180^{\circ}$ ). For the predicted [NII] 122 $\mu$ m luminosity of the S125 region, the CLOUDY value is also consistent with our calculation, and again shows a higher value compared with the observation, taking an integrated value and a smooth distribution between pointing positions. It may be that the nitrogen abundance in S125 is subsolar by about about a factor of two, similar to the abundance in M16 (Sankrit & Hester 2000). Alternatively, it may indicate too high an ionizing radiation field from the PHOENIX model atmosphere, which does not include the effects of a stellar wind.

The calculated values for the [NII] 205 $\mu$ m line from our model in the central position is $1.5\times 10^{-5}$ erg cm^-2 s^-1 sr^-1, or about 1/3 of the 122 $\mu$ m line lintensity. For the other lines also formed entirely in the HII region, we predict the following intensity values for the central position: I([OIII]88 $\mu {\rm m}) = 9.6\times 10^{-7}$ erg cm^-2 s^-1 sr^-1, I([OIII]52 $\mu {\rm m}) = 6.9\times 10^{-7}$ erg cm^-2 s^-1 sr^-1, and I([NIII]57 $~\mu\rm m) = 1.4\times 10^{-6}$ erg cm^-2 s^-1 sr^-1.

6 Discussion

The observations also show that the FIR line emission displays the same "excess emission'' as the continuum emission in a roughly symmetric region around and at the periphery of the HII region. For example, in order to account for the LWS continuum emission within the beam at position O, it is required that all the UV stellar flux in this direction is absorbed completely and only by the dust and re-emitted only in the FIR. This is not physically reasonable. We have earlier characterized this emission by subtracting our model flux from the observed flux (AE, e.g. Fig. 15). In Table 2 we have similarly subtracted our model line fluxes from the observed fluxes at the symmetrically placed positions D, F, M, and O for the [OI] 63 $\mu$ m and [CII] 158 $\mu$ m lines. We have also listed an approximate value for the FIR continuum emission for this "excess'' component by using the "excess'' in the 45-200 $\mu$ m range, but increased it by 20% to take account of emission below 45 $\mu$ m.

Table 3: "Additional'' component emission for the positions D, F, M and O $^{{\rm a}}$ .

Although the additional component values listed in Table 2 have additional uncertainty due to the subtraction, some further tentative conclusions can be drawn. Assuming PDR conditions, according to the calculations by Kaufman et al. (1999, their Figs. 3-4), the values for the line ratio in Table 2 imply $G_{0} \simeq 10$ and $n \gtrsim 10^{4}$ cm^-3. The intensity ratios ([OI]63 $\mu$ m + [CII]158 $\mu$ m)/FIR from Table 2, however, are very similar to the general values, but are also consistent with a high-density component, $n \gtrsim 10^{5}$ cm^-3 (cf. Kaufman et al. 1999, their Fig. 6).

We can compare the G₀ and n values given by our model with those derived from the observations together with the PDR models of Kaufman et al. (1999), recognizing thet these typically give more than one possible solution in the n, G₀ plane. In the present case, solutions can give a high G₀ value coupled with a low n value, or conversely a low G₀ value with a high n. To correct for the emission component from the HII region, we subtract our calculated contributions from the HII region alone from the observed intensities. The best determined values in the present observations are the intensity levels of the [CII] 158 $\mu$ m line and the line ratios [OI]63 $\mu$ m/[CII]158 $\mu$ m. Using these with the PDR models leads to two possible solutions for most of the observed positions. However, in all cases our blister values for G₀, n fall in the same part of the diagram with high G₀ and low n. Although the observed [OI]146 $\mu$ m/[OI]63 $\mu$ m line ratios are also available, they have significantly greater uncertainty. However, their use also points to the same (high G₀ with low n) part of the diagram. For example, for the central position (E,N) the observed values corrected for HII emission are: I([CII]158 $\mu {\rm m}) = 1.5\times 10^{-4}$ erg cm^-2 s^-1 sr^-1, I([OI]63 $\mu$ m)/I([CII]158 $\mu$ m) = 0.9, (I([OI]63 $\mu$ m)+I([CII]158 $\mu$ m))/ $I_{\rm {FIR}} = 6.6\times 10^{-3}$ , and I([OI]146 $\mu$ m)/I([OI]63 $\mu$ m) = 0.085. Using these values, the PDR models imply G₀ = 100 - 500 and $n\approx 10^{2}$ cm^-3. In comparison, the values in the present blister model at the PDR boundary for the central position are G₀ = 900 and n = 180 cm^-3. These parameters were set independently of the FIR line measurements, but , as shown, give line intensities in very good agreement with the observed values. In general for S125, constant density slab models tend to underestimate the radiation field at the HII/PDR boundary.

Kaufman et al. (1999) use an approximation to the FIR dust continuum of $I_{\rm {FIR}} \simeq 2.6\times 10^{-4}$ G₀ erg cm^-2 s^-1 sr^-1, which includes a factor of 2 for radiation absorbed outside the wavelength interval that defines G₀. From the blister model that provides a good match to the observations we find $I_{\rm {FIR}} \simeq 1.0\times 10^{-4}$ G₀ erg cm^-2 s^-1 sr^-1. A lower rate of dust emission is caused by a lower bolometric correction (1.35) and allowing for absorption of radiation by H₂ (photodissociation). The photoelectric heating efficiency is determined by the ratio (I([OI]63 $\mu$ m) + I([CII]158 $\mu$ m))/ $I_{\rm {FIR}}$ . An efficiency of $\simeq$ 10^-2 (Table 1) corresponds to a value $G_{0} T ^{1/2}/n_{\rm {e}} \approx 10 ^{4}$ K^1/2 cm³ in theories of photoelectric emission (Bakes & Tielens 1994; Weingartner & Draine 2001b). For the line of sight in position N, $G_{0} T^{1/2}/n_{\rm {e}}$ varies from $3\times 10^{5}$ at the PDR boundary to $2\times 10^{3}$ K^1/2 cm³ when $A_{V} \approx 1$ . The present observations and modeling parameters therefore give support to these descriptions of photoelectric heating.

Only collisional excitation of the fine structure levels have been included in our modeling. Addressing only the [OI] line ratios, Keenan et al. (1994) note that the $\rm ^{3}P_{1}$ and $\rm ^{3}P_{0}$ levels in OI can be populated by cascades from higher states that have been populated from the $\rm ^{3}P_{2}$ level through absorption of UV radiation. If we just include their effective rates of $7.8\times 10^{-11}~G$ s^-1 for indirect excitation of $\rm ^{3}P_{1}$ from $\rm ^{3}P_{2}$ and $1.7\times 10^{-11}~G$ s^-1 for indirect excitation of $\rm ^{3}P_{0}$ from $\rm ^{3}P_{2}$ , where Gis the UV radiation field normalized by Keenan et al. to the Gondhalekar et al. (1980) interstellar radiation field (G=1 corresponds to a flux of $1.5\times 10^{-3}$ erg cm^-2 s^-1), the 63 $\mu$ m and 146 $\mu$ m model line intensities for our lines of sight are then generally too high compared to the observations by factors $\gtrsim$ 1.5. However, the rate coefficients do depend on accurate values for the transition oscillator strengths and on the actual shape of the UV radiation field. Also, the model line fluxes could be lowered by using a lower gas phase oxygen abundance than assumed here, if the abundance is subsolar and/or if some of the oxygen is locked up in the dust.

Since chemistry has not been included in our modeling, it should be noted that this limits the calculations to the region where C is C⁺and O is OI. However, the PDR slab models show that this corresponds to $A_{V} \lesssim 4$ for a 30 000 K radiation field (Spaans et al. 1994), which encompasses our model region since this is generally where our calculation stops. Also, at these depths into the cloud, the gas temperature is becoming significantly less than the excitation temperature of the lines, and the contribution to the line intensity is small.

One main uncertainty in these calculations is the simplified treatment of line radiative transfer. However, it is difficult to judge the accuracy of the escape probability method, here used in the semi-infinite slab, one-dimensional approximation. Two-dimensional methods, such as those presented by Hogerheijde & van der Tak (2000) and by van Noort et al. (2002) would be very useful for blister calculations. Also, we have not allowed for any clumpiness of the gas in S125. While our modeling does not rule out clumpiness, it shows that, for this source at least, results consistent with the observations are obtained with a smooth density gradient from the HII region into the molecular cloud. It does, however, as discussed above, require that the gas temperature at the blister PDR boundary increases systematically with decreasing distance to the ionizing star.

In a recent paper, Herbig & Dahm (2002) have done visual and near-ir photometry of the cluster members in IC5146. They suggest a revised distance to the cluster of 1.2 kpc, but with an uncertainty of at least 0.2 kpc. A larger distance than our adopted one (960 pc) will primarily affect the physical scale of the emission region. Thus the off center beam positions will correspond to conditions slightly further away from the central star in our model nebula, with corresponding lower calculated continuum and line emission for the raster positions. This would make the postulated "excess emission'' a slightly greater fraction of the total. In addition, the line profiles (Figs. 7-9) would become narrower, which would reduce, but not eliminate, the required change in the PDR boundary temperature (Sect. 5).

7 Conclusions

It is clear from the emission mapping given by the blister model that the line emission shows an "excess'' in a region immediately surrounding the central position, similar to that shown by the dust continuum emission. This appears to be from a higher density ( n > 10⁴ cm^-3) region that may be heated by embedded sources to give emission components that are in addition to those accounted for by the blister model with a central ionizing star.

The present modeling gives the emission contributions from the various regions of S125 that together make up the observed value. From this, for example, the contribution to the [CII] and the [OI] line intensities emanating from the HII region are found to be $\lesssim$ 40% and $\lesssim$ 20%, respectively, showing that this should be taken into account in PDR modeling.

For interpreting the [OI] 63 $\mu$ m and [CII] 158 $\mu$ m lines, these are found to be moderately optically thick in the blister, whilst the [OI] 146 $\mu$ m line is optically thin with a region of slight negative optical depth. For the relatively low density conditions derived here for S125, however, this shows that the line intensities are affected by less than a factor of two.

Comparison with an equivalent analysis, using a one-dimensional constant density PDR slab model, shows that our blister model implies a higher value for the incident radiation at the PDR boundary.

Modeling far-infrared line emission from the HII region S125

1 Introduction