A&A 406, 357-362 (2003)
DOI: 10.1051/0004-6361:20030704
Understanding internetwork magnetic fields as
determined from visible and infrared spectral lines
L. R. Bellot Rubio 1 - M. Collados 2
1 - Kiepenheuer-Institut für Sonnenphysik,
Schöneckstr. 6, 79104 Freiburg, Germany
2 -
Instituto de Astrofísica de Canarias, 38200 La Laguna,
Tenerife, Spain
Received 25 February 2003 / Accepted 7 May 2003
Abstract
We present numerical experiments aimed at understanding why
near-infrared observations systematically deliver weak magnetic fields
in the internetwork, whereas analyses based on visible lines indicate
that kG fields are ubiquitous. Synthetic noisy Stokes V profiles of
the iron lines at 6302 Å and 1.565 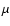 m have been produced under
varying conditions in an effort to simulate polarized spectra coming
from the internetwork. An inversion technique has been applied to the
profiles, as it is usually done with real observations, in order to
derive the distribution of magnetic fields in the simulated region. Our
results show that infrared lines yield distributions which are very
similar to those used as input for the simulation, while visible lines
are to a large extent affected by noise. Analyses based on the Fe I lines at 6302 Å may lead to an overabundance of kG fields if the
signal-to-noise ratio in Stokes V is poorer than about 10. A particular
example is shown where strong fields are retrieved in nearly 30% of the
pixels of a simulated internetwork region in which only fields of 200 G exist.
m have been produced under
varying conditions in an effort to simulate polarized spectra coming
from the internetwork. An inversion technique has been applied to the
profiles, as it is usually done with real observations, in order to
derive the distribution of magnetic fields in the simulated region. Our
results show that infrared lines yield distributions which are very
similar to those used as input for the simulation, while visible lines
are to a large extent affected by noise. Analyses based on the Fe I lines at 6302 Å may lead to an overabundance of kG fields if the
signal-to-noise ratio in Stokes V is poorer than about 10. A particular
example is shown where strong fields are retrieved in nearly 30% of the
pixels of a simulated internetwork region in which only fields of 200 G exist.
Key words: polarization - line: profiles -
Sun: infrared - Sun: photosphere - Sun: magnetic fields
Internetwork (IN) magnetic fields have attracted the interest of solar
physicists during the past few years (see, e.g., the review by Steiner 2003). One
reason for that is the suspicion that they may be responsible for a significant
fraction of the total magnetic flux of the sun. Another reason is that they hold
the key to decide whether the magnetism of the quiet photosphere is controlled
by a local dynamo (e.g., Emonet & Cattaneo 2001 and references therein) or
by other processes like, for example, the decay of active regions. Since the
magnetic field distribution at the surface is an expression of the relevant
physical mechanism, observational determinations of the field
strength distribution (in terms of probability density functions, or PDFs)
are important to distinguish between scenarios. The internetwork is preferred
for this characterization because the kG fields occurring in facular and
network regions are believed to be produced by other processes, most
notably convective collapse (Parker 1978; see also Solanki et al. 1996;
and Bellot Rubio et al. 2001).
From an observational point of view, the determination of magnetic field
PDFs in the internetwork is plagued with difficulties. The IN polarization
signals are very small because the magnetic field occupies a tiny fraction
of the resolution element. As a consequence, they are easily hidden by
noise. Cancellation of Stokes V signals due to mixed polarities in the
resolution element may also be important. Socas-Navarro & Sánchez Almeida
(2002) and Khomenko et al. (2003), for example, report that 35% and 30%
of the spatial points showing magnetic signal in their observed maps require
mixed polarities. This explains why internetwork fields remain elusive.
High sensitivity instruments are absolutely necessary for a reliable
characterization of their properties. Current grating spectropolarimeters
and narrow-band filters are just at the limit of the required sensitivity
if typical exposure times are used.
The IN magnetic field PDFs determined so far are contradictory (cf.
Steiner 2003). Analyses based on visible lines suggest that the
internetwork contains a sizeable fraction of fields in the kG range
(Grossmann-Doerth et al. 1996; Sánchez Almeida & Lites 2000;
Socas-Navarro & Sánchez Almeida 2002; Domínguez Cerdeña et al. 2003; but see Lites 2002). Analyses based on infrared spectral
lines, on the contrary, indicate that strong fields are very rare
and that weak fields dominate the PDF (Lin 1995; Collados 2001;
Khomenko et al. 2003). The particular scenario favored by each author
does not seem to depend on the data employed (spectrograph or narrow-band
filter observations), on the way the PDF is obtained (through Gaussian
fitting, Stokes V amplitude fitting, or profile inversion), or on the
assumptions regarding the model atmosphere (one or more components in the
resolution element), but only on the wavelength of the spectral lines
utilized. Several explanations have been offered to understand these
conflicting results. Part of the difference could be due to network
(kG) elements being present in the region under analysis. This is probably
the reason why the visible observations of Grossmann-Doerth et al. (1996)
revealed so many strong fields. Other explanations are based on the
different thermal and magnetic sensitivity of infrared and visible
lines (Sánchez Almeida & Lites 2000), although it is not clear
whether the proposed mechanisms are model-dependent or not. Changes
in the separation of the Zeeman components (and hence the saturation
of the polarization signal) start to be noticeable in Stokes V for
field strengths as low as 300-500 G in the case of infrared lines and
as high as 1000 G in the case of visible lines. The different field
strengths at which the transition from weak-field to strong-field
behavior takes place have been used to suggest that, if several
magnetic fields coexist in the resolution element, visible
observations would tend to detect the stronger fields, whereas
infrared lines would favor the weaker fields (Socas-Navarro 2003).
Here we argue that noise is essential for understanding the differences
between the PDFs retrieved from visible and near-infrared Stokes
profiles. Our suggestion is based on the results of a numerical experiment.
Synthetic Stokes V profiles of the Fe I lines at 6302 Å and 1.565 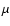 m
emerging from a simulated internetwork region have been generated under
varying conditions. After adding noise, the visible and infrared profiles have been
inverted separately in terms of a single magnetic component. This allows us
to investigate the properties of the resulting PDFs, and to assess how they
are influenced by the noise.
m
emerging from a simulated internetwork region have been generated under
varying conditions. After adding noise, the visible and infrared profiles have been
inverted separately in terms of a single magnetic component. This allows us
to investigate the properties of the resulting PDFs, and to assess how they
are influenced by the noise.
We synthesize the Stokes V profiles of the Fe I lines at 6301, 6302, 15 648 and 15 652 Å emerging from internetwork regions.
There is growing evidence, both from observations and from numerical
simulations, that magnetic fields are ubiquitous in the internetwork and
that all field strengths from zero to the thermal equipartition value of
about 1.5 kG are possible. This implies that magnetic fibrils of various
strengths may be present in the resolution element at moderate (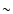 1 arcsec) angular resolution. We include these ingredients in our simulations
by considering that the polarization signals emerging from each resolution
element are produced by two spatially separated magnetic fibrils of different
field strengths. The number of magnetic components is restricted to two for
simplicity, but we note that having more components would not change
the results qualitatively. The magnetic field strength of the two atmospheres is assumed to be constant with optical depth. The
temperature stratifications are taken to be that of the quiet sun
(represented by the Harvard Smithsonian Reference Atmosphere of
Gingerich et al. 1971). A fraction
1 arcsec) angular resolution. We include these ingredients in our simulations
by considering that the polarization signals emerging from each resolution
element are produced by two spatially separated magnetic fibrils of different
field strengths. The number of magnetic components is restricted to two for
simplicity, but we note that having more components would not change
the results qualitatively. The magnetic field strength of the two atmospheres is assumed to be constant with optical depth. The
temperature stratifications are taken to be that of the quiet sun
(represented by the Harvard Smithsonian Reference Atmosphere of
Gingerich et al. 1971). A fraction 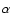 of the resolution
element is magnetized, with the first component contributing a
fraction
of the resolution
element is magnetized, with the first component contributing a
fraction 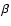 and the second the remaining
and the second the remaining 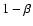 .
Thus,
the emergent Stokes V profiles are computed as
.
Thus,
the emergent Stokes V profiles are computed as
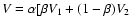 ], where Vi represents the signal
due to component i. The magnetic filling factor
], where Vi represents the signal
due to component i. The magnetic filling factor 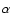 is
an important quantity in determining the amplitude of the
simulated Stokes V signal.
is
an important quantity in determining the amplitude of the
simulated Stokes V signal.
In order to mimic real observations, white noise is added to
the profiles at the level of 10-3 and 10-4 of the
continuum intensity 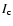 .
The interpretation of the
resulting circular polarization profiles is done by assuming
that there is only one single magnetic component in the resolution
element. This is a common assumption in analyses of the internetwork.
The Stokes V profiles are subject to two inversions (one for the
visible lines and other for the infrared lines) in order to
determine the parameters of the model atmosphere that provides
the best fit to the observations. To this end, we use the SIR code
developed by Ruiz Cobo & del Toro Iniesta (1992). SIR iteratively
modifies a guess model atmosphere by means of a non-linear,
least-squares algorithm until the synthetic profiles match the
observed ones. Depending on the application, the user decides
which atmospheric parameters are to be determined. In our case,
free parameters of the inversion are the magnetic field strength,
the magnetic filling factor, and the macroturbulent velocity.
The macroturbulence is allowed to vary in order to provide
a means to account for the broadening of the Stokes V profiles
induced by the existence of two magnetic fields, which cannot be
explained in terms of a single magnetic component. This additional
broadening is very noticeable in the infrared lines, but not in the
visible lines.
.
The interpretation of the
resulting circular polarization profiles is done by assuming
that there is only one single magnetic component in the resolution
element. This is a common assumption in analyses of the internetwork.
The Stokes V profiles are subject to two inversions (one for the
visible lines and other for the infrared lines) in order to
determine the parameters of the model atmosphere that provides
the best fit to the observations. To this end, we use the SIR code
developed by Ruiz Cobo & del Toro Iniesta (1992). SIR iteratively
modifies a guess model atmosphere by means of a non-linear,
least-squares algorithm until the synthetic profiles match the
observed ones. Depending on the application, the user decides
which atmospheric parameters are to be determined. In our case,
free parameters of the inversion are the magnetic field strength,
the magnetic filling factor, and the macroturbulent velocity.
The macroturbulence is allowed to vary in order to provide
a means to account for the broadening of the Stokes V profiles
induced by the existence of two magnetic fields, which cannot be
explained in terms of a single magnetic component. This additional
broadening is very noticeable in the infrared lines, but not in the
visible lines.
Let us assume that the actual distribution of magnetic fields in
the internetwork follows the law
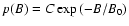 ,
where
,
where
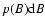 is the probability of occurrence of magnetic
fields with strengths from B to
is the probability of occurrence of magnetic
fields with strengths from B to
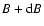 ,
and C is a
normalization constant. We take B0=250 G as indicated by the
infrared measurements of Collados (2001) and Khomenko et al. (2003).
,
and C is a
normalization constant. We take B0=250 G as indicated by the
infrared measurements of Collados (2001) and Khomenko et al. (2003).
The simulation starts by extracting at random two magnetic fields
from the actual distribution p(B). We then compute the
corresponding Stokes V signals, and combine them using a
value for 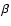 .
In accordance with recent observational results, we assume
that the magnetic atmospheres occupy a fraction
.
In accordance with recent observational results, we assume
that the magnetic atmospheres occupy a fraction
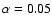 of the
resolution element. As many as 10 000 simulated profiles have
been produced in this way. The magnetic field distributions
inferred from the inversion of such profiles are presented in the
following sections for two values of
of the
resolution element. As many as 10 000 simulated profiles have
been produced in this way. The magnetic field distributions
inferred from the inversion of such profiles are presented in the
following sections for two values of 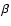 .
.
The situation in which only one magnetic field is present in the
resolution element can be modeled with 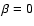 .
This case is
considered here because it represents the simplest scenario one
can imagine for the internetwork.
.
This case is
considered here because it represents the simplest scenario one
can imagine for the internetwork.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{h4342f1a.ps}}\vspace*{5mm}
\resizebox{8.8cm}{!}{\includegraphics{h4342f1b.ps}}
\end{figure}](/articles/aa/full/2003/28/aah4342/Timg20.gif) |
Figure 1:
Distribution of magnetic field strengths inferred from the
analysis of a simulated internetwork region (10 000 pixels) where the
actual distribution is
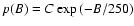 and each
resolution element contains one single magnetic field (
and each
resolution element contains one single magnetic field (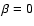 ).
Solid and dashed lines give the PDFs resulting from the infrared and the
visible lines, respectively. The dotted line represents the
original PDF. The binsize is 25 G. Top: Noise added to Stokes V at the level of 10-4 of the continuum intensity ).
Solid and dashed lines give the PDFs resulting from the infrared and the
visible lines, respectively. The dotted line represents the
original PDF. The binsize is 25 G. Top: Noise added to Stokes V at the level of 10-4 of the continuum intensity 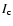 .
Bottom: Noise at the level of .
Bottom: Noise at the level of
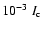 . . |
| Open with DEXTER |
Figure 1 shows the field strength distributions inferred from the
visible and infrared lines. When the noise is small (upper panel),
the PDF determined using the infrared lines is very similar to
the original distribution. By contrast, the PDF resulting from the visible
lines shows a pronounced deficit of weak fields below 400 G. With
larger noise at the level of
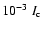 (lower panel), the infrared
lines still do an excellent job in recovering the original PDF down
to field strengths of about 350 G. However, the PDF delivered by
the visible lines bears little resemblance with the true PDF.
The most prominent feature of the distribution is the peak at
about 900 G, with very broad wings, especially towards lower
field strengths. Compared with the original PDF, there is an excess
of strong fields and a significant deficit of weak fields larger
than 200 G. Indeed, most pixels are interpreted as being characterized
by field strengths smaller than 100 G or larger than 800 G. Thus, one
would conclude from the visible PDF that the simulated IN region
contains a sizeable fraction of kG fields, while in reality
there are very few strong fields in it.
(lower panel), the infrared
lines still do an excellent job in recovering the original PDF down
to field strengths of about 350 G. However, the PDF delivered by
the visible lines bears little resemblance with the true PDF.
The most prominent feature of the distribution is the peak at
about 900 G, with very broad wings, especially towards lower
field strengths. Compared with the original PDF, there is an excess
of strong fields and a significant deficit of weak fields larger
than 200 G. Indeed, most pixels are interpreted as being characterized
by field strengths smaller than 100 G or larger than 800 G. Thus, one
would conclude from the visible PDF that the simulated IN region
contains a sizeable fraction of kG fields, while in reality
there are very few strong fields in it.
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{h4342f2a.ps}}\vspace*{5mm}
\resizebox{8.3cm}{!}{\includegraphics[clip]{h4342f2b.ps}}
\end{figure}](/articles/aa/full/2003/28/aah4342/Timg22.gif) |
Figure 2:
Distribution of magnetic field strengths inferred from the
analysis of a simulated internetwork region (10 000 pixels) where the actual
distribution is
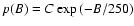 and two magnetic fibrils
coexist in each resolution element with
and two magnetic fibrils
coexist in each resolution element with
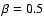 .
Solid and dashed
lines represent the PDFs resulting from the infrared and the visible lines,
respectively. The dotted line gives the original field strength
distribution. Top: Noise added at the level of .
Solid and dashed
lines represent the PDFs resulting from the infrared and the visible lines,
respectively. The dotted line gives the original field strength
distribution. Top: Noise added at the level of
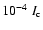 .
Bottom: Noise at the level of .
Bottom: Noise at the level of
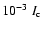 . . |
| Open with DEXTER |
The situation in which there are two magnetic fields in the same
resolution element is modeled here by setting
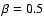 ,
i.e.,
both fields contribute to the Stokes V profile with the same weight.
In the absence of any observational result concerning the dependence
of the magnetic filling factor on field strength in internetwork
regions, the choice of
,
i.e.,
both fields contribute to the Stokes V profile with the same weight.
In the absence of any observational result concerning the dependence
of the magnetic filling factor on field strength in internetwork
regions, the choice of
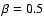 seems appropriate.
seems appropriate.
Figure 2 shows the PDFs resulting from the visible and infrared
lines in this case. Despite the different number of magnetic components
in the resolution element, the new PDFs are very similar to those
presented in Fig. 1. The only difference is that the peaks are slightly
broader and more shifted towards stronger fields. Independently of the
noise, the infrared lines deliver magnetic field PDFs which are in
reasonable accord with the actual distribution. Indeed, above 400 G
the infrared PDFs are well described by an exponential law of the
form
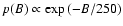 .
The visible lines, however, are
very much affected by the noise. As the noise level increases,
the peak of the distribution moves to stronger fields. The maximum
of the PDFs determined from the visible lines occurs at 500 G with
noise of
.
The visible lines, however, are
very much affected by the noise. As the noise level increases,
the peak of the distribution moves to stronger fields. The maximum
of the PDFs determined from the visible lines occurs at 500 G with
noise of
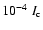 ,
and at 900 G with noise of
,
and at 900 G with noise of
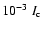 .
Again, one would conclude that a significant fraction
of pixels in the simulated region contains strong fields. This is
true for noise levels of about
.
Again, one would conclude that a significant fraction
of pixels in the simulated region contains strong fields. This is
true for noise levels of about
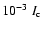 (typical of
current spectropolarimetric observations). Much lower noise levels,
at least by a factor of ten, would be needed for the visible lines
to recover the true distribution of magnetic fields.
(typical of
current spectropolarimetric observations). Much lower noise levels,
at least by a factor of ten, would be needed for the visible lines
to recover the true distribution of magnetic fields.
![\begin{figure}
\par\resizebox{8.6cm}{!}{\includegraphics[clip]{h4342f3.ps}}
\end{figure}](/articles/aa/full/2003/28/aah4342/Timg24.gif) |
Figure 3:
Distribution of magnetic field strengths determined from
an inversion of the Stokes V profiles of the visible lines emerging
from a simulated internetwork region where only fields of 200 G are present.
Noise of
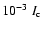 has been added to the Stokes V profiles.
If the resulting PDF is taken at face value, 27% of the pixels would
be associated with strong fields (>800 G).
has been added to the Stokes V profiles.
If the resulting PDF is taken at face value, 27% of the pixels would
be associated with strong fields (>800 G). |
| Open with DEXTER |
The excess of strong fields indicated by the visible lines is
particularly disturbing. In order to understand this behavior,
we have repeated the analysis assuming that all field strengths
in the simulated internetwork region are equal to 200 G, i.e.,
no strong fields exist. The results of this experiment, carried
out with noise in the profiles at the level of
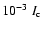 and
and
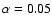 ,
are summarized in Fig. 3. Again, the
visible lines yield a peak of strong fields at around 0.9 kG, with
most of the pixels being assigned field strengths of less than 100 G. Taken at face value, the retrieved PDF indicates that 27% of the pixels contain kG fields. This leads us to
conclude that noise is capable of modifying the polarization signals
in such a way that the inversion code interprets them as
being caused by strong fields. At high noise levels, the
small changes in the Zeeman splitting of the visible lines
cannot be used as a diagnostics, and the ratio of Stokes V
amplitudes of the two lines is severely affected. As a result,
both strong and weak fields are compatible with the observations.
Figure 4 shows one such example. The observed profile has been
synthesized using a magnetic field of 200 G and noise of
,
are summarized in Fig. 3. Again, the
visible lines yield a peak of strong fields at around 0.9 kG, with
most of the pixels being assigned field strengths of less than 100 G. Taken at face value, the retrieved PDF indicates that 27% of the pixels contain kG fields. This leads us to
conclude that noise is capable of modifying the polarization signals
in such a way that the inversion code interprets them as
being caused by strong fields. At high noise levels, the
small changes in the Zeeman splitting of the visible lines
cannot be used as a diagnostics, and the ratio of Stokes V
amplitudes of the two lines is severely affected. As a result,
both strong and weak fields are compatible with the observations.
Figure 4 shows one such example. The observed profile has been
synthesized using a magnetic field of 200 G and noise of
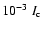 .
The inversion of this profile suggests
a magnetic field of 1250 G. The Stokes V signal corresponding
to such a strong field is given by the thick solid line. In
view of the quality of the fit, one would never say that the
inferred value of 1250 G is erroneous. Only when the best-fit
profile is compared with the original Stokes V spectrum
without noise (the smooth thin solid line of Fig. 4) do
differences in the amplitude and position of the peaks
become apparent.
.
The inversion of this profile suggests
a magnetic field of 1250 G. The Stokes V signal corresponding
to such a strong field is given by the thick solid line. In
view of the quality of the fit, one would never say that the
inferred value of 1250 G is erroneous. Only when the best-fit
profile is compared with the original Stokes V spectrum
without noise (the smooth thin solid line of Fig. 4) do
differences in the amplitude and position of the peaks
become apparent.
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{h4342f4.ps}}
\end{figure}](/articles/aa/full/2003/28/aah4342/Timg25.gif) |
Figure 4:
Stokes V signal simulated with a magnetic field strength
of 200 G,
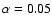 ,
and noise at the level of ,
and noise at the level of
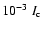 (thin solid line). For this particular realization
of the noise, the best-fit profile (thick solid line) indicates
a field strength of 1250 G. The smooth thin solid line is the
original spectrum without noise.
(thin solid line). For this particular realization
of the noise, the best-fit profile (thick solid line) indicates
a field strength of 1250 G. The smooth thin solid line is the
original spectrum without noise. |
| Open with DEXTER |
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{h4342f5.ps}}
\end{figure}](/articles/aa/full/2003/28/aah4342/Timg26.gif) |
Figure 5:
Position of the peak of the PDF inferred from the visible lines
as a function of the signal-to-noise ratio in Stokes V. Only fields of 200 G are present in the original distribution. |
| Open with DEXTER |
We may expect the situation to improve as the SNR of the
observations increases. At low noise levels, the different
Zeeman splittings and Stokes V amplitude ratios induced by
strong and weak fields cannot be confused any more. Since the
inversion code has much more information, the derived
field strengths become closer to the real values. This
is demonstrated in Fig. 5, where the peak of the PDF determined from the inversion of the visible lines is
plotted as a function of the signal-to-noise ratio (SNR)
in Stokes V![[*]](/icons/foot_motif.gif) . As before, we assume
that all magnetic fields in the simulated region are equal to 200 G.
In order to produce Fig. 5,
different noises have been added to the profiles, leading
to SNRs in Stokes V in the range 1-30. Strictly speaking,
Fig. 5 represents only the case in which all magnetic fields
have strengths of 200 G. However, it should be valid also for
any field weaker than about 1 kG. The curve in Fig. 5 slowly
converges to 200 G, but for typical noise levels the maximum
of the PDF occurs at much stronger fields. Indeed, a minimum SNR of 10 is required in the Stokes V signal of the
Fe I 6302.5 Å line if the PDF is not to peak above 600 G.
Adopting reasonable numbers for the polarization signal emerging
from the internetwork, this limit corresponds to SNRs of
roughly
. As before, we assume
that all magnetic fields in the simulated region are equal to 200 G.
In order to produce Fig. 5,
different noises have been added to the profiles, leading
to SNRs in Stokes V in the range 1-30. Strictly speaking,
Fig. 5 represents only the case in which all magnetic fields
have strengths of 200 G. However, it should be valid also for
any field weaker than about 1 kG. The curve in Fig. 5 slowly
converges to 200 G, but for typical noise levels the maximum
of the PDF occurs at much stronger fields. Indeed, a minimum SNR of 10 is required in the Stokes V signal of the
Fe I 6302.5 Å line if the PDF is not to peak above 600 G.
Adopting reasonable numbers for the polarization signal emerging
from the internetwork, this limit corresponds to SNRs of
roughly
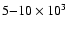 in the continuum intensity.
in the continuum intensity.
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{h4342f6a.ps}}\vspace*{4mm}
\resizebox{8.3cm}{!}{\includegraphics{h4342f6b.ps}}
\end{figure}](/articles/aa/full/2003/28/aah4342/Timg32.gif) |
Figure 6:
Top: simulated (solid line) and best-fit (dashed line)
profiles of the visible lines for 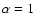 and
and
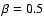 .
The
fit is so good that the dashed line is indistinguishable. Bottom: same
for the infrared lines. .
The
fit is so good that the dashed line is indistinguishable. Bottom: same
for the infrared lines. |
| Open with DEXTER |
The most important conclusion that can be drawn from these
experiments is that internetwork magnetic field PDFs resulting
from visible lines are very sensitive to noise in the profiles.
Empirically determined PDFs showing maxima at large field strengths
should be regarded with suspicion, especially if short exposure
times were used during the observations.
Another interesting outcome of the numerical experiments presented in
Sect. 3 is the fact that the PDFs retrieved from the infrared lines
for the cases 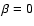 and
and
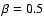 are essentially the same
down to about 400 G. This implies that the original distribution is
recovered in a statistical sense independently of whether the resolution
elements are occupied by one or more magnetic components. In order to
understand this result, let us consider the simple situation in which
two magnetic components having field strengths of 200 and 1200 G coexist
in the resolution element and the filling factor of the weak field
component,
are essentially the same
down to about 400 G. This implies that the original distribution is
recovered in a statistical sense independently of whether the resolution
elements are occupied by one or more magnetic components. In order to
understand this result, let us consider the simple situation in which
two magnetic components having field strengths of 200 and 1200 G coexist
in the resolution element and the filling factor of the weak field
component, 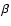 ,
varies from 0 to 1. The two limiting cases
correspond to only strong or weak fields being present in the resolution element.
For simplicity, no noise is added to the profiles.
,
varies from 0 to 1. The two limiting cases
correspond to only strong or weak fields being present in the resolution element.
For simplicity, no noise is added to the profiles.
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{h4342f7.ps}}
\end{figure}](/articles/aa/full/2003/28/aah4342/Timg33.gif) |
Figure 7:
Field strengths inferred from the fit of
simulated profiles assuming that they are produced
by one magnetic atmosphere, as a function of 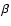 (the
fraction of magnetized area covered by weak fields).
The Stokes V spectra have been constructed by mixing
the signals of two atmospheres having magnetic
fields of 200 G and 1200 G.
(the
fraction of magnetized area covered by weak fields).
The Stokes V spectra have been constructed by mixing
the signals of two atmospheres having magnetic
fields of 200 G and 1200 G. |
| Open with DEXTER |
Figure 6 displays, as an example, the Stokes V profiles of the
visible and infrared lines when 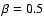 .
The visible lines
and Fe I 15 652 Å show no obvious trace of two different magnetic
fields due to the small Zeeman splittings. This is not the case for
the infrared Fe I line at 15 648 Å. With a Landé factor of 3,
the signals generated by the strong and weak field components are
clearly visible due to the huge splitting of the former. The dashed
lines give the best-fit profiles resulting from the inversion. As
can be seen, the fit is excellent for the visible lines and somewhat
worse for the infrared lines. If one magnetic atmosphere is used to
interpret the Stokes V signal of Fe I 15 648 Å, the inferred
field strength lies somewhere in between the original 200 and 1200 G
in order to have an intermediate Zeeman splitting. The Stokes V
amplitude of Fe I 15 652 Å induced by such a field is too small,
as can be seen in the lower panel of Fig. 6. The misfit could be
removed by increasing the field strength, but this would lead to a
much worse fit to Fe I 15 648 Å. The best compromise is then an
intermediate value which fits equally well (or worse) the Zeeman
splitting of Fe I 15 648 Å and the Stokes V amplitude of 15 652 Å. Hence, if two components are present in the resolution
element, we may expect that the field strength determined from
the infrared lines will not correspond to any of the original
fields unless the fraction of area occupied by one of them is
very large.
.
The visible lines
and Fe I 15 652 Å show no obvious trace of two different magnetic
fields due to the small Zeeman splittings. This is not the case for
the infrared Fe I line at 15 648 Å. With a Landé factor of 3,
the signals generated by the strong and weak field components are
clearly visible due to the huge splitting of the former. The dashed
lines give the best-fit profiles resulting from the inversion. As
can be seen, the fit is excellent for the visible lines and somewhat
worse for the infrared lines. If one magnetic atmosphere is used to
interpret the Stokes V signal of Fe I 15 648 Å, the inferred
field strength lies somewhere in between the original 200 and 1200 G
in order to have an intermediate Zeeman splitting. The Stokes V
amplitude of Fe I 15 652 Å induced by such a field is too small,
as can be seen in the lower panel of Fig. 6. The misfit could be
removed by increasing the field strength, but this would lead to a
much worse fit to Fe I 15 648 Å. The best compromise is then an
intermediate value which fits equally well (or worse) the Zeeman
splitting of Fe I 15 648 Å and the Stokes V amplitude of 15 652 Å. Hence, if two components are present in the resolution
element, we may expect that the field strength determined from
the infrared lines will not correspond to any of the original
fields unless the fraction of area occupied by one of them is
very large.
This intuitive idea is confirmed in Fig. 7, where the field strengths
estimated from the visible and infrared lines are plotted as a function
of 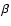 .
The visible lines deliver strong magnetic fields up to
.
The visible lines deliver strong magnetic fields up to
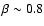 ,
whereas the infrared lines return all field strengths from 1200 G to 200 G as
,
whereas the infrared lines return all field strengths from 1200 G to 200 G as 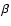 varies from 0 to 1. Visible lines favor
strong fields because the signal due to the weak
field component is about five times smaller than that of the strong
field, hence it does not contribute significantly to the total
profile until
varies from 0 to 1. Visible lines favor
strong fields because the signal due to the weak
field component is about five times smaller than that of the strong
field, hence it does not contribute significantly to the total
profile until 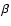 is relatively large. For
is relatively large. For
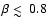 ,
the ratio of Stokes V amplitudes as well as the Zeeman splitting
of the visible lines indicate strong fields, and this is what the
inversion code returns. The infrared lines, on the other hand,
deliver field strengths which are somewhere in between the true fields present in the
resolution element. Of course, the assumption of one magnetic
component precludes a more realistic description of the various
fields that may contribute to the observed signals. In spite of
that, the picture drawn from the infrared lines is correct
in a statistical sense, because the true PDF is recovered
when a large number of pixels (i.e., the whole field of view) is
considered. Thus, the PDFs resulting from the interpretation of
infrared observations in terms of one single magnetic component
are probably valid even if several magnetic fields coexist in the
resolution element.
,
the ratio of Stokes V amplitudes as well as the Zeeman splitting
of the visible lines indicate strong fields, and this is what the
inversion code returns. The infrared lines, on the other hand,
deliver field strengths which are somewhere in between the true fields present in the
resolution element. Of course, the assumption of one magnetic
component precludes a more realistic description of the various
fields that may contribute to the observed signals. In spite of
that, the picture drawn from the infrared lines is correct
in a statistical sense, because the true PDF is recovered
when a large number of pixels (i.e., the whole field of view) is
considered. Thus, the PDFs resulting from the interpretation of
infrared observations in terms of one single magnetic component
are probably valid even if several magnetic fields coexist in the
resolution element.
In this paper we have presented the results of Montecarlo simulations
aimed at understanding the internetwork magnetic field distributions
derived from visible and infrared spectral lines. Stokes V profiles
of the Fe I lines at 6302 Å and 1.565 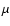 m have been synthesized
assuming different magnetic components in the resolution element and
different noise levels. The visible and infrared lines have been inverted
separately in order to determine the magnetic field distributions of
a simulated internetwork region. This strategy has allowed us to
assess the range of validity of the resulting distributions.
m have been synthesized
assuming different magnetic components in the resolution element and
different noise levels. The visible and infrared lines have been inverted
separately in order to determine the magnetic field distributions of
a simulated internetwork region. This strategy has allowed us to
assess the range of validity of the resulting distributions.
Three main conclusions can be drawn from our numerical
experiments:
- The infrared lines do a reasonably good job in retrieving the PDF
used as input for the simulation down to a few hundred Gauss, where the
weak field regime may be considered to take over. This is true even if several
magnetic fibrils are present in the resolution element, giving
strong support to the observational PDFs obtained by Lin (1995),
Collados (2001), and Khomenko et al. (2003).
- Visible lines are very sensitive to noise when dealing with
low-amplitude polarization signals such as those found in internetwork
regions. The magnetic field leaves its imprint mainly in the amplitude
of the circular polarization profiles. As a consequence, it cannot be
determined reliably at high noise levels. A particular example has
been presented where the inversion of spectra of visible lines with
noise of
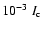 reveals strong fields in 30% of the
spatial points, although only fields of 200 G were used as input.
Infrared lines are much less sensitive to noise because of the
larger Zeeman splitting.
reveals strong fields in 30% of the
spatial points, although only fields of 200 G were used as input.
Infrared lines are much less sensitive to noise because of the
larger Zeeman splitting.
- Signal-to-noise ratios in Stokes V better than about 10
are needed to be confident about kG fields inferred from visible
lines. This limit corresponds to signal-to-noise ratiosof
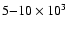 in the continuum intensity for the conditions
prevailing in the internetwork.
in the continuum intensity for the conditions
prevailing in the internetwork.
In order to reconcile the results of analyses based on visible and
infrared observations, some authors have suggested that weak and kG fields coexist in the internetwork, with the strong fields occupying
a tiny fraction of the resolution element (otherwise the infrared
lines would detect them easily). While such an scenario cannot be
ruled out, we warn that noise is an important ingredient
for understanding the internetwork magnetic field distributions
determined observationally. Noise affects the measurement of intrinsic
field strengths from very weak polarization signals, especially in the
visible. This may well explain the different magnetic field distributions derived
from visible and infrared lines.
Our results suggest that internetwork magnetic field studies would
greatly benefit from lower noise levels. Until larger solar telescopes
become operational, the obvious way to improve the SNR of spectropolarimetric
measurements is to use longer effective exposure times.
Acknowledgements
Comments and suggestions by Héctor Socas-Navarro and Oskar Steiner are
gratefully acknowledged. This work has been partially funded by the
Deutsche Forschungsgemeinschaft and by
the Spanish Ministerio de Ciencia y Tecnología through project
AYA2001-1649.
-
Bellot Rubio, L. R., Rodríguez Hidalgo, I., Collados, M.,
Khomenko, E., & Ruiz Cobo, B. 2001, ApJ, 560, 1010
In the text
NASA ADS
-
Collados, M. 2001, ASP Conf. Ser., 236, 255
In the text
-
Domínguez Cerdeña, I.,
Kneer, F., & Sánchez Almeida, J. 2003, ApJ, 582, L55
In the text
NASA ADS
- Emonet, T., &
Cattaneo, F. 2001, ApJ, 560, L197
In the text
NASA ADS
-
Gingerich, O., Noyes, R. W., Kalkofen, W., & Cuny, Y. 1971, Sol. Phys., 18,
347
In the text
NASA ADS
-
Grossmann-Doerth, U., Keller, C. U., & Schuessler, M. 1996,
A&A, 315, 610
In the text
NASA ADS
-
Khomenko, E., Collados, M., Solanki, S. K., Lagg, A., & Trujillo Bueno, J. 2003,
A&A, in press
In the text
-
Lin, H. 1995, ApJ, 446, 421
In the text
NASA ADS
-
Lites, B. W. 2002, ApJ, 573, 431
In the text
NASA ADS
-
Parker, E. N. 1978, ApJ, 221, 368
In the text
NASA ADS
-
Ruiz Cobo, B., & del Toro Iniesta, J. C. 1992, ApJ, 398, 375
In the text
NASA ADS
-
Sánchez Almeida, J., & Lites, B. W. 2000, ApJ, 532, 1215
In the text
NASA ADS
-
Socas-Navarro, H. 2003, ASP Conf. Ser., in press
In the text
-
Socas-Navarro, H., & Sánchez Almeida, J. 2002, ApJ, 565, 1323
In the text
NASA ADS
-
Solanki, S. K., Zufferey, D., Lin, H., Rüedi, I., & Kuhn, J. R. 1996, A&A, 310, L33
In the text
NASA ADS
-
Steiner, O. 2003, in Proc. NATO Advanced Research Workshop: Turbulence, Waves, and
Instabilities in the Solar Plasma, ed. R. Erdelyi, & K. Petrovay
(Dordrecht: Kluwer), in press
In the text
Copyright ESO 2003
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{h4342f1a.ps}}\vspace*{5mm}
\resizebox{8.8cm}{!}{\includegraphics{h4342f1b.ps}}
\end{figure}](/articles/aa/full/2003/28/aah4342/Timg20.gif)
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{h4342f2a.ps}}\vspace*{5mm}
\resizebox{8.3cm}{!}{\includegraphics[clip]{h4342f2b.ps}}
\end{figure}](/articles/aa/full/2003/28/aah4342/Timg22.gif)
![\begin{figure}
\par\resizebox{8.6cm}{!}{\includegraphics[clip]{h4342f3.ps}}
\end{figure}](/articles/aa/full/2003/28/aah4342/Timg24.gif)
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{h4342f4.ps}}
\end{figure}](/articles/aa/full/2003/28/aah4342/Timg25.gif)
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{h4342f5.ps}}
\end{figure}](/articles/aa/full/2003/28/aah4342/Timg26.gif)
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{h4342f6a.ps}}\vspace*{4mm}
\resizebox{8.3cm}{!}{\includegraphics{h4342f6b.ps}}
\end{figure}](/articles/aa/full/2003/28/aah4342/Timg32.gif)
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{h4342f7.ps}}
\end{figure}](/articles/aa/full/2003/28/aah4342/Timg33.gif)