A&A 406, 273-280 (2003)
DOI: 10.1051/0004-6361:20030746
Surface imaging of stellar non-radial pulsations
I. Inversions of simulated data
S. V. Berdyugina1,2 - J. H. Telting3 - H. Korhonen4
1 - Astronomy Division, University of Oulu,
PO Box 3000, 90401 Oulu, Finland
2 -
Institute of Astronomy, ETHZ, 8092 Zurich, Switzerland
3 -
Nordic Optical Telescope, Apartado 474, 38700 S/C de La Palma,
Canarias, Spain
4 -
Astrophysical Institute Potsdam, An der Sternwarte 16,
14482 Potsdam, Germany
Received 10 February 2003 / Accepted 13 May 2003
Abstract
We investigate capability of the stellar surface imaging technique for
studying stellar non-radial pulsations on the basis of inversions of
time series of variable line profiles without making assumptions on
the specific shape of the pulsations. The inversion results in an
image of the stellar surface in which sectoral and tesseral modes can be
distinguished in many cases, and the pulsational degree 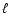 and the
azimuthal order |m| can be determined.
We find that sectoral and tesseral modes with
and the
azimuthal order |m| can be determined.
We find that sectoral and tesseral modes with
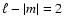 (or any even number) can be successfully restored under various conditions
(different inclinations of the rotational axis, surface temperature or
velocity fluctuations due to pulsations). Tesseral modes with
(or any even number) can be successfully restored under various conditions
(different inclinations of the rotational axis, surface temperature or
velocity fluctuations due to pulsations). Tesseral modes with
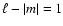 (or any odd number) do not show significant line profile
variations at higher inclinations of the rotational axis, and, thus, no
information can be recovered from line profiles. At lower inclinations,
only the azimuthal order |m| of such modes can be recovered.
We conclude that stellar surface imaging is a useful technique
for pulsation-mode identification.
(or any odd number) do not show significant line profile
variations at higher inclinations of the rotational axis, and, thus, no
information can be recovered from line profiles. At lower inclinations,
only the azimuthal order |m| of such modes can be recovered.
We conclude that stellar surface imaging is a useful technique
for pulsation-mode identification.
Key words: stars: imaging - stars: oscillations
Internal structure of stars can be studied by means of
asteroseismology, i.e. by observing and analysis of stellar
oscillations. Observed oscillation frequencies depend on the
properties of the star and, thus, constrain the stellar structure and
evolution models. Furthermore, it is important to identify
oscillation modes, namely to assign a pulsational degree and azimuthal
number to the observed frequency. Recent reviews on
pulsation-mode identification methods are presented by Aerts & Eyer
(2000), Balona (2000), Mantegazza (2000), and
Telting (2003).
Stellar non-radial pulsations (NRP) on rapidly rotating stars are
observed spectroscopically as systematic line-profile variations (lpv). The pulsations re-distribute the flux in a rotationally
broadened profile due to combined effects of the pulsational velocity
field and temperature fluctuations. With the Fourier analysis of time
series of profiles, dominant frequencies of pulsations can be
found. Then, the pulsational degree 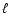 ,
the azimuthal order mand the velocity amplitude of the pulsations can be derived with an
appropriate data set (Gies & Kullavanijaya 1988; Schrijvers
et al. 1997; Telting & Schrijvers 1997; Schrijvers &
Telting 1999). The difficulties arise when the value of |m|is determined. It is generally assumed that
,
the azimuthal order mand the velocity amplitude of the pulsations can be derived with an
appropriate data set (Gies & Kullavanijaya 1988; Schrijvers
et al. 1997; Telting & Schrijvers 1997; Schrijvers &
Telting 1999). The difficulties arise when the value of |m|is determined. It is generally assumed that 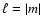 ,
i.e. that the
pulsation modes are sectoral. However, Telting & Schrijvers
(1997) showed that in some cases the value of |m| can be
estimated from line profiles.
,
i.e. that the
pulsation modes are sectoral. However, Telting & Schrijvers
(1997) showed that in some cases the value of |m| can be
estimated from line profiles.
A great help in the identification of the pulsation modes can be provided
by the technique of stellar surface imaging based on inversions of a time
series of line profiles into an instant stellar image. The idea of surface
imaging (or Doppler imaging) was invented by Deutsch (1958) and was
first used to map chemical inhomogeneities on Ap stars. The further
development of the method by Deutsch (1970), Falk & Wehlau
(1974), Goncharsky et al. (1977) and many others has lead to a
fully functional method for mapping stellar surface structures. Surface
imaging is an ill-posed inversion problem, and many different methods have
been used for solving it, e.g., Maximum Entropy Method (Vogt & Penrod
1983; Vogt et al. 1987), Tikhonov Regularization
(Goncharsky et al. 1977; Piskunov et al. 1990) and Occamian
Approach (Berdyugina 1998). Nowadays, surface imaging is widely
used for mapping temperature, abundance and magnetic field fluctuations on
the surfaces of magnetically active, rapidly rotating hot Ap stars and
cool G-K-M stars.
In this paper, we study how surface imaging technique can be used for
mapping stellar NRP. We perform inversions of theoretical line profiles
calculated for various pulsation modes and show that the inversions result
in images of the stellar surface in which sectoral and tesseral modes can
be distinguished. Our results apply to p-mode oscillations in rotating 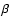 Cephei and
Cephei and 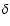 Scuti variables.
Scuti variables.
We calculated 14 sets of profiles of the Si III 4552 Å line
for a test star with the following parameters:
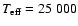 K,
K,
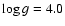 ,
,
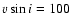 km s-1.
The time series of simulated spectra were generated with the
model presented by Telting & Schrijvers (1997) and Schrijvers &
Telting (1999).
In different sets, the test star is assumed to pulsate in different modes,
sectoral or tesseral, with either temperature or velocity fluctuations.
This is done in order to demonstrate how the method works
for different
km s-1.
The time series of simulated spectra were generated with the
model presented by Telting & Schrijvers (1997) and Schrijvers &
Telting (1999).
In different sets, the test star is assumed to pulsate in different modes,
sectoral or tesseral, with either temperature or velocity fluctuations.
This is done in order to demonstrate how the method works
for different 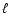 and |m| of NRP. For instance, the following
cases are of particular interest: (i) sectoral mode implying
and |m| of NRP. For instance, the following
cases are of particular interest: (i) sectoral mode implying
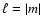 ;
(ii) tesseral mode with
;
(ii) tesseral mode with
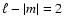 which is symmetric
with respect to the equator; (iii) tesseral mode with
which is symmetric
with respect to the equator; (iii) tesseral mode with
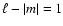 which is antisymmetric with respect to the equator as it
has one node line coinciding with the equator.
Also, by choosing different
values of the inclination of the stellar rotation axis, i, we test the
sensitivity of the solution to this parameter.
A summary of the calculated models is given in Table 1.
We assume that the test star oscillates with the frequency 15 cycles/day (in the observers' frame)
in all pulsation modes. This results, however, in different pattern-rotation
periods
which is antisymmetric with respect to the equator as it
has one node line coinciding with the equator.
Also, by choosing different
values of the inclination of the stellar rotation axis, i, we test the
sensitivity of the solution to this parameter.
A summary of the calculated models is given in Table 1.
We assume that the test star oscillates with the frequency 15 cycles/day (in the observers' frame)
in all pulsation modes. This results, however, in different pattern-rotation
periods 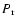 ,
which are given in Table 1.
The line profiles were simulated with S/N=500 for 22 rotational phases covering
a whole rotation of a single pulsation.
,
which are given in Table 1.
The line profiles were simulated with S/N=500 for 22 rotational phases covering
a whole rotation of a single pulsation.
Table 1:
Calculated models of NRP for the test star pulsating with the
frequency 15 cycle/day.
To perform inversions of the simulated data and recover the pulsation
patterns, we assume for simplicity that the lpv are caused only by
temperature fluctuations, despite the fact that the simulations included
also velocity variations.
For a rapidly-rotating star the rotational broadening of
line profiles is significantly larger than the local line profile at a
single point on the stellar surface. Therefore, a temperature or
velocity fluctuation on the stellar surface results
in a "bump'' in the profile. As the pulsation pattern rotates, this
"bump'' moves across the profile over a velocity
range that depends on the latitude
of the fluctuation (see e.g. Vogt & Penrod 1983).
Inversion of a time series of stellar
line profiles results in a map, or image, of the stellar surface.
Given a set of stellar atmosphere models, the
stellar image reflects the distribution of effective
temperatures of the models across the stellar surface, as usual for
the surface imaging technique. The stellar surface is considered as a
set of elemental areas,  ,
where the temperature values have to be
determined from the observational data set
,
where the temperature values have to be
determined from the observational data set  .
To achieve this, we
solve the equation
.
To achieve this, we
solve the equation
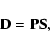 |
(1) |
where 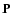 denotes the Point Spread Function (PSF), or
the response operator, which determines the transformation of the image to
the data, or the model. Elements of the matrix
denotes the Point Spread Function (PSF), or
the response operator, which determines the transformation of the image to
the data, or the model. Elements of the matrix 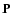 are proportional
to local line profiles and local areas.
are proportional
to local line profiles and local areas.
A set of local line profiles have been calculated for a temperature
range of
20 000-30 000 K and
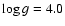 using the stellar atmosphere
models by Kurucz (1993). A code used for synthetic spectrum
calculations is described in detail by Berdyugina (1991). It
includes calculation of opacities, intensities and fluxes in the
continuum and lines. In order to take into account limb darkening
effect, the local line profiles have been calculated for ten angular
points on the stellar disk.
The stellar surface was divided by the
coordinate grid of
using the stellar atmosphere
models by Kurucz (1993). A code used for synthetic spectrum
calculations is described in detail by Berdyugina (1991). It
includes calculation of opacities, intensities and fluxes in the
continuum and lines. In order to take into account limb darkening
effect, the local line profiles have been calculated for ten angular
points on the stellar disk.
The stellar surface was divided by the
coordinate grid of
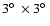 ,
and the temperature of each
pixel was recovered in the inversion.
,
and the temperature of each
pixel was recovered in the inversion.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4304F1.EPS}
\end{figure}](/articles/aa/full/2003/28/aah4304/Timg27.gif) |
Figure 1:
Inversion results for the sectoral mode
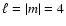 with
only temperature fluctuations (Set 1).
The image is shown in the cylindrical and spherical
projection. Because of significant inclination of the stellar
rotation axis, the pulsations are not completely recovered in the
subequatorial zone.
with
only temperature fluctuations (Set 1).
The image is shown in the cylindrical and spherical
projection. Because of significant inclination of the stellar
rotation axis, the pulsations are not completely recovered in the
subequatorial zone. |
| Open with DEXTER |
Since the surface imaging problem is a typical inverse problem, which
tries to determine the true properties of the phenomena from the
observed effects, a special method must be used to solve it.
Here, we use the Occamian approach to inverse problems which
was applied to the surface imaging problem by Berdyugina (1998).
With simulated data and test calculations it was shown that the
Occamian approach can restore stellar images under various
conditions. The method was also successfully used for temperature
mapping of cool stars (see e.g. Berdyugina et al. 1998, 1999).
Note that our inversion technique is free from assumptions that
it is the pulsations that cause line profile variations.
In contrast with many other techniques, we do
not assume that the surface-feature distribution is to be in the form
of spherical harmonics or any other presupposed shape. This provides
an opportunity to test with real data if such an assumption made in
previous studies is reliable. Also, we do not make any assumptions if
pulsation modes are of sectoral or tesseral type.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4304F2A.EPS}\par\vspace*{...
...}\par\vspace*{4mm}
\includegraphics[width=8.8cm,clip]{H4304F2C.EPS}
\end{figure}](/articles/aa/full/2003/28/aah4304/Timg28.gif) |
Figure 2:
Inversion results for the sectoral mode
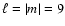 with temperature and velocity fluctuations (Sets 2-4). with temperature and velocity fluctuations (Sets 2-4). |
| Open with DEXTER |
For sectoral modes we considered two cases with temperature
fluctuations of 10%:
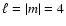 and
and
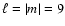 .
The latter
case was also studied for two values of velocity fluctuations: 3 and 10 km s-1. The inversion results are shown in
Figs. 1 and 2.
.
The latter
case was also studied for two values of velocity fluctuations: 3 and 10 km s-1. The inversion results are shown in
Figs. 1 and 2.
In all cases, the recovered images of the test star show a distinct
sectoral structure, in good agreement with the input pulsation
patterns. Because of significant inclination of the rotational axis
(i=60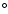 ), the pulsations are not completely recovered in the
subequatorial zone and, thus, look as shifted in latitude. This,
however, does not disturb the mode identification. The amplitude of
temperature fluctuations is restored reasonably well.
), the pulsations are not completely recovered in the
subequatorial zone and, thus, look as shifted in latitude. This,
however, does not disturb the mode identification. The amplitude of
temperature fluctuations is restored reasonably well.
The velocity fluctuations interpreted in terms of temperature
fluctuations also result in well-defined pulsation patterns.
The shapes of bumps in the images correspond well to the shapes of
bumps in spectra. Particularly, in the case of velocity fluctuations of 10 km s-1, dips in the line profiles, being narrower than
the bumps, result in narrow bright regions in the image
(the bottom image in Fig. 2), while broader dark regions
correspond to the line profile bumps. Such shapes, if observed, can
therefore serve as a signature of strong velocity fields in the
pulsations.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4304F3A.EPS}\par\vspace*{...
...}\par\vspace*{4mm}
\includegraphics[width=8.8cm,clip]{H4304F3C.EPS}
\end{figure}](/articles/aa/full/2003/28/aah4304/Timg29.gif) |
Figure 3:
Inversion results for the symmetrical tesseral mode 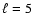 ,
|m|=3 with temperature fluctuations at different inclinations (Sets 5-7). ,
|m|=3 with temperature fluctuations at different inclinations (Sets 5-7). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4304F5A.EPS}\par\vspace*{2mm}
\includegraphics[width=8.8cm,clip]{H4304F5B.EPS}
\end{figure}](/articles/aa/full/2003/28/aah4304/Timg31.gif) |
Figure 5:
Inversion results for the antisymmetric tesseral mode 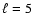 ,
|m|=4 with temperature fluctuations at different inclinations (Sets 11-12). ,
|m|=4 with temperature fluctuations at different inclinations (Sets 11-12). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4304F6A.EPS}\par\vspace*{2mm}
\includegraphics[width=8.8cm,clip]{H4304F6B.EPS}
\end{figure}](/articles/aa/full/2003/28/aah4304/Timg32.gif) |
Figure 6:
The same as Fig. 5 for velocity fluctuations (Sets 13-14). |
| Open with DEXTER |
The inversion results for the tesseral mode 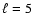 and |m|=3 with
temperature fluctuations of 10% and velocity fluctuations of 10 km s-1 are shown in Figs. 3 and 4,
respectively. Such a mode consists of three rows of a tesseral
pattern which is symmetrical with respect to the equator.
The two cases have been tested for three different
inclinations of the rotation axis to the line of sight: 55
and |m|=3 with
temperature fluctuations of 10% and velocity fluctuations of 10 km s-1 are shown in Figs. 3 and 4,
respectively. Such a mode consists of three rows of a tesseral
pattern which is symmetrical with respect to the equator.
The two cases have been tested for three different
inclinations of the rotation axis to the line of sight: 55 ,
70
,
70 ,
and 85
,
and 85 .
.
The recovered images again show rather distinct structures
in good agreement with the input pulsation patterns. At lower
inclination, the subequatorial zone is not well recovered and
high-latitude structures dominate the image. Also, as was obtained for
sectoral modes, the structures look shifted to higher latitudes at
lower inclinations, while this effect is completely gone at the
inclination of 85 .
.
For temperature
fluctuations, light and dark regions in the images as well as
corresponding dips and bumps in line profiles are of about the same
size and shape. For velocity fluctuations, bumps are noticeably broader than
dips in line profiles, that results in more extended dark regions in
the recovered images. This again may serve as an indication of strong
prevailing velocity fields in pulsations, if observed (see also
Schrijvers et al. 1997).
The inversion results for the tesseral mode 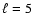 and |m|=4 with
temperature fluctuations of 10% and velocity fluctuations of 10 km s-1 are shown in Figs. 5 and 6,
respectively. Such a mode consist of two rows of tesseral
patterns which are antisymmetric with respect to the equator.
The two cases have been tested for two different
inclinations of the rotation axis to the line of sight: 55
and |m|=4 with
temperature fluctuations of 10% and velocity fluctuations of 10 km s-1 are shown in Figs. 5 and 6,
respectively. Such a mode consist of two rows of tesseral
patterns which are antisymmetric with respect to the equator.
The two cases have been tested for two different
inclinations of the rotation axis to the line of sight: 55 and 85
and 85 .
.
We found that this is a rather difficult case. For instance,
if the rotation axis is perpendicular to the line of sight,
Doppler shifts in either side of the stellar equator are equivalent.
Further, if temperature or velocity fluctuations at the same Doppler
shift on different sides of the equator are of opposite signs, as it
occurs in case of antisymmetric tesseral modes, the resulted signal in
the line profile at this Doppler shift will stay unchanged, as there
would be no fluctuations at all. Therefore, line profile variations
are rather small for these modes at higher inclinations (see
bottom line profiles in Figs. 5 and 6), and the
inversion procedure cannot deduce true pulsation patterns.
Relatively good
results can be achieved at lower inclinations, as seen from the
top plots in Figs. 5 and 6, especially for temperature
fluctuations. The structure recovered at i=55 clearly
indicates the azimuthal number |m|=4. However, because the surface
imaging technique is based on the analysis of Doppler shifts of local
line profiles, the procedure cannot distinguish the equivalent shifts
on different sides of the stellar equator and produces the known effect
of reflection of recovered structures with respect to the equator. It
is especially noticeable in case of antisymmetric pulsation patterns,
while it is successfully masked in case of symmetric modes. Its
appearance, therefore, may provide some hints for the
mode to be antisymmetric.
clearly
indicates the azimuthal number |m|=4. However, because the surface
imaging technique is based on the analysis of Doppler shifts of local
line profiles, the procedure cannot distinguish the equivalent shifts
on different sides of the stellar equator and produces the known effect
of reflection of recovered structures with respect to the equator. It
is especially noticeable in case of antisymmetric pulsation patterns,
while it is successfully masked in case of symmetric modes. Its
appearance, therefore, may provide some hints for the
mode to be antisymmetric.
For obtaining reasonable results from the inversions,
certain requirements have to be fulfilled.
First, observed spectra should be
of high resolution (
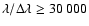 )
and
high signal-to-noise ratio (
)
and
high signal-to-noise ratio (
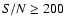 ). Chosen spectral lines
should be sensitive to NRP and show significant line profile
variations. It is also preferable if they are not blended.
The rotation of the star must be fast enough to use the
technique (
). Chosen spectral lines
should be sensitive to NRP and show significant line profile
variations. It is also preferable if they are not blended.
The rotation of the star must be fast enough to use the
technique (
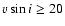 km s-1). The spectra should cover at
least one full pattern-rotation period with good time resolution. More
rotations are needed for obtaining a reliable frequency of NRP.
Further, the spectra should be reduced to exclude systematic radial
velocity variations, e.g., due to orbital motion in binary systems.
km s-1). The spectra should cover at
least one full pattern-rotation period with good time resolution. More
rotations are needed for obtaining a reliable frequency of NRP.
Further, the spectra should be reduced to exclude systematic radial
velocity variations, e.g., due to orbital motion in binary systems.
The second group of requirements concerns a set of input geometrical
and physical parameters which are needed for synthetic spectra
calculations. The geometrical parameters are
the inclination of the rotational axis to the line of sight i,
projection of the equatorial rotational velocity 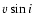 ,
and
observed oscillation frequency f or pattern-rotation period.
The physical parameters are the effective temperature of the star
,
and
observed oscillation frequency f or pattern-rotation period.
The physical parameters are the effective temperature of the star
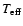 ,
surface gravity
,
surface gravity 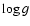 ,
micro- and macroturbulent
velocities. The accurate physical parameters are important for
deducing physical properties of the pulsations, such as amplitudes of
temperature and velocity fluctuations on the stellar surface. For the
mode identification purpose, however, these parameters are not crucial
and should only result in a good fit to the average observed line
profile. Moreover, the stellar effective temperature is not fixed in
inversions and can be fine-tuned by iterations. Synthetic spectra
calculations should account for limb darkening of the stellar
disk and for blends, including possible contribution from a companion
in binary systems.
,
micro- and macroturbulent
velocities. The accurate physical parameters are important for
deducing physical properties of the pulsations, such as amplitudes of
temperature and velocity fluctuations on the stellar surface. For the
mode identification purpose, however, these parameters are not crucial
and should only result in a good fit to the average observed line
profile. Moreover, the stellar effective temperature is not fixed in
inversions and can be fine-tuned by iterations. Synthetic spectra
calculations should account for limb darkening of the stellar
disk and for blends, including possible contribution from a companion
in binary systems.
The most critical stellar parameters for the NRP mode identification
are the geometrical parameters.
While 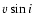 and f can be directly deduced from
spectral observations with good accuracy, the inclination angle ican be only estimated with high uncertainty. In this section, we
investigate the influence of errors in these parameters on the result
of inversions. Some tests for uneven cool spot distribution
with the present inversion method,
including effects of low S/N and errors in
and f can be directly deduced from
spectral observations with good accuracy, the inclination angle ican be only estimated with high uncertainty. In this section, we
investigate the influence of errors in these parameters on the result
of inversions. Some tests for uneven cool spot distribution
with the present inversion method,
including effects of low S/N and errors in
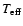 ,
,
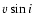 and i,
can be also found in the paper by Berdyugina (1998).
and i,
can be also found in the paper by Berdyugina (1998).
For a sample of parameter errors we carried out inversions for two sets of simulations: sectoral mode with
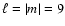 (Set 2) and
tesseral mode with
(Set 2) and
tesseral mode with 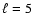 ,
|m|=3 (Set 6).
,
|m|=3 (Set 6).
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{H4304F7A.EPS}\hspace*{2mm}
\includegraphics[width=4.3cm,clip]{H4304F7B.EPS} }\end{figure}](/articles/aa/full/2003/28/aah4304/Timg39.gif) |
Figure 7:
The images of the Sets 2 and 6 (left and right) recovered with
the true inclination of the rotational axis of 60 and 70
and 70 ,
respectively, and pairs of values deviating from those by ,
respectively, and pairs of values deviating from those by 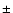 15 15 . . |
| Open with DEXTER |
Originally, Sets 2 and 6 have been calculated for the inclination
angles i of 60 and 70
and 70 respectively
(Table 1). To estimate the effect of inclination errors, which
can be quite large, we allowed the inclination angle to vary by
respectively
(Table 1). To estimate the effect of inclination errors, which
can be quite large, we allowed the inclination angle to vary by 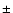 15
15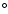 for both sets. The results are shown in Fig. 7.
for both sets. The results are shown in Fig. 7.
In all cases, the recovered images of the test star show distinct
pulsational patterns, in good agreement with the input images.
There is no noticeable changes in the structures except small
latitudinal shifts, which occur because of changes of the sub-observed
latitude on the stellar disk.
We conclude that errors in the inclination angle do not significantly
effect the recovered pulsation pattern and, thus, will not influence the
mode identification.
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{H4304F8A.EPS}\hspace*{2mm}
\includegraphics[width=4.3cm,clip]{H4304F8B.EPS} }\end{figure}](/articles/aa/full/2003/28/aah4304/Timg40.gif) |
Figure 8:
The images of the Sets 2 and 6 (left and right) recovered with
the true rotational velocity of 100 km s-1 and two values
deviating from that by 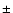 5 km s-1. 5 km s-1. |
| Open with DEXTER |
To estimate the effect of rotational velocity errors
we allowed it to vary by 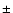 5 km s-1 for both sets.
The results are shown in Fig. 8. As was known from previously
published tests (Berdyugina 1998), underestimating of the
rotational velocity results in darkening (cooling) the polar regions,
while overestimating results in their brightening. This effect is very
well seen in the images for the sectoral mode (left column in Fig. 8).
In case of the tesseral mode (right column in Fig. 8),
the effect of smaller rotational velocity is seen in the enhancement of
the dark patterns near the pole and of the bright patterns near the
equator. The opposite behaviour is found for the case when the
rotational velocity is overestimated.
5 km s-1 for both sets.
The results are shown in Fig. 8. As was known from previously
published tests (Berdyugina 1998), underestimating of the
rotational velocity results in darkening (cooling) the polar regions,
while overestimating results in their brightening. This effect is very
well seen in the images for the sectoral mode (left column in Fig. 8).
In case of the tesseral mode (right column in Fig. 8),
the effect of smaller rotational velocity is seen in the enhancement of
the dark patterns near the pole and of the bright patterns near the
equator. The opposite behaviour is found for the case when the
rotational velocity is overestimated.
We conclude that errors in the rotational velocity influence
significantly the contrast of the recovered pattern in the latitudinal
direction, while they do not influence the mode identification.
For the sectoral mode (Set 2) we allowed the frequency to vary by 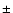 0.1 cycle/day. This corresponds to the changes of the pattern-rotation period by
0.1 cycle/day. This corresponds to the changes of the pattern-rotation period by 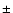 0.1 h, which is about 0.7%. The result is shown in the left column
of Fig. 9. The frequency perturbation appears in the visible
polar region as a pseudo-pulsation pattern with lower azimuthal number (
0.1 h, which is about 0.7%. The result is shown in the left column
of Fig. 9. The frequency perturbation appears in the visible
polar region as a pseudo-pulsation pattern with lower azimuthal number (
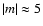 ).
).
For the tesseral mode (Set 6) we allowed the frequency to vary by 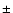 0.2 cycle/day. This corresponds to the changes of the pattern-rotation period by
0.2 cycle/day. This corresponds to the changes of the pattern-rotation period by 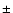 0.06 h, which is 1.25%. The result is shown in the right
column of Fig. 9. The frequency perturbation affects
significantly the structure of the equatorial and subequatorial pulsation
patterns.
0.06 h, which is 1.25%. The result is shown in the right
column of Fig. 9. The frequency perturbation affects
significantly the structure of the equatorial and subequatorial pulsation
patterns.
We conclude that errors in the pulsation frequency influence
significantly the result of inversions. Although the sectoral and tesseral
modes can be still distinguished, the clearness of the pattern can be
significantly destroyed. For applying the inversion technique to real
data, we suggest to test a sample of frequencies and look for the most
clear pattern.
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{H4304F9A.EPS}\hspace*{2mm}
\includegraphics[width=4.3cm,clip]{H4304F9B.EPS} }\end{figure}](/articles/aa/full/2003/28/aah4304/Timg42.gif) |
Figure 9:
The images of the Sets 2 and 6 (left and right) recovered with
the true pulsation frequencies (in the middle row) and two values
deviating from those. |
| Open with DEXTER |
We showed that the traditional Doppler imaging technique can be successfully
used for mapping stellar non-radial p-mode pulsations in terms of temperature
fluctuations. The technique results in an image of the stellar surface in which
sectoral and tesseral modes can be distinguished and the pulsational
degree 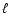 and the azimuthal order |m| can be determined.
and the azimuthal order |m| can be determined.
We found that sectoral and tesseral modes with
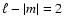 (or any even number), which are symmetric with respect to the equator, can be
successfully restored under various conditions. Temperature
fluctuations produce
a regular pattern of hot and cool regions. Strong velocity fluctuations,
interpreted in terms of temperature fluctuations, result in a pattern
with broad cool regions and narrow hot regions. This may serve as a
diagnostics of strong velocity fields in NRP.
(or any even number), which are symmetric with respect to the equator, can be
successfully restored under various conditions. Temperature
fluctuations produce
a regular pattern of hot and cool regions. Strong velocity fluctuations,
interpreted in terms of temperature fluctuations, result in a pattern
with broad cool regions and narrow hot regions. This may serve as a
diagnostics of strong velocity fields in NRP.
Difficulties arise when
pulsation modes are antisymmetric with respect to the equator, i.e. when
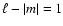 or any odd number. In such modes one node line
coincides with the equator, and opposite sign pulsation
fluctuations appear at almost equivalent Doppler shifts in
either sides of the equator. At higher inclinations, this cancels out
line profile variations and no information can be recovered. At
lower inclinations, the lpv are rather significant, but only the azimuthal
number |m| can be successfully determined. A reflection pattern in
the recovered image may suggest for the presence of an antisymmetric
tesseral mode. Note that in symmetric modes such a reflection is
hidden in the symmetric pattern.
or any odd number. In such modes one node line
coincides with the equator, and opposite sign pulsation
fluctuations appear at almost equivalent Doppler shifts in
either sides of the equator. At higher inclinations, this cancels out
line profile variations and no information can be recovered. At
lower inclinations, the lpv are rather significant, but only the azimuthal
number |m| can be successfully determined. A reflection pattern in
the recovered image may suggest for the presence of an antisymmetric
tesseral mode. Note that in symmetric modes such a reflection is
hidden in the symmetric pattern.
We tested the influence of errors in the inclination of the
rotational axis to the line of sight, rotational velocity and
pulsation frequency. We found that variations in the first two
parameters do not disturb significantly the pulsation pattern and,
thus, do not influence the mode identification. This is in contrast
with the effect of errors in the frequency (or pattern-rotation
period), which appeared to be critical for the inversions.
We conclude that stellar surface imaging represents a novel technique
for the pulsation mode identification that is complementary to
other Doppler-imaging mode-identification methods. Surface imaging
might especially aid in the determination of |m| for rotating stars.
We present an application of the surface imaging method on the
bright early-type B star  Sco in a separate paper
(Berdyugina et al. 2003).
Sco in a separate paper
(Berdyugina et al. 2003).
The present surface imaging technique is to be further developed for
recovering the velocity field of NRP along with the temperature
fluctuations. This will allow for studying physical properties of
pulsations and constraining their models. Also, it will make it possible
to draw some constraints on the photometric variability of pulsating
stars and compare them with observations.
-
Aerts, C., & Eyer, L. 2000, in Delta Scuti and Related Stars,
ed. M. Breger, & M. Montgomery, ASP Conf. Ser., 210, 113
In the text
-
Balona, L. A. 2000, MNRAS, 319, 606
In the text
NASA ADS
-
Berdyugina, S. V. 1991, Izv. Krymsk. Astrofiz. Obs., 83, 102
In the text
-
Berdyugina, S. V. 1998, A&A, 338, 97
In the text
NASA ADS
-
Berdyugina, S. V., Berdyugin, A. V., Ilyin, I., & Tuominen, I. 1998, A&A, 340, 437
In the text
NASA ADS
-
Berdyugina, S. V., Berdyugin, A. V., Ilyin, I., & Tuominen, I. 1999, A&A, 350, 626
In the text
NASA ADS
-
Berdyugina, S. V., Telting, J. H., Korhonen, H., & Schrijvers, C. 2003, A&A,
406, 281
In the text
-
Deutsch, A. 1958, in Electromagnetic Phenomena in Cosmological
Physics, ed. B. Lehnert, IAU Symp. 6 (Dordrecht: Reidel), 209
In the text
-
Deutsch, A. 1970, AJ, 159, 985
In the text
-
Falk, A. F., & Wehlau, W. H. 1974, AJ, 192, 409
In the text
-
Gies, D. R., & Kullavanijaya, A. 1988, ApJ, 326, 813
In the text
NASA ADS
-
Goncharsky, A. V., Stepanov, V. V., Khokhlova, V. L., & Yagola, A. G. 1977,
Sov. Astron. Lett., 3, 147
In the text
NASA ADS
-
Kurucz, R. L. 1993, Kurucz CD No. 13
In the text
-
Mantegazza, L. 2000, in Delta Scuti and Related Stars,
ed. M. Breger, & M. Montgomery, ASP Conf. Ser., 210, 138
In the text
-
Piskunov, N.E., Tuominen, I., & Vilhu, O. 1990, A&A, 230, 363
In the text
NASA ADS
-
Schrijvers, C., & Telting, J. H. 1999, A&A, 342, 453
In the text
NASA ADS
-
Schrijvers, C., Telting, J. H., Aerts, C., Ruymaekers, E., & Henrichs, H. F. 1997,
A&AS, 121, 343
In the text
NASA ADS
-
Telting, J. H. 2003, in Asteroseismology Across the HR Diagram, ed.
M. J. Thompson, M. S. Cunha, & M. J. P. F. G. Monteiro (Kluwer)
In the text
-
Telting, J. H., & Schrijvers, C. 1997, A&A, 317, 723
In the text
NASA ADS
-
Vogt, S. S., & Penrod, G. D. 1983, ApJ, 275, 661
In the text
NASA ADS
-
Vogt, S. S., Penrod, G. D., & Hatzes, A. P. 1987, ApJ, 321, 496
In the text
NASA ADS
Copyright ESO 2003
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4304F1.EPS}
\end{figure}](/articles/aa/full/2003/28/aah4304/Timg27.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4304F2A.EPS}\par\vspace*{...
...}\par\vspace*{4mm}
\includegraphics[width=8.8cm,clip]{H4304F2C.EPS}
\end{figure}](/articles/aa/full/2003/28/aah4304/Timg28.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4304F3A.EPS}\par\vspace*{...
...}\par\vspace*{4mm}
\includegraphics[width=8.8cm,clip]{H4304F3C.EPS}
\end{figure}](/articles/aa/full/2003/28/aah4304/Timg29.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4304F4A.EPS}\par\vspace*{...
...}\par\vspace*{4mm}
\includegraphics[width=8.8cm,clip]{H4304F4C.EPS}
\end{figure}](/articles/aa/full/2003/28/aah4304/Timg30.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4304F5A.EPS}\par\vspace*{2mm}
\includegraphics[width=8.8cm,clip]{H4304F5B.EPS}
\end{figure}](/articles/aa/full/2003/28/aah4304/Timg31.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4304F6A.EPS}\par\vspace*{2mm}
\includegraphics[width=8.8cm,clip]{H4304F6B.EPS}
\end{figure}](/articles/aa/full/2003/28/aah4304/Timg32.gif)
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{H4304F7A.EPS}\hspace*{2mm}
\includegraphics[width=4.3cm,clip]{H4304F7B.EPS} }\end{figure}](/articles/aa/full/2003/28/aah4304/Timg39.gif)
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{H4304F8A.EPS}\hspace*{2mm}
\includegraphics[width=4.3cm,clip]{H4304F8B.EPS} }\end{figure}](/articles/aa/full/2003/28/aah4304/Timg40.gif)
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{H4304F9A.EPS}\hspace*{2mm}
\includegraphics[width=4.3cm,clip]{H4304F9B.EPS} }\end{figure}](/articles/aa/full/2003/28/aah4304/Timg42.gif)